Impact Force Mechanism of a Trimaran Model and Its Experimental Validation

Abstract

In recent years, trimarans have been used in high-speed transport and in warships, but studies of them have made little progress. We designed a trimaran model and used it to perform a water-entry experiment to find a way to reduce the slamming pressure. The process of the model entering the water was divided into several steps, and different theoretical models were designed for each step, together with their force analysis. Relying on our experimental platform, we designed three flexible coating thicknesses and six drop heights as the different working conditions. With an analysis of the results under these experimental conditions, the experiment clearly indicates that the flexible cladding on the model can decrease the impact force when the model slams into water. Furthermore, the theoretical models and their corresponding force analyses are validated by the experimental results.

1. Introduction

Trimarans have excellent stability, seakeeping, and rapidity and are widely used in high-speed transport and in warships. Compared to the mono-hull ship, it has the advantages of better overall arrangement for the wider flight deck, stronger survivability as a kind of warship, and smaller resistance as a type of transport. In adverse sea conditions, trimarans’ sheaves will move due to strong wind and a high wave load. Although the duration of the impact pressure is relatively short, its peak value is very large. The mild impact pressure will cause the deformation of or fatigue damage to the hull structure, and the serious impact pressure will even be a threat to the safety of the hull and may result in serious marine accidents. For military ships, the bang will affect the ship’s electronic equipment, and for civilian ships, the bang will affect the passengers’ experience and cause unnecessary panic. To date, many trimaran accidents have been caused by water slamming, and thus, the prediction of the slamming load due to water has received much attention. For example, the Onomichi maru, weighing 66,874 tons, sank due to water slamming in the early 1980s. It is therefore necessary to find a way to reduce the water-slamming pressure.

Research on water slamming dates back to Von Karman in 1929. It involves potential flow theory [1], the conservation of momentum [2], and elastomer angles, as well as the changes in elastic effect when a wedge-shaped body enters the water [3]. The model structure for water-slamming experiments can be a sphere or cone [4], structures with different sections [5], a flat bottom [6], a V shape with an areal ship profile [7], a large wedge plate frame with different stiffnesses [8], or a wedge [9]. In the last decade, the research on the slamming force has focused on simulation [10,11]. For example, using CFD-FEA is a possible way to simulate the slamming and the green water loads on a sailing ship, and it is a method that combines computational fluid dynamics (CFD) and finite element analysis (FEA) solvers [12]. Furthermore, the simulation of green water and the slamming loads of ships shows that high-frequency components of the freak waves have a significant impact on the frequencies of peak pressure in the bow and deck area [13]. After finding ways to perform the simulation, people were able to predict water-slamming loads in different situations. Arbitrary Lagrangian–Eulerian (ALE) finite element method is one of the ways to perform the prediction, and it was used to study the impact between the flat panel and calm water [14]. However, by comparing the results from the experiment and the simulation, it was found that the numerical results might be larger than the experimental results by as high as 21% [15]. As the accuracy of the prediction of the slamming pressure was unacceptable, the fully coupled ALE algorithm was used to improve the accuracy [16]. However, the discretization of ALE will cause uncertainty in the simulation [17]. Another approach to the prediction of the slamming loads was presented by combining the seakeeping theory and CFD technology [18].

Some recent studies on trimarans are available. The peak pressure value was found to increase when the heel angle enlarges on the lower side of the trimaran [19].

There are many articles on simulations of the slamming pressure and the factors that influence the slamming pressure in the literature. However, little progress has been made in the field of reducing water slamming [20]. One of the possible ways to reduce the slamming pressure is to use the air-cushion effect [21]. In this paper, flexible cladding is placed in certain places where the peak water-slamming load is huge in order to decrease its influence on the ship.

2. Experiment Model Design

In order to ensure the similarity of the trimaran model and a real ship, the model came from the profile data of the cross-section at one-fourth of the whole length to the theback-end of the ship, but at a ratio of 1:100. The photos of the trimaran model are shown in Figure 1.

Figure 1. Photos of the trimaran model.

The model is symmetrical. It can be simplified to a two-dimensional parametric model, as illustrated in Figure 2. The thickness of the model is 20 cm, and the yellow points in the figure are the positions of the measuring points for the slamming pressure. A1 and A2 are two positions of fixtures, and S1 is the center point, where the speed is measured. The curved parts of the model are approximated by straight segments, shown as the blue lines in Figure 2, for computational purposes. The calculations in the theoretical analysis section verify that these simplifications are reasonable by comparing the results from te experiment and the theoretical calculation.

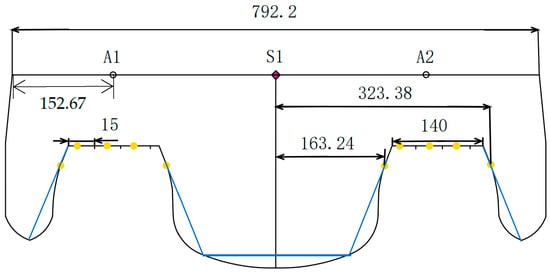
Figure 2. Two-dimensional parametric model of the trimaran model (in mm). The simplified model is identified by blue lines.

3. Force Analysis of the Trimaran Model

The process of the model entering the water can be divided into four stages, and a force analysis for each stage is given in this section.

Stage 1: Free fall in the air

At this stage, three forces are exerted on the model, namely air resistance $F_{\mathrm{a}}$, gravity $F_{\mathrm{g}}$, and guide rail friction resistance $F_{\mathrm{f}}$. The schematic of force analysis is shown in Figure 3.

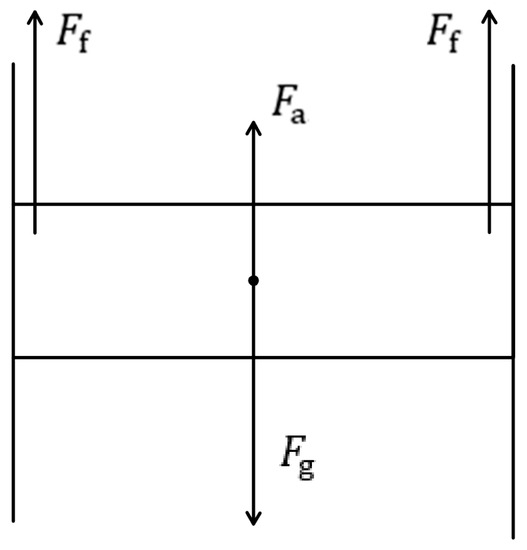
Figure 3. The schematic of force analysis for stage 1.

The resultant force is given by

$$F_1=F_{\mathrm{g}}-(F_{\mathrm{a}}+F_{\mathrm{f}})$$

(1)

which determines the speed $v$ of the model when it touches water.

The air resistance can be estimated by

$$F_{\mathrm{a}}=\frac{1}{2}C{\rho }_{\mathrm{a}}S{v}^2,$$

(2)

where $C$ is air dragging coefficient, considered to be slightly smaller than 1 due to the shape of the model; ${\rho }_{\mathrm{a}}$ is density of air and normally ${\rho }_{\mathrm{a}}=1.293$ kg/${\mathrm{m}}^3$; $S$ is the windward area of the object and approximately $S=0.8\times 0.2=0.16$ ${\mathrm{m}}^2$; and $v$ is the motion speed of the model relative to the air, and $v\approx 2$ m/s according to [8]. The air resistance is considered $F_{\mathrm{a}}<0.2$ N and is negligible compared to gravity (240 N) [8].

By the law of conservation of energy, we have

$$F_{1}h=\frac{1}{2}m{v}^2,$$

(3)

where $h$ is the height of the trimaran model relative to the water surface, and $m$ is the mass.

Stage 2: Main hull entering the water

When the bottom of the model enters the water, it will receive a reaction force from the water. At this stage, seven forces are applied to the model, namely, air resistance $F_{\mathrm{a}}$, gravity $F_{\mathrm{g}}$, guide-rail friction resistance $F_{\mathrm{f}}$, the buoyancy of water $F_{\mathrm{b}}$, the water’s impact force on the main hull $F_{\mathrm{w}1}$, the impact force on auxiliary hulls $F_{\mathrm{w}2}$, and the impact force on the connection bridge by splatter water $F_{\mathrm{w}3}$. The schematic of force analysis is shown in Figure 4.

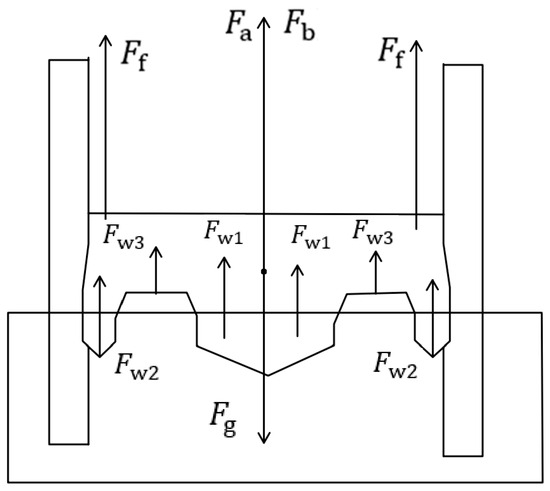
Figure 4. The schematic of force analysis for stage 2.

The resultant force $F_2$ is given by

$$F_2=F_{\mathrm{g}}-(F_{\mathrm{a}}+F_{\mathrm{f}}+F_{\mathrm{b}}+F_{\mathrm{w}1}+F_{\mathrm{w}2}+F_{\mathrm{w}3}).$$

(4)

$F_{\mathrm{w}3}$ is hard to calculate, and it was obtained experimentally.

In order to calculate the buoyancy of water $F_{\mathrm{b}}$, the main hull and the auxiliary hulls are approximated by three cubes. The bottom areas of the auxiliary hulls are approximately $0.073\times 0.20=0.0146{\mathrm{m}}^2$, and that of the main hull is approximately $0.327\times 0.20=0.0654{\mathrm{m}}^2$.

(i)

Slamming the flat plate into the water

The impact force is given by

$$F=0.5{\rho }_{\mathrm{w}}{\complement }_{\mathrm{s}}{A}_{\mathrm{p}}{v}^2,$$

(5)

where ${\rho }_{\mathrm{w}}$ is the water density, ${\complement }_{\mathrm{s}}$ is the slamming coefficient, $A_{\mathrm{p}}$ is the water-contacting area $0.327\times 0.20=0.0654{\mathrm{m}}^2$, and $v$ is the speed of the flat plate relative to water.

Equation (5) is used to calculate the slamming force when the main hull enters the water.

(ii)

Wagner’s theoretical model

Wagner’s theoretical model is illustrated in Figure 5. The impact force is given as [2]

$$F=\frac{{\rho }_{\mathrm{w}}{\pi }^3{v}^{3}t}{{\left(2\mathrm{t}\mathrm{a}\mathrm{n}\alpha \right)}^2},$$

(6)

where ${\rho }_{\mathrm{w}}$ is water density, $v$ is the speed of an object relative to water, $t$ is the width of one side, and $\alpha$ is the angle between the tangent of the model and the water.

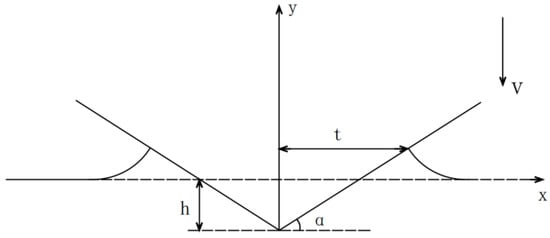
Figure 5. Wagner’s theoretical model.

Equation (6) is used to calculate the slamming force when the auxiliary hulls enter the water. In order to use (6), the measuring points on the side of the trimaran model, as shown in Figure 1 and Figure 2, need to be simplified.

Stage 3: Connection bridge entering the water

The connection bridge entering water means that the largest sectional area of the trimaran model submerges into the water and will receive a reaction force $F_{\mathrm{w}4}$. At this stage, force on the trimaran model is $F_3$, which is the result of air resistance $F_{\mathrm{a}}$, gravity $F_{\mathrm{g}}$, buoyancy of water $F_{\mathrm{b}}$, the impact force on the connection bridge part $F_{\mathrm{w}4}$, and the guide rail friction resistance $F_{\mathrm{f}}$, given by

$$F_3=F_{\mathrm{g}}-F_{\mathrm{a}}-F_{\mathrm{f}}-F_{\mathrm{w}4}-F_{\mathrm{b}}.$$

(7)

The schematic of force analysis is shown in Figure 6.

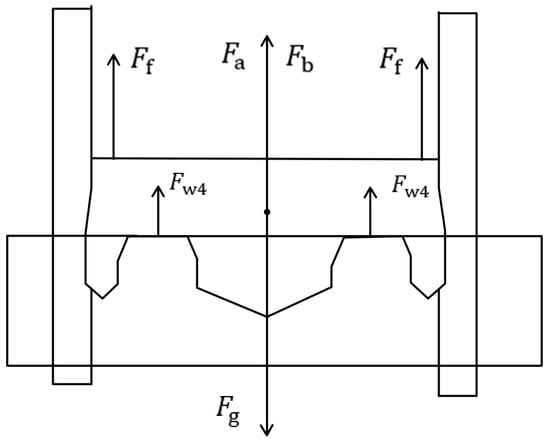
Figure 6. The schematic of force analysis for stage 3.

Stage 4: Trimaran model sinking to the bottom of the water tank

At this stage, three forces are applied to the model, namely gravity $F_{\mathrm{g}}$, the buoyancy of water $F_{\mathrm{b}}$, and the guide-rail friction resistance $F_{\mathrm{f}}$. The model falls to the bottom of the water tank at a decreasing speed.

4. Experiment Design

4.1. Layout of Measuring Points

This experiment was planned to raise the model to a specified height and then release it. In this process, the pressure on the measuring points was measured, and the speed of the model could be calculated by taking the derivative of the displacement of the model.

The layout of measuring points is shown in Figure 7.

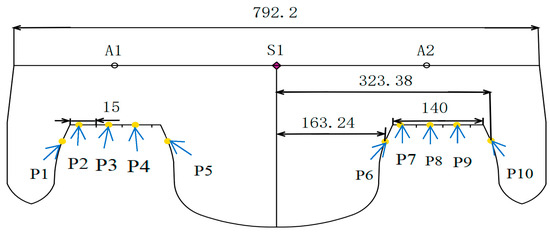
Figure 7. Layout of measuring points.

4.2. Experiment Procedure

The falling body’s experiment platform was our laboratory’s own design. It is 3.5 m high, and it can be used to perform a slamming experiment on a falling body from a height of 2.5 m, as shown in Figure 8. The platform is composed of supporting frames, guide-rail frames, sliding frames, and a limiting device for raising and releasing the trimaran model. During the experiment, the sliding frame and the model went into the water together. By fixing a weight on the frame, the model can always go into the water completely despite the large buoyancy force relative to the weight of the model.

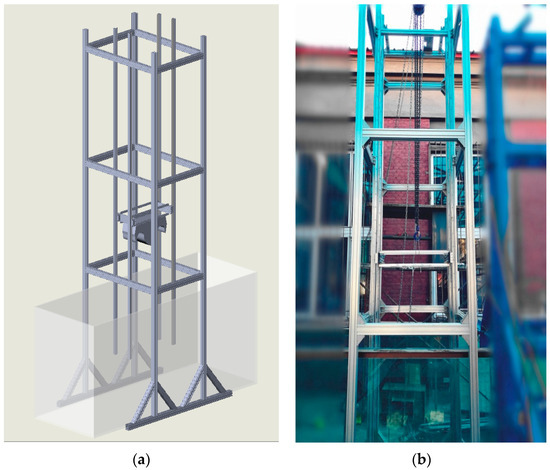
Figure 8. Falling experiment frame: (a) 3D picture, (b) the platform.

In addition to the frame, other instruments were used, including a glass tank, pressure transducers, displacement transducers, data acquisition instruments, high-speed cameras, and other auxiliary test equipment.

The principle of the experiment is to lift the model to a preset height and then release it. The model moved into the water at a certain speed after the falling motion, and thumping occurred. Throughout the process of water slamming, the slamming pressure at the measuring points on the model and the overall displacement curve could be obtained through the devices withy pressure sensors. By taking the derivative of the displacement curve, the speed of the model when entering the water could be obtained. The experiment process was divided into the following steps.

(i)

Calibration of sensors

Ten pressure sensors and one displacement sensor were used in this experiment. To ensure the accuracy of calibration, each pressure sensor matches a signal amplifier, and it can measure the pressure of a 100 m water column. A pressure calibrator was used to calibrate them to an accuracy with an error margin under 1%.

(ii)

Installation, release, and data collection

The pressure sensors were installed on the model, and the model was fixed at the sliding frame using some fixtures. The hook on the frame was connected to a decoupling device, and the drop height was changed by raising or lowering the sliding frame. One side of all the sensors was linked to the data-acquisition device DH5902N, which was connected to a computer. When system installation was completed, the model was raised to a proper height, according to a prespecified working condition. After the Balance Clearing button on the software interface was pressed, the experiment setup was ready.

(iii)

Setting of the working conditions

To decrease the influence of data-acquisition errors, guide rail friction, and model burr, a diverse set of experiment heights were set. Due to limited space, five of them are shown in Table 1.

Table 1. Setting of the working conditions.

Number	Processing Method	$\mathbf{Scale} \mathbf{on} \mathbf{Guide} \mathbf{Rail} \mathit{H}$ (cm)	Remarks
1	Without flexible cladding	$H_{11}=10$ $H_{12}=15$ $H_{13}=20$ $H_{14}=30$ $H_{15}=40$ $H_{16}=50$	$\mathrm{Real} \mathrm{drop} \mathrm{height}=H+10.6$ cm
2	Flexible cladding of 1 mm thickness, non-opening
3	Flexible cladding of 2 mm thickness, non-opening
4	Flexible cladding of 4 mm thickness, non-opening
5	Flexible cladding of 1 mm thickness, opening at positions of pressure sensors

The flexible cladding and how it was used are shown in Figure 9.

Figure 9. Flexible cladding.

Processing methods 1–4 were designed to explore the effect of flexible cladding with different thicknesses, and processing method 5 was used to verify the effect of flexible cladding on reducing slamming pressure.

5. Water-Slamming Experiment and Force Analysis

5.1. Data Processing

The data of slamming pressure and displacement were collected through DH5902N, and then the data were processed as follows.

(1)

The data were cleaned by filtering the noisy data arising from the unstable power supply and human-made movement.

(2)

The actual speed was derived from the data measured using the displacement sensors. Due to the friction on the guide rail, the water-entry speed calculated from the drop height is inaccurate.

(3)

The peak value of the data measured by the pressure sensors was recorded and the displacement data were differentiated to obtain the speed. Then, the slamming coefficient could be derived from the speed and pressure data.

5.2. Slamming Experiment When the Trimaran Entered the Water

The experiment data include ten slamming pressure signals, two acceleration signals, and one displacement signal. The working conditions needed to be repeated several times to ensure the accuracy of the data. The data from the same conditions have similar trends and peak values.

5.2.1. Experiment without Flexible Cladding

For this group, the results of all the processed curves for a certain drop height are listed here as an example, and the subsequent data are only listed in Table 2. The processed data curves under the H16 working conditions are shown in Figure 10. Figure 11 gives the raw data.

Table 2. Experiment without flexible cladding.

Working Condition	H11			H12			H13
	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient
P01	27,480.2	1.534	23.36	29,835.9	1.466	27.77	30,384.1	1.562	24.91
P02	36,281.8	1.534	30.84	45,019.8	1.541	37.92	41,038.5	1.596	32.22
P03	28,308.6	1.534	24.06	34,970.3	1.483	31.80	31,898.7	1.623	24.22
P04	18,139.5	1.534	15.42	19,830.9	1.546	16.59	19,869.8	1.596	15.60
P05	11,799.7	1.283	14.34	13,128.7	1.373	13.93	14,460.7	1.402	14.71
P06	10,164.7	1.283	12.35	14,691.0	1.373	15.59	13,099.9	1.402	13.33
P07	14,135.8	1.444	13.56	15,306.5	1.477	14.03	15,032.3	1.509	13.20
P08	29,783.5	1.466	27.72	31,638.4	1.515	27.57	34,132.7	1.592	26.93
P10	31,434.6	1.466	29.25	28,924.7	1.521	25.01	36,065.3	1.592	28.46
	H14			H15			H16
P01	30,384.1	1.562	24.91	31,540.7	1.761	20.34	57,849.5	1.772	36.85
P02	41,038.5	1.596	32.22	50,928.1	1.817	30.85	53,697.0	1.870	30.71
P03	31,898.7	1.623	24.22	51,839.3	1.786	32.50	48,982.7	1.828	29.32
P04	19,869.8	1.596	15.60	23,013.6	1.828	13.77	21,497.6	1.870	12.30
P05	14,460.7	1.402	14.71	18,892.2	1.539	15.95	15,017.5	1.522	12.97
P06	13,099.9	1.402	13.33	19,620.1	1.547	16.40	12,238.8	1.477	11.22
P07	15,032.3	1.509	13.20	16,545.6	1.670	11.87	19,016.0	1.659	13.82
P08	34,132.7	1.592	26.93	39,170.9	1.790	24.45	40,130.2	1.865	23.08
P10	36,065.3	1.592	28.46	39,475.1	1.787	24.72	42,549.5	1.844	25.03

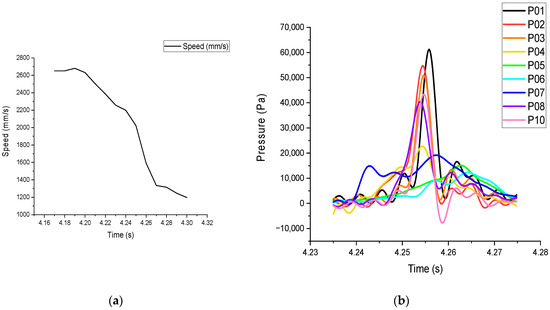
Figure 10. Speed and pressure versus time. (a) Speed versus time, (b) pressure versus time.

Figure 11. Raw data.

The test data and the calculated slamming-pressure coefficients for each working condition are listed in Table 2.

The slamming-pressure coefficient is calculated by

$$k=\frac{p_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}}{0.5\rho V^2}$$

(8)

where $p_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$ is the peak slamming pressure, $\rho$ is the fluid density, and $V$ is the velocity of the model when the peak slamming pressure is achieved.

As observed in Figure 10, the trimaran model slowed down during this period, especially after the slamming pressure reached the peak.

The slamming-pressure coefficient from the falling experiment without flexible cladding at six different heights (H11–H16)is shown in Figure 12.

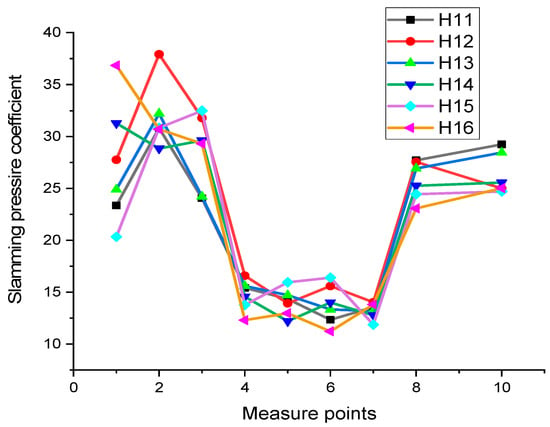
Figure 12. Slamming-pressure coefficient in the case without flexible cladding.

In Figure 7, P2, P9 and P3, P8 are two pairs of measuring points that are symmetrical, and the slamming pressures measured at these points are high. In contrast, while P4, P7 and P5, P6 are also symmetrical, the corresponding slamming pressures are low.

For H11–H16, the obtained slamming-pressure coefficients have a similar varying trend. As the drop height increased, the water-entry speed increased, while the slamming pressure dropped slightly. This is due to the fact that air entered the water when the model entered the water quickly, leading to a decrease in the slamming pressure and its coefficient.

5.2.2. Experiment in the Case of Flexible Cladding with a 1 mm Thick Silica Gel Plate

The test data and the calculated slamming-pressure coefficients for each working condition are listed in Table 3.

Table 3. Experiment with 1 mm silica gel sheet.

Working Condition	H11			H12			H13
	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient
P01	1915.4	1.640	1.42	1607.1	1.668	1.16	1590.7	1.781	1.00
P02	646.0	1.640	0.48	1248.9	1.668	0.90	1116.4	1.781	0.70
P03	1289.0	1.556	1.06	1833.4	1.668	1.32	2452.3	1.741	1.62
P04	1957.8	1.556	1.62	2407.9	1.668	1.73	3010.5	1.741	1.99
P05	2608.8	1.556	2.16	2891.3	1.634	2.17	3439.9	1.741	2.27
P06	2019.2	1.556	1.67	1914.7	1.634	1.43	2959.1	1.741	1.95
P07	2114.5	1.640	1.57	1665.3	1.725	1.12	1690.2	1.781	1.07
P08	1853.1	1.640	1.38	1262.4	1.725	0.85	1473.1	1.781	0.93
P10	1915.4	1.640	1.42	1607.1	1.668	1.16	1590.7	1.781	1.00
	H14			H15			H16
P01	1886.5	1.925	1.02	2313.2	2.049	1.10	1923.5	2.091	0.88
P02	1089.0	1.925	0.59	1907.9	2.049	0.91	1606.1	2.091	0.73
P03	2115.6	1.925	1.14	2460.8	2.049	1.17	1989.5	2.054	0.94
P04	2578.8	1.925	1.39	3117.4	2.049	1.49	2616.9	2.091	1.20
P05	3532.2	1.925	1.91	2891.3	2.049	1.38	3385.6	2.091	1.55
P06	6669.4	2.136	2.92	2358.0	2.049	1.12	2874.2	2.091	1.31
P07	2127.2	2.030	1.03	2684.6	2.183	1.13	2693.5	2.184	1.13
P08	1682.5	2.030	0.82	4946.5	2.105	2.23	2409.6	2.184	1.01
P10	1886.5	1.925	1.02	2313.2	2.049	1.10	1923.5	2.091	0.88

For the relationships of speed and pressure versus time, we chose height H16 as an example. The characteristic curves of speed and pressure versus time are shown in Figure 13.

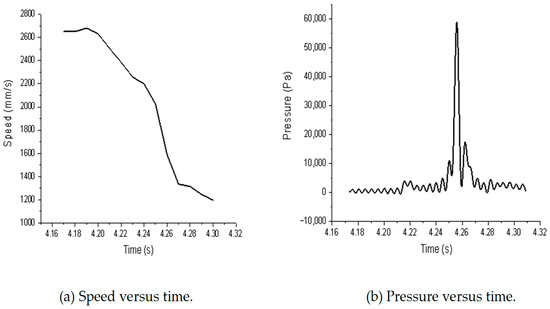
Figure 13. Speed and pressure versus time in the case of 1 mm thick flexible cladding.

As observed from Figure 13, the trimaran model slowed down gradually, especially after the slamming pressure reached the peak. At 4.18 s, the model entered the water and began to slow down. And at around 4.245 s, the connection bridge hit the water.

The data from falling experiment are shown in Figure 14 for six different heights (H11–H16).

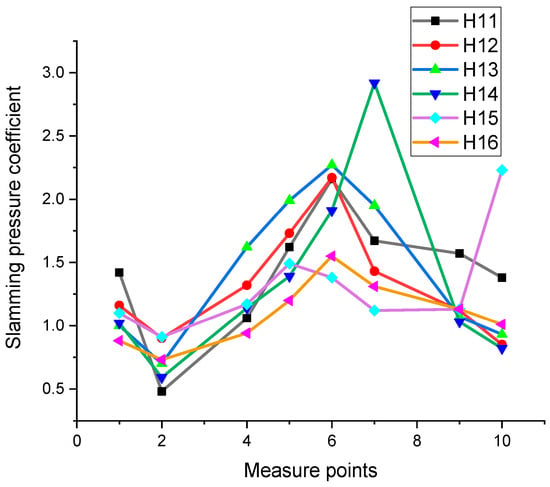
Figure 14. Slamming-pressure coefficient in the case of 1 mm thick flexible cladding.

As observed in Figure 14, with an increase in drop height, the coefficient of the slamming pressure drops. Furthermore, as shown in Figure 14 the coefficient is a little greater than 1 in most cases. This is because the silica gel plate turns part of the water pressure into air pressure.

5.2.3. Experiment in the Case of Flexible Cladding with a 2 mm Thick Silica Gel Plate

The test data and the calculated slamming-pressure coefficients for each working condition are listed in Table 4.

Table 4. Experiment with 2 mm silica gel sheet.

Working Condition	H11			H12			H13
	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient
P01	3754.7	1.549	3.13	4623.9	166.1	3.35	5073.9	1.689	3.56
P05	5710.5	1.549	4.76	5114.6	161.7	3.91	5411.7	1.689	3.79
P06	5808.7	1.549	4.84	6730.3	161.7	5.15	5857.0	1.689	4.11
P10	4691.9	1.549	3.91	4652.8	161.7	3.56	6515.3	1.701	4.50
	H14			H15			H16
P01	4287.2	1.788	2.68	5229.5	179.1	3.26	6028.0	1.989	3.05
P05	5905.8	1.788	3.69	5087.4	179.1	3.17	4899.8	1.934	2.62
P06	6853.0	1.788	4.29	5188.9	179.1	3.24	6026.6	1.853	3.51
P10	5024.6	1.882	2.84	5592.8	189.8	3.11	7169.8	2.146	3.11

To study the relationships of speed and pressure versus time, we choose height H16 as an example. The characteristic curves of speed and pressure versus time are shown in Figure 15.

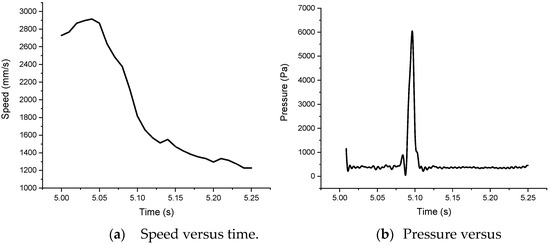
Figure 15. Speed and pressure versus time in the case of 2 mm thick flexible cladding.

As observed in Figure 15, the trimaran model slowed down during this period, especially after the slamming pressure reached its peak.

The data collected for six different heights (H11–H16) are shown in Figure 16. As observed in Figure 16, with an increase in drop height, the coefficient of slamming pressure dropped.

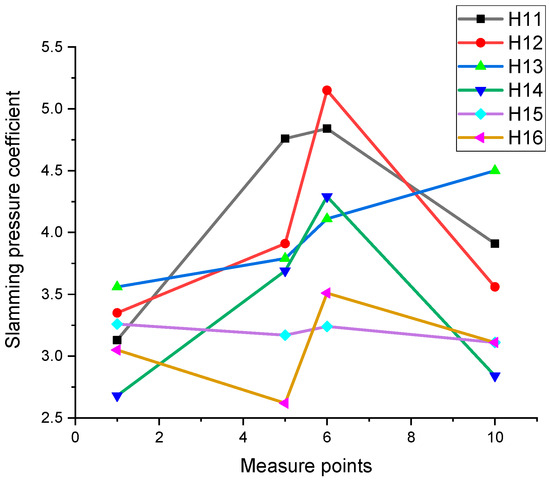
Figure 16. Slamming-pressure coefficient with 2 mm thick flexible cladding.

5.2.4. Experiment in the Case of Flexible Cladding with a 4 mm Thick Silica Gel Plate

The test data and the calculated slamming-pressure coefficients for each working condition are listed in Table 5.

Table 5. Experiment with 4 mm silica gel sheet.

Working Condition	H11			H12			H13
	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient
P01	358.2	1.500	0.32	506.4	1.647	0.37	648.5	1.774	0.41
P02	621.7	1.500	0.55	582.7	1.647	0.43	900.3	1.774	0.57
P04	1125.3	1.371	1.20	2168.0	1.538	1.83	1996.3	1.603	1.55
P05	1385.8	1.371	1.47	2343.8	1.538	1.98	2212.1	1.603	1.72
P06	1811.4	1.567	1.48	2027.2	1.519	1.76	2156.8	1.774	1.37
P07	1654.5	1.567	1.35	1764.2	1.519	1.53	2108.8	1.774	1.34
	H14			H15			H16
P01	788.9	1.937	0.42	888.9	2.132	0.39	2531.8	2.175	1.07
P02	860.1	1.937	0.46	1015.1	2.132	0.45	2019.2	2.175	0.85
P04	2104.6	1.688	1.48	2481.5	2.010	1.23	1987.0	1.976	1.02
P05	2306.2	1.688	1.62	2850.0	2.010	1.41	2420.1	1.976	1.24
P06	3876.1	2.090	1.77	2551.4	2.132	1.12	3635.8	2.175	1.54
P07	3441.1	2.090	1.58	1943.5	2.132	0.86	2913.3	2.175	1.23

To study the relationships of speed and pressure versus time, we chose height H16. The characteristic curves of speed and pressure versus time are shown in Figure 17.

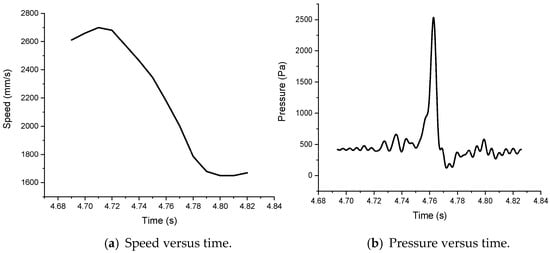
Figure 17. Speed and pressure versus time in the case of 4 mm thick flexible cladding.

As observed in Figure 17, the trimaran model slowed down during this period, especially after the slamming pressure reached the peak.

The data collected for six different heights (H11–H16) are shown in Figure 18. As shown in Figure 18, with an increase in drop height, the coefficient of slamming pressure again dropped. This verifies that the data are reasonable.

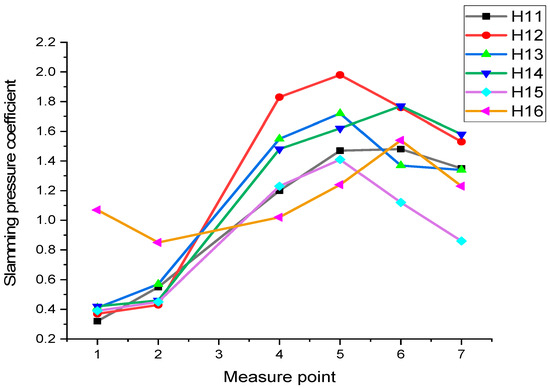
Figure 18. Slamming-pressure coefficient for 4 mm thick flexible cladding.

5.2.5. Experiment in the Case of Flexible Cladding with 1 mm Thickness, Opening at the Positions of Pressure Sensors

The test data and the calculated slamming-pressure coefficients for each working condition are listed in Table 6.

Table 6. Experiment with 1 mm silica gel sheet, opening at the positions of pressure sensors.

Working Condition	H11			H12			H13
	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient	Pressure/Pa	Speed m/s	Slamming-Pressure Coefficient
P01	34,893.9	2.242	13.88	45,097.6	2.183	18.93	36,727.5	1.965	19.02
P02	24,180.1	2.362	8.67	21,502.5	2.183	9.02	24,345.6	2.073	11.33
P05	8601.0	2.037	4.15	16,472.8	1.927	8.87	10,080.4	1.965	5.22
P06	27,845.2	2.117	12.43	19,826.0	2.061	9.33	24,044.9	1.965	12.45
P08	46,355.4	2.419	15.84	41,194.1	2.273	15.95	31,151.7	2.073	14.50
P10	35,696.1	2.314	13.33	28,860.4	2.183	12.11	10,955.9	2.073	5.10
	H14			H15			H16
P01	28,300.8	1.753	18.42	27,736.3	1.716	18.84	25,999.6	1.515	22.66
P02	25,237.7	1.855	14.67	21,832.9	1.716	14.83	20,406.8	1.557	16.84
P05	5114.6	1.692	3.57	5209.9	1.570	4.23	5880.3	1.432	5.74
P06	19,260.1	1.692	13.46	11,229.2	1.621	8.55	13,374.1	1.515	11.65
P08	24,869.8	1.753	16.19	21,926.3	1.757	14.21	18,934.6	1.432	18.47
P10	20,193.8	1.753	13.14	23,321.6	1.716	15.84	17,098.5	1.579	13.72

The data collected for six different heights (H11–H16) are shown in Figure 19. As shown in Figure 19, with an increase in drop height, the coefficient of slamming pressure again dropped. This verifies that the data are reasonable.

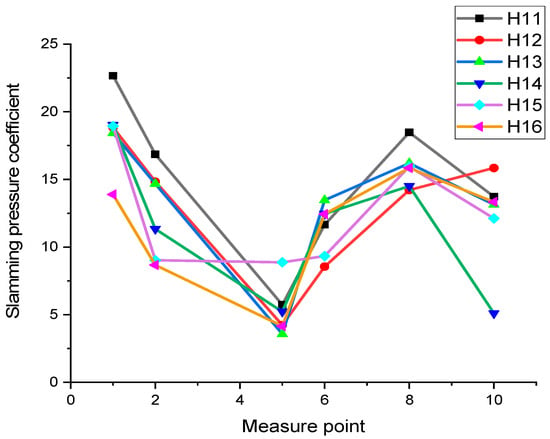
Figure 19. Slamming-pressure coefficient for a 1 mm thick flexible cladding, opening at positions of pressure sensors.

5.3. Summary and Analysis of Experimental Results

Experimental data, including the slamming-pressure coefficients and measuring points, are summarized in Table 7.

Table 7. Experiment data.

Working Condition	H11				H12				H13
Measure Point	1 mm Thick	2 mm Thick	4 mm Thick	No Clad	1 mm Thick	2 mm Thick	4 mm Thick	no Clad	1 mm Thick	2 mm Thick	4 mm Thick	No Clad
P1	1.42	3.13	0.32	23.36	1.16	3.35	0.37	27.77	1.00	3.56	0.41	24.91
P5	2.16	4.76	1.47	14.34	1.73	3.91	1.98	13.93	1.99	3.79	1.72	14.71
P6	1.67	4.84	1.48	12.35	2.17	5.15	1.76	15.59	2.27	4.11	1.37	13.33
P10	1.38	3.91	1.35	29.25	0.85	3.56	1.53	25.01	0.93	4.50	1.34	28.46
	H14				H15				H16
P1	1.02	2.68	0.42	31.29	1.10	3.26	0.39	20.34	0.88	3.05	1.07	36.85
P5	1.39	3.69	1.62	12.20	1.49	3.17	1.41	15.95	1.20	2.62	1.24	12.97
P6	1.91	4.29	1.77	14.00	1.38	3.24	1.12	16.40	1.55	3.51	1.54	11.22
P10	0.82	2.84	1.58	25.57	2.23	3.11	0.86	24.72	1.01	3.11	1.23	25.03

As seen in Table 7, compared to the data obtained from the model without flexible cladding, the slamming-pressure coefficient obtained from the group covered with a 2 mm thickness is very small; however, the measured slamming-pressure coefficients are several times larger than those obtained from the group covered with a 1 mm thickness. This may be because the thickness of 1 mm is very small, resulting in the silicone sheet being pasted on the wooden stick (shown in Figure 1) too tightly so that there was an air cushion between the pressure sensor and the water. In such a case, although the thickness is small, the reduction in slamming pressure is quite obvious. This shows that if there is space (an air cushion) between the surface flexible cladding and the trimaran model, the reduction in slamming pressure is obvious.

By comparing the 2 mm and 4 mm thickness, we find that as the thickness increases, the slamming-pressure coefficient becomes smaller and smaller until it approaches a constant when the thickness is big enough.

In order to reduce the influence of the air cushion, processing method 5 was designed. The experimental data, including the slamming-pressure coefficients and measuring points, are summarized in Table 8.

Table 8. Experimental data of coefficients of the model without flexible cladding and the model with a 1 mm thickness silica gel plate, opening at the positions of the pressure sensors.

Working Condition	H11			H12			H13
Measure Point	Without Cladding	With Cladding	Difference	Without Cladding	With Cladding	Difference	Without Cladding	With Cladding	Difference
P1	23.36	22.66	−3.0%	27.77	18.84	−32.2%	24.91	18.42	−26.1%
P2	30.84	18.64	−45.4%	37.92	14.83	−60.9%	32.22	14.67	−54.5%
P6	12.35	11.65	−5.7%	15.59	8.55	−45.2%	13.33	13.46	+1.0%
P8	27.72	18.47	−33.4%	27.57	14.21	−48.5%	26.93	16.19	−39.9%
P10	29.25	13.72	−53.1%	25.01	15.84	−36.7%	28.46	13.14	−53.8%
	H14			H15			H16
P1	31.29	19.02	−39.2%	20.34	18.93	−6.9%	36.85	13.88	−62.3%
P2	28.85	11.33	−60.7%	30.85	9.02	−70.8%	30.71	8.67	−71.8%
P6	14.00	12.45	−11.1%	16.40	9.33	−43.1%	11.22	12.43	+10.8%
P8	25.27	14.50	−42.6%	24.45	15.95	−34.8%	23.08	15.84	−31.4%
P10	25.57	5.10	−80.1%	24.72	12.11	−51.0%	25.03	13.33	−46.7%

For the same working conditions and the same measuring point, the measured and calculated slamming-pressure coefficients of the original model are almost always larger than the measured and calculated bang-pressure coefficients of the original model covered with a 1 mm open-cell silica gel sheet. Thus, we can draw the conclusion that surface flexible cladding (silica gel plate) can reduce the slamming pressure.

6. Theoretical Analysis of the Experiments

(i)

Pressure measured at the side measuring points

At the falling stage, as the four measuring points P1, P5, P6, and P10 are on the side, we can use (6) to calculate the slamming pressure. Since they are bilaterally symmetrical, only the pressures on P1 and P5 are calculated using (6), where $\rho$ = 1003 kg/${\mathrm{m}}^3$ and $v$ is set to 2 m/s, which is the average speed for H16. For P1, $t\approx 0.073$ m, and $\mathrm{t}\mathrm{a}\mathrm{n}\beta \approx 2$, we have $F=1135$ N. We can obtain the result that the pressure on P1 is $P\approx \mathrm{57,361}$ Pa, which is very close to the actually measured pressure (57,849.5 Pa).

Similarly, at P5, $\rho =1003$ kg/${\mathrm{m}}^3$, $v=2$ m/s, $t\approx 0.163$ m, and $\mathrm{t}\mathrm{a}\mathrm{n}\beta \approx 2$. We have $F=2523.2$ N and $P\approx \mathrm{15,480}$ Pa, which is very close to the pressure actually measured (15,017.5 Pa).

(ii)

Pressure of the main hull when entering the water

Water entry at the main hull can be regarded as the plate’s water slamming, and we use (5) for flat water slamming to estimate the slamming pressure, where $\rho =1003$ kg/${\mathrm{m}}^3$, $C_{\mathrm{s}}=5.15$ for the flat, $A_{\mathrm{p}}=0.327\times 0.20=0.0654$ m², and $v=2.7$ m/s according to the data. We have $F=1227.7$ N and $P\approx \mathrm{18,771}$ Pa.

(iii)

Pressure of auxiliary hulls when entering water

Due to the left–right symmetry of the trimaran model, only the left side needs to be calculated. The force is calculated using (6), where $\mathsf{\rho }$ = 1003 kg/m³; $v$ = 2 m/s, which is the average speed for H16; t = 0.073 m; and $\mathrm{t}\mathrm{a}\mathrm{n}\beta \approx 1$, according to Figure 2. As a result, $F=2260$ N and $P\approx \mathrm{17,000}$ Pa

(iv)

Pressure of trimaran when connection bridge entering water

The connection bridge entering water resembles the plate’s water slamming. Thus, we can use (5) to estimate the slamming force. Furthermore, as the model is in left–right symmetry, only values for one side need to be calculated. If we only consider the connection bridge, the slamming force is calculated using (5). As a result, by calculating P07 as an example, we have $F=233.604$ N and $P\approx \mathrm{16,686}$ Pa, which is close to the pressure actually measured (19,016.0 Pa).

7. Conclusions

This article aims to find a possible way to reduce the slamming pressure, in order to improve the safety of trimarans during navigation. In the model shown in Figure 1, the data measured for the two pairs of symmetrical measuring points on the outer connection bridges are large. On the contrary, the data measured for the two other pairs of symmetrical measuring points on the inner connection bridges are small. As the height changed, the slamming-pressure coefficient changed in a similar way. With an increase in the drop height, the slamming-pressure coefficient dropped slightly. The falling speed of the model decreased rapidly due to the force from the water. This was the most prominent after the slamming force reached its peak.

When flexible claddings of 1 mm, 2 mm, or 4 mm thick silica gel plate were coated on the model, it was obvious that they could reduce the slamming force significantly, especially when there was air between the model and the flexible cladding. Meanwhile, a thicker surface of flexible cladding could reduce the force more significantly. However, this led to a blunt effect. In the same working conditions, when the thickness was increased from 1 mm to 4 mm, the change in the measured slamming pressure was small. When the thickness was increased from 0 mm to 2 mm, the slamming-pressure coefficient decreased by around 75–80%. However, from 0 mm to 4 mm, it only decreased by around 80–90%. The thickness increased a lot, but the effect did not actually improve much.

The results from the force model and the main hull’s force-prediction model are in close agreement with those obtained from the experiment. Thus, our experiment confirms that the theoretical model is effective. For the same working conditions, the model with flexible cladding will reduce the pressure by nearly 50%. And our experiment validates that it is possible to reduce the slamming pressure of the trimaran to improve security by using flexible cladding.