Improving Characteristics of FPGA-Based FSMs Representing Sequential Blocks of Cyber-Physical Systems

Abstract

This work proposes a method for hardware reduction in circuits of Mealy finite state machines (FSMs). The circuits are implemented as networks of interconnected look-up table (LUT) elements. The FSMs with twofold state assignment and encoding of output collections are discussed. The method is based on using two LUT-based cores to implement systems of partial Boolean functions. One of the cores uses only maximum binary codes, while the second core is based on the use of extended state codes. The hardware reduction is based on diminishing the number of transformed maximum binary codes. This leads to FPGA-based FSM circuits with three levels of logic blocks. Each logic block has a single level of LUTs. As a result, partial functions are represented by single-LUT circuits. The article shows a step-by-step procedure for the transition from the initial form of the FSM representation to its logical circuit (a network of programmable look-up table elements, flip-flops, and interconnects). The results of experiments conducted with standard benchmarks show that the proposed approach produces LUT-based FSM circuits with significantly better area characteristics than for circuits produced by such methods as Auto and One-Hot of Vivado, JEDI, and twofold state assignment. Compared to these methods, the number of LUTs is reduced from 9.44% to 69.98%. Additionally, the proposed method leads to the following phenomenon: the maximum operating frequency is slightly improved as compared with FSM circuits based on twofold state assignment (up to 0.6%). The negative effect of these improvements is an increase in power consumption. However, it is extremely insignificant (up to 1.56%). As the values of the FSM’s main characteristics grow, there is an increase in the gain from the application of the proposed method. The conditions for applying the proposed method are determined. A generalized architecture consisting of three blocks of partial functions and a method for synthesizing an FSM with this architecture are proposed. A method for selecting one of the seven architectures generated by the generalized architecture is proposed.

1. Introduction

Our world is characterized by the widespread distribution of various cyber-physical systems (CPSs) into all spheres of human activity [1,2,3]. Currently, intensive research is being carried out in the field of designing and ensuring the safety of the operation of CPSs [4,5,6,7,8,9]. As the name suggests, these systems include digital (cybernetic) parts interacting with physical objects [10,11,12]. Very often, these digital parts include various sequential blocks [3,11]. These blocks can implement, for example, various security algorithms [13]. To improve the overall quality of a cybernetic part, it is necessary to optimize characteristics of its sequential blocks. In the current paper, we discuss a case where the sequential blocks of digital parts are represented by finite state machines (FSMs) [14].

Very often, the models of Mealy FSMs are used for the specification of sequential blocks [14,15]. The process of FSM design requires balancing the values of the occupied chip area, the maximum operating frequency, and power consumption [16,17]. We discuss a case where FSM circuits are designed with field-programmable gate arrays (FPGAs). The look-up table (LUT) elements are the basic elements used for implementing FSM circuits. As follows from [18,19], the circuit area has the greatest influence on the values of other characteristics. The area can be reduced due to jointly applying various methods of structural decomposition. In our paper [20], we propose an optimization method based on jointly applying the methods of twofold state assignment (TSA) and encoding of output collections. As a result, LUT-based FSM circuits have exactly three logic levels. Let us point out that FPGAs are very popular in modern digital systems design [5,7,8].

In this paper, we focus our attention on FPGA chips produced by AMD Xilinx [21] because this corporation is the largest manufacturer of FPGA chips. To implement an FSM circuit, we use configurable logic blocks (CLBs) that include four main components: LUTs, programmable flip-flops, dedicated multiplexers, and fast interconnections. To obtain a multi-CLB circuit, the system of inter-CLB programmable interconnects should be used. The proposed method reduces the values of LUT counts in the multi-level circuits of Mealy FSMs.

The main principle of TSA-based FSMs assumes using two types of internal state codes [20]. Each state is represented by both a maximum binary state code (MBC) and an extended state code (ESC) [20]. Such an approach allows for reducing FSM hardware compared to methods based solely on MBCs. However, the approach in [20] is connected with some overhead. Namely, an additional state transformer block should convert MBCs into ESCs. This converter consumes additional LUTs and interconnections. In this paper, we show how to reduce the noted overhead.

The main contribution of this paper boils down to the following. We have proposed: (1) a novel design method aimed at reducing the LUT counts in the circuits of FPGA-based Mealy FSMs with twofold state assignment and encoding of output collections; (2) a generalized FSM architecture, including three blocks of partial Boolean functions (PBFs); (3) a method of choosing one of seven possible FSM architectures based on the generalized architecture. To reduce hardware, we propose to use at least two cores of logic [22]. The first core generates PBFs based on MBCs. The second core uses ESCs for this purpose. This approach allows for reducing hardware in the state transformer circuit because now only a part of the MBCs is transformed into ESCs. The scientific novelty of the proposed approach also includes an improvement in the known method of encoding of output collections by some additional variables. This encoding is done so that each of the cores includes some additional variables that do not occur in the second core. Thanks to this approach, the number of LUTs generating additional variables is reduced. Our current research shows that joint usage of these two approaches leads to FSM circuits having fewer LUTs compared to FSM circuits based on the approach in [20]. The experimental results show that the proposed approach does not lead to significant deterioration of FSM temporal characteristics.

The remainder of the article is organized as follows. Section 2 presents the background of FPGA-based Mealy FSM design. Section 3 includes an analysis of relevant works. Section 4 is devoted to representing a main idea of the proposed method. An example of FSM synthesis is discussed in Section 5. The conducted experiments are analyzed in Section 6. A generalized FSM architecture is discussed in Section 7. Finally, Section 8 is a short conclusion that summarizes the results.

2. Background Information for FPGA-Based Mealy FSMs

A Mealy FSM has M internal states, L external inputs, and N outputs used by other blocks of a CPS. To organize interstate transitions, special internal objects are used. These include R1 state variables and R1 input memory functions (IMFs). These objects are combined into corresponding sets S, I, O, SV, and D [14], which represent the following: $S=\{s_1,\dots ,s_M\}$, $I=\{i_1,\dots ,i_L\}$, $O=\{o_1,\dots ,o_N\}$, $SV=\{T_1,\dots ,T_{R1}\}$, and $D=\{D_1,\dots ,D_{R1}\}$. The sets S, I, and O uniquely follow from, for example, the FSM state transition graph (STG) [23]. However, the value of the parameter R1 is chosen by the circuit designer during the state assignment stage [23].

In the case of MBCs [24], the following formula determines the value of R1:

$$R1=\lceil {log}_{2}M\rceil .$$

(1)

Formula (1) determines the number of bits for MBCs (this is the minimum possible number for the given number of states). In the case of one-hot state assignment [24], the value of R1 is equal to the number of states ($R1=M$).

The state variables $T_r\in SV$ create so-called full state codes $FC\left(s_m\right)$. Each state code bit corresponds to a flip-flop from a register RG. The register is controlled by IMFs and two special pulses, Res and Clk [25]. The pulse Res executes the initialization of the FSM operation. This pulse sets an FSM in the initial state $s_1\in S$. The pulse Clk determines the instant of state code loading into RG. The r-th bit of $FC\left(s_m\right)$ is determined by the value of $D_r\in D$. Like the vast majority of researchers, we use D flip-flops to organize the register RG [26].

The following internal resources of FPGA fabric are involved in implementing an FSM circuit: LUTs, flip-flops, programmable interconnections, a synchronization tree, and programmable input–outputs [27,28]. In this paper, we consider a case where FPGAs of AMD Xilinx [25] are used.

A LUT is a functional generator having $S_L$ inputs and a single output [24,29]. A LUT may keep a truth table of any Boolean function it depends on up to $S_L$ Boolean arguments. Nowadays, the value of $S_L$ does not exceed 6. However, using dedicated multiplexers, the number of inputs can be increased to 8 (within a single CLB) [27]. If the number of Boolean arguments exceeds 8, then a corresponding function is represented by a multi-CLB circuit. This leads to the necessity of minimizing the number of LUTs and their levels in the resulting circuit [30,31]. In this paper, we denote by the symbol LUTer a block consisting of LUTs, multiplexers, flip-flops, and interconnections. All these elements are programmable [32].

Two systems of Boolean functions (SBFs) represent an FSM logic circuit. They are the following [17]:

$$D=D(SV,I);$$

(2)

$$O=O(SV,I).$$

(3)

These SBFs define a so-called P Mealy FSM whose architecture is shown in Figure 1 [14].

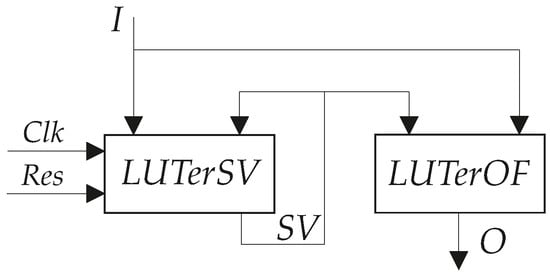
Figure 1. Architecture of P Mealy FSM.

In Figure 1, the block LUTerSV implements IMFs (2). The IMFs determine the next state code (a code of the state of transition). The flip-flops of register RG are distributed among the elements of LUTerSV. The pulses Clk and Res control the operation of flip-flops. The block LUTerOF generates output functions (3).

The analysis of SBFs (2) and (3) shows that their functions depend on variables $T_r\in SV$ and $i_l\in I$. Each function $f_b\in D\cup Y$ depends on $R_b\le R1$ state variables and $L_b\le L$ inputs. The number of LUT levels in the corresponding circuit depends on the following condition:

$$R_b+L_b\le S_L.$$

(4)

If (4) holds, then there is a single LUT in the corresponding logic circuit. The FSM circuit is single-level if condition (4) holds for each function belonging to SBFs (2) and (3). In this case, the resulting FSM circuit is characterized by the best possible values of its main characteristics. This means that this circuit requires the minimum possible chip area, that it consumes the minimum possible power, and that it represents the fastest possible solution.

Even average FSMs can have up to 10 state variables and 30 inputs [14]. Therefore, each function belonging to (2) and (3) may have up to 40 arguments. However, the number of LUT inputs is extremely small ($S_L=6$). In this regard, the probability of violation of the condition (4) is very high. In the case of violation, various optimization methods are used to improve the characteristics of an FSM circuit. In this paper, we discuss a case where condition (4) is violated.

3. Analysis of Related Work

Methods for improving spatial characteristics of FSM circuits are discussed in thousands of scientific works. For example, they can be found in [18,19,25,30,32,33,34,35,36,37,38]. To estimate the chip area required for a LUT-based circuit, the designers use the values of LUT counts [18]. Therefore, reducing the value of LUT count leads to a decrease in the area occupied by the circuit. This goal can be achieved using: 1. an optimal state assignment; 2. a functional decomposition (FD) of SBFs (2) and (3); and 3. a structural decomposition (SD) of the FSM logic circuit [19].

The optimal state assignment excludes some literals from sum-of-products (SOPs) of functions (2) and (3) [39]. In the best case, this exclusion allows for implementing a single-level Mealy FSM circuit. One of best state assignment methods is JEDI, which is distributed together with the CAD tool SIS [40]. In the work of [41], results of applying JEDI to FSMs from the library LGSynth93 are shown [42]. These results show that JEDI allows for excluding up to 3 literals from SOPs (2) and (3), representing the benchmark FSMs. Therefore, using JEDI can turn multi-level circuits into single-level ones only for rather simple FSMs [32].

Using either FD or SD leads to representing SBFs (2) and (3) by systems of partial Boolean functions [34,43]. Each PBF should depend on no more than $S_L$ arguments. In this case, each PBF will be represented by a single-LUT circuit. Applying any type of decomposition produces multi-level FSM circuits. However, there is a fundamental difference in the resulting interconnection system for different decomposition methods [19]. Applying the functional decomposition leads to FSM circuits with a “spaghetti-type” irregular interconnect system. In such a system, the same inputs and state variables may appear at any place on the circuit. Let us point out that the system of interconnections has a regular character for SD-based FSM circuits. An SD-based FSM circuit consists of large blocks [19]. Each block has its unique systems of input variables and output functions, which can differ from FSM inputs $i_l\in I$ and state variables $T_r\in SV$. Due to this, SD-based circuits have better quality than the equivalent FD-based circuits [19].

One such method is the encoding of FSM output collections (OCs) [19]. A collection $O_q\subseteq O$ is a set of outputs $o_n\in O$ that are generated simultaneously during the same interstate transition. If a particular STG has H interstate transitions, then the number of OCs, Q, differs from 1 to H [19].

To encode Q OCs by maximum binary codes $K\left(O_q\right)$, R2 variables are enough:

$$R2=\lceil {log}_{2}Q\rceil .$$

(5)

These variables create the set $AV=\{a_1,\dots ,a_{R2}\}$. There are two SBFs representing the system of FSM outputs [19]:

$$AV=AV(SV,I);$$

(6)

$$O=O\left(AV\right).$$

(7)

Applying this approach turns P Mealy FSM into PY Mealy FSM (Figure 2).

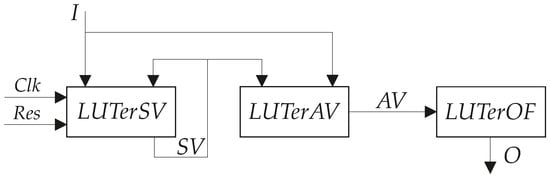
Figure 2. Architecture of PY Mealy FSM.

In the LUT-based PY Mealy FSM, the block LUTerSV implements SBF (2). The block LUTerAV generates the additional variables represented by SBF (6). The block LUTerOF produces the FSM outputs represented by SBF (7).

As follows from the research [44], this approach allows for reducing the chip area necessary for generating FSM outputs compared to this parameter if the outputs are represented by SBF (3). However, this gain reduces the value of the maximum operating frequency compared to an equivalent P Mealy FSM. To optimize characteristics of PY Mealy FSMs, the encoding of OCs may be connected with a twofold state assignment [20], leading to $P_{T}Y$ Mealy FSMs. We will discuss them a bit further.

To execute the TSA, we should find a partition ${\pi }_S$ of the set S by K classes. Each class includes compatible states. States $s_m$, $s_j\in S$ are compatible if their inclusion in the same class of the partition ${\pi }_S$ does not lead to the following phenomenon: the required number of LUT inputs exceeds the maximum number of inputs of LUT $S_L$. Why such a phenomenon is possible will be clear from the further text of the article. Three sets characterize any class $S^k\in {\pi }_S$. These sets consist of: 1. inputs determining transitions from states $s_m\in S^k$ (a set $I^k\subseteq I$ including $L_k$ elements); 2. outputs produced during the transitions from these states (a set $O^k\subseteq O$); and 3. IMFs determining MBCs of transition states (a set $D^k\subseteq D$). If the encoding of OCs is used, then the set $O^k\subseteq O$ is replaced by set $A{V}^k\subseteq AV$. The set $A{V}^k$ includes additional variables equal to 1 in the codes of OCs generated during the transitions from states $s_m\in S^k$.

Each class $S^k\in {\pi }_S$ includes $M_k$ compatible states $s_m\in S$. Inside each class, the states are encoded by partial codes $PC\left(s_m\right)$. These codes have $R_k$ bits:

$$R_k=\lceil {log}_2(M_k+1)\rceil .$$

(8)

To create the partial codes, a set ASV of additional state variables is created. The states $s_m\in S^k$ are encoded using the variables $v_r\in AS{V}^k$. The sets $AS{V}^k$ create the set ASV, which includes R3 elements:

$$R3=R_1+...+R_K.$$

(9)

If a state $s_m\in S$ is compatible with states $s_p\in S^k$, then including this state into $S^k$ satisfies the condition:

$$R_k+L_k\le S_L(k\in \{1,\dots ,K\}).$$

(10)

This approach leads to a $P_{T}Y$ Mealy FSM. In $P_{T}Y$ Mealy FSMs, each state $s_m\in S$ has two codes. One of them is a maximum binary full state code $FC\left(s_m\right)$, and the second is a partial state code $PC\left(a_m\right)$. The second code determines a particular state as an element of a particular class.

Each class $S^k\in {\pi }_S$ determines the following two systems of PBFs:

$$D^k=D^k(AS{V}^k,I^k);$$

(11)

$$A{V}^k=A{V}^k(AS{V}^k,I^k).$$

(12)

To obtain the final values of additional variables and IMFs, the following SBFs should be created:

$$D_r=\underset{k=1}{\overset{K}{\bigvee }}{D}_r^k(r\in \{1,\dots ,R1\});$$

(13)

$$A{V}_r=\underset{k=1}{\overset{K}{\bigvee }}A{V}_r^k(r\in \{1,...,R2\}).$$

(14)

Next, the codes of the OCs should be transformed into FSM outputs. The outputs are represented by SBF (7). Additionally, the full state codes should be transformed into the corresponding partial codes. The transformation is represented by the following SBF:

$$ASV1=ASV1\left(SV\right).$$

(15)

SBFs (11) and (12) define the first level of a $P_{T}Y$ Mealy FSM circuit. SBFs (13) and (14) determine its second level. Finally, SBFs (7) and (15) represent the third circuit level. The architecture of a $P_{T}Y$ Mealy FSM is shown in Figure 3.

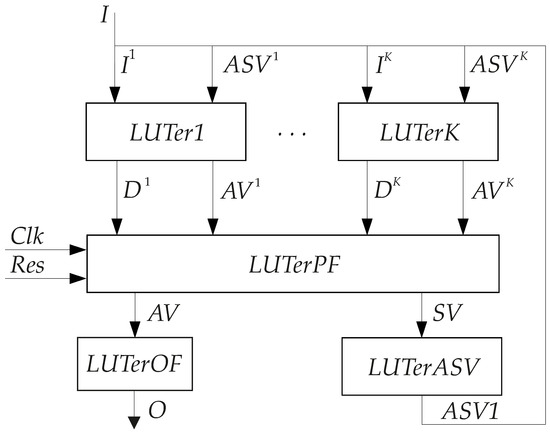
Figure 3. Architecture of $P_{T}Y$ Mealy FSM.

In this architecture, the block LUTerk generates PBFs (11) and (12). The block LUTerPF implements the system of disjunctions (13) and (14). This block includes the distributed RG controlled by the pulses Clk and Res. The block LUTerOF implements the outputs represented by SBF (7). The block LUTerASV implements SBF (15). Therefore, it executes the transformation of state codes.

Our previous research [20] shows that the LUT-based circuits of $P_{T}Y$ FSMs have better characteristics than the circuits of equivalent PY FSMs. If the conditions

$$K\le S_L,$$

(16)

$$R2\le S_L$$

(17)

hold, then the circuits of $P_{T}Y$ FSMs are three-level and are faster than the equivalent PY Mealy FSMs.

Let us represent the circuit (Figure 3) as a combination of a core of partial functions (CorePF) and a functional transformer. The core includes blocks LUTer1–LUTerK. The functional transformer includes all other blocks shown in Figure 3. This leads to the generalized diagram of a $P_{T}Y$ FSM (Figure 4).

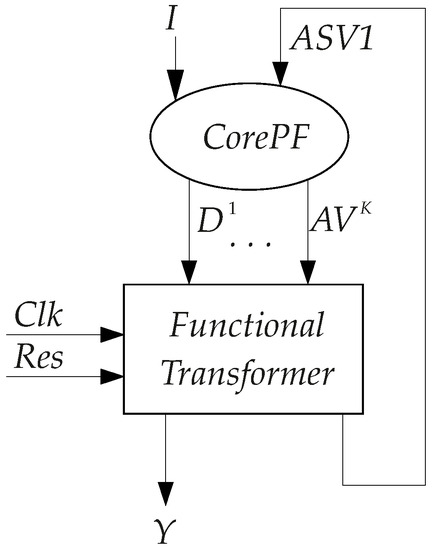
Figure 4. Generalized diagram of a $P_{T}Y$ Mealy FSM.

Analysis of the generalized diagram shows the following peculiarity: the transformation of full codes into partial codes $PC\left(s_m\right)$ is executed for all FSM states. However, there is a case when there is no need in the code transformation. If, for some state $s_m\in S$, condition (4) holds, then, for this state, all PBFs are represented by single-LUT circuits. If we take into account this property, we can reduce the cardinality number of the partition ${\pi }_S$. Additionally, the number of state variables R3 can be reduced as compared to its value for the equivalent $P_{T}Y$ FSM. In this paper, we propose a method based on taking into account the mentioned property.

4. Analysis of Our Current Approach

The transitions from state $s_m\in S$ are determined by elements of a set $I\left(s_m\right)\subseteq I$. There are $L\left(s_m\right)\le L$ elements in the set $I\left(s_m\right)\subseteq I$. If the condition

$$L\left(s_m\right)+R1\le S_L$$

(18)

holds, then it is enough for a single LUT to represent a circuit for any PBF generated during the transitions from $s_m\in S$. Therefore, for such states, it makes sense to use the full state codes for generating PBFs. If the condition (18) is violated, then the corresponding codes $FC\left(s_m\right)$ should be transformed into partial codes. This allows for creating a class of states $S^0\subset S$ whose maximum binary codes do not require the transformation. Therefore, the partition based on (10) should be constructed only for the states $s_m\notin S^0$.

Based on the above-mentioned statement, we propose to use the ideas from our paper [22]. First of all, we should divide the set S by disjoint sets $S^0$ and $S1=S\backslash S^0$. If a state $s_m\in S$ satisfies condition (18), then this state is included in the set $S^0$. The states $s_m\in S^0$ create a block CoreFC. Otherwise, the state $s_m\in S$ belongs to the set S1. The states $s_m\in S1$ form a block CorePC. Obviously, only the codes of states $s_m\in S1$ should be transformed.

CoreFC determines the sets $I1\subseteq I$, $AV1\cup A{V}^0\subseteq AV$, and $D^0\subseteq D$. The input $i_l\in I1$ causes the transitions from states creating the CoreFC. The set AV1 consists of additional variables $a_r\in AV$ produced only during the transitions from states creating the CoreFC. The set $A{V}^0$ consists of the additional variables produced by both FSM cores. The set $D^0$ includes functions $D_r\in D$ produced during the transitions creating the CoreFC. Therefore, the circuit of CoreFC is determined by the following SBFs:

$$D^0=D^0(SV,I1);$$

(19)

$$AV1=AV1(SV,I1);$$

(20)

$$A{V}^0=A{V}^0(SV,I1).$$

(21)

To synthesize CorePC, it is necessary to create the partition ${\pi }_{S2}=\{S^1,\dots ,S^J\}$ of the set S1. This can be done using the same approach as the one creating ${\pi }_S$. CorePC determines the sets $I2\subseteq I$ and $AV2\subseteq AV$. Their purpose is clear from the previous analysis.

Three sets ($I_{PC}^j$, $A{V}_{PC}^j$, $D_{PC}^j$) are determined by each class $S^j$ of the partition ${\pi }_{S2}$. Their meaning follows from the previous text. The state variables from the set ASV2 encode the states $s_m\in S1$. The codes of states $s_m\in S^j$ are created from elements of the set $AS{V}^j\subseteq ASV2$. There are R4 elements in the set $ASV2(R4=R_1+R_2+...+R_J)$. The following SBFs determine the circuit of CorePC:

$$D_{PC}^j=D_{PC}^j(ASV{2}^j,I_{PC}^j);$$

(22)

$$A{V}_{PC}^j=A{V}_{PC}^j(ASV{2}^j,I_{PC}^j).$$

(23)

To generate the final values of additional variables, FSM outputs, and state variables, we should use the functional transformer. This block is similar to the one used in the $P_{T}Y$ FSM (Figure 3). Using this information, we propose to transform $P_{T}Y$ FSMs into $P_{2T}Y$ Mealy FSMs (Figure 5).

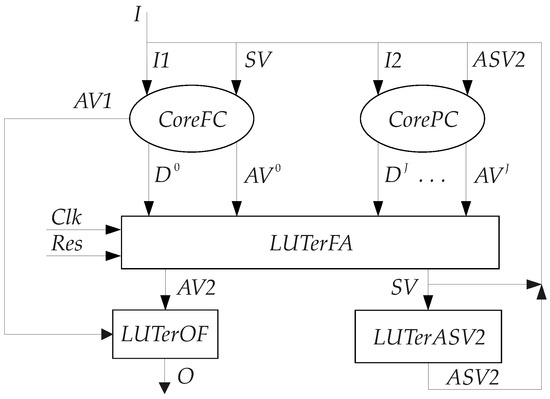
Figure 5. Architecture of the $P_{2T}Y$ Mealy FSM.

In the proposed two-core FSM, the block CoreFC implements SBFs (19)–(21). The block CorePC implements SBFs (22) and (23). The block LUTerFA is a functional assembler implementing the following disjunctions:

$$D_r=\underset{j=1}{\overset{J}{\bigvee }}{D}_r^j(r\in \{1,...,R1\});$$

(24)

$$AV{2}_r=\underset{j=1}{\overset{J}{\bigvee }}A{V}_r^j(r\in \{1,...,R2\}).$$

(25)

The block LUTerFA includes a distributed full state code register whose informational inputs are connected with IMFs (24). The register is controlled by pulses Clk and Res. The block LUTerOF implements SBF (7) where $AV=AV1\cup AV2$. The block LUTerASV2 implements SBF:

$$ASV2=ASV2\left(SV\right).$$

(26)

Let us analyze the proposed solution. The partition ${\pi }_{S2}$ has J classes. Obviously, the following conditions take place:

$$J\le K;$$

(27)

$$R4\le R3.$$

(28)

Due to the validity of condition (27), we can state that the circuit of the $P_{2T}Y$ Mealy FSM (Figure 5) is not slower than the circuit of the equivalent FSM $P_{T}Y$ (Figure 3). Due to the validity of condition (28), we can state that the circuit of CorePC for FSM $P_{2T}Y$ should perform better LUT counts than it does for block CorePF of the equivalent FSM $P_{T}Y$. The same is true for block LUTerASV of the equivalent FSMs $P_{T}Y$ and $P_{2T}Y$. Therefore, we could expect that a circuit of $P_{2T}Y$ FSM (Figure 5) requires a smaller area and is not slower compared to a circuit of equivalent $P_{T}Y$ FSM (Figure 3). These assumptions of ours have been confirmed by the conducted studies, the results of which are given in Section 6.

Let us show the features of our method in comparison with the methods proposed in [20,22]. In the article [20], we discussed $P_{T}Y$ FSMs with two-fold state assignment and encoding of output collections. The $P_{2T}Y$ FSMs have the following differences. First, in $P_{T}Y$ FSMs, the codes of all states are converted, while in $P_{2T}Y$ FSMs, only a part of the code is converted. This allows for optimizing the code converter circuit (compared to the circuit used in equivalent $P_{T}Y$ FSMs). Secondly, the use of two cores allows us to encode OCs such that some variables $a_r\in AV$ are generated only by the LUTs of CoreFC. This allows for reducing the number of LUTs generating output signals (compared to this number for equivalent $P_{T}Y$ FSMs). In the article [22], we discussed so-called $P_{2}C$ FSMs, where two cores of LUTs are used. However, $P_{2}C$ FSMs are based on one-hot encoding of outputs. In $P_{2T}Y$ FSMs, we use maximum binary codes of output collections. This allows for reducing the number of LUTs generating output signals (compared to this number for equivalent $P_{2}C$ FSMs).

In this paper, we propose a synthesis method aimed at LUT-based $P_{2T}Y$ Mealy FSMs. The synthesis process starts from the FSM state transition graphs [17]. Next, these graphs are transformed into equivalent state transition tables (STTs) [17]. The sequence of steps of the proposed method is the following:

• Creating an STT of P Mealy FSM.
• Pre-formation of sets $S^0$ and S1.
• Pre-formation of partition ${\pi }_{S2}$ of set S1.
• Final formation of sets $S^0$ and S1 and partition ${\pi }_{S2}$.
• Creating full state codes $FC\left(s_m\right)$.
• Encoding of output collections $O_q\subseteq O$ and finding SBF (7).
• Creating a table of CoreFC and deriving SBFs (19)–(21).
• Encoding of states $s_m\in S^j$ by partial state codes $PC\left(s_m\right)$.
• Generating tables describing the blocks of CorePC and deriving systems (22) and (23).
• Creating a table of LUTerFA and SBFs (24) and (25).
• Creating a table of LUTerASV and systems (26).
• Creating the $P_{2T}Y$ Mealy FSM circuit.

To show that the model of $P_{2T}Y$ FSM is used to synthesize FSM A, we use the symbol $P_{2T}Y\left(A\right)$. Let us explain how to execute the steps of the proposed design method.

5. Synthesis Example

We discuss a synthesis example for Mealy FSM A1 (Figure 6). To implement the FSM circuit, we use LUTs with $S_L=5$.

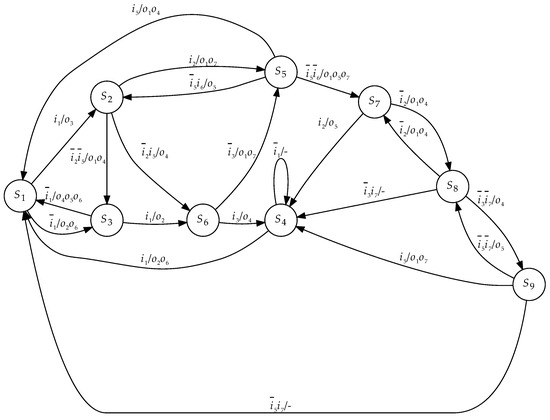
Figure 6. Initial STG.

The FSM states correspond to the STG vertices [17]. To show interstate transitions, the vertices are connected by arcs. An STG includes H arcs. The h-th arc $(h\in \{1,...,H\left\}\right)$ is marked by a pair $<I_h,O_h>$. In this pair, the symbol $I_h$ stands for a conjunction of either FSM inputs $i_l\in I$ or their complements. This is an input signal. The set $O_h\subseteq O$ includes FSM outputs $o_n\in O$ generated during the transition number h.

The STG (Figure 6) determines the following sets: $S=\{s_1,...,s_9\}$, $I=\{i_1,...,i_7\}$, and $O=\{o_1,...,o_7\}$. Therefore, the FSM A1 is characterized by $M=9$, $L=N=7$. There are 22 arcs in the initial STG. This gives 22 transitions among the states of FSM A1.

Step 1. This step is omitted if an FSM is represented by STT. The transformation is executed in the following way [14]. The STT includes H lines. Each line corresponds to an STG arc. Each transition is characterized by its current state $s_C$, the next state $s_T$, inputs $I_{CT}$ (for the h-th arc, this is the signal $I_h$), outputs $O_{CT}$ (for the h-th arc, this is the OC $O_h$), and h. Therefore, each arc determines the columns $s_C$, $s_T$, $I_{CT}$, $O_{CT}$, and h. Table 1 is an STT of A1.

Table 1. STT of FSM A1.

${\mathit{S}}_{\mathit{C}}$	${\mathit{S}}_{\mathit{T}}$	${\mathit{I}}_{\mathit{CT}}$	${\mathit{O}}_{\mathit{CT}}$	q	h
$s_1$	$s_2$	$i_1$	$o_3$	4	1
	$s_3$	$\overline{i_1}$	$o_2{o}_6$	5	2
$s_2$	$s_5$	$i_2$	$o_1{o}_7$	2	3
	$s_6$	$\overline{i_2}{i}_5$	$o_4$	3	4
	$s_3$	$\overline{i_2}\overline{i_5}$	$o_1{o}_4$	6	5
$s_3$	$s_6$	$i_1$	$o_2$	8	6
	$s_1$	$\overline{i_1}$	$o_4{o}_5{o}_6$	10	7
$s_4$	$s_1$	$i_1$	$o_2{o}_6$	5	8
	$s_4$	$\overline{i_1}$	–	1	9
$s_5$	$s_1$	$i_5$	$o_1{o}_4$	6	10
	$s_2$	$\overline{i_5}{i}_6$	$o_5$	7	11
	$s_7$	$\overline{i_5}\overline{i_6}$	$o_1{o}_5{o}_7$	9	12
$s_6$	$s_4$	$i_3$	$o_4$	3	13
	$s_5$	$\overline{i_3}$	$o_1{o}_7$	2	14
$s_7$	$s_4$	$i_2$	$o_5$	7	15
	$s_8$	$\overline{i_2}$	$o_1{o}_4$	6	16
$s_8$	$s_7$	$i_3$	$o_1{o}_5{o}_7$	9	17
	$s_4$	$\overline{i_3}{i}_7$	–	1	18
	$s_9$	$\overline{i_3}\overline{i_7}$	$o_5$	7	19
$s_9$	$s_4$	$i_5$	$o_1{o}_7$	2	20
	$s_1$	$\overline{i_5}{i}_7$	–	1	21
	$s_8$	$\overline{i_5}\overline{i_7}$	$o_5$	7	22

This table uniquely corresponds to the STG (Figure 6). We add the column q into Table 1 to show the subscripts of output collections.

Step 2. The following values of $L\left(s_m\right)$ can be found from the analysis of Table 1: $L\left(s_m\right)=1$ for states $s_1$, $s_3$, $s_4$, $s_6$, $s_7$; $L\left(s_m\right)=2$ for states $s_2$, $s_5$, $s_8$, $s_9$. Additionally, $M=9$. Using (1) gives $R1=4$. As follows from the initial conditions of the example, $S_L=5$. Therefore, condition (18) takes place for states with $L\left(s_m\right)=1$. Thus, the following sets can be created: $S^0=\{s_1,s_3,s_4,s_6,s_7\}$ and $S2=\{s_2,s_5,s_8,s_9\}$. As follows from our analysis, some states may be transferred from $S^0$ to S2. Thus, the elements of these sets can be changed. From Table 1, we can find the sets $I1=\{i_1,i_2,i_3\}$ and $I2=\{i_2,i_3,i_5,i_6,i_7\}$.

Step 3. Using known approach [20], we can find the partition ${\pi }_{S2}=\{S^1,S^2\}$ of the set S1. It includes the classes $S^1=\{s_2,s_5\}$ and $S^2=\{s_8,s_9\}$. Because the set S1 is a preliminary one, this partition is also preliminary. Each class includes $M_j=2$ elements. Using (8) gives the following relation: $R_1=R_2=2$. Using (9) gives $R3=4$. Therefore, there is a set of state variables $ASV2=\{v_1,...,v_4\}$.

Step 4. The classes $S^j\in {\pi }_{S2}$ determine the following sets of inputs: $I^1=\{i_2,i_5,i_6\}$ and $I^2=\{i_3,i_5,i_7\}$. Therefore, we have $L_1=L_2=3$. This means we cannot add new inputs in these sets due to violation of condition (10). Each set $S^j\in {\pi }_{S2}$ can include up to 3 elements without violation of (10). Therefore, one additional state can be added to each of the sets $S^j\in {\pi }_{S2}$.

The method of state redistribution is discussed in detail in the paper [22]. In our current paper, we just show the result of redistribution, which is the following: $S^0=\{s_1,s_3,s_4\}$ and $S1=\{s_2,s_5,s_6,s_7,s_8,s_9\}$. The redistribution gives the following classes: $S^1=\{s_2,s_5,s_7\}$ and $S^2=\{s_6,s_8,s_9\}$. Now, we obtain $M_1=M_2=3$. Using these values and Formula (8), we can see that $R_1=R_2=2$ and $R4=4$. Therefore, the total number of state variables $v_r\in ASV2$ does not change, but now the set $S^0$ includes fewer elements. Now we can expect a decrease in the value of the LUT count for the circuit of CoreFC.

Step 5. There are $M=9$ elements in the set S. Therefore, using (1) gives $R1=4$. This value determines the sets $SV=\{T_1,...,T_4\}$ and $D=\{D_1,...,D_4\}$. As shown in [17], it is necessary to cover the states from the same class using the minimum possible number of generalized cubes of R1-dimensional Boolean space. Such an outcome decreases the number of literals in functions (19)–(21). One of the possible outcomes is shown in Figure 6. To encode the states by MBCs, we used the algorithm JEDI [40].

As we can see from the analysis of the resulting Karnaugh map (Figure 7), the states $s_m\in S^0$ are covered by the generalized cube 00xx. The states $s_m\in S^1$ are represented by the generalized cube x100. The cube 1x00 covers the states $s_m\in S^2$. Therefore, for our example, each class is placed into a single generalized cube.

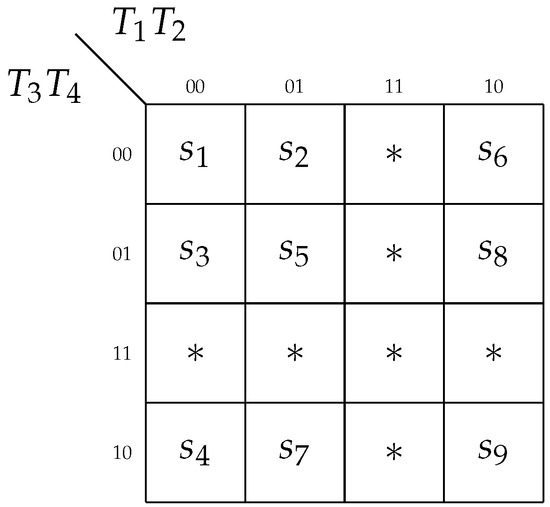
Figure 7. Maximum binary state codes for FSM A1.

Step 6. The analysis of Table 1 gives $Q=10$ output collections. They are the following: $O_1=\varnothing$, $O_2=\{o_1,o_7\}$, $O_3=\left\{o_4\right\}$, $O_4=\left\{o_3\right\}$, $O_5=\{o_2,o_6\}$, $O_6=\{o_1,o_4\}$, $O_7=\left\{o_5\right\}$, $O_8=\left\{o_2\right\}$, $O_9=\{o_1,o_5,o_7\}$, and $O_{10}=\{o_4,o_5,o_6\}$. Using (5) gives $R2=4$ and the set $AV=\{a_1,...,a_4\}$.

Each literal in the sum-of-product (SOP) of a Boolean function corresponds to an interconnection between the input source and a corresponding LUT. To reduce the number of interconnections, the number of literals in SOPs should be decreased. To encode the output collections, we used the methods presented in classical work [17]. Using the approach from [17] gives the codes shown in Figure 8.

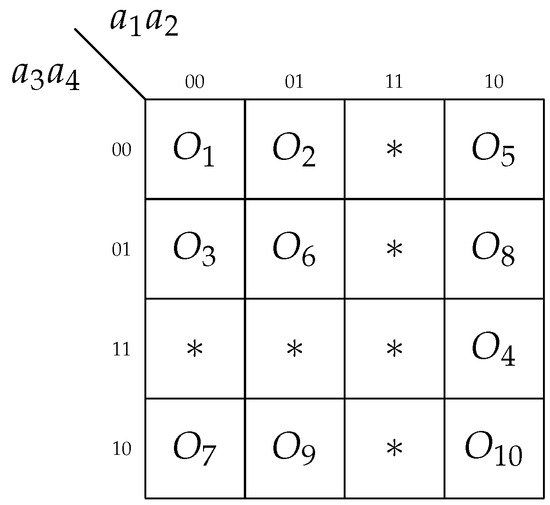
Figure 8. Codes of output collections for Mealy FSM A1.

We encoded the OCs in a way where the variable $a_1\in AV$ is generated only by one LUT of CoreFC. To do this, we have analyzed Table 1. The analysis of Table 1 shows that the following OCs are generated during the transitions from states $s_m\in S^0$: $O_4$, $O_5$, $O_8$, and $O_{10}$. Therefore, we have divided the Karnaugh map (Figure 8) into two parts. The first part corresponds to $a_1=0$, and the second part corresponds to $a_1=1$. We have placed the OCs $O_4$, $O_5$, $O_8$, and $O_{10}$ into the second part. Now, we can obtain the following system of functions:

$$\begin{array}{cc}\hfill & o_1=O_2\vee O_6\vee O_9=a_2;\\ \hfill & o_2=O_5\vee O_8=a_1\overline{a_3};\\ \hfill & o_3=O_4\vee O_{10}=a_1{a}_3;\\ & o_4=O_3\vee O_6=\overline{a_1}{a}_4;\\ \hfill & o_5=O_7\vee O_9\vee O_{10}=a_3\overline{a_4};\\ \hfill & o_6=O_5\vee O_{10}=a_1\overline{a_4};\\ \hfill & o_7=O_2\vee O_9=a_2\overline{a_4}.\end{array}$$

(29)

The SBF (29) determines the circuit of LUTerOF. The function $o_1$ is represented by a corresponding output of LUTerFA. Therefore, the circuit of LUTerOF consists of 6 LUTs. Analysis of system (29) shows that there are 12 literals in the SOPs of the implemented functions. This determines 12 interconnections between LUTerOF and other circuit blocks. Using the results of [19] gives the maximum number of interconnections. In our case, it is equal to $R2\ast Q=28$. Thus, due to using the proposed approach, the number of interconnects is reduced by 2.33 times.

Step 7. To construct the table of CoreFC, it is necessary to select the lines of STT with transitions from states $s_m\in S^0$. In the discussed case, we should select lines 1–2 and 6–9 of STT (Table 1). The table of CoreFC includes 5 additional columns (compared to the baseline STT). These columns are: $FC\left(s_C\right)$, $FC\left(s_T\right)$, $D_h^0$, $A{V}_h^0$, and $AV{1}_h$. There is a self-explanatory meaning of columns $FC\left(s_C\right)$ and $FC\left(s_T\right)$. The column $D_h^0$ includes IMFs creating the code $FC\left(s_T\right)$ (to load it into the code register). The column $A{V}_h^0$ includes the additional variables $a_r\in AV$ equal to 1 in codes of generated OCs. These variables are also produced by some blocks of LUTerPC. The column $AV{1}_h$ includes the additional variables $a_r\in AV$ generated only by the block CoreFC. Obviously, these variables are not produced by any block of LUTerPC. Table 2 represents the block CoreFC for the given example.

Table 2. Table of CoreFC for Mealy FSM A1.

${\mathit{S}}_{\mathit{C}}$	$\mathit{FC}\left({\mathit{S}}_{\mathit{c}}\right)$	${\mathit{S}}_{\mathit{T}}$	$\mathit{FC}\left({\mathit{S}}_{\mathit{T}}\right)$	$\mathit{I}{1}_{\mathit{h}}$	${\mathit{AV}}_{\mathit{h}}^0$	$\mathit{AV}{1}_{\mathit{h}}$	${\mathit{D}}_{\mathit{h}}^0$	h
$S_1$	0000	$S_2$	0100	$i_1$	$a_3{a}_4$	$a_1$	$D_2$	1
		$S_3$	0001	$\overline{i_1}$	–	$a_1$	$D_4$	2
$S_3$	0001	$S_6$	1000	$i_1$	$a_4$	$a_1$	$D_1$	3
		$S_1$	0000	$\overline{i_1}$	$a_3$	$a_1$	–	4
$S_4$	0010	$S_1$	0000	$i_1$	–	$a_1$	–	5
		$S_4$	0010	$\overline{i_1}$	–	–	$D_3$	6

The columns $A{V}_h^0$ and $AV{1}_h$ are created in the following manner. For example, there is an OC $O_4$ written in line 1 of Table 1. Analysis of Figure 8 gives the code $K\left(O_4\right)=1011$. This code determines the variables $a_1$, $a_3$, and $a_4$. Therefore, the first line of Table 2 includes the variables $a_3$ and $a_4$ in the column $A{V}_h^0$, as well as the variable $a_1$ in the column $AV{1}_h$. All other lines of Table 2 are created using a similar approach.

Using Table 2, we can obtain SBFs (19)–(21). For example, the function $a_1\in AV$ is represented as the following:

$$a_1=\overline{T_1}\overline{T_2}\overline{T_3}\vee \overline{T_1}\overline{T_2}{T}_3{i}_1.$$

(30)

The block CoreFC determines the set $D^0=D$. We will show a bit later the SOPs for functions $D_1^0$ and $a_3^0$.

Step 8. The codes for states $s_m\in S^1$ use the variables $v_1,v_2\in SV$. The codes for states $s_m\in S^2$ are based on the variables $v_3$, $v_4\in SV$. The code combination $v_1=v_2=0$ indicates that a particular state belongs to a class other than $S^1$. The code combination $v_3=v_4=0$ indicates that a particular state belongs to a class other than $S^2$. Due to the fulfillment of condition (10), the codes do not affect the number of LUTs in the circuit of CorePC. Therefore, the partial state codes can be arbitrary. We have chosen the following approach: the smaller the subscript (m) of a state, the more nulls its partial code contains. The obtained partial state codes are shown in Figure 9.

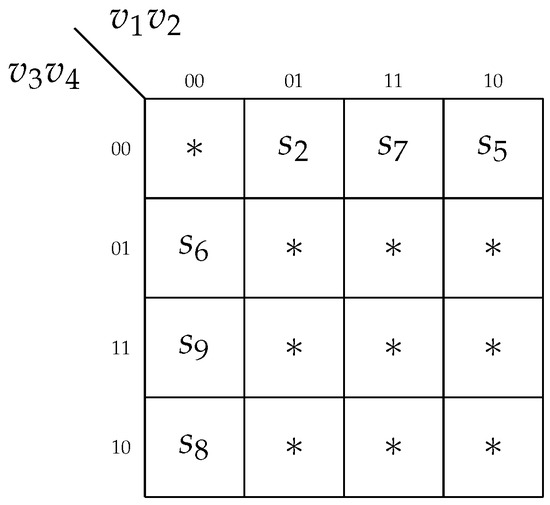
Figure 9. Partial state codes for Mealy FSM A1.

Using Figure 9, we can obtain the following partial codes: $PC\left(s_2\right)=PC\left(s_6\right)=01$, $PC\left(s_5\right)=PC\left(s_8\right)=10$, and $PC\left(s_7\right)=PC\left(s_9\right)=11$. Using them allows for creating tables representing CorePC.

Step 9. The block CorePC includes two blocks of LUTs. The block $CorePC\left(S^1\right)$ corresponds to the set $S^1$, whereas the block $CorePC\left(S^2\right)$ corresponds to the set $S^2$. The table of $CorePC(S^1$) (Table 3) is based on lines 3–5, 10–12, and 15–16 (Table 1). Table 4 represents the block $CorePC\left(S^2\right)$. The table is constructed using the lines 13–14 and 17–22 of the initial STT.

Table 3. Table of CorePC($S^1$).

${\mathit{S}}_{\mathit{C}}$	$\mathit{PC}\left({\mathit{S}}_{\mathit{c}}\right)$	${\mathit{S}}_{\mathit{T}}$	$\mathit{FC}\left({\mathit{S}}_{\mathit{T}}\right)$	$\mathit{I}{2}_{\mathit{h}}$	${\mathit{AV}}_{\mathit{h}}^1$	${\mathit{D}}_{\mathit{h}}^1$	h
$S_2$	01	$S_5$	0101	$i_2$	$a_2$	$D_2{D}_4$	1
		$S_6$	1000	$\overline{i_2}{i}_5$	$a_4$	$D_1$	2
		$S_3$	0001	$\overline{i_2}\overline{i_5}$	$a_2{a}_4$	$D_3$	3
$S_5$	10	$S_1$	0000	$i_5$	$a_2{a}_4$	–	4
		$S_2$	0100	$\overline{i_5}\overline{i_6}$	$a_3$	$D_2$	5
		$S_7$	0110	$\overline{i_5}\overline{i_6}$	$a_2{a}_3$	$D_2{D}_3$	6
$S_7$	11	$S_4$	0010	$i_2$	$a_3$	$D_3$	7
		$S_8$	1001	$\overline{i_2}$	$a_2{a}_4$	$D_1{D}_4$	8

Table 4. Table of CorePC($S^2$).

${\mathit{S}}_{\mathit{C}}$	$\mathit{PC}\left({\mathit{S}}_{\mathit{c}}\right)$	${\mathit{S}}_{\mathit{T}}$	$\mathit{FC}\left({\mathit{S}}_{\mathit{T}}\right)$	$\mathit{I}{2}_{\mathit{h}}$	${\mathit{AV}}_{\mathit{h}}^1$	${\mathit{D}}_{\mathit{h}}^1$	h
$S_6$	01	$S_4$	0010	$i_3$	$a_4$	$D_3$	1
		$S_5$	0101	$\overline{i_3}$	$a_2$	$D_2{D}_4$	2
$S_8$	10	$S_7$	0110	$i_3$	$a_2{a}_3$	–	3
		$S_4$	0010	$\overline{i_3}{i}_7$	–	$D_2$	4
		$S_9$	1010	$\overline{i_3}\overline{i_7}$	$a_3$	$D_2{D}_3$	5
$S_9$	11	$S_4$	0010	$i_5$	$a_2$	$D_3$	6
		$S_1$	0000	$\overline{i_5}{i}_7$	–	–	7
		$S_8$	1001	$\overline{i_5}\overline{i_7}$	$a_3$	$D_1{D}_4$	8

In these tables, the current states are represented by their partial codes $PC\left(s_C\right)$; the states of transition are represented by their full codes $FC\left(s_T\right)$. The column $O_{CT}$ of STT is replaced by the columns $A{V}_h^1$ and $A{V}_h^2$, respectively. These columns include additional variables equal to 1 in the codes of the OCs.

The transparent approach is used to construct SBFs (22) and (23). For example, the functions $D_1^0$, $D_1^1$, and $D_1^2$ are represented as:

$$\begin{array}{cc}\hfill & D_1^0=\overline{T_1}\overline{T_2}{T}_4{i}_1;\\ & D_1^1=\overline{v_1}{v}_2\overline{i_2}{i}_5\vee v_1{v}_2\overline{i_2};\\ \hfill & D_1^2=v_3\overline{v_4}\overline{i_3}\overline{i_7}\vee v_3{v}_4\overline{i_5}\overline{i_7}.\end{array}$$

(31)

In the same way, we can obtain the following SOPs:

$$\begin{array}{cc}\hfill & a_3^0=\overline{T_1}\overline{T_2}\overline{T_3}\overline{T_4}{i}_1\vee \overline{T_1}\overline{T_2}\overline{T_3}\overline{T_4}\overline{i_1};\\ & a_3^1=v_1\overline{v_2}\overline{i_5}\vee v_1{v}_2{i}_2;\\ \hfill & a_3^2=v_3\overline{v_4}{i}_3\vee v_3\overline{v_4}\overline{i_3}\overline{i_7}\vee v_3{v}_4\overline{i_5}\overline{i_7}.\end{array}$$

(32)

Step 10. The block LUTerFA is based on Table 5. Table 5 includes the following columns: Function (this is an assembled function produced by LUTerFA), CoreFC, and CorePC. If some function belonging to the set $D\cup AV$ is generated by a LUT of the block CoreFC, then there is a 1 in the intersection of the row containing this function and the column CoreFC. The opposite situation is marked by 0. The column CorePC is divided by J subcolumns corresponding to the classes $S^j(j\in \{1,\dots ,J\})$. The same principle is in play for placing either 1 or 0 in the rows of this part of Table 5.

Table 5. Table of LUTerFA.

Function	$\mathit{CoreFC}$	$\mathit{CorePC}$
		${\mathit{S}}^{\mathbf{1}}$	${\mathit{S}}^{\mathbf{2}}$
$D_1$	1	1	1
$D_2$	1	1	1
$D_3$	1	1	1
$D_4$	1	1	1
$a_1$	1	0	0
$a_2$	0	1	1
$a_3$	1	1	1
$a_4$	1	1	1

We use Table 2 to fill the rows of column CoreFC of Table 5. To fill the rows of subcolumn $S^1$$\left(S^2\right)$, we use Table 3 (Table 4).

Table 5 determines the R1 + R2 disjunctions of partial Boolean functions. The following disjunctions represent the circuit of the block LUTerFA:

$$\begin{array}{cc}\hfill & D_1=D_1^0\vee D_1^1\vee D_1^2;D_2=D_2^0\vee D_2^1\vee D_2^2;\\ & D_3=D_3^0\vee D_3^1\vee D_3^2;D_4=D_4^0\vee D_4^1\vee D_4^2;\\ \hfill & a_1=a_1^0;a_2=a_2^1\vee a_2^2;\\ \hfill & a_3=a_3^0\vee a_3^1\vee a_3^2;a_4=a_4^0\vee a_4^1\vee a_4^2.\end{array}$$

(33)

Step 11. The block LUTerASV transforms the full codes $FC\left(s_m\right)$ into the partial state codes $PC\left(s_m\right)$. This transformation is not executed for the states $s_m\in S^0$. The table of LUTerASV includes the following columns: $s_m$, $FC\left(s_m\right)$, $PC\left(s_m\right)$, and $A{V}_m$. The last column includes the symbols of additional variables equal to 1 in the codes $PC\left(s_m\right)$. In the discussed case, the full state codes are taken from Figure 7; the partial state codes are taken from Figure 9. Using these codes, we can create Table 6.

Table 6. Table of LUTerASV.

${\mathit{S}}_{\mathit{m}}$	$\mathit{FC}\left({\mathit{S}}_{\mathit{m}}\right)$	$\mathit{PC}\left({\mathit{S}}_{\mathit{m}}\right)$	${\mathit{AV}}_{\mathit{m}}$
$s_2$	0100	0100	$v_2$
$s_5$	0101	1000	$v_1$
$s_6$	1000	0001	$v_4$
$s_7$	0110	1100	$v_1{v}_2$
$s_8$	1001	0010	$v_3$
$s_9$	1010	0011	$v_3{v}_4$

Obviously, using Table 6 gives us the perfect SOPs [17] of SBF (12). To minimize the number of interconnections between the blocks LUTerFA and LUTerASV, we transform Table 6 into a multi-functional Karnaugh map (Figure 10).

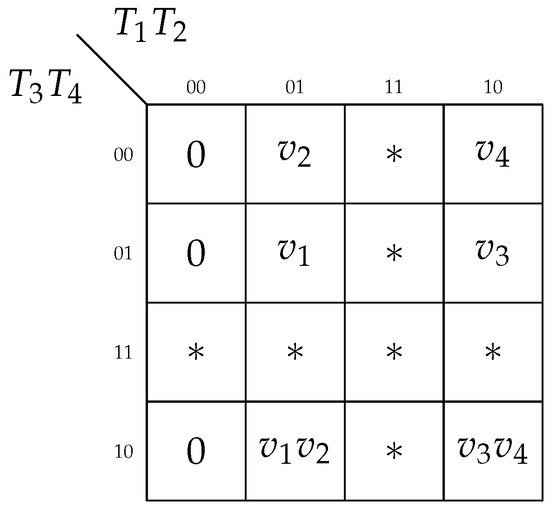
Figure 10. Karnaugh map for SBF ASV2(SV).

Figure 10 is based on Figure 7. This transformation is done in an obvious way. We have simply replaced the symbols of states from Figure 7 with symbols of corresponding additional variables. Additionally, the codes of states $s_m\in S^0$ are “do not care” code combinations. Using Figure 10 gives us the following SBF:

$$\begin{array}{cc}\hfill & v_1=T_2{T}_4\vee T_2{T}_3;\\ & v_2=T_2\overline{T_4};\\ \hfill & v_3=T_1{T}_4\vee T_1{T}_3;\\ \hfill & v_4=T_1\overline{T_4}.\end{array}$$

(34)

There are 10 literals in SBF (34). If each function from (12) is represented by its perfect SOP, then these SOPs have $R1\ast R4=16$ literals. Therefore, using the multi-functional Karnaugh map allows for reducing the number of interconnections by 1.6 times. As shown in [31], the fewer interconnections a circuit has, the less power it consumes.

Step 12. During this step, various technology mapping procedures should be executed [45,46]. If the FPGA chip used is produced by AMD Xilinx, then their CAD tool Vivado [47] should be applied for implementing an FSM circuit. In the next section, we show some results based on using this CAD package to implement FSM circuits. Experiments allow us to compare the effectiveness of the proposed method in relation to some known methods.

At the end of this section, we will show how to estimate the hardware amount in the circuits of FSMs $P_{2T}Y\left(A1\right)$ and $P_{T}Y\left(A1\right)$. We start from FSM $P_{2T}Y\left(A1\right)$. To find the LUT counts for circuits of CoreFC, CorePC (the first logic level), and LUTerFA (the second logic level), it is necessary to analyze Table 5 (the table of LUTerFA). Each symbol “1” in this table corresponds to a LUT from the first logic level. In the table, there are 21 “1” symbols. Therefore, the first-level circuits consist of 21 LUTs. If a row of the table includes more than a single 1, then this row corresponds to a LUT from the second logic level. There are 7 LUTs in the circuit of LUTerFA. This can be found from Table 5. To find the LUT counts for blocks LUTerOF and LUTerASV creating the third logic level, we should analyze SOPs (29) and (34), respectively. If an SOP includes at least two literals, then it determines a LUT of the third logic level. As follows from (29), there are 6 such SOPs. The analysis of (34) shows that the system includes 4 such SOPs. Therefore, the third logic level includes 10 LUTs. Summing up the number of LUTs for different levels, we see that the circuit of FSM $P_{2T}Y\left(A1\right)$ includes $21+7+10=38$ LUTs.

To estimate the number of LUTs in the circuit of FSM $P_{T}Y\left(A1\right)$, it is necessary to find the compatibility classes for the set of states. Using the approach [20] gives the partition with $K=3$. There are the following relations between the classes of ${\pi }_S$ and ${\pi }_{S2}$: $S^1=S^0$, $S^2=S^1$, and $S^3=S^2$. This means that the table of LUTerPF (FSM $P_{T}Y\left(A1\right)$) is the same as Table 5. This gives 21 LUTs for the first logic level consisting of the blocks LUTer1–LUTer3. Also, there are 7 LUTs in the circuit of LUTerPF. The blocks LUTerOF are the same for both FSMs (each of which includes 6 LUTs). However, there is $R3=6$. This gives 6 LUTs in the block LUTerASV. In total, 12 LUTs create the third logic level of FSM $P_{T}Y\left(A1\right)$. Summing up the number of LUTs for different levels, we see that there are $21+7+12=40$ LUTs in the circuit of $P_{T}Y\left(A1\right)$.

Therefore, for such a simple FSM, we see a gain of 5.3% due to the transition from $P_{T}Y\left(A1\right)$ to $P_{2T}Y\left(A1\right)$. For more complex FSMs, the gain can be much higher. This statement is confirmed by the results of the research shown in the next section.

6. Experimental Results

As a basis for comparing the efficiency of different synthesis methods, we use the benchmark FSMs from the library [42]. The library includes 48 benchmarks of varying complexity (numbers of states, inputs, outputs, output collections, and interstate transitions). The STTs of benchmark FSMs are represented using the format KISS2. These benchmarks have been used by different designers as a representative sample to compare the main characteristics of proposed and known FSM circuits [33,34,36]. To give an idea of the complexity of these benchmarks, we show their characteristics in [19,42].

As a rule, in research, FSMs are considered as stand-alone units. In this case, the stability of the output signals is not one of the main design problems. However, in our current paper, we consider Mealy FSMs as some parts of digital systems. As follows, for example, from [14], Mealy FSMs are unstable. This means that input fluctuations result in output fluctuations. The output fluctuations can cause operation failure in a digital system. Output stabilization can be achieved due to using a synchronous input register (AIR) [19]. The following is a principle of interaction of an FSM and other digital system blocks (Figure 11).

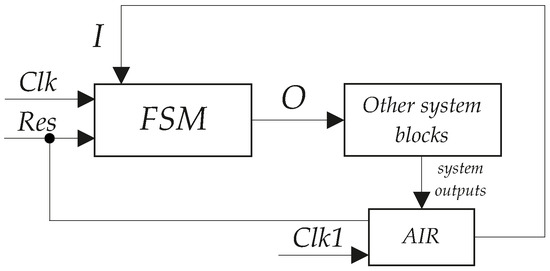
Figure 11. Interaction of FSM with other system blocks.

The system outputs are treated as FSM inputs forming the set I. As long as there are transients in the digital system, the synchronization signal Clk1 is equal to zero. This actually disconnects the FSM from other system blocks. When system outputs are stable, they are loaded into the AIR. Due to this, fluctuations in the system outputs do not affect the FSM output values. Of course, there is some overhead connected with this approach. Obviously, AIR consumes additional resources of the FPGA fabric. It also consumes some additional power and increases the value of FSM cycle time. Therefore, we took into account this overhead in our research.

In experiments, we use the Virtex-7 VC709 Evaluation Platform (xc7vx690tffg1761-2) [38]. Its FPGA chip xc7vx690tffg1761-2, produced by AMD Xilinx, is a base for implementing FSM circuits. For LUTs of this chip, there is $S_L=6$. The step of technology mapping is executed by the CAD tool Vivado v2019.1 (64-bit) [47]. To create tables with experimental results, we use data from the reports produced by Vivado. The VHDL-based FSM models are used to connect the benchmarks with Vivado. We use the CAD tool K2F [10] to create VHDL codes corresponding to initial KISS2-based benchmark files.

From the Vivado reports, we have derived the following characteristics of $P_{2T}Y$ Mealy FSM circuits: the number of LUTs (LUT count), value of cycle time, maximum operating frequency, and power consumption. As a basis for comparison, we have chosen four different FSMs. They are the following: 1. P Mealy FSMs with MBCs produced by the Auto method of Vivado; 2. P Mealy FSMs with one-hot state codes produced by the One-Hot method of Vivado; 3. JEDI-based P Mealy FSMs; and 4. $P_{T}Y$-based FSMs with twofold state assignment [20]. We did not compare $P_{2T}Y$ and PY Mealy FSMs. This is because $P_{T}Y$ FSMs have better characteristics than equivalent PY Mealy FSMs [20]. Therefore, if the proposed approach allows for improving characteristics compared to $P_{T}Y$, then the results obtained will obviously be better than the results for equivalent PY Mealy FSMs.

As follows from [19,42], the values of LUT counts and other LUT-based FSM circuits’ characteristics strongly depend on the relation between the values of $L+R1$ and $S_L$. In the discussed case, there is $S_L=6$. The benchmarks used have 5 complexity levels (C0–C4). These levels are determined in the following order. The benchmarks have the level C0 if $R1+L\le 6$. The level C0 determines trivial FSMs. The benchmarks have the level C1 if $6<R1+L\le 12$. The level C1 determines simple FSMs. The benchmarks have the level C2 if $12<R1+L\le 18$. The level C2 determines average FSMs. The benchmarks have the level C3 $18<R1+L\le 24$. The level C3 determines big FSMs. The benchmarks have the level C4 if $R1+L>24$. The level C4 determines very big FSMs.

The results of experiments are shown in Table 7 (the LUT counts), Table 8 (the minimum cycle times), Table 9 (the maximum operating frequencies), and Table 10 (the consumed power). There is a similar organization for each of these tables. Benchmark names are in the table rows. The investigated methods are shown in the table columns. The complexity of a particular benchmark is shown in the last column. The row “Sum” includes results of summation for corresponding columns. In the row “Percentage”, we show the percentage of the summarized characteristics of various FSM circuits with respect to $P_{2T}Y$-based FSMs.

Table 7. Experimental results (LUT counts).

Benchmark	Auto	One-Hot	JEDI	$\mathit{PTY}$	Our Approach	Complexity
bbara	21	21	14	13	12	C1
bbsse	40	44	31	26	22	C1
bbtas	7	7	7	10	10	C0
beecount	22	22	17	13	11	C1
cse	47	73	43	35	31	C1
dk14	19	30	13	13	11	C1
dk15	18	19	15	11	10	C1
dk16	17	36	14	12	12	C1
dk17	7	14	7	10	10	C0
dk27	4	6	5	9	9	C0
dk512	11	11	10	12	12	C0
donfile	33	33	26	21	17	C1
ex1	79	83	62	47	44	C2
ex2	11	11	10	10	9	C1
ex3	11	11	11	12	12	C0
ex4	21	19	18	14	12	C1
ex5	11	11	11	12	12	C0
ex6	29	41	27	24	20	C1
ex7	6	7	6	6	6	C1
keyb	50	68	47	41	38	C1
kirkman	54	70	51	40	35	C2
lion	4	7	4	7	7	C0
lion9	8	13	7	9	9	C0
mark1	28	28	25	21	18	C1
mc	7	10	7	9	9	C0
modulo12	8	8	8	10	10	C0
opus	33	33	27	24	20	C1
planet	138	138	95	80	76	C2
planet1	138	138	95	80	76	C2
pma	102	102	94	81	73	C2
s1	73	107	69	60	54	C2
s1488	132	139	116	93	89	C2
s1494	134	140	118	101	92	C2
s1a	57	89	51	43	39	C2
s208	23	42	21	19	16	C2
s27	10	22	10	9	9	C1
s386	33	46	29	23	19	C1
s420	29	50	28	24	20	C4
s510	67	67	51	44	38	C4
s820	13	13	13	11	10	C1
s832	106	100	86	72	67	C4
s840	98	97	80	70	62	C4
sand	143	143	125	107	101	C3
shiftreg	3	7	3	8	8	C0
sse	40	44	37	31	27	C1
styr	102	129	90	78	73	C2
tma	52	46	46	37	32	C2
Sum	2099	2395	1780	1542	1409
Percentage, %	148.97	169.98	126.33	109.44	100.00

Table 8. Experimental results (cycle time in nanoseconds).

Benchmark	Auto	One-Hot	JEDI	$\mathit{PTY}$	Our Approach	Complexity
bbara	8.811	8.811	8.352	9.394	9.601	C1
bbsse	10.096	9.642	9.213	9.763	9.924	C1
bbtas	8.497	8.497	8.451	9.497	9.497	C0
beecount	9.605	9.605	8.941	9.568	9.740	C1
cse	10.558	9.840	9.343	9.570	9.764	C1
dk14	8.821	9.395	8.762	9.964	9.070	C1
dk15	8.797	8.998	8.735	9.890	9.009	C1
dk16	9.491	9.320	8.672	9.327	9.539	C1
dk17	8.617	9.587	8.617	9.617	9.617	C0
dk27	8.325	8.424	8.369	9.325	9.325	C0
dk512	8.566	8.566	8.477	9.566	9.566	C0
donfile	9.033	9.034	8.509	7.916	7.628	C1
ex1	10.425	10.955	9.454	8.496	8.496	C2
ex2	8.635	8.635	8.596	9.566	9.738	C1
ex3	8.731	8.731	8.707	9.731	9.731	C0
ex4	9.214	9.315	8.874	9.745	9.902	C1
ex5	9.147	9.147	9.119	10.147	10.147	C0
ex6	9.564	9.772	9.330	9.701	9.863	C1
ex7	8.598	8.578	8.584	9.582	9.751	C1
keyb	10.121	10.699	9.666	10.063	10.174	C1
kirkman	10.971	10.392	10.280	10.621	10.300	C2
lion	8.539	8.501	8.541	9.595	9.595	C0
lion9	8.470	8.998	8.444	9.427	9.427	C0
mark1	9.825	9.825	9.343	9.942	10.063	C1
mc	8.688	8.719	8.682	9.688	9.688	C0
modulo12	8.302	8.302	8.299	9.302	9.302	C0
opus	9.684	9.684	9.275	10.290	10.353	C1
planet	11.264	11.264	9.073	9.897	9.791	C2
planet1	11.264	11.264	9.073	9.897	9.791	C2
pma	10.634	10.634	9.681	10.015	9.963	C2
s1	10.623	11.154	10.156	10.669	10.308	C2
s1488	11.013	11.372	10.155	10.314	10.299	C2
s1494	10.487	10.654	9.878	10.630	10.163	C2
s1a	10.313	9.462	9.704	10.385	10.185	C2
s208	9.503	9.434	9.361	9.859	9.684	C2
s27	8.672	8.862	8.662	9.671	9.832	C1
s386	9.676	9.494	9.311	9.905	10.198	C1
s420	9.864	9.780	9.755	9.719	9.632	C4
s510	9.742	9.742	9.155	9.689	9.115	C4
s820	10.691	10.641	9.775	10.317	10.416	C1
s832	10.975	10.638	9.866	9.697	9.233	C4
s840	9.195	9.228	9.158	9.108	9.032	C4
sand	12.390	12.390	11.652	10.995	10.895	C3
shiftreg	8.302	7.265	7.091	8.802	8.802	C0
sse	10.096	9.642	9.455	10.165	10.260	C1
styr	11.067	11.497	10.666	11.540	11.646	C2
tma	9.831	10.495	9.821	10.247	10.197	C2
Sum	453.73	454.88	431.08	460.81	458.25
Percentage, %	99.01	99.27	94.07	100.56	100.00

Table 9. Experimental results (maximum operating frequency in MHz).

Benchmark	Auto	One-Hot	JEDI	$\mathit{PTY}$	Our Approach	Complexity
bbara	113.496	113.496	119.727	106.456	104.152	C1
bbsse	99.049	103.713	108.539	102.428	100.766	C1
bbtas	117.687	117.687	118.336	105.295	105.295	C0
beecount	104.112	104.112	111.839	104.520	102.669	C1
cse	94.713	101.626	107.030	104.488	102.422	C1
dk14	113.364	106.439	114.134	100.361	110.248	C1
dk15	113.675	111.137	114.487	101.111	111.002	C1
dk16	105.362	107.294	115.316	107.219	104.835	C1
dk17	116.049	104.308	116.049	103.982	103.982	C0
dk27	120.122	118.709	119.494	107.240	107.240	C0
dk512	116.740	116.740	117.963	104.537	104.537	C0
donfile	110.706	110.696	117.517	126.323	131.093	C1
ex1	95.922	91.281	105.777	117.700	117.700	C2
ex2	115.808	115.808	116.340	104.540	102.692	C1
ex3	114.536	114.536	114.846	102.766	102.766	C0
ex4	108.530	107.352	112.690	102.621	100.991	C1
ex5	109.327	109.327	109.661	98.553	98.553	C0
ex6	104.556	102.333	107.183	103.082	101.394	C1
ex7	116.306	116.576	116.495	104.364	102.550	C1
keyb	98.806	93.466	103.453	99.375	98.291	C1
kirkman	91.148	96.232	97.272	94.152	97.084	C2
lion	117.110	117.634	117.083	104.226	104.226	C0
lion9	118.065	111.136	118.421	106.080	106.080	C0
mark1	101.781	101.781	107.032	100.585	99.372	C1
mc	115.102	114.694	115.174	103.221	103.221	C0
modulo12	120.454	120.454	120.498	107.505	107.505	C0
opus	103.265	103.265	107.818	97.181	96.590	C1
planet	88.777	88.777	110.222	101.038	102.132	C2
planet1	88.777	88.777	110.222	101.038	102.132	C2
pma	94.039	94.039	103.293	99.855	100.375	C2
s1	94.134	89.653	98.465	93.731	97.009	C2
s1488	90.800	87.934	98.472	96.960	97.101	C2
s1494	95.357	93.861	101.236	94.074	98.396	C2
s1a	96.963	105.687	103.048	96.297	98.188	C2
s208	105.231	106.000	106.825	101.426	103.260	C2
s27	115.314	112.842	115.449	103.400	101.705	C1
s386	103.348	105.329	107.401	100.964	98.059	C1
s420	101.378	102.249	102.514	102.891	103.822	C4
s510	102.648	102.648	109.226	103.205	109.704	C4
s820	93.537	93.975	102.300	96.932	96.006	C1
s832	91.117	94.001	101.354	103.126	108.309	C4
s840	108.755	108.364	109.196	109.795	110.717	C4
sand	80.711	80.711	85.821	90.949	91.784	C3
shiftreg	120.454	137.645	141.028	113.612	113.612	C0
sse	99.049	103.713	105.760	98.375	97.468	C1
styr	90.359	86.979	93.754	86.657	85.867	C2
tma	101.719	95.284	101.819	97.588	98.065	C2
Sum	4918.26	4910.30	5157.58	4811.82	4840.96
Percentage, %	101.60	101.43	106.54	99.40	100.00

Table 10. Experimental results (consumed power in watts).

Benchmark	Auto	One-Hot	JEDI	$\mathit{PTY}$	Our Approach	Complexity
bbara	0.961	0.961	0.880	0.898	0.911	C1
bbsse	2.651	1.637	2.144	2.228	2.243	C1
bbtas	0.900	0.900	0.900	0.923	0.923	C0
beecount	2.011	2.011	1.401	1.489	1.497	C1
cse	1.389	1.450	1.322	1.346	1.362	C1
dk14	3.339	3.710	3.332	3.341	3.368	C1
dk15	1.783	2.285	1.779	1.772	1.788	C1
dk16	3.334	3.109	2.879	2.881	2.895	C1
dk17	2.268	2.302	2.258	2.286	2.286	C0
dk27	1.524	1.210	1.514	1.539	1.539	C0
dk512	1.852	1.852	1.701	1.743	1.743	C0
donfile	1.076	1.076	0.970	0.992	1.034	C1
ex1	4.564	3.430	2.804	2.612	2.688	C2
ex2	0.735	0.753	0.709	0.698	0.712	C1
ex3	0.758	0.758	0.758	0.798	0.798	C0
ex4	1.980	1.659	1.605	1.625	1.641	C1
ex5	0.754	0.754	0.752	0.775	0.775	C0
ex6	2.675	4.256	2.648	2.673	2.691	C1
ex7	1.359	1.548	1.361	1.382	1.412	C1
keyb	1.524	1.502	1.506	1.528	1.541	C1
kirkman	2.204	2.355	1.950	1.854	1.892	C2
lion	0.909	0.996	0.914	0.953	0.953	C0
lion9	1.100	1.337	1.095	1.112	1.112	C0
mark1	1.851	1.851	1.633	1.661	1.683	C1
mc	0.827	0.941	0.823	0.863	0.863	C0
modulo12	0.915	0.915	0.919	0.941	0.941	C0
opus	1.750	1.750	1.689	1.708	1.734	C1
planet	4.553	4.553	2.887	2.914	3.121	C2
planet1	4.553	4.553	2.887	2.914	3.121	C2
pma	1.818	1.818	1.701	1.726	1.747	C2
s1	3.133	3.578	2.966	3.089	3.118	C2
s1488	4.430	4.544	3.996	4.001	4.108	C2
s1494	3.527	3.626	3.430	3.523	3.596	C2
s1a	1.770	2.458	1.656	1.672	1.689	C2
s208	1.858	3.311	1.740	1.769	1.784	C2
s27	1.148	2.342	1.157	1.164	1.183	C1
s386	1.682	1.824	1.552	1.571	1.593	C1
s420	1.960	3.443	1.909	1.812	1.861	C4
s510	2.166	2.166	1.714	1.643	1.685	C4
s820	1.128	1.197	1.124	1.142	1.151	C1
s832	2.662	2.409	2.071	1.915	1.932	C4
s840	2.704	2.695	2.436	2.264	2.283	C4
sand	1.640	1.640	1.479	1.421	1.443	C3
shiftreg	0.879	0.959	0.868	0.899	0.899	C0
sse	1.651	1.727	1.520	1.543	1.561	C1
styr	4.506	5.233	3.649	3.721	3.751	C2
tma	2.020	1.745	1.752	1.781	1.803	C2
Sum	96.78	103.13	84.74	85.11	86.45
Percentage, %	111.95	119.29	98.02	98.44	100.00

From Table 7, we can find that, compared to other investigated methods, the circuits of $P_{2T}Y$-based FSMs consume a minimum number of LUTs. The proposed approach provides the following gain: 1. 48.97% regarding the Auto-based FSMs; 2. 69.98% regarding the One-Hot-based FSMs; 3. 26.33% regarding the JEDI-based FSMs; and 4. 9.44% regarding the $P_{T}Y$-based FSMs. In our opinion, this gain is associated with a decrease in the amount of transformed state codes compared to $P_{T}Y$-based FSMs. Due to this, the LUT count in LUTerASV is less than 1 for the code transformer of equivalent $P_{T}Y$-based FSMs. Additionally, the gain can be achieved due to reducing the cardinality number of the partition of states. The fulfillment of the condition $(J+1)<K$ provides a decrease in the required number of LUT inputs for elements of LUTerFA compared to that of the LUTs of LUTerPF. This phenomenon can lead to a decrease in the LUT count.

The following phenomenon is clear from Table 7: if an FSM has the complexity C0, then there are the same LUT counts for equivalent FSMs based on collection encoding. Moreover, in this case, other FSMs have better values of LUT counts than $P_{T}Y$- and $P_{2T}Y$-based FSMs. We can explain this in the following way. If an FSM has the complexity C0, then the condition (4) takes place. In this case, each SOP (2) and (3) is implemented by a single LUT. Therefore, in this case, there is no need to use various structural decomposition methods. However, regardless of the validity of condition (4), the encoding of output collections is executed for both $P_{T}Y$- and $P_{2T}Y$-based FSMs. As a result of this, the block LUTerOF is used. This block consumes additional LUTs compared to other researched methods. Due to validity of (4), there are no partial functions for FSMs having the complexity C0. As a result, there is no need to assemble blocks (LUTerFA and LUTerPF). This means that both $P_{T}Y$ and $P_{2T}Y$ FSMs degenerate into equivalent PY FSMs.

Now, let us analyze the temporal characteristics of FSM circuits. They are represented in Table 8 (the cycle time measured in nanoseconds) and Table 9 (the maximum operating frequency measured in megahertz).

Analysis of Table 8 shows that JEDI-based FSMs are the fastest. It also shows that $P_{T}Y$-based FSMs are marginally slower than circuits of $P_{2T}Y$-based FSMs (the average loss is 0.56%). At the same time, the proposed approach generates circuits with worse time characteristics than the circuits of P FSMs. The Auto-based FSMs are 0.09% faster than the $P_{2T}Y$-based FSMs. The One-Hot-based FSMs are 0.73% faster than the $P_{2T}Y$-based FSMs. Finally, JEDI-based FSMs are 5.93% faster than $P_{2T}Y$-based FSMs. If the FSM complexity exceeds C0, then both $P_{T}Y$- and $P_{2T}Y$-based FSMs have three-level circuits. At the same time, it is difficult to estimate a priori the number of logic levels in circuits of P FSMs. It all depends on the number of literals in the implemented sum-of-products.

As follows from Table 8, if FSM complexity is equal to C0, then cycle times are the same for equivalent $P_{2T}Y$- and $P_{T}Y$-based FSMs. This phenomenon takes place because, in this case, both $P_{2T}Y$- and $P_{T}Y$-based FSMs turn into PY FSMs. However, if we look at the most complex FSMs having the complexity C4, we will see that the proposed method allows for obtaining the fastest circuits. Thus, the performance of $P_{2T}Y$ FSMs becomes better and better as the synthesized FSMs become more complex.

As follows from Table 9, an average, the circuits of $P_{2T}Y$ FSMs are slower compared to circuits of P-based FSMs. Our approach loses 1.6% to Auto-based FSMs. It loses 1.43% to One-Hot–based FSMs. The JEDI-based FSMs have the greatest gain (6.54%). Only $P_{T}Y$-based FSMs are a bit slower than $P_{2T}Y$-based FSMs. Obviously, the reasons for the loss in frequency are the same as the reasons for the loss in cycle time. Additionally, analysis of Table 9 shows that, starting with complexity level C2, our method allows us to produce faster circuits compared to other methods under study.

It is known [48] that one of the most important characteristics of FSM circuits is their power consumption. In particular, it is important in the case of mobile and autonomous cyber-physical systems [49]. Very often, a designer should make the choice among the area-temporal characteristics and the power consumption of a particular device. The values of power consumption can be taken from the Vivado reports. The power consumption is measured for the maximum possible value of the operating frequency. We show the experimental results for power consumption in Table 10.

The proposed method reduces the numbers of LUTs in FSM circuits compared with this characteristic of equivalent $P_{T}Y$-based FSMs. Very often, such improvement results in an increase in power consumption [19]. This phenomenon takes place for our method. However, as follows from comparison of $P_{T}Y$- and $P_{2T}Y$-based FSMs (Table 10), $P_{T}Y$ FSMs have a very small gain in power consumption. Compared to $P_{T}Y$-based FSMs, the loss in power consumption averages 1.55%. Additionally, JEDI-based FSMs require less power than equivalent $P_{2T}Y$ FSMs. The proposed approach allows for obtaining FSM circuits with less power consumption than for both Auto-based FSMs (11.95% of gain) and One-Hot-based FSMs (19.29% of gain).

If FSMs have complexity C0, then both $P_{T}Y$ and $P_{2T}Y$ FSMs have equal values of power consumption. If the FSM complexity exceeds C0, then $P_{T}Y$ FSMs always require less power than equivalent $P_{2T}Y$ FSMs. We see the following reason for this situation. In $P_{T}Y$ FSMs, the state variables enter only block LUTerASV. In contrast to this, in $P_{2T}Y$ FSMs, the outputs of LUTerFA are connected with two blocks (LUTerASV and CoreFC). It is known [31] that interconnections consume up to 70% of power. Therefore, the more interconnections, the more power is consumed.

Let us sum up some results of the comparison of equivalent $P_{T}Y$ and $P_{2T}Y$ FSMs. If FSMs have complexity C0, then there are the same values of basic characteristics for both models. For other levels of complexity, $P_{2T}Y$ FSMs have better spatial characteristics (the required FPGA chip area) than they do in their single-core counterparts based on twofold state assignment. For rather simple FSMs, $P_{T}Y$ FSMs have better temporal characteristics. However, as the complexity increases, the cycle times (and maximum operating frequencies) of $P_{2T}Y$ FSMs gradually become better than in their single-core counterparts. The FSM circuits based on the proposed method always require more power. However, this loss is very small (it does not exceed 2% on average). This comparison leads to the following conclusion: $P_{2T}Y$ FSMs should be used instead of $P_{T}Y$ FSMs if the required chip area is the main optimality criterion of designed LUT-based circuits. This conclusion is supported by diagrams shown in Figure 12.

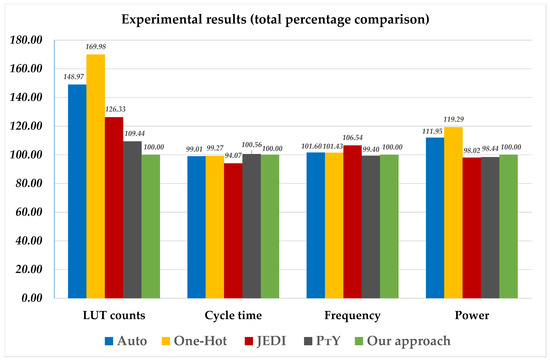
Figure 12. Percent summary of results.

Under certain conditions, the proposed method can be applied to implement the LUT-based circuit of any sequential block. In this case, neither the algorithm for the functioning of this block nor the scope of the digital system in which this block operates is important. The possibility of applying the model of $P_{2T}Y$ FSM depends on the distribution of inputs $i_l\in I$ between the states $s_m\in S$. If this distribution leads to the fulfillment of condition (4), then there is no need for optimization (because the circuit of P FSM has the best possible characteristics). If condition (4) is violated but the distribution leads to the fulfillment of condition (10), then the method can be applied. Otherwise, it is impossible to find a partition of the set of states for which each partial function is represented by a single-LUT circuit. The proposed method can be applied only if condition (18) is satisfied for some states $s_m\in S$. In this case, the corresponding partial functions depending on the state variables $T_r\in SV$ are implemented using single-LUT circuits. The more states that satisfy condition (18), the greater the gain from applying our method compared to using $P_{T}Y$ FSMs. However, if condition (18) is satisfied for all states, then there is no point in applying either $P_{2T}Y$ or $P_{T}Y$ FSMs. In this case, both of these models degenerate into a PY FSM. Thus, it is advisable to use the proposed method only if condition (18) is satisfied for a number of states (but not for all M states), and condition (10) for the rest.

7. Generalized FSM Architecture

Unfortunately, there is a condition where the proposed method cannot be applied. For a given FSM, let the set of states include at least a single state $s_m\in S$ for which the following condition is satisfied:

$$L\left(s_m\right)\ge S_L.$$

(35)

It is obvious that the state satisfying condition (35) cannot be included in either set $S^0$ or set S1. To obtain partial functions generated during transitions from this state, it is necessary to apply the methods of functional decomposition. Thus, to take into account the presence of such states, it is necessary to introduce a CoreFD based on functional decomposition into the architecture of $P_{2T}Y$ FSM shown in Figure 5.

We propose to split the set S by three disjoint sets ($S^0$, $S2$, $S3$). The set $S^0\subseteq S$ includes states satisfying condition (18). The set $S3\subseteq S$ includes states satisfying condition (35). The set $S2\subseteq S$ includes the rest of the states, i.e., $S2=S/(S^0\cup S3)$. The transitions from states $s_m\in S3$ are determined by FSM inputs creating the set I3. To encode these states, it is necessary to create the set of state variables ASV3. This set includes its own unique state variables. Three sets of PBFs are generated by LUTs of CoreFD: $D^F$ (IMFs generated during the transitions from states $s_m\in S3$); $A{V}^F$ (additional variables encoding the OCs generated during the transitions from states $s_m\in S3$); and AV3 (unique additional variables encoding the OCs generated during the transitions from states $s_m\in S3$). Therefore, the following partial SBFs are generated by LUTs of CoreFD:

$$D^F=D^F(ASV3,I3);$$

(36)

$$AV3=AV3(ASV3,I3);$$

(37)

$$A{V}^F=A{V}^F(ASV3,I3).$$

(38)

We denoted as $P_{F2T}Y$ the proposed generalized architecture of the LUT-based FSM circuit. Here the letter “F” means the presence of the block CoreFD. The proposed generalized architecture is shown in Figure 13.

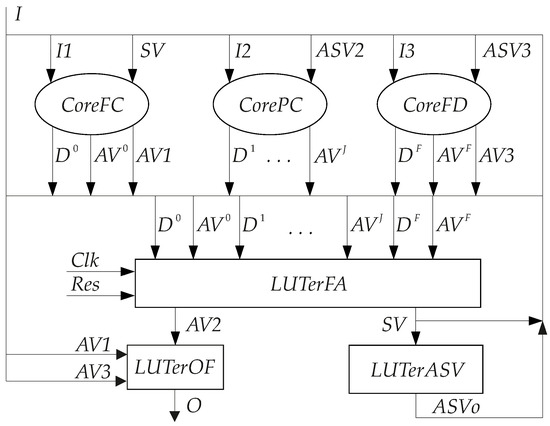
Figure 13. Generalized architecture of $P_{F2T}Y$ Mealy FSM.

The generalized architecture (Figure 13) includes three cores of PBFs. CoreFC generates PBFs for states satisfying condition (18). CoreFD generates PBFs for states satisfying condition (35). CorePC generates PBFs for the rest of the states.

In the $P_{F2T}Y$ FSM, LUTerFA generates the full functions represented by the following systems of disjunctions:

$$D=D(D^0,D^1,...,D^J,D^F);$$

(39)

$$AV2=AV2(A{V}^0,A{V}^1,...,A{V}^J,A{V}^F).$$

(40)

LUTerOF implements SBF (7). However, now the set AV is represented in the following form: $AV=AV1\cup AV2\cup AV3$. To encode the states of a $P_{F2T}Y$ FSM, the set $AS{V}_0$ is used, where $AS{V}_0=SV\cup ASV2\cup ASV3$. Therefore, LUTerASV generates the SBF:

$$AS{V}_0=AS{V}_0\left(SV\right).$$

(41)

Naturally, the proposed architecture is universal. In this paper, we propose the following method for synthesizing an FSM with a generalized architecture:

• Creating an STT of a P Mealy FSM.
• Pre-formation of sets $S^0$, S2, and S3.
• Pre-formation of partition ${\pi }_{S2}$ of set S2.
• Final formation of sets $S^0$ and S2 and partition ${\pi }_{S2}$.
• Creating full state codes $FC\left(s_m\right)$ for states $s_m\in S$.
• Encoding of output collections $O_q\subseteq O$ and finding SBF (7).
• Creating a table of CoreFC and deriving SBFs (19)–(21).
• Encoding of states $s_m\in S^j$ by partial state codes $PC\left(s_m\right)$.
• Generating tables describing the blocks of CorePC and deriving systems (22) and (23).
• Encoding of states $s_m\in S3$ by partial state codes $PC\left(s_m\right)$.
• Generating tables describing the blocks of CoreFD and deriving systems (36)–(38).
• Creating a table of LUTerFA and SBFs (39) and (40).
• Creating a table of LUTerASV and system (41).
• Implementing a $P_{F2T}Y$ Mealy FSM circuit using internal resources of a particular FPGA chip.

We hope that all the presented steps of this method are clear from the previous text. We do not, however, consider this method in detail. This will be the subject of a separate study. Now we will show that the generalized architecture (Figure 13) generates 6 more architectures. Three conditions are used for this purpose. The fulfillment of condition (18) indicates the presence of the block CoreFC in the FSM circuit architecture. This means that the set $S^0$ contains at least one element. The fulfillment of condition (35) indicates the presence of the block CoreFD. In this case, the set S3 contains at least one element. Finally, the fulfillment of the condition

$$S_L>L\left(s_m\right)>S_L-R1$$

(42)

indicates the presence of the block CorePC. In this case, the set S2 contains at least one element. We show the possible FSM models in Table 11. Additionally, the table rows contain conditions (or their conjunctions) in which a particular architecture should be used.

Table 11. Possible FSM models.

${\mathit{S}}^0$	$\mathit{S}2$	$\mathit{S}3$	Model	Conditions
FC	PC	FD
0	0	1	$P_{F}Y$	(35)
0	1	0	$P_{T}Y$	(42)
0	1	1	$P_{FT}Y$	(35) and (42)
1	0	0	$PY$	(18)
1	0	1	$P_{FF}Y$	(18) and (35)
1	1	0	$P_{2T}Y$	(18) and (42)
1	1	1	$P_{F2T}Y$	(18), (35), and (42)

The first three columns of the table contain the names of the sets ($S^0$, $S2$, $S3$) and corresponding architectural blocks (CoreFC, CorePC, CoreFD). The fourth column contains the model designation. The fifth column shows which combination of conditions leads to the model from a particular row. If there is a zero (one) at the intersection of the column with the block and the row with the model, then this block is not included (is included) in the FSM architecture corresponding to this row.

For example, if all states satisfy condition (35), then the architecture includes only CoreFD. We denote this architecture by the symbol $P_{F}Y$. This is the first row of Table 11. If some of states satisfy condition (35) and others satisfy condition (42), then the architecture includes blocks CorePC and CoreFD (row 3). This leads to $P_{FT}Y$ FSMs, and so on. The last row corresponds to the generalized FSM architecture, including three cores of partial functions.

Using Table 11 and generalized architecture, we can obtain the architecture for any model represented by this table. Obviously, it is possible to transform the design method for $P_{F2T}Y$ FSMs into a design method for any other model. In this case, of particular interest is the implementation of Step 2 of the proposed method and the definition of a model corresponding to its outcome. We have presented the algorithm for performing these steps in Figure 14.

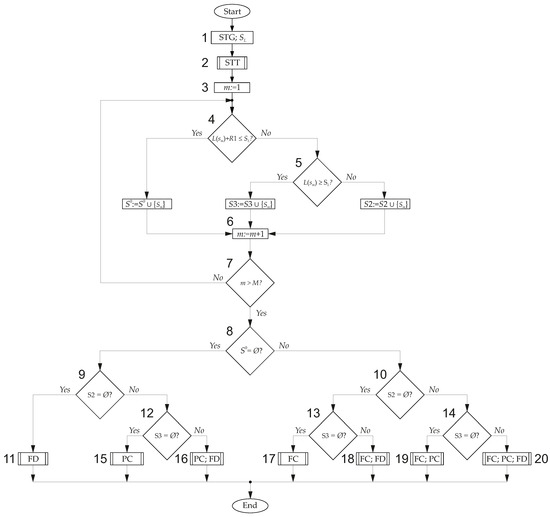
Figure 14. Selection of FSM model.

Let us consider this algorithm. Block 1 shows the initial information (FSM is represented by STG and the FPGA chip is represented by the number of inputs of the LUT element). Next, this STG must be converted to the equivalent STT (block 2).

The distribution of states over sets $S^0,S2,S3$ is performed in a cycle, including blocks 3–7. The distribution starts from the first state (block 3). In block 4, condition (18) is checked. If this condition is met (output “Yes” from block 4), then the state $s_m\in S$ is placed in set $S^0$ (block FC). If this condition is violated (output “No” from block 4), then condition (42) is checked (block 5). If this condition is met (output “Yes” from block 5), then the state $s_m\in S$ is placed in set S3 (block FD). If this condition is violated (output “No” from block 5), then the state $s_m\in S$ is placed in set S2 (block PC). The analysis of the next state begins (block 6). If all states are distributed (output “Yes” from block 7), then the FSM architecture selection begins (transition to block 8). Otherwise (output “No” from block 7), the analysis continues (transition to block 4).

To choose an architecture, we analyze whether empty sets are obtained in the process of distributing states. The analysis begins with checking the set $S^0$ (block 8). As follows from Table 11, if the set $S^0$ is empty (output “Yes” from block 8), then the choice is made among three architectures ($P_{F}Y$, $P_{T}Y$, $P_{FT}Y$). Set S2 is analyzed (block 9). If it is empty (output “Yes” from block 9), then the FSM $P_{F}Y$ is selected (block 11). If set S2 is not empty (output “No” from block 9), then set S3 is analyzed (block 12). If it is empty (output “Yes” from block 12), then the FSM $P_{T}Y$ is selected (block 15). If set S3 is not empty (output “No” from block 12), then the FSM $P_{FT}Y$ is selected (block 16).

If the set $S^0$ is not empty (output “No” from block 8), then the choice is made among four architectures ($PY$, $P_{FF}Y$, $P_{2T}Y$, $P_{F2T}Y$). Set S2 is analyzed (block 10). If it is empty (output “Yes” from block 10), then set S3 is analyzed (block 13). If S3 is empty (output “Yes” from block 13), then the FSM PY is selected (block 17). If S3 is not empty (output “No” from block 13), then the FSM $P_{FF}Y$ is selected (block 18). If set S2 is not empty (output “No” from block 10), then set S3 is analyzed (block 14). If S3 is empty (output “Yes” from block 14), then the FSM $P_{2T}Y$ is selected (block 19). If S3 is not empty (output “No” from block 14), then the FSM $P_{F2T}Y$ is selected (block 20).

Thus, the architecture has been chosen, and it is necessary to proceed to the synthesis of the corresponding FSM model. We hope that the relationship between Table 11 and the algorithm (Figure 14) is transparent enough.

8. Conclusions

Modern FPGAs are widely used in the design of cyber-physical systems [13]. These chips are very powerful: a single FPGA chip is enough for implementing practically any block (either combinational or sequential) of modern CPSs [50]. The reverse side of the FPGA universality is an extremely small number of LUT inputs [21,51]. This is a serious drawback that significantly complicates the design process. As a result, various methods of functional decomposition should be applied in the step of technology mapping. It is known that FD-based circuits are multi-level. The disadvantages of layered circuits are well known: they are slower and less energy efficient than equivalent single-level counterparts.

Better results can be obtained by replacing the functional decomposition with the structural one [10]. This is proved, for example, in the work [19]. In the paper [20], the FSM circuit optimization is achieved due to using the twofold state assignment and encoding of output collections. The resulting $P_{T}Y$ FSM circuits have better values of LUT counts than their FD-based counterparts. However, the twofold state assignment is connected with the transformation of maximum binary state codes into their extended equivalents. As a result, a code transformer should be used that consumes some additional resources of the FPGA fabric.

To reduce the LUT count in the circuits of $P_{T}Y$-based FSMs, we propose to use two LUT-based blocks (cores). To do this, we use the main ideas from the paper [22]. Both cores generate systems of partial Boolean functions. This leads to $P_{2T}Y$ FSMs having the following peculiarity: one of the cores uses the MBCs, whereas the second core uses the partial state codes. Our approach reduces LUT counts and slightly improves temporal characteristics as compared to equivalent $P_{T}Y$-based FSMs. The overhead of the proposed method is a rather insignificant increase in consumption of power (up to 1.56% on average). We hope the proposed $P_{2T}Y$ FSMs can function as an efficient tool for implementing FPGA-based sequential devices in modern cyber-physical systems.

The conducted experiments have shown that, under certain conditions, the proposed method allows for better results than methods based entirely on either maximum binary or one-hot state codes. If some partial functions are implemented using a single LUT, then our method allows for improving the spatial, temporal, and energy characteristics of the LUT-based circuits of sequential blocks. We think that our method can be modified to take into account the use of state assignment methods other than the twofold one. In this, we see the further directions for the proposed method development.

Under certain conditions, the transition from the proposed model to other models is possible (Table 11). In the most general case, the FSM architecture consists of three cores of partial functions. There are also three dual-core architectures. One of the directions of our further research is the development of synthesis methods and the study of the characteristics of LUT-based FSM circuits based on these two- and three-core models.