Abstract
In modern information technology systems, secure storage and transmission of personal and sensitive data are recognized as important tasks. These requirements are achieved through secure and robust encryption methods. Argon2 is an advanced cryptographic algorithm that emerged as the winner in the Password Hashing Competition (PHC), offering a concrete and secure measure. Argon2 also provides a secure mechanism against side-channel attacks and cracking attacks using parallel processing (e.g., GPU). In this paper, we analyze the existing GPU-based implementation of the Argon2 algorithm and further optimize the implementation by improving the performance of the hashing function during the computation process. The proposed method focuses on enhancing performance by distributing tasks between CPU and GPU units, reducing the data transfer cost for efficient GPU-based parallel processing. By shifting several stages from the CPU to the GPU, the data transfer cost is significantly reduced, resulting in faster processing times, particularly when handling a larger number of passwords and higher levels of parallelism. Additionally, we optimize the utilization of the GPU’s shared memory, which enhances memory access speed, especially in the computation of the hash value generation process. Furthermore, we leverage the parallel processing capabilities of the GPU to perform efficient brute-force attacks. By computing the H function on the GPU, the proposed implementation can generate initial blocks for multiple inputs in a single operation, making brute-force attacks in an efficient way. The proposed implementation outperforms existing methods, especially when processing a larger number of passwords and operating at higher levels of parallelism.
1. Introduction
Graphics Processing Units (GPUs) are processors with remarkable parallel processing capabilities that accelerate computations for large-scale data. Research based on this technology has received consistent attention and continues to progress as a field. The domain of research utilizing GPUs spans various areas and, among them, the investigation into password decryption has been an ongoing endeavor in recent years.
Chu-Hsing Lin et al. [1] conducted a study utilizing cloud computing and GPU parallel computing to find hash collisions in SHA-1, which is still widely used today. While SHA-1 is a popular hash function in the context of IoT, this research demonstrates the security vulnerabilities of SHA-1 and highlights the need for stronger hash functions. They implemented a simple hash value matching algorithm on the Hadoop cloud system and NVIDIA GeForce GTX650Ti GPU parallel system, measuring the execution time and speed based on various numbers of nodes and threads. To break the hash value of a 7-digit code word within a minute, approximately 110 physical computers (330 compute nodes) were required and the GTX650Ti GPU exhibited similar performance to 120 worker nodes. This indicates that SHA-1 is not secure in the era of cloud computing and GPU parallelization.
Ibrahim Alkhwaja et al. [2] evaluated the performance of parallel computing techniques in brute-force algorithms and dictionary attacks. To do so, they implemented password cracking programs using various languages and tools such as Python, C++, and hashcat, and analyzed the impact of hardware configurations (CPU, GPU, and CUDA) and character sets. The experimental results showed that parallel processing using GPUs and CUDA significantly improved the speed and accuracy of password cracking. This research provides valuable insights into the development of password cracking techniques and contributes to raising awareness about the vulnerabilities of passwords and potential ways to strengthen them.
Radek Hranický et al. [3] conducted a study on distributed password cracking using BOINC and hashcat. BOINC is a framework for network computing, while hashcat is a tool that utilizes GPUs to efficiently crack various hash algorithms. The paper proposes a strategy for effectively partitioning and allocating tasks based on hashcat’s different attack modes and introduces the Fitcrack system, which implements this strategy. Fitcrack features a user-friendly web interface called WebAdmin and utilizes the BOINC client along with Runner, a hashcat wrapper. Furthermore, a comparison between Fitcrack and another distributed cracking tool called Hashtopolis is presented to analyze the strengths and weaknesses of Fitcrack.
GPU-driven decryption techniques leverage parallel processing capabilities effectively, leading to impressive performance in the decryption process. This plays a pivotal role in detecting and addressing vulnerabilities in encryption algorithms.
In this paper, we perform the optimization of the Argon2 hashing function using GPUs. Argon2 is an advanced password hashing function that emerged as the winner in the Password Hashing Competition (PHC), and is regarded as a robust algorithm [4,5]. It is considered as the next-generation password hashing function and is expected to be widely used.
Argon2 provides a secure mechanism against cracking attacks [5,6]. Therefore, due to this mechanism, Argon2 does not show much efficiency in parallel implementations using GPUs. To compensate for this, I would like to propose an implementation using a more efficient GPU through task distribution of CPU and GPU. The contributions of this paper are as follows.
Contributions
Efficient Argon2 Implementation on GPU: The main contribution of this study is the development of a more efficient implementation of Argon2. We improved performance by utilizing both the CPU and GPU, and efficiently distributing tasks. By shifting the processing of several stages from the CPU to the GPU, we significantly reduced the data transfer cost. This new method resulted in faster processing times compared to previous implementations, particularly when dealing with a larger number of passwords and higher levels of parallelism than previous works.
GPU Shared Memory Utilization: The proposed approach optimally uses the GPU’s shared memory, which provides faster memory access. This is particularly beneficial in the computation of process, where a hash value is repeatedly generated until the desired output size is achieved.
GPU Parallel Processing for Brute-Force Attacks: Another significant contribution is leveraging the GPU’s parallel processing capabilities for efficient brute-force attacks. By performing the H function computation on the GPU, the proposed implementation can generate initial blocks for multiple inputs in a single operation, thus resulting in optimal brute-force attacks.
In-depth Performance Evaluation of Argon2: The performance evaluation reveals that our proposed implementation performs better than existing ones, especially when processing a larger number of passwords and at higher levels of parallelism than previous works.
2. Related Work
2.1. Password Hash Algorithm
Password hashing algorithms are important functions used in cryptography that take an input (or ‘plaintext’) and return a fixed-size string of bytes, typically a ‘digest’ that is unique for each unique input. Hash functions are deterministic, meaning that they always return the same output for the same input. Password hashing algorithms play a crucial role in maintaining the security of stored passwords. Instead of storing a user’s actual password, a system stores the hash of that password. During the login process, when a user enters their password, the system applies the hash function to this password and compares the result with the stored hashed password. If the two hashes match, the user is granted access. Well-designed password hashing algorithms possess several important characteristics. Firstly, it should be computationally difficult to compute the original input given only the hash output, a property known as ‘pre-image resistance’. Secondly, given a specific input and its hash, it should be computationally difficult to find a different input with the same hash, a property known as ‘second pre-image resistance’. Thirdly, it should be difficult to find two different inputs that produce the same hash output, a property known as ‘collision resistance’. Lastly, the algorithm should be able to use random data known as ‘salt’ as additional input, which prevents identical passwords from producing identical hash outputs and protects against attacks using pre-computed tables of hash outputs (rainbow tables [7]). Examples of password hashing algorithms include bcrypt, scrypt, Argon2, and PBKDF2 [6,8,9,10,11]. Among these, bcrypt and Argon2 are widely recommended because they include built-in salting and their computational cost makes brute-force attacks slower. Notably, Argon2 was the winner of the Password Hashing Competition in July 2015 and is considered the state-of-the-art technology.
2.2. Argon2
Argon2 [6] is one of the algorithms used for password hashing, with the purpose of transforming a user’s plaintext password into a hashed format. This algorithm is notably the winner of the Password Hashing Competition in 2015. Fundamentally, Argon2 has several configurable parameters that allow adjustments to CPU and memory usage. There are three variants of Argon2: Argon2d, Argon2i, and Argon2id.
- Argon2d maximizes data dependence to fortify resistance against parallel hardware such as GPUs. However, this variant can be sensitive to side-channel attacks.
- Argon2i, conversely, is designed to resist side-channel attacks, but may sacrifice some resistance against parallel hardware.
- Argon2id combines the two aforementioned approaches, operating like Argon2i in the early stages and like Argon2d in the subsequent stages. This hybrid aims to amalgamate the advantages of both and is currently the most broadly recommended variant.
One of Argon2’s most salient features is its ability to optimize both CPU and memory usage simultaneously, increasing the cost for attackers attempting brute-force attacks to guess the password. Furthermore, Argon2 uses unique salts, preventing hash collisions among users employing the same password. Salts are random values added to the password, modifying the process of hash generation; therefore, even with identical passwords, each user will generate a unique hash. This characteristic is crucial in thwarting precomputed hash attacks such as rainbow tables. Internally, the Argon2 algorithm consists of several stages, as depicted in Figure 1.
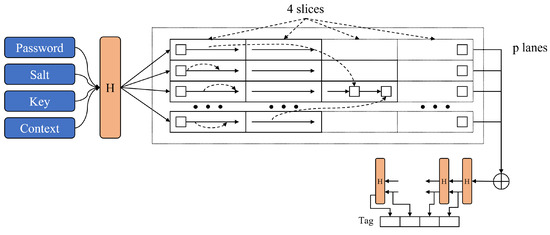
Figure 1.
Algorithm of Argon2.
- Initialization: The algorithm first creates an initial block using input values received from the user such as password, salt, and optionally provided secret data (associated data). This initial block fills a sequence of blocks using memory.
- Block Filling: The algorithm then populates these memory blocks up to the set memory amount. Each block’s computation depends on previous blocks, making this stage data-dependent. Argon2d and Argon2i take distinct approaches during this block-filling process.
- Final Block Creation: After filling all blocks, the algorithm selects one block as the final block.
- Hash Generation: Finally, the algorithm passes this final block to a hash function to generate the final password hash.
These stages work together to ensure the security and strength of the password hashing process in Argon2. By utilizing memory-hard operations and data dependence, Argon2 aims to make password cracking attempts more computationally expensive and time-consuming.
Argon2 strives to maximize data dependence, aiming to make attacks like brute force or GPU-based attacks more difficult. Because of this, Argon2 is widely recognized as a robust password hashing algorithm.
The input parameters used in the Argon2 algorithm can be summarized as follows:
- Password: The user’s password. This is used to generate the encrypted hash value.
- Salt: A randomly generated value. The salt is added to each user’s password to enhance the encryption process. This ensures that users with the same password do not have the same hash value.
- Time Cost: A parameter that adjusts the amount of time consumed during the encryption process. A higher time cost increases the security by requiring more time for encryption but it may result in a slower processing speed.
- Memory Cost: A parameter that adjusts the amount of memory used for encryption. A higher memory cost requires more memory for encryption, increasing the computational cost for an attacker trying to crack the password.
- Parallelism Degree: A parameter that determines the number of threads or tasks processed concurrently. A higher parallelism degree allows for more simultaneous processing, resulting in faster encryption.
In addition, parameters such as Lane Count, Iterations, and Type are also used in the Argon2 algorithm. These parameters have an impact on the security and performance of the Argon2 algorithm and need to be appropriately adjusted.
2.3. Blake2b Hash Function
Blake2b is a high-performance cryptographic hash function that efficiently generates fixed-size, short digests for data. It is based on the original BLAKE algorithm and is optimized for 64-bit platforms. The algorithm utilizes a block cipher-based round function to transform input data into a hash and incorporates bitwise operations and nonlinear transformations to modify the internal state. This process minimizes the risks of collision attacks and pre-image attacks. Blake2b can be easily applied to various use cases and security requirements by utilizing unique keys, salts, and personalization parameters. Overall, Blake2b is recognized as a reliable cryptographic hash function that combines fast processing speed with high security.
Additionally, Blake2b is an algorithm that allows flexible configuration of the output hash length. This means that the length of the generated hash can be adjusted according to specific needs. As a result, Blake2b can produce digests of various lengths, making it versatile for different purposes. This flexibility enables Blake2b to be widely used and facilitates the generation of optimized digests tailored to specific applications. Therefore, Blake2b is not dependent on a fixed output length and is evaluated as a cryptographic hash function that provides both flexibility and stability.
Internally, the Argon2 algorithm utilizes the Blake2 hash function. Blake2 participated in the SHA-3 competition but ultimately was not victorious, losing to Keccak. Nevertheless, Blake2 remains fast and secure, supporting outputs of various lengths, making it valuable in many projects.
In Argon2, the Blake2 hash function is employed in the following key parts:
- Initialization: Blake2b is used to generate the initial block.
- Block Filling: Blake2b is used in the computation of each block, based on previous blocks.
- Final Hash Generation: The final block is passed to the Blake2b hash function to generate the final password hash.
2.4. Graphics Processing Units
The use of GPUs has become an integral and widespread component in modern computing systems. These GPUs are highly parallel processors with significant arithmetic and memory bandwidth capabilities that far surpass those of CPUs [12,13,14]. For our study, we utilized an Nvidia RTX 3060 Laptop GPU, which boasts an impressive 3840 cores and operates at a clock rate of 1702 MHz. It is important to note that clock rates may vary depending on the specific GPU manufacturer. The GPU we used is designed with the Ampere architecture, which has a Compute Capability (CC) of 8.3. CC refers to the device’s ability to perform computations.
To leverage the parallel processing power of the GPU, we employed the Compute Unified Device Architecture (CUDA), a GPGPU (General-Purpose Computing on Graphics Processing Units) technology. CUDA allows programmers to write parallel processing code using the C language. Developed and maintained by Nvidia, CUDA requires an Nvidia GPU and the corresponding stream processing driver. The CUDA GPU architecture comprises functional kernels, threads, blocks, grids, and warps (bundles of 32 threads) that run on the GPU. Multiple warps execute concurrently on a Streaming Multi-processor (SM), enabling efficient parallel computation [14,15].
The GPU provides several memory types, including register, shared memory, local memory, constant memory, texture memory, and global memory.
- Global memory is the largest memory on the GPU and is commonly used for storing and accessing data. However, it is the slowest memory due to its off-chip location.
- Local memory is used to temporarily store register values when the number of registers used by a thread exceeds the available capacity. Excessive usage of local memory can impact performance as it relies on global memory.
- Texture memory is read-only memory designed for efficient data visualization. It allows for optimized texture access patterns.
- Constant memory is read-only memory that can be initialized before executing the kernel function. It utilizes a separate constant cache within global memory, resulting in faster access when multiple threads access the same address.
- Shared memory is memory shared among threads within a block. Although it provides a smaller memory space, it offers fast access speed. Shared memory employs a banking mechanism, allowing 32 threads executed in warp units to access it simultaneously, minimizing latency.
CUDA manages GPU memory by dividing it into on-chip and off-chip memory. Register and shared memory are located on-chip for faster access, while other memory types reside off-chip. Maximizing on-chip memory can help reduce memory transmission delays and enhance performance. Efficient utilization of the available on-chip memory size is crucial.
3. Implementation
We propose optimizing the implementation for Argon2id as our target variant. Argon2id combines the stability of Argon2i and the parallelism of Argon2d. It ensures stability by initially using Argon2i’s data-dependent approach and later enables parallel processing through independent memory filling similar to Argon2d. By doing so, Argon2id combines the strengths of both algorithms to provide a more efficient password hashing scheme.
3.1. Previous Implementation [16]
The Argon2 encryption algorithm consists of three stages: initialization (init), filling memory blocks (fill memory blocks), and termination (final). In the previous GPU implementation, as shown in the left of Figure 2, only the ‘fill memory blocks’ stage was processed on the GPU.
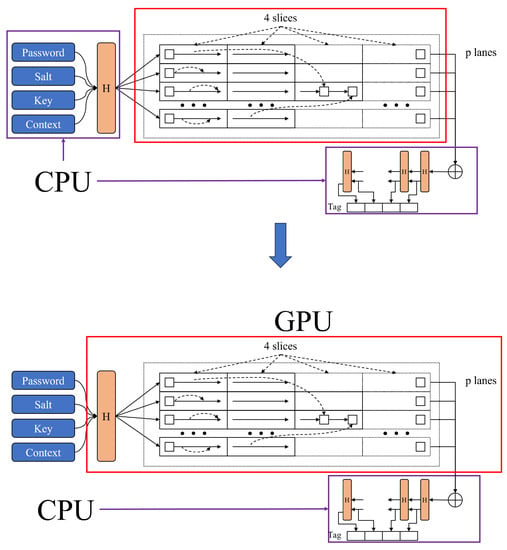
Figure 2.
Changes in workload distribution between CPU and GPU.
A key advantage of this approach is that the Blake hash function works quickly on the CPU, making it efficient for processing small amounts of passwords. However, this does not hold true when processing multiple passwords. Even though Blake2b operations are performed quickly on the CPU, when handling a large number of passwords, more computations can be done on the GPU.
In the ‘init’ stage of Argon2, various parameters (such as password and salt) are inputted and the blake2b hash function is applied to obtain a 64-byte hash value. This hash value is then used to generate the initial memory block for further computations. The size of the generated memory block is determined by the following formula.
Lanes × 2 × ArgonBlockSize(1024 − Byte)
‘Lanes’ refers to the number of rows in the memory block and ‘ArgonBlockSize’ is 1024 bytes. Therefore, if ‘lanes = 1’, the size of the initial memory block generated in the ‘init’ stage is 2048 bytes.
As mentioned, the size of the initial memory block generated after the ‘init’ stage is larger compared to the input parameters, resulting in an increased amount of data transferred from the CPU to the GPU. Consequently, the overall computational speed is slowed down. In the ‘final’ stage, multiple blocks are also selected and copied to the CPU for the calculation of the final hash. Similar to the previous stages, the problem of significant copying costs arises as multiple memory blocks are selected and copied to the CPU for processing.
We have discovered that the size of the data to be copied is large and we have focused on optimizing this aspect.
3.2. Our Implementation
To solve these issues, we propose a new technique that processes both stages—‘init’ and ‘fill memory blocks’—on the GPU, aiming to handle multiple passwords. By doing this, the amount of data transferred to the GPU is significantly less than that of the data after initialization in the previous implementation. This reduces the delay in data transfer from the CPU to the GPU. The same reduction applies to the ‘final’ stage.
3.2.1. Advantages from the Perspective of Memory
GPUs are designed for parallel processing of large data sets and processing of these significant amounts of data requires copying to GPU memory. The data transfer process has a significant impact on GPU performance. CUDA supports various features such as stream mechanisms and directly storing data in fixed memory to reduce the cost of data transfer. This means that the data transfer process affects GPU performance. We have tried to reduce the cost of copying these data.
By performing the initial block creation process, which was traditionally executed on the CPU, on the GPU, we reduce the cost of data transfer. The process of creating an initial memory block and the method for reducing data copy cost are as follows.
Blake2b supports various output lengths and the output length parameter can be adjusted to obtain the desired length of the hash value. Therefore, the output length of Blake2b can be set according to the required length in the application. As shown in Figure 3, the initial block creation process can be divided into two stages. The first stage is the h1 process, where the initial hash value is generated using the input parameters. The parameters used in this stage are summarized in Section 2.2. The input parameters are used to generate an initial hash value of 64 bytes in length through the blake2b hash function. This generated value is then expanded to a size of 1024 bytes to fill the initial memory block of Argon2.
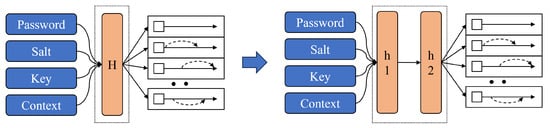
Figure 3.
The initialization stage of Argon2.
The process of expansion described above corresponds to the h2 step in the diagram. In h2, the initial hash value is used as the basis to generate a 1024-byte value through blake2b, which supports various output lengths. This resulting 1024-byte hash value corresponds to a single initial memory block. This can increase depending on the parameters, as it involves the number of lanes and the need to generate two initial memory blocks for each lane.
In the previous implementation, the computation of H(h1 + h2) was performed on the CPU. However, in our approach, we divided it so that the h1 process is still computed on the CPU, while the h2 process is computed on the GPU. Through the analysis mentioned above, we observed that the initial hash value generated in h1 is a small size of 64 bytes. In the previous implementation, the data size before copying from the CPU to the GPU was a minimum of 2048 bytes, which is significantly larger compared to the small data size in h1.
By looking at the numbers alone, the data size in the previous implementation is only around 3% of the total. This indicates that the cost of copying data from the CPU to the GPU is significantly reduced. While the size of the data to be copied has decreased, there is a trade-off in moving the processing from the CPU to the GPU. This is because more computations need to be performed on the GPU, resulting in increased workload for the GPU. We need to analyze the comparison between the decrease in data transfer cost and the increase in computational workload on the GPU to determine the efficiency of our implementation.
Also, to achieve efficient implementation of the h2 process moved to the GPU, we utilize the GPU’s shared memory. Shared memory on the GPU has faster memory access compared to global memory, providing advantages in terms of read and write speeds [17,18]. The h2 computation process involves generating a 64-byte hash value and using the generated hash value as input to generate the next 64-byte hash value, repeating this process until the desired output size is achieved. In other words, to create a 1024-byte memory block, this hashing process is performed 16 times, resulting in significant memory accesses. In summary, shared memory on the GPU is leveraged to optimize the computation of the h2 process. By using shared memory, which offers faster memory access, the repeated hashing process for generating the required memory block can be executed more efficiently on the GPU.
3.2.2. Advantages from the Perspective of Cracking
By leveraging GPUs for parallel optimization implementation, it is possible to handle different input values in parallel during a brute-force attack. This means that the high parallel processing capabilities of GPUs can be utilized to compute multiple input values simultaneously and produce results. Utilizing the parallel processing capabilities of GPUs can enhance the speed and efficiency of brute-force attacks, enabling faster and more effective decryption of passwords. Such techniques are considered crucial research topics in the fields of password decryption and security, attracting interest from both attackers and defenders. Due to its specialization in parallel processing, GPUs can effectively utilize the parallel optimization implementation of the ‘init’ stage in Argon2. If the H function computation is performed on the CPU, it would require generating individual initial blocks for each different input. However, by performing the computation on the GPU, the same operation can be applied to all inputs, enabling the generation of initial blocks in a single computation. This allows for the efficient utilization of the GPU’s parallel processing capabilities, resulting in a more efficient implementation of the ‘init’ stage in Argon2. In the case where the parameters other than the input password are the same, as depicted in Figure 4, only the parameter information is transmitted and each thread can perform the hashing operation for different passwords.
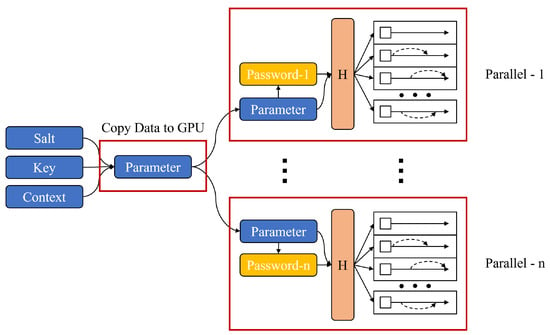
Figure 4.
Parallel implementation structure of Argon2 from a cracking point of view.
However, Argon2 is designed to utilize a significant amount of memory in order to prevent cracking attacks using GPUs. Additionally, the computation process and implementation of Argon2 become more complex and challenging depending on the parameters. In this study, we did not carry out an implementation based on the structure depicted in Figure 4; instead, we propose theoretical implementation techniques.
4. Evaluation
The implementation and benchmarking were carried out using an AMD Ryzen 7 4800H CPU and an NVIDIA GTX 3060 laptop GPU. The implementation was carried out using CUDA in Visual Studio, utilizing CUDA version 11.8 runtime. The project was built in release mode to measure performance during execution. Furthermore, for additional comparative analysis, additional performance measurements were conducted solely using the CPU on a 2018 15-inch MacBook Pro equipped with a 2.6 GHz 6-core Intel Core i7. The proposed technique proved more efficient as the number of passwords to be processed increased. Therefore, we gradually increased the number of passwords processed in parallel and compared the performance with the previous implementation. We compared the time taken based on three parameters: memory cost (m) at 1 MB, time cost (t) at 1, and parallelism (p) at 1, by incrementally increasing t and p, respectively. The password length was selected as 64 bytes and the output length as 32 bytes.
4.1. Comparison with Reference Code
To compare performance against using only the CPU, measurements were taken using the reference code. In this case, the parameters remained consistent as described above. The performance results for both the implementation utilizing both the CPU and GPU, and the implementation using only the CPU are presented in Table 1. The CPU–GPU configuration measured the time taken for parallel computation of 32 passwords and calculated the time for hashing a single password. Overall, using the GPU in conjunction with the CPU demonstrated a speed approximately five to six times faster compared to using only the CPU.

Table 1.
Performance comparison with CPU-only performance (parameters: t = 1, p = 1, m = 1024, output length = 32 byte).
4.2. Comparison with Existing CPU–GPU Implementation
Figure 5 and Table 2, Table 3 and Table 4 compare the performance of our implementation with that of the previous one at the parallelism levels (p) of 1, 2, and 4 for the Argon2d id version. The relationship between the Number of Passwords and Total Time (ms) was compared. As seen in Figure 6, overall, the time approximately doubles each time the number of passwords doubles. The increase in time decreases as the number of passwords being processed increases. As illustrated in Table 1, the time per password decreases as the number of passwords increases. This is most prominent in GPU computation. When processing 4096 passwords, it deals with 128 times more passwords than when processing 32 but the computation time increases by about 25 times. This confirms that more efficient operations are possible when there are more passwords processed in parallel on the GPU. However, it is relatively inefficient in terms of data transfer time between the CPU and GPU. The greatest delay in GPU computation was confirmed to be the data transfer time between the CPU and the GPU. Generally, our implementation has a shorter processing time than the existing implementation. It was more efficient when there were more passwords being processed and when the level of parallelism was higher. The increase in the level of parallelism affected the delay in data transfer between the CPU and GPU. In the case of the existing implementation, computation was somewhat reduced but, in our implementation, the time taken increased when the number of passwords was large (more than 1024). The difference between the two implementations was not significant at a parallelism level of 1 but, as the level of parallelism increased, the performance difference became more significant and the difference increased as the number of passwords increased. In our work, as the fillblock operation and finalize operation run on the GPU, the amount of memory transfer between the CPU and GPU is reduced, and the computation time in the kernel increased. Therefore, although the computation was more efficient in the existing implementation, the overall time was reduced by reducing the larger delay factor, the data transfer time between the CPU and the GPU. These characteristics were the same in the i version and d version, as shown in Figure 6 and Figure 7, and Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10.
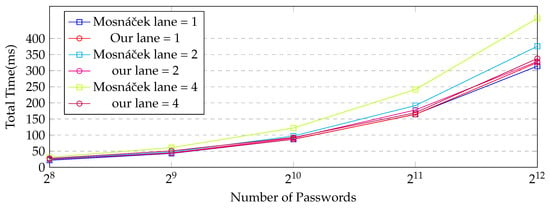
Figure 5.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 1, 2, and 4 for Argon2id versions.

Table 2.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 1 for Argon2id versions (Ours/Mosnáček).

Table 3.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 2 for Argon2id versions (Ours/Mosnáček).

Table 4.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 4 for Argon2id versions (Ours/Mosnáček).
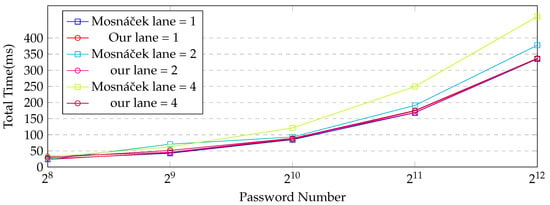
Figure 6.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 1, 2, and 4 for Argon2i versions.
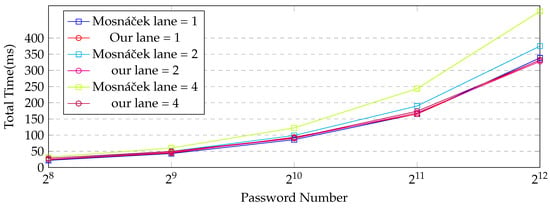
Figure 7.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 1, 2, and 4 for Argon2d versions.

Table 5.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 1 for Argon2i versions (Ours/Mosnáček).

Table 6.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 2 for Argon2i versions (Ours/Mosnáček).

Table 7.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 4 for Argon2i versions (Ours/Mosnáček).

Table 8.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 1 for Argon2d versions (Ours/Mosnáček).

Table 9.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 2 for Argon2d versions (Ours/Mosnáček).

Table 10.
Comparison of the performance of the implementation with that of the previous implementation at levels of parallelism (p) of 4 for Argon2d versions (Ours/Mosnáček).
5. Conclusions
In this study, we proposed a new implementation technique for Argon2 that leverages GPU for both the ‘init’ and ‘fill memory blocks’ stages, aiming to efficiently handle multiple passwords. This implementation significantly reduces the amount of data transferred from CPU to GPU, consequently decreasing the overall delay in data transfer. By shifting the processing of the ‘h2’ process from CPU to GPU, we further reduced the data transfer cost. The proposed method capitalizes on the GPU’s shared memory, which offers faster memory access, optimizing the computation of the ‘h2’ process. The repeated hashing process needed to generate the required memory block can be executed more efficiently on the GPU. The proposed approach also takes advantage of GPU’s parallel processing capabilities for an efficient execution of brute-force attacks. By performing the H function computation on the GPU, initial blocks for multiple inputs can be generated in a single operation, resulting in a more efficient implementation of the ‘init’ stage in Argon2. Through rigorous evaluation, we found that, as the number of passwords to be processed concurrently increased, the proposed method exhibited enhanced performance. Even though the computation time in the kernel increased, the proposed technique reduced the overall time by decreasing the significant delay factor (i.e., the data transfer time between the CPU and GPU). Overall, the proposed implementation demonstrated a more efficient execution time compared to the existing one, particularly when processing a larger number of passwords and at higher levels of parallelism. A more efficient execution time means more hash operations can be carried out in the same amount of time. This can be expected to reduce the cost of cracking attacks by showing less energy consumption when performing the same hash operation. Although Argon2 is designed to utilize significant memory to prevent cracking attacks, our findings reveal that an optimized implementation leveraging the GPU can provide substantial advantages in terms of performance and efficiency. This research suggests a promising direction for future developments and improvements in the password decryption and security fields.
Author Contributions
Investigation, S.E., H.K. and M.S.; Writing—original draft, S.E.; Writing—review & editing, H.S.; Supervision, H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2021-0-00540, Development of Fast Design and Implementation of Cryptographic Algorithms based on GPU/ASIC, 100%).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lin, C.H.; Liu, J.C.; Chen, J.I.Z.; Chu, T.P. On the Performance of Cracking Hash Function SHA-1 Using Cloud and GPU Computing. Wirel. Pers. Commun. 2019, 109, 491–504. [Google Scholar] [CrossRef]
- Alkhwaja, I.; Albugami, M.; Alkhwaja, A.; Alghamdi, M.; Abahussain, H.; Alfawaz, F.; Almurayh, A.; Min-Allah, N. Password Cracking with Brute Force Algorithm and Dictionary Attack Using Parallel Programming. Appl. Sci. 2023, 13, 5979. [Google Scholar] [CrossRef]
- Hranickỳ, R.; Zobal, L.; Ryšavỳ, O.; Kolář, D. Distributed password cracking with BOINC and hashcat. Digit. Investig. 2019, 30, 161–172. [Google Scholar] [CrossRef]
- Hatzivasilis, G.; Papaefstathiou, I.; Manifavas, C. Password hashing competition-survey and benchmark. Cryptol. ePrint Arch. 2015. Available online: https://eprint.iacr.org/2015/265 (accessed on 8 July 2023).
- Wetzels, J. Open sesame: The password hashing competition and Argon2. arXiv 2016, arXiv:1602.03097. [Google Scholar]
- Biryukov, A.; Dinu, D.; Khovratovich, D. Argon2: New generation of memory-hard functions for password hashing and other applications. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbrucken, Germany, 21–24 March 2016; pp. 292–302. [Google Scholar]
- Kumar, H.; Kumar, S.; Joseph, R.; Kumar, D.; Singh, S.K.S.; Kumar, A.; Kumar, P. Rainbow table to crack password using MD5 hashing algorithm. In Proceedings of the 2013 IEEE Conference on Information & Communication Technologies, Thuckalay, India, 11–12 April 2013; pp. 433–439. [Google Scholar]
- Provos, N.; Mazieres, D. Bcrypt Algorithm; USENIX: Berkeley, CA, USA, 1999; Available online: https://www.usenix.org/legacy/events/usenix99/provos/provos_html/node5.html (accessed on 8 July 2023).
- Percival, C.; Simon, J. The Scrypt Password-Based Key Derivation Function. No.rfc7914. 2016. Available online: https://www.rfc-editor.org/rfc/rfc7914?trk=public_post_comment-text (accessed on 11 July 2023).
- Moriarty, K.; Kaliski, B.; Rusch, A. Pkcs# 5: Password-Based Cryptography Specification Version 2.1. RFC 8018. 2017. Available online: https://www.rfc-editor.org/info/rfc8018 (accessed on 16 July 2023). [CrossRef]
- Ertaul, L.; Kaur, M.; Gudise, V.A.K.R. Implementation and performance analysis of pbkdf2, bcrypt, scrypt algorithms. International Conference on Wireless Networks (ICWN). 2016, p. 66. Available online: http://mcs.csueastbay.edu/~lertaul/PBKDFBCRYPTCAMREADYICWN16.pdf (accessed on 21 July 2023).
- Owens, J.D.; Houston, M.; Luebke, D.; Green, S.; Stone, J.E.; Phillips, J.C. GPU computing. Proc. IEEE 2008, 96, 879–899. [Google Scholar] [CrossRef]
- Choi, H.; Seo, S.C. Fast implementation of SHA-3 in GPU environment. IEEE Access 2021, 9, 144574–144586. [Google Scholar] [CrossRef]
- Iwai, K.; Nishikawa, N.; Kurokawa, T. Acceleration of AES encryption on CUDA GPU. Int. J. Netw. Comput. 2012, 2, 131–145. [Google Scholar] [CrossRef]
- CUDA C Programming Guide V6.0. Available online: https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html (accessed on 11 July 2022).
- GPU Is Unfriendly for WebDollar-argon2-gpu for WebDollar. Available online: https://github.com/WebDollar/argon2-gpu (accessed on 1 July 2023).
- Chen, L.; Agrawal, G. Optimizing mapreduce for gpus with effective shared memory usage. In Proceedings of the 21st International Symposium on High-Performance Parallel and Distributed Computing, Minneapolis, MN, USA, 27 June–1 July 2022; pp. 199–210. [Google Scholar]
- Fang, M.; Fang, J.; Zhang, W.; Zhou, H.; Liao, J.; Wang, Y. Benchmarking the GPU memory at the warp level. Parallel Comput. 2018, 71, 23–41. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).