Abstract
This paper presents a characterization of the pore structure of tight-pore sandstones of the Achimov suite and examines the application of Lattice–Boltzmann method (LBM) simulations to estimate the permeabilities of rock formations with a single-scale porosity. Porosity is characterized by pore volume distribution, pore throat connectivity, and tortuosity, which are calculated from 3D computer tomography pore network maps. The tight sandstones are poorly permeable, with permeabilities from 0.7 to 13 mD. For comparison, sandstones and carbonates with higher porosity and permeability from the existing database are also considered. For the more permeable reference samples with wider pores (250 µm), LBM simulations show good agreement with the experiments and somewhat outperform the selected state-of-the-art direct simulations from the literature. For samples with the tightest pores and lowest porosity, LBM simulations tend to somewhat overestimate the permeability in comparison with the direct simulation methods, whereas for samples of higher porosity, a slight underestimation is obtained. We explain the inconsistencies by an interplay between the compressibility effects neglected by our LBM simulations in wider pores and the friction at the pore-wall interface, which is underestimated due to the use of the bounce-back conditions. However, the general agreement with experimental and direct simulation methods is very reasonable and suitable for practical use, which means that LBM is fast, highly parallel, and computationally sound even in tight pores.
1. Introduction
Digital Rock Physics (DRP) complements laboratory studies in efforts to understand mechanical, thermal and transport properties as well as obtain characteristics of natural porous media important for water resources, oil recovery, composite manufactures, etc. The two fundamental components of the DRP are (1) a detailed characterization of the sample morphology and (2) property prediction from the structure. The typical workflow of DRP first involve digital reconstruction of the three-dimensional pore space matrix with computer tomography (CT), nowadays based on artificial intelligence [1]. Then, the methods of computational physics are applied to calculate the structure-property relationships. The analysis of the geometry of the pore space is traditionally based on the theoretical interpretation of gas adsorption data [2,3], mercury or another liquid intrusion [4], positron annihilation, etc. Each of those methods is optimal for a particular type of sample and sensitive to pores of a certain diameter range. The primary result is the pore size distribution (PSD), although some methods are sensitive to finer geometric features, such as the pore throat distributions and ink-bottle effects [5]. Detailed 3D structures available from the segmentation of CT images allow a finer characterization of the pore geometry that is not limited to the overall porosity, surface area and PSD (at the resolution scale), but also include pore throat, pore volume distributions, and pore tortuosity characterization [6]. However, 3D maps are available for relatively small sample sizes. If the pore space resolution is in a micron-range, the sample mass is in the milligram range, while gas sorption data are available for approximately 10g samples. Thus, the representativeness of the structures remains an issue. Other problems are related to CT scanner resolution, as well as the segmentation artifacts of the images [7], although modern machine learning-based methods have improved reconstruction. The finer the pore structure, the more severe these issues become [8,9]. After the 3D structure is processed, a variety of computational tools can be involved in predictions of the structure—property relationships. The most attention is paid to the permeability of single-phase and multi-phase flows through the pore network and the relationship of the flows to the pore network topology and mineral composition. Machine learning techniques can be applied to such relationships to restore the pore structure from 2D images [10,11] and predict flows without any physics-based simulations. Such predictions for multi-component solid structures have greatly expanded the capacity for fluid flow simulations in geological solids, the manufacture of porous and fibrous materials, textiles, and pharmaceutical dosages, where fluid wicking is a topical problem [12]. This, however, is a difficult work that requires computationally efficient and standardized numerical simulation tools with precisely known applicability limits for the estimation of fluid flows.
Single phase and multiphase fluids could be simulated with a variety of models, the choice of which is determined by the core of the applied problem. In the case of flows in the geometry of the pore space, the direct solution of the Navier–Stokes (NS) equations is the most common approach. It deals with systems of conservation equations for macroscopic properties and explicitly defined phase boundaries. On the contrary, the Lattice–Boltzmann method (LBM) has gained rapidly in popularity over the last few years [13]. In LBM, densities and velocities are computed for fictive particles on a lattice with streaming and collision processes using “local rules”, which provide unmatched computational efficiency and versatility. Phase boundaries are calculated from the densities. LBM has been demonstrated to handle the dynamics of quite complex systems, processes, and interactions (e.g., disjoining forces), including foams and gas filtration [14,15]. The main obstacle to the routine engineering applications of LBM in fluid flow simulations is a lack of understanding of the applicability in “tight” systems, that is, when the feature size (be it the pore width, fiber thickness, etc.) becomes comparable with the effective voxel size. It should be noted that NS solvers often also succumb to poor convergence in tight media [16]. Recent efforts invested in the development of direct methods [17,18,19], such as Direct Hydrodynamic (DHD) simulations [20] and Dimp-Hydro Solver (DiMP) [17], substantially improved flow predictions in tight pore samples at a certain cost in computational efficiency and versatility.
As for LBM, most efforts were traditionally invested in DRP. A classical Lattice–Boltzmann method with the Bhatnagar–Gross–Krook collision operator (BGK-LBM) showed very good (up to 95%) agreement with experimental data on the permabilities of wide pore samples [21,22]. However, the sample size and mesh resolution, which were up to the standards of 2010, are outdated in 2023. The relaxation time dependencies for the wall boundary conditions may cause poor stability. The multiple-relaxation-time (MRT) [23,24,25,26] approach, the most general and advanced relaxation model of today, has become common practice and improved the accuracy due to the generalization of the equation in terms of momenta. It also allows the bulk viscosity to be chosen independently of the shear viscosity, thus supporting the Galilean invariance. However, it is also more laborous to code, and it becomes computationally more expensive if not coded efficiently. In Ref. [16], LBM-MRT simulations overestimated the permeability of rock samples with moderate pore sizes by 30 to 100%, which is comparable to the errors of different experimental methods and sufficient for practical purposes. MRT and the off-lattice boundary [27,28] improved the accuracy of permeability predictions to 7–8% for moderate pore sizes [29]. However, this approach requires an exact determination of the wall interfaces, which are unavailable in most digitized rock structures, excepting the usage of the marching cubes algorithm. Taking into account the pore size effects [30] and coupling LBM with finite differences calculations for the refinement of the pre-boundary layers [31], is also quite promising.
However, success has been almost exclusively reported with structures of moderate to high porosity ( 0.2), with developed networks of reasonably large pores (0.1–2 mm) [16,22,32,33]. The applicability limits of LBM in tight pore media remain unexplored, and are of substantial interest, accompanied by recent progress in LBM simulations of complex fluids and the trend towards the development of tight pore hydrocarbon reservoirs with a very little open porosity, where structure–permeability relationships may be decisive for efficient filtration. The pore structure–permeability relationships were studied in the literature. Attention was paid to characteristic pore length, overall volume and tortuosity [34]; Euler characteristics [35]; connectivity and pore size distribution [36]. However, again, practically all of these studies deal with more porous systems. The structure of tight sandstone collectors and the relationship between topology and permeability remain unclear. In this paper, we evaluate the accuracy of single phase LBM simulations in sandstone and carbonate samples of different pore sizes, digital sample sizes, and resolution. We compare samples from different sources and validate the LBM simulations against experiments on permeability and direct NS solvers, which are considered here as state-of-the-art. The other goal of the paper is to relate the permeabilities to the structural features of the rock pore network, namely throat sizes and coordination numbers that characterize the pore connectivity along the pore size distributions and pore network tortuosity. This paper is structured as follows. First, we discuss the available samples, data sources, and digital representation (Section 2.1). The simulations are briefly described in Section 2.2. The structure of the samples is explored in Section 3.1, and the permeabilities are calculated in Section 3.2. The Appendix A and Appendix B describe the computational performance and the tortuosity calculations, and Section 4 concludes the report.
2. Materials and Methods
2.1. The Samples
Considered in this paper are mostly sandstones, chosen because of their relatively simple isotropic porosity, which makes the comparison of simulations (performed on small samples, 1–20 mm) to experimental studies (3–50 cm) the most straightforward and valid. The relative simplicity of the sandstone pore structure was evidenced by a 3D pore network reconstruction from 2D images using machine learning in a limited database [10]. Another reason to choose sandstones is the availability of reconstructed 3D maps of the pore space, for which experimental and simulation results have been reported in the literature.
We start with relatively wide pore sandstones from the Imperial College of London (ICL) collection [37]. The resolution of the 3D maps is 2.85 to 10.0 µm/voxel (lower than the other samples considered here), and the physical size ranges from 1.155 mm to 4.5 mm. The structures are mapped on relatively coarse grids, from to voxels. For these samples, both experimental data and Pore Network Model (PNM) simulations are available from the literature [38,39]. The experiments were carried out in the most classical manner: by injecting fluid (water) mass flow with the pressure measured on the inlet and outlet of each sample.
Group 2 also contains selected samples from the ICL collection [37]: two sandstones and two carbonates. For these samples, we did not find experimental data, but their permeability was extensively modeled in the literature [40,41,42]. On average, they are less porous and less permeable than the samples from group 1. They are selected for this study because the pore structure maps available for them are much larger (1000 cubic voxels) than for the samples of group 1, making the maps suitable for pore network characterization. As a benchmark for permeability calculations, we used the finite volume CFD simulations from Raeini et al. [40].
Our target samples are classical tight sandstones from the Achimov formation [43]. They form two groups, here referred to as group 3 and group 4. For both groups, CT images were obtained with a spatial resolution 1.2 µm/voxel (that is, substantially finer compared to the maps for groups 1 and 2). For group 3, the 3D pore maps were reconstructed using an algorithm that utilizes the spatial covariance of the image in conjunction with indicator kriging to determine object edges [7] (Figure 1). The use of indicator kriging makes the thresholding local and guarantees smoothness in the threshold surface. The samples of group 4 are approximately twice as large and mapped with the same spatial resolution. They were reconstructed using a combination of “heavy” band-pass (Fourier transform) and bilateral filters for denoising and local thresholding. Random walk-based algorithms were applied in the binarization of the 3D maps of the samples in both groups 3 and 4. For both groups, we do not have experimental data, but direct simulations (DHD, DiMP) have been reported [7].
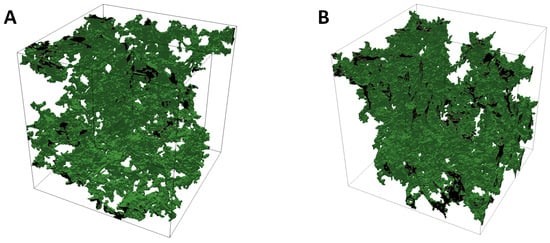
Figure 1.
Three-dimensional maps of tight-pore sandstones of the Achimov suite: (A) 3_E sample with overall porosity of 7%; (B) 3_B sample with overall porosity of 5.3%. Green represents the pore walls; the inner pore space is shown in black. The cube size is 720 µm.
2.2. Lattice–Boltzmann Simulations
The LBM simulations of the permeability of samples are performed in Palabos [44], an open source computational fluid dynamics software, which is a well-established software package tested in multiple LBM applications [45,46,47]. Its modern architecture and storage organization [44] allow efficient parallelization in massive computations. A large library of models and boundary conditions allows for the facile adaptation to a particular phenomenon. The methodology is straightforward: The flow of fluid through the reconstructed digital pore matrix is imposed by a fixed pressure gradient between the inlet and outlet faces of the sample. All simulations were held in LB units, represented as a two-step conversion from physical units to dimensionless, which do not depend on real physical sizes of the system, then from dimensionless to discretized, in order to convert to space and time grid-related units [48]. The gradient is implemented using the common relationship between density and pressure in LBM: [49], where —is dimensionless pressure, is the speed of sound in LB units, and —density in LB units.
Since the permeability is independent of the pressure, the density at the inlet boundary is constant and equal to , and the density at the outlet is varied in the interval depending on the sample. The resulting gradient values were primarily aimed at the stability and accuracy of the LBM [49]. The methodology implies that the system obeys the Darcy law, which requires .
To avoid the artificial anisotropic velocity slip at the solid boundaries caused by the choice of relaxation time(s), we apply the MRT collision operator [23], which provides a more precise ratio between the kinematic and bulk viscosities of the flow. At the solid wall, the half-bounce-back boundary condition (HBB-BC) [50] is applied. HBB-BC effectively places an impenetrable boundary exactly between the cells. This approach helps improve the momentum exchange algorithm and maintain the Galilean invariance. It also alleviates the effect of the “staircase” approximation of complex curved boundaries [49], which is one of the major limitations of LBM in complex geometries. Because all of the samples from the dataset were already voxelized and there was no information about isosurfaces of the wall interfaces, the off-lattice BCs that could potentially improve the accuracy are not applicable. The faces, which are not the inlet or outlet, are padded by symmetry boundary condition.
Simulations are assumed to converge to a steady state when the mean kinetic energy deviation over 1000 iterative steps decreases below . The relaxation time is , which provides optimal stability and accuracy of the simulation according to Asinari et al. [51]. In LB simulations of sample 3_C, we experienced problems with convergence because of the substantial number of narrow pores less than 4 voxels in diameter. That is, the CT resolution is insufficient for a permeability evaluation of such tight pores. To avoid the issue, we artificially increased the map resolution by scaling the matrix twofold and interpolating the boundary regions using the nearest-neighbor method (0-order interpolation). Such a technique is quite common [7,52].
3. Results
3.1. Pore Structure Characterization
The porosity of the samples is estimated as the fraction of the void space in the sample map. More important is the effective porosity that only accounts for the open pores’ space (all isolated voids are excluded). Both quantities are shown in Table 1. The samples from group 1 are the most porous, and the Achimov samples from groups 3 and 4 are the least porous among the sandstones considered here: for example, sample 1_LV60A is 8.5 times more porous than sample 3_B. Carbonates from the ICL database (group 2) are also relatively low in porosity compared to other samples from groups 1 and 2, but still more porous than the Achimov sandstones (groups 3, 4). We also estimate the mean pore size from PSD, calculated using the machine learning framework [53]. The mean pore radius ranges from 5 to 9 voxels, which is sufficient for performing the simulations [52].

Table 1.
Samples used in the present study: discretization, resolutions and porosity.
As mentioned, the samples from group 1 are the most porous, and their digital maps are the smallest. The pore morphologies of wide pore sandstones were extensively studied by Dong et al. [54]. For these reasons, we do not discuss the pore characteristics of this group here. For finer discretized maps of the samples from groups 2, 3 and 4, we calculate pore volume distributions and characterize the pore connectivity and pore network tortuosity. Using the Euclidean distance transform (EDT) [55], for each pore voxel, the largest sphere non-overlapping with the walls is found. Each pore space voxel is assigned the radius of the maximum inscribed sphere (MISA). The field contains as many maximum spheres as the binary image contains pore space voxels. Clearly, some void voxels would be part of multiple spheres. The set of maximum spheres has to be reduced to a subset of containing spheres by searching for each void voxel for the largest sphere in which this voxel was contained. This implies that the spheres contained within a larger sphere are eliminated. This method enables the dissection of a continuous pore space to an integer number of effective pores and thus calculates the pore volume distribution (PVD), as well as characterizes the connectivity and tortuosity.
Figure 2 shows the pore volume distribution obtained from the MISA analysis.
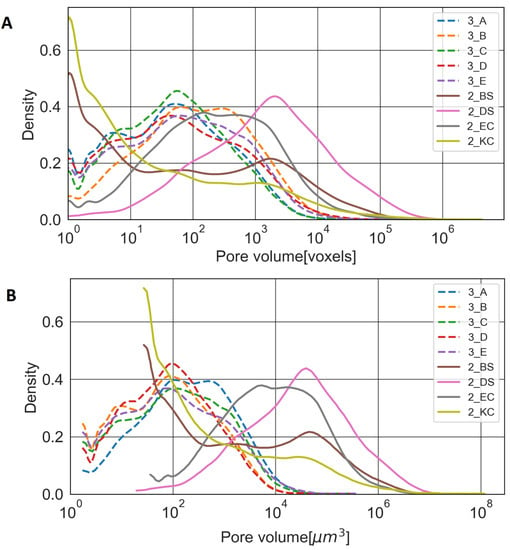
Figure 2.
Pore volume distributions for samples of Groups 2 and 3 (A) in voxels and (B) in µm3.
There is a visible difference between the pore structure of the reference sandstones and carbonates from the ICL database (group 2) and the Achimov sandstones (groups 3 and 4). All Achimov sandstones have unimodal pore volume distributions with the mode at 420–900 µm3 (Table A1), which approximately corresponds to an 8 µm pore radius. The mode of the pore volume distribution only slightly varies with the overall porosity. The reference samples (group 2) are more diverse. 2_BS and 2_KC samples (Bentheimer sandstone and Ketton carbonate) have a large share of very small pores that have a low influence on overall permeability. At the same time, they have a higher fraction of pores of much high volume compared to Achimov sandstones. The other two samples, 2_EC and 2_DS (also one sandstone and one carbonate), have unimodal pore volume distributions similar to the Achimov sandstones, but the modes are shifted to volumes 2–3 orders of magnitude larger, with the 3_DS sandstone having the largest average pore size. It is peculiar that within groups 2 (we do not of course pretend on any generalization) neither the prevailing mineral nor the overall porosity correlate with the type of pore volume distribution.
The pore coordination number refers to the compartmentalized representation of the pore space obtained with the MISA algorithm and measures the number of pores with which a given pore shares throat voxels [6] (Table A1). is the pore throat coordination number, which is the number of effective pores connected by each junction connects. Most junctions, of course, only connect two neighboring pores, which basically means a narrowing in the channel through which the fluid flows. Since the ratio between junction diameter and channel diameter is unknown, it is difficult to say how narrows affect flow. The connectivity R is characterized by the concentration of junctions connecting more than two pores, and can be represented as:
where is the total volume of the system, is the average pore volume, and j is the index of junction. Such a normalization by a characteristic pore volume makes the concentration independent of spatial resolution.
Figure 3 demonstrates the connectivity of the pore networks. mean values are available in Table A1. One can observe that the junctions with high coordination numbers (>4) are so rare that they can hardly influence the permeabilities. The most important junctions, therefore, are those that connect three different pores. The connectivity varies substantially even within the same group. For example, sample 3_B has a very low concentration of three-pore and four-pore junctions compared to other group 3 samples, 3_D in particular. In general, Achimov sandstones are poorly connected to the reference samples from group 2. Sample 1D has the best connected network, according to the EDT analysis. The same sample has the widest pores among the Achimov sandstones.
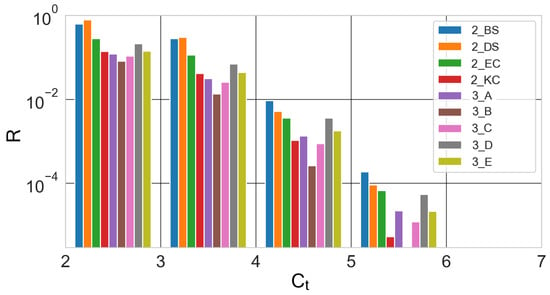
Figure 3.
Concentration of junctions (R) to pore throat coordination number (), connecting two, three, four and five pores for samples of groups 1 and 3. Junction concentration is the number of junctions in the digitized sample.
3.2. Pore Network Permeabilities
Each LB simulation produces stationary velocity and and pressure fields (Figure 4). Typically, high-velocity zones are observed in the throats leading to larger pores and in the pores of low tortuosity. It is possible to visually distinguish several connected pores through which the main flow passes, as well as the dead-end pores. Generally, the flow in samples with wider pores is more uniform. The contrast between fast-moving and slow-moving sectors for wide pore samples is not as pronounced as in the tighter pore sandstones of low porosity. Examples are shown in Figure 4.
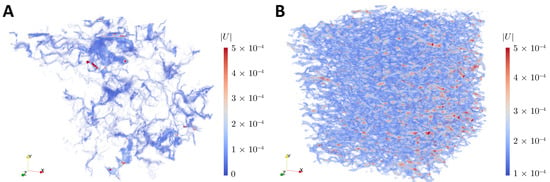
Figure 4.
Magnitude of the velocity field for (A) tight-pore Achimov sandstone sample 3_E with 6.4%porosity (B) wide-pore sandstone sample 1_LV60A with higher porosity (37.7%) (see Table 1).
Absolute permeability is calculated with the Darcy’s law equation:
where is the mean velocity of flow, obtained from LBM simulation; is the dynamic viscosity in LB units; is the density difference between inlet and outlet in LB units. For conversion to physical units, the LB units should be multiplied by a characteristic scale. For permeability, it leads to , where s is the sample resolution. Table 2 shows the results of the permeability calculations in comparison with the experimental data [38,39] and the results obtained by other methods that are considered the most accurate today and applied as modern benchmarks [7,38,39]. First, we can observe that the permeability predictions for the wide pore sandstones made with the LBM methods agree with the experiments quite well. The largest discrepancy obtained is approximately 16%, and most of the results fall within 10% of the experimental value, which is comparable to the experimental error and certainly sufficient for practical purposes. We cannot clearly say that LBM systematically underestimates or overestimates the permeability, although our values tend to be lower compared to the experiments.

Table 2.
Comparison of the calculated absolute permeability k by different methods.
In general, the comparison with experiments is affected by two artifacts that are related to the size of the digital map. First of all, for samples of low porosity, the percolation effects are quite important. The percolation of pore networks in a smaller body is typically achieved at lower porosity than in a larger body with a similar structure, unless the characteristic feature scale of the pore network is much smaller than the system size [56]. In our digitized rock structures, the size of the system and the scale of the characteristic geometric features of the pore network are somewhat comparable, which is evidenced by the tortuosity maps presented in Appendix B. In an infinite porous system, the ratio of the length of the shortest path through the porous network to the Euclidian distance between the same two points should converge to a constant as the distance increases. In the Achimov sandstone samples considered here, the tortuosity maps show non-uniform and anisotropic structures with no visible asymptotic relationship. This means that the characteristic scale of the pore network topology is comparable to the size of the digitized sample. This artifact should facilitate percolation and, therefore, increase the calculated permeability. On the other hand, the limited size of the 3D map effectively cuts off the channels that cross the side boundaries of the digitized sample. Therefore, the channels that cross the side boundaries become dead-end pores, the effective porosity decreases, and the permeability decreases as well. The smaller the digitized sample size is, the higher the fraction of channels that are effectively cut off. To what extent each of the factors matters is hard to say, and a detailed study of the system size would be required for that. These considerations (which, surprisingly, have received little attention in the literature) apply to all CFD methods, not only to LBM.
Comparison of the LBM permeabilities with those obtained with PoreNetwork models [39,40] for group 1 shows very reasonable agreement and no clear trends. The largest difference is obtained for the 1_C1 sample, where the LBM estimate is twice as high. On the contrary, the permeability of the 1_S9 sandstone sample was 1.5 times lower than the PNM result. The discrepancies appear random, with no clear trend. We should say that our results show somewhat better agreement with the experiment, and at least the LBM calculations showed no large discrepancies. The PNM solver underestimates the permeability of the 1_C1 sample by the factor of 2 and overestimates the permeability of the 1_S9 sample by 70%, while the LBM estimates fall with 10% from the experimental result for both systems. However, in general, the discrepancies are by no means dramatic for both methods.
The samples from group 2 are somewhat tighter. Since the experiments are not available, we can only compare them with the same simulation benchmark of the OpenFOAM finite volume solver [40]. Again, the agreement between the LBM and DNS calculations is reasonable and does not show any clear trend. Yet again, LB showed substantially higher permeability (compared to DNS) for the least permeable sample, 2_EC carbonate. The same tendency was noted above for the group 1 sample. At the same time, the permeability of the Bentheimer sandstone sample (2_BS) has a wide PVD with a high share of very narrow pores but higher share of wide pores (which contribute the most to the permeability); LBM underestimated the permeability by 20% compared to the ICL direct simulations [40].
We relate this difference to two important factors in the LBM modeling. First, at high pressure gradients applied in sandstone permeability measurements, the compressibility of the fluid becomes important for the overall flow. In most LBM simulations, including those reported here, the compressibility is ignored and, therefore, the permeability is somewhat overestimated. At the same time, an artificial and anisotropic slip caused by the bounce-back boundary condition applied in our LBM simulations effectively decreases the viscosity–dependent friction between the pore fluid and the wall. The tighter the pores, the more pronounced this distortion is, leading to an overall overestimation of the permeability of tight-pore samples by the LBM.
Considering the tightest samples of this work, the Achimov sandstones of groups 3 and 4, we observe that the overprediction of the permeability by LBM becomes somewhat systematic. Unfortunately, the rigorous test against the experimental data is not available. However, LBM shows a higher permeability compared to both DHD and DiMP for all Achimov sandstone samples considered here, while DHD and DiMP results are reasonably close and show no clear trends when compared with each other (for example, DHD permeability is higher for the 3_B sample and lower for the 3_C sample compared to the DiMP permeability). Overall, the largest discrepancies between LBM and other methods are obtained for the tightest pore samples with the lowest permeabilities (3_C and 3_E). The exception is sample 3_B, which is poorly permeable, and yet, the results obtained by LBM and DHD are quite close. In fact, the larger discrepancy between DiMP and LBM permeabilities (sample 4_B) is no worse than the diescrepancy between the PNM results from [40] and the experiment for wide-pore sandstone 1_S2. In no case did we observe a dramatic disagreement that would certainly prohibit the practical application of LBM as the method for permeability prediction.
It might have also been expected that the artificial effect of friction reduction in LB were more pronounced for physically large samples. The longer the path the fluid needs to take “from start to finish”, the more important the friction forces become. Thus, for larger samples with larger geometry discretization error and more wall boundary voxels, higher deviations of LB calculations from the benchmark results were expected. However, the permeability calculations for group 2 do not show a larger disagreement between the LBM and DHD/DiMP results compared to those for group 1.
In a comparison between the geometric characteristic of the pore structure and the permeabilities calculated with LBM, we can assume that the overall porosity and the pore volume distribution strongly influence the permeability, while the role of connectivity is not obvious. The general correlation between porosity and permeability is apparent. In group 3, samples 3_A, 3_B, 3_C, and 3_E have a comparable porosity. Among them, sample 3_B has the highest fraction of wider pores and has the highest permeability, while sample 3_C has the lowest share of wider pores and the lowest permeability. At the same time, the lower pore throat coordination number in sample 3_B compared to the other Achimov sandstones from group 3 does not appear to decrease the permeability. Thus, overall, it is the volume occupied by relatively wide pores that makes a difference in terms of permeability rather than the pore throat coordination.
4. Conclusions
In this work, for the first time, we evaluate the Lattice–Boltzmann method for permeability prediction on substantial collections of sandstones and carbonates, both highly porous with open porosity and tight pore (6–10 µm) sandstones of the Achimov suite. We also analyze the pore sizes and connectivity and relate them to the permeability.
Our main conclusion is that LB with multiple relaxation times and half-bounce-back boundary conditions at the pore walls quantitatively predict permeabilities with a reasonable accuracy even in tight pore sandstones of low porosity. For samples of high porosity and wider pores (1_S1, 1_S2, 1_S9,1_C1) LBM results showed a somewhat better agreement with the experiments than the state-of-the-art direct Navier–Stokes solvers. For tight-pore samples, the agreement between LBM and other state-of-the-art calculations is satisfactory: the difference between LB permeabilities and those obtained by DiMP simulations is of the same order as the difference between two direct simulation methods, DiMP and DHD.
Generally LBM tends to:
- Somewhat overpredict the permeability of very tight pore least permeable samples due to underestimations of fluid–wall friction caused by the application of half-bounce-back boundary conditions;
- Somewhat underestimate the permeabilities of more permeable samples with open porosity due to a neglect of the compressibility effects.
The permeability shows, as expected, a strong dependence on the effective porosity (and therefore with the average pore size that in our samples is strongly correlated with porosity, as well) and the pore volume distribution, in particular. However, the parameters of the network connectivity, in particular the pore throat coordination numbers, do not appear to influence the permeability in the sample considered in this work. It is not clear how general this observation is, because the pore structure is related to the process of the formation of geological samples and might be quite different for different types of rock formations. For some manufactured materials, the connectivity characteristics proved very important for fluid transport [57,58].
Speaking of requirements to the resolution of the digital porosity maps, this work confirms that the pore width should be larger than at least four voxels. If this is not the case, the LB solver experiences stability problems and shows poor convergence. In order to obtain a more stable simulation, the map can be scaled by the factor of two and the walls interpolated to achieve a smoother structure. What remains unclear is the role of the box size in comparison with the pore network feature size. Our geometrical analysis showed that in all considered samples, the box is not much larger than the topological features of the pore network: all maps showed a substantial anisotropy. For wide pore sandstones, this did not seem to create a problem, as the calculated permeabilities compared well with the experimental values. For tighter samples, where the scale of the pore network geometric features is expected to be larger in comparison with the available box size, the effect of the limited map size is expected to be more severe. However, we cannot draw a clear conclusion on the importance of the anisotropy effect without experimental data.
Author Contributions
Conceptualization, A.V. and A.O.; methodology, A.O.; software, A.O.; validation, A.O.; formal analysis, A.V.; investigation, A.O.; resources, A.V.; data curation, A.V.; writing—original draft preparation, A.O.; writing—review and editing, A.V.; visualization, A.O.; supervision, A.V.; project administration, A.V.; funding acquisition, A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Department of Science and Higher Education of Russian Federation (Center of excellence grant 075-10-2022-011). Calculations were performed on Zhores computational facilities [59] purchased with the support of the Skolkovo Foundation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All datasets and computational packages are referred to in this paper.
Acknowledgments
The authors thank D. Orlov (Skoltech Center for Petroleum Engineering) for stimulating discussions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Tables

Table A1.
Pore structure characterization parameters.
Table A1.
Pore structure characterization parameters.
| Sample | 3_A | 3_B | 3_C | 3_D | 3_E | 2_BS | 2_DS | 2_EC | 2_KC |
|---|---|---|---|---|---|---|---|---|---|
| Average pore volume (voxel), | 260 | 561 | 256 | 527 | 458 | 2824 | 11,376 | 1846 | 2642 |
| Average pore volume (µm3), | 450 | 970 | 442 | 911 | 793 | 76,533 | 222,162 | 67,028 | 71,350 |
| Max pore volume (voxel), | 34,855 | 45,593 | 101,760 | 93,878 | 84,046 | 674,770 | 659,394 | 438,012 | 1,548,038 |
| 2.222 ± 0.437 | 2.148 ± 0.36 | 2.204 + 0.419 | 2.271 ± 0.473 | 2.256 ± 0.459 | 2.328 ± 0.492 | 2.284 + 0.462 | 2.303 ± 0.480 | 2.240 ± 0.440 | |
| 6.462 ± 7.161 | 4.736 ± 4.265 | 6.209 ± 7.229 | 7.817 ± 9.854 | 7.175 ± 8.529 | 12.316 + 16.101 | 10.300 ± 13.227 | 8.465 ± 13.487 | 7.568 + 10.033 |

Table A2.
Computational resources, time costs and performance of the simulations.
Table A2.
Computational resources, time costs and performance of the simulations.
| Sample Pack | Computational Resources | CPU | Time, Seconds | Number of Iterations | MLUPS * Per Core |
|---|---|---|---|---|---|
| Group 1 | 60 CPU cores | Intel Xeon Gold 6136 | ∼9000 | ∼12,000–25,000 | 5.2 |
| Group 2 | 80 CPU cores | Intel Xeon Gold 6230 | ∼72,000–86,400 | ∼20,000–40,000 | 4.8 |
* MLUPS—million lattices updated per second.
Appendix B. Tortuosity Computations
The evaluation of tortuosity was carried out only on the samples of group 1. The ratio is obtained for all points of the sample belonging to the pore space, and is shown in Figure A1. In a network with high tortuosity, always substantially exceeds as the path through the pore space, which is substantially longer than the shortest path (that is the Euclidian distance). However, if the pore network is a single scale (which is assumed for sandstones) and the digitized sample size is much larger compared to the pore network characteristic scale, the should asymptotically converge to a constant as increases (that is, the map should asymptotically converge to the red line at high d). Since we observe otherwise, we have to conclude that our sample size is not much larger than the typical feature of the pore space.
The obtained geometric characteristics of the samples of group 1 characterize them as highly heterogeneous-possessing in the strongly branched structure, on the one hand, and with a low connectivity of pores, on the other. Low porosity samples, with relatively narrow pores and a large number of throat interfaces, present a high difficulty in terms of the analysis and approaches to the extraction of hydrocarbons from reservoirs of this type.
The small physical dimensions of the pores, combined with the relatively low resolution of the tomography, as evidenced by the small voxel volume of pores, will allow one to assess the limits of the applicability of various PSS methods.
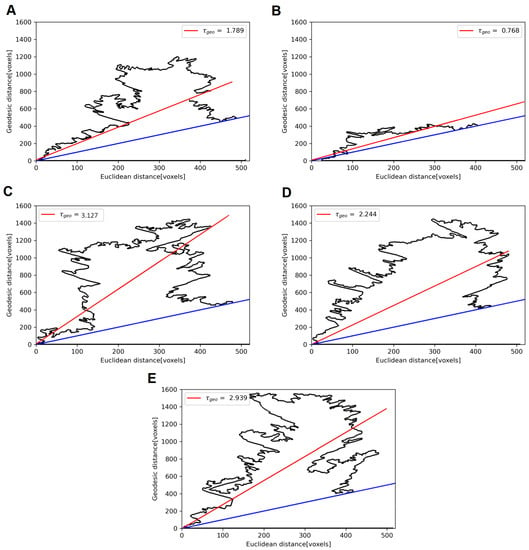
Figure A1.
Geodesic distances plotted against the corresponding Euclidean distances. Left to right, top to bottom—(A–E) sample from the group 1. Red line is the linear approximation of the tortuosity; blue line—separation of “non-representative” data ().
References
- Baraboshkin, E.; Demidov, A.; Orlov, D.; Koroteev, D. Core box image recognition and its improvement with a new augmentation technique. Comput. Geosci. 2022, 162, 105099. [Google Scholar] [CrossRef]
- Karnauhov, A. The Texture of Dispersed and Porous Materials; Novosibirsk Science: Novosibirsk, Russia, 1999; p. 470. [Google Scholar]
- Ravikovitch, P.I.; Vishnyakov, A.; Russo, R.; Neimark, A.V. Unified Approach to Pore Size Characterization of Microporous Carbonaceous Materials from N2, Ar, and CO2 Adsorption Isotherms. Langmuir 2000, 16, 2311–2320. [Google Scholar] [CrossRef]
- Klobes, P.; Meyer, K.; Munro, P.G. Porosity and Specific Surface Area Measurements for Solid Materials, national g ed; NIST: Gaithersburg, MD, USA, 2006. [Google Scholar] [CrossRef]
- Felipe, C.; Rojas, F.; Kornhauser, I.; Thommes, M.; Zgrablich, G. Mechanistic and experimental aspects of the structural characterization of some model and real systems by nitrogen sorption and mercury porosimetry. Adsorpt. Sci. Technol. 2006, 24, 623–643. [Google Scholar] [CrossRef]
- Hormann, K.; Baranau, V.; Hlushkou, D.; Höltzel, A.; Tallarek, U. Topological analysis of non-granular, disordered porous media: Determination of pore connectivity, pore coordination, and geometric tortuosity in physically reconstructed silica monoliths. New J. Chem. 2016, 40, 4187–4199. [Google Scholar] [CrossRef]
- Orlov, D.; Ebadi, M.; Muravleva, E.; Volkhonskiy, D.; Erofeev, A.; Savenkov, E.; Balashov, V.; Belozerov, B.; Krutko, V.; Yakimchuk, I.; et al. Different methods of permeability calculation in digital twins of tight sandstones. J. Nat. Gas Sci. Eng. 2021, 87, 103750. [Google Scholar] [CrossRef]
- Pot, V.; Zhong, X.; Baveye, P.C. Effect of resolution, reconstruction settings, and segmentation methods on the numerical calculation of saturated soil hydraulic conductivity from 3D computed tomography images. Geoderma 2020, 362, 114089. [Google Scholar] [CrossRef]
- Cnudde, V.; Masschaele, B.; Dierick, M.; Vlassenbroeck, J.; Hoorebeke, L.V.; Jacobs, P. Recent progress in X-ray CT as a geosciences tool. Appl. Geochem. 2006, 21, 826–832. [Google Scholar] [CrossRef]
- Sudakov, O.; Burnaev, E.; Koroteev, D. Driving digital rock towards machine learning: Predicting permeability with gradient boosting and deep neural networks. Comput. Geosci. 2019, 127, 91–98. [Google Scholar] [CrossRef]
- Santos, J.E.; Xu, D.; Jo, H.; Landry, C.J.; Prodanović, M.; Pyrcz, M.J. PoreFlow-Net: A 3D convolutional neural network to predict fluid flow through porous media. Adv. Water Resour. 2020, 138, 103539. [Google Scholar] [CrossRef]
- Markl, D.; Zeitler, J.A. A Review of Disintegration Mechanisms and Measurement Techniques. Pharm. Res. 2017, 34, 890–917. [Google Scholar] [CrossRef]
- Succi, S. Lattice Fluid Dynamics: Thirty-five Years Down the Road. Comptes Rendus. Mécanique 2022, 350, 1–12. [Google Scholar] [CrossRef]
- Zacharoudiou, I.; Boek, E.S.; Crawshaw, J. The impact of drainage displacement patterns and Haines jumps on CO2 storage efficiency. Sci. Rep. 2018, 8, 15561. [Google Scholar] [CrossRef]
- Ataei, M.; Shaayegan, V.; Costa, F.; Han, S.; Park, C.B.; Bussmann, M. LBfoam: An open-source software package for the simulation of foaming using the Lattice Boltzmann Method. Comput. Phys. Commun. 2021, 259. [Google Scholar] [CrossRef]
- Saxena, N.; Hofmann, R.; Alpak, F.O.; Berg, S.; Dietderich, J.; Agarwal, U.; Tandon, K.; Hunter, S.; Freeman, J.; Wilson, O.B. References and benchmarks for pore-scale flow simulated using micro-CT images of porous media and digital rocks. Adv. Water Resour. 2017, 109, 211–235. [Google Scholar] [CrossRef]
- Balashov, V.A.; Savenkov, E.B.; Chetverushkin, B.N. Dimp-Hydro Solver for Direct Numerical Simulation of Fluid Microflows within Pore Space of Core Samples. Math. Models Comput. Simul. 2020, 12, 110–124. [Google Scholar] [CrossRef]
- Pimanov, V.; Lukoshkin, V.; Toktaliev, P.; Iliev, O.; Muravleva, E.; Orlov, D.; Krutko, V.; Avdonin, A.; Steiner, K.; Koroteev, D. On a workflow for efficient computation of the permeability of tight sandstones. arXiv 2022, arXiv:2203.11782. [Google Scholar]
- Verri, I.; Della Torre, A.; Montenegro, G.; Onorati, A.; Duca, S.; Mora, C.A.; Radaelli, F.; Trombin, G. Development of a Digital Rock Physics workflow for the analysis of sandstones and tight rocks. J. Pet. Sci. Eng. 2017, 156, 790–800. [Google Scholar] [CrossRef]
- Koroteev, D.; Dinariev, O.; Evseev, N.; Klemin, D.; Nadeev, A.; Safonov, S.; Gurpinar, O.; Berg, S.; van Kruijsdijk, C.; Armstrong, R.; et al. Direct Hydrodynamic Simulation of Multiphase Flow in Porous Rock. Int. Symp. Soc. Core Anal. 2013, 1–12. [Google Scholar]
- Arns, C.H.; Adler, P.M. Fast Laplace solver approach to pore-scale permeability. Phys. Rev. E 2018, 97, 1–9. [Google Scholar] [CrossRef]
- Boek, E.S.; Venturoli, M. Lattice-Boltzmann studies of fluid flow in porous media with realistic rock geometries. Comput. Math. Appl. 2010, 59, 2305–2314. [Google Scholar] [CrossRef]
- D’Humières, D.; Ginzburg, I.; Krafczyk, M.; Lallemand, P.; Luo, L.S. Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef]
- Ginzbourg, I.; Adler, P.M. Boundary flow condition analysis for the three-dimensional lattice Boltzmann model. J. De Phys. II 1994, 4, 191–214. [Google Scholar] [CrossRef]
- Ginzburg, I.; D’Humières, D. Multireflection boundary conditions for lattice Boltzmann models. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2003, 68, 1–30. [Google Scholar] [CrossRef]
- Gray, F.; Boek, E. Enhancing Computational Precision for Lattice Boltzmann Schemes in Porous Media Flows. Computation 2016, 4, 11. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, T.S. Lattice Boltzmann model for incompressible flows through porous media. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2002, 66, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Filippova, O.; Hänel, D. Grid Refinement for Lattice-BGK Models. J. Comput. Phys. 1998, 147, 219–228. [Google Scholar] [CrossRef]
- Rao, P.; Schaefer, L. Permeability estimation on tomographic images using curved boundary schemes in the lattice Boltzmann method. Adv. Water Resour. 2020, 143, 103685. [Google Scholar] [CrossRef]
- Chen, L.; Fang, W.; Kang, Q.; De’Haven Hyman, J.; Viswanathan, H.S.; Tao, W.Q. Generalized lattice Boltzmann model for flow through tight porous media with Klinkenberg’s effect. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 91. [Google Scholar] [CrossRef]
- Yi, J.; Xing, H. Finite element lattice Boltzmann method for fluid flow through complex fractured media with permeable matrix. Adv. Water Resour. 2018, 119, 28–40. [Google Scholar] [CrossRef]
- Zambrano, M.; Volatili, T.; Mancini, L.; Pitts, A.; Giorgioni, M.; Tondi, E. Pore-scale dual-porosity and dual-permeability modeling in an exposed multi-facies porous carbonate reservoir. Mar. Pet. Geol. 2021, 128, 105004. [Google Scholar] [CrossRef]
- Zambrano, M.; Tondi, E.; Mancini, L.; Lanzafame, G.; Trias, F.X.; Arzilli, F.; Materazzi, M.; Torrieri, S. Fluid flow simulation and permeability computation in deformed porous carbonate grainstones. Adv. Water Resour. 2018, 115, 95–111. [Google Scholar] [CrossRef]
- Berg, C.F. Permeability Description by Characteristic Length, Tortuosity, Constriction and Porosity. Transp. Porous Media 2014, 103, 381–400. [Google Scholar] [CrossRef]
- Liu, Z.; Herring, A.; Robins, V.; Armstrong, R.T. Prediction of Permeability From Euler Characteristic of 3D Images. In Proceedings of the International Symposium of the Society of Core Analysts, Vienna, Austria, 27 August–1 September 2017; pp. 1–12. [Google Scholar]
- Soares, J.; Andrade, P. A model for permeablility of carbonate rocks based on pore connectivity and pore size. In Proceedings of the 15th International Congress of the Brazilian Geophysical Society & EXPOGEF, Rio de Janeiro, Brazil, 31 July–3 August 2017; pp. 977–981. [Google Scholar] [CrossRef]
- Micro-CT Images of Sandstone and Carbonate Rocks[Dataset]. 2015. Available online: https://www.imperial.ac.uk/earth-science/research/research-groups/pore-scale-modelling/micro-ct-images-and-networks/ (accessed on 20 January 2020).
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Direct simulations of two-phase flow on micro-CT images of porous media and upscaling of pore-scale forces. Adv. Water Resour. 2014, 74, 116–126. [Google Scholar] [CrossRef]
- Dong, H.; Blunt, M.J. Pore-network extraction from micro-computerized-tomography images. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 1–11. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Bijeljic, B.; Blunt, M.J. Generalized network modeling: Network extraction as a coarse-scale discretization of the void space of porous media. Phys. Rev. E 2017, 96, 1–17. [Google Scholar] [CrossRef]
- Suzuki, A.; Miyazawa, M.; Minto, J.M.; Tsuji, T.; Obayashi, I.; Hiraoka, Y.; Ito, T. Flow estimation solely from image data through persistent homology analysis. Sci. Rep. 2021, 11, 1–13. [Google Scholar] [CrossRef]
- Muljadi, B.P.; Blunt, M.J.; Raeini, A.Q.; Bijeljic, B. The impact of porous media heterogeneity on non-Darcy flow behaviour from pore-scale simulation. Adv. Water Resour. 2016, 95, 329–340. [Google Scholar] [CrossRef]
- Orlov, D.; Ebadi, M.; Koroteev, D.; Makhotin, I.; Belozerov, B.; Krutko, V.; Yakimchuk, I.; Evseev, N. Dataset for Different Methods of Permeability Calculation in Thin-Pore Tight Sandstones[Dataset]. 2020. Available online: https://data.mendeley.com/datasets/s7dn6jvrpw/1 (accessed on 5 May 2020).
- Latt, J.; Malaspinas, O.; Kontaxakis, D.; Parmigiani, A.; Lagrava, D.; Brogi, F.; Belgacem, M.B.; Thorimbert, Y.; Leclaire, S.; Li, S.; et al. Palabos: Parallel Lattice Boltzmann Solver. Comput. Math. Appl. 2021, 81, 334–350. [Google Scholar] [CrossRef]
- Park, S.w.; Lee, J.; Yoon, H.; Shin, S. Microfluidic Investigation of Salinity-Induced Oil Recovery in Porous Media during Chemical Flooding. Energy Fuels 2021, 35, 4885–4892. [Google Scholar] [CrossRef]
- Kotsalos, C.; Latt, J.; Beny, J.; Chopard, B. Digital blood in massively parallel CPU/GPU systems for the study of platelet transport. Interface Focus 2020, 11, 20190116. [Google Scholar] [CrossRef]
- Poureslami, P.; Siavashi, M.; Moghimi, H.; Hosseini, M. Pore-scale convection-conduction heat transfer and fluid flow in open-cell metal foams: A three-dimensional multiple-relaxation time lattice Boltzmann (MRT-LBM) solution. Int. Commun. Heat Mass Transf. 2021, 126, 105465. [Google Scholar] [CrossRef]
- Latt, J. Choice of Units in Lattice Boltzmann Simulations. 2008. Available online: https://api.semanticscholar.org/CorpusID:106402853 (accessed on 5 May 2020).
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method—Principles and Practice; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Kutay, M.E.; Aydilek, A.H.; Masad, E. Laboratory validation of lattice Boltzmann method for modeling pore-scale flow in granular materials. Comput. Geotech. 2006, 33, 381–395. [Google Scholar] [CrossRef]
- Asinari, P.; Karlin, I.V. Quasiequilibrium lattice Boltzmann models with tunable bulk viscosity for enhancing stability. Phys. Rev. E 2010, 81, 016702. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.; Gray, F.; Crawshaw, J.; Boek, E. Micro-computed tomography pore-scale study of flow in porous media: Effect of voxel resolution. Adv. Water Resour. 2016, 95, 276–287. [Google Scholar] [CrossRef]
- Rabbani, A.; Babaei, M.; Shams, R.; Wang, Y.D.; Chung, T. DeePore: A deep learning workflow for rapid and comprehensive characterization of porous materials. Adv. Water Resour. 2020, 146, 103787. [Google Scholar] [CrossRef]
- Dong, H. Micro-CT Imaging and Pore Network Extraction. Ph.D. Thesis, Imperial College London, London, UK, 2008. [Google Scholar]
- Schouten, T.E.; Van Den Broek, E.L. Fast exact Euclidean distance (FEED): A new class of adaptable distance transforms. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2159–2172. [Google Scholar] [CrossRef] [PubMed]
- Neimark, A.V. Multiscale percolation systems. Sov. Phys. 1989, 96, 1386–1396. [Google Scholar]
- Vishnyakov, A.; Mao, R.; Lee, M.T.; Neimark, A.V. Coarse-grained model of nanoscale segregation, water diffusion, and proton transport in Nafion membranes. J. Chem. Phys. 2018, 148, 024108. [Google Scholar] [CrossRef]
- Lee, M.T.; Vishnyakov, A.; Neimark, A.V. Coarse-grained model of water diffusion and proton conductivity in hydrated polyelectrolyte membrane. J. Chem. Phys. 2016, 144, 014902. [Google Scholar] [CrossRef]
- Zacharov, I.; Arslanov, R.; Gunin, M.; Stefonishin, D.; Bykov, A.; Pavlov, S.; Panarin, O.; Maliutin, A.; Rykovanov, S.; Fedorov, M. “Zhores”—Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology. Open Eng. 2019, 9, 512–520. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).