Abstract
This study aims to investigate the elastic–plastic response of a clamped-clamped beam struck by a rigid heavy mass with a low velocity at any point on the span. The impact system is simplified as a single-degree-of-freedom (SDoF) mass-spring model to formulate the beam’s equations of motion during loading and unloading. With the consideration of material elasticity and large deflection, elastic–plastic analytical solutions are derived to predict the global deformation behavior of the beam. Validation and comparison are conducted against numerical simulations performed using ABAQUS, and satisfactory agreement is achieved for the predictions of the structural dynamic behavior. Meanwhile, a parametric study is presented to assess the influence of the impact location on the characteristic response parameters, which suggests that the structural stiffness increases as the impact location approaches the beam’s support. The findings drawn from analytical and numerical studies can be useful in the anti-impact design of engineering structures.
1. Introduction
Impact on flexible structures is common in a wide range of engineering fields, such as marine, automobile and civil engineering. In order to provide useful information on the preliminary designs of structures and systems subjected to impact, the demand for deep insight into the impact performance and response mechanism of main structural members, such as restrained beams, has rapidly increased.
In order to predict the nonlinear response of dynamically loaded structures with high efficiency, some efforts have been made to develop simplified analytical approaches. Most theoretical analyses adopt the rigid-plastic approximations, reviewed and discussed in detail by Jones [1]. Nevertheless, given that material elasticity is found to play a significant role in accurate predictions of important response characteristics, such as the spring-back and deformation energy dissipation [2,3,4,5,6,7,8], the incorporation of material elasticity is essential in developing a more accurate analytical model for structures under impact.
The equivalent single-degree-of-freedom (SDoF) mass-spring model is an important tool that has been widely used to predict the dynamic behavior of elastic–plastic structures due to its simplicity and accuracy [9,10]. In fact, owing to the high complexity of the material and geometric nonlinear behavior of the actual structures, the equivalent resistance functions in the SDoF model are often determined by experimental and/or numerical methods [11,12,13]. Hence, some simplifications are employed so as to develop an analytical solution of the SDoF model. Several representative research studies on predicting the impact response of beams using the SDoF model are reviewed here. For example, on the basis of the traditional equivalent SDoF method considering only flexural behavior, while the influence of the axial force on the bending moment is ignored [14], Stochino and Carta [15] examined the dynamic responses of reinforced concrete beams under blast and impact loads. In order to simulate the behavior of structures that undergo large displacements more accurately, some improved SDoF models are proposed [16]. Wang et al. [17] numerically and theoretically investigated the dynamic response of axially loaded CFST members with the fixed-sliding boundary conditions subjected to lateral impact at its mid-span. A constant axial force was applied to the sliding support. The effect of the axial force was incorporated into the classical SDoF model to calculate the deflection, and reasonable accuracy was obtained when compared with the numerical simulation. Heng et al. [18] presented a non-linear elastic–plastic SDoF model for a steel beam-column subjected to impact at any point on its span. Although this model assumes a linear yield surface to account for the interaction between axial force and bending moment, the changes of axial forces along the beam are ignored until the formation of the plastic hinges at the three critical locations, i.e., the two fixed ends and the impact point. Noticeably, although the influence of the material elasticity on the loading behavior of the structures is considered in the previously mentioned SDoF methods, the unloading behavior is still neglected. One such improvement in the SDoF model is made by Shi et al. [19] to predict the elastic–plastic behavior of the clamped-clamped beam under the impact of a heavy mass with a low velocity at its mid-span. The explicit expressions of the resistance functions of the beam are proposed during the loading/unloading/elastic vibration stage. This model adopts a non-linear relation between the axial force and the bending moment to account for the membrane effect. In their recent study [20], the strain hardening effect on the structural resistance of an elastic-linear strain hardening beam is estimated for the problem of repeated impacts.
It is clear from the review of the existing literature that limited elastic–plastic analytical studies have been performed to estimate the deformation behavior of flexible structures under impact. To contribute to the inadequate research in this aspect is the direct motivation for undertaking the present work. Herein, for deep insight into the impact performance and response mechanism of structures, an attempt is made to develop an improved SDoF approach for a fully clamped beam under impact at any point along the span, which extends the author’s previous work [19] focusing on symmetrical impact to a wider range of impact cases, i.e., to include unsymmetrical impact. The organization of the paper is as follows. Section 2 establishes a new SDoF model. Section 3 gives details of the finite element model. Section 4 presents the comparisons between the analytical and numerical predictions. Finally, Section 5 gives the conclusions of the present study. The primary contribution of this paper is the development of the non-linear SDoF model to elucidate the effect of impact location on some characteristic response parameters, which can be useful in the preliminary design to protect the engineering structures against impact.
2. SDoF Model for Low-Velocity Heavy-Mass Impact
Consider a clamped-clamped beam of span l with a solid rectangular cross-section of width B and thickness H, transversely struck by a rigid wedge with a heavy mass m0 and a low velocity V0 at a point l1 from the left-hand support, as shown in Figure 1. Without loss of generality, the dimension l1 is taken as smaller than l2 = l − l1. The contact width between the wedge and the beam is assumed to be negligibly small in comparison to the beam length. The beam is assumed to be made of elastic-perfectly plastic material, with the mass density ρ, Young’s modulus E, the yield stress σ0 and Poisson’s ratio ν.
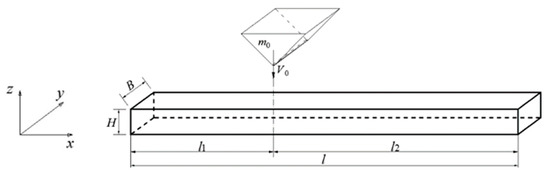
Figure 1.
A heavy mass m0 with a low velocity V0 striking a clamped beam at a point l1 from the left-hand support.
It is common to simulate the impact process using a mass-spring system, which has been demonstrated to provide reliable assessment of structural responses under impact [21]. The impact problem can be simplified as an equivalent SDoF model, of which the dynamic equilibrium equation is written as Equation (1), the detailed derivation of which can be found in [19].
where W, and are the transverse deflection, velocity and acceleration of the beam at the impact point; F(W) is the quasi-static resistance of the beam; and is the equivalent mass of the beam, which can be calculated by an integration of the kinetic energy over the length of the beam [15]:
where μ = ρBH is the mass per unit length of beam; x is the global coordinate along the length direction of the beam, and the origin x = 0 is located at the impact point; and is the transverse velocity field of the beam.
The beam’s resistance is assumed to be governed by the bending moment M and axial force N, while the transverse shear effect can be neglected [22]. This assumption seems reasonable since the effect of axial force dominates the response for the transverse deflections larger than the beam thickness even when the impact location is close to the support of the beam. Thus, based on the moment equilibrium of the fully clamped beam shown in Figure 2, the beam’s resistance in any regime can be expressed as:
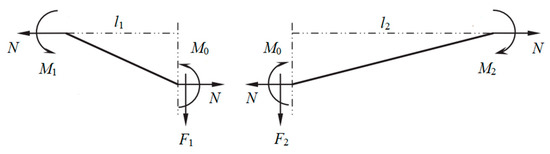
Figure 2.
Force and moment analyses on the fully clamped beam quasi-statically loaded at x = 0. M1, M2 and M0: the bending moments at the two supports and the loading point of the beam, respectively.
In what follows, a complete impact process is composed of two components, loading and unloading, for which the analytical predictions of the beam’s behavior are given below.
2.1. Loading Stage
The loading stage is divided into a number of regimes corresponding to the formation of plastic hinges when using the square yield condition Equation (4) relating M and N for the plastic flow in a rectangular cross-section. The derivation of Equation (4) can be found in [1]. The details of the response of the elastic–plastic beam during each are given below.
where Mp = σ0H2B/4 and Np = σ0HB are the fully plastic bending moment and fully plastic axial force, respectively, for the beam with a rectangular-shaped cross-section.
Regime I represents pure elastic deformations developed in the beam with the shape function w1(x) approximated as
The explanation to illustrate this approximated shape function will be given later in this section.
The axial force following Hooke’s law of elasticity in this regime can thus be given by
The expressions for the elastic bending moment based on the simple technical theory of bending are used here [18]:
where I = BH3/12 is the section moment of inertia and W is the displacement of the beam at the loading location x = 0.
Regarding the assumed shape function, it is worth mentioning that in the elastic regime, the maximum deflection does not occur at the loading point, but the maximum deformation point gets closer to the loading point as the beam’s deformation increases. In addition, the assumed shape function in this regime is only used to calculate the axial force N, while the elastic bending moment M is obtained based on the classical bending theory of beams to weaken the influence of the assumed shape function on the establishment of the elastic loading path. The shape function defined in Equation (5), which satisfies the boundary condition, therefore seems reasonable to facilitate a simplified analytical solution that can take into account the influence of the elastic deformations.
Substitution of Equations (6)–(9) into Equation (3) gives the following:
The velocity profile of the beam, taking the same form as the shape of the transverse displacement profile (see Equation (5)), is substituted into Equation (2), and then the equivalent mass of the beam can be given as the following:
With the assumption that the striker and the struck region of the beam reach the same velocity immediately after impact and maintain contact during impact [19,20], the initial velocity of the beam at the impact location just after impact, , can be calculated from the conservation of linear momentum:
Thus, substituting Equations (10) and (11) into Equation (1), the dynamic response in this regime can be obtained with the initial conditions for Regime I, namely and .
The general conditions for Regime I are as follows: M0 < MN, M1 < MN and M2 < MN, where MN is the bending moment at a plastic hinge related to axial force N:
It is evident from Equations (7)–(9) that M1 > M0 > M2 for l1 < l2, which suggests that the initiation of plastic yielding occurs at the left support x = −l1. Thus, the terminating condition for Regime I is M1 = MT at the inception of yield t = t1y.
At t = t1y, the critical displacement W1y, obtained by substituting Equations (6) and (7) into Equation (4), and the instantaneous velocity are used as the initial condition for Regime II.
Regime II represents the elastic–plastic deformations developed in the beam when the plastic hinge has formed at the left support x = −l1.
To simplify the theoretical analysis of the unloading path, the deformation shape function is assumed to remain the same as that defined in Equation (5) until the plastic hinges are formed at the two supports and the impact point. As a result, the equivalent mass of the beam in regimes II and III can be estimated by Equation (11).
In addition, owing to the fact that the bending moment dominates the beam’s behavior under a relatively smaller deformation, it is reasonable to assume that prior to the plastic hinge formation at the impact point, the elastic behavior in terms of the axial force persists [20].
With these assumptions, in this regime, the axial force can be calculated via Equation (6), and the bending moments at x = −l1, l2 and 0 can be calculated via Equations (13), (8) and (9), respectively. Then, when substituting the corresponding values of M and N into Equation (3), the beam’s resistance during this regime can be obtained as
The general conditions for Regime II are: M0 < MN, M1 = MN and M2 < MN. This regime continues until a critical displacement W2y is attained to define the plasticity hinge formation at x = 0 for M0 > M2. Thus, the terminating conditions for this regime are M0 = MN at t = t2y. When the terminating conditions for Regime II have been reached, the response of the beam is about to enter the next regime, with the initial conditions, namely W = W2y and .
Regime III represents the elastic–plastic deformations developed in the beam when the plastic hinges have formed at the left support and the impact point, and plastic yielding is about to occur at the right point.
In this regime, the axial force N and the bending moment M2 are obtained via Equations (6) and (9), respectively, while the bending moments M0 and M1 are obtained by Equation (13). Hence, the beam’s resistance during this regime can be formulated as
The general conditions for Regime III are M0 = MN, M1 = MN and M2 < MN. This regime continues until the plasticity hinge forms at the support x = l2, implying that the terminating condition for this regime is M2 = MN at time t = t3y.
The critical displacement W3y when reaching the terminating condition of Regime III is attained from Equation (4) with the substitution of Equations (6) and (9). The axial force N = N3y at W = W3y is obtained by Equation (6), which is used as the initial value to determine the dependence of the axial force on the displacement of the beam in Regime IV.
Regime IV represents the elastic–plastic deformations developed in the beam when the plastic hinges have formed at the supports and the loading point.
In order to ensure continuity of the transverse displacement profile at W = W3y and to highlight the characteristic that plastic hinges have formed at the supports and the loading point in this regime, the deformation shape function of the beam in this regime is given as
Here, based on the normality rule of plasticity, a similar method to that developed by Campbell and Charlton [23] is adopted for the predictions on the elastic–plastic behavior of the fully clamped beam loaded at any point on the span.
The total increment in axial tension is given as
The total increment in axial extension can be divided into the elastic and plastic components of axial tension, because the elastic extensions occur in the portions of the beam between the plastic hinges. The increment in the elastic extension is expressed as .
Thus, the increment in the plastic extension is given as
which predicts the rate of extension of the beam centre line as
The rate of rotation across all plastic hinges developing at the supports and the loading point is given as
The normality rule of plasticity requires the following:
Substitution of Equations (19) and (20) into Equation (21) gives
This first-order differential equation involving two variables, N and W, can be solved with the initial conditions N = N3y at W = W3y using Mathematica software version 11.3. The differential equation solution is valid from W = W3y until the establishment of a membrane state, i.e., N = Np at W = Wp. Thus, the bending moment for a specific displacement W can be given via Equation (13). Consequently, from Equation (3), the beam’s resistance during this regime is determined as
In such a case where W ≥ W3y, the transverse velocity field is obtained by taking the derivative of w2(x) defined in Equation (16) with respect to time:
Substituting Equation (24) into Equation (2), the equivalent mass of the beam in this regime is determined as
The initial conditions are W3y and at t = t3y. The general conditions for Regime IV are M0 = M1 = M2 = MN and N < Np. The terminating conditions for this regime are N = Np and M = 0 at time t = tp.
Regime V represents that full plastic deformation develops along the beam and a membrane state is reached for impact with sufficiently large kinetic energy. Thus, substituting M0 = M1 = M2 = 0 and N = Np into Equation (3) gives the following loading path:
Since the transverse velocity field remains unchanged, the equivalent mass of the beam in this regime can be calculated by Equation (25).
The initial conditions for this stage are Wp and at t = tp. At the end of the loading stage, say at tm, the displacement of the beam reaches its maximum value, and the velocity of the impact system decreases to zero, namely, and , which are also the initial conditions of the unloading stage.
With the obtained load-deformation relations and the equivalent mass of the beam in each regime, the global dynamic response of the beam during loading can be obtained analytically by solving Equation (1), when using and at the end of the preceding regime as the initial conditions. The loading regimes of the beam from elastic through elastic–plastic to plastic deformation are summarised in Figure 3, the initial condition and general condition given in each regime.
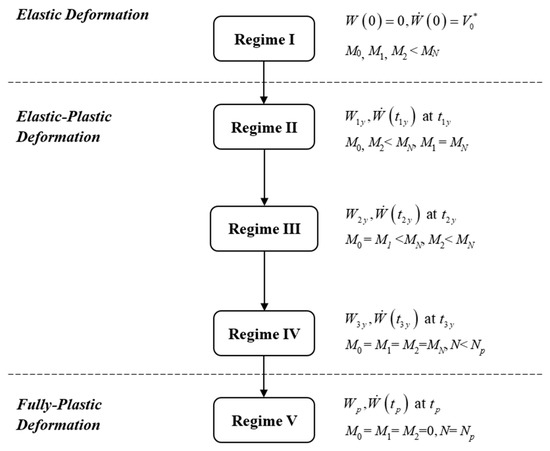
Figure 3.
A summary of the loading regimes.
2.2. Unloading Stage
After attaining the maximum deflection, the beam rebounds due to the material elasticity.
Equation (3) is rewritten to obtain the unloading path as
where M1m, M0m and M2m are the bending moments at x = −l1, 0 and l2 at the peak point W = Wm, respectively; Nm is the axial force at the peak point W = Wm; ΔM1, ΔM0 and ΔM2 are the change of the bending moments at x = −l1, 0 and l2 during unloading; ΔN is the change of the axial force during unloading; and Wu is the displacement of the beam at x = 0 during unloading.
It is evident that the quantities Fm and Nm at the unloading point in Equation (27) can be determined from the theoretical analysis of the loading path, while the changes of the bending moment and the axial force are unknown, which is relevant to the change of the shape function of the beam during the unloading stage.
Unloading is widely regarded as an elastic process [24], and thus the change of the displacement profile during unloading is
where ΔW = Wm − Wu.
Accordingly, the changes of the bending moment and the axial force related to ΔW are
where Δε is the change of the axial strain, given as
where wm(x) is the shape function at the maximum deflection Wm, and wu(x) = wm(x) − Δw(x) is the shape function during unloading.
For unloading from a maximum displacement Wm ≤ W3y, the first term at the right-hand side of Equation (33), Δε1, can be determined by using the shape function w1(x) defined in Equation (5):
For unloading from a maximum displacement Wm ≥ W3y, Δε1 can be determined by using the shape function w2(x) defined in Equation (16), expressed as
On the other hand, the second term at the right-hand side of Equation (33), Δε2, only depends on Δw(x). Thus, Δε2 can be determined when using Equation (28), expressed as
Now, ΔN can be obtained from Equation (32) for unloading from any peak displacement Wm. Thus, the unloading path from any loading regimes can be determined from Equation (27) when using the values of Fm, Tm, ΔN and ΔM in the corresponding regime.
Since the velocity field of the beam during unloading takes the same form as that in Regime I during loading, the equivalent mass of the beam can be calculated by Equation (11).
At the end of this stage t = tf, the impact force applied to the beam decreases to zero, and the velocity and displacement at the impact point of the beam are given as
where Vr is the absolute value of the rebound velocity of the striker, and the negative sign denotes its direction being opposite to that of the initial velocity V0; Wf is defined as the final displacement at the end of the restitution phase.
3. Finite Element Model
In the following, the proposed SDoF model is validated against the numerical simulations performed using the commercial software ABAQUS/Explicit version 6.14.
The numerically examined beam with a size of l × B × H = 500 × 20 × 8 mm3 is made of an elastic-perfectly plastic material with mass density ρ = 7850 kg/m3, yield strength σ0 = 300 MPa, Young’s modulus E = 206 GPa and Poisson ratio v = 0.3. The beam is modelled as deformable bodies using C3D8R, an eight-node linear brick element with reduced integration. In order to model a clamped boundary condition, constraints limiting all degrees of freedom are assigned to both ends of the beam.
The striker is modelled as a rigid wedge to ensure no deformation and is relatively sharp with a small radius (r~1 mm) at the tip to model the concentrated force. Contact between striker and beam is accounted for by applying the “Surface to Surface Contact.”
For the striker, the mass m0 = 30 kg and velocity V0 = 2.0 m/s are assigned to the reference point to ensure a relatively larger ratio of m0/ and to weaken the influence of the necking phenomenon [19]. The motion of the striker is allowed only in the horizontal direction to transversely impact the beam at a point l1 from the left-hand support. To analyse the influence of the impact location on the overall dynamic behavior of the beam, numerical simulations are performed with four impact locations, i.e., l1/l = 1/8, 1/4, 3/8 and 1/2.
Convergence tests on different mesh sizes are performed using the impact case with l1/l = 1/2. The mesh sizes of 1 mm, 1.5 mm, 2 mm and 4 mm are tested. The dependence of the characteristic response parameters, namely, the spring-back (i.e., Wm − Wf) and maximum contact force on the mesh size, are plotted in Figure 4. To balance the simulation accuracy and the computational cost, the mesh size is selected as 1.5 mm in the numerical study.
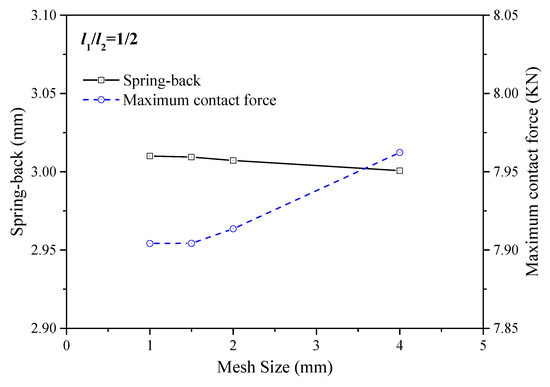
Figure 4.
Spring-back and maximum contact force versus different mesh sizes.
4. Validation of the Proposed SDoF Model
For the purpose of validating the proposed SDoF model, the analytical and numerical results are compared in terms of the overall dynamic response histories and some characteristic response parameters.
4.1. Overall Dynamic Response Histories
Figure 5a,b illustrates the velocity time history and the force-displacement relations resulting from the SDoF and numerical models.
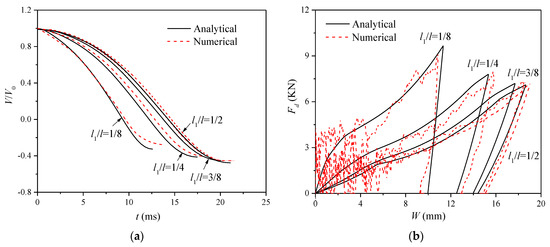
Figure 5.
Comparisons of response characters between the SDoF and numerical models. (a) Velocity-time history of the striker. (b) Impact force-displacement curve.
It transpires from Figure 5a that the analytical results correlate well with the numerical results in terms of the variation of the velocity of the striker with time. The velocity of the impact system decreases to zero until reaching the maximum displacement at the end of the loading stage and then increases to Vr with an opposite direction due to the elastic strain energy stored in the beam. To study the influence of the impact location on the variation of velocity with time, a parameter av = (V0 + Vr)/tf, which represents the average rate of change of velocity over the response time, is introduced here. It is found from Figure 5a that with the increasing l1/l, av becomes smaller and so does its changing rate.
One can see from Figure 5b that the proposed SDoF model can successfully predict the relevance of the impact force to the beam deflection at the impact point, except for a slight difference in the unloading path caused by the difference in the maximum deflection and the change of the transverse displacement profile assumed in Equation (28). The main characteristics of the predicted impact force-displacement responses can be summarised as follows. The growth of the impact force is almost linearly proportional to further increases in deflection for the sufficiently larger displacement behavior of a beam. Different from the almost overlapping loading paths for the central impact cases with different impact velocities analysed in [19], it is evident that the slope of the loading path becomes smaller with the increase of l1/l. To illustrate this phenomenon, a fully plastic beam with T = Tp is taken as an example. It is revealed from Equation (26) that as l1 approaches l2, the slope of the loading path decreases and gets its minimum in the central impact case with l1 = l2. Likewise, the variation of the slope of the unloading path with l1/l shows the same trend as that of the loading path, which can be explained from the perspective of the elastic strain energy. With the approximation of the unloading path as a linear function of ΔW, the slope during unloading can be estimated as
where Ee is the elastic strain energy stored in the beam.
It will be shown in Figure 6c that with an increase of l1/l, the rebound velocity Vr increases while the maximum impact force Fm decreases, with detailed analysis referring to Section 4.2. Thus, it follows from Equation (38) that the slope of the unloading path Ku decreases with an increasing l1/l.
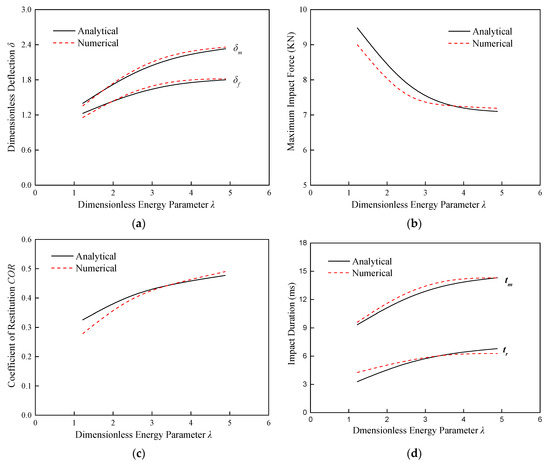
Figure 6.
Dependence of characteristic parameters of an elastic–plastic beam on the impact location. COR = Vr/V0 is defined as the coefficient of restitution. (a) Variation of δm and δf with λ. (b) Variation of Fm with λ. (c) Variation of COR with λ. (d) Variation of tm and tr with λ.
4.2. Characteristic Response Parameters of Beam under Impact at Any Point
The dimensionless external dynamic energy parameter is introduced in Equation (39) to convert the influence of impact location on the beam’s behavior to that of the impact energy.
It is evident from Equation (39) that λ is in proportion to l1/l, which ranges from zero to 1/2.
Figure 6a–d illustrates the variation trends of the maximum/final displacement and the impact duration with λ resulting from the SDoF and numerical models.
For comparison purpose, the dimensionless maximum and final displacements, i.e., δm = Wm/H and δf = Wf/H obtained from the theoretical and numerical predictions, are plotted against λ in Figure 6a. Satisfactory agreement is observed, although the proposed SDoF model predicts a slightly larger deflection with the increase of λ, owing to the neglect of the thinning effect of the beam with a sufficiently larger displacement, as analysed for the displacement-time history curve in Figure 5a. It is shown from Figure 6a that both the maximum and final displacements show an increasing trend with an increase of λ. Meanwhile, the spring-back ΔW = Wm − Wf corresponding to the gap between the δm − λ and δf − λ curves is seen to increase with an increase of λ and attains its maximum value in the central impact. To explain this phenomenon, a similar analysis to that on the slope of the unloading path can be conducted to approximate the spring-back ΔW, written as
It is revealed from the comparisons between Equations (38) and (40) that the variation tendency of ΔW is opposite that of Ku with λ. Thus, the spring-back of the beam attains its maximum value in the central impact with l1 = l2 and decreases with the increase of l1/l.
It is evident from Figure 6b that the SDoF analysis provides reasonable agreement with the numerical predictions for the dependence of the maximum impact force on the impact location. With an increase of λ due to an increasing l1/l, the maximum impact force decreases, which can be attributed to the decrease of the beam’s resistance. Specifically speaking, the dynamic loading path can be approximated as a linear model due to its characteristics, as illustrated in Figure 6b. Thus, the maximum impact force Fm can be approximated by
where K is the slope of the loading path, and Ek = m0/2 is the impact kinetic energy of the striker.
As pointed out in Section 4.1, there is an increase in K with a decreasing l1/l, which implies a greater structural resistance mainly owing to the axial force when a relatively large deformation develops in the beam. Thus, it follows from Equation (41) that a larger l1/l inducing a smaller K will result in a smaller Fm.
However, it is found that in the impact cases with a relatively smaller λ, the maximum impact force predicted by the proposed analytical model is evidently larger than the corresponding numerical prediction. This is possibly caused by the neglect of the bending wave propagation in the beam in the analytical model. In the early stage, when the beam is accelerated to obtain the same velocity of the striking mass, the bending wave propagation in the beam can result in the kinetic energy loss of the impact system. For the case with a smaller λ, the bending wave propagation is somewhat significant due to the boundary effect. Nevertheless, generally speaking, compared to the numerical results, the current analytical model with a relative error within 5.4% gives a satisfactory prediction of the maximum impact force.
It is observed from Figure 6c that the numerical and analytical results generally show the same variation trends of the rebound velocity with λ, despite a slight difference, especially for a smaller λ. It is notable that Vr increases with an increasing λ induced by an increasing l1/l, which implies that the more symmetrical load allows for more elastic energy absorbed by the beam. It can be explained as follows. With the aid of Equation (39), a larger l1/l with a specific kinetic energy can be equivalent to a larger kinetic energy in a central impact case. Besides, it has been demonstrated that a larger impact energy results in a larger elastic strain energy, i.e., a larger rebound velocity [19]. Thus, the rebound velocity attains its maximum value in the central impact corresponding to the largest λ amongst the examined cases with different impact locations.
Furthermore, the variations of loading and unloading durations, namely tm and tr, respectively, with λ are plotted in Figure 6d, which shows that tm and tr increase with an increasing λ. This characteristic can be explained from the point of view of momentum. At t = tm, the impact force reaches its maximum value, and the velocity of the striker decreases to zero. Thus, it follows from the principle of momentum that the initial momentum I0 and the residual momentum If of the impact system can be expressed as
For simplicity, two linear functions are adopted to model the variations of impact force with time during loading and unloading. Thus, the duration during loading, tm, and the duration during unloading, tr = tf − tm, can be approximated from Equation (42), written as
Now, combined with the variation tendencies of Fm and Vr with λ shown in Figure 6b,c, respectively, it is revealed from Equation (43) that tm and tr both increase with an increase of λ, which results in an increase of the impact duration tf.
Thus, it is revealed from Equation (43) that tm and tr both increase with an increase of λ, which results in an increase of the impact duration tf.
In order to quantitatively assess the accuracy of the analytical model, it is necessary to analyse the ratios of numerical to analytical predictions in terms of the characteristic response parameters, i.e., Wm, Wf, Fm, COR, tm and tr. Table 1 presents the corresponding mean values and the standard deviations of the ratios obtained for the four different values of λ. It is notable that for all the analysed parameters, the mean values are quite close to 1, while the standard deviations approach zero. This demonstrates that the proposed analytical model, although with some simplifying assumptions, can offer a satisfactory approximation of the dynamic response of a beam on condition of a heavy mass with a low impact velocity, at least within the range of parameters examined (the largest value of λ is 4.9). Nevertheless, it should be mentioned that the necking phenomenon can become significant with further increase in the structural deflection due to a larger λ. Thus, one should be extremely cautious and careful when applying this model to the impact cases with comparatively larger initial kinetic energy.

Table 1.
Mean and standard deviation of the ratio between the numerical and analytical values.
5. Conclusions
In this study, a nonlinear SDoF model is presented to obtain the dynamic response of an elastic-perfectly plastic beam subjected to low-velocity heavy-mass impact at any point along the span. The nonlinear elastic–plastic behavior of the SDoF model is characterised by a series of resistance functions during the loading/unloading process, which incorporates the geometric and material nonlinearities.
The proposed model allows for investigation of the effects of impact location on the dynamic performance of a beam. The results show that under the same initial impact energy, by comparison with symmetrical impact on a clamped beam, an unsymmetrical situation can lead to more plastic energy dissipation with a smaller maximum/final deflection, owing to the increasing stiffness of the loading and unloading paths. It suggests that a symmetrical impact case shall be given much focus in a displacement-based impact design of structures.
This analytical model is validated by the ABAQUS simulations. It is demonstrated that the proposed SDoF model can be an efficient and accurate tool for estimating the dynamic response characteristics of an elastic–plastic beam under symmetrical and unsymmetrical impacts. Nevertheless, in order to make this model applicable to a wider range of impact energy, further research should include strain rate sensitivity and strain hardening effects, which can improve the structural resistance.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jones, N. Structural Impact, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Jones, N. Pseudo-shakedown phenomenon for the mass impact loading of plating. Int. J. Impact Eng. 2014, 65, 33–39. [Google Scholar] [CrossRef]
- Karagiozova, D.; Yu, T.X.; Shi, S.Y.; Zhu, L. On the influence of elasticity on the large deflections response of circular plates to uniform quasi-static pressure. Int. J. Mech. Sci. 2017, 131, 894–907. [Google Scholar] [CrossRef]
- Shi, S.Y.; Zhu, L.; Yu, T.X. Elastic-plastic response of clamped square plates subjected to repeated quasi-static uniform pressure. Int. J. Appl. Mech. 2018, 10, 1850067. [Google Scholar] [CrossRef]
- Zhu, L.; Shi, S.Y.; Jones, N. Dynamic response of stiffened plates under repeated impacts. Int. J. Impact Eng. 2018, 117, 113–122. [Google Scholar] [CrossRef]
- Ren, J.; Zhao, Z.; Zhou, Y.; Qiang, L.; Lu, T.J. Springback of a fully-clamped metallic beam loaded impulsively. Int. J. Mech. Mater. Des. 2022, 18, 435–459. [Google Scholar] [CrossRef]
- He, X.; Guedes Soares, C. Experimental study on the dynamic behavior of beams under repeated impacts. Int. J. Impact Eng. 2021, 147, 103724. [Google Scholar] [CrossRef]
- He, X.; Guedes Soares, C. Numerical study on the pseudo-shakedown of beams under repeated impacts. Ocean. Eng. 2021, 242, 110137. [Google Scholar] [CrossRef]
- Rigby, S.E.; Tyas, A.; Bennett, T. Single-Degree-of-Freedom response of finite targets subjected to cleared blast loads. Int. J. Impact Eng. 2014, 66, 37–47. [Google Scholar] [CrossRef]
- Feldgun, V.R.; Yankelevsky, D.Z.; Karinski, Y.S. A nonlinear SDOF model for blast response simulation of elastic thin rectangular plates. Int. J. Impact Eng. 2016, 88, 172–188. [Google Scholar] [CrossRef]
- Fischer, K.; Häring, I. SDOF response model parameters from dynamic blast loading experiments. Eng. Struct. 2009, 31, 1677–1786. [Google Scholar] [CrossRef]
- Yu, J.; Guo, Y. Nonlinear SDOF model for dynamic response of structures under progressive collapse. J. Eng. Mech. 2016, 142, 04015103. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Influence of global stiffness and equivalent model on prediction of impact response of RC beams. Int. J. Impact Eng. 2018, 113, 88–97. [Google Scholar] [CrossRef]
- Biggs, J.M. Introduction to Structural Dynamics; McGrawHill: New York, NY, USA, 1964. [Google Scholar]
- Stochino, F.; Carta, G. SDOF models for reinforced concrete beams under impulsive loads accounting for strain rate effects. Nucl. Eng. Des. 2014, 276, 74–86. [Google Scholar] [CrossRef]
- Qasrawi, Y.; Heffernan, P.J.; Fam, A. Dynamic behavior of concrete filled FRP tubes subjected impact loading. Eng. Struct. 2015, 100, 2120225. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Song, J.; Zhao, S.; Wang, Z.; Zeng, Y.; Feng, X. Deflection Calculation Based on SDOF Method for Axially Loaded Concrete-Filled Steel Tubular Members Subjected to Lateral Impact. Hindawi Ltd. 2020, 2020, 6301018. [Google Scholar] [CrossRef]
- Heng, P.; Hjiaj, M.; Battini, J.M.; Limam, A. An enhanced SDOF model to predict the behaviour of a steel column impacted by a rigid body. Eng. Struct. 2017, 152, 771–789. [Google Scholar] [CrossRef]
- Shi, S.Y.; Zhu, L.; Yu, T.X. Dynamic modelling of elastic-plastic beams under impact. Int. J. Impact Eng. 2019, 126, 1–10. [Google Scholar] [CrossRef]
- Shi, S.Y.; Yu, T.X.; Zhu, L. Analytical and numerical modelling of repeated impacts on elastic-strain hardening beams. Int. J. Mech. Mater. Des. 2023, 19, 207–222. [Google Scholar] [CrossRef]
- Wu, K.Q.; Yu, T.X. Simple dynamic models of elastic–plastic structures under impact. Int. J. Impact Eng. 2001, 25, 735–754. [Google Scholar] [CrossRef]
- Qin, Q.; Wang, T.J. Low-velocity impact response of fully clamped metal foam core sandwich beam incorporating local denting effect. Compos. Struct. 2013, 96, 346–356. [Google Scholar] [CrossRef]
- Campbell, T.I.; Charlton, T.M. Finite deformation of a fully fixed beam comprised of a non-linear material. Int. J. Mech. Sci. 1972, 15, 415–422. [Google Scholar] [CrossRef]
- Brake, M.R. An analytical elastic-perfectly plastic contact model. Int. J. Solids Struct. 2012, 49, 3129–3141. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).