Spiking Neural P Systems with Rules Dynamic Generation and Removal

Abstract

Spiking neural P systems (SNP systems), as computational models abstracted by the biological nervous system, have been a major research topic in biological computing. In conventional SNP systems, the rules in a neuron remain unchanged during the computation. In the biological nervous system, however, the biochemical reactions in a neuron are also influenced by factors such as the substances contained in it. Based on this motivation, this paper proposes SNP systems with rules dynamic generation and removal (RDGRSNP systems). In RDGRSNP systems, the application of rules leads to changes of the substances in neurons, which leads to changes of the rules in neurons. The Turing universality of RDGRSNP systems is demonstrated as a number-generating device and a number-accepting device, respectively. Finally, a small universal RDGRSNP system for function computation using 68 neurons is given. It is demonstrated that the variant we proposed requires fewer neurons by comparing it with five variants of SNP systems.

1. Introduction

Membrane computing (MC) [1], proposed in 1998, is a distributed parallel computational method inspired by the working process of biological cells. The computational models of MC are also known as membrane systems or P systems. P systems can be roughly classified into three groups according to the biological cells they imitate: cell-like P systems, tissue-like P systems, and neural-like P systems.

In neural-like P systems, spikes are used to represent information. Two classes of neural-like P systems have been proposed: axon P systems (AP systems) [2] and spiking neural P systems (SNP systems) [3]. An AP system has a linear structure, so that each node of this system can only send spikes to its neighboring left and right nodes. An SNP system has a directed graph structure, where neurons are represented as the nodes in the directed graph and the synapses between neurons are represented by directed arcs.

SNP systems, which also belong to the spiking neural network [4], have become a major research issue as soon as they were proposed. The research related to SNP systems mainly includes four aspects: variant model design, computational power proof, algorithm design (application), and implementation. Theoretical research mainly includes variant model design and computational power proof, while algorithmic research mainly includes algorithm design (application) and implementation. Under the continuous research of a wide range of scholars, several different variants of SNP systems have been proposed. Numerical SNP (NSNP) systems [5,6,7] are a variant of SNP systems inspired by numerical P systems, in which information is encoded by the values of variables and processed by continuous functions. Compared to the original SNP systems, NSNP systems are no longer discrete, but have a continuous numerical nature, which is useful for solving real-world problems. Homogeneous SNP (HSNP) systems [8,9,10,11] are a restricted variant of SNP systems in which each neuron has the same set of rules, making HSNP systems simpler than the original SNP systems. SNP systems with communication on request (SNQP systems) [12,13,14,15,16] are proposed by adding a communication strategy to the original SNP systems in which neuron request spikes from neighboring neurons according to the number of spikes it contains, and no spikes are consumed or produced during the computation. SNP systems with anti-spikes [17,18,19,20] are proposed by considering the anti-spikes and annihilation rules in the original SNP systems. In SNP systems with anti-spikes, the usual spikes and anti-spikes will annihilate each other when they meet in the same neuron. SNP systems with weights [21,22,23,24,25] are proposed by introducing synaptic weights to the original SNP systems in which the number of spikes received by a neuron depends on not only the number of spikes sent by its presynaptic neurons, but also the synaptic weights between neurons.

In addition, as a kind of bio-inspired computational model, SNP systems have many excellent characteristics. First, neurons are not fully connected to each other; therefore, the topological structure of SNP systems is sparse and simple. In SNP systems, information is transmitted only when meeting a specific value, so their information transmission is characterized by low power consumption. Additionally, because SNP systems are a kind of parallel computational model, the tasks can be processed in parallel, reducing the processing time required to be consumed significantly. In addition, the working mechanism of SNP systems is special. In SNP systems, spikes are used to represent information, and the information is processed and transmitted by using spiking rules. In SNP systems, a neuron can contain multiple rules and use regular expression as a control condition for the rules, allowing the neuron to freely select rules to use depending on the number of spikes. It is because of these characteristics that SNP systems have good performance in many kinds of applications [26,27], such as time series forecasting [28,29,30,31], pattern recognition [32,33], image processing [34,35,36,37], etc.

Generally, the rules of neurons in SNP systems are set in the initial state and cannot be changed during the computation process. However, in biological neurons, biochemical reactions are usually changed according to factors such as different substances in the neuron. Motivated by this, spiking neural P systems with rules dynamic generation and removal (RDGRSNP systems) is proposed. In RDGRSNP systems, rules in the rule set of a neuron can be added and removed during the computation process.

Our contribution is to propose a new variant of SNP systems called RDGRSNP systems. This new variant enriches the research on SNP systems. In RDGRSNP systems, the application of rules causes the number of spikes in the neuron to change, which causes the rules in the neuron to change. This makes the rules in RDGRSNP systems no longer constant like the traditional SNP systems, but dynamically changing during the computation. This is not considered by previous theoretical studies on SNP systems. Therefore, our proposed RDGRSNP systems are closer to biological nervous systems and fit better with biological facts than the original SNP systems. In addition, our proposed RDGRSNP systems can improve the ability of adaptive regulation of SNP systems based on dynamical change of rules according to the different substances in neurons.

This paper will be structured as follows: in Section 2, we introduce the proposed RDGRSNP systems and an illustrative example; in Section 3, we demonstrate the Turing universality of RDGRSNP systems when used as a number-generating device and a number-accepting device, respectively. In Section 4, a small universal RDGRSNP system for simulating function computation is constructed. In Section 5, the work of this paper is summarized.

2. SNP Systems with Rules Dynamic Generation and Removal

This section presents the definition of SNP systems with rules dynamic generation and removal and explains them with an illustrative example.

2.1. Definition and Description

In this subsection, we introduce the formal definition of RDGRSNP systems using abstract notation and a detailed description of the definition.

2.1.1. Definition

An RDGRSNP system $\mathrm{\Pi }$ of degree m consists of the following tuples:

$$\mathrm{\Pi }=(O,{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n,R,syn,in,out)$$

(1)

where

(1)

O is a single alphabet with only one element a used to represent a spike.

(2)

${\sigma }_1,{\sigma }_2,\dots ,{\sigma }_m$ denote m neurons in $\mathrm{\Pi }$, and ${\sigma }_i$ is represented by tuple ${\sigma }_i=(n_i,R_i)$, where

(a)

$n_i$ denotes the number of spikes in neuron ${\sigma }_i$.

(b)

$R_i$ denotes the rule set contained in neuron ${\sigma }_i$, where $R_i\subseteq R$.

(3)

R is the rule set of $\mathrm{\Pi }$, which contains rules of the following two forms:

(a)

$r_i:E/a^c\to a^p;{\alpha }_1{r}_1,{\alpha }_2{r}_2,\dots ,{\alpha }_l{r}_l$. A rule of this form is called the spiking rule with rules dynamic generation and removal, where E is a regular expression defined on the single alphabet O, and c and p denote the number of spikes consumed and produced with $c\ge p$, $r_1,r_2,\dots ,r_l$ denoting the l rules in R, and ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_l\in \{+,-,0\}$ are the labels. The spiking rule with rules dynamic generation and removal $r_i:E/a^c\to a^p;{\alpha }_1{r}_1,{\alpha }_2{r}_2,\dots ,{\alpha }_l{r}_l$ can be applied when the number of spikes in the neuron satisfies conditions $a^{n_i}\in L\left(E\right)$ and $a^{n_i}\ge a^c$. Furthermore, the spiking rule with rules dynamic generation and removal can be abbreviated as $r_i:a^c\to a^p;{\alpha }_1{r}_1,{\alpha }_2{r}_2,\dots ,{\alpha }_l{r}_l$ when $a^c\in L\left(E\right)$.

(b)

$r_i:a^s\to \lambda ;{\alpha }_1{r}_1,{\alpha }_2{r}_2,\dots ,{\alpha }_l{r}_l$. A rule of this form is called the forgetting rule with rules dynamic generation and removal, where $s\ge 0$ denotes the number of spikes consumed, with the additional restriction that for all the spiking rules with rules dynamic generation and removal $r_i:E/a^c\to a^p;{\alpha }_1{r}_1,{\alpha }_2{r}_2,\dots ,{\alpha }_l{r}_l$, there is $a^s\notin E$. Similarly, $r_1,r_2,\dots ,r_l$ denotes the l rules R, and ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_l\in \{+,-,0\}$ are the labels.

(4)

$syn=\left\{\right(i,j\left)\right\}$ denotes the set of synapses, where $(i,j)\in \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}$ and $i\ne j$.

(5)

$in,out\in \{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_m\}$ denotes the input and output neurons, respectively.

2.1.2. Description

The definition of RDGRSNP systems proposed above is described here in detail. We mainly describe the process of applying rules in RDGRSNP systems, how the rules are executed in RDGRSNP systems, and the state and graphical definition of RDGRSNP systems.

When neuron ${\sigma }_i$ applies a spiking rule with rules dynamic generation and removal, $r_i:E/a^c\to a^p;{\alpha }_1{r}_1,{\alpha }_2{r}_2,\dots ,{\alpha }_l{r}_l$, c spikes in ${\sigma }_i$ are consumed, and p spikes are sent along synapse $(i,j)$ to postsynaptic neuron ${\sigma }_j$. Meanwhile, neuron ${\sigma }_i$ adjusts its rule set $R_i$ as follows. When ${\alpha }_k=+$, ${\alpha }_k{r}_k$ can be abbreviated to $r_k$, indicating that rule $r_k$ is added to the rule set $R_i$ of neuron ${\sigma }_i$. If rule $r_k$ already exists $R_i$, no rule is repeatedly added. When ${\alpha }_k=-$, it means that rule $r_k$ is removed from the rule set $R_i$ of neuron ${\sigma }_i$. If rule $r_k$ does not exist in $R_i$, no rule is removed. When ${\alpha }_k=0$, ${\alpha }_k{r}_k$ can be omitted and not written, and it means that rule $r_k$ is neither added to nor removed from the rule set $R_i$ of neuron ${\sigma }_i$.

When neuron ${\sigma }_i$ applies a forgetting rule with rules dynamic generation and removal $r_i:a^s\to \lambda ;{\alpha }_1{r}_1,{\alpha }_2{r}_2,\dots ,{\alpha }_k{r}_k$, s spikes in ${\sigma }_i$ are removed and no spikes are sent. Meanwhile, ${\sigma }_i$ adjusts its rule set, operating in the same way as when applying the spiking rule with rules dynamic generation and removal.

Note that an RDGRSNP system $\mathrm{\Pi }$ is parallel on the system level and sequential on the neuron level. There is a global clock used to mark steps throughout the system. When a neuron contains only one applicable rule, the neuron must apply it. When a neuron contains two or more applicable rules, the neuron can only non-deterministically choose one to apply. When no rule is applicable in the neurons of $\mathrm{\Pi }$, the system stops computing.

In general, the state of the system at each step is represented by the number of spikes in each neuron at that step. However, in the proposed RDGRSNP system $\mathrm{\Pi }$, since rules can be generated and removed dynamically, the rules contained in each neuron should also be included in the state of system $\mathrm{\Pi }$. That is, the state of $\mathrm{\Pi }$ is represented by the number of spikes and the rules in each neuron, symbolized as $C_t=⟨(n_1,R_1),(n_2,R_2),\dots ,(n_m,R_m)⟩$. The initial state of $\mathrm{\Pi }$ is represented by $C_0$. When the number of spikes and the rule sets contained in the neurons of $\mathrm{\Pi }$ do not change, the system stops computing.

Regarding the graphical definition, rounded rectangles are used to represent neurons, and directed line segments are used to represent synapses between neurons. In an RDGRSNP system, the result of a computation is defined by the time interval between the first two spikes sent to the environment $env$ by the output neuron ${\sigma }_{out}$.

2.2. An Illustrative Example

In Figure 1, an illustrative example is given to elaborate the definition of RDGRSNP systems. In this example, both ${\sigma }_1$ and ${\sigma }_2$ initially have one spike, and ${\sigma }_{out}$ initially has two spikes, so the initial state is $C_0=⟨(1,\left\{r_3\right\}),(1,\{r_3,r_4\}),(2,\left\{r_1\right\})⟩$.

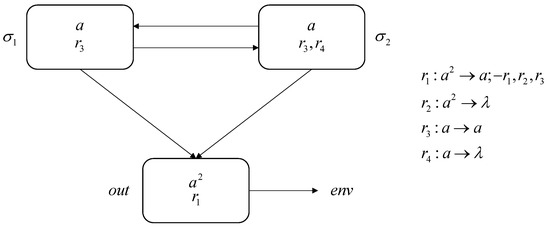
Figure 1. An Illustrative Example.

At step 1, neuron ${\sigma }_1$ applies $r_3:a\to a$ to send one spike to ${\sigma }_2$ and ${\sigma }_{out}$. The output neuron ${\sigma }_{out}$ applies the spiking rule with rules dynamic generation and removal $r_1:a^2\to a;-r_1,r_2,r_3$, consumes two spikes, sends the first spike to $env$, removes $r_1$, and adds $r_2$ and $r_3$. As for neuron ${\sigma }_2$, the number of spikes contained can satisfy the two rules $r_3$ and $r_4$, so it will non-deterministically choose one rule to apply.

Suppose at step 1, neuron ${\sigma }_2$ applies $r_3:a\to a$ and sends one spike to ${\sigma }_1$ and ${\sigma }_{out}$. At step 2, ${\sigma }_1$ applies $r_3:a\to a$ again and sends one spike to ${\sigma }_2$ and ${\sigma }_{out}$, respectively. As for the output neuron ${\sigma }_{out}$, it contains two spikes and rules $r_2$ and $r_3$, so it applies rule $r_2:a^2\to \lambda$, forgetting the two included spikes. Thereafter, if neuron ${\sigma }_2$ continues to apply rule $r_3:a\to a$, the system will continue to repeat the cycle until neuron ${\sigma }_2$ chooses rule $r_4:a\to \lambda$ to apply.

Suppose at step n, where $n\ge 1$, neuron ${\sigma }_2$ chooses rule $r_4:a\to \lambda$ to apply, so it does not send spikes outward. In addition, neuron ${\sigma }_1$ sends one spike to ${\sigma }_{out}$. Therefore, at step $n+1$, ${\sigma }_{out}$ has only one spike, applies rule $r_3:a\to a$, and sends the second spike to $env$.

Thus, ${\sigma }_{out}$ sends the first two spikes with a time interval of $(n+1)-1=n$, where $n\ge 0$, i.e., all positive integers.

3. The Turing Universality of SNP Systems with Rules Dynamic Generation and Removal

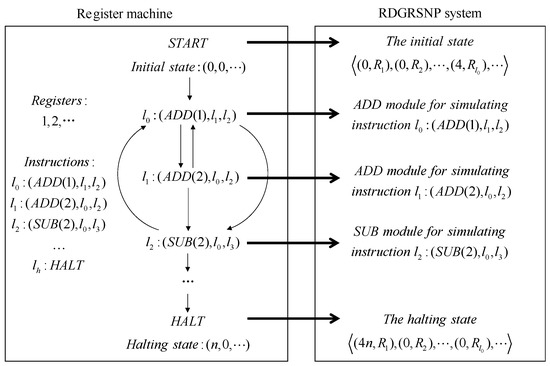
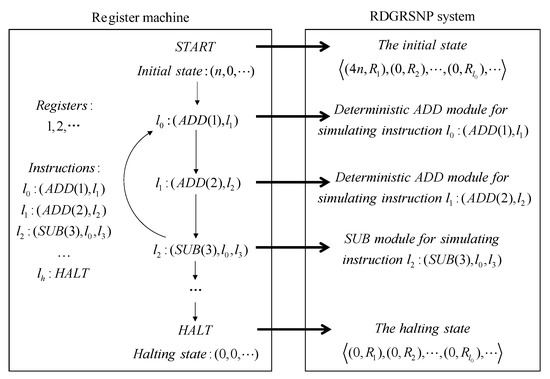
This section is used to prove the Turing universality of RDGRSNP systems when used as a number-generating device and a number-accepting device, respectively. It has been shown that register machines can be used to characterize Turing computable sets of numbers (NRE), so we demonstrate the Turing universality of RDGRSNP systems by simulating register machines.

For a register machine $M=(m,H,l_0,l_h,I)$, m denotes the number of registers r in the register machine M, H is a label set in which each label corresponds to an instruction in the instruction set I, $l_0$ denotes the start instruction, $l_h$ denotes the halt instruction, and I denotes an instruction set. The instructions in I have the following three forms:

(1)

$l_i:(ADD\left(r\right),l_j,l_k)$, the instruction indicates that: add one to the number in r and then jump non-deterministically to $l_j$ or $l_k$;

(2)

$l_i:(SUB\left(r\right),l_j,l_k)$, the instruction indicates that: if the number in r is not zero, subtract the number by one and jump to $l_j$; if the number in r is zero, jump directly to $l_k$;

(3)

$l_h:HALT$, the instruction is the halt instruction, indicating that M stops computing.

In the number-generating mode, all registers in M are initially empty, and M starts from $l_0$ and executes until $l_h$. After the computation is finished, all registers except register 1 are empty, and the number generated by M is stored in register 1. It is assumed that there is no $l_i:(SUB\left(r\right),l_j,l_k)$ for the instructions related to register 1, i.e., the number in register 1 will not be subtracted.

In the number-accepting mode, all registers of M except register 1 are initially empty, and the number to be accepted is stored in register 1. If M can reach the halt instruction $l_h:HALT$, it proves that the number is accepted by M. Note that the instruction $l_i:(ADD\left(r\right),l_j,l_k)$ needs to be changed to deterministic $l_i:(ADD\left(r\right),l_j)$ in the number accepting mode.

In this paper, we use $N_{2}RDGRSNP\left(\mathrm{\Pi }\right)$ and $N_{acc}RDGRSNP\left(\mathrm{\Pi }\right)$ to denote the set of numbers that can be generated and accepted by a RDGRSNP system, respectively.

In the proofs of this paper, we use neuron ${\sigma }_{l_i}$ to denote instruction $l_i$, neuron ${\sigma }_r$ to denote register r, and auxiliary neurons ${\sigma }_{l_i^{\left(j\right)}}$ for module construction, where $j\in N^{+}$. In addition, we stipulate that the simulation of instruction $l_i$ starts when ${\sigma }_{l_i}$ has four spikes.

Theorem 1.

$N_{2}RDGRSNP\left(\mathrm{\Pi }\right)=NRE$

Proof. 

By Turing Church’s theorem, there is $N_{2}RDGRSNP\left(\mathrm{\Pi }\right)\subseteq NRE$, so it is sufficient if we can prove $NRE\subseteq N_{2}RDGRSNP\left(\mathrm{\Pi }\right)$. For $NRE\subseteq N_2\left(\mathrm{\Pi }\right)$, we simulate the register machine to prove it by following the process shown in Figure 2.   □

Figure 2. The flowchart of the SNP system with rules dynamic generation and removal simulating register machine in the number-generating mode.

In the initial state, all neurons are empty except neuron ${\sigma }_{l_0}$. Four spikes in neuron ${\sigma }_{l_0}$ are used to trigger the simulation of computation. The simulation of computation follows the simulation of the instructions in the register machine until neuron ${\sigma }_{l_h}$ receives four spikes. When neuron ${\sigma }_{l_h}$ receives four spikes, it means that the computation process in the register machine is successfully simulated, and the FIN module starts to output the computation result stored in register 1.

ADD module: The ADD module is used to simulate instruction $l_i:(ADD\left(r\right),l_j,l_k)$, as shown in Figure 3. This module consists of six neurons and eight rules.

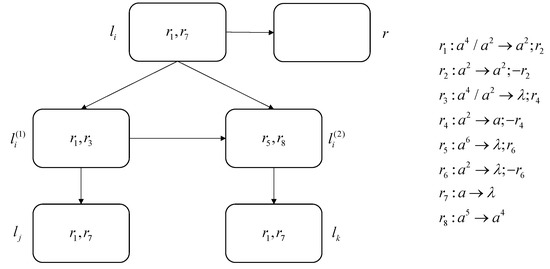
Figure 3. ADD module.

Suppose that at step t, ${\sigma }_{l_i}$ has four spikes and starts simulating instruction $l_i:(ADD\left(r\right),l_j,l_k)$. In neuron ${\sigma }_{l_i}$, the spiking rule with rules dynamic generation and removal $r_1:a^4/a^2\to a^2;r_2$ is applied, consuming two spikes, sending two spikes to ${\sigma }_r$, ${\sigma }_{l_i^{\left(1\right)}}$, and ${\sigma }_{l_i^{\left(2\right)}}$ and adding $r_2:a^2\to a^2;-r_2$. At step $t+1$, ${\sigma }_{l_i}$ has two spikes with $r_1$, $r_2$, and $r_7$. Therefore, ${\sigma }_{l_i}$ applies rule $r_2:a^2\to a^2;-r_2$, sending two spikes to ${\sigma }_r$, ${\sigma }_{l_i^{\left(1\right)}}$, and ${\sigma }_{l_i^{\left(2\right)}}$ and removing $r_2$. At step $t+1$, ${\sigma }_r$ receives two spikes again, for a total of four spikes, corresponding to the number in register r add one. In addition, ${\sigma }_{l_i^{\left(1\right)}}$ has four spikes with rules $r_1$ and $r_2$. Since both rules can be applied, neuron ${\sigma }_{l_i^{\left(1\right)}}$ non-deterministically chooses one to apply. The situations are as follows:

(1)

When neuron ${\sigma }_{l_i^{\left(1\right)}}$ chooses rule $r_1:a^4/a^2\to a^2;r_2$ to apply, it consumes two spikes, sends two spikes to neurons ${\sigma }_{l_j}$ and ${\sigma }_{l_i^{\left(2\right)}}$, and adds rule $r_2:a^2\to a^2;-r_2$. At step $t+3$, ${\sigma }_{l_i^{\left(2\right)}}$ applies the forgetting rule with rules dynamic generation and removal $r_5:a^6\to \lambda ;r_6$, consumes the six spikes it contains, and adds rule $r_6:a^2\to \lambda ;-r_6$. In neuron ${\sigma }_{l_i^{\left(1\right)}}$, since it contains two spikes with rules $r_1$, $r_2$, and $r_3$, rule $r_2:a^2\to a^2;-r_2$ is applied, sending two spikes to neurons ${\sigma }_{l_j}$ and ${\sigma }_{l_i^{\left(2\right)}}$, and removing rule $r_2$. At step $t+4$, ${\sigma }_{l_i^{\left(2\right)}}$ applies $r_6:a^2\to \lambda ;-r_6$, consuming two spikes and removing rule $r_6$. In addition, neuron ${\sigma }_{l_j}$ receives two spikes, containing four spikes in total and starts simulating $l_j$.

(2)

When neuron ${\sigma }_{l_i^{\left(1\right)}}$ chooses rule $r_3:a^4/a^2\to \lambda ;r_4$ to apply, it consumes two spikes and adds rule $r_4$. At step $t+3$, ${\sigma }_{l_i^{\left(1\right)}}$ contains two spikes with rules $r_1$, $r_3$, and $r_4$. Thus, the spiking rule with rules dynamic generation and removal $r_4:a^2\to a;-r_4$ is applied, sending one spike to neurons ${\sigma }_{l_j}$ and ${\sigma }_{l_i^{\left(2\right)}}$, respectively, and removing rule $r_4$. At step $t+4$, ${\sigma }_{l_j}$ applies $a\to \lambda$, forgetting the one spike from neuron ${\sigma }_{l_i^{\left(1\right)}}$. In addition, $r_8:a^5\to a^4$ is applied in neuron ${\sigma }_{l_i^{\left(2\right)}}$, sending four spikes to ${\sigma }_{l_k}$. At step $t+5$, ${\sigma }_{l_k}$ contains four spikes and starts simulating $l_k$.

Table 1 lists five variants of SNP systems and the number of neurons they require to construct the ADD module. From Table 1, it can be seen that DSNP, PASNP, PSNRSP, MPAIRSNP, and SNP-IR require 7, 8, 11, 9, and 8 neurons, respectively, while RDGRSNP requires 6. Therefore, the proposed RDGRSNP system in this paper requires the least number of neurons.

Table 1. The comparison of the number of neurons required to construct the ADD module.

Variants of SNP Systems	Number of Neurons
DSNP [38]	7
PASNP [39]	8
PSNRSP [40]	11
MPAIRSNP [41]	9
SNP-IR [42]	8
RDGRSNP	6

SUB module: The SUB module is used to simulate instruction $l_i:(SUB\left(r\right),l_j,l_k)$, as shown in Figure 4. This module consists of six neurons and twelve rules.

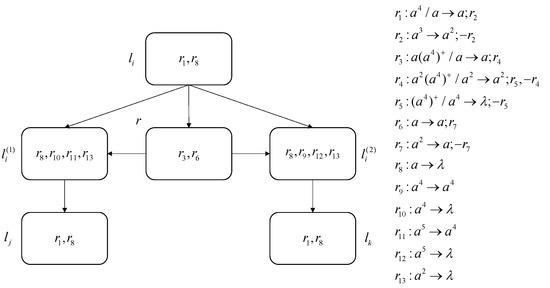
Figure 4. SUB module.

Suppose that neuron ${\sigma }_{l_i}$ contains four spikes at step t and starts simulating instruction $l_i:(SUB\left(r\right),l_j,l_k)$. Neuron ${\sigma }_{l_i}$ applies the spiking rule with rules dynamic generation and removal $r_1:a^4/a\to a;r_2$, sends one spike to ${\sigma }_{l_i^{\left(1\right)}}$, ${\sigma }_{l_i^{\left(2\right)}}$, and ${\sigma }_r$, and adds $r_2$ to the rule set. At step $t+1$, ${\sigma }_{l_i}$ remains with three spikes with rules $r_1$, $r_2$, and $r_8$, so ${\sigma }_{l_i}$ applies the spiking rule with rules dynamic generation and removal $r_2:a^3\to a^2;-r_2$, sends two spikes to the postsynaptic neuron, and removes the rule $r_2$. In ${\sigma }_{l_i^{\left(1\right)}}$ and ${\sigma }_{l_i^{\left(2\right)}}$, the forgetting rule is applied, forgetting one spike. In addition, different rules are applied in neuron ${\sigma }_r$ depending on whether the initial state contains spikes or not in the following two cases:

(1)

If ${\sigma }_r$ contains $4n(n\ge 1)$ spikes, then at step $t+1$, ${\sigma }_r$ applies $r_3:a{\left(a^4\right)}^{+}/a\to a;r_4$, consumes one spike, and sends it to ${\sigma }_{l_i^{\left(1\right)}}$ and ${\sigma }_{l_i^{\left(2\right)}}$. Thus, at step $t+2$, both ${\sigma }_{l_i^{\left(1\right)}}$ and ${\sigma }_{l_i^{\left(2\right)}}$ have three spikes. Additionally, neuron ${\sigma }_r$ contains $4n+2$ spikes with rules $r_3$, $r_4$ and $r_6$. Thus, the spiking rule with rules dynamic generation and removal $r_4:a^2{\left(a^4\right)}^{+}/a^2\to a^2;r_5,-r_4$ is applied, sending two spikes to ${\sigma }_{l_i^{\left(1\right)}}$ and ${\sigma }_{l_i^{\left(2\right)}}$, adding rule $r_5$, and removing rule $r_4$. At step $t+3$, ${\sigma }_r$ applies $r_5:{\left(a^4\right)}^{+}/a^4\to \lambda ;-r_5$, forgetting four spikes. Thus, at step $t+4$, ${\sigma }_r$ has $4n-4$ spikes, corresponding to the number in register r subtracted by one. Additionally, at step $t+3$, ${\sigma }_{l_i^{\left(1\right)}}$ applies $r_{11}:a^5\to a^4$ to send four spikes to ${\sigma }_{l_j}$. In neuron ${\sigma }_{l_i^{\left(2\right)}}$, the forgetting rule $r_{12}:a^5\to \lambda$ is applied. At step $t+4$, ${\sigma }_{l_j}$ contains four spikes, simulating instruction $l_j$.

(2)

If neuron ${\sigma }_r$ does not contain spikes, then at step $t+1$, the spiking rule with rules dynamic generation and removal $r_6:a\to a;r_7$ is applied, sending one spike to ${\sigma }_{l_i^{\left(1\right)}}$ and ${\sigma }_{l_i^{\left(2\right)}}$ and adding $r_7$. At step $t+2$, ${\sigma }_r$ has $r_3$, $r_6$, and $r_7$ with two spikes, so the spiking rule with rules dynamic generation and removal $r_7:a^2\to a;-r_7$ is applied, removing rule $r_7$. Thus, at step $t+3$, the auxiliary neuron ${\sigma }_{l_i^{\left(1\right)}}$ applies rule $r_{10}:a^4\to \lambda$, while ${\sigma }_{l_i^{\left(2\right)}}$ applies rule $r_9:a^4\to a^4$, sending spikes to ${\sigma }_{l_k}$. At step $t+4$, ${\sigma }_{l_k}$ contains four spikes, simulating instruction $l_k$.

Table 2 lists five variants of SNP systems and the number of neurons they require to construct the SUB module. From Table 2, it can be seen that DSNP, PASNP, PSNRSP, MPAIRSNP, and SNP-IR require 7, 10, 15, 8, and 8 neurons, respectively, while RDGRSNP requires 6. Therefore, the proposed RDGRSNP system in this paper requires the least number of neurons.

Table 2. The comparison of the number of neurons required to construct the SUB module.

Variants of SNP Systems	Number of Neurons
DSNP [38]	7
PASNP [39]	10
PSNRSP [40]	15
MPAIRSNP [41]	8
SNP-IR [42]	8
RDGRSNP	6

FIN module: The FIN module is used to simulate the halt instruction $l_h:HALT$ and output the numbers generated by system $\mathrm{\Pi }$, as shown in Figure 5. The generated number n is represented by the time interval between the first two spikes sent to the environment $env$ by the output neuron. The FIN module constructed in this paper consists of three neurons and six rules.

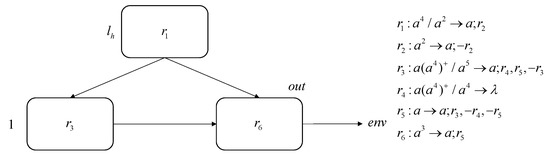
Figure 5. FIN module.

Suppose that at step t, ${\sigma }_{l_h}$ has four spikes, starts simulating instruction $l_h:HALT$ and outputting the computation results. Neuron ${\sigma }_{l_h}$ applies the spiking rule with rules dynamic generation and removal $r_1:a^4/a^2\to a;r_2$, sends one spike to ${\sigma }_1$ and ${\sigma }_{out}$, and adds $r_2$ to it. Thus, at step $t+1$, neuron ${\sigma }_{l_h}$ applies $r_2:a^2\to a;r_2$, sends one spike to ${\sigma }_1$ and ${\sigma }_{out}$, and removes $r_2$. Neuron ${\sigma }_1$ applies the spiking rule with rules dynamic generation and removal $r_3:a{\left(a{}^4\right)}^{+}/a^5\to a;r_4,r_5,-r_3$, consuming five spikes, sending one spike to the output neuron ${\sigma }_{out}$, adding rules $r_4$ and $r_5$, and removing rule $r_3$. At step $t+2$, ${\sigma }_{out}$ applies $r_6:a^3\to a;r_5$ sending the first spike to $env$ and adding $r_5$. So, starting from step $t+2$, neuron ${\sigma }_1$ will forget four spikes at each step until step $t+n+1$, where $n\ge 1$.

At step $t+n+1$, ${\sigma }_1$ has only one spike with rules $r_4$ and $r_5$. Therefore, it applies the spiking rule with rules dynamic generation and removal $r_5:a\to a;r_3,-r_4,-r_5$, sends one spike to ${\sigma }_{out}$, adds $r_3$, and removes rules $r_4$ and $r_5$. At step $t+n+2$, ${\sigma }_{out}$ applies $r_5:a\to a;r_3,-r_4,-r_5$ to send the second spike to $env$. Thus, the time interval between the first two spikes sent by ${\sigma }_{out}$ to the environment is $(t+n+2)-(t+2)=n$, i.e., the number stored in register 1 when the computation stops.

Table 3 lists five variants of SNP systems and the number of neurons they require to construct the FIN module. From Table 3, it can be seen that DSNP, PASNP, PSNRSP, MPAIRSNP, and SNP-IR require 4, 9, 8, 8, and 5 neurons, respectively, while RDGRSNP requires 3. Therefore, the proposed RDGRSNP system in this paper requires the least number of neurons.

Table 3. The comparison of the number of neurons required to construct the FIN module.

Variants of SNP Systems	Number of Neurons
DSNP [38]	4
PASNP [39]	9
PSNRSP [40]	8
MPAIRSNP [41]	8
SNP-IR [42]	5
RDGRSNP	3

Theorem 2.

$N_{acc}RDGRSNP\left(\Pi \right)=NRE$

Proof 

Similarly, by Turing Church’s theorem, we have $N_{acc}RDGRSNP\left(\mathrm{\Pi }\right)\subseteq NRE$, so we only need to prove $NRE\subseteq N_{acc}RDGRSNP\left(\mathrm{\Pi }\right)$. For $NRE\subseteq N_{acc}\left(\Pi \right)$, we simulate the register machine to prove it by following the process shown in Figure 6.   □

Figure 6. Flowchart of the RDGRSNP system simulating the register machine in number-accepting mode.

In the initial state, neuron ${\sigma }_1$ contains $4n$ spikes, corresponding to the number n to be accepted in the register machine, neuron ${\sigma }_{l_0}$ contains four spikes for triggering the simulation of computation, and all the remaining neurons are empty. The simulation of computation follows the simulation of instructions in the register machine until neuron ${\sigma }_{l_h}$ receives four spikes. When neuron ${\sigma }_{l_h}$ receives four spikes, it means that the computation process in the register machine is simulated successfully, the computation stops, and the number is accepted.

First, in the number-accepting mode, we need the INPUT module to read the number to be accepted. The number n to be accepted is represented by the time interval between the first two spikes entered, i.e., the spike train entered is: ${10}^{n-1}1$.

INPUT module: The INPUT module is used to read the number to be accepted, as shown in Figure 7. This module consists of nine neurons and seven rules.

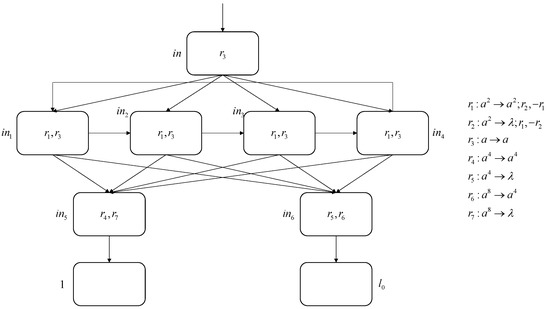
Figure 7. INPUT module.

Suppose that at step 0, ${\sigma }_{in}$ receives one spike, so at step 1, ${\sigma }_{in}$ applies $r_3:a\to a$ and sends one spike to auxiliary neurons ${\sigma }_{i{n}_1}$, ${\sigma }_{i{n}_2}$, ${\sigma }_{i{n}_3}$, and ${\sigma }_{i{n}_4}$, respectively. Starting from step 2, auxiliary neurons ${\sigma }_{i{n}_1}$, ${\sigma }_{i{n}_2}$, ${\sigma }_{i{n}_3}$, and ${\sigma }_{i{n}_4}$ will send spikes in a cycle and send one spike to ${\sigma }_{i{n}_5}$ and ${\sigma }_{i{n}_6}$, respectively. For neuron ${\sigma }_{i{n}_5}$, it applies $r_4:a^4\to a^4$ to send four spikes to ${\sigma }_1$; for neuron ${\sigma }_{i{n}_6}$, it applies rule $r_5:a^4\to \lambda$ to forget the received four spikes. The above process will continue until the input neuron ${\sigma }_{in}$ receives another spike.

At step n, ${\sigma }_{in}$ receives another spike, so at step $n+1$, ${\sigma }_{in}$ applies $r_3:a\to a$ again, sends one spike to ${\sigma }_{i{n}_1}$, ${\sigma }_{i{n}_2}$, ${\sigma }_{i{n}_3}$, and ${\sigma }_{i{n}_4}$. At step $n+2$, ${\sigma }_{i{n}_1}$, ${\sigma }_{i{n}_2}$, ${\sigma }_{i{n}_3}$, and ${\sigma }_{i{n}_4}$ all apply the spiking rule with rules dynamic generation and removal $r_1:a^2\to a^2;r_2,-r_1$, send two spikes to neurons ${\sigma }_{i{n}_5}$ and ${\sigma }_{i{n}_6}$, remove rule $r_1$, and add rule $r_2$. Thus, at step $n+3$, these four auxiliary neurons apply rule $r_2:a^2\to \lambda ;r_1,-r_2$ to forget two spikes. At step $n+3$, both neurons ${\sigma }_{i{n}_5}$ and ${\sigma }_{i{n}_6}$ receive eight spikes. Neuron ${\sigma }_{i{n}_5}$ applies rule $r_7:a^8\to \lambda$ to forget the spikes in it. Neuron ${\sigma }_1$ receives four spikes at step $n+2$, so it contains $4n$ spikes. In ${\sigma }_{i{n}_6}$, rule $r_6:a^8\to a^4$ is applied to send four spikes to ${\sigma }_{l_0}$. Then, neuron ${\sigma }_{l_0}$ contains four spikes, simulating the starting instruction $l_0$.

Table 4 lists five variants of SNP systems and the number of neurons they require to construct the INPUT module. From Table 4, it can be seen that DSNP, PASNP, PSNRSP, MPAIRSNP, and SNP-IR require 6, 6, 10, 6, and 9 neurons, respectively, while RDGRSNP requires 9. However, this is acceptable because the INPUT module will be used only once in the number-generating mode and will not have a great impact on the overall number of neurons.

Table 4. The comparison of the number of neurons required to construct the INPUT module.

Variants of SNP Systems	Number of Neurons
DSNP [38]	6
PASNP [39]	6
PSNRSP [40]	10
MPAIRSNP [41]	6
SNP-IR [42]	6
RDGRSNP	9

In the number-generating mode, the SUB instruction in M does not change, so we can continue to use the SUB module in Theorem 1 above. Since the system stop means that the input numbers are accepted, an additional FIN module is no longer needed to output the computation results. However, in the number-accepting mode, the ADD instruction in M is no longer in the non-deterministic form of $l_i:(ADD\left(r\right),l_j,l_k)$, but in the deterministic form of $l_i:(ADD\left(r\right),l_j)$. Therefore, this paper provides a deterministic ADD module, as shown in Figure 8. This module consists of only three neurons and three rules.

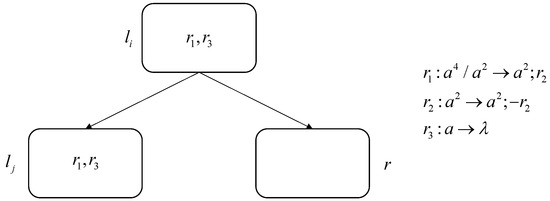
Figure 8. Deterministic ADD module.

In this deterministic ADD module, ${\sigma }_{l_i}$ sends spikes to ${\sigma }_r$, simulating the operation of adding one to the number of register r and, at the same time, sends spikes to ${\sigma }_{l_j}$, causing instruction $l_j$ to start being simulated.

Table 5 lists five variants of SNP systems and the number of neurons they require to construct the deterministic ADD module. From Table 5, it can be seen that DSNP, PASNP, PSNRSP, MPAIRSNP, and SNP-IR require 4, 3, 5, 3, and 3 neurons, respectively, while RDGRSNP requires 3. Therefore, PASNP, MPAIRSNP, SNP-IR and the proposed RDGRSNP system in this paper require the least number of neurons.

Table 5. The comparison of the number of neurons required to construct the deterministic ADD module.

Variants of SNP Systems	Number of Neurons
DSNP [38]	4
PASNP [39]	3
PSNRSP [40]	5
MPAIRSNP [41]	3
SNP-IR [42]	3
RDGRSNP	3

4. Small Universal SNP System with Rules Dynamic Generation and Removal

This section presents a small universal RDGRSNP system used to simulate function computation and demonstrates that the RDGRSNP system we proposed requires fewer neurons by comparing it with five variants of SNP systems.

Theorem 3.

A small universal RDGRSNP system using 68 neurons can implement function simulation.

Regarding Theorem 3, we continue to prove it by simulating a register machine. In $M_u$ [41], for simulating the function computation shown in Figure 9, there always exists a recursive function g such that ${\theta }_x\left(y\right)=M_u(g\left(x\right),y)$ holds for any ${\theta }_x\left(y\right)$, where ${\theta }_x\left(y\right)$ is any one function of the fixed enumeration $({\theta }_1,{\theta }_2,\dots )$ of all unary partial recursive functions, $M_u$ denotes a universal register machine, and $g\left(x\right)$ and y are two parameters with $x,y\in N$ stored in registers 1 and 2, respectively. The register machine $M_u$ for the simulating function computation stops when the execution reaches $l_h:HALT$. The result of the computation is stored in register 0.

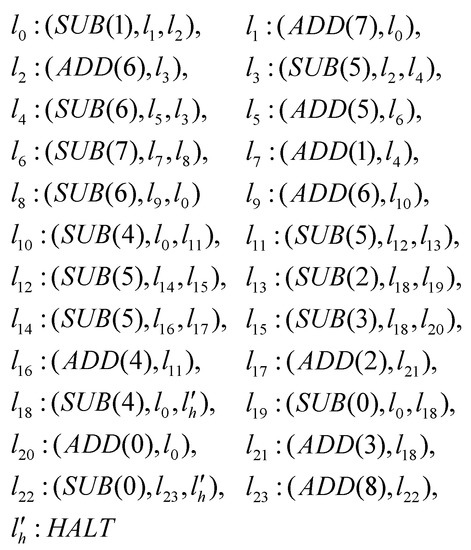
Figure 9. Register machine $M_u$.

Proof 

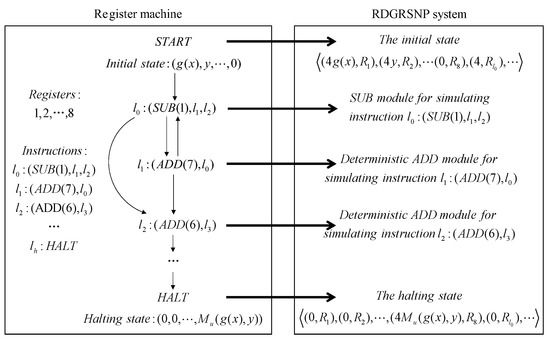
For Theorem 3, we simulate the register machine to prove it by following the process shown in Figure 10.

Figure 10. The flowchart of a small universal RDGRSNP system simulating a register machine.

In the initial state, neuron ${\sigma }_1$ contains $4g\left(x\right)$ spikes, corresponding to parameter $g\left(x\right)$ in register 1, neuron ${\sigma }_2$ contains $4y$ spikes, corresponding to parameter y in register 2, neuron ${\sigma }_{l_0}$ contains four spikes for triggering the simulation of computation, and all the remaining neurons are empty. The simulation of computation follows the simulation of instructions in the register machine until neuron ${\sigma }_{l_h}$ receives four spikes. When neuron ${\sigma }_{l_h}$ receives four spikes, it means that the computation process of the register machine is successfully simulated and the computation stops. Meanwhile, the FIN module is triggered and used to output the computation result.

In $M_u$, the SUB instruction in the form of $l_i:(SUB\left(r\right),l_j,l_k)$, the halt instruction $l_h:HALT$, and the deterministic ADD instruction in the form of $l_i:(ADD\left(r\right),l_j)$ are included. Thus, we can continue to use the SUB, FIN, and deterministic ADD module, as proposed in Theorems 1 and 2 above. In addition, since two registers are needed to store parameters $g\left(x\right)$ and y, respectively, this paper makes a little change to the INPUT module in Theorem 2 above, as shown in Figure 11. We still use the time interval between two spikes to represent the input number, so the input sequence is ${10}^{g\left(x\right)-1}{10}^{y-1}1$.

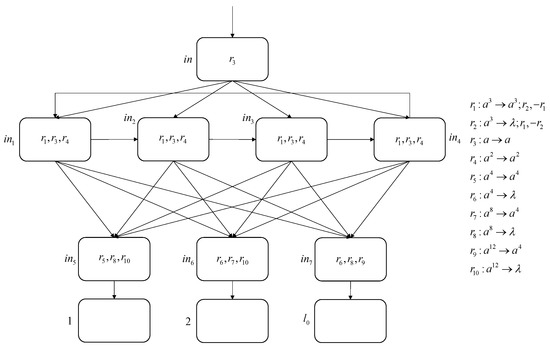
Figure 11. INPUT module in register machine $M_u$.

Suppose that at step 0, ${\sigma }_{in}$ receives the first spike, so at step 1, ${\sigma }_{in}$ applies $r_3:a\to a$ and sends one spike to the four auxiliary neurons ${\sigma }_{i{n}_1}$, ${\sigma }_{i{n}_2}$, ${\sigma }_{i{n}_3}$, and ${\sigma }_{i{n}_4}$. Thus, from step 2, these four auxiliary neurons send spikes in a cycle by applying rule $r_3:a\to a$, and all send one spike to ${\sigma }_{i{n}_5}$, ${\sigma }_{i{n}_6}$, and ${\sigma }_{i{n}_7}$. For neuron ${\sigma }_{i{n}_5}$, starting at step 3, it continuously applies $r_5:a^4\to a^4$ to send four spikes to ${\sigma }_1$, by which the first input number is stored in ${\sigma }_1$, while for neurons ${\sigma }_{i{n}_6}$ and ${\sigma }_{i{n}_7}$, they continuously apply rule $r_6:a^4\to \lambda$ to forget four spikes. The process continues until the input neuron receives the second spike.

At step $g\left(x\right)$, ${\sigma }_{in}$ receives the second spike, so at step $g\left(x\right)+1$, ${\sigma }_{in}$ applies $r_3:a\to a$ again, sends one spike to neurons ${\sigma }_{i{n}_1}$, ${\sigma }_{i{n}_2}$, ${\sigma }_{i{n}_3}$, and ${\sigma }_{i{n}_4}$. Thus, starting at step $g\left(x\right)+2$, these four neurons apply rule $r_4:a^2\to a^2$ to send two spikes in a cycle, while sending two spikes to their postsynaptic neurons ${\sigma }_{i{n}_5}$, ${\sigma }_{i{n}_6}$, and ${\sigma }_{i{n}_7}$. Similarly, for neuron ${\sigma }_{i{n}_6}$, starting at step $g\left(x\right)+3$, it applies rule $r_7:a^8\to a^4$ continuously to send four spikes to the neuron ${\sigma }_2$, by which the second input number is stored in ${\sigma }_2$. For neurons ${\sigma }_{i{n}_5}$ and ${\sigma }_{i{n}_7}$, they apply rule $r_8:a^8\to \lambda$ to forget the spikes. The process continues until ${\sigma }_{in}$ receives the third spike. In addition, ${\sigma }_1$ receives four spikes sent from ${\sigma }_{i{n}_5}$ at step $g\left(x\right)+2$. Therefore, ${\sigma }_1$ contains $4g\left(x\right)$ spikes, which corresponds to the number $g\left(x\right)$ in register 1.

At step $g\left(x\right)+y$, ${\sigma }_{in}$ receives the third spike, so at step $g\left(x\right)+y+1$, ${\sigma }_{in}$ applies $r_3:a\to a$ again and sends one spike to ${\sigma }_{i{n}_1}$, ${\sigma }_{i{n}_2}$, ${\sigma }_{i{n}_3}$, and ${\sigma }_{i{n}_4}$. At step $g\left(x\right)+y+2$, neurons ${\sigma }_{i{n}_1}$, ${\sigma }_{i{n}_2}$, ${\sigma }_{i{n}_3}$, and ${\sigma }_{i{n}_4}$ all contain three spikes with rules $r_1$, $r_3$, and $r_4$, so they all apply the spiking rule with rules dynamic generation and removal $r_1:a^3\to a^3;r_2,-r_1$, send three spikes to neurons ${\sigma }_{i{n}_5}$, ${\sigma }_{i{n}_6}$, and ${\sigma }_{i{n}_7}$, and add rule $r_2$ and remove rule $r_1$. At step $g\left(x\right)+y+3$, neurons ${\sigma }_{i{n}_1}$, ${\sigma }_{i{n}_2}$, ${\sigma }_{i{n}_3}$, and ${\sigma }_{i{n}_4}$ all apply the forgetting rule with rules dynamic generation and removal $r_2:a^3\to \lambda ;r_1,-r_2$, forget three spikes, and remove rule $r_2$ and add rule $r_1$ again. Meanwhile, both neurons ${\sigma }_{i{n}_5}$ and ${\sigma }_{i{n}_6}$ contain 12 spikes and apply rule $r_{10}:a^{12}\to \lambda$ to forget these 12 spikes. Neuron ${\sigma }_{i{n}_7}$ applies rule $r_9:a^{12}\to a^4$ to send four spikes to ${\sigma }_{l_0}$. In addition, ${\sigma }_2$ receives four spikes sent by neuron ${\sigma }_{i{n}_6}$ at step $g\left(x\right)+y+2$, so it has $4y$ spikes, which corresponds to the number y in register 2. At step $g\left(x\right)+y+4$, ${\sigma }_{l_0}$ contains four spikes, simulating the starting instruction $l_0$.

Table 6 lists five variants of SNP systems and the number of neurons they need to build the INPUT module in the register machine. From Table 6, it can be seen that DSNP, PASNP, PSNRSP, MPAIRSNP, and SNP-IR require 9, 9, 13, 9, and 9 neurons, respectively, while RDGRSNP requires 11. However, this is acceptable because the INPUT module will be used only once during the simulation of function calculation and will not have a great impact on the overall number of neurons.

Table 6. The comparison of the number of neurons required to construct the INPUT module in register machine $M_u$.

Variants of SNP Systems	Number of Neurons
DSNP [38]	9
PASNP [39]	9
PSNRSP [40]	13
MPAIRSNP [41]	9
SNP-IR [42]	9
RDGRSNP	11

According to the INPUT, deterministic ADD, SUB, and FIN modules described above, a small universal RDGRSNP system for simulating function ${\theta }_x\left(y\right)=M_u(g\left(x\right),y)$ consists of 71 neurons, as follows:

(1)

Neurons used to start simulating instructions: 25

(2)

Neurons used to simulate registers: 9

(3)

Auxiliary neurons in the ADD module: 0

(4)

Auxiliary neurons in the SUB module: $2\times 14=28$

(5)

The input and auxiliary neurons in the INPUT module: 8

(6)

The output neuron in the FIN module: 1

We can also further reduce the number of neurons by compound connections between modules, and the following is the specific structure of compound connections between modules.

Figure 12 represents the composite connection of a set of consecutive ADD instructions $l_i:(ADD\left(r^{\prime }\right),l_g)$ and $l_g:(ADD\left(r^{\prime \prime }\right),l_j)$. We put ${\sigma }_{r^{\prime }}$ from the former module into the latter module, removing ${\sigma }_{l_g}$.

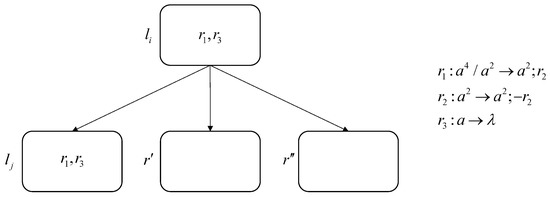
Figure 12. Compound connection of ADD–ADD.

Figure 13 represents the compound connection of a set of consecutive ADD instruction $l_i:(ADD\left(r^{\prime }\right),l_g)$ and SUB instruction $l_g:(SUB\left(r^{\prime \prime }\right),l_j,l_k)$. We put the neuron ${\sigma }_{r^{\prime }}$ of the former ADD module into the later SUB module, removing ${\sigma }_{l_g}$.

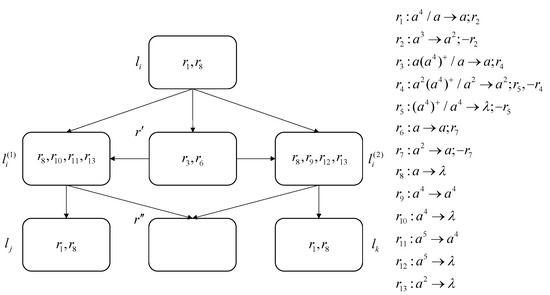
Figure 13. Compound connection of ADD–SUB.

By the compound connection between the modules mentioned above, we remove three neurons ${\sigma }_{l_{21}}$, ${\sigma }_{l_6}$, and ${\sigma }_{l_{10}}$, so that the number of neurons required to build a small universal RDGRSNP system for simulating function ${\theta }_x\left(y\right)=M_u(g\left(x\right),y)$ is reduced from 71 to 68.

Table 7 lists several variants of SNP systems and the number of neurons they require to construct a small universal SNP system for simulating function computation. From the table, it can be seen that five variants of SNP systems, DSNP, PASNP, PSNRSP, MPAIRSNP, and SNP-IR, require 81, 121, 151, 95, and 100 neurons, respectively, while the RDGRSNP system proposed in this paper requires only 68.

Table 7. The comparison of the number of neurons required to construct a small universal SNP system for simulating function computation.

Variants of SNP Systems	Number of Neurons
DSNP [38]	81
PASNP [39]	121
PSNRSP [40]	151
MPAIRSNP [41]	95
SNP-IR [42]	100
RDGRSNP	68

In the construction of SNP systems, the number of neurons is generally used to measure the computational resources required to build a system. A smaller number of neurons means fewer computational resources are required to build a system; conversely, a larger number of neurons means more resources are required to build a system. Therefore, the smaller the number of neurons needed to construct the SNP system, the better. As we can see in Table 7, our proposed RDGRSNP systems require fewer neurons to build a small universal SNP system for simulating function ${\theta }_x\left(y\right)=M_u(g\left(x\right),y)$. This means that a RDGRSNP system needs only fewer computational resources compared to other systems. Thus, our proposed RDGRSNP systems have an advantage.   □

5. Conclusions

In conventional SNP systems, the rules contained in neurons do not change during the computation process. However, biochemical reactions in biological neurons tend to be different depending on factors such as the substances in the neuron. Considering this motivation, RDGRSNP systems are proposed in this paper. In RDGRSNP systems, neurons apply rules to update the rule set. In Section 2, we give the definition of RDGRSNP systems and illustrate how RDGRSNP systems work with an illustrative example.

In Section 3, we demonstrate the computational power of RDGRSNP systems by simulating the register machines. Specifically, we demonstrate that RDGRSNP systems are Turing universal when used as a number-generating device and a number-accepting device. Subsequently, in Section 4, we construct a small universal RDGRSNP system by using 68 neurons. By comparing with five variants of SNP systems, DSNP, Asynchronous RSSNP, PASNP, PSNRSP, MPAIRSNP, and SNP-IR, it is demonstrated that the RDGRSNP system proposed in this paper requires only fewer resources to construct a small universal RDGRSNP system for simulating function computation.

Our future research will focus on the following areas. Although the computational power of RDGRSNP systems has been demonstrated, the potential of RDGRSNP systems goes far beyond that. SNP systems have shown excellent capabilities in solving NP problems, and we have demonstrated the advantage of RDGRSNP systems compared with other variants of SNP systems. Therefore, we believe that RDGRSNP systems can perform better in solving NP problems.

RDGRSNP systems proposed in this paper work in sequential mode. However, there are other modes of operation such as asynchronous mode that have not been discussed. In asynchronous mode, the neurons in the system can choose to apply or not to apply the rules at each step. Of course, these rules also need to satisfy control conditions to be applied. Therefore, neurons have more autonomy in asynchronous mode. Many variants of SNP systems have been discussed working in asynchronous mode. An exploration of RDGRSNP systems working in asynchronous mode is also a future research direction for this paper.