Optimal Solution of Environmental Economic Dispatch Problems Using QPGPSO-ω

Abstract

The renewable energy sources (RESs)-based economic dispatch problem (EDP) is of vital importance for modern power systems. Environmental pollution, climatic degradation, and rapidly growing prices of continuously depleting fossil fuels have encouraged researchers to consider mechanisms for RES implementation and optimal operations. This paper presents a quasi-oppositional population-based global particle swarm optimizer with inertial weights (QPGPSO-ω) to solve environment friendly EDPs. The optimization technique is applied to solve the EDP under different scenarios including cases where only renewable energy sources (RESs) are used and the cases where combined emission–economic dispatch (CEED) problem is taken into account. The scenario for RESs includes a combination of six wind, five solar PV, and four biofuel systems for power generation. EDPs are considered without any constraints, and the variability of resources is depicted over time, along with the regional load-sharing dispatch (RLSD). The case of CEED considers ten thermal units with the valve point loading (VPL) effect and transmission losses. The results obtained by the proposed QPGPSO-ω algorithm are better than the reported results employing other optimization methods. This is shown by the lower costs achieved up to USD 8026.1439 for the case of only RES-based EDPs, USD 1346.8 for the case of RES-based EDPs with RLSD, and USD 111,533.59 for the case of CEED. Thus, the proposed QPGPSO-ω algorithm was effective in solving the various adopted power dispatch problems in power system.

1. Introduction

1.1. Background and Motivation

Environmental sustainability, rapid depletion and constantly fluctuating prices of fossil fuels are currently forcing the incorporation of renewable energy sources (RESs) into power grids [1,2]. The recent research predominantly focused on exploring energy generation using various renewable resources [3,4,5]. However, these RESs present their own limitations, both climatic and technical, as their resource availability is subject to variations caused by climate conditions. In addition, the extraction of bulk power from major renewable energy sources (such as solar and wind) is primarily feasible in locations that are situated far away from major load centers. Thus, there is a requirement for properly designed dispatch mechanisms to transmit the produced power from the source to the load in an efficient and economically effective manner [6,7].

RESs have issues; however, they still manage to produce good results in their power generation performance, such as wind; biofuel and solar systems produced approximately 700, 671, and 659 GWs of installed capacity till 2020 [8,9]. However, the high variability of resource availability requires a well-designed metaheuristic optimization algorithm for the calculation of economic dispatch (ED) [10]. The developed ED algorithm should not only provide the efficient dispatch of power, but also account for the penalties imposed as a result of resource variability.

Pakistan presents a significant potential for RESs and there is a growing trend towards utilizing these emission-free resources for power generation. The authors conducted an extensive survey of the availability of wind resources in the southern regions of Pakistan, as documented in [11,12]. A detailed survey of the regions rich in solar-based power generation in Pakistan and the prospects of its hybridization with wind energy sources was presented in [13,14]. In [15,16,17], the authors deliberated on the potential of extractable bio-fuel-based energy in the country and examined various scenarios for extracting energy from waste materials. The authors in [18,19,20] provided a comprehensive analysis of several renewable energy-based projects that were executed in various appropriate locations to generate environment friendly electricity.

The ED problem (EDP) is a computational mechanism used to determine the optimal distribution of generated electric power in order to meet the load demand, while minimizing the production cost [21]. Obtaining the optimum solution for EDPs is a critical requirement for a sustainable power network, while considering various operational constraints. The developed algorithm should not only consider the operational limitations of RESs, but also the constraints of thermal systems, such as ramp rate limits (RRLs), and prohibited operating zones (POZs) should be taken into account [22,23].

1.2. Literature Review

Initially, deterministic techniques were employed to achieve the optimal solution for basic EDPs. These classical techniques were effective in optimizing small- to medium-scale thermal power systems, without taking into account the operational constraints [24,25,26]. However, the shortcomings of these deterministic algorithms became evident when attempting to solve complex dispatch problems that involved operational constraints. Modern power systems comprise a significant number of generating units and necessitate the consideration of several operational constraints, such as RRL, POZ, losses, and multiple fuel cost functions. Accomplishing feasible solutions in such systems mandates the utilization of sophisticated optimization algorithms.

The researchers worked on the development of metaheuristic optimization algorithms for achieving the optimal solution of constraints-based EDPs incorporating thermal and hybrid power systems. The utilization of the genetic algorithm (GA) and its variants for obtaining optimal solutions to various categories of EDPs was surveyed by the authors in [27,28], and they also compared the performance of these algorithms. In [29,30], the authors presented a review and application of the artificial bee colony (ABC) algorithm and its hybridized variant for solving the multi-area economic dispatch (MAED) problem. They also considered factors, such as of POZ, losses, VPL effects, tie-line constraints, and multiple fuel scenario.

A comprehensive analysis of the utilization of the standard PSO and its various variants for obtaining optimal solutions to both constrained and unconstrained EDPs was presented in [24,25,26,31,32,33,34]. Additionally, the authors also compared the performance of these algorithms with other notable metaheuristic techniques. However, the focus was primarily on achieving optimal solutions for EDPs based on thermal power plants (TPPs). The application of the bat algorithm (BA) and its variants for solving different instances of EDPs, while taking into account the integration of wind power systems, was presented in [35,36]. The developed algorithms were evaluated on 25 benchmark standard functions, and the outcomes were compared with other metaheuristic techniques for the selected test cases [37].

Due to the escalating power demand (PD) and the high rate of carbon emissions from TPPs, the integration of RESs into existing power networks is of utmost importance [38,39]. According to the research, load frequency control is challenging because of uncertain power generation and variable load demands [40,41,42]. The designed version of the PSO approach was utilized to attain an optimal solution for various categories of EDPs that involved both TPPs and RESs. In [43], the authors addressed the optimization of EDPs by taking into account the concept of virtual power plants (VPPs) comprising wind farms and hybridized TPPs. However, they did not consider the penalty costs associated with under- and overestimations of the wind power framework. The resolution of EDPs that involve wind and PV frameworks, as well as TPP combinations, was presented in [44], with the consideration of penalty functions only for the wind power system. In [45], the authors presented the mathematical expressions for calculating the costs of power systems that integrate wind and solar PVs with conventional TPPs. EDPs involving a combination of a PV system and a biofuel plant as an alternative to fossil fuels was solved in [46].

The extensive utilization of TPPs leads to a high emission rate of hazardous substances that cause severe environmental pollution and negatively impact the health of the general public [47]. In addition to the integration of RESs, the researchers also emphasized the importance of developing mechanisms for the optimal calculation of emissions with the goal of reducing them [48,49,50,51,52]. The incorporation of economic and environmental considerations is essential to attain eco-friendly power-generation and dispatch mechanisms, which can be achieved through a combined CEED approach.

1.3. Research Focus

Global particle swarm optimizer with inertial weights (GPSO-ω) is a variant of PSO algorithm, which is a stochastic optimization technique used to solve complex optimization problems. QPGPSO-ω, which is an extension of GPSO-ω, was utilized in [53] for the solution of ED-IEEE standard (3, 6, 13, 15, 40, and 140) units for Korean grid thermal test systems under various constraints. QPGPSO-ω outperformed several other methods in solving the EDP, showcasing superior results. However, in this study, QPGPSO-ω is applied to address the challenges of EDPs specifically related to the integration of RESs and the consideration of CEED. The main focus of this study is as follows:

• Validation of the QPGPSO-ω methodology for solving only RES-based EDs with resource variability.
• Validation of the QPGPSO-ω methodology for solving regional load sharing dispatch.
• Utilization of QPGPSO-ω to solve the CEED problem for ten-unit TPPs, which is a significant challenge in power systems due to various constraints, such as VPL effects and losses.

1.4. Paper Organization

The study is structured in the following sections. Section 2 provides the mathematical formulations of the EDPs under consideration. In Section 3, the proposed methodology is described in detail, including a flowchart and pseudocode. The results and their implications are discussed in Section 4, whereas the concluding remarks are mentioned in Section 5.

2. Mathematical Formulations

RESs are considered as the future of electric power generation systems due to several factors, such as environmental concerns caused by conventional resources, their rapid depletion, and fluctuating prices. The primary challenge for the large-scale implementation of RES-based power generation, especially in developing countries, is the considerable distance between major load centers and optimal sites for large-scale RES-based power generation. The objective function and mathematical formulations for the operational limitations of the considered power systems are presented in the following sub-sections.

2.1. Objective Function

The cost function for the power framework comprising only RESs is presented in (1):

$${Cost}_{Total}=\sum _{i=1}^N\left[\begin{array}{c}{\displaystyle \sum _{j=1}^{N_{wi}}}{f}_{wij}(P_{wij})+{\displaystyle \sum _{j=1}^{N_{si}}}{f}_{sij}(P_{sij})+{\displaystyle \sum _{j=1}^{N_{bi}}}{f}_{bij}(P_{bij})\end{array}\right]$$

(1)

The objective function in (1) was designed by the total cost incurred in generating electric power from wind, PV, and biofuel-based plants, and is taken from [54]. $f_{wij}\left(P_{wij}\right), f_{sij}\left(P_{sij}\right), f_{bij}\left(P_{bij}\right)$ in (1) represent the cost functions of j^th wind, PV, and biofuel-based plants in region i. The mathematical relations for the computation of extractable power and its respective cost from the mentioned RESs are presented in the proceeding sub-section.

2.2. Formulations for the Consideration of Resource Variability

RESs, due to their intermittent nature, require the consideration of over- and underestimations of the resources and corresponding power availability. Overestimation occurs when the estimated power and its corresponding costs are lower than the actual available resource and the resulting power and cost from wind sources. On the other hand, underestimation refers to a situation where the extracted power and its associated costs are higher than the predicted values. The mathematical representations for the overestimation, underestimation, and the direct generation cost of wind resources are provided in (2)–(4) respectively:

$$f_{wij}\left(P_{wij}\right)=C_{pwij}\left(P_{wav,ij}-P_{wsh,ij}\right)+C_{rwij}\left(P_{wsh,ij}-P_{wav,ij}\right)\times \left(k_{wij}\times P_{wav,ij}\right)$$

(2)

$$C_{rwij}\left(P_{wsh,ij}-P_{wav,ij}\right)=k_{rwij}\times \underset{0}{\overset{P_{wsh,ij}}{\int }}(P_{iwsh,ij}-w_{ij})f_{wij}(w_{ij}){dw}_{ij}$$

(3)

$$C_{pwij}\left(P_{wav,ij}-P_{wsh,ij}\right)=k_{pwij}\times \underset{P_{wsh,ij}}{\overset{P_{wr,ij}}{\int }}(w_{ij}-P_{iwsh,ij})f_{wij}(w_{ij}){dw}_{ij}$$

(4)

where the power generated by the j^th wind turbine in region i is represented as $P_{wij}$. Additionally, the coefficients representing the direct, penalty, and reserve costs of the j^th wind turbine in region i are denoted as $k_{wij}$, $k_{pwij}$, and $k_{rwij}$, respectively. The cut-in, cut-out, and rated speeds of wind are represented as v_cut-in, v_cut-out, and v_r, respectively [55]. Similarly, the penalties for over- (reserve) and underestimations, as well as the direct cost associated with PV-based generation, are presented in (5)–(7):

$$f_{sij}\left(P_{sij}\right)=k_{sij}\times P_{sav,ij}+C_{psij}\left(P_{sav,ij}-P_{ssh,ij}\right)+C_{rsij}\left(P_{ssh,ij}-P_{sav,ij}\right)$$

(5)

$$C_{rsij}\left(P_{ssh,ij}-P_{sav,ij}\right)=f_s\left(P_{sav,ij}<P_{ssh,ij}\right)\times \left[E\left(P_{sav,ij}<P_{ssh,ij}\right)\right]\times k_{rsij}$$

(6)

$$C_{psij}\left(P_{sav,ij}-P_{ssh,ij}\right)=k_{psij}\times \left[E\left(P_{sav,ij}>P_{ssh,ij}\right)-P_{ssh,ij}\right]\times f_s\left(P_{sav,ij}>P_{ssh,ij}\right)$$

(7)

The power output extracted from the solar PV system, generated by the j^th solar plant in the designated i region, is represented as $P_{sij}$. The coefficients associated with the costs for direct, penalty, and reserve expenses for the j^th PV plant in the I region are specified as $k_{sij}$, $k_{psij}$, and $k_{rsij}$, respectively. The terms $f_s\left(P_{sav,ij}>P_{ssh,ij}\right)$, $f_s\left(P_{sav,ij}<P_{ssh,ij}\right)$ taken from Equations (6) and (7), respectively, represent the potential for the excess and deficiency of scheduled power from the PV source. Also, $\left[E\left(P_{sav,ij}>P_{ssh,ij}\right)-P_{ssh,ij}\right]$, $\left[E\left(P_{sav,ij}<P_{ssh,ij}\right)\right]$ indicate the anticipated PV power that exceeds or falls below the planned corresponding output [56].

The third RES considered for power supply was biofuel. To determine the computational cost of power generation from biofuel, a quadratic cost function is employed, as described in (8) [34,57]:

$$f_{bij}\left(P_{bij}\right)=a\times P_i^2+b\times P_i+c$$

(8)

where a, b, and c represent the coefficients for the quadratic cost function.

2.3. Regional Load Sharing Dispatch (RLSD)

RLSD is classified as the exchange or sharing of available energy from multiple sources, which are distributed across different regions. Numerically it is presented as (9):

$$\sum _{i=1}^{N_{areas}}{P}_{N_{i,max}}\ge \sum _{i=1}^N{P}_{B_i}+\sum _{i=1}^N{P}_{W_i}+\sum _{i=1}^N{P}_{S_i}$$

(9)

where $P_N$, $P_B$, $P_W$, and $P_S$ represent the power values from the entire system, biofuel, wind, and PV sources, respectively, which can be mutually used according to the regional requirements. Variable N represents the region of the power production resources [58].

2.4. Combined Emissions Economic Dispatch (CEED)

The calculation for the CEED problem is performed through (10) and (11), given in [48,49].

$$Emissions=E\left(P_i\right)=\sum _{i=1}^N({\alpha }_i+{\beta }_i{P}_i+{\gamma }_i{P}_i^2)+{\zeta }_{i}exp({\lambda }_i{P}_i)$$

(10)

$$CEED=\sum _{I=1}^N\left[\begin{array}{c}\begin{array}{c}\{a_i+b_i{P}_i+a_i{P}_i^2+\left|e_i\right.\sin {(f}_i(P_i^{min}-P_i)\left.)\right|\}\\ +PP{F}_i\times ({\alpha }_i+{\beta }_i{P}_i+{\gamma }_i{P}_i^2)+{\zeta }_{i}exp({\lambda }_i{P}_i)\end{array}\end{array}\right]$$

(11)

The emission coefficients for the i^th generating unit are represented by ${\alpha }_i$, ${\beta }_i$, ${\gamma }_i$, ${\zeta }_i$, and ${\lambda }_i$. The price-penalty factor (PPF) associated with the emissions is provided in (12) [48]:

$$PP{F}_i=\frac{f_{th,max}{(P}_i)}{E_{max}{(P}_i)}$$

(12)

3. Description of the Proposed Algorithm

3.1. Overview of GPSO-ω

GPSO-ω was suggested in [59] by expanding the functionality of PSO. GPSO-ω initializes N distinctive solutions with N distinctive velocity vectors. In order to identify the most optimum point in each situation, the GPSO-ω search begins with exploring random locations as a possible solution to the problem. Evaluating these random locations/solutions for the desired objective sets directions for developing new solutions, often referred to as updated solutions [60]. The updated solutions further recursively undergo an evaluation process till a termination criterion is reached.

The equation presented below demonstrates that positioning vectors are upgraded towards the most optimum solution on the basis of their personal positioning along with the positioning of the best possible solution. c₁ and c₂ can be used to control an individual’s share to the total propagation of solutions. The solutions are updated using velocity and position updates based on the following equations:

$$\begin{array}{c}{V}_i\left(k\right)=\omega \left(k\right)\times V_i\left(k-1\right)+c_1{r}_1\left(k\right)\times [P_B\left(k-1\right)-X_i\left(k-1\right)\\ +c_2{r}_2\left(k\right)\times [G_B\left(k-1\right)-X_i\left(k-1\right)]\end{array}$$

(13)

$$X_i\left(k\right)=X_i\left(k-1\right)+V_i\left(k\right)$$

(14)

where c₁ and c₂ denote accelerating constants, r₁(k) and r₂(k) denote two random numbers, ω indicates inertial weight, P_B describes the particle’s personal best position, G_B shows the particle’s best position within the whole swarm, and V_i(k) and X_i(k) denote the velocity and positioning of the i^th solution in k^th iteration, respectively.

3.2. Overview of QPGPSO-ω

Opposition-based learning (OBL) was, at first, suggested by Tizhoosh in 2005 for initiating the population to improve the convergence speed of existent meta-heuristic optimization methodologies [61]. The quasi-opposition population (QOP) strategy is based on quasi-opposition initialization and quasi-opposition generation jumping, which allow optimal starting candidate arrangements to be obtained by utilizing inverse points, even when past data about the solutions are not available. The QOP technique considers both the population, at present, and its quasi-inverse population, simultaneously, in order to attain an optimal candidate arrangement. An equivalent strategy can be constantly applied to each solution in the present population [62]. This methodology has been widely incorporated into many optimization techniques to enhance their optimization potential.

QPGPSO-ω is a variant of PSO that incorporates an opposition-based mechanism, which aids in avoiding local minima and enhances the possibility to find a global optimal solution. QPGPSO-ω divides the swarm’s particles into two categories: explorer and opponent particles. Explorer particles move towards the global optimum, while the opponent particles move away from it. The quasi-opposite population advances in the following manner:

An inverse number is defined for each configuration in the population as follows:

$$X_0=min+max-X_i$$

(15)

$$X_{qoi}=rand\left[\frac{(min+\max )}{2},(X_0)\right]$$

(16)

where $X_i$ is the i^th d-dimensional solution at a specific iteration. $X_0$ denotes the inverse number of this i^th solution and $X_{qoi}$ represents the respective opposite population [53].

In Equation (15), the inverse number is calculated by subtracting the original number from the sum of the minimum and maximum values in the range. Essentially, it transforms the original number in such a way that the closer the original number is to the maximum value, the closer the inverse number will be to the minimum value, and vice versa.

The difference between GPSO-ω and QPGPSO-ω lies in their update mechanisms that are elaborated below:

• In GPSO-ω, the velocity and position of each particle are updated based on the global best solution found to date by the entire swarm. On the other hand, in QPGPSO-ω, the velocity and position of each particle are updated based on the quasi-best solution found by a subset of particles, called the quasi-population, randomly selected from the entire swarm.
• The quasi-population is updated in each iteration by selecting the best particles from the entire swarm.
• In QPGPSO-ω, the velocity update includes three components:
  • The inertia component that helps the particle maintain its previous velocity.
  • The cognitive component that encourages the particle to move towards its personal best solution.
  • The social component that causes the particle to move towards the quasi-best solution found by the quasi-population.
• By using a subset of particles to update the velocity and position of each particle, QPGPSO-ω reduces the computational cost and enhances the exploration capability of the algorithm.
• Moreover, by incorporating the quasi best solution found by the quasi population, QPGPSO-ω is able to avoid premature convergence and achieve better solutions in terms of cost and emissions.

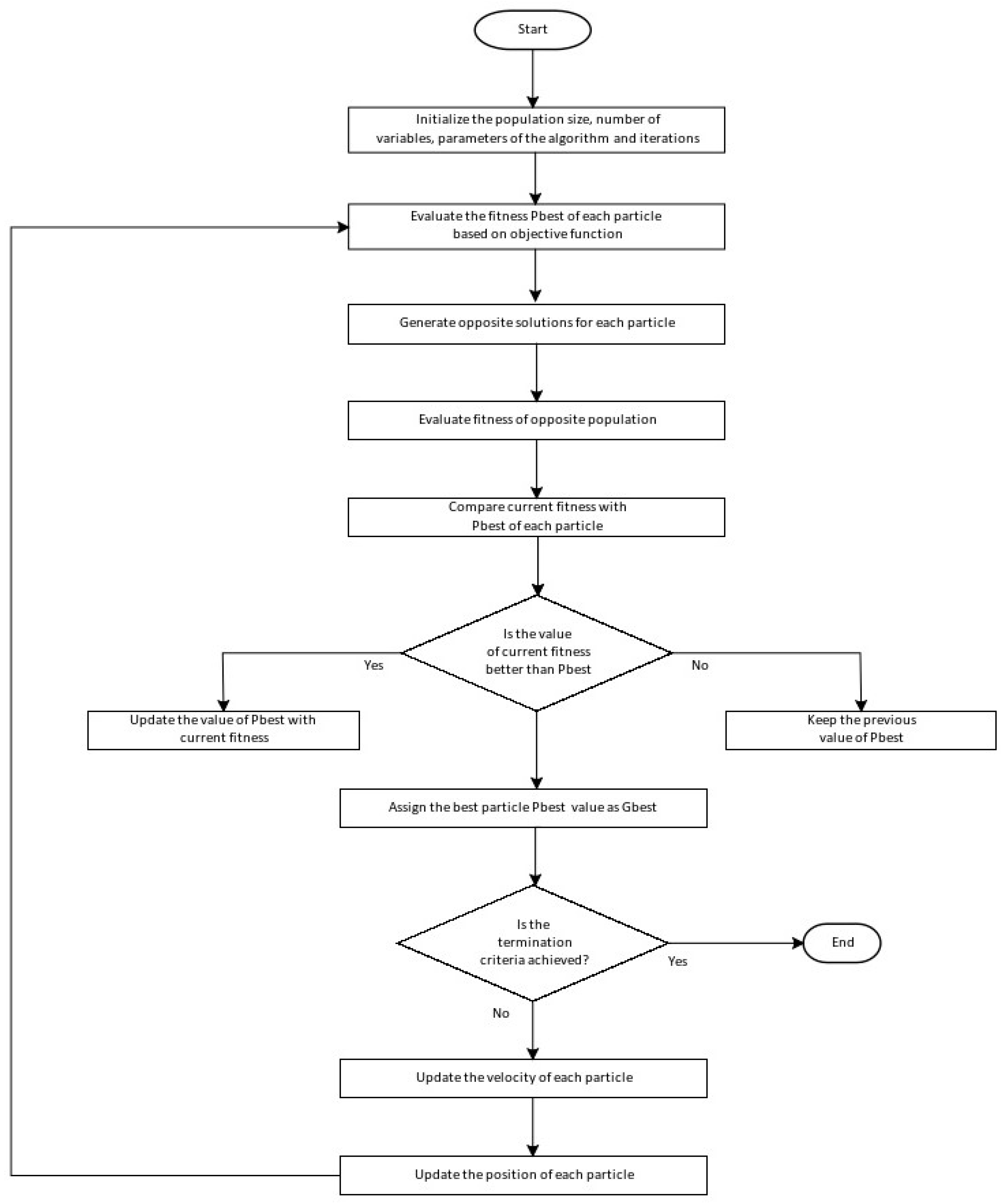
The flowchart of the proposed QPGPSO-ω is presented in Figure 1.

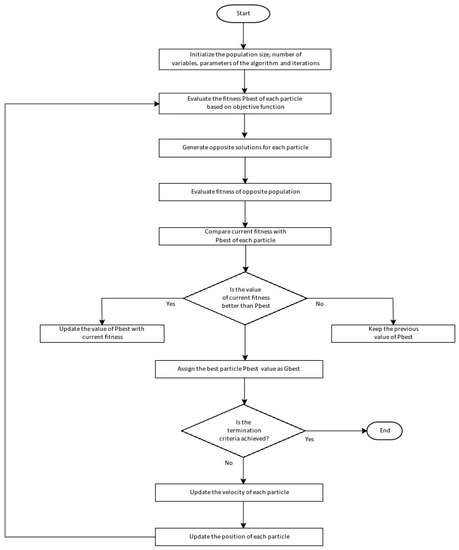
Figure 1. Flowchart of the proposed QPGPSO-ω.

The decision-making block illustrated in Figure 1 shows the process of updating the best-position value (Pbest) in each iteration. If the recently calculated value of Pbest is found to be better than the previous value, it is adopted as the current best value (represented by the branch “yes”). On the other hand, if the recently calculated value is not better, the previous value is retained as the Pbest (represented by the branch “no”).

In the final decision block of the algorithm, a similar approach is followed. If the Gbest value is achieved, the algorithm will terminate and the final solution will be displayed (case of the branch “yes”). Otherwise, the velocity of each particle is updated based on its current velocity, Pbest and Gbest values, followed by the position update (case of the branch “no”). The iterative process continues until the termination criterion is satisfied and the algorithm provides the most optimal solution for the considered dispatch problem.

The QPGPSO-ω methodology is demonstrated through a pseudocode [53] (Algorithm 1).

Algorithm 1. QPGPSO-ω Pseudocode

Initialize N, d-dimensional velocity vectors $V_i\left(j\right)$, and solutions $X_i\left(j\right)$ within the specified range of the search space.

Initialize iteration j = 0

for 1st iteration do initialize $G_{pi}\left(0\right)$ = $X_i\left(0\right)$ end for

for i = 1:N do

Calculate the initial fitness of each particle

${fit(G}_B\left(0\right))=\mathrm{m}\mathrm{i}\mathrm{n} ({fit(G}_{pi}\left(0\right)\left)\right)$

$G_B\left(0\right)$ corresponding to $index fit\left(G_B\left(0\right)\right)$ end for

for j = 1:maxiter do

Compute $w\left(j\right)=0.9-0.5/maxiter$

Update $V_i\left(j\right)$ and $X_i\left(j\right)$

Calculate the opposite number $X_0$ and generate corresponding quasi-opposite population $X_{qoi}$

Update $X_i\left(j\right)=\{\begin{array}{cc}{X}_{qoi}\hfill & \hfill if fit\left(X_{qoi}\right)<fit\left(X_i\left(j\right)\right)\\ X_i\left(j\right)\hfill & \hfill else\end{array}$

Update $G_{pi}\left(j\right)=\{\begin{array}{l}{X}_i\left(j\right) if fit{(X}_i\left(j\right))<fit(G_{pi}\left(j-1\right))\\ G_{pi}\left(j-1\right) else\end{array}$

Update ${fit(G}_B\left(j\right))=\mathrm{m}\mathrm{i}\mathrm{n}({fit(G}_{pi}\left(j\right)\left)\right)$

Update $G_B\left(j\right)$ corresponding to ${fit(G}_B\left(j\right))$

end for Print best solution $G_B\left(maxiter\right)$ and best fitness ${fit(G}_B\left(maxiter\right))$

4. Results and Discussion

The QPGPSO-ω algorithm proposed in this study was utilized to tackle environmentally significant EDPs. The EDP scenarios considered include power systems comprising solely RESs, as well as thermal systems incorporating CEED. The simulation parameters employed for the algorithm throughout the paper are specified in Table 1, unless mentioned otherwise.

Table 1. Parameters and their corresponding values for QPGPSO-ω.

No.	Parameter	Range	Value
1	C1, C2	[1.5–3]	2.5
2	Uniform pdf (probability density function), r	[0–1]	0.5

The values of the unique parameter r and cognitive and social components c₁ and c₂ are given in Table 1. The simulation for the accomplishment of the optimum cost values for the considered EDPs was performed in MATLAB with versatile characteristics [63].

QPGPSO-ω was employed for solving various EDPs of RESs, along with the CEED problem. The combinations of sources for the test cases are given below:

• Only RES-based EDPs solved through QPGPSO-ω (15 units);
• Only RES-based EDPs with time-varying loads solved through QPGPSO-ω (hourly variation);
• Only RES-based EDPs with MAED/RLSD solved through QPGPSO-ω;
• TPPs of ten units with CEED, losses, and VPL solved through QPGPSO-ω.

To obtain the optimal cost values and identify the best solution among the compared optimization techniques, the algorithm was utilized to solve the mentioned EDPs. Multiple trials were conducted, amounting to up to thirty iterations, with varying values of the parameters listed in Table 1.

Throughout these trials, the algorithm aimed to minimize costs while considering the operational constraints imposed by the EDPs. The algorithm’s performance was evaluated based on the achieved cost and emission values, ensuring that both economic and environmental factors were taken into account.

4.1. Case 1 of Only RESs without Constraints

In case 1, QPGPSO-ω was employed to solve the EDP for the power system comprising only RESs without considering any constraints.

The simulation was conducted using specific power plants located in different regions of Pakistan. Four biofuel power plants located in Rahim Yar Khan (RYK), Punjab; five PV plants commissioned in Bahawalnagar and Sahiwal, Punjab; and six wind-based frameworks deployed in Jhimpir, Sindh, were selected for the study. The climatic conditions and applied requisites of the considered resources were taken from [20,64,65] and presented in Table 2.

Table 2. Parameters for the RESs utilized for test case 1.

Regional Distribution	Project	Capacity (MW)	Area	Irradiance/Rated Velocity
Region 1	M/S R.Y.K Mills Limited	30	Rahim Yar Khan	NA
	M/S Hamza-Sugar Mills Limited	15	Rahim Yar Khan
	M/S J.D.W Sugar-Mills (Unit II)	26.4	Rahim Yar Khan
	M/S Cheniot-Power Limited	62.4	Rahim Yar Khan
Region 2	Harrapa Solar (private) Limited	18	Sahiwal	Rad min = 150 Rad max = 1000 P.V Mean = 5.2 P.V Std. Dev. = 0.6 P.V Reserve = 3 P.V Over est. = 1.5 P.V direct cost = 1.6
	Adam-jee Power-Generation (private) Limited.	10	Noorsar, Bahawalnagr
	Asia-Petroleum Limited.	30	Noorsar, Bahawalnagr
	M/S Safe Solar Power (private) Limited	10.3	Bahawalnagr
	Asia-Petroleum Limited.	30	Bahawalnagr
Region 3	Three Gorgeous Wind-Farm (private) Limited	49.5	Jhimpir	Vcut-in = 05 m/s Vcut-out = 25 m/s Overestimation = 5 Underestimation = 1 Kp factor = 1
	Sapphire Wind-Power Company Limited	52.8	Jhimpir
	FFC Energy Limited	49.5	Jhimpir
	Zorla Energi Pakistan (private) Limited	56.4	Jhimpir
	Yunus Energy Limited	50	Jhimpir
	Metro Power Co., Limited	50	Jhimpir

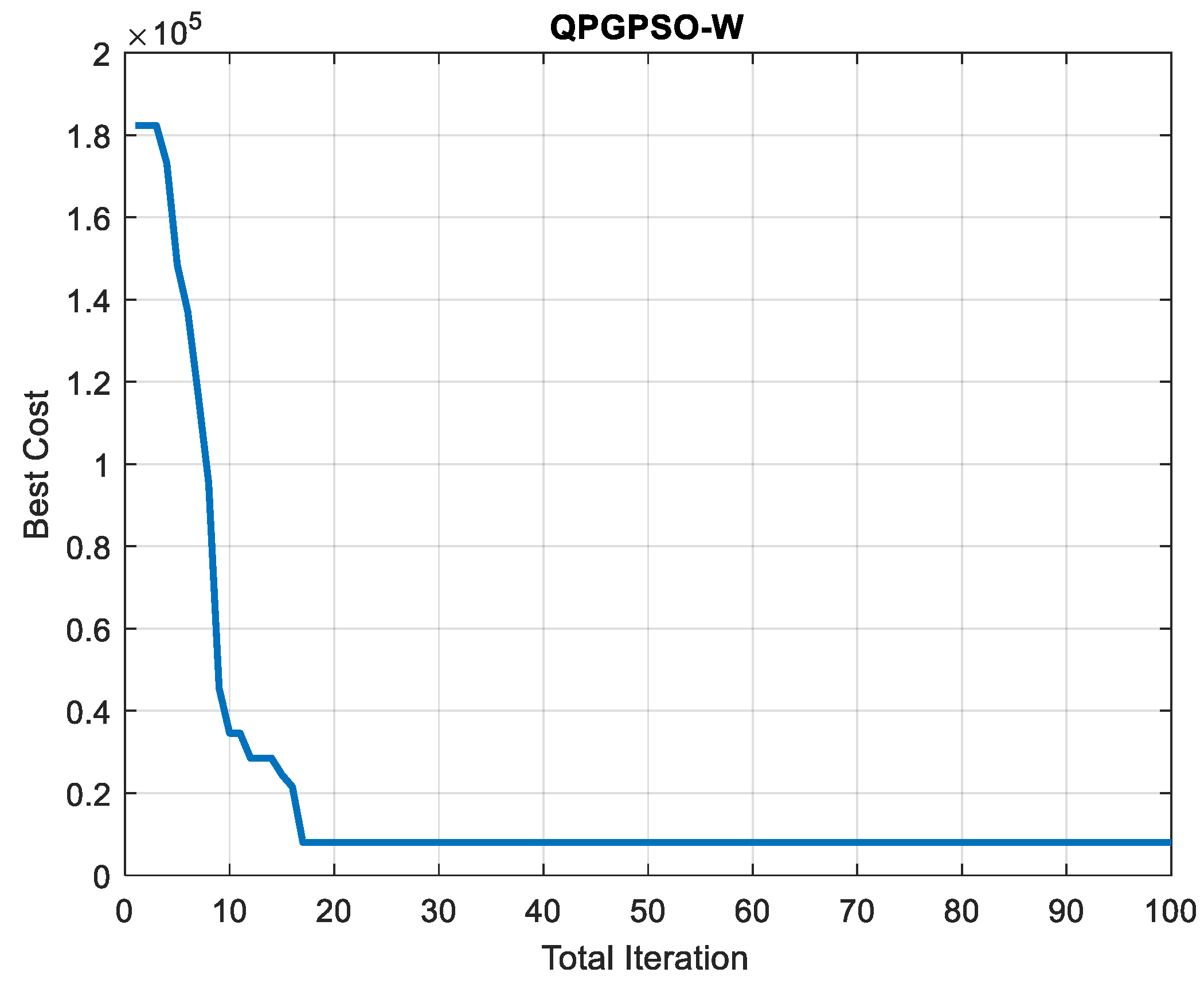
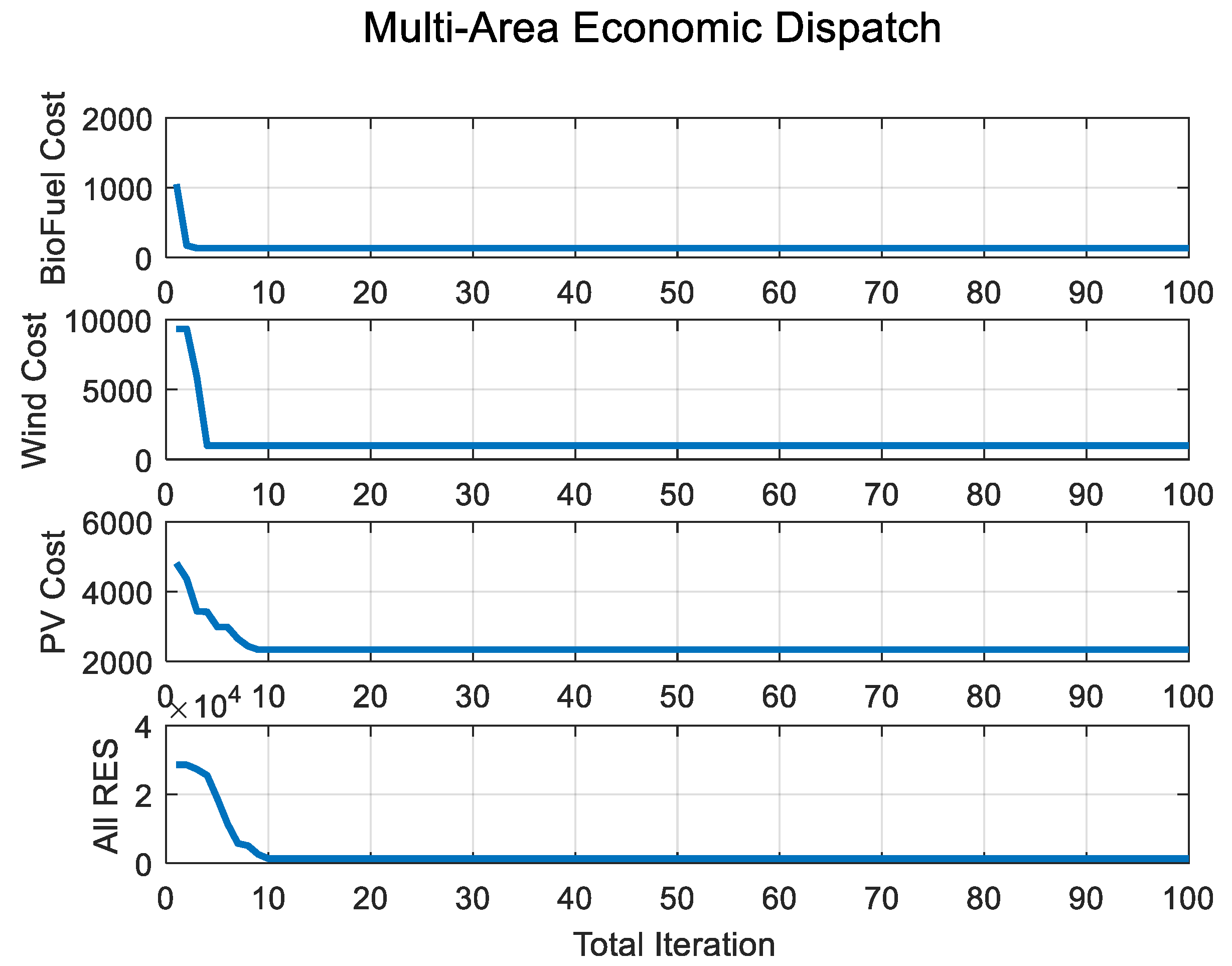
The QPGPSO-ω algorithm was simulated for 30 sequential trials, and the average results obtained from these trials are presented in Figure 2. The figure illustrates the convergence behavior of the algorithm, indicating the progressive improvement in cost values for the same power demand (PD) as the iteration’s progress. The 17th iteration is identified as the point of convergence where the algorithm achieves optimal cost values. Table 3 provides a comprehensive power and cost comparison between the QPGPSO-ω algorithm and other prominent optimization techniques implemented for the case of RES-only systems [66].

Figure 2. Cost convergence curve of RES-based EDPs without constraints.

Table 3. Produced powers with the corresponding costs of each source for case 1.

RES	QPGPSO-ω (MW)	QPGPSO-ω (USD)	HPSO_BA (MW)	HPSO_BA Cost (USD)	MHPSO_BAAC (MW)	MHPSO_BAAC Cost (USD)	MHPSO_BAAC_χ (MW)	MHPSO_BAAC_χ Cost (USD)
P1	26.35	1168.798	23.715	1169.7981	26.35	1168.798	26.35	1168.7981
P2	62.4	2734.124	62.4	2739.1242	62.4	2734.124	62.4	2734.1242
P3	30	1355.04	30	1358.04	30	1355.04	30	1355.04
P4	15	1050.702	15	1056.7025	15	1050.7025	15	1050.7025
P5	7.1176	54.9	7.29	54.9	9	54.9	8.9617	54.9
P6	1.4425	30.5	8	30.9	0.4289	30.5	4.9123	30.5
P7	15	91.5	15	91.8	15	91.5	15	91.5
P8	4.9421	31.3589	3.2018	31.8589	5.0209	31.3589	3.4607	31.3589
P9	15	91.5	15	91.8	15	91.5	15	91.5
P10	13.86	227.7	12.471	227.7	12.474	227.7	8.8787	227.7
P11	15.792	259.44	14.0002	259.44	14.4174	259.44	15.2875	259.44
P12	13.86	227.7	11.4819	227.7	13.86	227.7	13.3501	227.7
P13	13.915	242.88	14.784	242.88	13.9812	242.88	14.784	242.88
P14	11.4	230	14	230	14	230	14	230
P15	14	230	14	230	14	230	14	230
PTotal	260	8026.1429	260	8046.1438	260	8026.1435	260	8026.1438

4.2. Case 2 of Only RESs with Resource Variability

For the mentioned case, resource and load variations within a day were taken into account. Table 4 provides an overview of different time periods, along with the corresponding PD, average solar irradiance, and wind speed values during those specific periods [20,64,65].

Table 4. Time slots and the system parametric values for case 2.

Period (h)	Power Demand (MW)	Solar Irradiance (W/m2)	Wind Speed (m/s)
00–01	200	000	8.7
01–02	195	000	8.5
02–03	190	000	8.4
03–04	180	000	8.3
04–05	185	000	8.2
05–06	190	100	8.1
06–07	200	150	8.0
07–08	210	200	7.9
08–09	215	250	7.5
09–10	220	325	7.1
10–11	225	360	7.3
11–12	230	400	7.1
12–13	235	450	6.7
13–14	242	510	6.8
14–15	249	600	6.7
15–16	260	660	6.9
16–17	250	525	7.1
17–18	246	400	7.4
18–19	243	290	7.6
19–20	245	200	7.8
20–21	231	000	8
21–22	225	000	8.3
22–23	216	000	8.5
23–00	205	000	8.7

The results presented in Table 5 indicate that the power generation from wind and PV resources exhibits variations throughout the day, due to the availability of these resources. As wind speed and solar irradiance fluctuate, the power output from these renewable sources also varies accordingly. On the other hand, the power generation from the biofuel resource remains relatively constant, as its supply is less prone to variations. The results obtained through the QPGPSO-ω algorithm for the cost of power production were compared with the techniques introduced in [66]. As observed in the comparison, the results obtained using QPGPSO-ω exhibit a slight improvement.

Table 5. Comparative analysis of QPGPSO-ω with prominent methodologies for test case 2.

Time Period Hours (h)	QPGPSO-ω		HPSOBA		MHPSO-BAAC		MHPSO-BAAC-χ
	(MW)	(USD)	(MW)	(USD)	(MW)	(USD)	(MW)	(USD)
00–01	200	8029.8	200	8030	200.2	8030	202.15	8030
01–02	195.7	8060	195.7	8060.78	195.87	8060.8	196.04	8060.8
02–03	190.51	8076	190.51	8076.2	193.07	8076.2	190.47	8076.2
03–04	181.14	8075.9	181.14	8076.2	185.3	8076.2	181.61	8076.2
04–05	193.97	8090.8	193.97	8091.6	190.4	8091.6	187.57	8091.6
05–06	190.64	8093.5	190.64	8094	195.3	8093.8	190.16	8094
06–07	204.84	8094.3	204.84	8095.1	203.5	8095	201.03	8095.1
07–08	212.20	8095.1	212.20	8096.2	212.14	8092.6	210.4	8096.2
08–09	217.31	8143.3	217.31	8143.6	220.25	8143.6	215.07	8143.6
09–10	221.28	8175.8	221.28	8176.2	220.14	8176.1	221.02	8176.2
10–11	226.51	8142.9	226.51	8143.1	225.26	8143	226.55	8143.1
11–12	227.12	8162.5	227.12	8162.5	230.67	8162.5	223.72	8162.5
12–13	226.11	8171.4	226.11	8171.9	232.7	8179.1	230.52	8179.1
13–14	230.32	8177.1	230.32	8177.4	232.75	8176.7	229.30	8177.4
14–15	228.27	8159.4	228.27	8159.4	231.42	8158.8	238.72	8160
15–16	245.38	8119.2	245.38	8119.2	248.31	8119.2	248.68	8119.2
16–17	237.42	8119	237.42	8119.2	243.54	8119.15	242.79	8119.2
17–18	229.4	8115.8	229.4	8116.3	242.37	8116.2	238.16	8116.2
18–19	226.45	8116.3	226.45	8116.8	229.76	8116.7	234.43	8116.43
19–20	231.65	8111.2	231.65	8111.6	230.62	8111.5	229.78	8111.6
20–21	219.35	8137.3	219.35	8137.8	224.57	8137.8	224.55	8137.8
21–22	225.48	8091.3	225.48	8091.6	225	8091.6	225.11	8091.6
22–23	216.13	8060	216.13	8060.8	217.76	8060.7	216.30	8060.8
23–00	207.06	8030	207.06	8030	205.92	8030	205.12	8030

In Table 5, a comparison is provided between the developed algorithm and techniques utilized for solving RES-based EDPs [63]. The table demonstrates that the developed algorithm exhibits slightly superior results in terms of cost reduction across nearly half of the time slots.

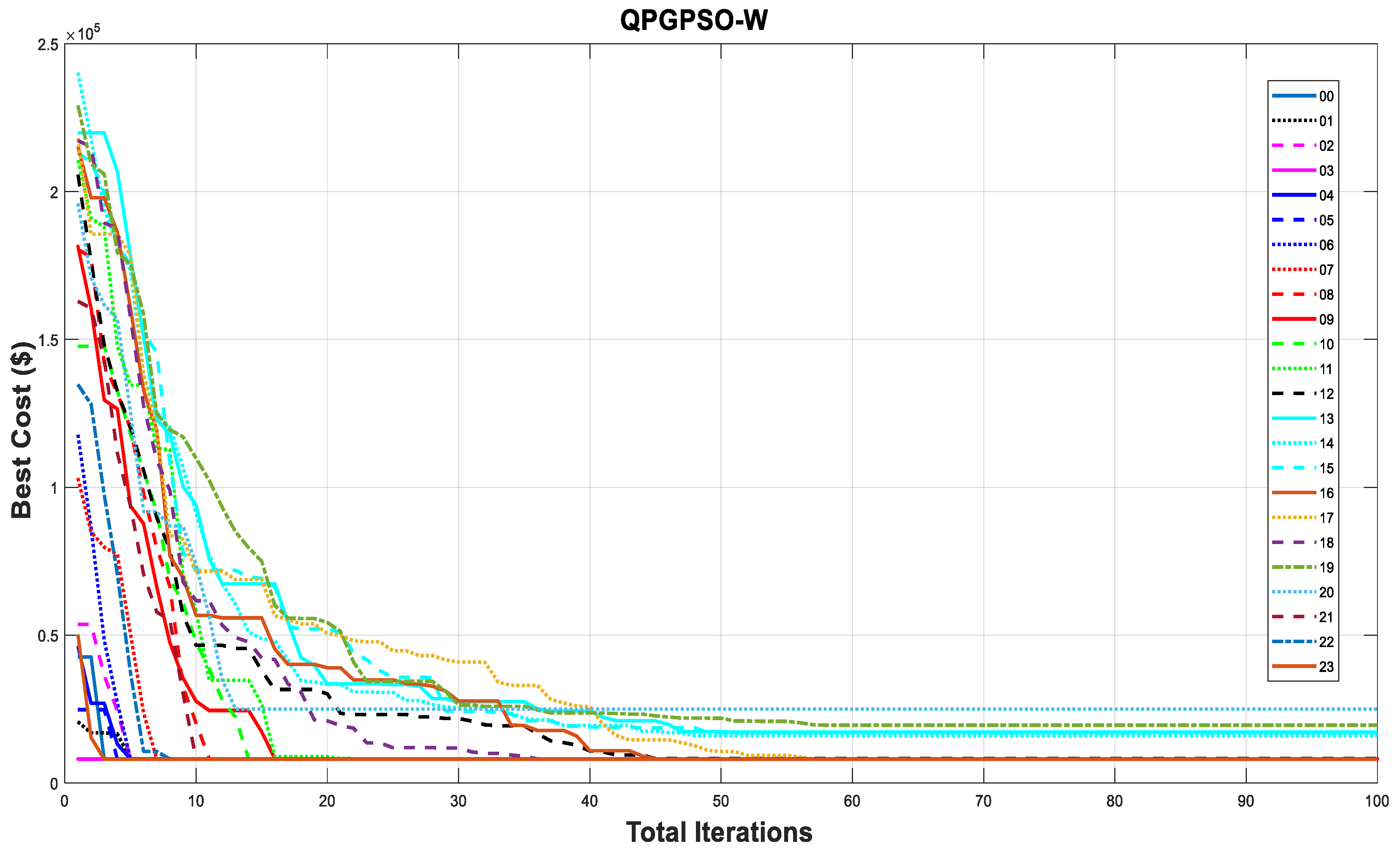
Furthermore, Figure 3 showcases the convergence curves for case 2, illustrating the progressive reduction in costs over the 23 time slots of the day. The graph visually represents the algorithm’s ability to optimize power generation and achieve cost efficiency throughout the different time periods.

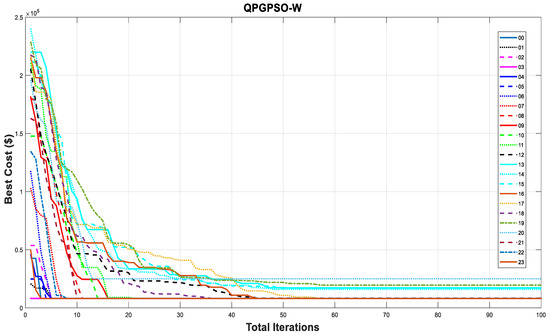
Figure 3. Cost convergence curve of RES-based EDPs with resource variability.

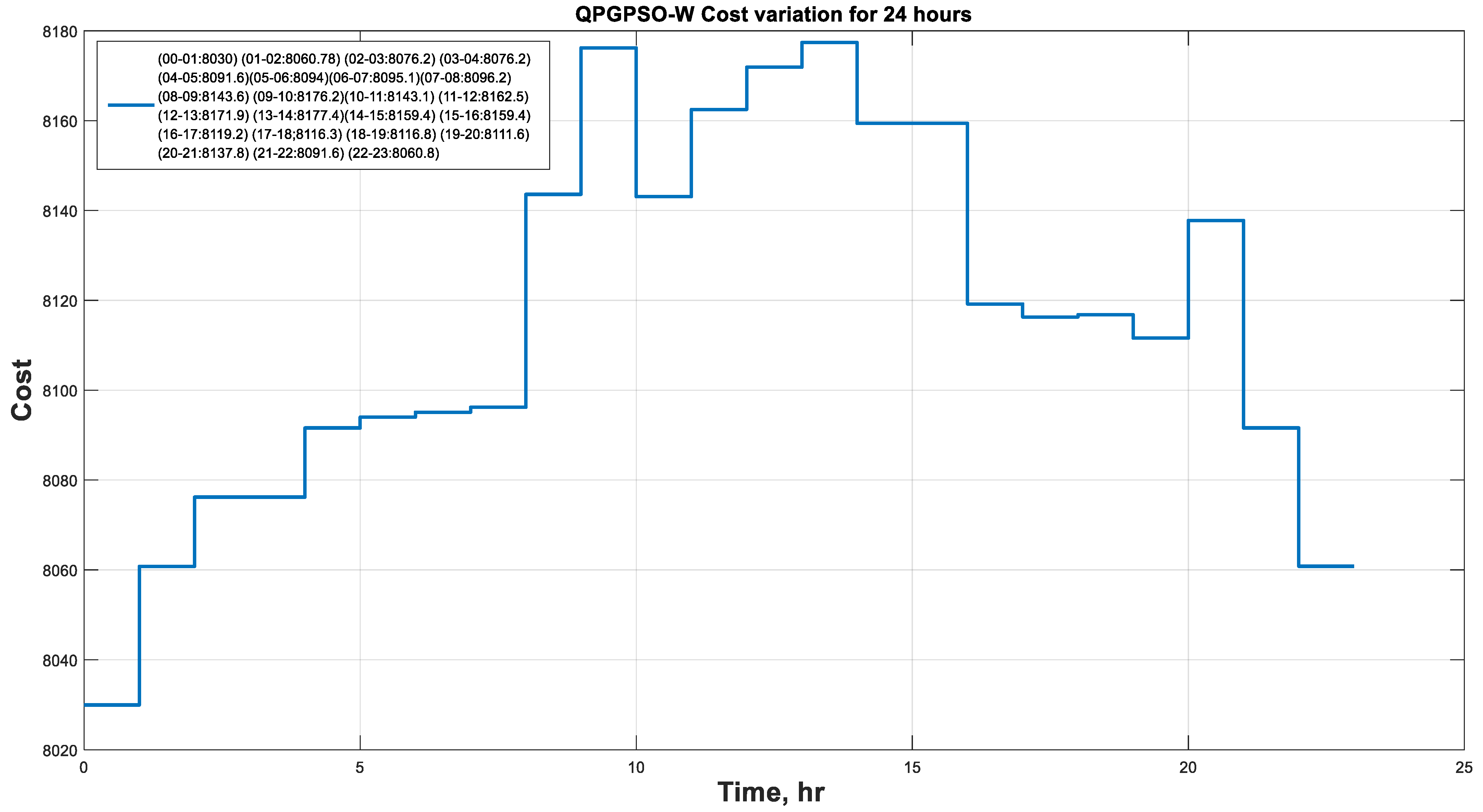
Figure 4 illustrates the variations in cost during the peak (16–20) and low (00–04) load hours. The cost of power generation fluctuated during these time slots, primarily due to the changes in solar radiation.

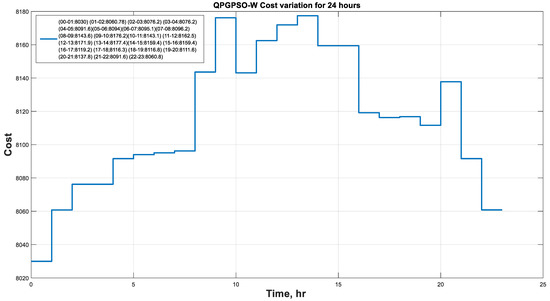
Figure 4. Cost convergence curve of RES-based EDPs with load and supply variations for 24 h.

4.3. Case 3 of RESs with RLSD

The QPGPSO-ω algorithm utilizes a set of variables for simulation purposes, and their specifications are provided in Table 1. On the other hand, Table 2 presents the parametric values assigned to RESs considered in the study. The scientific calculations for the case of RLSD were performed according to (10). Furthermore, Table 6 showcases the power production results and their associated costs when considering regional availability constraints. The table provides insights into the performance of different resources when meeting both individual and collective power demands using RESs.

Table 6. QPGPSO-ω cost calculations for EDPs of RESs with RLSD in case 3.

Power Values of the Biofuel, Wind, and PV Sources
PG and PC	Biofuel		Wind		PV		All RESs
	MW	USD	MW	USD	MW	USD	BF (MW)	BF (USD)	W (MW)	W (USD)	PV (MW)	PV (USD)
P1	26.15	26.35	18.92	157.4	14	42.37	26.15	26.5	28.92	158.4	14	42.7
P2	62.4	62.4	26.55	180	8.933	23.54	62.4	62.4	26.55	180.9	8.933	23.4
P3	29	30	27.72	157.4	22.2	70.62	29	30	29.72	158	12.2	70.2
P4	13.5	14	23.54	167.96	6.847	23.20	13.5	14	28.54	168.9	6.87	24.20
P5	-	-	27.99	159	22.2	70.62	-	-	27.99	158	18.2	70.2
P6	-	-	27	158	-	-	-	-	27.9	159	-	-
PT	131.05	-	151.72	-	74.18	-	131.05	-	169.62	-	60.2	-
CT	-	132.75	-	979.76	-	230.35	-	132.9	-	983.2	-	230.7
PD	130		150		80		130		150		80
Pavailable	1.05		1.72		−5.82		0.87
PD overall	360						360.87@ 1346.8

The given values presented in Table 6 were obtained by taking the average values for the 30 trials. Once the PD was met, any surplus power in the region was denoted as P_available, which could be distributed and shared with other regions. However, power sharing among regions was only possible when the value of P_available was positive, indicating that there was a surplus power available after fulfilling the PD. Conversely, a negative value of P_available signified that the resource was inadequate to meet the power demands, and thus power sharing was not feasible. Figure 5 illustrates the cost convergence curves for both the individual regional resource supply and mutual power sharing scenarios.

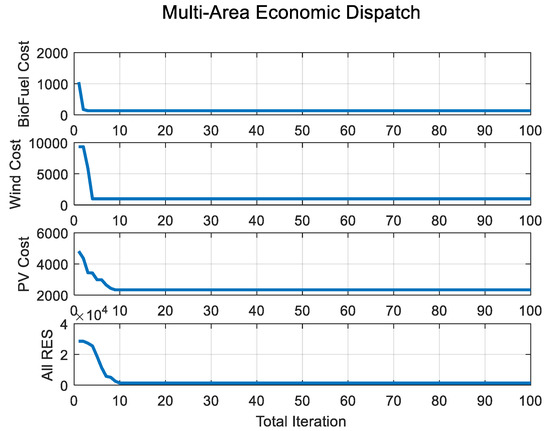
Figure 5. Cost convergence curve of RES-based EDPs with RLSD.

Table 7 presents a comparative analysis of the cost calculation for EDPs of RESs with RLSD using different techniques for the case of ED.

Table 7. Comparison table for cost calculations for EDPs of RESs with RLSD.

Methods	Generated Power (MW)	Min. Cost (USD)
HPSOBA [66]	361.977	1351.344
MHPSO-BAAC [66]	360.139	1350.448
MHPSO-BAAC-χ [66]	360.567	1350.344
QPGPSO-ω	360.870	1346.800

Table 7 validated the efficacy of QPGPSO-ω compared to various methodologies presented in the literature.

4.4. Case 4 of Ten Thermal Units (CEED + VPL + Losses)

The test scenario involved ten thermal-based generating units, taking into account the VPL and power losses, as well as the combined emission economic dispatch (CEED). The specifications and parameters of the thermal TPPs, as well as their corresponding emissions, were obtained from [49]. The mathematical expressions used in the analysis are given by (11) and (12). Furthermore, Table 8 presents the power production and corresponding costs for each of the considered plants when simulated using the QPGPSO-ω algorithm.

Table 8. Produced powers and their corresponding costs of the individual plants for case 4.

Plant No.	QPGPSO-ω (MW)	QPGPSO-ω ($)	QPGPSO-ω (lb)
P1	55	3645.188	307.474
P2	80	4837.056	332.4252
P3	94.1025	5460.377	302.58
P4	111.10	6752.469	314.458
P5	81.09	4897.367	57.87
P6	82.215	5158.461	60.396
P7	300	15,936.28	466.1098
P8	340	18,034.35	655.8089
P9	470	23,455.1	905.7544
P10	470	23,356.94	902.882
PT	2083.5	-	-
CT	-	111,533.59	-
Ploss	83.402	-	-
E (lb)	-	-	4305.76
PPF	25.903	-	-

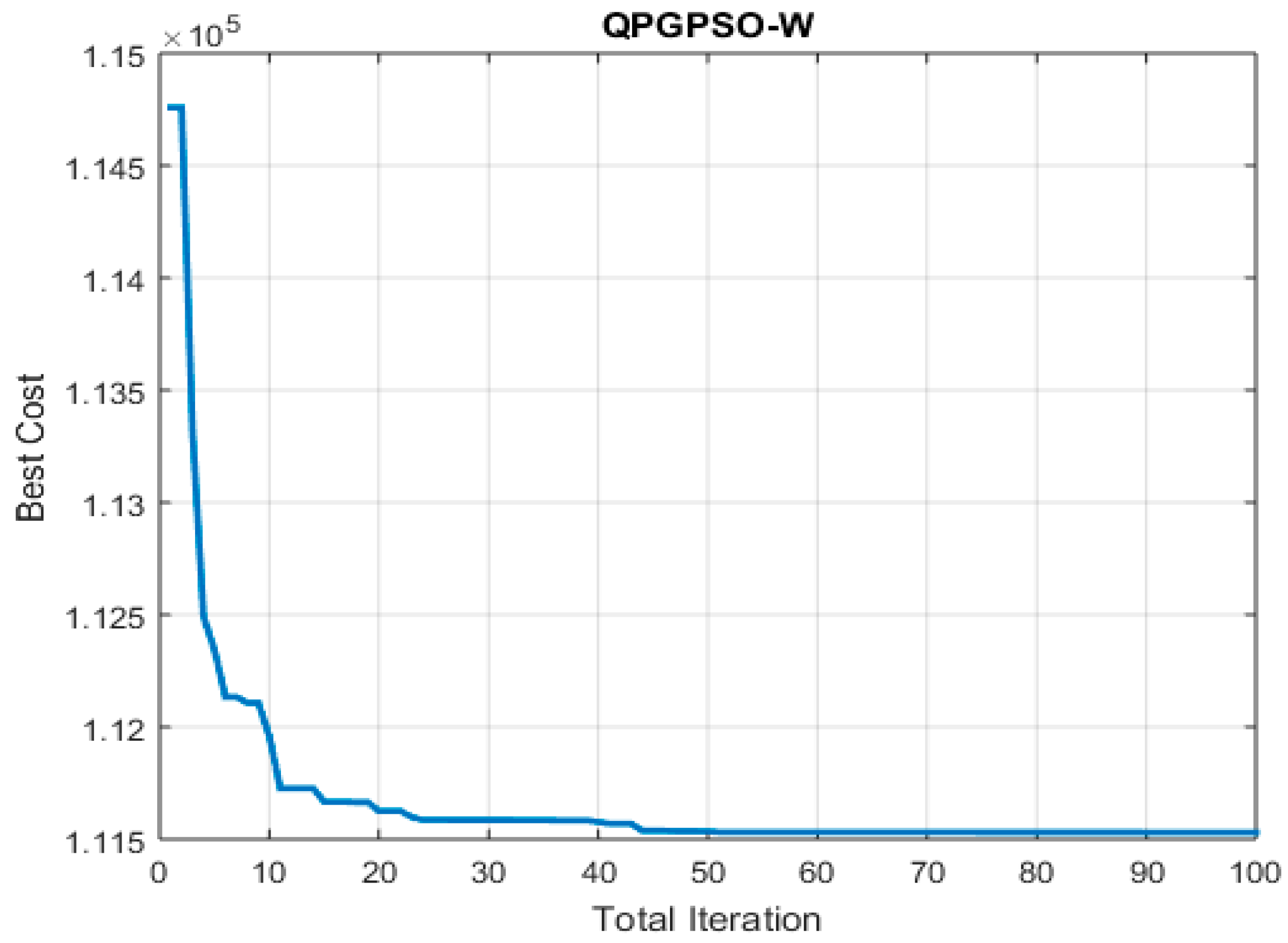
Figure 6 illustrates the cost convergence curve for the CEED case, showing the progression of cost values as the algorithm iteratively updated and refined the solutions.

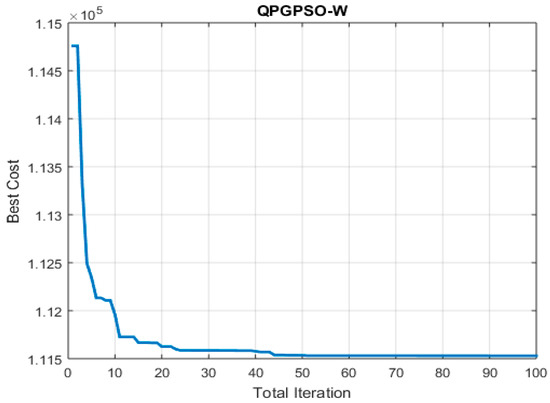
Figure 6. Cost convergence curve of EDP problem.

Table 9 presents a comprehensive comparative analysis of the cost, emissions, and computational time for various prominent techniques used to solve the EDPs.

Table 9. Comparison of QPSPSO-ω for CEED case.

Methods	Min. Cost (USD)	Average Cost (USD)	E (lb)	CPU Time (s)
EMOCA [49]	113,444.8500	-	4113.9800	2.90
MSA [51]	113,350.0000	-	4102.4000
QPSO [53]	119,005.3000	121,621.7500	4041.9171	-
GQPSO [53]	112,429.7444	113,102.4627	4032.9320	-
LAPO [67]	113,412.3500	-	4115.5730	3.109
SMA [68]	113,490.0000	-	4108.6000	-
PDE [68]	113,510.0000	-	4111.4000	4.23
ABC-PSO [68]	113,420.0000	-	4120.1000	-
MODE [68]	113,484.0000	-	4124.9000	3.82
NSGAII [68]	113,539.0000	-	4130.2000	6.02
SPEA-2 [68]	113,520.0000	-	4109.1000	7.53
BSA-WSM [69]	112,559.8061	-	4223.7248	-
GWO [70]	111,729.4238	-	4247.5200	-
MHPSO-BAAC [66]	106,278.0500	109,728.0500	4318.8900	2.242
MHPSO-BAAC-χ [66]	106,236.1500	109,632.1500	4310.9500	2.362
QPGPSO-ω	111,533.5900	111,649.8210	4305.7600	2.358

Overall, the combination of the quasi-population-based approach and the inertial weight parameter in QPGPSO-ω results in an effective exploration of the search space, a balanced trade-off between exploration and exploitation, and convergence to favorable solutions. Comparisons with other techniques validated the superior performance of QPGPSO-ω in terms of cost and emissions reduction, with slightly improved computational times. Therefore, QPGPSO-ω stood out as a promising optimization approach for similar problems, offering efficient and effective solutions.

5. Conclusions

The paper presented the implementation of QPGPSO-ω to solve environmentally significant EDPs consisting of scenarios of only RESs and a case of a thermal system with a CEED problem. The RES-based system comprised three cases: (i) without constraints, (ii) with resource and load variability, and (iii) RLSD. The scenario of thermal system consisted of ten thermal-based generating units having VPLs, losses, and CEED. The comparative analysis of the QPGPSO-ω with several reported methods has shown the efficacy of the proposed technique in terms of cost minimization and achieving a fast convergence. Our research findings suggest that the incorporation of RESs can be an effective way to tackle the challenges of the CEED problem as it offers an economical and environmental friendly solution for an optimal power dispatch. We are of the opinion that the optimization based methods can serve as an effective tool for power system operators and planners to optimize power system operations while minimizing costs and reducing emissions. Future research can explore the applicability of QPGPSO-ω in other energy optimization problems and investigate the practicality of implementing the proposed approach in real-world power systems.