Abstract
Graph neural network (GNN), as a widely used deep learning model in processing graph-structured data, has attracted numerous studies to apply it in the link prediction task. In these studies, observed edges in a network are utilized as positive samples, and unobserved edges are randomly sampled as negative ones. However, there are problems in randomly sampling unobserved edges as negative samples. First, some unobserved edges are missing edges that are existing edges in the network. Second, some unobserved edges can be easily distinguished from the observed edges, which cannot contribute sufficiently to the prediction task. Therefore, using the randomly sampled unobserved edges directly as negative samples is difficult to make GNN models achieve satisfactory prediction performance in the link prediction task. To address this issue, we propose a policy-based training method (PbTRM) to improve the quality of negative samples. In the proposed PbTRM, a negative sample selector generates the state vectors of the randomly sampled unobserved edges and determines whether to select them as negative samples. We perform experiments with three GNN models on two standard datasets. The results show that the proposed PbTRM can enhance the prediction performance of GNN models in the link prediction task.
1. Introduction
The graph neural network (GNN) model is one of the most representative deep learning models capable of operating on graph-structured data, which has been widely used in tasks such as node classification [1], graph clustering [2], and graph classification [3]. Identifying missing edges from the unobserved edges in a network is the objective of the link prediction task [4]. To achieve better performance in the link prediction task, there is increasing interest among many researchers to utilize GNN models in their studies [5,6,7,8,9,10,11,12].
Inspired by the variational auto-encoder (VAE), Kipf et al. [5] propose a graph auto-encoder (GAE) framework, which is adopted by the benchmarking GNN models [13] in the link prediction task. Many studies [6,8,9,11,12] have also adopted the GAE framework and made some refinements to it. In these studies, observed edges in the network are utilized as positive samples, and unobserved edges in the network are randomly sampled as negative samples with the same number as the positive ones. However, we find two cases may happen during randomly sampling unobserved edges in a network, which impact the prediction performance of GNN models in the link prediction task. In the first case, some of the randomly sampled unobserved edges are missing edges that actually exist in the network. Choosing such missing edges as negative samples results in false negative samples, which harm the prediction performance of GNN models. In the second case, some of the randomly sampled unobserved edges can be easily distinguished from the observed edges by GNN models. Choosing such easily distinguishable unobserved edges as negative samples results in easy negative samples, which are insufficient for the training of GNN models. Because of the aforementioned two cases, it is requisite to select high-quality negative samples from unobserved edges for the training of GNN models to enhance their prediction performance in the link prediction task.
In this work, a policy-based training method (PbTRM) is proposed to improve the negative sampling procedure of GNN models in the link prediction task. The proposed PbTRM still utilizes observed edges as positive samples. The difference from the previous studies is that we design a negative sample selector to select high-quality negative samples from randomly sampled unobserved edges. In more detail, a policy network is employed as the core module of the negative sample selector. For each randomly sampled unobserved edge, the negative sample selector obtains its state vector, which is the input to the policy network. Subsequently, the policy network outputs an action for each randomly sampled unobserved edge, which determines whether to select it as a negative sample. Extending the Policy Gradient [14], we use the change in the prediction performance of the GNN model as the reward for the policy network, where the reward of the improved prediction performance is positive. The parameters of the policy network are updated after finishing a sampling period. Finally, we illustrate the effectiveness of the proposed PbTRM with three GNN models, including GCN [1], GraphSAGE [15], and GAT [16]. The experimental results demonstrate that the proposed PbTRM enhances the prediction performance of these GNN models on two standard datasets, i.e., Cora [17] and CiteSeer [17], in the link prediction task.
In summary, the contributions of this work are as follows:
- We introduce a negative sample selector, which employs a policy network as its core module, to reduce the impact of existing false and easy negative samples in the training set for the GNN models in the link prediction task.
- Armed with the negative sample selector, we design a policy-based training method (PbTRM), which generates the negative samples through the negative sample selector in each sampling period and updates the parameters of the policy network after finishing a sampling period.
- We demonstrate the effectiveness of the proposed PbTRM by experiments with three GNN models on two datasets. In the remainder of the experiments, we also illustrate the influence of the sampling period on the proposed PbTRM.
The remainder of our paper is organized as follows: The problem definition of our work and related work of the GNN models in the link prediction task is presented in Section 2. Section 3 introduces the proposed negative sample selector and policy-based training method in this work. Section 4 reports the experimental setup and results of our work. Section 5 makes the conclusion and discusses the potential future work.
2. Preliminary
2.1. Problem Definition
A network dataset usually consists of the node set , the observed edge set , and the feature matrix of nodes, which can be expressed as a simple undirected graph [4]. The observed edge set and unobserved edge set constitute the universal set , i.e., . Some edges in the unobserved edge set are missing edges that actually are existing edges. The unobserved edge set consists of missing edges and non-existing edges. The link prediction task aims to find these missing edges in based on the information contained by the structure and node features of [4].
In the network dataset, we cannot know which edges in are missing edges [18]. Therefore, in this work, we divide the observed edge set into three subsets: the set for training, the set for validation and the set for testing. Here, ,. The edges in set are used as the observed edges, and the edges in set are used as the unobserved edges. The edges in set and are used as missing edges to evaluate the prediction performance of GNN models during and after training, respectively. Here, ).
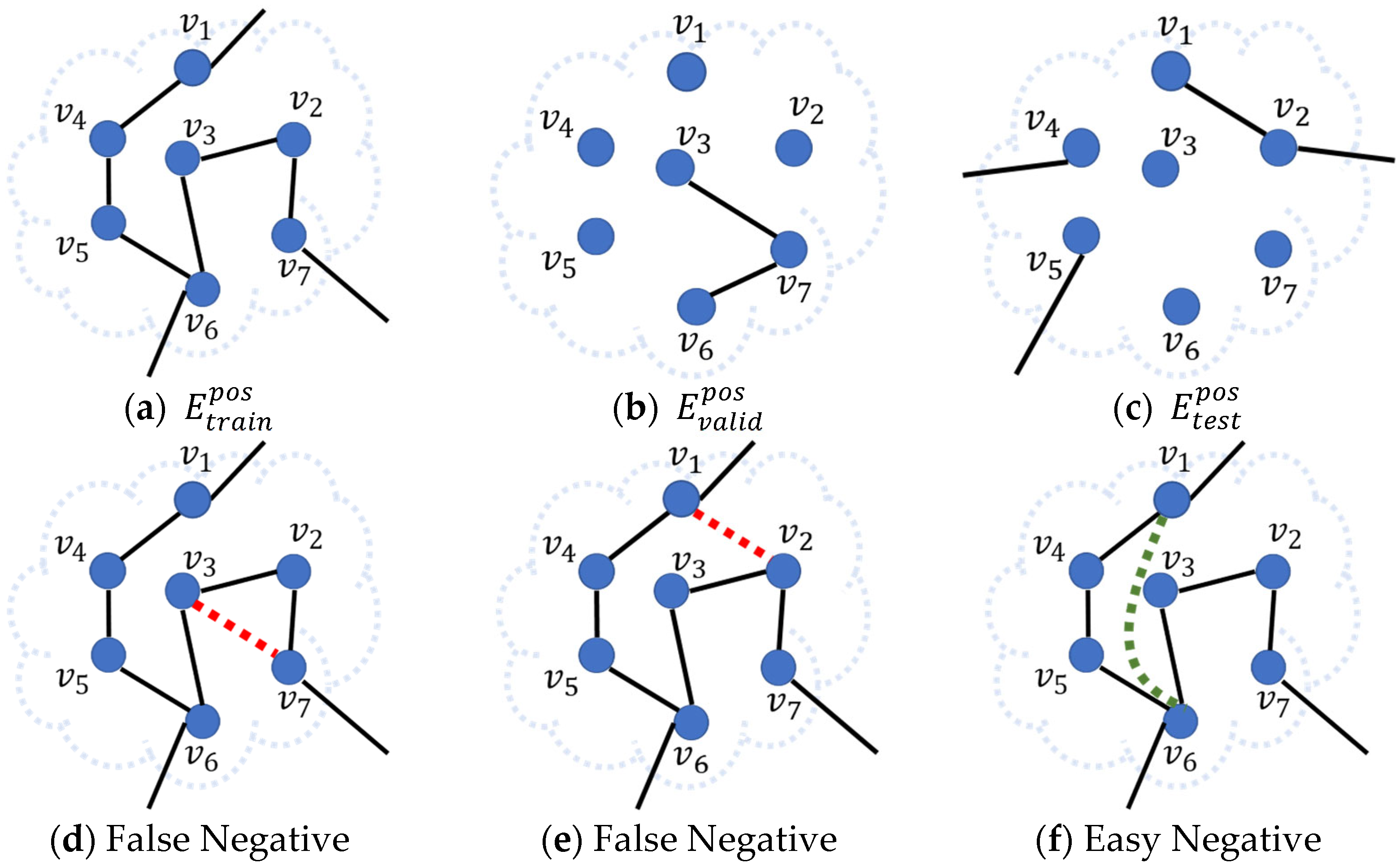
In previous studies, edges in are used as positive samples, and edges in are randomly sampled as negative samples during the training process of GNN models. However, it is not possible to know in advance which edges in are missing edges. Choosing missing edges as negative samples results in false negative samples. In another scenario, some of the edges randomly sampled from can be easily distinguished from the edges in by GNN models. Choosing such easily distinguishable unobserved edges as negative samples results in easy negative samples. In more detail, several examples of false and easy negative samples are shown in Figure 1. In Figure 1d,e the edges and are missing edges in and , which are shown in Figure 1b,c, respectively. Whether the edge or is sampled as a negative sample, the sampled edge will conversely be regarded as a non-existing edge by GNN models, resulting in poor prediction performance of GNN models. In Figure 1f, if the edge can be easily distinguished from observed edges in shown in Figure 1a, choosing it as a negative sample contributes insufficiently to the prediction performance of GNN models. Considering the aforementioned two problems, the purpose of this work is to select high-quality negative samples from the to form the negative sample set for the training of GNN models.
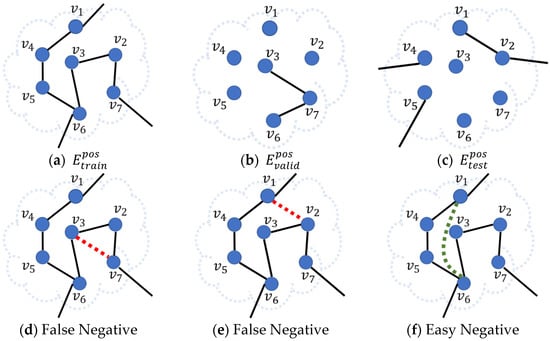
Figure 1.
Examples of false and easy negative samples. Edges in (a–c) represent the edges in , and respectively. The missing edges, including edge in (d) and edge in (e), are sampled as negative samples, which mislead GNN models. The easily distinguishable edge in (f) is sampled as a negative sample, which contributes insufficiently to GNN models.
2.2. Graph Neural Network in Link Prediction Task
Graph neural network (GNN) models are deep learning models operating directly on graph-structured data, which are generalizations of the convolutional neural network in the non-Euclidean domain [19]. Here, we only briefly introduce several typical GNN models. Bruna et al. [20] propose the Spectral Graph CNN extending convolutions to general graphs by using the graph Fourier transform. The Spectral Graph CNN is the pioneering work of GNN models. Kipf et al. [1] propose the graph convolutional network (GCN), which aggregates information in one-hop neighborhoods of each node. Hamilton et al. [15] present the GraphSAGE, which obtains the convolved features of nodes by sampling and aggregating their neighbors. Velickovic et al. [16] present the graph attention network (GAT) taking advantage of masked self-attention in the graph convolutional architecture.
As an important task in graph mining, increasing studies attempt to introduce the aforementioned GNN models into the link prediction tasks. In the study of Zhang et al. [7], the authors find that the over-reliance on predefined assumptions about the existence of edges limits the performance of traditional link prediction methods. They propose a link prediction method (SEAL) using GNN to automatically evaluate the existence of edges from the subgraph. Zhu et al. [10] propose a framework, named NBFNet, that can be utilized in the link prediction task. The NBFNET framework leverages a GNN model to obtain edge representations from the paths between two nodes. Moreover, this framework is applicable to both homogeneous graphs and knowledge graphs. Inspired by variational auto-encoder (VAE), Kipf et al. [5] propose two models, including variational graph auto-encoder (VGAE) and graph auto-encoder (GAE). Due to the ability of GAE to incorporate the feature of nodes, benchmarking GNN models [13] and many studies [6,8,9,11,12] in the link prediction tasks have adopted the graph auto-encoder (GAE) framework. The methods using the GAE framework generally have two modules, including the encoder and decoder. Berg et al. [6] propose a GC-MC framework, which is an extension of the GAE framework solving the matrix completion in the form of link prediction. In the GC-MC framework, the encoder generates node features through message passing, and the decoder utilizes a bilinear operation to evaluate the existence of edges. The Graphite proposed by Grover et al. [8] also has an encoder and decoder. The authors use GNN models as the encoder and use an iterative approach with two steps to calculate the edge probabilities in a graph. Salha et al. [9] propose a FastGAE framework to accelerate the training process of the GAE framework in real-world graphs. This framework introduces a node sampling approach and constructs the decoder on the subgraph. Guo et al. [11] propose a MSVGAE framework to remove the deficiency of the GAE framework and employ a self-supervised learning method to make sufficient use of the graph attributes. Salha-Galvan et al. [12] propose a message-passing scheme that takes advantage of both structure and community information in a graph. The message-passing scheme can be used in the encoder of the GAE framework, which is shown to be effective in the link prediction task.
3. Methodology
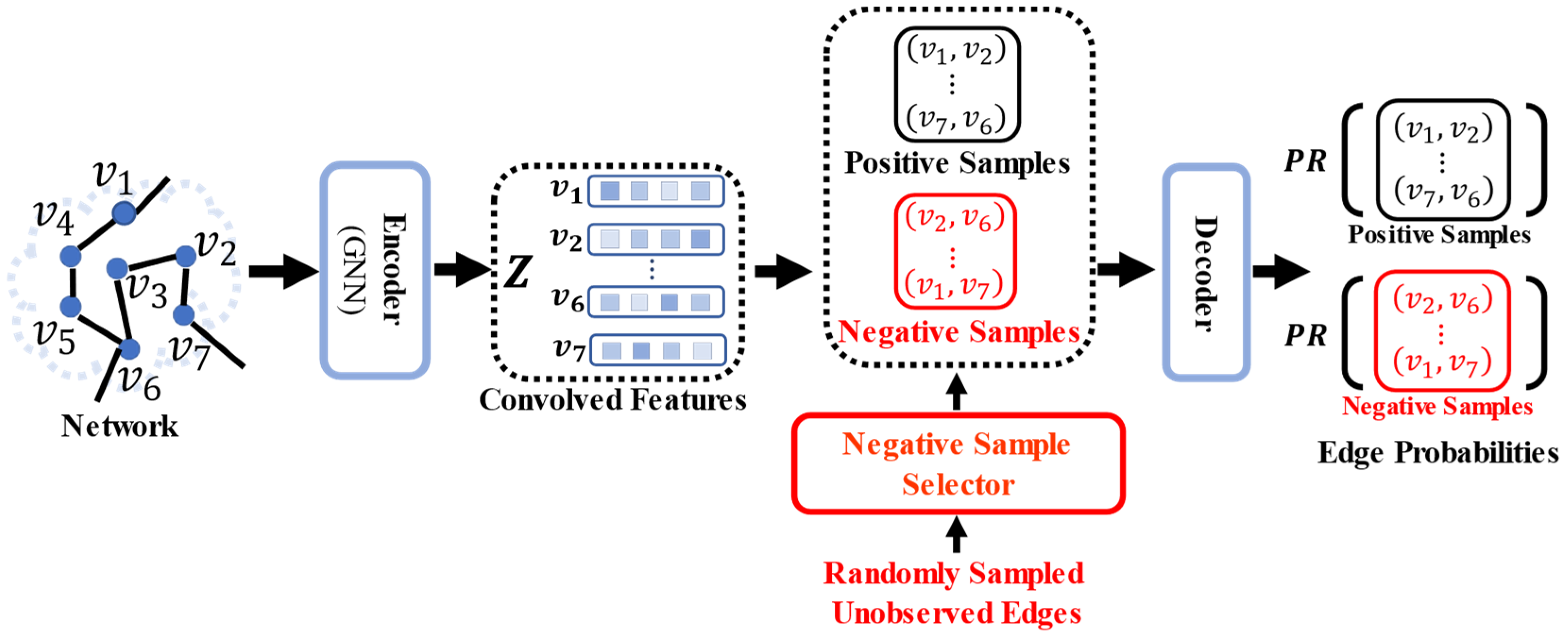
The primary goal of this work is to augment the quality of negative samples for the training of GNN models. As shown in Figure 2, a network is used as the input to the encoder. A GNN model is used as the encoder to obtain the convolved feature matrix for all nodes in the node set . Observed edges in are used as positive samples. Different from previous studies, a negative sample selector is designed to select high-quality negative samples from randomly sampled unobserved edges. The decoder calculates the pair-wise distances of the convolved features, which are used as the edge probabilities of the positive and negative samples.
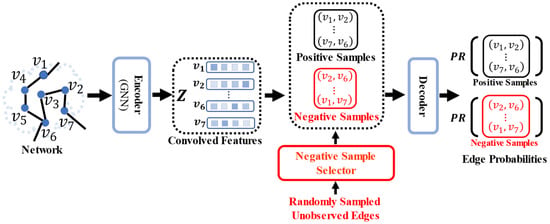
Figure 2.
The training procedure of GNN models with the proposed PbTRM in the link prediction task. GNN models are used as the encoder to extract the convolved features of nodes in the input network. The decoder calculates the edge probabilities of positive and negative samples.
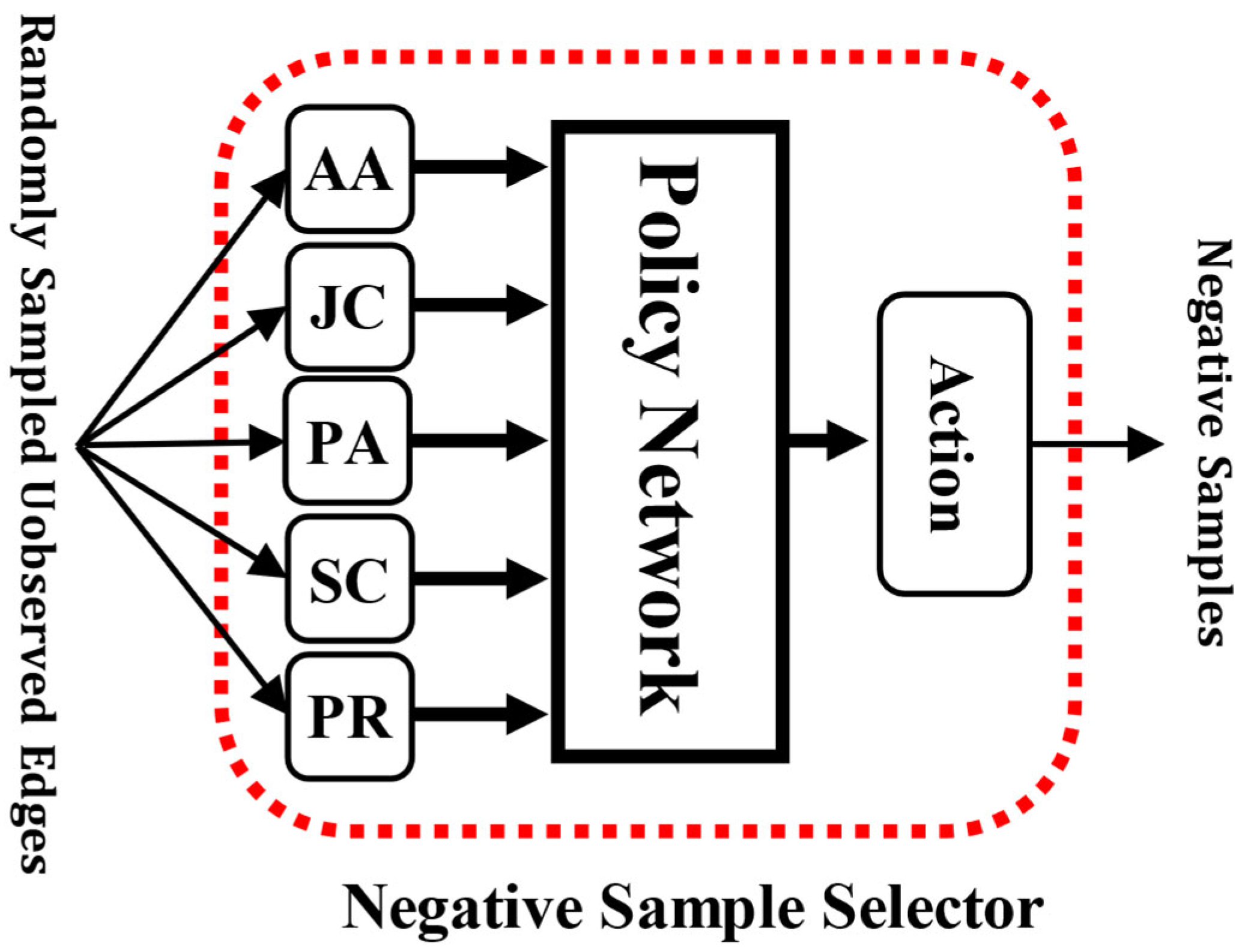
As the core contribution in this work, the architecture of the negative sample selector is shown in Figure 3. In the following sections, we present its architecture and training procedure in detail.
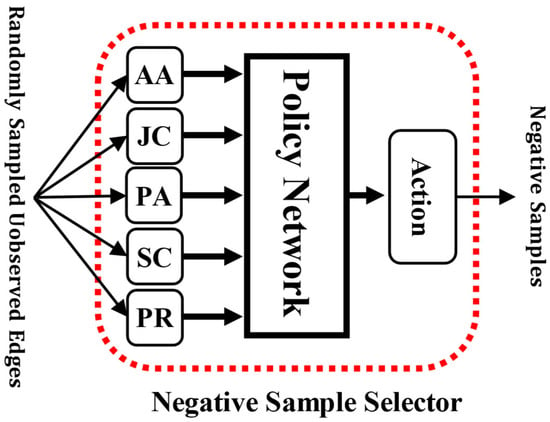
Figure 3.
The architecture of the negative sample selector. The conceptions of the AA, JC, PA, SC, PR, and Action are introduced in Section 3.1 and Section 3.2.
3.1. The Inputs for the Negative Sample Selector
The negative sample selector takes the randomly sampled unobserved edges as inputs. To promote the negative sample selector to select high-quality negative samples from the randomly sampled unobserved edges, a state vector is designed for each randomly sampled unobserved edge. Two kinds of information are utilized to compose the state vector of a randomly sampled unobserved edge.
To avoid choosing missing edges as negative samples, the negative sample selector needs to evaluate the existence of the randomly sampled unobserved edges. Therefore, we use similarity-based matrices, including the Adamic-Adar (AA) [21], Jaccard Coefficient (JC) [22], and Preferential Attachment (PA) [23], and the Spectral Clustering (SC) [24] method to obtain four evaluated score functions. The evaluated score functions are denoted as , , , and for the AA, JC, PA matrices, and SC method, respectively.
In another scenario, some of the randomly sampled unobserved edges can be easily distinguished from the observed edges in by the GNN model. These easily distinguishable negative samples contribute insufficiently to the GNN model. Therefore, we use the edge probability of each unobserved edge in the current sampling period to reflect the ability of the GNN model to distinguish it from observed edges in . The easily distinguishable negative samples are with lower edge probabilities, while the hard distinguishable ones are with higher edge probabilities.
Combining the aforementioned two kinds of information, the negative sample selector builds a state vector for each randomly sampled unobserved edge. For a randomly sampled unobserved edge , its state vector can be expressed as follows:
where is the concatenation operator.
3.2. The Outputs of the Negative Sample Selector
The action for each randomly sampled unobserved edge is determined given its state vector. To achieve this, we design a policy network that is implemented as a fully connected neural network. The policy network is denoted as , where is its parameter set. For a randomly sampled unobserved edge , the policy network takes its state vector as input and outputs the action probability for it, which is expressed as follows:
The action probabilities output from the policy network determine the actions for the randomly sampled unobserved edges. For a randomly sampled unobserved edge , its action is determined by the following policy function :
where represents the action to select the unobserved edge as a negative sample, and represents to drop it. With the output actions, the randomly sampled unobserved edges are filtrated by the negative sample selector, and high-quality negative samples are generated.
3.3. The Reward for the Policy Network
To facilitate the policy network to pick high-quality negative samples, the reward is extended as an indicator reflecting the quality of the generated negative samples in . However, since none of the supervised information can be provided to quantify the quality of negative samples in , we design the reward relayed on the influence of on the prediction performance of the GNN model. In contrast to the previous sampling period, the negative samples in are updated by the negative sample selector in the current sampling period. Therefore, we use the change in the prediction performance of the GNN model in adjacent sampling periods to define the reward as follows:
where the and represent the prediction performance of the GNN model in the current and previous sampling periods, respectively. Equation (4) means the reward for the policy network is positive corresponding to the improved prediction performance of the GNN model in the current sampling period.
The prediction performance of the GNN model is evaluated on the validation set with the metrics including the area under the ROC curve (AUC) [5] and average precision (AP) [5], which is expressed as follows:
Here, and represent the AUC and AP values of the GNN model on , respectively.
3.4. The Updating Procedure of the Policy Network
The parameters of the policy network are updated following the Policy Gradient [14], which is a reinforcement learning approach directly optimizing the policy network by gradient descent. The policy network takes the state vectors of the randomly sampled unobserved edges as inputs and outputs the actions for them. After finishing a sampling period, the policy network obtains a reward . In this sampling period, we define the objective function of the policy network as follows:
where the is the set of the randomly sampled unobserved edges in this sampling period.
To use the gradient descent, the derivative of the objective function is calculated as follows:
The purpose of the training of the policy network is to maximize the expected reward. Therefore, its parameters are updated following the gradient descent [14]:
where the is the learning rate of the policy network.
Armed with the introduction of the negative sample selector, the negative sampling procedure in this work is described in Algorithm 1.
| Algorithm 1: The negative sampling procedure with the negative sample selector |
| INPUT: Network and number of required negative samples OUTPUT: Negative sample set |
|
3.5. The Training Procedure of the GNN Model with PbTRM in the Link Prediction Task
Compared to the training procedure of GNN models in the previous studies, the differences in this work are described as follows:
The randomly sampled unobserved edges are sequentially input into the negative sample selector. The negative sample selector obtains state vectors of the randomly sampled unobserved edges and feeds the state vectors into the policy network. According to the actions output from the policy network, high-quality negative samples are selected from the randomly sampled unobserved edges to compose the negative sample set . The state vectors and actions of the randomly sampled unobserved edges are recorded to update the parameters of the policy network.
In this work, we set a sampling period in the proposed PbTRM, where each sampling period contains training epochs. To calculate the reward for the policy network, we need a base value of the prediction performance of the GNN model before the first update of the policy network. Therefore, we construct the negative sample set by randomly sampling from unobserved edges in the first sampling period. The prediction performance of the GNN model, which is evaluated in the first sampling period, is set as the base value. Starting from the second sampling period, the negative sample set is updated by the negative sample selector following Algorithm 1, and the policy network is updated according to the reward, state vectors, and actions in this sampling period.
The detailed training procedure of the GNN model with PbTRM in the link prediction task is described in Algorithm 2.
| Algorithm 2: The policy-based training method (PbTRM) |
| INPUT: Network and value of a sampling period OUTPUT: Edge probabilities of edges in |
| 1:a for epoch in : 2: if or : #In the first training epoch of a sampling period 3: if epoch = 1: #In the first training epoch of the first sampling period 4: Obtain the negative sample set by randomly sampling from 5: else: 6: Obtain the negative sample set following Algorithm 1 7: Calculate the edge probabilities of the edges in and 8: Calculate the loss function value for the GNN model 9: Update the parameters of the GNN model according to the loss function value 10: if or : #In the last training epoch of a sampling period 11: Evaluate the prediction performance of the GNN model following Equation (5) 12: if epoch = : #In the last training epoch of the first sampling period 13: # Base value for the first update of the policy network 14: else: 15: 16: Calculate the reward for the policy network following Equation (4) 17: Update the parameters of the policy network following Equation (8) 18: 19: end for 20: Calculate the edge probabilities of edges in |
4. Experiments
4.1. Datasets
In this work, we employ two standard datasets, including Cora [17] and CiteSeer [17]. Table 1 summarizes the split details of these two datasets. We split 10% and 20% of the observed edges in the datasets into the validation and test sets as positive samples, respectively. The same number of randomly sampled unobserved edges are used as negative samples in the validation and test sets.

Table 1.
The split details of two datasets in this work.
4.2. Implementation Details
The implementation details of experiments in this work are described as follows.
In this work, all experiments are performed on a computer with a 2 GHz quad-core processor and 16 GB memory. To illustrate the effectiveness of the proposed PbTRM, we utilize three GNN models as the encoder, including GCN, GraphSAGE, and GAT. The PyTorch Geometric [25] is used to construct the GCN, GraphSAGE, and GAT in this work. For the GCN, we construct it with two graph convolutional layers, where the output sizes of the first layer and second layer are 128 and 64, respectively. The GraphSAGE is constructed with two SAGE layers, whose output sizes of two layers are the same as the GCN. As for the GAT, its first layer is the graph attention layer that uses multi-headed attention with 4 heads, and the input size of the second graph attention layer is 512.
The GCN, GraphSAGE, and GAT models in this work use the same decoder. In the decoder, the dot product of convolved features is used to calculate the edge probability. During the training procedure of GNN models, the binary cross entropy with logits backward is used as the loss function to calculate the loss of the predicted edge probability. All GNN models in this work are trained for 100 epochs.
The policy network is implemented as a two-layer fully connected network, whose input and output sizes are 5 and 2, respectively.
4.3. Effectiveness of the PbTRM
We conduct the experiment with the GCN, GraphSAGE, and GAT models on the datasets, including Cora and CiteSeer. The datasets are spilt following Table 1. To verify the effectiveness of the proposed PbTRM, we train the GNN models with two different methods. The GNN models trained with the proposed PbTRM, denoted as GNN+PbTRM, generate negative samples in the training sets by using the negative sample selector following Algorithm 1. The GNN models, which generate the negative samples in the training set by randomly sampling unobserved edges, are used as benchmarking GNN models. For a fair comparison, the values of a sampling period for the GNN+PbTRM and benchmarking GNN models are all set as 1. When value is set to 1, the GNN+PbTRM and benchmarking GNN models update the negative samples in their training sets in each training epoch. The prediction performance of the benchmarking GNN models is used as the baseline performance. The prediction performance is evaluated by two standard metrics in the link prediction task, including AUC [5] and AP [5], and the results are listed in Table 2 and Table 3.

Table 2.
The comparison of prediction performance between GNN+PbTRM and benchmarking GNN models on Cora.

Table 3.
The comparison of prediction performance between GNN+PbTRM and benchmarking GNN models on CiteSeer.
From Table 2 and Table 3, it can be observed that the AUC and AP values of the GCN, GAT, and GraphSAGE models trained with the proposed PbTRM are all higher than those of corresponding benchmarking GNN models. In comparison to their benchmarking GNN models, the GNN+PbTRM models employ the negative sample selector to select high-quality negative samples from the randomly sampled unobserved edges. The parameters of the policy network are updated at the end of each sampling period, which promotes the negative sample selector to perform better. The augmented AUC and AP values indicate that the negative samples generated by the negative sample selector can make the GNN models outperform their baseline performance, which demonstrates the effectiveness of the proposed PbTRM.
In this experiment, we also observed that the time required by the training of the GNN+PbTRM models is longer than that of the benchmarking GNN methods. In the proposed PbTRM, it is necessary for the randomly sampled unobserved edges to be selected by the negative sample selector, and then the parameters of the policy network need to be updated in each sampling period. While the aforementioned two steps increase the time required by the training of the GNN+PbTRM models, they enhance the prediction performance of the GNN+PbTRM models. This shows that although the time consumption of the proposed PbTRM is longer than that of the random sampling of the unobserved edges, it is necessary for the effectiveness of the proposed PbTRM.
4.4. Influence of the Sampling Period
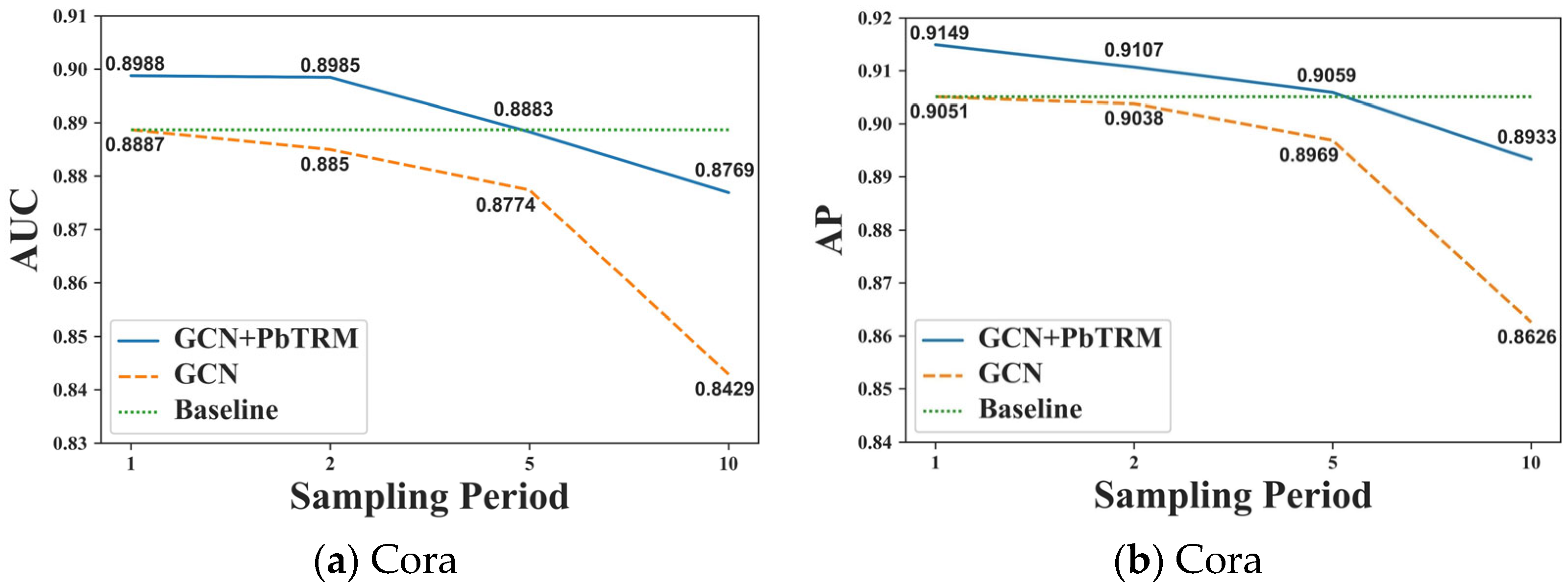
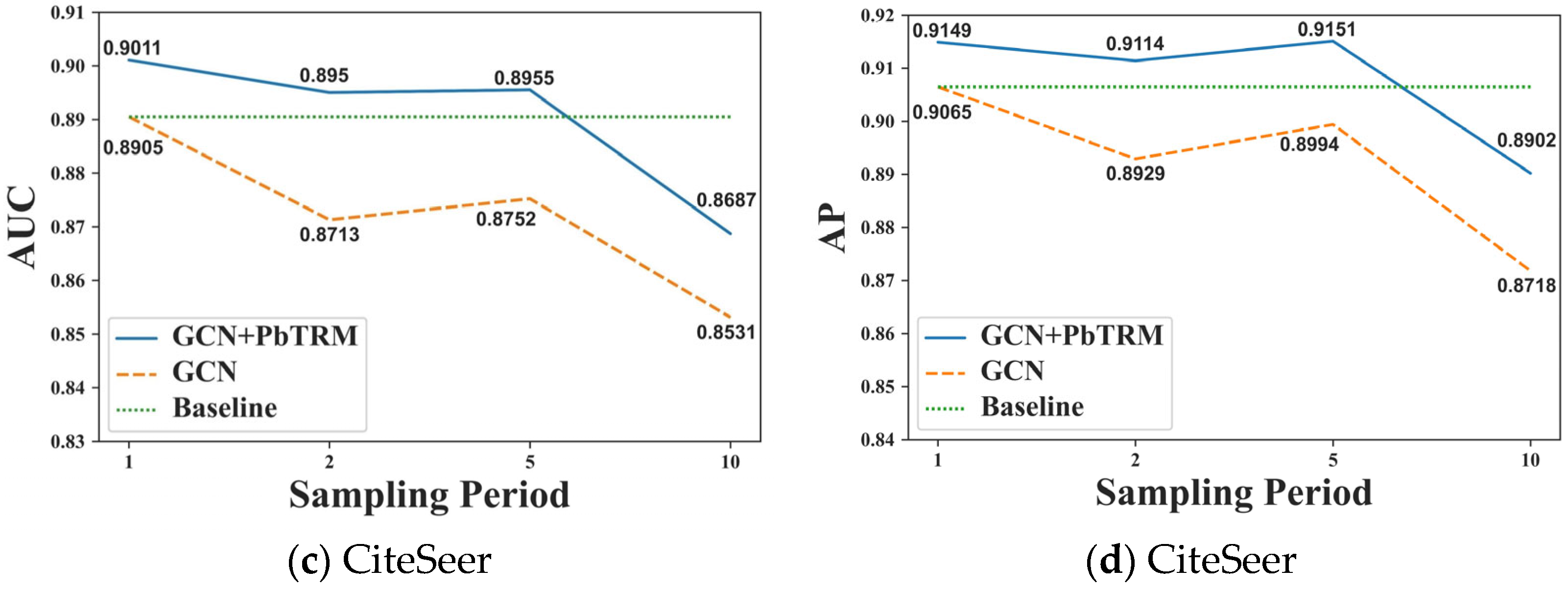
In this experiment, we study the influence of the sampling period on the proposed PbTRM. The prediction performance of the GCN+PbTRM model is compared to its benchmarking GCN model by searching the value in a range of . The value for the benchmarking GCN model means that the negative samples in its training set are updated by randomly sampling unobserved edges after finishing training epochs. To illustrate the effectiveness of the proposed PbTRM, the prediction performance of the benchmarking GCN model, whose value is set as 1, is used as the baseline performance. The experimental results are illustrated in Figure 4a–d.
Figure 4.
The changes in prediction performance of GCN+PbTRM and benchmarking GCN models on different values of a sampling period.
On the Cora dataset, the AUC and AP values of the GCN+PbTRM model with the value of 1 and 2 are higher than the baseline performance and fell to around the baseline performance when the value is equal to 5. On the CiteSeer dataset, the AUC and AP values of the GCN+PbTRM model keep higher than the baseline performance when is equal to 1, 2, and 5. Given these results, the proposed PbTRM is workable when the value of is set to be a relatively low value. As the value of increases, the training of the policy network in the negative sample selector becomes insufficient, which results in the poor prediction performance of the GCN+PbTRM model. The update frequency of negative samples in keeps decreasing with the increasing value, which can be another reason for the decreasing prediction performance of both the GCN+PbTRM and benchmarking GCN models.
5. Conclusions
In this work, we identify the problem in randomly sampling unobserved edges as negative samples, where the false and easy negative samples limit the prediction performance of GNN models in the link prediction task. We proposed a policy-based training method (PbTRM) to improve the negative sampling procedure. In the proposed PbTRM, randomly sampled unobserved edges are fed into the negative sample selector. The negative sample selector obtains the state vectors of the randomly sampled unobserved edges and outputs actions for them. According to the actions of the randomly sampled unobserved edges, high-quality negative samples are selected from them for the training of GNN models. We conduct comprehensive experiments with three GNN models. The experimental results show that the proposed PbTRM can enhance the prediction performance of GNN models on two standard datasets in the link prediction task.
One limitation of this work is that the time consumption of the proposed PbTRM is longer than that of the random sampling method used in previous studies. In future work, we intend to improve the efficiency of the proposed PbTRM by reducing its time consumption. Moreover, we also plan to conduct further experiments to illustrate the effectiveness of the PbTRM on larger network datasets.
Author Contributions
Data curation, Y.S.; software Y.S. and Z.H.; writing—original draft preparation, Y.S.; writing—review and editing, Y.S., G.L., Z.H. and C.Y.; visualization, Y.S. and C.Y.; supervision, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities (grant No. 2662022JC005 and 2662021JC008) and HZAU-AGIS Cooperation Fund (grant No. SZYJY2022001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All datasets used in this work are available in the PyTorch Geometric [25].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Tsitsulin, A.; Palowitch, J.; Perozzi, B.; Müller, E. Graph Clustering with Graph Neural Networks. arXiv 2020, arXiv:2006.16904. [Google Scholar]
- Zhang, M.; Cui, Z.; Neumann, M.; Chen, Y. An end-to-end deep learning architecture for graph classification. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Kumar, A.; Singh, S.S.; Singh, K.; Biswas, B. Link prediction techniques, applications, and performance: A survey. Phys. A Stat. Mech. Its Appl. 2020, 553, 124289. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- van den Berg, R.; Kipf, T.N.; Welling, M. Graph convolutional matrix completion. arXiv 2017, arXiv:1706.02263. [Google Scholar]
- Zhang, M.; Chen, Y. Link Prediction Based on Graph Neural Networks. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 5171–5181. [Google Scholar]
- Grover, A.; Zweig, A.; Ermon, S. Graphite: Iterative generative modeling of graphs. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 2434–2444. [Google Scholar]
- Salha, G.; Hennequin, R.; Remy, J.B.; Moussallam, M.; Vazirgiannis, M. FastGAE: Scalable Graph Autoencoders with Stochastic Subgraph Decoding. Neural Netw. 2021, 142, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Zhang, Z.; Xhonneux, L.P.; Tang, J. Neural Bellman-Ford Networks: A General Graph Neural Network Framework for Link Prediction. In Proceedings of the 35th Conference on Neural Information Processing Systems, Virtually, 6–14 December 2021; pp. 29476–29490. [Google Scholar]
- Guo, Z.; Wang, F.; Yao, K.; Liang, J.; Wang, Z. Multi-Scale Variational Graph AutoEncoder for Link Prediction. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining, Tempe, AZ, USA, 21–25 February 2022; pp. 334–342. [Google Scholar]
- Salha-Galvan, G.; Lutzeyer, J.F.; Dasoulas, G.; Hennequin, R.; Vazirgiannis, M. Modularity-Aware Graph Autoencoders for Joint Community Detection and Link Prediction. arXiv 2022, arXiv:2202.00961. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Vinel, A. Benchmarking Graph Neural Networks on Link Prediction. arXiv 2021, arXiv:2102.12557. [Google Scholar]
- Sutton, R.S.; Mcallester, D.; Singh, S.; Mansour, Y. Policy Gradient Methods for Reinforcement Learning with Function Approximation. In Proceedings of the 12th International Conference on Neural Information Processing Systems, Denver, CO, USA, 29 November–4 December 1999. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yang, Z.; Cohen, W.W.; Salakhutdinov, R. Revisiting Semi-Supervised Learning with Graph Embeddings. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 40–48. [Google Scholar]
- Lu, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. Its Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph Neural Networks: A Review of Methods and Applications. arXiv 2018, arXiv:1812.08434. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2014, arXiv:1312.6203. [Google Scholar]
- Adamic, L.A.; Adar, E. Friends and neighbors on the web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Jaccard, P. Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bull. Soc. Vaud. Des Sci. Nat. 1901, 37, 241–272. [Google Scholar]
- Barabâsi, A.-L.; Jeong, H.; Néda, Z.; Ravasz, E.; Schubert, A.; Vicsek, T. Evolution of the social network of scientific collaborations. Phys. A Stat. Mech. Its Appl. 2002, 311, 590–614. [Google Scholar] [CrossRef]
- Lei, T.; Huan, L. Leveraging social media networks for classification. Data Min. Knowl. Discov. 2011, 23, 447–478. [Google Scholar] [CrossRef]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).