Aerodynamic Drag Reduction on Speed Skating Helmet by Surface Structures

Abstract

The aerodynamic drag for speed skating helmets with surface structures was investigated in this work by using numerical and experimental methods. Computational fluid dynamic (CFD) research was performed to analyze the detail of the flow field around the helmets. The simplified helmet models, with riblet and bump surface structures, were analyzed using the CFD simulations. The pressure distribution and velocity field around the helmets were obtained through the CFD analysis. The CFD results showed that the boundary layer separation position was obviously delayed, and the pressure changed to a higher value at the back area for structured helmets. Therefore, the aerodynamic drag for the structured helmet was lower than that of the original model. According to the CFD results, three types of helmets, with the of riblet and bump surface structure printed on the helmets by using flexible film, were tested in a wind tunnel. A full-scaled skater mannequin of half a body was used in the experiment to simulate the actual skating process. Compared with the original helmet, a drag reduction rate of 7% was achieved for the helmet with the bump at the middle region in the wind tunnel experiment, at the average speed in competitions for skaters.

1. Introduction

Aerodynamic drag plays an important role in competitive games such as short-track speed skating. Many drag reduction methods have been adopted in recent years, such as optimized postures and drag reduction skating suits. In addition to these, researchers also concentrated on helmets that must be used in formal competitions as protection gear. However, not many reports about aerodynamic performance of skating helmets could be found. Taking cycling helmets as the example, Len Brownlie [1,2] used the wind tunnel method to study competitive time trial cycling helmets and provided an analytical procedure to test the drag of those helmets. Firoz Alam [3] also studied the competitive cycling helmets with dimples and ribbed structures using wind tunnel tests, and the results showed that the frontal area played a critical role in pressure drag and that the dimple helmet might provide a marginal improvement to the aerodynamic performance. It was also found in the research by L. Underwood [4] that the frontal area influenced the wake region of the helmet. Computational fluid dynamics (CFD) are useful to understand the mechanisms of drag reduction and flow field, and has been used in much research regarding competition sports [5,6]. It was found that the tail shapes of cycling helmets were important to the total drag by influencing the pressure behind the athletes [7,8,9,10].

Drag reducing by surface structure as a passive control method without energy inputting has attracted many researchers. The drag reduction method with riblets is one of the few techniques that has been successfully applied in both the laboratory and aerodynamic configurations. Inspired by the shark skin, many researchers attempted to make replicas and optimize the geometry at different flow fields [11]. The drag reduction performance of the riblet surface with different cross-sectional shapes was studied through experiments. Walsh obtained a frictional drag reduction of 8% under turbulent flow conditions [12]. Bechert et al. tested the drag reduction characteristics of the riblet structured surfaces with various cross-sectional shapes, including sawtooth, semicircular, and rectangular riblets [13]. The results showed that the riblet surface with the sawtooth structure had a better drag reduction effect compared with others. The aforementioned riblet surfaces with various cross-sectional shapes were proposed by scaling on the placoid scales from the shark skin, and the direction of riblet structure was parallel to the velocity. The convergent and divergent riblet structures that were not parallel to the velocity direction had been studied by K. Keoltzsch [14], and the velocity filed close to the wall was obtained by experiments. Dean et al. [15] obtained a surface with a drag reduction rate of 10% by duplicating, scaling, and optimizing the ridged structure of the placoid scales from the shark skin.

For curved surfaces where the flow is separated from the surface, the surface structure can also reduce the resistance by influencing the transformation of fluid from laminar to turbulent. The longitudinal grooves, which are parallel to velocity, can suppress the spanwise vortex, such as V-groove [16] and U-groove [17]. Meanwhile, spanwise surface structures on cylindrical surfaces, i.e., vertical to the velocity direction, could change the separation point because of the interaction of fluid and groove [2,18], and still worked even if the depth of the groove was very shallow [19]. The circular dimple surface is another uniform surface structure that can create a disturbance in the boundary layer to accelerate the transition from laminar to turbulent. Frohlich studied the possibility of drag reduction in baseball sports [20], and this structure attracted more attention to the drag reduction field afterward. Many researchers studied the dimple structures on the cylinder model and obtained the drag reduction effect [21,22]. In addition, other types of dimples, such as hexagonal geometry showed similar drag reduction effects [23]. The velocity profile around dimple and separate points was measured on the sphere [24,25] to reveal the drag reduction mechanism of the dimples.

Herein, we report the design of a skating helmet with surface structures to reduce the aerodynamic drag. The CFD method with the LES turbulence model was employed to analyze the details of the flow field in the model of the skating helmet. The real helmets with surface structure had also been fabricated, and wind tunnel experiments were performed using the structured helmets on a full-scale mannequin.

2. Numerical Approach

2.1. Computational Conditions and Helmet Models

The CFD method was used in this study to observe the fluid detail around the helmet models. The actual flow field around the athlete is very complex, so reasonable and necessary assumptions are made in the CFD process. To easily construct the surface structure on the helmet surface, an ellipsoid was used to approximate the shape of the helmet. The dimensions of the ellipsoid are shown in Figure 1, and it was very close to the helmet in geometry. Here, it was assumed that the ellipsoid model was similar to the actual helmet in terms of flow field properties, and the influence of the details of the actual helmet could be omitted. At the same time, we also assumed that the movement of the athlete’s arms and legs in skating had little effect on the helmet, as they were moving behind and below the shoulders of the skater. Underneath the simulated helmet model, a support structure was designed to simulate the off-the-ground position in the actual process. The support consisted of two parts: one was a cylindrical shape close to the helmet, which was used to simulate the athlete’s face, and the other had a variable cross-section to simulate the athlete’s neck and below. In order to reduce the calculation task, the influence of the torso far from the helmet was ignored here. The support with a smooth surface was extended to the ground, so that there were no cross-sections in the computational domain and its impact on the flow field would be avoided. The height between the center of the helmet and the ground was H = 1 m, and the helmet was tilted forward 45° to simulate the athlete’s position, which agreed with the mannequin used in wind tunnel experiments.

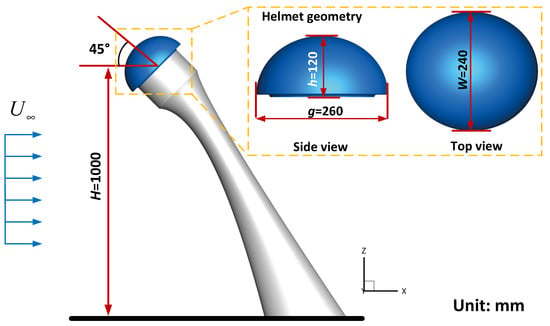
Figure 1. The simplified helmet model with geometrical dimensions used in CFD simulations.

As shown in Figure 2, the computational domain was a rectangular box, which was 2H in width and height and 6H in the streamwise direction. The helmet model was located 1.5H from the inlet surface. A uniform velocity field of x direction ($U=14 \mathrm{m}/\mathrm{s}$) was set on the inlet surface with zero turbulence intensity. The outlet surface was defined as the pressure outlet with zero gauge pressure. The helmet surface, as well as the support surface, was set as the smooth no-slip wall, on which the air had no relative velocity to the model because of the viscosity. The ground surface was also set with a no-slip condition, and defined as the moving wall with the same velocity ($U=14 \mathrm{m}/\mathrm{s}$) at x direction as defined at the inlet face, which could simulate the relative velocity between the athlete and the ground during skating competitions. Other surfaces on the rectangular domain were set as the symmetry boundary, which means that the velocity and pressure gradient were zero in the normal direction of the surface. It was assumed that the property of air remained constant in the skating process. Reference density, temperature, and pressure of 1.225 $\mathrm{kg}/{\mathrm{m}}^3$, 15 °C, and 101,325 Pa were adopted in the simulation, respectively.

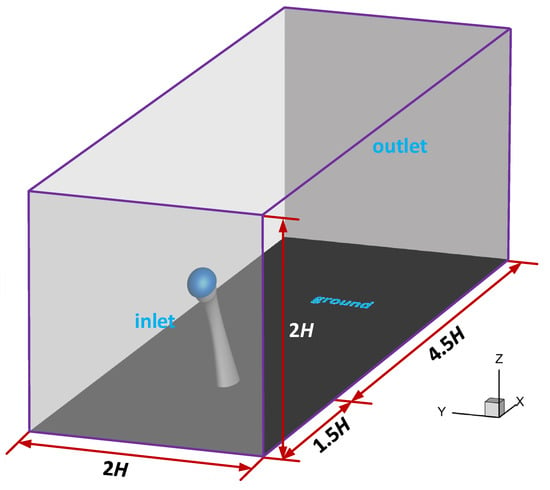
Figure 2. The computational domain in CFD simulations.

Another two types of structured helmet models, as shown in Figure 3, were simulated in the CFD analysis besides the original one. The height of the riblets in Figure 3a is h = 1 mm, and the cross section is an equilateral triangle. The space between two riblets is s = 10 mm. Figure 3b is the helmet model with bumps in the middle region. The height and diameter of the bumps is h = 0.5 mm and d = 3 mm, respectively. The bumps have a staggered arrangement on the helmet surface, and the space between two bumps is s = 6 mm.

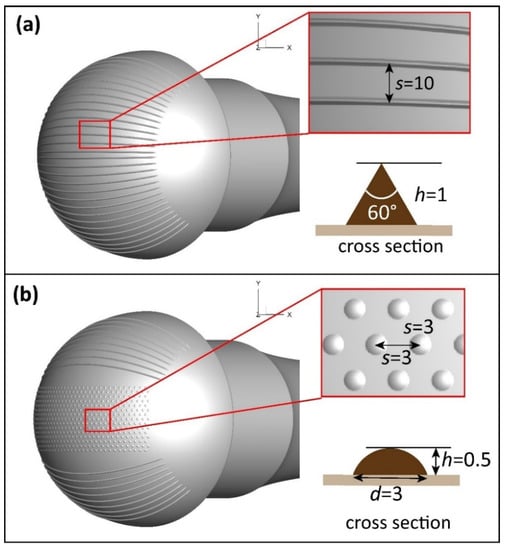
Figure 3. The helmet model with surface structure used in the CFD simulations; (a) the riblet structured helmet model, (b) the bumped helmet model.

2.2. Slover Conditions and Mesh Convergence Research

The CFD analysis was performed with the Ansys fluent 2020 R1. To catch the vortex around the helmet and in the wake region, a large eddy simulation (LES) turbulence model was adopted in our numerical analysis. LES is the widely accepted model in the industry to solve a variety of problems, in which turbulence models for the RANS equations are either inaccurate, or do not supply sufficient information. The governing equations employed for the LES are obtained by filtering the time-dependent Navier–Stokes equations. The filtering process effectively filters out the eddies whose scales are smaller than the grid spacing used in the computation. The filtered equations are written as follows.

$$\frac{\partial {\overline{u}}_i}{\partial x_i}=0$$

(1)

$$\frac{\partial {\overline{u}}_i}{\partial t}+u_j\frac{\partial {\overline{u}}_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial \overline{p}}{\partial x_j}+\frac{\partial }{\partial x_j}\left[\nu \left(\frac{\partial {\overline{u}}_i}{\partial x_j}+\frac{\partial {\overline{u}}_j}{\partial x_i}\right)+{\tau }_{ij}\right]$$

(2)

Here, $\nu$ is the kinematic viscosity of fluid, and $\overline{u}$ and $\overline{p}$ are the filtered velocity and pressure, respectively. In the spatially filtered Navier–Stokes equations, the stress term ${\tau }_{ij}=\overline{u_i}\overline{u_j}-{\overline{u}}_i{\overline{u}}_j$ is molded using the eddy-viscosity type SGS model of Smagorinsky, which is based on Boussineq’s assumption,

$${\tau }_{ij}-\frac{2}{3}{k}_t{\delta }_{ij}=-2{\nu }_t\left({\overline{S}}_{kk}-\frac{1}{3}{\overline{S}}_{kk}{\delta }_{ij}\right)$$

(3)

$${\overline{S}}_{ij}=\frac{1}{2}\left(\frac{\partial {\overline{u}}_i}{\partial x_j}+\frac{\partial {\overline{u}}_j}{\partial x_i}\right)$$

(4)

where ${\overline{S}}_{ij}$ is the rate of strain tensor computed from the resolved scales, ${\nu }_t$ is the SGS viscosity and $k_t$ is the turbulent kinetic energy.

The unsteady pressure-based solver was used in our simulations and the SIMPLE scheme was chosen in pressure–velocity coupling. The second order scheme was set for the pressure and the bounded central differencing for the momentum with respect to the spatial discretization, while the gradients were evaluated as the least squared cell based gradients. The time step for the unsteady solver was set to ${10}^{-5}$ s, and the total time was 2 s for every simulation. The residuals of continuity and velocity were monitored as the convergence criteria, which were the order of ${10}^{-3}$ for continuity and the order of ${10}^{-5}$ for velocity (x, y, z components) at every time step. The drag of every helmet model was analyzed to confirm whether the flow field had reached stability.

The schematic of the mesh in the computational domain is shown in Figure 4. An unstructured mesh was established and refined near the helmet as well as in the wake region. The maximum element size, minimum element size, and growth rates were defined as 50 mm, 0.1 mm, and 1.2, respectively. A polygon surface mesh was defined on the surface of the helmet and the support, and a refinement was also applied to the surface structure (bumps and riblets). Regarding the boundary layer mesh, a prismatic inflation of 20 layers with the first layer height of 0.01 mm and the growth rate of 1.2 was applied.

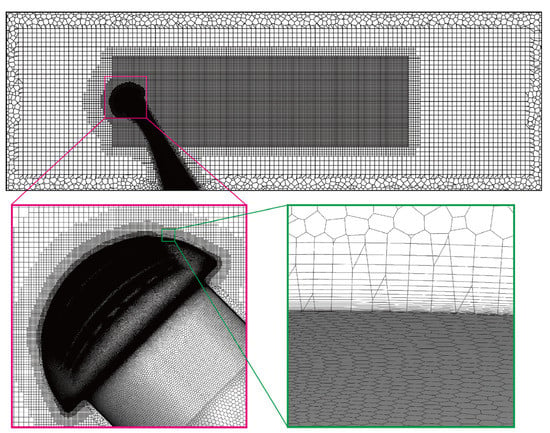
Figure 4. The schematic of the mesh in the computational domain.

A mesh convergence study had been performed on the original helmet model with 4 sets of meshes, as shown in Table 1. The coefficient of aerodynamic drag ($C_{\mathrm{d}}$) was calculated in this study as

$$C_{\mathrm{d}}=\frac{F_{\mathrm{d}}}{\frac{1}{2}\rho A{U}^2}$$

(5)

where $F_{\mathrm{d}}$ was the drag force, $\rho$ was the density of air, A was the frontal area, and U was the free stream velocity. Figure 5 shows that the computations with mesh M3 and mesh M4 yielded insignificant changes to results in terms of time-averaged drag coefficient, which did not show a difference up to the fourth decimal. Therefore, mesh M3 had a good balance in between the sufficient grid resolution and the simulation efficiency.

Table 1. The finite element mesh used in simulations and the results of the grid convergence study.

Mesh	Elements	${\mathit{C}}_{\mathit{d}}$
M1	7,316,086	0.32416
M2	8,779,304	0.33005
M3	14,505,131	0.33202
M4	20,200,985	0.3322

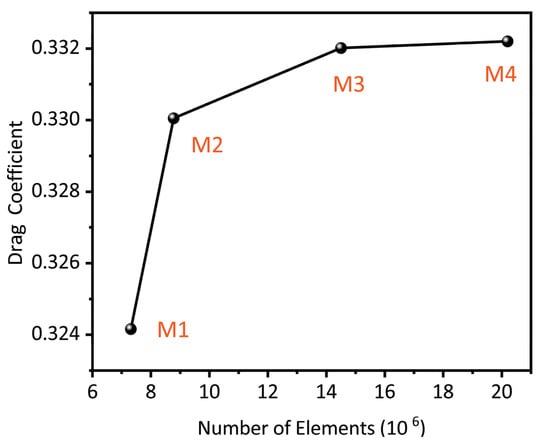
Figure 5. Grid convergence study for $C_d$ with respect to the number of elements in the computational domain.

3. Experiment Method and Fabrication Process

A full-scale skater model without arms or legs was used in the wind tunnel experiment. This model was obtained by scanning an athlete in skating posture with the head tilted to 45°. In order to simulate the actual competition process as much as possible, the head, the face, and the neck, which were close to the helmet in the model, were completely preserved, while the lower part of the torso was simplified to reduce the resistance. Moreover, the cross-section of the simplified lower support was streamlined, as shown in Figure 1. The point of this treatment was that the change in resistance with speed would be more stable compared with a cylindrical support, which helped to reduce experimental errors. There were some marks on the head of this model to ensure that the test helmets would be at the same position every time, in order to reduce the systematic errors. The schematic of the wind tunnel experiment is shown in Figure 6.

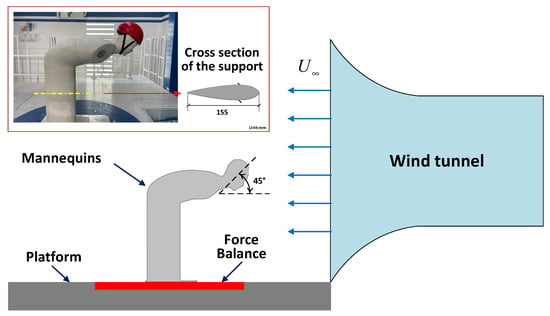
Figure 6. Schematic of the wind tunnel experiment.

The experiments were conducted in an open jet wind tunnel which had a rectangular cross section of 2.5 m × 3 m (width × height). This wind tunnel was specially designed for sports training and has high flow field quality. The turbulence intensity was less than 0.75%; therefore, the velocity is consistent, with very little fluctuation. The boundary layer thickness near the wind tunnel ground was measured at a velocity of 20 m/s, and the result showed that the thickness was about 80 mm, which was much smaller than the height of the mannequin. The blockage ratio was approximately 3% in our experiments. The whole test object was placed in the center of the wind tunnel and about 4 m from the outlet. The experiments were performed in a series free stream velocities ($U$) from 6 m/s to 24 m/s. The Reynolds number ($Re=WU/\nu$, where $U$, $W$, and $\nu$ were the free stream velocity, the helmet width, and the kinematic viscosity of the air, respectively) based on the free stream velocity and the helmet width was from $1\times {10}^4$ to $2\times {10}^5$. The drag force on the model was measured by a force balance installed under the test platform of the wind tunnel. The measuring range of the balance was 300 N in the streamwise direction. The balance was also calibrated before the experiment, and the uncertainty was less than 0.07%. The sampling frequency in this experiment was 1200 Hz, and the sampling time on each velocity value was 10 s. Each helmet was measured for five rounds to reduce the systematic error, and the results were averaged, with standard deviations calculated.

Four types of helmets were tested in this wind tunnel experiment, including three helmets with surface structures and one original helmet without any structure as the control. Figure 7a shows the distribution of surface structures on tested helmets. The helmet surface was divided into three parts, where different types of surface structures were used. Region A and C were located on the sides of the helmet, while region B was on the top. According to the helmet shape and the drag reduction effect of the surface structure, the riblet structure had been used in Region A and C on all structured helmets. The surface structure used in region B had two types, namely riblets and bumps. as shown in Figure 7b,c. The riblet structure used in Region B had a cross-section shape of a regular triangle, as defined by the height (h) and the space (s), which was the same as those in Region A and C. The bumps were spherical and defined by three parameters, namely height (h), diameter (d), and space (s). Detailed parameters of the surface structures used in four types of test helmets are shown in Table 2.

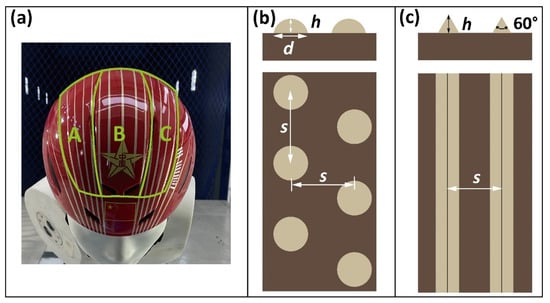
Figure 7. (a) the position to print surface structure on helmet; the surface structure parameters of bumps (b) and riblets (c).

Table 2. Parameters of surface structure used in four types of helmets tested in wind tunnel experiments (unit: mm).

Helmet Type	Region A and C		Region B
	Riblets		Riblets		Bump
	h	s	h	s	h	d	s
Type 1	0.5	10	0.5	10	Null
Type 2	0.5	10	Null		0.5	3	6
Type 3	0.5	10	Null		0.5	3	4
Original	Smooth Surface

It was difficult to process the surface structure directly on the helmet surface because of its irregular curved surface. The thermal cured flexible films made by polydimethylsiloxane (PDMS) and the epoxy resin were used to fabricate the riblets and bumps. The fabrication process of the surface structure is shown in Figure 8. The templates were made from a flat plate of aluminum by carving. Then, a thin layer of PDMS was covered on the template surface. After curing at 80 °C for 20 min, a flexible structured film was obtained. Then, the surface of the helmet was coated with epoxy resin and imprinted by the flexible structured film. After the epoxy resin was completely cured, the flexible structured film was removed to complete the preparation of the designed surface structure. As-prepared helmets for wind tunnel experiments are shown in Figure 9.

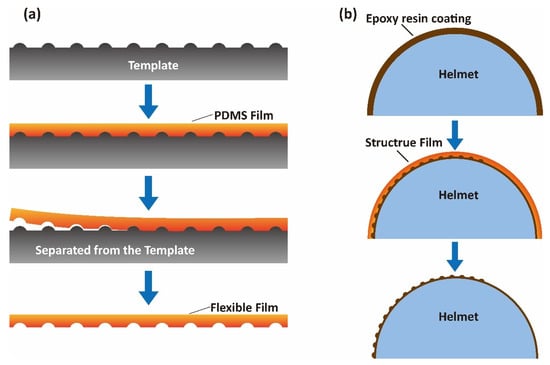
Figure 8. Schematic of fabrication method of surface structure on the helmet surface. (a) The fabrication of flexible film with structure; (b) the process of printing on the helmet surface.

Figure 9. The helmets tested in the wind tunnel experiments. (a) is the original helmet; (b) is the type 1 helmet with all riblets; (c,d) are the type 2 and type 3 helmets with bumps at the middle region, respectively.

4. Results and Discussion

4.1. CFD and Experiment Results

The free stream velocity of the CFD simulations was 14 m/s ($Re=2.3\times {10}^5$) in this research, because it was the typical velocity in competitions. The drag coefficients of the CFD results were summarized in Figure 10. It was found that the drag coefficient of the bumped helmet model was lower than others, which was consistent with the wind tunnel experiment results. The rate of drag reduction ($\eta$) can be defined as

$$\eta =\frac{F_{d1}-F_{d2}}{F_{d1}}\times 100\%$$

(6)

where $F_{d1}$ and $F_{d2}$ are the drag forces of the helmets with and without surface structure, respectively. The drag reduction rate of the riblet helmet and the bump helmet compared with original helmet model were approximately 2.4% and 4.2%, respectively.

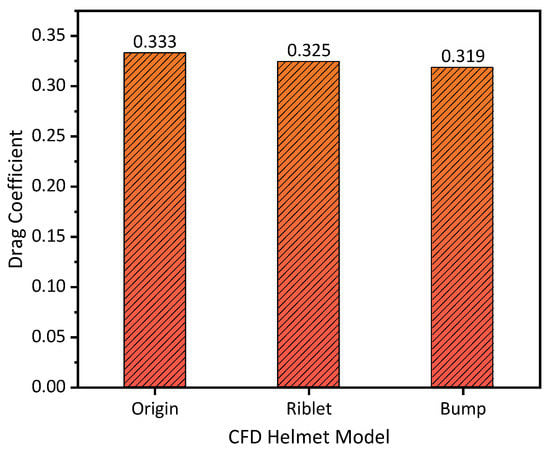
Figure 10. Drag coefficient of the results for three types of helmets used in the CFD simulations.

According to the CFD results, the drags of structured helmets were measured by experiment. In addition, a helmet with smaller space between bumps (type 4) was tested to further analyze the drag reduction effect of the bump structure. The experiment results are plotted in Figure 11, where the $C_d$ values are averaged over five rounds of the sampling process. The error bars based on the standard deviation are also presented in Figure 10a, and the relative standard deviation was less than 1.4%. As shown in Figure 11a, $C_d$ of all tested helmets kept a high value when Re was less than $1.2\times {10}^5$, and showed a significant decrease as Re increased from $1\times {10}^5$ to $2\times {10}^5$. This phenomenon was due to the torso and supporter of the model, and the helmets had a less significant impact on that. It was clear that the $C_d$ of the original helmet was higher than that of structured helmets. Figure 11b shows the $\eta$ of structured helmets compared with those without surface structure. It was found that the range of Re based on free stream velocity could be divided into two parts, as $Re<1.4\times {10}^5$ and $Re>1.4\times {10}^5,$ according to the $\eta$ of the structured helmets. For the range of $Re<1.4\times {10}^5$, the drag of the type 2 helmet was lower than the drag of others, and the $\eta$ value of the type 2 helmet was approximately 9% in Re =$1.2\times {10}^5$. However, when $Re>1.4\times {10}^5$, the $\eta$ of the type 3 helmet was significantly higher than the others (approximately 7% in $Re=2\times {10}^5)$. During competitions, the usual velocities of athletes are approximately 10–20 m/s, corresponding to a Re range of $1.6\times {10}^5$ and $3.2\times {10}^5$. As a result, the type 3 helmet with the bump will have lower drag than others in this velocity range.

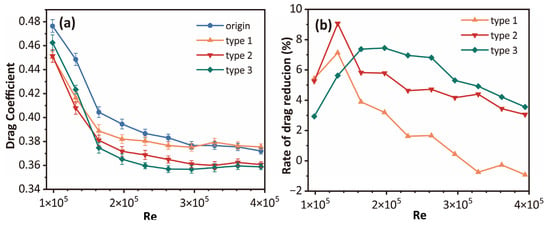
Figure 11. The wind tunnel results for $C_d$ and $\eta$: (a) the $C_d$ respect to Re, (b) $\eta$ respect to Re.

For all structured helmets, the $\eta$ values varied similarly in the range of Re >$1.4\times {10}^5$, which indicated that the surface structures of the helmets caused the increased aerodynamic resistance with the increasing free stream velocity. For the type 1 riblet helmet, the downward trend of $\eta$ was more significant than others, and when $Re>3\times {10}^5$, the drag for the type 1 helmet was higher than original helmet as the $\eta$ went to negative value. For type 2 and type 3 helmets, which both had bumps at the middle region, the trend of $\eta$ decreased in a similar way, especially in $Re>3\times {10}^5$.

From the results of the CFD analysis and wind tunnel experiments, it was clear that both riblet and bump structures had obvious drag reduction effects on the skating helmet. According to the CFD results, the drag for the bumped helmet was lower than that of the riblet one, which was verified by the experiment results. The bumped helmet with small spacing (type 4) was the best model with the lowest drag in the wind tunnel experiments. It must be noted that the $C_d$ and $\eta$ of CFD results showed differences from the experiments in numerical value, because the CFD model simplified the torso which was used in the wind tunnel tests to reduce the cost of simulations. Based on the above results, the experiment results agreed with the CFD analysis, which confirmed the validity of the CFD results. Additionally, more details of the flow field could be obtained from the CFD results to analyze the interaction between the surface structure and the fluid; thereby, it became possible to analyze the drag reduction mechanism of the surface structure.

4.2. Fluid Field Profile

The pressure drags accounted for 96% of the total aerodynamic drags according to the CFD results. As a result, the pressure distribution on the helmet surface played an important role in aerodynamic drag. The pressure coefficient was defined as

$$C_p=\frac{P-P_0}{\frac{1}{2}\rho U^2}$$

(7)

Figure 12a–c presented the iso-surface of zero streamwise velocity around the helmet models that were colored by $C_p$. The direction of local velocity of air was opposite on both side of the iso-surface, which meant that the flow separation occurred on helmet surfaces. The separation line of the original helmet model mostly kept a line; however, for the riblet helmet model and the bump helmet model, the separation lines were obviously delayed, especially on the helmet sides. For the middle region of the helmets, the riblet structure did not have noticeable influence on separation line, while the bump structure was able to delay the separation line significantly. The flow separation could lead to generation of a low pressure region, thus increasing the pressure drag. Figure 12d–f illustrated the $C_p$ contour on helmet model surfaces. The distribution of $C_p$ on the windward side for all simulated models was similar, and the microstructure did not influence the pressure at this region. Obvious differences could be found at the rear region of the helmet. For the original helmet model, the low-pressure region at the rear that caused the pressure drag was much larger than that of the riblet structured helmet or the bumped helmet.

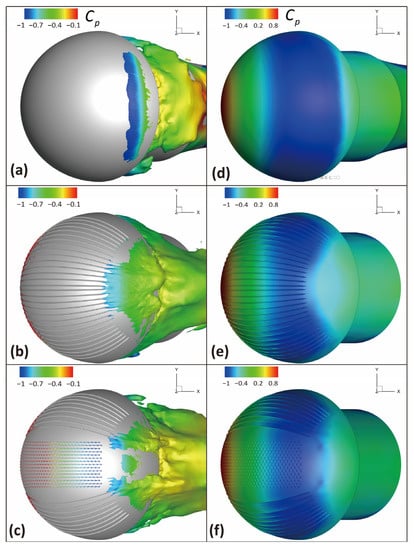
Figure 12. (a–c) The iso-surface of zero velocity: (a) original, (b) riblet, (c) bump. (d–f) The contour of pressure on the helmet surface: (d) original, (e) riblet, (f) bump.

Figure 13 presented the $C_p$ along the midline of the helmet. It was found that $C_p,$ for all CFD helmet models, had almost the same values at the frontal region, and separated with the increase in $\theta$. This difference in pressure reflected the changes of the fluid field near the helmet surface that were caused by the surface structures. With the increase in the air flow distance on the helmet surface (the increase in $\theta$), the interaction between the air and the surface structure was gradually enhanced, and finally, the flow properties changed. The decrease in $C_p$ was due to the conversion process of kinetic energy of fluid to pressure energy. For the original helmet model, the pressure was especially lower than the structured models at $\theta >90°$, which led to a higher pressure drag. It was noted that $C_p$ for the original helmet model was higher than others at the end of the helmet surface, and it was revealed that less kinetic energy was lost within the flow boundary layer for the original model compared with the structured ones. On the other hand, the surface structures increased the resistance of the fluid along the surface, including frictional resistance and local pressure resistance. The local pressure separation could be observed from Figure 12b,c around the riblet structures and bumps, which was the reason for increased local pressure resistance. As mentioned above, the frictional resistance and local pressure resistance were only a tiny fraction of the total drag of the helmet; therefore, these phenomena had scant impact on the total drag.

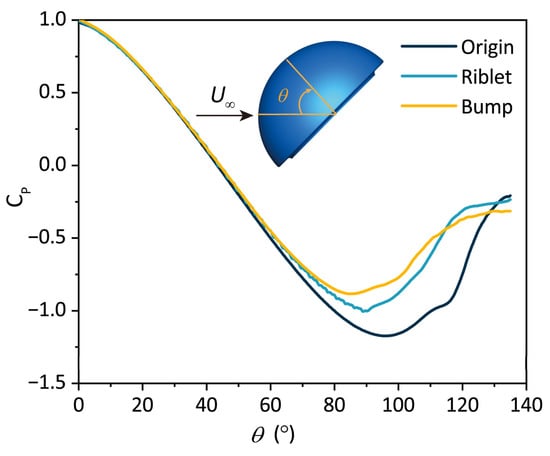
Figure 13. Pressure coefficient distribution on the midline of the CFD helmet surface.

The pressure drag and separation position were closely related to the boundary layer of the air near the helmet surface. Figure 14 presented the dimensionless root mean square (RMS) as $\sqrt{\overline{{u^{\prime }}^2}}/U$ at different positions near the surface, where $u^{\prime }$ was the fluctuating velocity, $U$ was the free stream velocity, and r was the distance from the surface. The RMS of fluctuation velocity could present local turbulence intensity. The fluctuating velocity for all helmet models in the vicinity of $\theta =60°$ had a large value far from the surface, as shown in Figure 14a. It was believed that this flow fluctuation was caused by air hitting the surface of the helmet, and this turbulence intensity dissipated rapidly in the region outside of the boundary layer. At the position of $\theta =90°,$ $\sqrt{\overline{{u^{\prime }}^2}}/U$ for the original helmet was much smaller compared with others, and the turbulence far from the surface had dissipated completely. For the riblet helmet model, the peak of $\sqrt{\overline{{u^{\prime }}^2}}/U$ was significantly higher than the bump model at $\theta =90°$, which was related to the riblet height. The turbulence had been suppressed at the valley between two adjacent riblets, and the vortex had been lifted to the top of the riblets. In addition, the riblets also interacted with airflow at their top region, thereby generating a strong velocity fluctuation. For the bump helmet, however, $\sqrt{\overline{{u^{\prime }}^2}}/U$ had a significant increase near the surface at the position of $\theta =90°$. The airflow interacted with the staggered bumps and became unstable. Therefore, the boundary layer transformed from laminar to turbulent rapidly. Kinetic energy was transferred from outside of the boundary layer to the inside; thus, the flow could overcome the adverse pressure gradient, and the separation line moved downstream.

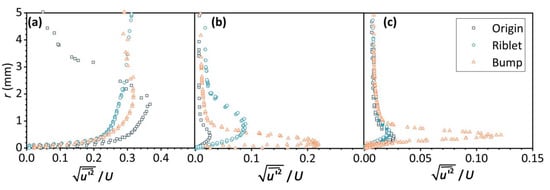
Figure 14. The dimensionless RMS of the fluctuating velocity as $\sqrt{\overline{{u^{\prime }}^2}}/U$ at different position: (a) $\theta =60°$, (b) $\theta =90°$, (c) $\theta =120°$.

Figure 15a–c illustrated the vortex iso-surfaces based on Q criterion ($Q=1\times {10}^5)$. For the original helmet, the vortex generated in the wake region where the flow had separated from the surface, and the airflow was stable before the separation. However, the situation was completely different for the helmet model with surface structure. Many vortices were generated on two sides of the structured helmet, where the riblet structures were situated. Figure 15d–f presents the streamlines on the CFD helmet surfaces. It was found from the streamlines at the two sides of the helmet that there was an obvious angle between the riblet and the velocity direction, and as a result, the vortex was generated from the top of the riblet structures. The boundary layer of airflow could easily transform from laminar to turbulence under this condition. As shown in Figure 15d–f, there was a large difference in surface streamline between the original and riblet/bumped models. The velocity direction also changed in the valley of the riblets compared with the original model, which elucidated the delayed separate position on the side of the helmet (Figure 12). However, there were very few vortices at the middle region of the helmet, where the riblet structures were parallel to the streamlines that had almost no effect on the boundary layer. Therefore, the separation positions were almost the same for the type 1 helmet and the original model. Bumps in the middle region had a different effect compared with the riblets. A vortex was generated from the bumps and promoted the transition of the boundary layer. This had an agreement with the separation position and the turbulence intensity, as shown in Figure 12 and Figure 14.

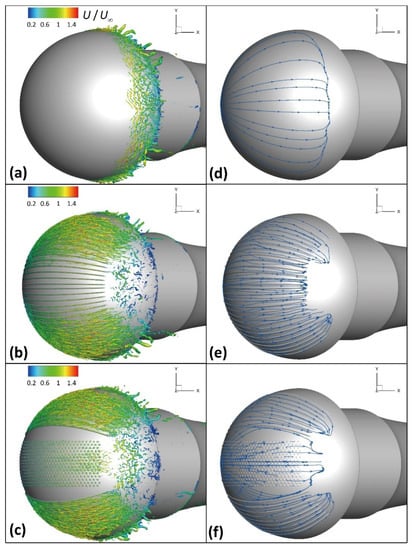
Figure 15. The vortex iso-surface based on the Q criterion at (Q = 10,000) of CFD helmet models: (a) original model, (b) riblet model, (c) bumped model; (d–f) surface streamline on the original and structured models.

To assess the contribution of the drag reduction by helmets to the overall average drag of the skater, a full-scale complete mannequin was tested in the wind tunnel. The drag ratio of the simplified mannequin to the complete one is shown in Figure 16. It was found that the ratio of the drag changed by approximately 12% with the increase in velocity. Referring to the experiment results shown in Figure 11, the total drag reduction rate was approximately 0.84% at the velocity range of 12–16 m/s, which is just as important when every second counts.

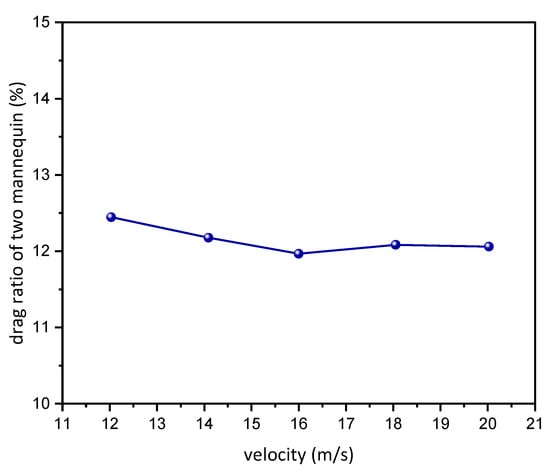
Figure 16. The drag ratio of the simplified mannequin to the complete one.

5. Conclusions

In this paper, numerical simulations and wind tunnel experiments on the skate helmet with drag reduction surface structures were presented. It was found from the CFD results that the boundary layer separation position was delayed for structured helmets, especially the helmet with bump structure at the middle region. The boundary layer of air flow was disturbed by the bumps at the middle region of the helmet, and transformed from the laminar to turbulence, while the riblet structures had limited effects on the boundary layer at this region, because it was parallel to the velocity direction. The vortex was also generated from the riblet region at the sides of the structured helmets, and the velocity direction changed due to the riblet at the valley. Therefore, the separate position was delayed on all structured helmets compared with the original helmet in this region. The pressure distribution on the helmet surface changed due to the delayed separate position; therefore, the pressure drag reduced. The wind tunnel results agreed well with the CFD results, that the drag of structured helmets were all lower than that of the original helmet at the usual speeds of skating competitions. A maximum drag reduction rate of 7% was obtained for the bumped helmet, compared with the original one, in the wind tunnel experiment.