Abstract
The Stellarator is a magnetic configuration considered a realistic candidate for a future thermonuclear fusion commercial reactor. The most widely accepted scaling law of the energy confinement time for the Stellarator is the ISS04, which employs a renormalisation factor, fren, specific to each device and each level of optimisation for individual machines. The fren coefficient is believed to account for higher order effects not ascribable to variations in the 0D quantities, the only ones included in the database used to derive ISS04, the International Stellarator Confinement database. This hypothesis is put to the test with symbolic regression, which allows relaxing the assumption that the scaling laws must be in power monomial form. Specific and more general scaling laws for the different magnetic configurations have been identified and perform better than ISS04, even without relying on any renormalisation factor. The proposed new scalings typically present a coefficient of determination R2 around 0.9, which indicates that they basically exploit all the information included in the database. More importantly, the different optimisation levels are correctly reproduced and can be traced back to variations in the 0D quantities. These results indicate that fren is not indispensable to interpret the data because the different levels of optimisation leave clear signatures in the 0D quantities. Moreover, the main mechanism dominating transport, in reasonably optimised configurations, is expected to be turbulence, confirmed by a comparative analysis of the Tokamak in L mode, which shows very similar values of the energy confinement time. Not resorting to any renormalisation factor, the new scaling laws can also be extrapolated to the parameter regions of the most important reactor designs available.
1. Stellarator Configurations: Optimisation and the Scaling of the Confinement Time
The Stellarator is a toroidal magnetic confinement device for the achievement of thermonuclear fusion, with potentially sufficient efficiency to become a realistic candidate for the final commercial reactor [1]. The main, common specificity of the various Stellarator configurations is that they use external magnets to generate nearly all the confining fields. The fact that Stellarators do not require any plasma current to form and sustain the configuration presents some very substantial advantages [2]. First, they are not affected by those plasma terminating instabilities called disruptions, which frequently occur in Tokamaks and are a potential showstopper on the route to the reactor. Secondly, relying on externally generated fields, the Stellarator is inherently a steady state device, contrary to the Tokamak, which would probably need challenging and expensive external current drive to operate continuously and not in pulse mode [3]. Thirdly, Stellarator plasmas are much more externally controlled by design, and therefore, being less self-organised, their extrapolation into the future generation of machines should be less uncertain.
On the other hand, in the first generations of Stellarator devices, the energy confinement was severely affected by neoclassical losses, related to the asymmetries inherent in the 3D topology of the fields [4]. The strategy of designing the coils without too much regard for the plasma behaviour proved to be inadequate. Modern Stellarator machines are now conceived with a completely different approach, in which a plasma equilibrium with good neoclassical confinement properties is analysed first, and then, the external coils are configured to approximate the required magnetic fields as much as possible. The most recent devices, such as W7-X, have been built not only taking into account neoclassical transport but are also optimized relative to ideal MHD stability. They are basically stable to all ideal MHD perturbations, as described in [5,6].
These new configurations have certainly benefitted greatly from the substantial progress in theoretical understanding of neoclassical transport [7]. On the other hand, the most consequential aspects of energy transport remain too difficult to properly understand with only numerical simulations. Therefore, in the last years, the community has collected an international database explicitly built to investigate the confinement properties of the Stellarator configuration. This International Stellarator Confinement DB contains 0D quantities from all the major devices in the world. (0D quantities are global values, characterising the whole plasma). It has therefore been the basis for the identification of the most widely accepted scaling law for the Stellarator confinement time τE, the so called ISS04. This scaling is in power law monomial form and, in order to fit the experimental data acceptably, it employs a dimensionless renormalisation factor, called fren, for each device and for each sufficiently different optimisation level. In the traditional interpretation, fren is considered to reflect the different aspects of the optimisation, which cannot be accounted for by 0D quantities.
The assumptions adopted to derive and interpret the ISS04 scaling have been critically tested with a new approach to data fitting, called Symbolic Regression (SR) via Genetic Programming (GP) and briefly overviewed in Section 2. The main characteristics of the available database (DB) are summarised in Section 3. The deployment of the proposed methodology to analyse the DB, without any recourse to renormalisation factors, shows that power laws are too rigid and that the main Stellarator magnetic configurations can be better interpreted with different models (Section 4) [8]. The flexibility of the non-power law scalings, identified with SR via GP, are shown to properly reproduce also the signature left on the 0D quantities by the optimisation (Section 5). After optimisation for neoclassical transport, it seems therefore that the transport in Stellarator is dominated by turbulence, being very similar to the Tokamak in L mode (Section 6). Extrapolation to the demonstrative reactor is also reported in Section 6. The possible consequences of the aforementioned evidence are discussed in the last section of the paper.
2. Brief Overview of Symbolic Regression via Genetic Programming for the Extraction of Scaling Laws from Empirical Databases
Symbolic Regression (SR) via Genetic Programming (GP) [9,10,11,12,13] is the analysis technique, which has been developed to identify, minimizing various metrics, the most appropriate mathematical expressions to describe a physical system directly from the data, with a minimum of a priori hypotheses. Traditional linear and non-linear regression techniques simply try to find the best parameters of predefined equations, by fitting the available data. Consequently, a mathematical model of the phenomenon to be investigated must be already available, before starting the analysis of the experimental evidence. Consequently, the objective of the fitting routines is simply to identify the parameters of mathematical models, whose basic structure has been already decided on the basis of prior information. On the contrary, SR via GP searches for the best functional form of the equations directly from the data. This is achieved by manipulating various building blocks such as algebraic operators, analytical functions, constants, and state variables. New models are derived by combining previous equations with the typical operators of genetic programming, namely, mutation, crossover, etc. [14]. Finally, the best equations, which are expected to better correspond to the physics underlying the observed data, are retained.
Various metrics can be adopted to determine the quality of the obtained equations. To maximize the reliability of the results, in our applications two traditional model selection criteria, the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC), have been implemented. Both indicators try to find the best trade-off between goodness of fit and complexity of the models. They can be interpreted as cost functions, in the sense that the better the models the lower their value [15]. If the quality of the DBs is not sufficient to converge on a single best model, the approach of the Pareto Frontier (PF) is adopted [16]. The PF is the set of non-dominated optimal solutions, which means the set of best models, one for each level of complexity. Typically, the Pareto Frontier presents a shape similar to the letter L in the plane of fitness function value versus complexity. The models around the inflexion point are the most important candidates to consider because they constitute the best compromise between goodness of fit and complexity. Once the best functional form for the scaling has been identified with symbolic regression, the final values of the parameters and their confidence intervals are derived with non-linear regression modelling (NLM) [17,18]. In the case of the shearless devices, due to the quite heterogeneous character of the entries, a form of constrained minimisation has been implemented, and the confidence intervals have therefore been obtained with the method of the bootstrap.
3. The International Stellarator Confinement Database and the ISS04 Scaling Law
To allow for this study to be as general as possible, the largest publicly available database of the energy confinement in Stellarators has been analysed [19]. The International Stellarator Confinement DB comprises entries from the eight most relevant machines operated in the world at the time of its constitution: ATF, CHS, Heliotron E, Heliotron J, LHD, TJ-II, W7-A, and W7-AS. For the sake of comparison with the literature and with specific experiments [20,21], the same variables and selection criteria reported in [22] for the derivation of the ISS04 scaling have been adopted (ISHCDB 26). An overview of the analysed database is provided in Table 1.

Table 1.
The main quantities in the International Stellarator Confinement database and their range of values. The meaning of the symbols is the usual: a is the minor radius, R the major radius, P the input power, ne the average electron density, B the on-axis magnetic field, and the rotational transform at two thirds of the minor radius.
As a cautionary note, some limitations of the DB have to be mentioned. With regard to the physics, the discharges included present quite different plasma wall interactions: the database indeed contains devices with different plasma facing components, diverted plasmas and limited plasmas, and a variety of wall conditioning techniques. The heating schemes, neutral beam, and electron cyclotron resonance are also different. The underlying hypothesis is therefore that these dissimilarities do not influence dramatically the main confinement properties of the plasmas. The statistical limitations of the database will be discussed later in the paper.
Notwithstanding the aforementioned deficiencies, the International Stellarator confinement DB was used to derive the most widely accepted scaling law for the energy confinement time in Stellarators: the so-called ISS04 [22]. The ISS04 scaling law is reported as Equation (1) for the reader’s convenience and was obtained with log regression, assuming therefore a priori that its most appropriate mathematical form is a power law monomial.
In Equation (1), a indicates the minor radius, R the major radius, B the magnetic field on axis, ne the average plasma density, and 2/3 the rotational transform at two thirds of the minor radius. It is worth mentioning that, since in the literature the uncertainties affecting fren are not reported, it is impossible to calculate the confidence intervals of Equation (1).
To fit the data of the various machines, the ISS04 scaling law requires introducing a renormalization factor, called , specific to each device or even to different ranges of the operational parameters in the same machine [22]. This renormalization coefficient is commonly believed to account for different levels of optimization, determined by the fine tuning of quantities not leaving a signature in the 0D entries included in the DB.
The use of a renormalisation factor to determine the ISS04 poses several issues. First, the statistical coherence and soundness of the approach are doubtful. Secondly, such a fudge factor tends to obscure more than clarify the underlying physics. Another significant limitation resides in the lack of confidence intervals, which cannot be quantified, because the uncertainties in are not available. This is a particularly relevant drawback for extrapolation, one of the fundamental reasons scaling laws are derived in the first place. Indeed, in general, one of the main objectives of empirical scaling laws consists of providing guidance to the planning of new experiments and the design of new devices.
Another delicate issue affecting the DB relates to the rotational transform. Indeed, it proves quite problematic to extract the dependence of τE on the rotational transform from the DB. This is mainly the unfortunate consequence of two factors: the design of certain devices and the experimental programme of others. The heliotron/torsatron family of devices, due to engineering constraints, presents a very strong collinearity between the rotational transformand the aspect ratio. In their turn, W7-A and W7-AS machines do not scan a significant range of . Consequently, it is difficult to isolate the effect of the rotational transform on τE. To alleviate this deficiency, an approach, similar to the one devised in [22] to obtain ISS04, has also been implemented to derive the scalings reported in this work. TJ-II dependence of τE on the rotational transform is used as first guess for symbolic regression. This approach works quite well for the devices with shear, whose scaling shows a power law dependence on with an exponent not much different from the one of TJ-II. On the other hand, for the shearless configurations much weaker dependencies on would be better supported by the International Stellarator Confinement Database, a subject discussed more extensively in the next section.
4. Scaling Laws for Different Magnetic Configurations
As reported in [8], a simple analysis indicates that the database is not really homogenous. In this respect, it should be remembered that the International Stellarator Confinement Database includes two main types of magnetic configurations with respect to the rotational transform profile, with and without shear. The first class includes the devices ATF, CHS, HELE, HELJ, and LHD, whereas the shearless devices are W7-A, W7-AS, and TJ-II. Visual inspection of the database reveals that the dependencies of the energy confinement time on the regressors can be different for these two types of configurations. Consequently, it seems natural to particularise the scaling laws for these two different groups of machines. The characteristics of the two corresponding data subsets are reported in Table 2.

Table 2.
The two data subsets analysed in the present work.
For the magnetic configuration with shear, the scaling law obtained, by applying SR via GP to the corresponding entries of the International Stellarator Confinement Database, is
Equation (2) is not a simple power law, and its performances are slightly better than the ISS04 for this subset of the database, as reported in Table 3.

Table 3.
Comparison of ISS04 and the non-power law scalings for the machines with and without shear.
The entries of the shearless devices are more inhomogeneous, and indeed for these devices, the fren of ISS04 ranges from 0.25 to 1. Moreover, the dependence from is quite difficult to determine, and indeed, as mentioned in [22], it was derived from a different set of data not included in the International Stellarator Confinement DB. It has therefore been decided to provide more freedom to the nonlinear fit of the model, selected by SR via GP, by implementing a non-linear least-square fit with constrained coefficients [23]. To perform the fit, a regularization term has been added to the loss function so that it becomes:
This technique of constrained regularisation complicates the derivation of solid confidence intervals, which have to be obtained with the bootstrap, using the basic percentile technique [24]. In the rest of the paper, the intervals reported have been calculated at 95% confidence level. It is probably worth mentioning that, to the authors’ knowledge, this combination of constrained fit and bootstrap is a methodological solution applied for the first time to the investigation of scaling laws for Stellarators.
The scaling laws obtained for the shearless magnetic configuration, deploying SR via GP and a constrained non-linear least-square fit, are the following:
where is the avarage Major radius of the dataset.
The statistical performances of these non-power law scalings are also reported in Table 3; they are both very competitive with ISS04. On the other hand, the trend is for the fit to improve its quality with lower exponents of . The actual scaling of the energy confinement time with will probably have to be reassessed with specific experiments for the shearless configurations because the traditional exponent is not really supported by the International Stellarator Confinement database at least for the shearless configuration.
It is probably worth stating again that, contrary to ISS04, Equations (2)–(4) have been obtained without any renormalisation factor. The scalings are not in power law form because they contain exponential terms, which are essential to obtain good fits. The performances of the models identified with SR via GP are very competitive compared with the results of ISS04. Indeed, some have slightly better statistical indicators, which is an interesting result, since in the DB fren ranges between 0.25 and 1, an interval quite substantial. The proposed scalings can improve in the ISS04 thanks to their flexibility.
It should also be noted that the R-squared (R2) is very high, about 0.9 for all scaling laws obtained with SR via GP. Considering that R2 represents the proportion of the dependent variable variance that is explained by the regressors, the obtained scalings basically account for all the information contained in the database. Around 10% of random errors in the estimates of the energy confinement times is indeed probably an overestimate of the accuracy of the entries in the DB. It is therefore not reasonable to expect R2 values higher than the ones already achieved.
The traditional log–log plots of the experimental energy confinement time versus the predictions of the various scaling laws are reported in Figure 1. They show a graphical comparison of the configurations with shear and without shear. Some trends of the ISS04 and the three scalings obtained with SR via GP are reported in Figure 2 over the parameters interval covered by the machines in the database. The scaling of the machines with shear seems to have a different dependence on the main engineering quantities than the shearless one. A significant difference in the exponents of the power law part of the scalings is particularly evident for magnetic field, plasma density, and major radius. On the other hand, great caution is indispensable in interpreting these visual representations of the equations. Indeed, for clarity’s sake, in these plots, only one parameter is scanned at the time, keeping all the others fixed at the value corresponding to their average in the database.
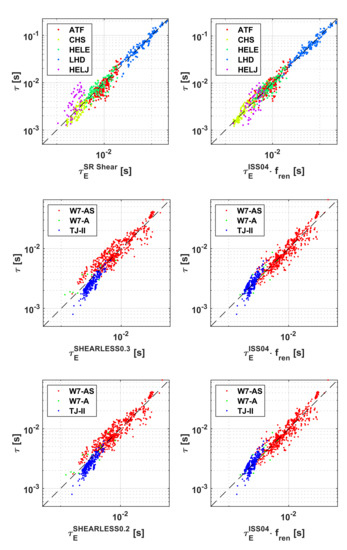
Figure 1.
The log-log plots for the comparison of the models and the data; the experimental values of τE are on the y axis and the estimates of the models on the x axis. (Left column) the models obtained with SR via GP. (Right columns) the corresponding estimates of ISS04.
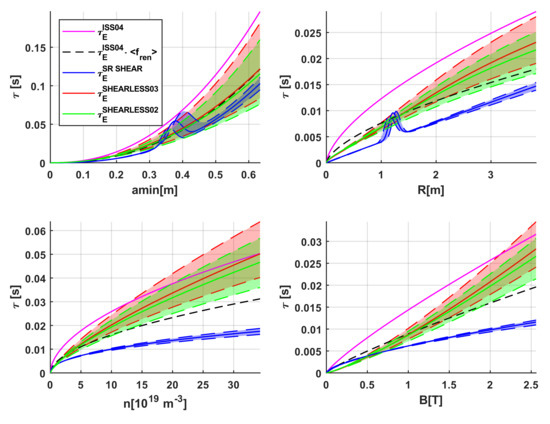
Figure 2.
The trends of the equations obtained with SR via GP compared to the ISS04. For the ISS04, two scalings are shown: one with a renormalization factor equal to 1 and one (indicated by <fren>) with the renormalization factor averaged over the entries in the DB.
The exponential terms, which have to be included in the scaling laws to obtain performance competitive with IS004 without using any renormalization factor, require some comments. They are indispensable to achieve a good fit of the database because its composition is quite heterogeneous, including machines of different magnetic configurations and various levels of optimisation. Power law monomials are not flexible enough to accommodate these differences satisfactorily. Indeed, it is the poor homogeneity of the database, which constitutes the main reason why fren had to be introduced to derive the ISS04. The new methodology of SR via GP allows relaxing the power law constraint, alleviating the rigidity of the scalings without relying on any renormalisation coefficient. The effects of the non-power law terms are shown graphically in Figure A1 and Figure A2. It is also worth mentioning, as supported again by the plots reported in Figure A1 and Figure A2, that not constraining the scalings to be power law monomials allows fitting quite well also the data of the individual devices. Normally the scaling laws for thermonuclear devices are designed to better fit the trends between devices but not the individual machines’ data (and this applies also to the Tokamak scalings [12,13]).
5. Scaling Laws and Optimisation
Even if the flexibility of the proposed non-power law scalings can explain why fren is not indispensable to fit the different devices, a fundamental point remains to be clarified. In the DB there are devices, particularly LHD and W7-AS, which present different levels of optimisation. This is confirmed by the fact that four different values of fren were necessary to fit the data of LHD with ISS04. In particular, LHD at R = 3.60 m is much better neoclassically optimized than LHD at R = 3.90. In the case of W7-AS, three different values of fren had to be used to properly reproduce the entries of the database. Since the need for renormalisation was interpreted as a way to take into account higher order effects not reflected in the 0D quantities, the effectiveness of unified scaling laws, obtained without fren, and valid for very different optimisation levels, needs explaining. The next two subsections are therefore devoted to investigating the relationship between the scalings obtained with SR via GP and fren. The analysis is based on calculating first the ratio between the scaling laws obtained with SR via GP and the ISS04. These ratios reproduce almost perfectly the trends of τE with fren. The parts of the non-power law scaling reflecting the trends of fren are then discussed in detail.
5.1. Non-Power Law Scalings and fren for Different Optimisation Levels of LHD
For the LHD device, the ratio between the scaling laws obtained with SR via GP and the ISS04 is indicated with RLHD/ISS04 and reads as follows:
In the top of Figure 3, the trend of the energy confinement time is plotted versus the ratio RLHD/ISS04. From these plots, it is easy to see how the scaling of Equation (2), obtained with SR via GP, can reproduce the effects of the various optimization levels on the 0D quantities equally well, if not better, than the renormalization factor fren. The ratio RLHD/ISS04 depends basically on major and minor radius, with a small residual effect on the magnetic field. The part of the ratio depending on the minor and major radii, RLHD/ISS04(a,R), is plotted vs. the major radius in Figure 4, while the other main trends are illustrated graphically in Figure A3, Figure A4, Figure A5 and Figure A6. For an easier visual comparison with fren, the values of this ratio have been averaged for each level of optimisation.
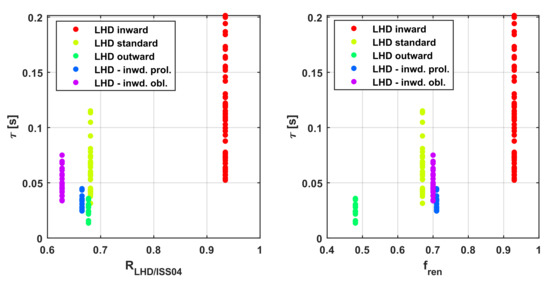
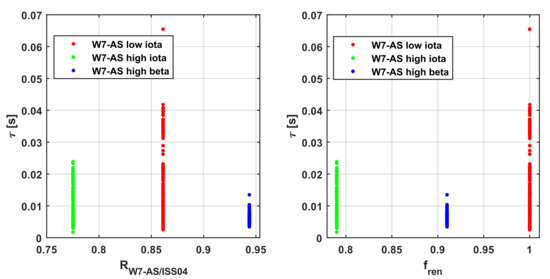
Figure 3.
(Top) comparison of the trend of the energy confinement time with RLHD/ISS04 and fren for LHD. (Bottom) comparison of the trend of the energy confinement time with RW-AS/ISS04.and fren for W7-AS (for = 0.3).
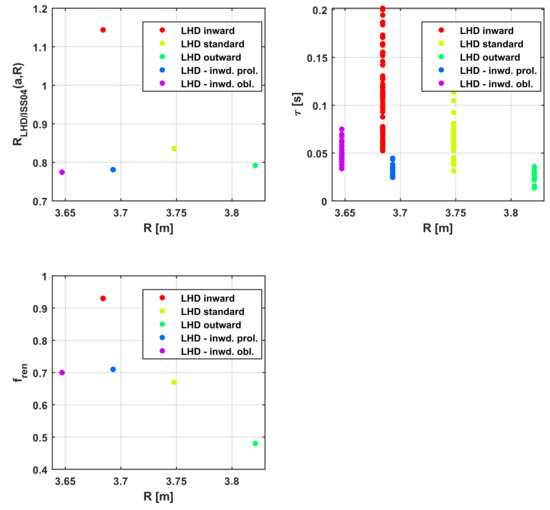
Figure 4.
Analysis of LHD data for various optimisation levels vs. the major radius. (Top left) The part of the model Equation (2), which depends on major and major radius RLHD/ISS04(a,R). (Top right) the actual confinement time in LHD vs. the major radius. (Bottom) trend of fren in ISS04 vs. the major radius.
In the light of the evidence reported in Figure 3 and Figure 4 and Figure A3, Figure A4, Figure A5 and Figure A6, it is possible to explain how the models, derived with SR via GP, can reproduce quite well the LHD entries at different optimization levels, on the basis of only 0D quantities and without any renormalisation factor. Thanks to its high exploratory capability, symbolic regression can capture the signature left in the 0D quantities by the different optimisation levels. Indeed, the part of the scalings including the geometrical quantities, RLHD/ISS04(a,R), fits quite well fren and basically takes into account the effects of the changes in the configurations implemented to optimise confinement. Moreover, the good quality of the fits, testified by the high values of the indicator R2, suggest that practically all the effects of the optimisation efforts in LHD can be ascribed to the modifications in the 0D quantities.
5.2. Non-Power Law Scalings and fren for Different Optimisation Levels of W7-AS
The same analysis reported in the previous subsection has also been performed for the other device, W7-AS, whose entries in the database present a significantly different level of optimisation. In the bottom plots of Figure 3, the trend of the energy confinement time is plotted versus the ratio RW-AS/ISS04. For a exponent of 0.3, the functional dependence of RW-AS/ISS04 is
The dependency does not change dramatically for the case of being elevated to 0.2. The ratio RW-AS/ISS04 is compared with fren in Figure 3. The part depending on the minor and major radii, RW7-AS/ISS04(a,R), is shown versus R in the plots of Figure 5 (while the other major dependencies are reported in Figure A3, Figure A4, Figure A5 and Figure A6). Again, for an easier visual comparison, the values of this ratio have been averaged for each level of optimisation.
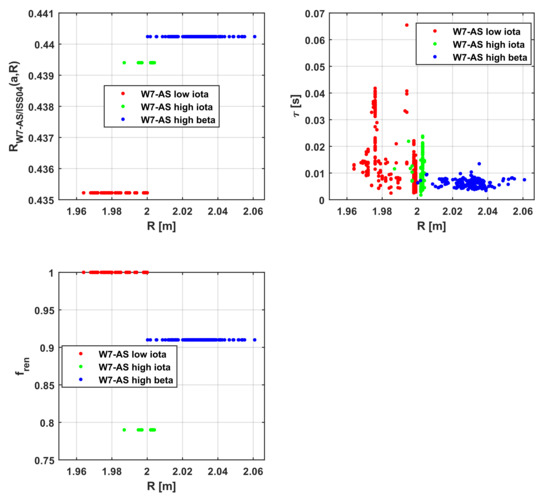
Figure 5.
Analysis of W7-AS data for various optimisation levels vs. the major radius. (Top left) The part of the model Equation (3), which depends on major and minor radius f(a,R). (Top right) the actual confinement time in W7-AS vs. the major radius. (Bottom) trend of fren in ISS04 vs. the major radius.
In the case of the shearless device W7-AS, the ratio RW7-AS/ISS04 depends strongly on plasma density and magnetic field, whereas in the case of LHD, the most important factors are geometrical, the minor and major radii. This evidence needs to be further investigated, but some points can be already emphasised. First, the completely different trends of RLHD/ISS04 and RW7-AS/ISS04 stress again the need for particularising the scaling laws for the different magnetic configurations, with and without shear. Second, the dubious and confusing nature of fren becomes even more evident. This arbitrary factor tends to obscure more than clarify the underlying trends and the phenomenology. On the other hand, a significant effort should be devoted to understanding the causes of the different forms of Equations (5) and (6), for example, by studying whether they are due to dissimilar approaches to optimisation or to intrinsic specificities of the magnetic configuration physics.
6. Comparison with the Tokamak in the L Mode of Confinement and Extrapolation to Stellarator Reactors
Extrapolation is always a delicate matter. In principle, data driven equations, such as those derived in the present work, have very limited validity out of sample, where they can indeed become misleading. On the other hand, the trends of the derived scaling laws near the already explored operational space can provide useful insight. This is the objective of Section 6.1, in which the comparison with the Tokamak in L mode seems to indicate that, in optimised configurations, the dominant transport mechanism in Stellarators is probably turbulence. Larger extrapolation should be mainly aimed at checking the basis consistency of the scaling laws, meaning that they do not take absurd turns, when particularised for a parameter region of interest far from that already explored. This is the objective of Section 6.2, devoted to investigating the predictions of the various scalings to the region covered by the Stellarator main proto-reactor designs.
6.1. Comparison with the Tokamak in L Mode of Confinement
To compare the scaling laws obtained for the Stellarator with the Tokamak’s, the International Tokamak Physics Activity (ITPA) International L-Mode Confinement (DB3v13f) Data Base has been considered [25]. The study therefore focusses on the scaling of τE in the L mode. Overall, the DB contains 1140 entries, identified using the same selection criteria adopted in [26]. As customary, to compare the two configurations, the scaling laws of the Tokamak have been reformulated by writing the current in terms of the safety factor q95 in the cylindrical approximation, corrected by the elongation [22]. For this confinement regime, the best credited scaling law in the literature is Equation (7), the so called ITER97 [27]. The methodology of symbolic regression via genetic programming has been applied also to the ITPA database of L-mode discharges [28]. The one obtained with SR is not a power law and is reported as Equation (8).
The non-power law scaling outperforms the power law according to all the statistical indicators, as reported in Table 4. Moreover, the database is large enough to perform an extrapolation exercise; the scaling laws (7) and (8) have been fitted to the small devices, and then, their accuracy in modelling JET data has been tested [27]. The capability of the non-power law scaling to extrapolate to JET is qualitatively better than the equation in the literature: indeed, the residuals of (8) are an order of magnitude smaller than the ones of (7) [27].

Table 4.
Comparison of the statistical indicators used to qualify the quality of the models: MSE is the mean square error, RMSE the root the mean square error, and k the number of parameters of the models.
As stated previously, since the models for the Stellarator confinement obtained with SR via GP do not include any renormalization factor, they can be compared with the scalings of the Tokamak in L mode. For the ISS04 it is assumed that fren = 1, which is a reasonable choice, since this is the value of renormalization factor typical of the largest devices and the best optimisation levels. A comparison of the predictions of the various models for a device of ITER engineering parameters is reported in Table 5. It is interesting to note that the estimates for the Stellarator configuration span practically the same interval than the two for the Tokamak. The extrapolation to ITER is probably still acceptable, since the gap in terms of operational parameters is not excessive. On the other hand, it should also be remembered that the assumption, underlying all these extrapolation exercises, is that the physics of the plasmas in devices of ITER dimensions will not be different from the ones of the present-day generation, an aspect that can be addressed only experimentally.

Table 5.
Extrapolations to ITER. The extrapolation of ISS04 have been obtained for fren = 1.
6.2. Extrapolation to the Demonstrative Reactor Region of the Parameter Space
This section is meant to compare the various scalings, for the configuration with and without shear, and to investigate their extrapolation to the next generation of devices and to the reactor. The legitimacy of this extrapolation exercise derives from the fact that no renormalization factor has been introduced to extract from the data the scaling laws with SR via GP. The use of ISS04 to estimate the confinement time of the reactor studies is not immediate, since it provides no guidance about the renormalization factor to be adopted in the calculations. In the following, for comparison’s sake, it is assumed that fren = 1.
The main devices investigated are reported in Table 6 together with their main engineering parameters [29,30,31]. The Helias configuration was the basis of HSR4 and HSR5 designs, and the quasi-axial symmetric NCSX is the reference for ARIES-CS. HSR/14 and HSR5/22 [30,31], being scaled versions of W7X, are expected to be run in shearless configurations. For completeness’ sake, it should be mentioned that in NCSX and ARIES-CS, the bootstrap current is expected to play a more important role than in the other configurations because it is meant to be responsible for an important fraction of the rotational transform.

Table 6.
Parameters of the reactor studies considered.
The estimates of the confinement time for the devices of Table 6 are summarised in Table 7. Inspection of the table suggests a couple of considerations. First, the predictions of ISS04 are basically confirmed by the results obtained with SR via GP. In any case, given the quality of the database available and the large extrapolations in most engineering parameters, the level of agreement of the new scalings with the IS004 is quite remarkable. On the other hand, the set of data for the shearless configuration includes devices with very different characteristics, as already emphasised in [22], in which they were attributed very different renormalization factors. Extreme caution is therefore appropriate to interpret the results for this configuration. In particular, the shearless devices extrapolate quite differently depending on the assumed dependence on the rotational transform, an aspect which will require careful experimental assessments in the future. It should also be stated one more time that the level of extrapolation from present day devices to the demonstrative reactor designs is very large, and there is no guarantee even that the physics of the energy transport will remain the same. The main objective of the exercise in this subsection is therefore not so much to provide accurate estimates of the energy confinement time but to verify that the various scalings do not present absurd unphysical trends out of samples, a check which is always recommended.

Table 7.
Estimates for the machines of Table 6.
7. The Need to Move beyond fren: Concluding Remarks
In this paper, it has been investigated whether good quality scaling laws, for the energy confinement time in Stellarators, can be obtained without having recourse to any renormalization factor. To this end, the main tool deployed has been symbolic regression via genetic programming. It has been shown how relaxing the constraint that the scaling laws have to be in power law form allows particularising the models for the main configurations, with and without shear. The quality of the models is very competitive with ISS04, even if the proposed scalings do not resort to any renormalisation factors. The obtained models can also reproduce quite well the different levels of optimisation of the Stellarator configuration. Indeed, at least for the cases included in the International Stellarator Confinement database, optimising the configuration for neoclassical transport implies changes in the 0D quantities, which have been properly picked up by SR via GP. An interesting result is that the quantities in the scalings reproducing fren are very different for the two magnetic configurations. In the case of the devices with shear, the different optimisation levels can be accounted for by a dependence on the geometric factors, mainly minor and major radii. In the shearless devices, the optimisation process seems to leave a signature mainly in magnetic field and plasma density. In this context, it is worth stating again that, in any case, the results obtained with SR via GP are completely agnostic about higher order effects, not leaving clear traces in the 0D quantities. The proposed methodology is fully data driven and therefore can account only for the information contained in the data. Consequently, whether the aforementioned dissimilarities are the result of different optimisation procedures or are inherent to the physics of the two magnetic configurations remains to be established. On the other hand, the obtained results and the comparison with the L mode Tokamak support the opinion that turbulence transport is the dominant effect in determining the Stellarator energy confinement time, once the devices are reasonably optimised for neoclassical transport [32].
In terms of future developments, it should be considered that the quite high R2 levels, achieved by the fits, indicate that the variance unaccounted for by the scalings is compatible with the random uncertainties to be associated with the entries of τE. Consequently, SR via GP has converged on models, which exploit all the information available in the database (if anything some have probably a tendency to overfit). It seems therefore only reasonable to state that further progress in the understanding would require an upgrade of the database, which is not completely satisfactory given the complexities of the configuration. Moreover, to investigate higher order effects, additional entries, such as turbulence measurements, also will have to be included; current profiles and radiation patterns have also proved to be essential to understand the behaviour of Tokamaks [33,34]. Another quite high priority would be to particularise the models for the devices with metallic plasma facing components, given the effects of these materials on the operation and performance of JET with the new ITER Like Wall [35,36]. The dependence of the energy confinement time on the rotational transform should also be clarified experimentally, to understand its actual form and whether it is the same for both main magnetic configurations.
Author Contributions
Conceptualization, A.M. and J.V.; methodology, A.M., E.P., L.S. and M.G.; software, L.S. and E.P.; validation, M.G. and J.V.; formal analysis, A.M. and L.S.; investigation, A.M. and E.P.; resources, M.G.; data curation, E.P. and L.S.; writing—original draft preparation, A.M.; writing—review and editing, A.M. and M.G.; visualization, L.S.; supervision, M.G. and J.V.; project administration, M.G. and J.V.; funding acquisition, M.G. and J.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by the Spanish Ministry of Economy and Competitiveness under the Project No. PID2019-108377RB-C31.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors would like to thank J.M.García-Regaña and J.L.Velasco for their help with the first analysis of the International Stellarator Confinement database.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Effects of the Exponential Terms on the Scaling Laws
This appendix reports the log–log plots of the non-power law scalings predictions versus the experimental energy confinement time. Different symbols are used to differentiate the predictions of the models with and without the non-power law term. The non-power law terms typically improve the quality of the fit to the entries in the database.
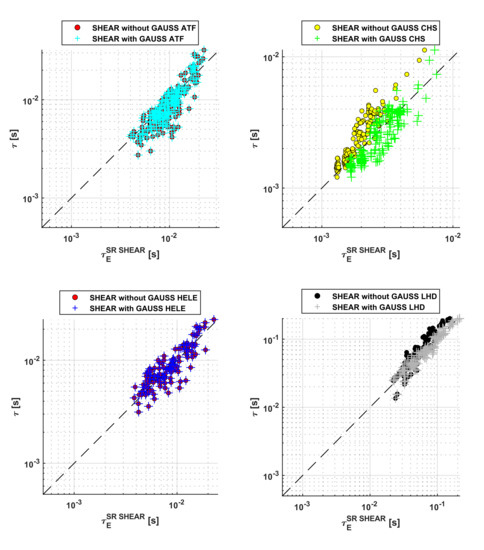
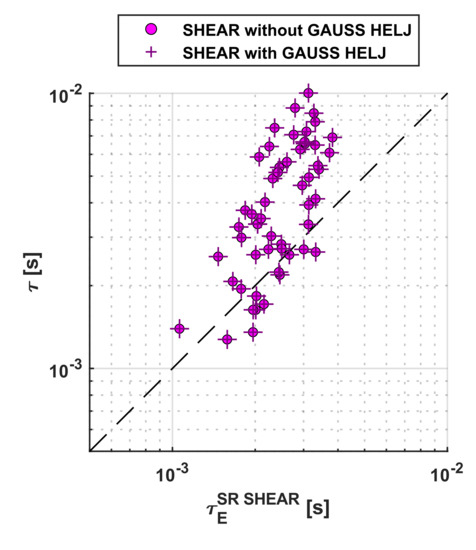
Figure A1.
Comparison of the scaling laws with and without the exponential term for the devices with shear. In the legend of the plots, GAUSS indicates the corrective non-power law term in the scaling laws.
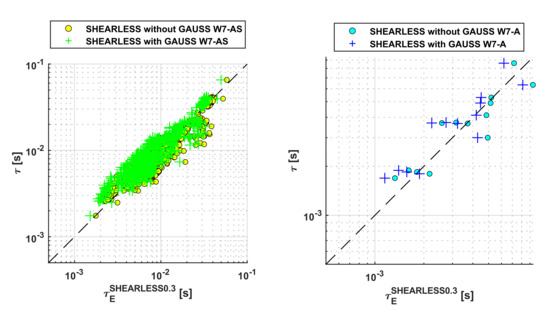
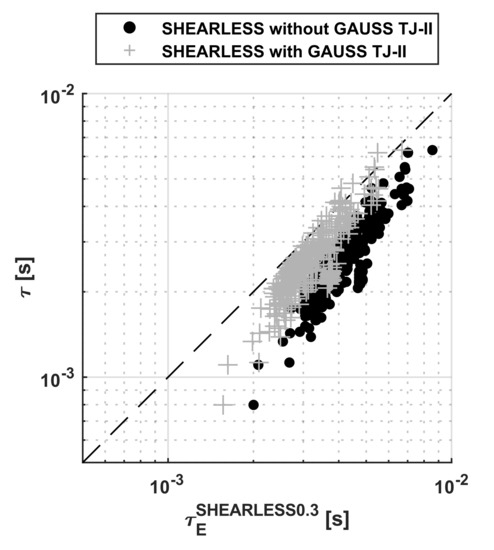
Figure A2.
Comparison of the scaling laws with and without the exponential term for the devices without shear. In the legend of the plots, GAUSS indicates the corrective non-power law term in the scaling laws.
Appendix B. Scaling Laws obtained with SR via GP and fren
This appendix is meant to illustrate graphically the main signatures left by the optimisation process on the 0D quantities, in both magnetic configurations, with and without shear.
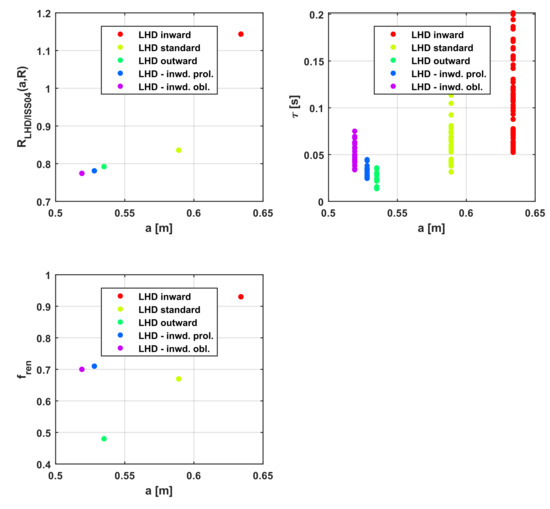
Figure A3.
Analysis of LHD data for various optimisation levels vs. the minor radius. (Left) The part of the model Equation (2), which depends on major and minor radius f(a,R). (Centre) The actual confinement time in LHD vs. the minor radius. (Right) Trend of fren in ISS04 vs. the minor radius.
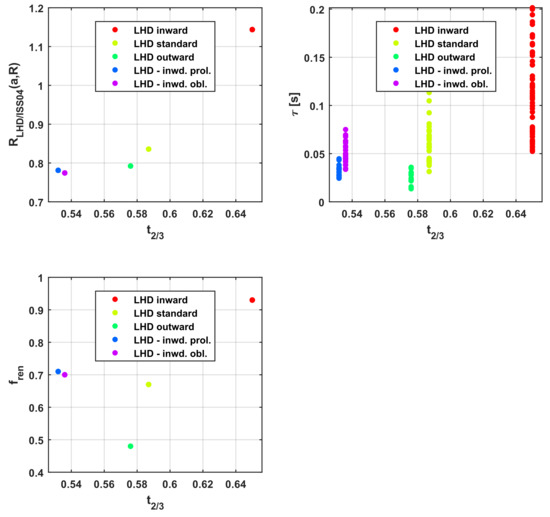
Figure A4.
Analysis of LHD data for various optimisation levels vs. iota. (Left) The part of the model Equation (2), which depends on major and minor radius f(a,R). (Centre) The actual confinement time in LHD vs. iota. (Right) Trend of fren in ISS04 vs.
.
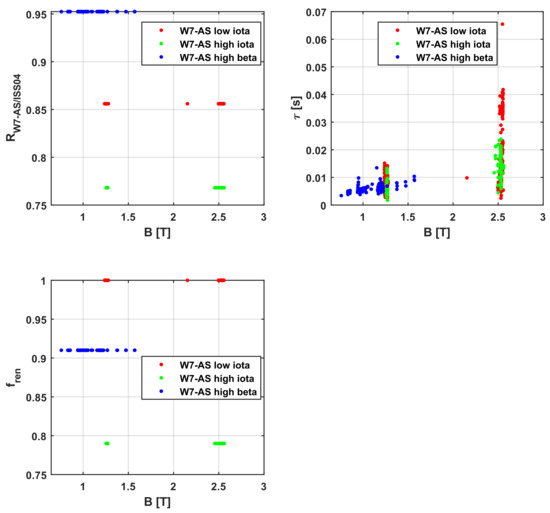
Figure A5.
Analysis of W7-AS data for various optimisation levels vs. the magnetic field and comparison with fren.
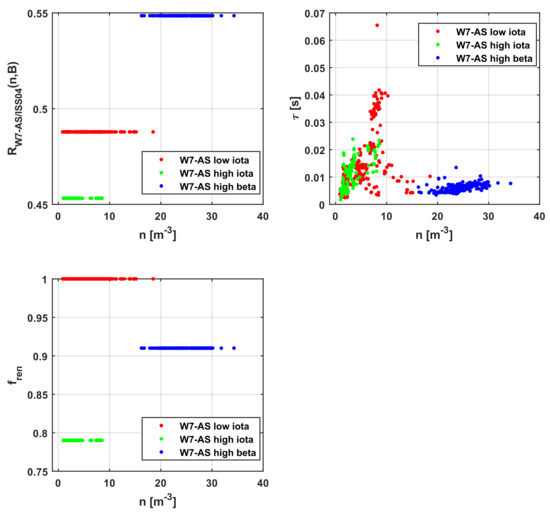
Figure A6.
Analysis of W7-AS data for various optimisation levels vs. the plasma density and comparison with fren.
References
- Wakatani, M. Stellarator and Heliotron Devices; Oxford University Press: Oxford, UK, 1998; ISBN 978-0-19-507831-2. [Google Scholar]
- Clery, D. After ITER, Many Other Obstacles for Fusion Power; Science Insider: Washington, DC, USA, 2013. [Google Scholar]
- Wesson, J. Tokamaks, 3rd ed.; Oxford Clarendon Press: Oxford, UK, 2004. [Google Scholar]
- Xu, Y. A general comparison between tokamak and stellarator plasmas. Matter Radiat. Extrem. 2016, 1, 192–200. [Google Scholar] [CrossRef]
- Fu, G.Y.; Ku, L.P.; Cooper, W.A.; Hirshman, S.H.; Monticello, D.A.; Redi, M.H.; Reiman, A.; Sanchez, R.; Spong, D.A. Magnetohydrodynamics stability of compact stellarators. Phys. Plasmas 2000, 7, 1809–1815. [Google Scholar] [CrossRef]
- Cooper, W.A. Stability of a compact three-period stellarator with quasiaxial symmetry features. Phys. Plasmas 2000, 7, 2546–2553. [Google Scholar] [CrossRef][Green Version]
- Boozer, A.H. Transport and isomorphic equilibria. Phys. Fluids 1983, 26, 496–499. [Google Scholar] [CrossRef]
- Murari, A.; Peluso, E.; Vega, J.; García-Regaña, J.M.; Velasco, J.L.; Fuchert, G.; Gelfusa, M. Scaling Laws of the Energy Confinement Time in Stellarators without Renormalization Factors. Nucl. Fusion 2021, 61, 096036. [Google Scholar] [CrossRef]
- Schmid, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Murari, A.; Lupelli, I.; Gelfusa, M.; Gaudio, P. Non-power law scaling for access to the H-mode in tokamaks via symbolic regression. Nucl. Fusion 2013, 53, 043001. [Google Scholar] [CrossRef]
- Murari, A.; Peluso, E.; Gelfusa, M.; Lupelli, I.; Lungaroni, M.; Gaudio, P. Symbolic regression via genetic programming for data driven derivation of confinement scaling laws without any assumption on their mathematical form. Plasma Phys. Control. Fusion 2015, 57, 014008. [Google Scholar] [CrossRef]
- Murari, A.; Peluso, E.; Gelfusa, M.; Lupelli, I.; Gaudio, P. A new approach to the formulation and validation of scaling expressions for plasma confinement in tokamaks. Nucl. Fusion 2015, 55, 7. [Google Scholar] [CrossRef]
- Murari, A.; Peluso, E.; Lungaroni, M.; Gelfusa, M.; Gaudio, P. Application of symbolic regression to the derivation of scaling laws for tokamak energy confinement time in terms of dimensionless quantities. Nucl. Fusion 2015, 56, 26005. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Jin, Y.; Sendhoff, B. Pareto-Based Multiobjective Machine Learning: An Overview and Case Studies. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 397–415. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer: New York, NY, USA, 1999; ISBN 978-0-7923-8278-2. [Google Scholar]
- Bates, D.; Watts, D. Nonlinear Regression Analysis and Its Applications; Wiley: New York, NY, USA, 1988. [Google Scholar]
- International Stellarator-Heliotron Profile Database Site. Available online: https://ishpdb.ipp-hgw.mpg.de/ (accessed on 9 March 2022).
- Dinklage, A.; Ascasibar, E.; Beidler, C.D.; Brakel, R.; Geiger, J.; Harris, J.H.; Kus, A.; Murakami, S.; Okamura, S.; Preuss, R.; et al. Assessment of Global Stellarator Confinement: Status of the International Stellarator Confinement Database. Fusion Sci. Technol. 2007, 51, 1–7. [Google Scholar] [CrossRef]
- Stroth, U.; Murakami, M.; Dory, R.A.; Yamada, H.; Okamura, S.; Sano, F.; Obiki, T. Energy confinement scaling from the international stellarator database. Nucl. Fusion 1996, 36, 8. [Google Scholar] [CrossRef]
- Yamada, H.; Harris, J.H.; Dinklage, A.; Ascasibar, E.; Sano, F.; Okamura, S.; Talmadge, J.; Stroth, U.; Kus, A.; Murakami, S.; et al. Characterization of energy confinement in net-current free plasmas using the extended International Stellarator Database. Nucl. Fusion 2005, 45, 1684–1693. [Google Scholar] [CrossRef]
- Majda, A.J.; Abramov, R.V.; Grote, M.J. Information Theory and Stochastics for Multiscale Nonlinear Systems; CRM Monograph Series v.25; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall: New York, NY, USA, 1993. [Google Scholar]
- ITPA Confinement Database Site. Available online: http://efdasql.ipp.mpg.de/hmodepublic/DataDocumentation/Datainfo/DB3v13/db3v13.html (accessed on 10 February 2018).
- McDonald, D.C.; Cordey, J.G.; Thomsen, K.; Kardaun, O.J.; Snipes, J.A.; Greenwald, M.; Sugiyama, L.; Ryter, F.; Kus, A.; Stober, J.; et al. Recent progress on the development and analysis of the ITPA global H-mode confinement database. Plasma Phys. Control. Fusion 2004, 46, 519–534. [Google Scholar] [CrossRef]
- Beidler, C.D.; Harmeyer, E.; Herrnegger, F.; Igitkhanov, Y.; Kendl, A.; Kisslinger, J.; Kolesnichenko, Y.I.; Lutsenko, V.V.; Nührenberg, C.; Sidorenko, I.; et al. The Helias reactor HSR4/18. Nucl. Fusion 2001, 41, 1759. [Google Scholar] [CrossRef]
- Murari, A.; Peluso, E.; Gaudio, P.; Gelfusa, M. Robust scaling laws for energy confinement time, including radiated fraction, in Tokamaks. Nucl. Fusion 2017, 57, 126017. [Google Scholar] [CrossRef]
- Najmabadi, F.; Raffray, A.R.; Abdel-Khalik, S.I.; Bromberg, L.; Crosatti, L.; El-Guebaly, L.; Garabedian, P.R.; Grossman, A.A.; Henderson, D.; Ibrahim, A.; et al. The ARIES-CS compact stellarator fusion power plant. Fusion Sci. Technol. 2008, 54, 655–672. [Google Scholar] [CrossRef]
- Warmer, F.; Beidler, C.D.; Dinklage, A.; Wolf, R. From W7-X to a HELIAS fusion power plant: Motivation and options for an intermediate-step burning-plasma stellarator. Plasma Phys. Control. Fusion 2016, 58, 074006. [Google Scholar] [CrossRef]
- Lin, M.-C.; Lu, P.-S. Injection-locked millimeter wave oscillator based on field-emission cathodes. J. Vac. Sci. Technol. B 2008. [Google Scholar] [CrossRef]
- Stroth, U.; Fuchert, G.; Beurskens, M.N.; Birkenmeier, G.; Schneider, P.A.; Scott, E.R.; Brunner, K.J.; Günzkofer, F.; Hacker, P.; Kardaun, O.; et al. Stellarator-tokamak energy confinement comparison based on ASDEX Upgrade and Wendelstein 7-X hydrogen plasmas. Nucl. Fusion 2021, 61, 016003. [Google Scholar] [CrossRef]
- Mazon, D.; Mazon, D.; Litaudon, X.; Moreau, D.; Pericoli-Ridolfini, V.; Zabeo, L.; Crisanti, F.; De Vries, P.; Felton, R.; Joffrin, E.; et al. Active control of the current density profile in JET. Plasma Phys. Control. Fusion 2003, 45, L47–L54. [Google Scholar] [CrossRef]
- Craciunescu, T.; Bonheure, G.; Kiptily, V.; Murari, A.; Tiseanu, I.; Zoita, V. JET-EFDA Contributors. A comparison of four reconstruction methods for JET neutron and gamma tomography. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 605, 374–383. [Google Scholar] [CrossRef]
- Pamela, J.; Romanelli, F.; Watkins, M.L.; Lioure, A.; Matthews, G.; Philipps, V.; Jones, T.; Murari, A.; Géraud, A.; Crisanti, F.; et al. The JET programme in support of ITER. Fusion Eng. Design. 2007, 82, 590–602. [Google Scholar] [CrossRef]
- Romanelli, F.; Laxåback, M. Overview of JET results. Nucl. Fusion 2011, 51, 094008. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).