Mutational Chemotaxis Motion Driven Moth-Flame Optimizer for Engineering Applications

Abstract

Moth-flame optimization is a typical meta-heuristic algorithm, but it has the shortcomings of low-optimization accuracy and a high risk of falling into local optima. Therefore, this paper proposes an enhanced moth-flame optimization algorithm named HMCMMFO, which combines the mechanisms of hybrid mutation and chemotaxis motion, where the hybrid-mutation mechanism can enhance population diversity and reduce the risk of stagnation. In contrast, chemotaxis-motion strategy can better utilize the local-search space to explore more potential solutions further; thus, it improves the optimization accuracy of the algorithm. In this paper, the effectiveness of the above strategies is verified from various perspectives based on IEEE CEC2017 functions, such as analyzing the balance and diversity of the improved algorithm, and testing the optimization differences between advanced algorithms. The experimental results show that the improved moth-flame optimization algorithm can jump out of the local-optimal space and improve optimization accuracy. Moreover, the algorithm achieves good results in solving five engineering-design problems and proves its ability to deal with constrained problems effectively.

1. Introduction

Optimization cases have been classified into many groups, such as single objective, multi-objective, and many-objective models [1,2], and according to each category, we need a different mathematical model for the optimization core [3]. In recent years, meta-heuristic algorithms have become an effective class of methods for solving real-world practical problems due to their excellent performance in dealing with high-dimensional optimization problems [4], such as resource allocation [5,6], task-deployment optimization [7], supply-chain planning [8], etc. There are numerous algorithms with terse principles and high optimization performance, such as particle swarm optimizer (PSO) [9,10], differential evolution (DE) [11], Equilibrium Optimizer (IEO) [12], Runge Kutta optimizer (RUN) [13], hunger games search (HGS) [14], slime mould algorithm (SMA) [15], Harris hawks optimization (HHO) [16], colony predation algorithm (CPA) [17], the weighted mean of vectors (INFO) [18], seagull optimization algorithm (SOA) [19], and so on. Also, due to their excellent performance, they have achieved very positive results in many fields, such as image segmentation [20,21], complex optimization problem [22], feature selection [23,24], resource allocation [25], medical diagnosis [26,27], bankruptcy prediction [28,29], gate-resource allocation [30,31], fault diagnosis [32], airport-taxiway planning [33], train scheduling [34], multi-objective problem [35,36], scheduling problems [37,38,39], and solar-cell-parameter identification [40]. Although these algorithms have a good ability to obtain the optimal solution, there is often the problem of the algorithm falling into deceptive optimization in practical applications. Therefore, researchers have aimed to further enhance the ability of the algorithms to jump out of the local optimal space.

Moth-flame optimization (MFO) [41] is a novel metaheuristic algorithm proposed by Mirjalili et al. in 2015, which was inspired by the flight characteristics of moths in nature. Once the algorithm was proposed, it was favored by many researchers because of its advantages, such as fewer parameters and ease of implementation. Therefore, within a few years, the algorithm has appeared frequently in practical application settings. For example, Yang et al. [42] developed a deep neural network to predict gas production in urban-solid waste. To improve the accuracy of prediction, MFO was used to optimize the deep-neural-network model, which effectively improved the prediction effect of the model and was conducive to improving environmental pollution.

In order to find the optimal-economic dispatch of the hybrid-energy system, Wang et al. [43] constructed an operation model based on the moth-flame algorithm to optimize the schedule of each unit, effectively reducing the system’s operating cost. Singh et al. [44] used the MFO algorithm to reasonably arrange the placement of multiple optical-network units in WiFi and simplify the network design. After using this algorithm, it was proved that the layout method could promote the reduction of deployment costs and improve network performance. Said et al. [45] proposed a segmentation method based on the MFO algorithm to solve the difficult segmentation problem of the liver image caused by factors such as liver volume in computer-medical-image segmentation. The structural-similarity index verified the method’s effectiveness, and the segmentation method’s accuracy was as high as 95.66%.

Yamany et al. [46] applied MFO to train multilayer perceptron and searched for the perceptron’s bias and weight, which reduced the error and improved the classification rate. Hassanien et al. [47] used the improved MFO in a study on the automatic detection of tomato diseases and the exploration ability of MFO for feature selection, significantly improving the classification accuracy of support-vector-machine evaluation. Allam et al. [48] chose MFO to estimate parameters in a three-diode model so that accurate parameter can be found quickly in experiments, and minimum RMSE error and average bias error were achieved. Singh et al. [49] proposed a moth-flame-optimization- guidance method to solve the data-clustering problem and verified the method’s effectiveness using Shape and UCI benchmark datasets. The cases above showed that MFO has been widely used in practical problems and has achieved good results in different fields.

As the scale of the problem rises, the simple and original MFO algorithm can no longer satisfy the complex high-dimensional and multimodal problems; thus, a large number of improved MFO variants have been proposed one after another. Kaur et al. [50] adopted the Cauchy-distribution function to enhance the algorithm’s exploration ability and improved the algorithm’s mining ability. Experiments showed that the improved algorithm promotes convergence speed and solution quality. Wang et al. [26] added chaotic-population initialization and chaotic-disturbance mechanisms in the algorithm to further balance the algorithm’s exploration and exploitation performance, and enhance the algorithm’s ability to jump out of the local optimum. Yu et al. [51] proposed an enhanced MFO, which added a simulate-annealing strategy to enhance the local exploitation and introduced the idea of a quantum-revolving gate to enhance its global exploration ability. Ma et al. [52] added inertia weight to balance the algorithm performance and introduced a small probability mutation in the position-update stage to enhance the ability of the algorithm to escape from the local optimal space.

Pelusi et al. [53] defined a hybrid phase in the MFO algorithm to balance the exploration and exploitation of the algorithm, and adopted the dynamic-crossover mechanism to the flame to enhance population diversity. Li et al. [54] proposed a novel variant of MFO, whose main optimization idea was to adopt differential evolution and opposite-learning strategies to the generation of flame. The improved shuffle-frog-jump algorithm was used as the local-search algorithm, and the individuals with poor fitness were eliminated through the death mechanism. Li et al. [55] proposed a dual-evolutionary learning MFO. The two optimization strategies in the algorithm were differential-evolutionary- flame generation and dynamic-flame-guidance strategy, which aimed to generate a high-quality flame to guide the moth to fly toward the optimal direction.

Li et al. [56] initialized the moth population by chaotic mapping, processed the cross-border individuals, and adjusted the distance parameters to improve the performance of MFO. The statistical results showed that chaotic mapping promotes the algorithm’s performance. Xu et al. [57] added a cultural-learning mechanism to MFO and performed a Gaussian mutation of the optimal flame, which increased the population diversity and enhanced the search ability of the algorithm. In order to overcome the problem of premature convergence of MFO, Sapre et al. [58] used opposition learning, Cauchy mutation and evolutionary-boundary-constraint-processing technology. Experiments showed that the enhanced MFO improved both in convergence and escape from local stagnation. Although many scholars have proposed optimization strategies for MFO from different perspectives, it still needs to be strengthened in terms of jumping out of the local optimal space and optimization accuracy.

To overcome the problem that the traditional MFO is prone to local optimality and poor optimization accuracy, this paper proposes a novel MFO-variant algorithm called HMCMMFO. To deal with the problem that MFO is vulnerable to deceptive optimality, this paper proposes a hybrid-mutation strategy that assigns dynamic weights to Cauchy and Gaussian mutation, which are applied to the individuals adaptively with the deepening of the optimization process. At the same time, to improve the optimization accuracy of the algorithm, chemotaxis-motion mechanism is proposed to better mine the solutions in the local space and improve the search efficiency. Based on the classical IEEE CEC2017 functions, experiments, such as mechanism combination, balanced-diversity analysis, and comparison of novel and advanced algorithms, were conducted to demonstrate the optimization effect of the MFO variant named HMCMMFO, of which the effectiveness and superiority were verified, and was then applied to engineering problems to realize its potential value better. Note that the main contributions of this study are as follows.

(1)

A hybrid-mutation strategy is proposed to enhance the exploration ability of the algorithm and the ability to jump out of the local optimum.

(2)

Chemotaxis-motion mechanism is proposed to guide the direction of the population to approach optimal solution and improve the algorithm’s local-exploitation capability.

(3)

HMCMMFO can obtain high-quality optimal solutions within the CEC 2017 test functions.

(4)

HMCMMFO is applied to five typical engineering cases to solve the constraint problems effectively.

The next part of the paper is structured into five sections, where Section 2 provides an overview of the MFO algorithm, Section 3 introduces two optimization strategies, Section 4 discusses the comparative experimental results, Section 5 presents applications of HMCMMFO to engineering problems, and Section 6 summarizes the full paper and introduces future work.

2. The Principle of MFO

MFO is a population-based, random-metaheuristic-search algorithm inspired by moths’ lateral positioning and navigation [41]. The main idea is that when a moth flies at a fixed angle with a flame as a reference, as the distance to the flame decreases, the moth will continuously adjust its angle to the light source during the flight to maintain a specific angle toward the flame, and finally its flight trajectory will be spiral-shaped. The mathematical model of this flight characteristic will be introduced as follows.

In the following matrix, n represents the number of moth populations, d denotes the problem dimension, and X means explicitly that n moths fly in the d-dimensional space.

$$X=\left[\begin{array}{ccc}{x}_{1,1}& \cdots & x_{1,d}\\ ⋮& \ddots & ⋮\\ x_{n,1}& \cdots & x_{n,d}\end{array}\right]$$

(1)

Equation (2) is the fitness-value matrix of the moth population, and the moth individual in each row in matrix X stores the fitness value in the $F_X$ matrix through the fitness function.

$$F_X={\left[F_{X1} F_{X2}\dots F_{Xn}\right]}^T$$

(2)

Each moth in the population needs a flame to correspond to it, so the matrix representing the flame and matrix X should be of the same size. The flame position matrix P and its fitness matrix $F_P$ are shown below:

$$P=\left[\begin{array}{ccc}{p}_{1,1}& \cdots & p_{1,d}\\ ⋮& \ddots & ⋮\\ p_{n,1}& \cdots & p_{n,d}\end{array}\right]$$

(3)

$$F_P={\left[ F_{P1} F_{P2}\dots F_{Pn}\right]}^T$$

(4)

The process of spiral flight in the process of a moth flying towards the fire is modeled. Since the position update of the moth is affected by the position of flame, its expression is shown in Equations (5) and (6).

$$X_i=S\left(X_i ,P_j\right)$$

(5)

$$S\left(X_i ,P_j\right)=\left|P_j-X_i\right|·e^{bt}·\cos \left(2\pi t\right)+P_j$$

(6)

where $X_i$ denotes the i-th moth, te $P_j$ represents the j-th flame, and S is the path function of moths flying towards the flame. In Equation (6), $\left|P_j-X_i\right|$ is the distance between the j-th flame and the i-th moth, b is the logarithmic-spiral-shape constant, and t is a random number in the range of [−1,1]. The updated positions of moths and flames are reordered according to their fitness, and the spatial position with better fitness is selected to be updated and used as the position of the next generation of flames.

Meanwhile, the number of flames is adaptively reduced to balance the global-exploration and local-exploitation ability of the algorithm, as shown in Equation (7).

$$l=round\left(n-it·\frac{n-1}{Maxit}\right).$$

(7)

where $it$ is the current number of iterations and $Maxit$ is the maximum number of iterations. As the number of flames decreases, moths corresponding to the reduced flames will update their positions according to the flames at present.

The pseudocode of the traditional MFO is shown in Algorithm 1.

Algorithm 1 Pseudocode of MFO

Input: The size of the population, n; the dimensionality of the data, dim; the maximum iterations, Maxit;

Output: The position of the best flame;

Initialize moth-population positions X;

it = 0;

while (it < Maxit) do

if it == 1

P = sort(Xit);

FP = sort(FXit);

else

P = sort(Xit−1, Xit);

FP = sort(FXit−1, FXit);

end if

Update l according to Equation (7);

Update the best flame;

for i = 1: size(X,1) do

for j = 1: size(X,2) do

Update parameters a, t;

if i <= l

Update X(i,j) according to Equation (6);

else

Update X(l,j) according to Equation (6);

end if

end for

end for

it = it + 1;

end while

return the best flame

3. Improvement Methods Based on MFO

3.1. Hybrid Mutation

MFO is prone to local stagnation in the process of finding the optimal solution. A certain degree of mutation in the population can increase the population’s diversity and improve the algorithm’s solution accuracy. Common mutation operations are Gaussian mutation and Cauchy mutation. The difference between the two is that the disturbance ability of Gaussian mutation is weaker and has a more robust local-exploitation ability, while the disturbance ability of Cauchy mutation is more vital than that of Gaussian mutation; it has a strong global-exploration ability [59]. For this reason, the mutation methods used in this paper are the hybrid mutation of Cauchy and Gaussian [60], and dynamic weights are assigned to the two mutation methods as the number of iterations increases. The formula for updating the individual position of the moth using hybrid mutations is shown below.

$$X_i^{it+1}=X_i^{it}\times \left[1+\delta \times \left\{\omega \times N\left(0,1\right)+\left(1-\omega \right)\times C\left(0,1\right)\right\}\right]$$

(8)

where $X_i^{it}$ is the current individual position of the moth, $X_i^{it+1}$ is the updated individual position, $N\left(0,1\right)$ is a Gaussian-distributed-random number, $C\left(0,1\right)$ is a random number subject to Cauchy distribution, $\delta$ is the inertia constant, which is taken as 0.3 in this paper, and $\omega$ is the dynamic weight, which is the ratio of the current iteration to the maximum iteration. When the algorithm is in the early stage, a larger weight is given to Cauchy mutation to promote the global exploration of the algorithm, while in the later stage of the algorithm, Gaussian mutation has a large weight, which is more beneficial to the exploitation of solution space. Combining the two mutation methods, hybrid mutation can increase the population’s diversity and enhance the algorithm’s ability to jump out of the local optimum.

3.2. Chemotaxis Motion

There is a possibility that the MFO algorithm has a situation where the current population individual has moved away from the optimal solution or still has a certain distance from the optimal solution during the iteration, so it is necessary to enhance the local-search ability of the algorithm. Inspired by the chemotaxis motion of bacterial-foraging-optimization algorithm [61], E. coli has two movement modes in the chemotaxis motion: flipping and forwarding. Flipping motion is the movement of bacteria in any direction by unit steps. Forwarding motion means that if the fitness of the individual position is improved after the bacteria moves in a specific direction, it will continue to move in this direction until the fitness is no longer improved or reaches a predetermined number of moving steps. Based on this idea, this paper adds the chemotaxis-motion strategy to the optimization process of MFO. The mathematical model of this strategy is shown below.

$$X_i^{it+1}=X_i^{it}+C\left(i\right)\times \frac{\Delta \left(i\right)}{\sqrt{{\Delta }^T\left(i\right)\Delta \left(i\right)}}.$$

(9)

where $C\left(i\right)$ is the step size of the chemotaxis motion, and $\Delta \left(i\right)$ is a random direction vector with a value range of [−1,1]. When the fitness of $X_i^{it+1}$ is less than the fitness of $X_i^{it}$, it means that moving in the current direction can get closer to the optimal solution, so the movement toward the direction continues. Cross-border judgment is made in each movement, and individual fitness before and after the chemotaxis motion is compared. If the updated position crosses the boundary or its fitness is worse than the fitness of the previous-generation individual, the current movement deviates from the optimal solution, and then the previous-generation individual is adopted. If the fitness of $X_i^{it+1}$ is better than that of $X_i^{it}$, the updated solution is adopted.

To address the characteristics of the two optimization strategies, this paper adopts hybrid mutations in the first half of the optimization process to increase population diversity and promote solution-space exploration. In the second half, chemotaxis-motion strategy is adopted to increase the possibility of an individual approaching the optimal solution and improve the algorithm’s search efficiency. The improved MFO pseudocode is given in Algorithm 2.

Algorithm 2 Pseudocode of HMCMMFO

Input: The size of the population, n; the dimensionality of the data, dim; the maximum iterations, Maxit;

the inertia constant, $\delta$; the chemotaxis-motion-step size, C;

Output: The position of the best flame;

Initialize moth population positions X;

it = 0;

while (it < Maxit) do

if it == 1

P = sort(Xit);

FP = sort(FXit);

else

P = sort(Xit-1, Xit);

FP = sort(FXit-1, FXit);

end

Update the best flame;

for i = 1: size(X,1) do

if $\frac{it}{Maxit}$ < 0.5

Update X according to Equation (8);

Judge whether X is out of bounds and deal with it;

else

Generate a random direction vector $\Delta \left(i\right)$;

Set k = 1;

while (k <= 10)

Update Xnew according to Equation (9);

If Xnew is out of bounds, the search will jump out of the loop;

Calculate the fitness before and after updating X;

If the fitness of Xnew is worse than that of X, the search will jump out of the loop, otherwise, it will be copied to X;

k = k + 1;

end while

end if

end for

Update l according to Equation (7);

for i = 1: size(X,1) do

for j = 1: size(X,2) do

Update parameters a, t;

if i <= l

Update X(i,j) according to Equation (6);

else

Update X(l,j) according to Equation (6);

end if

end for

end for

it = it + 1;

end while

return the best flame

The time complexity of HMCMMFO mainly depends on the number of evaluations (S), the number of moths (n), the problem dimension (d), and the maximum number of forwarding steps (m) for the chemotaxis motion. The time complexity of traditional MFO is calculated around three parts: population initialization, updating flame position, and updating moth position. The time complexity of these three parts is O(n × d), O((2n)²), and O(n × d), respectively. HMCMMFO in this paper adds two parts: hybrid mutation and chemotaxis motion based on the original MFO. The time complexity of hybrid mutation is O(n). When executing chemotaxis motion, the default is to move forward m steps each time the strategy is executed, and its time complexity is O(n × m). Hybrid-mutation strategy is adopted in the first half of the evaluations, and chemotaxis motion mechanism is adopted in the second half. Therefore, time complexity of HMCMMFO is O(HMCMMFO) = O(population initialization) + S × (O(updating flames position) + 0.5S × O(hybrid mutation) + 0.5S × O(chemotaxis motion) + O(updating moths position)). That is, the total time complexity is O(HMCMMFO) = (S + 1) × O(n × d) + S(O(4n²) + 0.5 × O(n) + 0.5 × O(n × m)).

For a clear understanding of the algorithm flow of the improved MFO in this paper, the flow of HMCMMFO is shown in Figure 1 below.

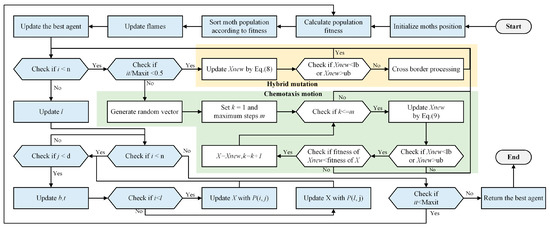
Figure 1. Flow chart of HMCMMFO.

4. Discussion of Experimental Results

In this section, a series of comparative experiments will be used to verify the superiority of HMCMMFO and the effectiveness of the optimization strategy proposed in this paper. A total of 30 benchmark functions of IEEE CEC 2017 are selected for the experimental test, and the specific function details are shown in Table 1. Among them, NO. denotes the serial number of the function, Functions represents the function name, Bound is the range of the function, and F(min) denotes the optimal value of the function. The experimental environment is intuitively displayed in Table S1 in the Supplementary Material, where N is the number of populations, set to 30 and dim is the dimension of the function. This paper sets the dimensions of IEEE CEC2017 functions to 30. At the same time, to ensure that the algorithm in the comparison experiment can give full play to its search performance, the evaluation times (Maxit) of the algorithm in this paper are set to 300,000 times. Meanwhile, to reduce the over-concentration or dispersion of the population caused by random initialization of the population, and thus losing the fairness of the experiment [62], all the test functions in this paper adopt 30 independently repeated experiments (Flod) and take the average value to objectively represent the optimization effect of the algorithm in each function.

Table 1. Description of the CEC2017 functions.

No.	Functions	Bound	F (min)
F1	Shifted and Rotated Bent Cigar Function	[−100,100]	100
F2	Shifted and Rotated Sum of Different Power Function	[−100,100]	200
F3	Shifted and Rotated Zakharov Function	[−100,100]	300
F4	Shifted and Rotated Rosenbrock’s Function	[−100,100]	400
F5	Shifted and Rotated Rastrigin’s Function	[−100,100]	500
F6	Shifted and Rotated Expanded Scaffer’s F6 Function	[−100,100]	600
F7	Shifted and Rotated Lunacek Bi_Rastrigin Function	[−100,100]	700
F8	Shifted and Rotated Non-Continuous Rastrigin’s Function	[−100,100]	800
F9	Shifted and Rotated Levy Function	[−100,100]	900
F10	Shifted and Rotated Schwefel’s Function	[−100,100]	1000
F11	Hybrid Function1 (N = 3)	[−100,100]	1100
F12	Hybrid Function2 (N = 3)	[−100,100]	1200
F13	Hybrid Function3 (N = 3)	[−100,100]	1300
F14	Hybrid Function4 (N = 4)	[−100,100]	1400
F15	Hybrid Function5 (N = 4)	[−100,100]	1500
F16	Hybrid Function6 (N = 4)	[−100,100]	1600
F17	Hybrid Function6 (N = 5)	[−100,100]	1700
F18	Hybrid Function6 (N = 5)	[−100,100]	1800
F19	Hybrid Function6 (N = 5)	[−100,100]	1900
F20	Hybrid Function6 (N = 6)	[−100,100]	2000
F21	Composition function1 (N = 3)	[−100,100]	2100
F22	Composition function2 (N = 3)	[−100,100]	2200
F23	Composition function3 (N = 4)	[−100,100]	2300
F24	Composition function4 (N = 4)	[−100,100]	2400
F25	Composition function5 (N = 5)	[−100,100]	2500
F26	Composition function6 (N = 5)	[−100,100]	2600
F27	Composition function7 (N = 6)	[−100,100]	2700
F28	Composition function8 (N = 6)	[−100,100]	2800
F29	Composition function9 (N = 3)	[−100,100]	2900
F30	Composition function10 (N = 3)	[−100,100]	3000

4.1. Parameters Sensitivity Analyses

4.1.1. Determination of the Parameter δ

In order to discuss the influence of δ in hybrid-Cauchy-and-Gaussian mutation on the algorithm’s accuracy, the parameter-sensitivity experiment of δ is carried out in this paper. If the value of δ is too large, the updated individual will exceed the space boundary. Therefore, this experiment adopts boundary control for the updated agent and reinitializes the individuals beyond the spatial range. Meanwhile, to ensure the experiment’s fairness, as per other AI work [63,64,65], this experiment adopts the single-variable principle to only assign different values to $\delta$, specifically $\delta i=\left[0.1, 0.2, \dots , 0.9\right]$. In addition, other experimental environments are described above.

In the 30 test functions, the average value of the optimal solution is obtained in each function by HMCMMFO with different $\delta$, and the most suitable $\delta$ is determined according to the average-ranking value of each algorithm. As shown in Table 2 below, ARV is the average ranking of the algorithm in the 30 functions, and Rank is the final ranking of the algorithm obtained according to ARV. From the data in the table, it can be seen that δ in the range from 0.1 to 0.5 has better results in solving the optimal values among the 30 functions, and their ARV and Rank are stronger than those of other δ. This is because larger δ will cause the population individual to cross the boundary, and out-of-bounds processing needs to be conducted; in this case, the hybrid-Cauchy-and-Gaussian-mutation strategy will become meaningless. Therefore, it can be concluded from the data that this strategy can play best role when the value of δ is 0.3.

Table 2. Comparison of HMCMMFO results with different δ.

	F1		F2		F3
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	7.99653 × 103	8.11122 × 103	2.02180 × 102	7.97128 × 100	3.00001 × 102	1.60450 × 10−3
$\mathrm{HMCMMFO}\delta 2$	8.21015 × 103	8.27410 × 103	2.02389 × 102	9.48917 × 100	3.00002 × 102	5.03969 × 10−3
$\mathrm{HMCMMFO}\delta 3$	7.07403 × 103	7.66029 × 103	2.04935 × 102	1.10703 × 101	3.00011 × 102	3.91913 × 10−2
$\mathrm{HMCMMFO}\delta 4$	9.21663 × 103	8.31977 × 103	2.13036 × 102	1.76469 × 101	3.00009 × 102	1.75611 × 10−2
$\mathrm{HMCMMFO}\delta 5$	8.96503 × 103	8.71510 × 103	2.12881 × 102	4.39056 × 101	3.00014 × 102	3.99256 × 10−2
$\mathrm{HMCMMFO}\delta 6$	8.95832 × 103	8.56015 × 103	2.62513 × 102	2.31404 × 102	3.00007 × 102	1.37536 × 10−2
$\mathrm{HMCMMFO}\delta 7$	7.85556 × 103	7.53276 × 103	2.57079 × 102	1.95675 × 102	3.00026 × 102	4.89904 × 10−2
$\mathrm{HMCMMFO}\delta 8$	9.56777 × 103	8.42754 × 103	2.20087 × 102	3.05948 × 101	3.00038 × 102	8.48057 × 10−2
$\mathrm{HMCMMFO}\delta 9$	7.74946 × 103	7.93181 × 103	2.94503 × 102	4.64133 × 102	3.00013 × 102	3.65740 × 10−2
	F4		F5		F6
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	4.79600 × 102	2.19971 × 101	5.65883 × 102	1.30092 × 101	6.02914 × 102	1.43321 × 100
$\mathrm{HMCMMFO}\delta 2$	4.83789 × 102	1.85106 × 101	5.69532 × 102	1.49643 × 101	6.04265 × 102	1.61646 × 100
$\mathrm{HMCMMFO}\delta 3$	4.77139 × 102	2.38766 × 101	5.66750 × 102	1.47806 × 101	6.05051 × 102	1.54771 × 100
$\mathrm{HMCMMFO}\delta 4$	4.80376 × 102	2.07554 × 101	5.65549 × 102	1.42534 × 101	6.06653 × 102	1.87038 × 100
$\mathrm{HMCMMFO}\delta 5$	4.79813 × 102	1.57313 × 101	5.66377 × 102	1.65492 × 101	6.07038 × 102	3.01397 × 100
$\mathrm{HMCMMFO}\delta 6$	4.76710 × 102	2.31167 × 101	5.67587 × 102	1.49385 × 101	6.08589 × 102	2.22007 × 100
$\mathrm{HMCMMFO}\delta 7$	4.81896 × 102	1.71013 × 101	5.72513 × 102	2.07946 × 101	6.08187 × 102	2.06391 × 100
$\mathrm{HMCMMFO}\delta 8$	4.82687 × 102	1.68842 × 101	5.70935 × 102	1.73829 × 101	6.08702 × 102	2.86039 × 100
$\mathrm{HMCMMFO}\delta 9$	4.83429 × 102	1.40439 × 101	5.74763 × 102	1.63916 × 101	6.09976 × 102	2.59386 × 100
	F7		F8		F9
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	8.08829 × 102	1.93631 × 101	8.66175 × 102	1.65266 × 101	1.02209 × 103	1.18813 × 102
$\mathrm{HMCMMFO}\delta 2$	8.11975 × 102	1.93645 × 101	8.61202 × 102	1.37233 × 101	1.05695 × 103	1.12437 × 102
$\mathrm{HMCMMFO}\delta 3$	8.13853 × 102	1.83122 × 101	8.65252 × 102	1.79224 × 101	1.08753 × 103	7.73680 × 101
$\mathrm{HMCMMFO}\delta 4$	8.24653 × 102	2.40904 × 101	8.61151 × 102	1.08887 × 101	1.12094 × 103	1.05606 × 102
$\mathrm{HMCMMFO}\delta 5$	8.23326 × 102	1.95622 × 101	8.64910 × 102	1.22870 × 101	1.19348 × 103	1.21825 × 102
$\mathrm{HMCMMFO}\delta 6$	8.29887 × 102	2.27070 × 101	8.66039 × 102	1.61677 × 101	1.23425 × 103	1.61509 × 102
$\mathrm{HMCMMFO}\delta 7$	8.33600 × 102	2.01543 × 101	8.66617 × 102	1.54959 × 101	1.27620 × 103	1.88407 × 102
$\mathrm{HMCMMFO}\delta 8$	8.28945 × 102	1.97034 × 101	8.69795 × 102	1.42669 × 101	1.30408 × 103	1.73771 × 102
$\mathrm{HMCMMFO}\delta 9$	8.36140 × 102	2.21724 × 101	8.68763 × 102	1.59392 × 101	1.30254 × 103	1.47192 × 102
	F10		F11		F12
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	3.68506 × 103	5.91426 × 102	1.20160 × 103	3.58494 × 101	2.67558 × 105	2.14441 × 105
$\mathrm{HMCMMFO}\delta 2$	3.78613 × 103	5.77981 × 102	1.20404 × 103	3.30579 × 101	2.75684 × 105	2.34504 × 105
$\mathrm{HMCMMFO}\delta 3$	4.01424 × 103	6.16844 × 102	1.20764 × 103	2.98736 × 101	2.10189 × 105	1.34071 × 105
$\mathrm{HMCMMFO}\delta 4$	4.23830 × 103	6.64904 × 102	1.20398 × 103	4.29623 × 101	2.78662 × 105	1.84968 × 105
$\mathrm{HMCMMFO}\delta 5$	4.12424 × 103	6.04695 × 102	1.21226 × 103	3.92513 × 101	2.94367 × 105	2.01289 × 105
$\mathrm{HMCMMFO}\delta 6$	4.40904 × 103	5.50600 × 102	1.21198 × 103	3.39188 × 101	2.63203 × 105	1.95176 × 105
$\mathrm{HMCMMFO}\delta 7$	4.32233 × 103	6.13896 × 102	1.21189 × 103	4.13867 × 101	2.44483 × 105	1.51160 × 105
$\mathrm{HMCMMFO}\delta 8$	4.43261 × 103	6.35888 × 102	1.20839 × 103	4.46607 × 101	2.37750 × 105	2.14237 × 105
$\mathrm{HMCMMFO}\delta 9$	4.39891 × 103	5.11591 × 102	1.22373 × 103	4.85077 × 101	2.42413 × 105	1.89349 × 105
	F13		F14		F15
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	3.33690 × 104	2.50935 × 104	2.81393 × 104	1.49900 × 104	2.01635 × 104	1.44834 × 104
$\mathrm{HMCMMFO}\delta 2$	2.89474 × 104	2.19148 × 104	2.25083 × 104	1.19023 × 104	1.17364 × 104	1.22589 × 104
$\mathrm{HMCMMFO}\delta 3$	3.91207 × 104	2.61488 × 104	2.98529 × 104	1.43223 × 104	1.38299 × 104	1.34655 × 104
$\mathrm{HMCMMFO}\delta 4$	4.52750 × 104	2.44167 × 104	2.96832 × 104	1.51745 × 104	1.87379 × 104	1.49142 × 104
$\mathrm{HMCMMFO}\delta 5$	3.47647 × 104	2.61895 × 104	2.11498 × 104	8.92111 × 103	8.07613 × 103	9.03779 × 103
$\mathrm{HMCMMFO}\delta 6$	3.59667 × 104	2.59839 × 104	2.73962 × 104	1.45910 × 104	1.15598 × 104	1.34873 × 104
$\mathrm{HMCMMFO}\delta 7$	3.56409 × 104	2.61362 × 104	3.32410 × 104	1.96918 × 104	8.27325 × 103	9.80176 × 103
$\mathrm{HMCMMFO}\delta 8$	4.00782 × 104	2.83890 × 104	2.78522 × 104	1.47880 × 104	9.22414 × 103	1.02606 × 104
$\mathrm{HMCMMFO}\delta 9$	3.70569 × 104	3.41490 × 104	3.25110 × 104	1.91208 × 104	8.78055 × 103	9.08876 × 103
	F16		F17		F18
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	2.26587 × 103	2.54360 × 102	2.03413 × 103	1.66456 × 102	2.32120 × 105	1.62629 × 105
$\mathrm{HMCMMFO}\delta 2$	2.22922 × 103	2.62825 × 102	1.98976 × 103	1.45363 × 102	3.03816 × 105	2.64694 × 105
$\mathrm{HMCMMFO}\delta 3$	2.18807 × 103	2.03828 × 102	1.96657 × 103	1.63256 × 102	3.02479 × 105	2.53518 × 105
$\mathrm{HMCMMFO}\delta 4$	2.27606 × 103	3.00368 × 102	1.93906 × 103	1.38437 × 102	2.18571 × 105	1.59221 × 105
$\mathrm{HMCMMFO}\delta 5$	2.25724 × 103	3.05542 × 102	1.93626 × 103	1.30135 × 102	2.11116 × 105	1.23450 × 105
$\mathrm{HMCMMFO}\delta 6$	2.19430 × 103	2.51897 × 102	1.94892 × 103	1.71728 × 102	2.38839 × 105	1.14788 × 105
$\mathrm{HMCMMFO}\delta 7$	2.17115 × 103	2.78175 × 102	1.96743 × 103	1.61969 × 102	2.21677 × 105	2.13197 × 105
$\mathrm{HMCMMFO}\delta 8$	2.18195 × 103	2.54818 × 102	1.97014 × 103	1.45771 × 102	2.68645 × 105	2.06891 × 105
$\mathrm{HMCMMFO}\delta 9$	2.25173 × 103	3.14991 × 102	1.94118 × 103	1.46154 × 102	2.30345 × 105	1.04406 × 105
	F19		F20		F21
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	2.45014 × 104	2.20795 × 104	2.36142 × 103	2.13054 × 102	2.37248 × 103	1.64518 × 101
$\mathrm{HMCMMFO}\delta 2$	2.71886 × 104	2.44299 × 104	2.29151 × 103	1.78105 × 102	2.36374 × 103	1.32328 × 101
$\mathrm{HMCMMFO}\delta 3$	2.38428 × 104	2.00474 × 104	2.31589 × 103	1.44362 × 102	2.35438 × 103	1.37493 × 101
$\mathrm{HMCMMFO}\delta 4$	2.66206 × 104	2.34198 × 104	2.27306 × 103	6.91329 × 101	2.35393 × 103	1.71400 × 101
$\mathrm{HMCMMFO}\delta 5$	2.37079 × 104	2.17911 × 104	2.21201 × 103	1.34726 × 102	2.35681 × 103	1.63814 × 101
$\mathrm{HMCMMFO}\delta 6$	2.37245 × 104	2.21257 × 104	2.23979 × 103	1.42513 × 102	2.36507 × 103	1.14326 × 101
$\mathrm{HMCMMFO}\delta 7$	2.91757 × 104	2.44700 × 104	2.27627 × 103	1.79039 × 102	2.35550 × 103	1.30317 × 101
$\mathrm{HMCMMFO}\delta 8$	3.17990 × 104	2.46838 × 104	2.30130 × 103	1.47551 × 102	2.36044 × 103	1.61065 × 101
$\mathrm{HMCMMFO}\delta 9$	3.29311 × 104	2.38761 × 104	2.29063 × 103	1.60959 × 102	2.36239 × 103	1.74163 × 101
	F22		F23		F24
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	4.02772 × 103	1.40382 × 103	2.72940 × 103	1.74092 × 101	2.89249 × 103	2.01833 × 101
$\mathrm{HMCMMFO}\delta 2$	4.63412 × 103	1.36568 × 103	2.71861 × 103	1.68920 × 101	2.89348 × 103	1.64088 × 101
$\mathrm{HMCMMFO}\delta 3$	4.79283 × 103	1.30998 × 103	2.72305 × 103	1.86821 × 101	2.88755 × 103	2.21572 × 101
$\mathrm{HMCMMFO}\delta 4$	4.14717 × 103	1.70499 × 103	2.72766 × 103	2.08506 × 101	2.90043 × 103	2.62559 × 101
$\mathrm{HMCMMFO}\delta 5$	4.67154 × 103	1.69790 × 103	2.72896 × 103	1.85336 × 101	2.89554 × 103	1.71822 × 101
$\mathrm{HMCMMFO}\delta 6$	4.51014 × 103	1.89522 × 103	2.72462 × 103	1.83384 × 101	2.89672 × 103	1.97406 × 101
$\mathrm{HMCMMFO}\delta 7$	4.32952 × 103	1.86939 × 103	2.72418 × 103	1.59060 × 101	2.89221 × 103	1.35818 × 101
$\mathrm{HMCMMFO}\delta 8$	4.43535 × 103	1.98141 × 103	2.72610 × 103	1.97684 × 101	2.90216 × 103	2.04542 × 101
$\mathrm{HMCMMFO}\delta 9$	4.24424 × 103	1.88557 × 103	2.73053 × 103	1.76783 × 101	2.90211 × 103	2.17068 × 101
	F25		F26		F27
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	2.88854 × 103	6.77121 × 100	4.35270 × 103	1.76935 × 102	3.21421 × 103	1.34401 × 101
$\mathrm{HMCMMFO}\delta 2$	2.88597 × 103	2.39509 × 100	4.28581 × 103	1.36642 × 102	3.21421 × 103	9.54168 × 100
$\mathrm{HMCMMFO}\delta 3$	2.88705 × 103	7.42716 × 100	4.33071 × 103	1.86552 × 102	3.21360 × 103	9.08677 × 100
$\mathrm{HMCMMFO}\delta 4$	2.88660 × 103	2.47058 × 100	4.39885 × 103	1.56521 × 102	3.21523 × 103	1.02152 × 101
$\mathrm{HMCMMFO}\delta 5$	2.88608 × 103	2.41853 × 100	4.36359 × 103	1.94143 × 102	3.21392 × 103	8.79104 × 100
$\mathrm{HMCMMFO}\delta 6$	2.88705 × 103	7.57731 × 100	4.35711 × 103	1.95361 × 102	3.21371 × 103	9.37593 × 100
$\mathrm{HMCMMFO}\delta 7$	2.88799 × 103	7.36339 × 100	4.40356 × 103	1.73217 × 102	3.21635 × 103	1.24228 × 101
$\mathrm{HMCMMFO}\delta 8$	2.88606 × 103	2.46422 × 100	4.42429 × 103	2.05940 × 102	3.21478 × 103	1.13235 × 101
$\mathrm{HMCMMFO}\delta 9$	2.88775 × 103	4.37929 × 100	4.45078 × 103	1.92314 × 102	3.21407 × 103	1.04529 × 101
	F28		F29		F30
	AVG	STD	AVG	STD	AVG	STD
$\mathrm{HMCMMFO}\delta 1$	3.17619 × 103	6.94854 × 101	3.68289 × 103	1.84964 × 102	1.26906 × 104	5.57223 × 103
$\mathrm{HMCMMFO}\delta 2$	3.18621 × 103	7.13906 × 101	3.57683 × 103	1.23870 × 102	1.40244 × 104	4.21658 × 103
$\mathrm{HMCMMFO}\delta 3$	3.16965 × 103	6.92289 × 101	3.61081 × 103	1.71466 × 102	1.21935 × 104	5.25786 × 103
$\mathrm{HMCMMFO}\delta 4$	3.16650 × 103	7.46658 × 101	3.62631 × 103	1.49335 × 102	1.21869 × 104	4.20930 × 103
$\mathrm{HMCMMFO}\delta 5$	3.17276 × 103	6.93366 × 101	3.62422 × 103	1.67782 × 102	1.50316 × 104	4.71045 × 103
$\mathrm{HMCMMFO}\delta 6$	3.16032 × 103	6.31060 × 101	3.57831 × 103	1.61502 × 102	1.33741 × 104	4.21481 × 103
$\mathrm{HMCMMFO}\delta 7$	3.15070 × 103	6.04520 × 101	3.62263 × 103	2.29452 × 102	1.26976 × 104	4.58287 × 103
$\mathrm{HMCMMFO}\delta 8$	3.18155 × 103	6.40737 × 101	3.66002 × 103	1.47621 × 102	1.25602 × 104	4.09736 × 103
$\mathrm{HMCMMFO}\delta 9$	3.14029 × 103	6.10406 × 101	3.68634 × 103	1.95530 × 102	1.40643 × 104	5.26455 × 103
	ARV	Rank
$\mathrm{HMCMMFO}\delta 1$	4.566667	4
$\mathrm{HMCMMFO}\delta 2$	4.333333	2
$\mathrm{HMCMMFO}\delta 3$	3.866667	1
$\mathrm{HMCMMFO}\delta 4$	4.7	5
$\mathrm{HMCMMFO}\delta 5$	4.466667	3
$\mathrm{HMCMMFO}\delta 6$	4.866667	6
$\mathrm{HMCMMFO}\delta 7$	5.3	7
$\mathrm{HMCMMFO}\delta 8$	6.4	8
$\mathrm{HMCMMFO}\delta 9$	6.5	9

4.1.2. Determination of Chemotaxis Motion Step Size

In order to select the most suitable step size, this experiment follows the single-variable principle. Only the parameter settings for the step size were changed, specifically $Ci=\left[0.01, 0.03, 0.05, 0.07, 0.09, 0.1, 0.3\right]$, and the rest followed the experimental setting described above. If the direction in the chemotaxis-motion strategy helps the individual move toward the optimal solution, the maximum number of motion steps is specified as 10 to avoid too many motion steps which increases the overhead of the algorithm. Table 3 below shows the solutions using different step lengths.

Table 3. Comparison of the results of HMCMMFO using different step sizes.

	F1		F2		F3
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	8.66303 × 103	7.84705 × 103	2.04834 × 102	1.33106 × 101	3.00878 × 102	4.65364 × 100
HMCMMFOstep2	7.97589 × 103	8.53624 × 103	2.00760 × 102	3.74399 × 100	3.00002 × 102	4.76692 × 10−3
HMCMMFOstep3	9.35529 × 103	8.74887 × 103	2.00604 × 102	3.30324 × 100	3.00002 × 102	7.33390 × 10−3
HMCMMFOstep4	6.89668 × 103	7.10186 × 103	2.01220 × 102	4.63905 × 100	3.00006 × 102	1.51866 × 10−2
HMCMMFOstep5	8.37666 × 103	8.18901 × 103	2.02887 × 102	1.06536 × 101	3.00002 × 102	6.01558 × 10−3
HMCMMFOstep6	6.84418 × 103	7.32319 × 103	2.01161 × 102	4.46624 × 100	3.00002 × 102	5.42726 × 10−3
HMCMMFOstep7	8.45848 × 103	7.75686 × 103	2.03841 × 102	1.11938 × 101	3.00002 × 102	4.28391 × 10−3
	F4		F5		F6
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	4.76064 × 102	2.00601 × 101	5.66023 × 102	1.53038 × 101	6.03610 × 102	1.85782 × 100
HMCMMFOstep2	4.84669 × 102	2.42338 × 101	5.65072 × 102	1.44465 × 101	6.03249 × 102	1.42262 × 100
HMCMMFOstep3	4.77161 × 102	2.52032 × 101	5.65874 × 102	1.61628 × 101	6.03415 × 102	1.91600 × 100
HMCMMFOstep4	4.77238 × 102	2.38403 × 101	5.66073 × 102	1.54412 × 101	6.03048 × 102	1.33092 × 100
HMCMMFOstep5	4.79878 × 102	2.11073 × 101	5.68237 × 102	1.16246 × 101	6.03160 × 102	1.36591 × 100
HMCMMFOstep6	4.78631 × 102	2.90738 × 101	5.65631 × 102	1.70457 × 101	6.03028 × 102	1.40687 × 100
HMCMMFOstep7	4.80517 × 102	2.68455 × 101	5.63865 × 102	2.00864 × 101	6.03027 × 102	1.71435 × 100
	F7		F8		F9
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	8.09803 × 102	2.23524 × 101	8.71397 × 102	1.85329 × 101	1.00859 × 103	8.06705 × 101
HMCMMFOstep2	8.10786 × 102	2.87670 × 101	8.65882 × 102	1.36839 × 101	1.00787 × 103	7.71723 × 101
HMCMMFOstep3	8.02920 × 102	2.05684 × 101	8.65062 × 102	1.55406 × 101	1.11090 × 103	2.45938 × 102
HMCMMFOstep4	8.09671 × 102	2.81699 × 101	8.64766 × 102	1.60089 × 101	1.06668 × 103	1.70977 × 102
HMCMMFOstep5	8.15750 × 102	2.10966 × 101	8.70045 × 102	1.93109 × 101	1.02977 × 103	7.25515 × 101
HMCMMFOstep6	8.14312 × 102	2.88166 × 101	8.60382 × 102	1.23858 × 101	1.06351 × 103	2.09531 × 102
HMCMMFOstep7	8.15832 × 102	2.32068 × 101	8.61928 × 102	1.59051 × 101	1.01560 × 103	8.16708 × 101
	F10		F11		F12
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	3.48260 × 103	6.58739 × 102	1.19133 × 103	3.43658 × 101	2.05355 × 105	1.81947 × 105
HMCMMFOstep2	3.55392 × 103	4.78136 × 102	1.20569 × 103	4.08568 × 101	1.85451 × 105	1.42475 × 105
HMCMMFOstep3	3.39803 × 103	4.88723 × 102	1.19695 × 103	3.15625 × 101	2.38687 × 105	2.14414 × 105
HMCMMFOstep4	3.54981 × 103	5.82920 × 102	1.20035 × 103	4.25845 × 101	2.53071 × 105	2.20994 × 105
HMCMMFOstep5	3.42152 × 103	4.81097 × 102	1.20382 × 103	3.66358 × 101	2.00713 × 105	1.33010 × 105
HMCMMFOstep6	3.63880 × 103	5.63713 × 102	1.19170 × 103	4.10747 × 101	2.98582 × 105	2.43926 × 105
HMCMMFOstep7	3.58965 × 103	4.99686 × 102	1.18150 × 103	3.10368 × 101	2.03903 × 105	1.58705 × 105
	F13		F14		F15
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	2.82176 × 104	2.39431 × 104	2.53297 × 104	1.39987 × 104	1.70620 × 104	1.42020 × 104
HMCMMFOstep2	2.94128 × 104	2.31020 × 104	2.27879 × 104	1.19290 × 104	1.86470 × 104	1.42804 × 104
HMCMMFOstep3	2.45448 × 104	2.21089 × 104	2.33637 × 104	1.30973 × 104	1.92008 × 104	1.41454 × 104
HMCMMFOstep4	2.85837 × 104	2.20365 × 104	2.06428 × 104	1.44728 × 104	1.99020 × 104	1.56693 × 104
HMCMMFOstep5	2.94851 × 104	2.51721 × 104	2.09628 × 104	1.22437 × 104	1.31878 × 104	1.31048 × 104
HMCMMFOstep6	3.88001 × 104	2.54849 × 104	1.87060 × 104	1.38225 × 104	1.97045 × 104	1.54835 × 104
HMCMMFOstep7	3.20569 × 104	2.39578 × 104	2.35105 × 104	1.31240 × 104	2.16252 × 104	1.62251 × 104
	F16		F17		F18
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	2.24731 × 103	2.40282 × 102	1.97406 × 103	1.61157 × 102	2.06004 × 105	1.71979 × 105
HMCMMFOstep2	2.23372 × 103	2.30237 × 102	2.00022 × 103	1.89506 × 102	2.20227 × 105	1.59302 × 105
HMCMMFOstep3	2.17411 × 103	2.47117 × 102	1.97994 × 103	1.38732 × 102	1.95129 × 105	1.22832 × 105
HMCMMFOstep4	2.22615 × 103	2.55121 × 102	2.01179 × 103	1.29681 × 102	2.23185 × 105	1.28914 × 105
HMCMMFOstep5	2.21992 × 103	3.23175 × 102	1.98371 × 103	1.57909 × 102	2.21492 × 105	1.92743 × 105
HMCMMFOstep6	2.15437 × 103	2.35643 × 102	1.96257 × 103	1.18271 × 102	2.64409 × 105	2.07695 × 105
HMCMMFOstep7	2.24883 × 103	2.62444 × 102	2.03128 × 103	1.48530 × 102	2.24798 × 105	1.68917 × 105
	F19		F20		F21
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	2.16109 × 104	2.11400 × 104	2.28848 × 103	1.33351 × 102	2.35638 × 103	1.34010 × 101
HMCMMFOstep2	2.19802 × 104	1.88487 × 104	2.30271 × 103	1.09320 × 102	2.36099 × 103	1.19829 × 101
HMCMMFOstep3	2.92007 × 104	2.30629 × 104	2.29251 × 103	1.56898 × 102	2.35663 × 103	1.31425 × 101
HMCMMFOstep4	2.46817 × 104	2.31719 × 104	2.32795 × 103	1.21269 × 102	2.36337 × 103	1.88726 × 101
HMCMMFOstep5	2.24346 × 104	2.04424 × 104	2.25983 × 103	1.47482 × 102	2.35918 × 103	1.78142 × 101
HMCMMFOstep6	2.41069 × 104	2.10334 × 104	2.33532 × 103	1.55709 × 102	2.35750 × 103	1.07666 × 101
HMCMMFOstep7	2.92545 × 104	2.15780 × 104	2.28679 × 103	1.51164 × 102	2.35688 × 103	1.34916 × 101
	F22		F23		F24
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	4.90416 × 103	7.02988 × 102	2.71162 × 103	1.47736 × 101	2.88149 × 103	1.65674 × 101
HMCMMFOstep2	4.18116 × 103	1.08442 × 103	2.70908 × 103	1.64223 × 101	2.88223 × 103	1.54699 × 101
HMCMMFOstep3	3.81072 × 103	1.32467 × 103	2.71173 × 103	1.62408 × 101	2.88204 × 103	1.11811 × 101
HMCMMFOstep4	4.02186 × 103	1.29459 × 103	2.71223 × 103	1.75592 × 101	2.88091 × 103	1.28149 × 101
HMCMMFOstep5	4.17377 × 103	1.21352 × 103	2.71392 × 103	1.93099 × 101	2.88374 × 103	1.49332 × 101
HMCMMFOstep6	3.77317 × 103	1.39412 × 103	2.70908 × 103	1.31521 × 101	2.88087 × 103	1.28877 × 101
HMCMMFOstep7	3.82962 × 103	1.32294 × 103	2.70730 × 103	1.47359 × 101	2.88032 × 103	1.36292 × 101
	F25		F26		F27
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	2.88713 × 103	3.01734 × 100	4.27411 × 103	2.28711 × 102	3.21428 × 103	1.20565 × 101
HMCMMFOstep2	2.88779 × 103	4.95017 × 100	4.25873 × 103	1.44133 × 102	3.21560 × 103	1.19838 × 101
HMCMMFOstep3	2.88772 × 103	7.50453 × 100	4.24224 × 103	1.33129 × 102	3.21352 × 103	1.07658 × 101
HMCMMFOstep4	2.89198 × 103	1.21144 × 101	4.29374 × 103	1.47012 × 102	3.21376 × 103	1.19883 × 101
HMCMMFOstep5	2.88688 × 103	2.23710 × 100	4.28584 × 103	1.98674 × 102	3.21268 × 103	1.28796 × 101
HMCMMFOstep6	2.88710 × 103	5.38606 × 100	4.23512 × 103	1.45781 × 102	3.21288 × 103	1.20503 × 101
HMCMMFOstep7	2.89106 × 103	1.43336 × 101	4.21557 × 103	2.92270 × 102	3.21270 × 103	1.13763 × 101
	F28		F29		F30
	AVG	STD	AVG	STD	AVG	STD
HMCMMFOstep1	3.16453 × 103	7.15106 × 101	3.62812 × 103	9.80410 × 101	1.23201 × 104	4.60316 × 103
HMCMMFOstep2	3.17521 × 103	7.82121 × 101	3.61384 × 103	1.34470 × 102	1.27183 × 104	4.44108 × 103
HMCMMFOstep3	3.15475 × 103	6.77392 × 101	3.63245 × 103	1.54113 × 102	1.19296 × 104	4.82325 × 103
HMCMMFOstep4	3.13913 × 103	5.87252 × 101	3.58077 × 103	1.32657 × 102	1.31280 × 104	4.92988 × 103
HMCMMFOstep5	3.16409 × 103	7.46936 × 101	3.57499 × 103	1.50803 × 102	1.35334 × 104	4.52054 × 103
HMCMMFOstep6	3.14385 × 103	6.48299 × 101	3.63710 × 103	1.40842 × 102	1.32345 × 104	4.73736 × 103
HMCMMFOstep7	3.17434 × 103	6.92739 × 101	3.61872 × 103	1.46426 × 102	1.29146 × 104	4.65148 × 103
	Overall Rank
	ARV	Rank
HMCMMFOstep1	4.033333	3
HMCMMFOstep2	4.166667	4
HMCMMFOstep3	3.566667	1
HMCMMFOstep4	4.466667	5
HMCMMFOstep5	4.033333	3
HMCMMFOstep6	3.7	2
HMCMMFOstep7	4.033333	3

From the above table, it can be seen that HMCMMFO using different step lengths obtained the optimal solution with a similar magnitude in most functions. This indicates that under the limitation of the maximum number of chemotaxis motion steps, the algorithms using different step sizes facilitate the moth’s approach to the optimal solution. Moreover, HMCMMFO using a step size of 0.05 has the smallest average-ranking value among the compared algorithms, which is more beneficial to enhance the search efficiency of the algorithm.

4.2. Impact of Optimization Strategies on MFO

HMCMMFO uses two optimization mechanisms, namely hybrid mutation and chemotaxis motion. To demonstrate the effect of the two strategies on the MFO, three different MFOs were developed to compare with the original algorithm by different combinations of the two strategies. As shown in Table 4 below, hybrid-mutation strategy is denoted by “HM,” and chemotaxis motion is represented by “CM”, with “1” indicating that the MFO uses this strategy and “0” indicating that it does not. For example, CMMFO indicates that only chemotaxis-motion strategy is adopted, and HMCMMFO indicates that both hybrid-mutation and chemotaxis-motion optimization strategies are used.

Table 4. Performance of the two strategies on MFO.

	Hybrid Mutation	Chemotaxis Motion
MFO	0	0
CMMFO	0	1
HMMFO	1	0
HMCMMFO	1	1

4.2.1. Comparison between Mechanisms

Table 5 below shows the average value and standard deviation of the optimal solution obtained by four different MFOs in the test function. The “+”, “−”, and “=” in the table indicate that the optimization accuracy of HMCMMFO is better than, worse than, or equal to the comparison algorithm, respectively. AVG represents the average value of the optimal solution obtained by the algorithm in the function, and STD is the standard deviation. The data in the table show that the average value and standard deviation of the optimal solution obtained by HMCMMFO in most functions are better than those of other algorithms, and the search performance is stable. The average ranking values of MFO variants with different strategies are stronger than that of the original MFO, which proves the effectiveness of the two optimization strategies. HMCMMFO with two strategies is better than the traditional algorithm in 29 functions, and their optimization performance is the same in only one function. Comparing the average ranking values of both, HMCMMFO is only about one-third of MFO. This shows that the two optimization strategies proposed in this paper are essential to improve the performance of the algorithm.

Table 5. Comparison of MFO results with different strategies.

	F1		F2		F3
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	9.88074 × 103	8.36593 × 103	2.57815 × 102	2.58794 × 102	3.00026 × 102	7.17286 × 10−2
CMMFO	9.01626 × 103	8.01713 × 103	2.00000 × 102	3.33524 × 10−4	3.00001 × 102	3.40189 × 10−3
HMMFO	4.46256 × 108	4.77887 × 108	1.48764 × 1019	7.29118 × 1019	1.26610 × 104	5.07162 × 103
MFO	1.43280 × 1010	9.64728 × 109	3.08359 × 1037	1.47328 × 1038	1.06204 × 105	6.27301 × 104
	F4		F5		F6
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.77557 × 102	2.31258 × 101	5.65091 × 102	1.22131 × 101	6.06060 × 102	1.53909 × 100
CMMFO	4.77661 × 102	1.94289 × 101	6.92106 × 102	4.49923 × 101	6.37071 × 102	1.10670 × 101
HMMFO	5.12020 × 102	1.47713 × 101	6.09776 × 102	1.57299 × 101	6.08643 × 102	1.63674 × 100
MFO	1.21151 × 103	7.57463 × 102	7.12338 × 102	5.05325 × 101	6.37028 × 102	1.10430 × 101
	F7		F8		F9
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	8.17282 × 102	2.25823 × 101	8.60641 × 102	1.62711 × 101	1.09963 × 103	1.29386 × 102
CMMFO	1.10897 × 103	1.82774 × 102	9.87306 × 102	4.24357 × 101	7.30599 × 103	2.19949 × 103
HMMFO	9.13037 × 102	1.75738 × 101	8.95471 × 102	1.26446 × 101	1.21187 × 103	1.31024 × 102
MFO	1.16361 × 103	2.30837 × 102	1.00535 × 103	3.71062 × 101	7.50263 × 103	2.59327 × 103
	F10		F11		F12
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.07312 × 103	5.96620 × 102	1.20139 × 103	3.81300 × 101	2.56822 × 105	1.79231 × 105
CMMFO	5.42916 × 103	5.94213 × 102	1.39367 × 103	1.01072 × 102	1.61037 × 105	9.63357 × 104
HMMFO	4.53305 × 103	4.67957 × 102	1.27039 × 103	3.28704 × 101	1.58438 × 107	9.83874 × 106
MFO	5.62479 × 103	8.53512 × 102	7.12357 × 103	6.57687 × 103	2.72064 × 108	5.35291 × 108
	F13		F14		F15
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.02651 × 104	2.45014 × 104	3.12846 × 104	2.09629 × 104	1.36877 × 104	1.47697 × 104
CMMFO	3.57362 × 104	2.52200 × 104	2.04073 × 104	9.06924 × 103	2.35051 × 104	1.71883 × 104
HMMFO	1.35146 × 106	5.64713 × 105	2.80552 × 104	1.41804 × 104	7.60219 × 104	7.02575 × 104
MFO	4.59919 × 107	2.47756 × 108	7.10991 × 104	9.99911 × 104	6.20266 × 104	5.13299 × 104
	F16		F17		F18
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.22691 × 103	3.07251 × 102	1.96813 × 103	1.61808 × 102	2.74032 × 105	2.23878 × 105
CMMFO	2.93507 × 103	3.00156 × 102	2.49429 × 103	2.31511 × 102	2.09121 × 105	1.76984 × 105
HMMFO	2.32223 × 103	2.20334 × 102	2.05634 × 103	1.84945 × 102	5.01800 × 105	4.35420 × 105
MFO	3.15072 × 103	3.86413 × 102	2.57387 × 103	2.85106 × 102	2.65915 × 106	7.32477 × 106
	F19		F20		F21
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.31613 × 104	2.26335 × 104	2.28316 × 103	1.67238 × 102	2.35584 × 103	1.68999 × 101
CMMFO	2.43818 × 104	2.12790 × 104	2.64263 × 103	2.20602 × 102	2.48656 × 103	4.02556 × 101
HMMFO	1.14206 × 105	6.47232 × 104	2.28963 × 103	1.47657 × 102	2.39520 × 103	1.25889 × 101
MFO	1.14474 × 107	3.46847 × 107	2.77829 × 103	2.48745 × 102	2.51140 × 103	5.28160 × 101
	F22		F23		F24
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.93530 × 103	1.59584 × 103	2.72477 × 103	1.52897 × 101	2.88764 × 103	1.53510 × 101
CMMFO	5.93190 × 103	1.61431 × 103	2.80777 × 103	3.43904 × 101	2.95894 × 103	3.77249 × 101
HMMFO	4.63810 × 103	1.66806 × 103	2.76685 × 103	1.56515 × 101	2.93080 × 103	1.38384 × 101
MFO	6.00588 × 103	1.40791 × 103	2.84127 × 103	3.13079 × 101	2.99268 × 103	2.96835 × 101
	F25		F26		F27
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.88676 × 103	2.25680 × 100	4.26794 × 103	1.29377 × 102	3.21293 × 103	9.60366 × 100
CMMFO	2.89025 × 103	9.52125 × 100	5.74402 × 103	4.98044 × 102	3.23401 × 103	2.04502 × 101
HMMFO	2.91451 × 103	1.74483 × 101	4.66563 × 103	1.47998 × 102	3.21993 × 103	9.73166 × 100
MFO	3.38300 × 103	5.44547 × 102	5.99749 × 103	4.07191 × 102	3.25580 × 103	2.56771 × 101
	F28		F29		F30
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	3.15714 × 103	5.94062 × 101	3.64233 × 103	1.78067 × 102	1.47158 × 104	4.86596 × 103
CMMFO	3.19869 × 103	6.89095 × 101	4.21224 × 103	3.21054 × 102	1.40666 × 104	5.94538 × 103
HMMFO	3.28424 × 103	4.08765 × 101	3.65353 × 103	1.55844 × 102	8.97401 × 105	5.11961 × 105
MFO	4.74021 × 103	1.07501 × 103	4.13419 × 103	2.98080 × 102	1.52611 × 106	5.67583 × 106
	+/−/=	ARV	Rank
HMCMMFO		1.333333	1
CMMFO	19/4/7	2.366667	2
HMMFO	24/0/6	2.4	3
MFO	29/0/1	3.9	4

To visualize the impact of the two optimization mechanisms on the optimization performance of MFO, convergence plots of nine test functions are selected in this experiment, as shown in Figure 2 below. HMMFO with hybrid-mutation strategy has a better optimization accuracy than the traditional MFO on eight functions. CMMFO with chemotaxis-motion mechanism has a significant optimization effect on F1 and F13, and can find the optimal solution at a faster speed, while it can also improve MFO in other functions to varying degrees. Among the nine function plots, HMCMMFO jumps downward in the middle of the evaluation and finds the optimal solution quickly. This is because, in the early stage of the evaluation, hybrid-mutation strategy is used to mutate the individual to avoid the algorithm falling into the local optimal space. By comparing the convergence curves of HMMFO and MFO in the figure, it can be proved that this strategy contributes to avoiding stagnation problem of the algorithm. A chemotactic- motion strategy is adopted in the later evaluation stage to help individuals approach the optimal solution. The effectiveness of this strategy is illustrated by comparing HMCMMFO with HMMFO, and it outperforms HMMFO in terms of optimization accuracy. Overall, the two strategies promote each other, which positively improves the optimization performance of MFO.

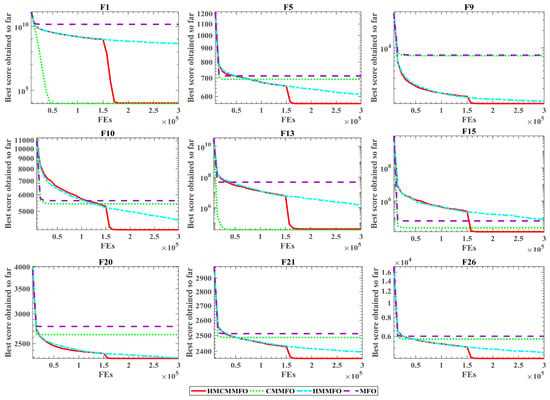
Figure 2. MFO convergence curves with different strategies.

4.2.2. Balance and Diversity Analysis of HMCMMFO and MFO

To further analyze the changes produced by the strategies proposed in this paper on the optimization performance of MFO, this section analyzes the diversity and balance of HMCMMFO and MFO. As shown in Figure 3 below, this section selects three functions from the 30 test functions for discussion, namely F1, F11, and F25. In the figure, the first column is the balance plots of HMCMMFO, the second column is the balance plots of MFO, and the third column is the diversity plots, including HMCMMFO and MFO.

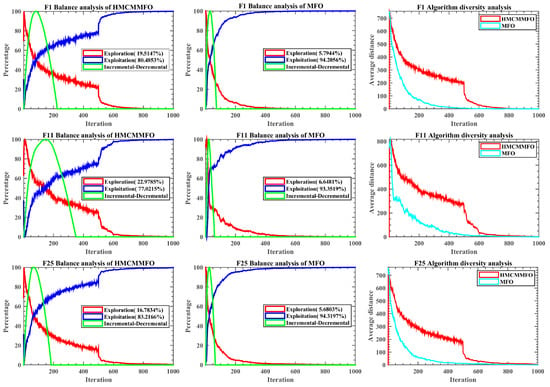
Figure 3. Balance-and-diversity-analysis plots.

There are three curves in the equilibrium graph’s first and second columns: exploration, exploitation, and incremental-decremental. Among them, the exploration curve represents the proportion of the global search process of the algorithm, the exploitation curve represents the proportion of the local-exploitation process of the algorithm, and the incremental-decremental curve is a dynamic curve that changes with the changes in the exploration and exploitation curves. When the global-exploration ability of the algorithm is greater than its local-exploitation ability, the incremental-decremental curve increases, and vice versa. The curve reaches the vertex position when the algorithm’s global-exploration ability and local-exploitation ability are equal. In the F1, F11, and F25 balance plots shown below, the global-exploration ability of traditional MFO is weak, but the local-exploitation ability is strong. Although the stronger local-exploitation ability helps the MFO algorithm to search for the solution space finely, global exploration that is too short will affect the population’s optimal solution and reduce its optimization accuracy. Moreover, the HMCMMFO proposed in this paper effectively improves the global-exploration ability of the algorithm. For example, the global-exploration stage of MFO in F1 only accounts for 5.7944%, while HMCMMFO accounts for 19.5147%, and still has a large proportion of the exploitation process. When HMCMMFO does not reach half of the maximum evaluation times, its exploration curve decreases slowly compared with MFO’s, and oscillation is large. When it exceeds half of the maximum evaluation times, the exploitation curve increases rapidly, and then the slope of the curve slowly approaches 0. The reason for this phenomenon is that the algorithm adopts hybrid mutation on the individual in the first half of the evaluation, which increases the exploration performance of the algorithm. The chemotaxis motion is adopted in the second half to guide the individual to approach the optimal solution, increasing the algorithm’s local-exploitation ability.

In the diversity plots, the horizontal coordinate indicates the number of iterations, and the vertical coordinate represents the diversity metric. The algorithm population is affected by random initialization, which leads to good population diversity at the beginning of the algorithm and gradually decreases as it keeps approaching the optimal solution. In F1, F11, and F25, the diversity curve of MFO decreases rapidly and approaches 0 in the middle of the iteration. A too-fast decline in diversity will lead the algorithm to local optimum, while too-fast convergence is not conducive to finding higher-quality optimal solutions. In the early stage of the iteration, HMCMMFO has a slow decline in diversity curve, rich diversity, and large fluctuation, which means that the hybrid mutation adopted in the early stage is helpful for the algorithm to explore the solution space comprehensively. HMCMMFO diversity drops fast when the algorithm just enters the second half of the iteration, which indicates that the chemotaxis-motion strategy can help an individual to approach the optimal solution effectively.

4.3. Impact of Optimization Strategies on MFO

In order to verify the strength of the optimization performance of HMCMMFO, six well-known MFO-variant algorithms are selected for comparison in this experiment. These algorithms are: CLSGMFO [28], LGCMFO [66], NMSOLMFO [67], QSMFO [51], CMFO [56], and WEMFO [68]. Table S2 in the Supplementary Material shows the parameter settings of these algorithms.

By comparing the average value and standard deviation of the optimal solutions obtained by these algorithms in the IEEE CEC2017 functions, the differences in optimization performance among them were explored. Table 6 shows the optimization results of the MFO variants in test functions. Among these, ARV indicates the algorithm’s average ranking value across all functions, and Rank is the final ranking obtained from ARV. According to the table data, HMCMMFO’s average values of optimum solutions are superior to other techniques in most functions. By comparing the standard deviations of the optimal solutions obtained by these MFO variants, it can be seen that the optimal performance of HMCMMFO in most functions is relatively stable and is at an upper-middle level. By comparing ARV and RANK, it can be found more intuitively that the ARV value of HMCMMFO is only 2.2, which ranks first among these algorithms. Compared with NMSOLMFO, with strong performance, HMCMMFO has more advantages.

Table 6. Comparison of MFO-variant algorithms.

	F1		F2		F3
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	7.45008 × 103	7.73709 × 103	2.08253 × 102	1.54018 × 101	3.00010 × 102	1.92062 × 10−2
CLSGMFO	9.77833 × 103	9.27666 × 103	1.54528 × 1012	5.62911 × 1012	4.41481 × 103	2.46828 × 103
LGCMFO	9.54047 × 103	7.48239 × 103	3.17117 × 1012	1.05059 × 1013	7.63227 × 103	3.40084 × 103
NMSOLMFO	1.00029 × 102	1.19294 × 10−1	2.00000 × 102	2.52539 × 10−7	3.00000 × 102	7.53173 × 10−10
QSMFO	7.76493 × 105	4.67365 × 105	1.65263 × 1014	8.76662 × 1014	1.65277 × 103	5.43654 × 102
CMFO	3.12151 × 108	7.85453 × 108	4.03821 × 1038	2.20987 × 1039	1.07744 × 105	3.18599 × 104
WEMFO	1.26782 × 104	8.16879 × 103	1.30928 × 1016	4.91342 × 1016	9.34514 × 103	4.04733 × 103
	F4		F5		F6
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.83921 × 102	1.00659 × 101	5.67565 × 102	1.58153 × 101	6.05821 × 102	1.49235 × 100
CLSGMFO	4.92717 × 102	3.18428 × 101	6.44607 × 102	3.75846 × 101	6.22085 × 102	1.14138 × 101
LGCMFO	4.96847 × 102	3.48442 × 101	6.49694 × 102	3.90103 × 101	6.15888 × 102	9.33071 × 100
NMSOLMFO	4.17466 × 102	2.80568 × 101	6.10793 × 102	3.63679 × 101	6.06714 × 102	2.26585 × 100
QSMFO	4.81483 × 102	4.03995 × 100	7.06033 × 102	2.19196 × 101	6.41868 × 102	1.87151 × 101
CMFO	5.76424 × 102	6.19701 × 101	7.29219 × 102	6.06530 × 101	6.52386 × 102	8.92716 × 100
WEMFO	4.86804 × 102	2.04131 × 101	6.69370 × 102	5.71347 × 101	6.30716 × 102	1.11558 × 101
	F7		F8		F9
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	8.17605 × 102	2.09013 × 101	8.64528 × 102	1.59203 × 101	1.11123 × 103	1.21983 × 102
CLSGMFO	9.00751 × 102	5.15106 × 101	9.30074 × 102	2.79516 × 101	3.50079 × 103	9.51979 × 102
LGCMFO	8.68081 × 102	4.90456 × 101	9.17209 × 102	2.64516 × 101	2.92376 × 103	7.90733 × 102
NMSOLMFO	8.64867 × 102	5.83245 × 101	9.03175 × 102	3.27945 × 101	1.59150 × 103	4.59537 × 102
QSMFO	8.52241 × 102	3.40663 × 101	9.29969 × 102	2.09746 × 101	4.11144 × 103	1.76071 × 103
CMFO	1.25439 × 103	1.41749 × 102	9.59348 × 102	4.02805 × 101	4.80020 × 103	1.23739 × 103
WEMFO	9.37825 × 102	6.98497 × 101	9.86209 × 102	4.71145 × 101	5.29982 × 103	2.17483 × 103
	F10		F11		F12
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.14337 × 103	6.76492 × 102	1.20406 × 103	4.01105 × 101	2.99045 × 105	2.13295 × 105
CLSGMFO	5.14610 × 103	5.92095 × 102	1.25692 × 103	7.26976 × 101	1.36113 × 106	3.12632 × 106
LGCMFO	4.66928 × 103	5.95099 × 102	1.22641 × 103	5.99199 × 101	1.69558 × 106	3.16562 × 106
NMSOLMFO	5.56026 × 103	6.27896 × 102	1.27211 × 103	7.16933 × 101	1.69407 × 104	1.44619 × 104
QSMFO	4.47754 × 103	4.15647 × 102	1.20220 × 103	3.21058 × 101	3.22319 × 106	1.99893 × 106
CMFO	7.23579 × 103	1.24780 × 103	4.85080 × 103	4.35495 × 103	2.94481 × 107	6.15277 × 107
WEMFO	5.20927 × 103	8.17462 × 102	1.37952 × 103	8.94922 × 101	1.97070 × 106	2.08794 × 106
	F13		F14		F15
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	3.42289 × 104	2.60128 × 104	2.93673 × 104	1.73593 × 104	1.32157 × 104	1.54584 × 104
CLSGMFO	2.10077 × 105	8.04303 × 105	3.64888 × 104	3.63694 × 104	9.03043 × 103	1.24897 × 104
LGCMFO	1.88965 × 105	8.04602 × 105	4.91007 × 104	4.31686 × 104	8.63513 × 103	8.92177 × 103
NMSOLMFO	1.65278 × 104	1.75963 × 104	2.90354 × 103	3.16045 × 103	8.66224 × 103	8.92571 × 103
QSMFO	1.53350 × 104	1.18018 × 104	5.43527 × 103	2.95458 × 103	3.46751 × 103	1.60762 × 103
CMFO	5.99018 × 107	3.27735 × 108	2.39223 × 105	3.66707 × 105	6.80532 × 104	1.00702 × 105
WEMFO	1.28597 × 105	1.50446 × 105	7.13607 × 104	5.30010 × 104	5.56216 × 104	3.97499 × 104
	F16		F17		F18
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.25628 × 103	2.45440 × 102	2.03304 × 103	1.98205 × 102	2.96542 × 105	2.37436 × 105
CLSGMFO	2.79035 × 103	3.27657 × 102	2.29013 × 103	2.63252 × 102	2.06182 × 105	1.87797 × 105
LGCMFO	2.65628 × 103	3.31587 × 102	2.23362 × 103	2.35792 × 102	2.86097 × 105	2.73568 × 105
NMSOLMFO	2.80008 × 103	3.17420 × 102	2.15480 × 103	2.02631 × 102	3.69755 × 104	1.74905 × 104
QSMFO	2.55393 × 103	2.90689 × 102	2.15129 × 103	2.49991 × 102	1.30576 × 105	6.48885 × 104
CMFO	3.06381 × 103	3.65806 × 102	2.38382 × 103	3.04997 × 102	2.65726 × 106	4.23158 × 106
WEMFO	2.71408 × 103	2.79634 × 102	2.20708 × 103	1.63247 × 102	7.09107 × 105	6.33762 × 105
	F19		F20		F21
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.81007 × 104	2.39984 × 104	2.32888 × 103	1.70978 × 102	2.35586 × 103	1.52030 × 101
CLSGMFO	7.90184 × 103	8.82683 × 103	2.48624 × 103	2.14519 × 102	2.42275 × 103	2.92180 × 101
LGCMFO	4.67956 × 103	2.20143 × 103	2.42374 × 103	1.79375 × 102	2.41380 × 103	3.13042 × 101
NMSOLMFO	4.67165 × 103	2.89003 × 103	2.52364 × 103	2.16870 × 102	2.39968 × 103	3.65319 × 101
QSMFO	5.90630 × 103	3.67545 × 103	2.60309 × 103	1.91367 × 102	2.44613 × 103	6.16862 × 101
CMFO	2.33164 × 106	9.43357 × 106	2.76036 × 103	2.60376 × 102	2.48904 × 103	5.10689 × 101
WEMFO	3.69983 × 104	4.15722 × 104	2.51147 × 103	1.99701 × 102	2.35586 × 103	1.52030 × 101
	F22		F23		F24
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.49134 × 103	4.14938 × 101	2.72355 × 103	1.95252 × 101	2.89131 × 103	1.63587 × 101
CLSGMFO	3.86489 × 103	1.63233 × 103	2.78920 × 103	4.14287 × 101	2.96303 × 103	4.96313 × 101
LGCMFO	2.30089 × 103	1.84713 × 100	2.77439 × 103	3.20033 × 101	2.94276 × 103	3.54360 × 101
NMSOLMFO	2.30060 × 103	1.24812 × 100	2.73741 × 103	5.56529 × 101	2.89207 × 103	3.09280 × 101
QSMFO	3.11602 × 103	1.88410 × 103	2.81666 × 103	5.34004 × 101	3.00679 × 103	6.75075 × 101
CMFO	6.02144 × 103	1.30649 × 103	2.99936 × 103	8.54328 × 101	3.11696 × 103	1.06157 × 102
WEMFO	7.91188 × 103	1.75562 × 103	2.80333 × 103	3.97615 × 101	2.96319 × 103	3.77158 × 101
	F25		F26		F27
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.88924 × 103	1.25732 × 101	4.33633 × 103	1.72102 × 102	3.21751 × 103	1.09748 × 101
CLSGMFO	2.89193 × 103	1.40971 × 101	4.10420 × 103	1.31229 × 103	3.29229 × 103	4.93810 × 101
LGCMFO	2.89213 × 103	1.58401 × 101	3.80797 × 103	1.16466 × 103	3.28270 × 103	3.28060 × 101
NMSOLMFO	2.89325 × 103	1.62354 × 101	4.28850 × 103	5.54938 × 102	3.24104 × 103	1.44964 × 101
QSMFO	2.88704 × 103	7.29022 × 100	4.17073 × 103	1.43435 × 103	3.20001 × 103	1.75060 × 10−4
CMFO	2.97389 × 103	5.35474 × 101	6.92114 × 103	8.93332 × 102	3.36460 × 103	1.38467 × 102
WEMFO	2.90061 × 103	2.39035 × 101	5.52994 × 103	4.55182 × 102	3.24074 × 103	2.45360 × 101
	F28		F29		F30
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	3.17875 × 103	6.87415 × 101	3.63537 × 103	1.78531 × 102	1.33965 × 104	4.89866 × 103
CLSGMFO	3.22498 × 103	2.50723 × 101	3.97385 × 103	2.38628 × 102	1.56889 × 105	4.17105 × 105
LGCMFO	3.22064 × 103	2.79571 × 101	3.88712 × 103	2.49899 × 102	3.45376 × 104	4.08926 × 104
NMSOLMFO	3.17597 × 103	6.70651 × 101	3.75346 × 103	2.47148 × 102	9.40010 × 103	3.56750 × 103
QSMFO	3.29991 × 103	2.37411 × 10−1	3.53423 × 103	1.69382 × 102	7.71247 × 103	5.33689 × 103
CMFO	3.39495 × 103	2.02412 × 102	4.48373 × 103	3.23986 × 102	2.17166 × 106	4.89252 × 106
WEMFO	3.38313 × 103	6.47108 × 102	4.10687 × 103	2.71645 × 102	3.02808 × 105	7.58156 × 105
	ARV	RANK
HMCMMFO	2.2	1
CLSGMFO	4.066667	5
LGCMFO	3.466667	4
NMSOLMFO	2.566667	2
QSMFO	3.4	3
CMFO	6.9	7
WEMFO	5.4	6

In order to further verify the difference between the optimization performance of HMCMMFO and other MFO variants, the experiment in this section uses the nonparametric Wilcoxon signed-rank test with a 5% significance level to compare the differences between these variant algorithms. When the data in the table are less than 0.05, it shows that HMCMMFO has obvious advantages, compared with other algorithms. As can be seen from Table S3 in the Supplementary Material, HMCMMFO is less than 0.05 in most functions, compared to other algorithms. Compared with CMFO and WEMFO, HMCMMFO has a better optimal solution in 28 functions, and the optimization effect of the remaining two functions is the same. Compared with CLSGMFO and LGCMFO, HMCMMFO obtains optimal values in 21 functions that are closer to the theoretically optimal solutions. Compared with the powerful NMSOLMFO, HMCMMFO still outperforms by a slight advantage. Overall, the improved algorithm proposed in this paper has a good optimization ability in these MFO-variant algorithms, which reflects that the optimization strategy adopted in this paper is both effective and strong in improving MFO performance.

In order to visualize the graphs of the optimization effect of the different algorithms in this experiment, as shown in Figure 4 below, the optimization-convergence plots of algorithms in nine functions are selected for display. In F1, although the optimal solution found by HMCMMFO in the early stage of algorithm evaluation is not as good as other algorithms, it continues to converge downward after 1.5 × 10⁵ evaluations, and the optimal solution found in the latter stage of evaluation is close to that of NMSOLMFO. In F9, the optimal solution found by HMCMMFO in the early stage of evaluation is better than that found by other algorithms at the end of the evaluation. Through the convergence plots of these nine functions, it can be found that there is a common feature, that is, before the 1.5 × 10⁵ evaluations of HMCMMFO, its optimization-convergence curve always shows a downward search trend, while the curves of other MFO variants converge early in the evaluation, the curve of HMCMMFO shows a rapid and continuous downward trend. This is because hybrid-mutation strategy is adopted in the early stage of evaluation, which enhances the algorithm’s ability to jump out of the local optimum and the algorithm’s global-exploration ability. In general, although HMCMMFO is not as fast as other algorithms in convergence speed, it performs better in optimization accuracy.

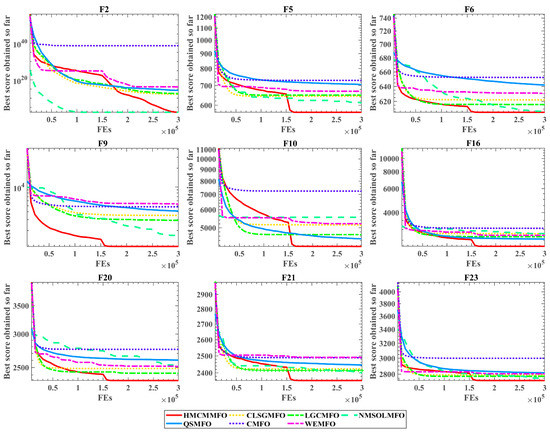
Figure 4. Convergence plots of the MFO variants.

4.4. Comparison with Original Algorithms

To strengthen the reliability of the optimization performance of HMCMMFO in this paper, the experiment in this section selected the popular and highly recognized meta-heuristic algorithms for comparison. These algorithms are sine cosine algorithm (SCA) [69], firefly algorithm (FA) [70], whale optimization algorithm (WOA) [71], grasshopper optimization algorithm (GOA) [72], and grey wolf optimizer (GWO) [73]. The parameter settings in these algorithms are shown in Table S4 in the Supplementary Material.

Table 7 below shows the optimization results of different novel algorithms in 30 test functions. Among the six algorithms, the average value of the optimal solution found by the HMCMMFO algorithm is closer to the theoretical optimal values of functions than other algorithms. As shown in the data in F2, the average optimal solutions obtained by the other five algorithms are not as good as that of HMCMMFO, and the numerical gap between them is large. By comparing the standard deviations, it can be seen that the optimization ability of HMCMMFO in most functions is more stable. From the final ranking, it can be seen clearly that HMCMMFO is in first place, and there is a significant gap between it and the second-ranked GOA in terms of average-ranking value, demonstrating that HMCMMFO has a significant advantage.

Table 7. Comparison of original algorithms.

	F1		F2		F3
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	9.80294 × 103	8.67716 × 103	2.10105 × 102	1.95548 × 101	3.00025 × 102	8.14402 × 10−2
SCA	1.22222 × 1010	1.96238 × 109	2.90172 × 1034	8.10053 × 1034	3.77999 × 104	5.92640 × 103
FA	1.44254 × 1010	1.24469 × 109	1.05613 × 1034	2.35540 × 1034	6.17194 × 104	6.95564 × 103
WOA	2.62081 × 106	1.45296 × 106	1.32144 × 1024	5.24072 × 1024	1.55853 × 105	5.63397 × 104
GOA	8.70605 × 107	3.38904 × 108	3.39750 × 1029	1.86088 × 1030	1.87791 × 103	3.41613 × 103
GWO	2.08506 × 109	1.37458 × 109	9.52398 × 1030	3.68834 × 1031	3.11186 × 104	1.09033 × 104
	F4		F5		F6
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.82113 × 102	1.68093 × 101	5.64407 × 102	1.85969 × 101	6.04935 × 102	1.81119 × 100
SCA	1.41644 × 103	2.88610 × 102	7.76337 × 102	1.86038 × 101	6.50345 × 102	5.13636 × 100
FA	1.36794 × 103	1.30754 × 102	7.60093 × 102	1.23883 × 101	6.44207 × 102	2.46820 × 100
WOA	5.37710 × 102	4.27357 × 101	7.89919 × 102	6.08936 × 101	6.68318 × 102	9.55672 × 100
GOA	5.02471 × 102	1.75301 × 101	6.22152 × 102	3.71558 × 101	6.26699 × 102	1.38950 × 101
GWO	5.99420 × 102	7.69352 × 101	5.98055 × 102	2.97506 × 101	6.06722 × 102	3.37262 × 100
	F7		F8		F9
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	8.17904 × 102	3.04063 × 101	8.64352 × 102	1.18965 × 101	1.14232 × 103	1.50046 × 102
SCA	1.13362 × 103	4.30939 × 101	1.05252 × 103	1.67232 × 101	5.72874 × 103	1.10108 × 103
FA	1.37609 × 103	3.87283 × 101	1.05363 × 103	1.06885 × 101	5.41486 × 103	5.35328 × 102
WOA	1.23989 × 103	8.26385 × 101	1.01339 × 103	5.49513 × 101	8.51073 × 103	2.93031 × 103
GOA	8.31785 × 102	2.47063 × 101	9.00602 × 102	2.54215 × 101	3.62090 × 103	2.04697 × 103
GWO	8.55401 × 102	3.13429 × 101	8.91975 × 102	1.81598 × 101	1.75641 × 103	4.84758 × 102
	F10		F11		F12
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	3.94563 × 103	7.83295 × 102	1.20235 × 103	4.27168 × 101	2.53419 × 105	1.95894 × 105
SCA	8.16479 × 103	2.19303 × 102	2.14661 × 103	3.21220 × 102	1.08585 × 109	2.83877 × 108
FA	8.01204 × 103	1.91427 × 102	3.59287 × 103	4.69048 × 102	1.57000 × 109	2.87851 × 108
WOA	6.07641 × 103	7.56256 × 102	1.57520 × 103	4.56758 × 102	5.38455 × 107	3.61079 × 107
GOA	4.77105 × 103	6.68543 × 102	1.31983 × 103	6.38855 × 101	7.19275 × 106	6.51294 × 106
GWO	4.40239 × 103	1.17408 × 103	2.06448 × 103	1.19279 × 103	7.96839 × 107	1.03465 × 108
	F13		F14		F15
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.97951 × 104	2.48147 × 104	2.81214 × 104	1.54518 × 104	1.41600 × 104	1.49864 × 104
SCA	4.08758 × 108	1.80993 × 108	1.46486 × 105	7.10065 × 104	1.50961 × 107	1.21193 × 107
FA	6.37347 × 108	1.47746 × 108	1.94565 × 105	9.03669 × 104	5.93363 × 107	2.68132 × 107
WOA	1.35499 × 105	8.18057 × 104	5.99596 × 105	6.14266 × 105	7.63819 × 104	5.26598 × 104
GOA	2.56136 × 106	1.30964 × 107	1.24840 × 104	1.18689 × 104	9.77789 × 104	5.72643 × 104
GWO	1.18806 × 107	3.62122 × 107	3.45932 × 105	8.19506 × 105	3.07587 × 105	7.36900 × 105
	F16		F17		F18
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.23270 × 103	2.82027 × 102	1.94649 × 103	1.57061 × 102	2.50879 × 105	2.27659 × 105
SCA	3.58651 × 103	2.01890 × 102	2.37142 × 103	1.61380 × 102	3.18469 × 106	1.74397 × 106
FA	3.41910 × 103	1.68782 × 102	2.52523 × 103	1.33623 × 102	4.34332 × 106	1.31134 × 106
WOA	3.40525 × 103	4.39797 × 102	2.56204 × 103	2.55239 × 102	2.97948 × 106	2.78891 × 106
GOA	2.66037 × 103	2.87847 × 102	2.11946 × 103	2.20818 × 102	3.59963 × 105	3.63171 × 105
GWO	2.37071 × 103	2.81933 × 102	2.00664 × 103	1.73227 × 102	7.57256 × 105	7.68810 × 105
	F19		F20		F21
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.60781 × 104	2.40778 × 104	2.27488 × 103	1.29918 × 102	2.35987 × 103	1.49386 × 101
SCA	2.34815 × 107	1.36479 × 107	2.62866 × 103	1.26935 × 102	2.54552 × 103	1.26107 × 101
FA	9.81301 × 107	4.53475 × 107	2.58205 × 103	7.80533 × 101	2.53884 × 103	1.00598 × 101
WOA	1.93056 × 106	1.33706 × 106	2.70029 × 103	2.06830 × 102	2.59499 × 103	7.74413 × 101
GOA	8.66939 × 105	6.48577 × 105	2.43412 × 103	1.22912 × 102	2.41908 × 103	3.62377 × 101
GWO	7.11832 × 105	8.45637 × 105	2.38103 × 103	1.86150 × 102	2.38440 × 103	1.59318 × 101
	F22		F23		F24
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.59104 × 103	1.52829 × 103	2.71925 × 103	1.74873 × 101	2.89330 × 103	1.66167 × 101
SCA	7.91014 × 103	2.44538 × 103	2.99551 × 103	3.07982 × 101	3.15983 × 103	2.47710 × 101
FA	3.84440 × 103	1.28648 × 102	2.90730 × 103	1.25120 × 101	3.06393 × 103	1.16914 × 101
WOA	6.81259 × 103	1.78682 × 103	3.02993 × 103	9.67257 × 101	3.16602 × 103	8.61215 × 101
GOA	5.84939 × 103	1.16893 × 103	2.77218 × 103	3.80386 × 101	2.93515 × 103	3.58702 × 101
GWO	4.33638 × 103	1.33978 × 103	2.76138 × 103	4.34565 × 101	2.91973 × 103	5.06338 × 101
	F25		F26		F27
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.88931 × 103	9.95669 × 100	4.32738 × 103	3.29400 × 102	3.21494 × 103	8.49659 × 100
SCA	3.23535 × 103	1.05916 × 102	6.88857 × 103	3.57567 × 102	3.40674 × 103	4.20371 × 101
FA	3.59245 × 103	1.00415 × 102	6.46760 × 103	1.78319 × 102	3.33506 × 103	1.54050 × 101
WOA	2.94543 × 103	3.03126 × 101	7.69008 × 103	1.15885 × 103	3.34929 × 103	6.62554 × 101
GOA	2.90327 × 103	2.01055 × 101	4.47919 × 103	7.19257 × 102	3.23620 × 103	2.51853 × 101
GWO	2.97106 × 103	3.00129 × 101	4.70175 × 103	3.96504 × 102	3.25009 × 103	2.29212 × 101
	F28		F29		F30
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	3.16137 × 103	6.37650 × 101	3.57164 × 103	1.44757 × 102	1.25015 × 104	4.92798 × 103
SCA	3.84001 × 103	1.11131 × 102	4.63200 × 103	2.43532 × 102	7.44453 × 107	2.66254 × 107
FA	3.88691 × 103	9.42419 × 101	4.71936 × 103	1.65719 × 102	8.84685 × 107	3.18824 × 107
WOA	3.30819 × 103	3.33857 × 101	4.81128 × 103	4.28659 × 102	1.28954 × 107	8.86520 × 106
GOA	3.26029 × 103	4.43678 × 101	3.84191 × 103	1.90477 × 102	3.84859 × 106	3.93893 × 106
GWO	3.41446 × 103	7.39254 × 101	3.74663 × 103	1.67931 × 102	6.83847 × 106	9.49355 × 106
	ARV	Rank
HMCMMFO	1.1	1
SCA	5	6
FA	4.933333	5
WOA	4.466667	4
GOA	2.6	2
GWO	2.9	3

Table S5 in the Supplementary Material shows the comparison results of using the Wilcoxon signed-rank test to evaluate HMCMMFO with other original metaheuristic algorithms. As can be seen from the data in Table S5, most of the results are far less than 0.05. It can be concluded that the optimization ability of HMCMMFO in most functions is significantly different from that of other algorithms. By comparing “+/−/=”, it can be found that, compared with SCA and WOA, HMCMMFO has a better optimization effect in the 30 functions than the two algorithms. Compared to FA, HMCMMFO is inferior to it in only one function. From the comparison results of GOA and GWO, only four functions of their optimization results are not significantly different, compared with HMCMMFO. GOA is inferior to HMCMMFO in 25 functions and GWO is inferior to HMCMMFO in 26 functions. In general, it can be seen that the improved algorithm proposed in this paper has a strong optimization ability and other advantages, compared with novel algorithms.

The convergence effect of HMCMMFO and other original algorithms is shown in Figure 5 below. In F2, these original algorithms find the optimal value in the early stage of evaluation and show convergence. However, HMCMMFO jumps out of the local optimum space and continues to search downward in the later stage of evaluation, and its solution is much better than those obtained by other algorithms. In F12, although GOA, GWO, and HMCMMFO show a downward trend throughout the evaluation process, the decline of GWO is significantly less than that of HMCMMFO and GOA, and its decline rate is not as fast as theirs. At the end of the evaluation, the curve of HMCMMFO still remains some distance from the curve of GOA. It can be seen that HMCMMFO has advantages in global-exploration ability. In F19 and F30, the optimal solution searched by HMCMMFO in the middle of the evaluation is already stronger than those found by the other algorithms after the whole evaluation. At the same time, HMCMMFO has a fast convergence speed and can find the optimal value quickly and accurately in the later stage of evaluation. In other functions, the optimal solution obtained by HMCMMFO is closer to the theoretical optimal solution in the test functions than those obtained by other algorithms, and the strong optimization performance of HMCMMFO can be seen from the optimization effect of the algorithm in Figure 5 below.

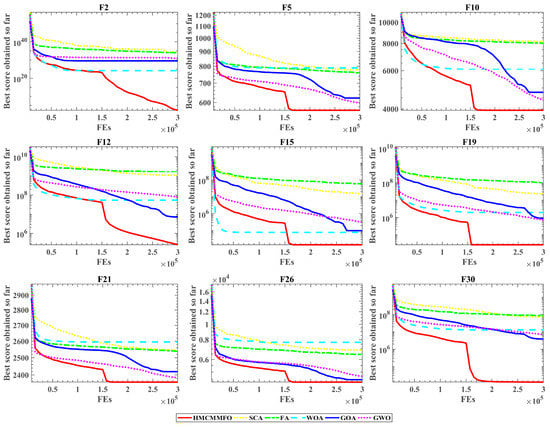
Figure 5. Convergence effect of original algorithms.

4.5. Comparison with Advanced Algorithms

This section compares HMCMMFO with typically advanced algorithms to further verify its effectiveness and superiority. The advanced algorithms are: FSTPSO [74], ALCPSO [75], CDLOBA [76], BSSFOA [77], SCADE [78], CGPSO [79], and OBLGWO [80]. Table S6 in the Supplementary Material shows the parameter settings of these advanced algorithms.

Table 8 below shows the average and standard-deviation results of the optimal solutions obtained by these eight advanced algorithms in the IEEE CEC2017 functions. The average ranking value of HMCMMFO is 1.466667, and, compared with the second-ranked ALCPSO algorithm, the average ranking value of the two is significantly different. PSO is a classical, swarm-intelligence algorithm with powerful optimization ability, and its variants FSTPSO, ACLPSO, and CGPSO are enhanced algorithms based on PSO. However, by comparing the results of HMCMMFO and these three PSO variants, HMCMMFO shows better averages and smaller standard deviations in most functions. From the data in the table as a whole, the optimization ability of HMCMMFO is better than these advanced algorithms.

Table 8. Comparison results of advanced algorithms.

	F1		F2		F3
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	9.04208 × 103	8.03368 × 103	2.05737 × 102	1.27916 × 101	3.00005 × 102	9.47002 × 10−3
FSTPSO	2.24935 × 1010	7.20644 × 109	3.38172 × 1037	1.01762 × 1038	8.76469 × 104	2.03541 × 104
ALCPSO	5.69193 × 103	6.76754 × 103	2.41025 × 1017	8.32693 × 1017	2.67799 × 104	3.63044 × 103
CDLOBA	5.01333 × 103	5.42594 × 103	1.13044 × 1012	3.71628 × 1012	1.26087 × 103	1.59138 × 103
BSSFOA	6.94886 × 1010	4.63503 × 109	4.96079 × 1059	1.90717 × 1060	1.05247 × 107	2.29879 × 107
SCADE	1.91644 × 1010	2.82685 × 109	2.85732 × 1037	1.02110 × 1038	6.18223 × 104	7.12746 × 103
CGPSO	1.41430 × 108	1.56060 × 107	1.02685 × 1014	7.37472 × 1013	7.74256 × 102	7.70923 × 101
OBLGWO	1.41222 × 107	6.42248 × 106	5.38329 × 1016	9.80940 × 1016	1.79685 × 104	5.24282 × 103
	F4		F5		F6
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.78053 × 102	1.94693 × 101	5.65518 × 102	1.09386 × 101	6.05534 × 102	2.09891 × 100
FSTPSO	4.25834 × 103	1.34899 × 103	8.09741 × 102	4.36397 × 101	6.67701 × 102	8.86637 × 100
ALCPSO	5.03845 × 102	3.76435 × 101	6.08908 × 102	2.48248 × 101	6.04422 × 102	4.76403 × 100
CDLOBA	4.82331 × 102	2.76442 × 101	8.82001 × 102	6.77780 × 101	6.71516 × 102	9.42381 × 100
BSSFOA	3.17512 × 104	2.92592 × 103	1.06410 × 103	3.68237 × 101	7.34761 × 102	5.65161 × 100
SCADE	3.45962 × 103	7.10815 × 102	8.27990 × 102	2.15557 × 101	6.60604 × 102	5.97788 × 100
CGPSO	4.84497 × 102	2.08597 × 101	7.84836 × 102	3.48166 × 101	6.61193 × 102	1.45069 × 101
OBLGWO	5.28375 × 102	3.03182 × 101	6.58444 × 102	3.92032 × 101	6.19614 × 102	1.60747 × 101
	F7		F8		F9
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	8.11945 × 102	1.75857 × 101	8.61893 × 102	1.11592 × 101	1.08570 × 103	7.80439 × 101
FSTPSO	1.26983 × 103	9.39213 × 101	1.05100 × 103	3.77858 × 101	7.37842 × 103	2.20220 × 103
ALCPSO	8.39120 × 102	2.44524 × 101	9.06292 × 102	2.66775 × 101	1.78237 × 103	8.05156 × 102
CDLOBA	2.59370 × 103	3.11305 × 102	1.11367 × 103	4.82036 × 101	9.94803 × 103	2.02410 × 103
BSSFOA	1.59163 × 103	2.05661 × 101	1.28217 × 103	2.30679 × 101	2.10390 × 104	2.77333 × 103
SCADE	1.18133 × 103	2.94610 × 101	1.08557 × 103	2.18091 × 101	8.29165 × 103	1.03456 × 103
CGPSO	9.30265 × 102	1.31675 × 101	1.01738 × 103	3.05058 × 101	6.40560 × 103	2.04473 × 103
OBLGWO	9.29796 × 102	6.46318 × 101	9.51157 × 102	2.84480 × 101	2.48274 × 103	1.50724 × 103
	F10		F11		F12
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	3.99206 × 103	6.42707 × 102	1.19044 × 103	3.51538 × 101	2.59550 × 105	1.73810 × 105
FSTPSO	7.10032 × 103	5.48307 × 102	3.67947 × 103	1.39061 × 103	2.08122 × 109	1.01824 × 109
ALCPSO	4.38956 × 103	4.71963 × 102	1.23543 × 103	5.47290 × 101	3.78287 × 105	4.51017 × 105
CDLOBA	5.61945 × 103	7.47000 × 102	1.33122 × 103	7.16582 × 101	3.35594 × 105	2.71621 × 105
BSSFOA	1.06223 × 104	3.52578 × 102	1.52698 × 108	1.94191 × 108	2.64859 × 1010	2.12389 × 109
SCADE	8.15302 × 103	2.60426 × 102	3.32858 × 103	4.38924 × 102	1.92116 × 109	5.52975 × 108
CGPSO	6.28405 × 103	5.85956 × 102	1.27621 × 103	3.59016 × 101	3.01121 × 107	1.49000 × 107
OBLGWO	5.31016 × 103	7.39178 × 102	1.30783 × 103	5.14082 × 101	1.50043 × 107	1.45532 × 107
	F13		F14		F15
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	3.05695 × 108	4.06431 × 108	2.78181 × 104	2.06399 × 104	1.26334 × 104	1.47346 × 104
FSTPSO	2.26316 × 104	2.09263 × 104	1.53374 × 105	3.13636 × 105	4.29129 × 104	2.96810 × 104
ALCPSO	1.91228 × 105	1.33831 × 105	2.66550 × 104	4.10110 × 104	1.19935 × 104	9.61744 × 103
CDLOBA	3.93413 × 1010	5.20883 × 109	4.28871 × 103	3.32841 × 103	9.85047 × 104	6.35953 × 104
BSSFOA	6.15265 × 108	3.05402 × 108	3.33185 × 108	3.49954 × 108	1.35846 × 109	1.43455 × 109
SCADE	5.43284 × 106	1.53440 × 106	3.36376 × 105	2.01937 × 105	1.10667 × 107	1.10265 × 107
CGPSO	1.99876 × 105	1.21607 × 105	1.38928 × 104	8.14814 × 103	5.21935 × 105	2.57225 × 105
OBLGWO	3.05695 × 108	4.06431 × 108	5.74416 × 104	4.46473 × 104	8.07591 × 104	5.75320 × 104
	F16		F17		F18
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.18654 × 103	2.53645 × 102	1.95862 × 103	1.53751 × 102	2.67430 × 105	1.22752 × 105
FSTPSO	3.77056 × 103	4.68395 × 102	2.61466 × 103	2.81489 × 102	1.99070 × 106	2.62927 × 106
ALCPSO	2.56164 × 103	2.65815 × 102	2.13464 × 103	1.83086 × 102	2.31803 × 105	3.48936 × 105
CDLOBA	3.37554 × 103	4.55811 × 102	2.84930 × 103	3.06689 × 102	1.19113 × 105	6.15026 × 104
BSSFOA	2.06437 × 104	4.54964 × 103	1.18493 × 105	4.29716 × 104	2.42077 × 108	1.41621 × 108
SCADE	3.79560 × 103	2.85942 × 102	2.53314 × 103	1.22389 × 102	5.10740 × 106	2.91497 × 106
CGPSO	2.94824 × 103	2.23716 × 102	2.43695 × 103	1.46966 × 102	2.27304 × 105	1.45495 × 105
OBLGWO	2.78036 × 103	3.85906 × 102	2.15965 × 103	1.88167 × 102	8.77316 × 105	7.94452 × 105
	F19		F20		F21
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.28653 × 104	2.37575 × 104	2.27049 × 103	1.47954 × 102	2.35533 × 103	1.27145 × 101
FSTPSO	5.97313 × 106	9.82037 × 106	2.81911 × 103	1.88576 × 102	2.60030 × 103	4.53346 × 101
ALCPSO	1.43683 × 104	1.26703 × 104	2.34131 × 103	1.63222 × 102	2.41626 × 103	2.92292 × 101
CDLOBA	6.76365 × 104	2.87225 × 104	2.88893 × 103	2.63286 × 102	2.61586 × 103	6.69569 × 101
BSSFOA	4.66464 × 109	1.39110 × 109	3.91874 × 103	6.28712 × 102	3.13228 × 103	6.09591 × 101
SCADE	2.45048 × 107	1.75808 × 107	2.74629 × 103	9.43193 × 101	2.57874 × 103	1.88650 × 101
CGPSO	1.64224 × 106	7.94663 × 105	2.68852 × 103	2.12709 × 102	2.53880 × 103	4.10711 × 101
OBLGWO	4.23299 × 105	3.46594 × 105	2.49005 × 103	1.37337 × 102	2.45559 × 103	3.49696 × 101
	F22		F23		F24
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	4.60599 × 103	1.39264 × 103	2.71533 × 103	1.52824 × 101	2.89092 × 103	1.72014 × 101
FSTPSO	8.17465 × 103	1.49814 × 103	3.35230 × 103	2.13670 × 102	3.42508 × 103	1.35019 × 102
ALCPSO	5.26114 × 103	1.68105 × 103	2.80839 × 103	6.12510 × 101	2.98866 × 103	4.49861 × 101
CDLOBA	6.48827 × 103	1.71007 × 103	3.19776 × 103	1.34188 × 102	3.30902 × 103	1.00817 × 102
BSSFOA	1.25049 × 104	4.15229 × 102	7.32713 × 103	7.61185 × 102	4.96946 × 103	8.54779 × 101
SCADE	4.57113 × 103	3.84997 × 102	3.01439 × 103	3.79839 × 101	3.17776 × 103	2.86583 × 101
CGPSO	4.61575 × 103	2.84604 × 103	3.09483 × 103	1.39474 × 102	3.24776 × 103	1.40199 × 102
OBLGWO	2.93436 × 103	1.60266 × 103	2.81928 × 103	4.27943 × 101	2.96521 × 103	3.26361 × 101
	F25		F26		F27
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	2.88662 × 103	2.31850 × 100	4.29885 × 103	1.66434 × 102	3.21537 × 103	1.10466 × 101
FSTPSO	3.80903 × 103	4.22414 × 102	8.64513 × 103	1.04959 × 103	3.75013 × 103	3.33357 × 102
ALCPSO	2.90160 × 103	2.29872 × 101	5.04676 × 103	5.28395 × 102	3.26136 × 103	4.44969 × 101
CDLOBA	2.92016 × 103	3.09550 × 101	9.91927 × 103	1.56755 × 103	3.51981 × 103	2.02790 × 102
BSSFOA	8.18323 × 103	8.20049 × 102	1.40078 × 104	1.47440 × 103	9.67126 × 103	6.85230 × 102
SCADE	3.45156 × 103	1.17093 × 102	7.41895 × 103	3.00524 × 102	3.43460 × 103	4.36814 × 101
CGPSO	2.91209 × 103	2.30965 × 101	4.66870 × 103	1.96387 × 103	3.24002 × 103	2.21509 × 102
OBLGWO	2.91070 × 103	1.58354 × 101	5.36174 × 103	7.06736 × 102	3.24087 × 103	1.75657 × 101
	F28		F29		F30
	AVG	STD	AVG	STD	AVG	STD
HMCMMFO	3.17923 × 103	7.13571 × 101	3.59993 × 103	1.36984 × 102	1.35419 × 104	5.06496 × 103
FSTPSO	4.68773 × 103	4.77235 × 102	5.40032 × 103	5.34498 × 102	2.44164 × 107	1.76436 × 107
ALCPSO	3.25431 × 103	4.58890 × 101	3.80554 × 103	2.11994 × 102	2.31032 × 104	3.00373 × 104
CDLOBA	3.19569 × 103	4.92004 × 101	5.02853 × 103	4.92660 × 102	2.01968 × 105	1.47051 × 105
BSSFOA	9.39323 × 103	6.87934 × 102	2.48753 × 104	1.84269 × 104	7.73967 × 109	5.30175 × 108
SCADE	4.30153 × 103	3.07323 × 102	5.09990 × 103	2.35088 × 102	1.03853 × 108	3.88292 × 107
CGPSO	3.24643 × 103	2.91921 × 101	4.38928 × 103	3.16194 × 102	4.79992 × 106	1.73866 × 106
OBLGWO	3.28167 × 103	4.17184 × 101	3.96194 × 103	2.37288 × 102	2.39098 × 106	1.61698 × 106
	ARV	Rank
HMCMMFO	1.466667	1
FSTPSO	6.233333	7
ALCPSO	2.533333	2
CDLOBA	4.666667	5
BSSFOA	7.966667	8
SCADE	5.733333	6
CGPSO	3.9	4
OBLGWO	3.5	3

To clearly understand the difference in optimization performance between advanced algorithms and HMCMMFO, the nonparametric Wilcoxon signed-rank test method at a 5% significance level is used for this experiment. As shown in Table S7 in the Supplementary Material, the results of most of the functions are less than 0.05, which shows that HMCMMFO has obvious advantages, compared with these algorithms. Compared with typical PSO variant algorithms, HMCMMFO outperforms FSTPSO by 30 functions and outperforms CGPSO by 26 functions. Compared with the powerful ALCPSO, HMCMMFO outperforms ALCPSO in 20 functions and has the same search results in 10 functions.

Figure 6 below shows the convergence effects of different advanced algorithms in nine test functions. In F2 and F12, HMCMMFO shows a downward exploration trend throughout the evaluation, while the other algorithms reach convergence early in the evaluation. In F5, F9, F16, F20, and F21, the accuracy of the optimal solution found by HMCMMFO in the early stage of evaluation is already better than the accuracy of the solution obtained at the end of evaluation by the other algorithms, except for ALCPSO. Although HMCMMFO is inferior to ALCPSO in the early stage, after continuous evaluation, the accuracy of the solution obtained by HMCMMFO exceeds that of ALCPSO in the middle of the evaluation. Through these convergence-effect plots, it can be seen that hybrid-mutation strategy effectively reduces the risk of the algorithm falling into deceptive optimal, and chemotaxis-motion mechanism improves the search efficiency of the MFO algorithm. With the support of these two optimization strategies, HMCMMFO has good advantages in optimization performance, compared with other advanced algorithms.

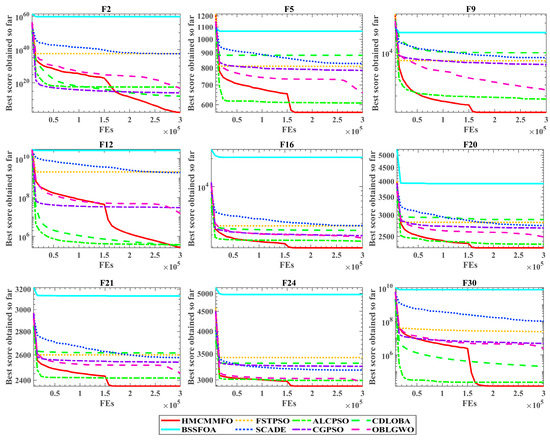
Figure 6. Convergence effect of advanced algorithms.

5. Engineering Design Problems

In this section, five classical engineering design problems are used to study the real-life application value of HMCMMFO’s optimization performance: tension-compression string, three-bar truss, pressure vessel, I-beam, and speed-reducer-design problems.

5.1. Tension-Compression String Problem

The engineering model is a typical engineering-constraint problem, which minimizes the weight of the spring under the constraints of model parameters. The parameters involved are wire diameter (d), average coil diameter (D), and the finite number of coils (N). Specific model details are shown below.

$$\mathrm{Consider}: \overrightarrow{x}=\left[x_1 x_2 x_3 \right]=\left[d D N\right]$$

$$\mathrm{Minimize}: f\left(\overrightarrow{x}\right)=x_1^2{x}_2\left(x_3+2\right)$$

$$\begin{gathered} \mathrm{Subject} \mathrm{to}: g_1\left(\overrightarrow{x}\right)=1-\frac{4x_2^3{x}_3}{\mathrm{71,785}{x}_1^4}\le 0, \\ {g}_2\left(\overrightarrow{x}\right)=\frac{4x_2^2-x_1{x}_2}{\mathrm{12,566}\left(x_2{x}_1^3-x_1^4\right)}+\frac{1}{5108x_1^2}\le 0, \\ {g}_3\left(\overrightarrow{x}\right)=1-\frac{140.45x_1}{x_2^2{x}_3}\le 0, \\ {g}_4\left(\overrightarrow{x}\right)=\frac{x_1+x_2}{1.5}-1\le 0. \end{gathered}$$

$$\mathrm{Variable} \mathrm{range}: 0.05\le x_1\le 2, 0.25\le x_2\le 1.3, 2\le x_3\le 150$$

Table 9 below shows the parameters and minimum weight obtained by the 11 methods for solving this problem. Through comparison, it is found that the improved algorithm proposed in this paper obtains the smallest spring weight of 0.012665, compared to the traditional mathematical methods and well-known metaheuristic algorithms. Compared with WEMFO, which is also an improved MFO algorithm, the minimum cost of HMCMMFO is much better than WEMFO. It can be seen that HMCMMFO can solve this problem effectively and with significant results.

Table 9. Comparison results of the tension-compression string problem.

Algorithm	Optimal Values for Variables			Optimum Cost
	d	D	N
HMCMMFO	0.051796	0.359300	11.13916	0.012665
EWOA [81]	0.051961	0.363306	10.91296	0.012667
IDARSOA [82]	0.051960	0.363240	10.91947	0.012670
Improved HS [83]	0.051154	0.349871	12.07643	0.012671
RO [84]	0.051370	0.349096	11.76279	0.012679
ES [85]	0.051989	0.363965	10.89052	0.012681
GSA [86]	0.050276	0.323680	13.52541	0.012702
Mathematical optimization [87]	0.053396	0.399180	9.185400	0.012730
SSA [88]	0.051207	0.345215	12.00403	0.126763
WEMFO [68]	0.050012	0.31674	14.197	0.012832

5.2. Tension-Compression String Problem

This engineering model contains three constraint functions and two parameters. The effective parameters are applied to the constraints to find the optimal cost. The specific details of this model are described below.

$$\mathrm{Objective} \mathrm{function}: f\left(x\right)=\left(2\sqrt{2}{x}_1+x_2\right)\times l$$

$$\begin{gathered} \mathrm{Subject} \mathrm{to}: g_1\left(x\right)=\frac{\sqrt{2}{x}_1+x_2}{\sqrt{2}{x}_1^2+2x_1{x}_2}P-\sigma \le 0, \\ {g}_2\left(x\right)=\frac{x_2}{\sqrt{2}{x}_1^2+2x_1{x}_2}P-\sigma \le 0, \\ {g}_3\left(x\right)=\frac{1}{\sqrt{2}{x}_2+x_1}P-\sigma \le 0. \end{gathered}$$

$$\mathrm{Variable} \mathrm{range}: 0\le x_i\le 1 \left( i=1, 2\right), l=100\mathrm{cm},P=2 {\mathrm{kN}/\mathrm{cm}}^2,\sigma =2 {\mathrm{kN}/\mathrm{cm}}^2$$

As shown in Table 10 below, the cost of HMCMMFO for this problem is 263.895843, with x₁ = 0.788673 and x₂ = 0.408253. Compared with other mature algorithms, HMCMMFO ranks first with the smallest optimum cost. It shows that the method proposed in this paper has advantages in solving the optimization problem, which can effectively reduce engineering consumption and help to solve practical problems in the real world.

Table 10. Comparison results of the three-bar design problem.

Algorithm	Optimal Values for Variables		Optimum Cost
	x1	x2
HMCMMFO	0.788673	0.408253	263.895843
AGOA [89]	0.788584	0.4085050	263.895849
MBA [90]	0.788565	0.4085597	263.895852
CLSCA [91]	0.78806	0.40998	263.8964
CS [92]	0.78867	0.40902	263.9716
GWO [73]	0.79477	0.39192	263.987
FOA [93]	0.768316	0.4691685	264.229309
CBA [94]	0.00871	0.98083	265.5966

5.3. Pressure Vessel Design Problem

The cylindrical-pressure-vessel-design problem is to reduce the manufacturing cost to satisfy the parameters and constraint functions. The model involves four parameters and four constraint functions, and its mathematical model is shown as follows.

$$\mathrm{Consider}: \overrightarrow{x}=\left[x_1 x_2 x_3 x_{4 }\right]=\mathrm{Consider} \left[T_s T_h R L\right]$$

$$\mathrm{Objective}:f{\left(\overrightarrow{x}\right)}_{min}=0.6224x_1{x}_3{x}_4+1.7781x_3{x}_1^2+3.1661x_4{x}_1^2+19.84x_3{x}_1^2$$

$$\begin{gathered} \mathrm{Subject} \mathrm{to}: g_1\left(\overrightarrow{x}\right)=-x_1+0.0193x_3\le 0, \\ {g}_2\left(\overrightarrow{x}\right)=-x_3+0.00954x_3\le 0, \\ {g}_3\left(\overrightarrow{x}\right)=-\pi x_4{x}_3^2-\frac{4}{3}\pi x_3^3+\mathrm{1,296,000}\le 0, \\ {g}_4\left(\overrightarrow{x}\right)=x_4-240\le 0. \end{gathered}$$

$$\mathrm{Variable} \mathrm{ranges}: 0\le x_1\le 99, 0\le x_2\le 99, 10\le x_3\le 200, 10\le x_4\le 200.$$

From Table 11 below, it can be seen that HMCMMFO can reduce the manufacturing cost of pressure vessels, compared with G-QPSO and CDE algorithms, which have strong optimization performance and do not exceed 6060. For this problem, the cost of HMCMMFO is 6059.714, the cost of G-QPSO is 6059.721, and the cost of CDE is 6059.734. Comparison shows that HMCMMFO is superior to the latter two algorithms. Furthermore, compared with the cost obtained by other typical algorithms, HMCMMFO has outstanding advantages and shows more competitive performance.

Table 11. Comparison results of pressure-vessel-design problem.

Algorithm	Optimal Values for Variables				Optimum Cost
	${\mathit{T}}_{\mathit{s}}$	${\mathit{T}}_{\mathit{h}}$	R	L
HMCMMFO	0.8125	0.4375	42.09845	176.6366	6059.714
G-QPSO [95]	0.8125	0.4375	42.09840	176.6372	6059.721
CDE [96]	0.8125	0.4375	42.09840	176.6376	6059.734
IDARSOA [82]	0.812500	0.4375	42.09711	177.1901	6072.430
AGOA [89]	0.812500	0.437500	41.73619	181.1778	6104.325
SCADE [78]	1.465138	0.679596	65.0882	13.36838	6126.139
GWO [73]	2.176906	0.614469	63.9998	15.78465	6199.028
Improved HS [83]	1.12500	0.625000	58.29015	43.69268	7197.730
Branch-and-bound [97]	1.12500	0.625000	47.70000	117.7100	8129.104
GSA [86]	1.12500	0.625000	55.98866	84.45420	8538.836

5.4. I-Beam Design Problem

The fourth engineering example aims to obtain the minimum vertical deflection in the I-beam structure. The model contains four parameters: the structure’s length, two thicknesses, and height. The details of the model are shown below.

$$\mathrm{Consider}: \overrightarrow{x}=\left[x_1 x_2 x_3 x_4\right]=\left[b h t_w t_f\right]$$

$$\mathrm{Minimize}: f\left(\overrightarrow{x}\right)=\frac{5000}{\frac{x_3{\left(x_2-2x_4\right)}^3}{12}+\frac{{x_1{x}_4}^3}{6}+2x_1{x}_4{\left(\frac{x_2-x_4}{2}\right)}^2}$$

$$\begin{gathered} \mathrm{Subject} \mathrm{to}: g\left(\overrightarrow{x}\right)=2x_1{x}_4+x_3\left(x_2-2x_4\right)\le 0, \\ {g}_1\left(\overrightarrow{x}\right)=\frac{18x_2\times {10}^4}{x_3{\left(x_2-2x_4\right)}^3+2x_1{x}_4\left(4x_4+3x_2\left(x_2-2x_4\right)\right)}+\frac{15x_1\times {10}^3}{\left(x_2-2x_4\right)x_3{}^3+2x_{4}b{x}_1{}^3}-6\le 0 \end{gathered}$$

$$\mathrm{Variable} \mathrm{ranges}: 10\le x_1\le 50, 10\le x_2\le 80, 0.9\le x_3\le 5, 0.9\le x_4\le 5$$

The minimum vertical deflection obtained by different algorithms in this model is shown in Table 12 below, where the result obtained by HMCMMFO is 0.013074; HMCMMFO obtains the same optimal cost as IDARSOA and SOS, and all three obtain the same value on the $x_1$, $x_2,$ and $x_3$, with only a small difference in $x_4$. It can be seen that HMCMMFO can effectively solve this problem and achieve desired results.

Table 12. Comparison results of the I-beam design.

Algorithm	Optimal Values for Variables				Optimum Cost
	$\mathit{b}$	$\mathit{h}$	${\mathit{t}}_{\mathit{w}}$	${\mathit{t}}_{\mathit{f}}$
HMCMMFO	50.0000	80.0000	0.9000	2.321792	0.013074
IDARSOA [82]	50.0000	80.0000	0.9000	2.321769	0.013074
SOS [98]	50.0000	80.0000	0.9000	2.3218	0.013074
CS [92]	50.0000	80.0000	0.9000	2.3217	0.013075
AGOA [89]	43.12663	79.91247	0.932602	2.671865	0.013295
ARSM [99]	37.0500	80.0000	1.7100	2.3100	0.015700
IARSM [99]	48.4200	79.9900	0.9000	2.4000	0.131000

5.5. Speed Reducer Design Problem

The model involves seven parameters, which are represented by $x_1$–$x_7$, and their meanings are the width of the end face (b), the tooth module (m), the number of teeth in the pinion (z), the length of the first shaft between the bearings (l₁), the length of the second shaft between bearings (l₂), the diameter of the first shaft (d₁), and the second shaft (d₂). The following constraints are carried out within the effective range of satisfying these parameters, and finally, the weight of the reducer is minimized. The specific details in this model are shown below.

$$\mathrm{Consider} \overrightarrow{x}=\left[x_{1 } x_2 x_3 x_4 x_5 x_6 x_7 \right]=\left[b m p l_{1 }{l}_2 d_1 d_2\right]$$

$$\begin{gathered} \mathrm{Minimize} f\left(\overrightarrow{x}\right)=0.7854x_1{x}_2^2\left(3.3333x_3^2+14.9334x_3-43.0934\right) \\ -1.508x_1\left(x_6^2+x_7^2\right)+7.4777\left(x_6^2+x_7^2\right)+0.7854\left(x_4{x}_6^2+x_5{x}_7^2\right) \end{gathered}$$

$$\begin{gathered} \mathrm{Subject} \mathrm{to}: g_1\left(\overrightarrow{x}\right)=\frac{27}{x_1{x}_3{x}_2^2}-1\le 0, \\ {g}_2\left(\overrightarrow{x}\right)=\frac{397.5}{x_1{x}_2^2{x}_3^2}-1\le 0, \\ {g}_3\left(\overrightarrow{x}\right)=\frac{1.93x_4^3}{x_2{x}_6^4{x}_3}-1\le 0, \\ {g}_4\left(\overrightarrow{x}\right)=\frac{1.93x_5^3}{x_2{x}_7^4{x}_3}-1\le 0, \\ {g}_5\left(\overrightarrow{x}\right)=\frac{{\left[{\left(745\left(\frac{x_4}{x_2{x}_3}\right)\right)}^2+16.9\times {10}^6\right]}^{\frac{1}{2}}}{110x_6^3}-1\le 0, \\ {g}_6\left(\overrightarrow{x}\right)=\frac{{\left[{\left(745\left(\frac{x_5}{x_2{x}_3}\right)\right)}^2+157.5\times {10}^6\right]}^{\frac{1}{2}}}{85x_7^3}-1\le 0, \\ {g}_7\left(\overrightarrow{x}\right)=\frac{x_2{x}_3}{40}-1\le 0, \\ g_8\left(\overrightarrow{x}\right)=\frac{5x_2}{x_1}-1\le 0, \\ g_9\left(\overrightarrow{x}\right)=\frac{x_1}{12x_2}-1\le 0, \\ {g}_{10}\left(\overrightarrow{x}\right)=\frac{1.5x_6+1.9}{x_4}-1\le 0, \\ g_{11}\left(\overrightarrow{x}\right)=\frac{1.1x_7+1.9}{x_5}-1\le 0. \end{gathered}$$

$$\begin{gathered} \mathrm{Variable} \mathrm{ranges}: 2.6\le x_1\le 3.6, 0.7\le x_2\le 0.8, 17\le x_3\le 28,7.3\le x_4\le 28, \\ 7.3\le x_5\le 8.3, 2.9\le x_6\le 3.9, 5.0\le x_7\le 5.5 \end{gathered}$$

Table 13 below shows the target values obtained by eight algorithms, including HMCMMFO, when solving this problem. These algorithms include novel metaheuristics and advanced algorithms. According to the data in the table, the weight of the model obtained by HMCMMFO is 2994.4711, which is smaller than that obtained by other algorithms and satisfies the goal of the model. Compared with SCA and GSA, HMCMMFO has a larger difference in the weight of the reducer. It can be seen that HMCMMFO can achieve good results when solving this problem, and can satisfactorily meet the requirements of industrial problems.

Table 13. Comparison results of speed-reducer-design problem.

Algorithm	Optimal Values for Variables							Optimum Cost
	$\mathit{b}$	$\mathit{m}$	$\mathit{p}$	${\mathit{l}}_{1 }$	${\mathit{l}}_2$	${\mathit{d}}_1$	${\mathit{d}}_2$
HMCMMFO	3.5	0.7	17	7.3	7.71532	3.350215	5.286654	2994.4711
AGOA [89]	3.5	0.7	17	7.310097	7.737602	3.350234	5.287056	2995.3092
IDARSOA [82]	3.50608	0.7	17	7.3	7.71926	3.353154	5.288364	2998.7797
GWO [73]	3.50669	0.7	17	7.380933	7.815726	3.357847	5.286768	3001.2880
PSO [100]	3.50001	0.7	17	8.3	7.8	3.352412	5.286715	3005.7630
SCA [69]	3.50875	0.7	17	7.3	7.8	3.461020	5.289213	3030.5630
GSA [86]	3.6	0.7	17	8.3	7.8	3.369658	5.289224	3051.1200

To sum up, research on the above five engineering examples shows that the HMCMMFO proposed in this paper is an effective method for solving engineering-constraint problems and has an excellent performance in solving practical problems. When it is applied to other fields in the future, such as recommender system [101,102], power-flow optimization [103], location-based services [104,105], road-network planning [106], human-activity recognition [107], information-retrieval services [108,109], image denoising [110], and colorectal-polyp-region extraction [111], it has the potential to perform well.

6. Conclusions and Future Work

The HMCMMFO proposed in this paper substantially improves optimization performance over the traditional MFO. By introducing a hybrid-mutation strategy, the diversity of the algorithm is increased, and its ability to jump out of the local optimal space is enhanced. A chemotaxis-motion strategy is adopted to guide individuals to move toward the optimal solution and improve the optimization accuracy of the algorithm. In the test functions of CEC2017, the most suitable parameter settings in the optimization strategy are determined through parameter-sensitivity analysis. MFO variants using different mechanisms are compared to prove the effectiveness of the improved strategy. Comparing HMCMMFO with MFO variants, original metaheuristics, and advanced algorithms proves that HMCMMFO has more superior optimization performance. Moreover, five typical engineering design examples are verified in this paper to discuss the application value of HMCMMFO in solving practical problems in the real world. The results show that HMCMMFO has significant advantages in solving constraint problems.

Due to the time-consuming nature of HMCMMFO in dealing with large-scale and complex problems, the next piece of research is planned to combine HMCMMFO with distributed platforms to deal with such problems in a parallel way. In addition, balancing the global-exploration and local-exploitation capabilities of HMCMMFO is crucial to improving the overall optimization performance of the algorithm. Therefore, the next piece of work will also investigate the flame-number formula of HMCMMFO and adopt a dynamic-adaptive mechanism based on the number of evaluations to balance the algorithm’s exploration and exploitation. At the same time, relying on the powerful optimization ability of HMCMMFO, its applications in image segmentation [21] and dynamic-landscape processing are also worthy research directions. In addition, future research can also be extended to a multi-objective optimization algorithm to solve more complex issues in real industrial environments.