Assessment of an Implicit Discontinuous Galerkin Solver for Incompressible Flow Problems with Variable Density
Abstract
:1. Introduction
2. Variable Density Incompressible Flow Model
3. Numerical Framework
3.1. Discontinuous Galerkin Discretization
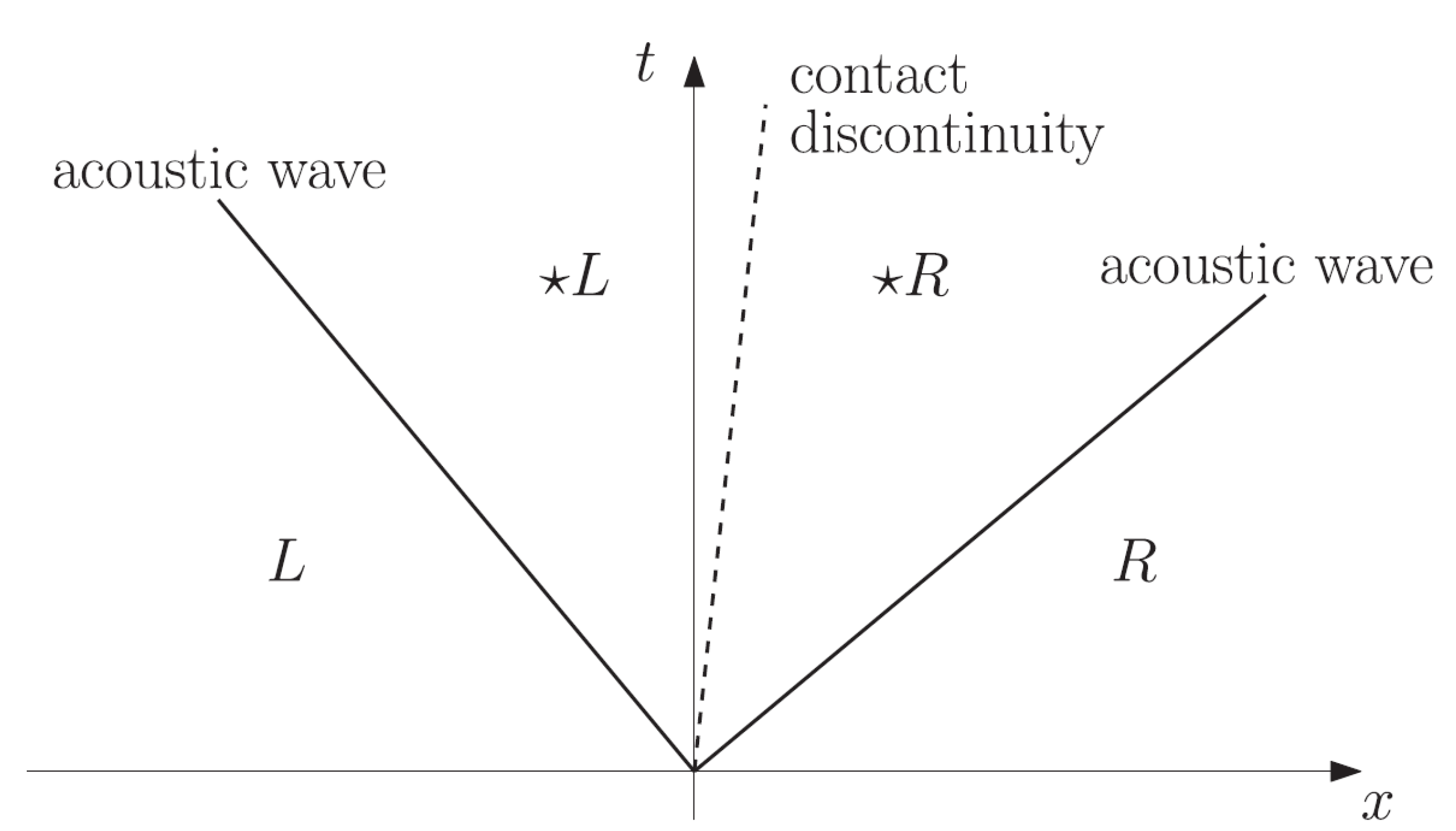
3.2. Riemann Solvers
3.3. Set of Working Variables
- linear
- exponential
- hyperbolic tangent-based
3.4. Shock Capturing for Material Interfaces
3.5. Implicit Time Integration
Time Step Adaptation
4. Numerical Results
4.1. Kovasznay Flow
4.2. Guermond–Quartapelle Manufactured Solution
4.3. Density Waves
- The linear advection of a sine density wave
- The linear advection of a square-density wave
4.4. 2D Droplet Impinging on a Thin Liquid Film
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DAE | differential-algebraic equation |
| DG | discontinuous Galerkin |
| ERS | exact Riemann solver |
| ESDIRK | explicit singly diagonally implicit Runge–Kutta |
| LTE | local truncation error |
| SDRS | switched density Riemann solver |
| VDI | variable density incompressible |
References
- Von Neumann, J.; Richtmyer, D. A Method for the Numerical Calculation of Hydrodynamic Shocks. J. Appl. Phys. 1950, 21, 232–237. [Google Scholar] [CrossRef]
- Hirt, C.; Amsden, A.; Cook, J. An arbitrary Lagrangian-Eulerian computing method for all flow speeds. J. Comput. Phys. 1974, 14, 227–253. [Google Scholar] [CrossRef]
- Glimm, J.; Graham, M.; Grove, J.; Li, X.; Smith, T.; Tan, D.; Tangerman, F.; Zhang, Q. Front tracking in two and three dimensions. Comput. Math. Appl. 1998, 35, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Dervieux, A.; Thomasset, F. A finite element method for the simulation of a Rayleigh-Taylor instability. In Approximation Methods for Navier-Stokes Problems; Springer: Berlin/Heidelberg, Germany, 1980; pp. 145–158. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Youngs, D. Time-dependent Multi-material flow with large fluid distortion. In Numerical Methods in Fluid Dynamics; Academic Press: Cambridge, MA, USA, 1982; Volume 24, pp. 273–285. [Google Scholar]
- Baer, M.; Nunziato, J. A two-phase mixture theory for the deflagration-to-detonation transition (ddt) in reactive granular materials. Int. J. Multiph. Flow 1986, 12, 861–889. [Google Scholar] [CrossRef]
- Abgrall, R.; Saurel, R. Discrete equations for physical and numerical compressible multiphase mixtures. J. Comput. Phys. 2003, 186, 361–396. [Google Scholar] [CrossRef]
- Murrone, A.; Guillard, H. A five equation reduced model for compressible two phase flow problems. J. Comput. Phys. 2005, 202, 664–698. [Google Scholar] [CrossRef] [Green Version]
- Saurel, R.; Pantano, C. Diffuse-Interface Capturing Methods for Compressible Two-Phase Flows. Annu. Rev. Fluid Mech. 2018, 50, 105–130. [Google Scholar] [CrossRef] [Green Version]
- Lions, P.L. Mathematical Topics in Fluid Mechanics: Incompressible Models; Clarendon Press: Oxford, UK, 1996; Volume 1. [Google Scholar]
- Chapelier, J.B.; de la Llave Plata, M.; Renac, F.; Lamballais, E. Evaluation of a high-order discontinuous Galerkin method for the DNS of turbulent flows. Comput. Fluids 2014, 95, 210–226. [Google Scholar] [CrossRef]
- Renac, F.; Plata, M.d.l.L.; Martin, E.; Chapelier, J.B.; Couaillier, V. Aghora: A high-order DG solver for turbulent flow simulations. In IDIHOM: Industrialization of High-Order Methods—A Top-Down Approach: Results of a Collaborative Research Project Funded by the European Union, 2010–2014; Kroll, N., Hirsch, C., Bassi, F., Johnston, C., Hillewaert, K., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 315–335. [Google Scholar] [CrossRef]
- De Wiart, C.C.; Hillewaert, K.; Bricteux, L.; Winckelmans, G. Implicit LES of free and wall-bounded turbulent flows based on the discontinuous Galerkin/symmetric interior penalty method. Int. J. Numer. Methods Fluids 2015, 78, 335–354. [Google Scholar] [CrossRef]
- Chapelier, J.B.; Plata, M.d.l.L.; Lamballais, E. Development of a multiscale LES model in the context of a modal discontinuous Galerkin method. Comput. Methods Appl. Mech. Eng. 2016, 307, 275–299. [Google Scholar] [CrossRef]
- Flad, D.; Gassner, G. On the use of kinetic energy preserving DG-schemes for large eddy simulation. J. Comput. Phys. 2017, 350, 782–795. [Google Scholar] [CrossRef] [Green Version]
- Krais, N.; Beck, A.; Bolemann, T.; Frank, H.; Flad, D.; Gassner, G.; Hindenlang, F.; Hoffmann, M.; Kuhn, T.; Sonntag, M.; et al. FLEXI: A high order discontinuous Galerkin framework for hyperbolic–parabolic conservation laws. Comput. Math. Appl. 2021, 81, 186–219. [Google Scholar] [CrossRef]
- Bassi, F.; Botti, L.; Colombo, A.; Rebay, S. Agglomeration based discontinuous Galerkin discretization of the Euler and Navier–Stokes equations. Comput. Fluids 2012, 61, 77–85. [Google Scholar] [CrossRef]
- Massa, F.; Bassi, F.; Botti, L.; Colombo, A. An implicit high-order discontinuous galerkin approach for variable density incompressible flows. In Droplet Interactions and Spray Processes; Lamanna, G., Tonini, S., Cossali, G.E., Weigand, B., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 191–202. [Google Scholar] [CrossRef]
- Gao, F.; Ingram, D.M.; Causon, D.M.; Mingham, C.G. The development of a Cartesian cut cell method for incompressible viscous flows. Int. J. Numer. Methods Fluids 2007, 54, 1033–1053. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y. An improved free surface capturing method based on Cartesian cut cell mesh for water-entry and -exit problems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 1843–1868. [Google Scholar] [CrossRef]
- Bassi, F.; Massa, F.; Botti, L.; Colombo, A. Artificial compressibility Godunov fluxes for variable density incompressible flows. Comput. Fluids 2018, 169, 186–200. [Google Scholar] [CrossRef]
- Manzanero, J.; Rubio, G.; Kopriva, D.A.; Ferrer, E.; Valero, E. An entropy–stable discontinuous Galerkin approximation for the incompressible Navier–Stokes equations with variable density and artificial compressibility. J. Comput. Phys. 2020, 408, 109241. [Google Scholar] [CrossRef] [Green Version]
- Leakey, S.; Glenis, V.; Hewett, C.J. A novel Godunov-type scheme for free-surface flows with artificial compressibility. Comput. Methods Appl. Mech. Eng. 2022, 393, 114763. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Hairer, E.; Gerhard, W. Solving Ordinary Differential Equations II; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Kennedy, C.A.; Carpenter, M.H. Additive Runge-Kutta schemes for convection-diffusion-reaction equations. Appl. Numer. Math. 2003, 44, 139–181. [Google Scholar] [CrossRef]
- Kennedy, C.A.; Carpenter, M.H. Diagonally Implicit Runge-Kutta Methods for Ordinary Differential Equations. A Review; Technical Report 20160005923; NASA, Langley Research Center: Hampton, VA, USA, 2016.
- Bassi, F.; Botti, L.; Colombo, A.; Di Pietro, D.; Tesini, P. On the flexibility of agglomeration based physical space discontinuous Galerkin discretizations. J. Comput. Phys. 2012, 231, 45–65. [Google Scholar] [CrossRef] [Green Version]
- Bassi, F.; Rebay, S.; Mariotti, G.; Pedinotti, S.; Savini, M. A high-order accurate discontinuous finite element method for inviscid and viscous turbomachinery flows. In Proceedings of the 2nd European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Antwerp, Belgium, 5–7 March 1997; Decuypere, R., Dibelius, G., Eds.; Technologisch Instituut: Hannover, Germany, 1997; pp. 99–108. [Google Scholar]
- Arnold, D.N.; Brezzi, F.; Cockburn, B.; Marini, L.D. Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 2002, 39, 1749–1779. [Google Scholar] [CrossRef]
- Hesthaven, J.S.; Warburton, T. Nodal Discontinuous Galerkin Methods; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef] [Green Version]
- Chorin, A.J. A numerical method for solving incompressible viscous flow problems. J. Comput. Phys. 1967, 2, 12–26. [Google Scholar] [CrossRef]
- Persson, P.O.; Peraire, J. Sub-cell shock capturing for discontinuous Galerkin methods. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibition, Reno, NV, USA, 9–12 January 2006; Volume 2. [Google Scholar] [CrossRef] [Green Version]
- Klöckner, A.; Warburton, T.; Hesthaven, J.S. Viscous Shock Capturing in a Time-Explicit Discontinuous Galerkin Method. Math. Model. Nat. Phenom. 2011, 6, 57–83. [Google Scholar] [CrossRef]
- Jaffre, J.; Johnson, C.; Szepessy, A. Convergence of the discontinuous Galerkin finite element method for hyperbolic conservation laws. Math. Model. Methods Appl. Sci. 1995, 5, 367–386. [Google Scholar] [CrossRef]
- Söderlind, G. Digital Filters in Adaptive Time-Stepping. ACM Trans. Math. Softw. 2003, 29, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Söderlind, G.; Wang, L. Adaptive time-stepping and computational stability. J. Comput. Appl. Math. 2006, 185, 225–243. [Google Scholar] [CrossRef] [Green Version]
- Noventa, G.; Massa, F.; Rebay, S.; Bassi, F.; Ghidoni, A. Robustness and efficiency of an implicit time-adaptive discontinuous Galerkin solver for unsteady flows. Comput. Fluids 2020, 204, 104529. [Google Scholar] [CrossRef]
- Ghidoni, A.; Massa, F.; Noventa, G.; Rebay, S. Assessment of an adaptive time integration strategy for a high-order discretization of the unsteady RANS equations. Int. J. Numer. Methods Fluids 2022, 94, 1923–1963. [Google Scholar] [CrossRef]
- Bassi, F.; Botti, L.; Colombo, A.; Ghidoni, A.; Massa, F. Linearly implicit Rosenbrock-type Runge–Kutta schemes applied to the Discontinuous Galerkin solution of compressible and incompressible unsteady flows. Comput. Fluids 2015, 118, 305–320. [Google Scholar] [CrossRef]
- Noventa, G.; Massa, F.; Bassi, F.; Colombo, A.; Franchina, N.; Ghidoni, A. A high-order Discontinuous Galerkin solver for unsteady incompressible turbulent flows. Comput. Fluids 2016, 139, 248–260. [Google Scholar] [CrossRef]
- Kelley, C.T.; Keyes, D.E. Convergence Analysis of Pseudo-Transient Continuation. SIAM J. Numer. Anal. 1998, 35, 508–523. [Google Scholar] [CrossRef] [Green Version]
- Balay, S.; Abhyankar, S.; Adams, M.; Brown, J.; Brune, P.; Buschelman, K.; Dalcin, L.; Dener, A.; Eijkhout, V.; Gropp, W.; et al. PETSc Users Manual; Argonne National Laboratory: Lemont, IL, USA, 2019. [Google Scholar]
- Kovasznay, L.I.G. Laminar flow behind a two-dimensional grid. Math. Proc. Camb. Philos. Soc. 1948, 44, 58–62. [Google Scholar] [CrossRef]
- Bassi, F.; Crivellini, A.; Di Pietro, D.A.; Rebay, S. An artificial compressibility flux for the discontinuous Galerkin solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 2006, 218, 794–815. [Google Scholar] [CrossRef]
- Shahbazi, K.; Fischer, P.F.; Ethier, C.R. A high-order discontinuous Galerkin method for the unsteady incompressible Navier–Stokes equations. J. Comput. Phys. 2007, 222, 391–407. [Google Scholar] [CrossRef]
- Cockburn, B.; Kanschat, G.; Schötzau, D. An Equal-Order DG Method for the Incompressible Navier–Stokes Equations. J. Sci. Comput. 2009, 40, 188–210. [Google Scholar] [CrossRef] [Green Version]
- Massa, F.; Ostrowski, L.; Bassi, F.; Rohde, C. An artificial Equation of State based Riemann solver for a discontinuous Galerkin discretization of the incompressible Navier–-Stokes equations. J. Comput. Phys. 2022, 448, 110705. [Google Scholar] [CrossRef]
- Botti, L.; Massa, F. HHO Methods for the Incompressible Navier-Stokes and the Incompressible Euler Equations. J. Sci. Comput. 2022, 92, 28. [Google Scholar] [CrossRef]
- Guermond, J.L.; Quartapelle, L. A Projection FEM for Variable Density Incompressible Flows. J. Comput. Phys. 2000, 165, 167–188. [Google Scholar] [CrossRef]
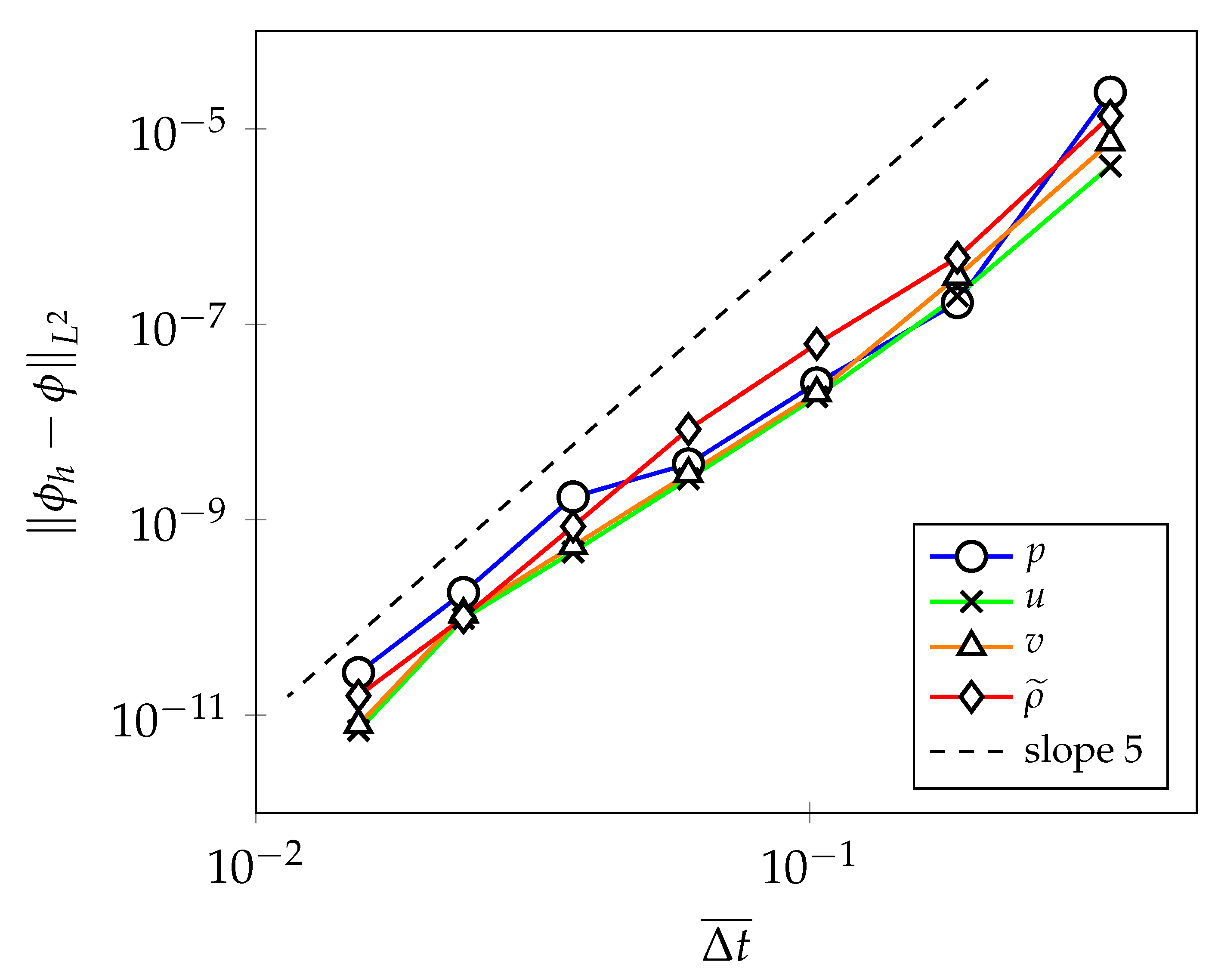






| i | Order | Order | Order | Order | |||||
|---|---|---|---|---|---|---|---|---|---|
| 3 | 2.01 | – | 7.91 | – | 1.54 | – | 2.11 | – | |
| 4 | 5.88 | 0.89 | 1.90 | 2.06 | 4.29 | 1.84 | 5.49 | 1.94 | |
| 5 | 1.58 | 1.90 | 4.38 | 2.12 | 1.07 | 2.00 | 1.21 | 2.18 | |
| 6 | 4.10 | 1.95 | 1.02 | 2.10 | 2.54 | 2.07 | 2.55 | 2.25 | |
| 7 | 1.05 | 1.96 | 2.43 | 2.07 | 5.99 | 2.09 | 5.51 | 2.21 | |
| 8 | 2.69 | 1.96 | 5.90 | 2.04 | 1.43 | 2.06 | 1.25 | 2.14 | |
| 3 | 2.41 | – | 4.22 | – | 1.11 | – | 1.16 | – | |
| 4 | 6.46 | 0.95 | 5.17 | 3.03 | 1.56 | 2.83 | 1.76 | 2.72 | |
| 5 | 1.70 | 1.93 | 6.53 | 2.99 | 2.15 | 2.86 | 2.36 | 2.90 | |
| 6 | 4.41 | 1.95 | 8.29 | 2.98 | 2.87 | 2.90 | 3.09 | 2.94 | |
| 7 | 1.13 | 1.97 | 1.05 | 2.98 | 3.74 | 2.94 | 3.98 | 2.96 | |
| 8 | 2.86 | 1.98 | 1.32 | 2.99 | 4.78 | 2.97 | 5.08 | 2.97 | |
| 3 | 1.46 | – | 3.45 | – | 7.77 | – | 2.11 | – | |
| 4 | 1.47 | 1.66 | 2.33 | 3.89 | 5.34 | 3.86 | 5.49 | 3.69 | |
| 5 | 1.56 | 3.24 | 1.50 | 3.96 | 3.61 | 3.89 | 1.21 | 3.72 | |
| 6 | 1.79 | 3.12 | 9.45 | 3.98 | 2.41 | 3.90 | 2.55 | 3.91 | |
| 7 | 2.16 | 3.05 | 5.93 | 3.99 | 1.58 | 3.93 | 5.51 | 4.06 | |
| 8 | 2.67 | 3.02 | 3.72 | 4.00 | 1.02 | 3.95 | 1.25 | 4.17 | |
| 3 | 1.50 | – | 1.05 | – | 2.82 | – | 6.36 | – | |
| 4 | 1.13 | 1.86 | 3.22 | 5.03 | 9.57 | 4.88 | 2.51 | 4.66 | |
| 5 | 7.83 | 3.86 | 9.93 | 5.02 | 3.04 | 4.97 | 9.11 | 4.79 | |
| 6 | 5.13 | 3.93 | 3.09 | 5.01 | 9.47 | 5.01 | 2.99 | 4.93 | |
| 7 | 3.28 | 3.97 | 9.66 | 5.00 | 2.94 | 5.01 | 9.12 | 5.04 | |
| 8 | 2.08 | 3.98 | 3.02 | 5.00 | 9.13 | 5.01 | 2.63 | 5.12 |
| Setup | ||
|---|---|---|
| A | 1.55 | 1.39 |
| B | 1.03 | 1.04 |
| C | 7.89 | 2.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassi, F.; Botti, L.A.; Colombo, A.; Massa, F.C. Assessment of an Implicit Discontinuous Galerkin Solver for Incompressible Flow Problems with Variable Density. Appl. Sci. 2022, 12, 11229. https://doi.org/10.3390/app122111229
Bassi F, Botti LA, Colombo A, Massa FC. Assessment of an Implicit Discontinuous Galerkin Solver for Incompressible Flow Problems with Variable Density. Applied Sciences. 2022; 12(21):11229. https://doi.org/10.3390/app122111229
Chicago/Turabian StyleBassi, Francesco, Lorenzo Alessio Botti, Alessandro Colombo, and Francesco Carlo Massa. 2022. "Assessment of an Implicit Discontinuous Galerkin Solver for Incompressible Flow Problems with Variable Density" Applied Sciences 12, no. 21: 11229. https://doi.org/10.3390/app122111229
APA StyleBassi, F., Botti, L. A., Colombo, A., & Massa, F. C. (2022). Assessment of an Implicit Discontinuous Galerkin Solver for Incompressible Flow Problems with Variable Density. Applied Sciences, 12(21), 11229. https://doi.org/10.3390/app122111229






