Experimental Study on Fractal Characteristics of Particle Size Distribution by Repeated Compaction of Road Recycling Crushed Stone

Abstract

In order to investigate the compaction characteristics of graded crushed stone under repeated utilization, it is necessary to improve the utilization rate of road recycling crushed stone and maintain its strength and stability during recycling. In the present study, repeated compaction characteristic curves of graded crushed stone were developed using repeated compaction and screening of the graded crushed stone. The correlations between the fractal dimension of particle size distribution and repeated compaction times, water content, and dry density were analyzed. The experimental results indicate that both the maximum dry density and the optimal water content increase as the repeated compaction times increase. The fractal dimension of the particle size distribution of the graded crushed stone used in this test is 2.33 to 2.57. The obtained results show that as the fractal dimension increases, the maximum dry density of the graded crushed stone increases. At a constant repeated compaction time, the fractal dimension of the particle size distribution of graded crushed stone increased and then decreased as the water content increased. In summary, the compaction performance of the structural layer of graded crushed stone can be tuned by adjusting the fractal dimension of the particle size distribution of the recycled pavement structural layer in practical applications. Moreover, the optimal graded materials can be prepared under the guidance of the fractal dimension, thereby achieving an optimized working performance of the recycled pavement structural layer.

1. Introduction

Graded crushed stone has excellent stability under different conditions, a high bearing capacity, and good fatigue resistance, making it an ideal choice in road construction. Currently, this material is widely used in the cushion and base of high-grade road pavement structures in China. Studies show that the compactness of the stone particles directly affects the strength of the graded crushed stone, thereby affecting the strength and stability of the pavement structural layer. Moreover, the structural instability of pavement and excessive permanent deformations mainly originate from the high porosity of graded crushed stone [1,2,3]. A review of the literature indicates that most investigations in this area focus on the influence of physical properties such as particle gradation on the mechanical properties of the graded crushed stone [4,5], and the elastic-plastic deformation of graded crushed stone under long-term loading [6,7]. With the rapid increase in construction in the past few years, the shortage of building materials has intensified, and the recycling of materials from the pavement structural layer has become a subject of interest [8,9]. In this regard, the performed analyses reveal that after long-term cyclic loads originating from the transportation of vehicles, the composition and properties of the pavement structural layer undergo great changes. Therefore, in-depth research on the compaction characteristics of graded crushed stone under cyclic loads is of great significance in the improvement of recycling graded crushed stone and ensuring its strength and stability during reuse.

In the field of road construction, it is prudent to use recycled graded crushed stone; however, the utilization rate of recycled graded crushed stone is still low. Especially in key engineering projects such as highways, recycled graded crushed stone is rarely used or basically not used. The main reason is that the use performance and methods of recycled graded crushed stone are insufficiently understood, and they cannot be used well. The fractal geometry theory has recently been proposed as a useful tool to solve complex engineering problems [10,11,12]. Fractal geometry has been widely used in the field of geomechanics since its formation in 1983 [13]. It has successfully solved many problems of geotechnical irregularity and randomness that cannot be solved by classical theoretical models, and achieved fruitful research results. In this regard, Turcotte [14] analyzed the experimental measurement data of the fragmentation distribution of various geological materials using different crushing methods and established a correlation between the fractal dimension, volume distribution function, and the mass distribution function of the crushed rock mass.

Moreover, Xie et al. [15,16,17] summarized the following three basic methods of applying fractal geometry to solve practical problems: the fractal model method, experimental measurement method and dimensional image method. Taking the fracture and fragmentation of rock as the research focus, they analyzed the relationship between the fractal dimension of bulk distribution and the microstructure, the loading method, and the shape and size of specimens from the perspective of energy dissipation. By analyzing the fractal characteristics of particle size distribution and compaction characteristics of silt and coarse-grained soil samples. Qin et al. [18,19,20,21,22] proposed a method to evaluate the effects of particle size distribution on compaction performance using the deviation coefficient of particle size distribution and establishing the relationship between the particle size distribution deviation coefficient and the maximum dry density. Zhu et al. [23,24,25,26] analyzed the relationship between gradation and compaction dry density through dry density testing. They obtained a good linear normalization law between particle size fractal dimension and maximum dry density, and proposed a method to optimize stone gradation based on the evaluation index of particle size fractal dimension. Yu et al. [27,28,29] established the relationship of axial displacement, compressive modulus, the fractal dimension of particle size distribution, and axial stress using confining compaction tests of saturated gradation of broken mudstone. Xu et al. [30] proposed the concept of “quasi-fractal dimension” and “true fractal dimension” for particle crushing based on the physical interpretation of particle crushing fractal dimension; they also established the relationship between particle crushing in the “quasi-fractal dimension” and crushing stress or crushing energy. Peng et al. [31] proposed a correlation between particle size fractal dimension and water content under different compaction conditions. The above research results analyze the fractal characteristics of rock after crushing and the relationship between crushed rock gradation and dry density using fractal theory. However, there are few studies on the fractal characteristics and changing laws of recycled graded crushed stone.

In the present study, the use of grading crushed stone regeneration was simulated by performing cyclic compaction and sieving tests on graded crushed stone particles; furthermore, the compaction and fractal characteristics of the particle size distribution of the samples were studied. To this end, the correlations between the fractal dimension of particle size distribution with cyclic compaction, water content, and dry density were obtained. This article will provide a reference for evaluating the compaction performance and structural strength of the newly formed pavement layer using the materials of the old pavement layer as graded crushed stones. It provides a new idea and method for optimizing the grading of recycled gravel.

2. Experiment

2.1. Instrument

Figure 1 shows the multi-functional electric compaction instrument (BKJ-Ⅲ, Hebei Tongli Instrument Equipment Co., Ltd., Cangzhou, China), used to perform experiments. Table 1 shows the main characteristics of the compaction instrument. All tests were carried out in accordance with the technical requirements of the Class C compaction test in the “Test Methods of Materials Stabilized with Inorganic Binders for Highway Engineering” (JTG E51-2009, China Communications Press: Beijing, China, 2009).

Figure 1. Multi-functional electric compaction instrument for repeated compaction tests.

Table 1. Main characteristics of the compaction instrument.

Hammer Quality	Height of Hammer Drop High	Work of Compaction	Barrel Inner Diameter	Barrel Height	Barrel Volume
4.5 kg	45 cm	2677 J	15.25 cm	12.0 cm	2177

2.2. Experimental Foundation

The particle composition of graded crushed stone is extremely complex and irregular. Under the action of compaction energy, particles of different sizes of graded crushed stone re-crush to different degrees. Its particle composition change process is relatively complex, and traditional geomechanics methods encounter many difficulties in quantitatively describing particle composition changes. Fractal geometry is a science that studies extremely irregular geometric figures. Fractal geometry mainly describes the self-similarity of things, including exact self-similarity, semi-self-similarity, and statistical self-similarity. Fractal dimension is the main concept of fractal geometry, which was first proposed by Hausdorff (1919). Fractal dimension overcomes the limitation that the dimension can only be an integer and can be used to analyze the inherent laws of irregular graphics.

In this section, fractal theory is introduced to describe the mass distribution of graded crushed stone after being compacted and broken; it was used by Turcotte to analyze the fragmentation of soil particles. According to the physical interpretation of the particle size distribution curve, the relationship between the sample size and the particle size of the crushed stone particles can be expressed as follows [32,33]:

$$p\left(<r\right)=\frac{{\left(r/r_{\max }\right)}^{3-D}-{\left(r_{\min }/r_{\max }\right)}^{3-D}}{1-{\left(r_{\min }/r_{\max }\right)}^{3-D}}$$

(1)

where r, r_min, and r_max are the particle size, minimum particle size, and maximum particle size of the graded crushed stone sample, respectively. Moreover, p(<r) denotes the ratio of the mass of particles with a particle size smaller than r to the total mass of the sample, and D is the fractional dimension of the particle.

Since the minimum size of sample particles (r_min) is limited to zero, Equation (1) can be simplified in the form below:

$$p\left(<r\right)={\left(r/r_{\max }\right)}^{3-D}$$

(2)

Taking the logarithm of both sides yields the following expression:

$$\lg p\left(<r\right)=\left(3-D\right)\lg p\left(r/r_{\max }\right)$$

(3)

where the coefficient (3−D) is the linear ratio of $\lg p\left(<r\right)$ to $\lg p\left(r/r_{\max }\right)$. Accordingly, the fractional dimension of the particle size distribution D of the sample can be obtained by fitting the terms $\lg p\left(<r\right)$ with $\lg p\left(r/r_{\max }\right)$ after compaction.

In the present study, the graded crushed stone samples with different water contents were compacted in different water-containing states; then, the samples were recovered and sieved. Moreover, the fractal dimension of the particle size distribution of graded crushed stone samples after compaction was obtained using Equation (3). A correlation was established between the fractal dimension of particle size distribution and water content. Then, these samples were repeatedly compacted and sieved to obtain the relationship between the fractal dimension of particle size distribution and cyclic compaction.

2.3. Sample Preparation

In the present study, graded crushed limestone, which is commonly used in the road pavement structural layer in the Liaoning area, was considered as the research object. The crushed value of the graded crushed stone was 12.6%. Figure 2 indicates that the samples were first sieved into 12 intervals using a standard square-hole sieve. According to the gradation requirements listed in Table 2, 5500 g samples were separated. In total, 5 uniformly blended samples were prepared for the tests.

Figure 2. Crushed stone samples with different particle sizes before blending.

Table 2. Initial gradation of samples before repeated compaction tests.

Sieve size/mm	26.5	19	16	13.2	9.5	4.75	2.36	1.18	0.6	0.3	0.15	0.075	Sieve bottom
Screening Ratio of Sub-Meter/%	0	2.5	12.0	11.0	16.5	23.0	11.5	7.5	5.0	3.5	2.5	1.5	3.5

2.4. Experimental Schemes

In order to clarify the effects of water content and cyclic compaction on the compaction and fractal characteristics of the particle size distribution of graded crushed stone, several samples with different water contents, including 2%, 3.5%, 5%, 6.5%, and 8% were prepared [34]. According to the requirements of the “Test Methods of Materials Stabilized with Inorganic Binders for Highway Engineering” (JTG E51-2009), each sample was equally divided into three parts for packaging during the test, and each layer of the samples was compacted 98 times The test results were recorded and the compacted samples were recovered after compaction. The recovered graded crushed stone was dried at a constant temperature of 105 °C and subjected to a screening test after drying. Throughout the experimental process, the above test process was repeated 5 times. The specific test scheme is shown in Table 3, and the workflow is shown in Figure 3.

Table 3. Experimental scheme for repeated compaction characteristics of graded crushed stone.

Sample No.	Water Content/%	Experiment Method
1	2.0	Compaction→Recovery→Drying→Screening For each sample, this process is repeated 5 times
2	3.5
3	5.0
4	6.5
5	8.0

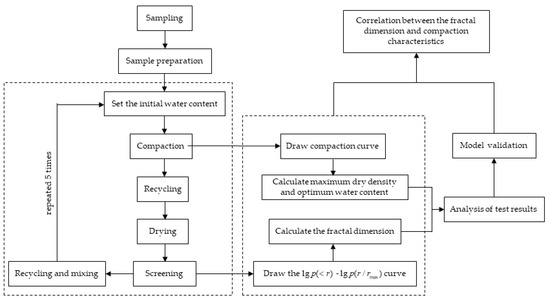
Figure 3. Workflow of repeated compaction test method.

The dry density of graded crushed stone after each compaction was calculated according to Equation (4):

$${\rho }_d=\frac{{\rho }_{\omega }}{1+0.01\omega }$$

(4)

where ${\rho }_d$ is the dry density of the sample, ${\rho }_{\omega }$ is the wet density of the sample, and $\omega$ is the water content of the sample.

Then, the compaction curves were drawn based on the test results, and the maximum dry density and optimized water content were obtained accordingly. Based on the obtained results, the $\lg p\left(<r\right)$-$\lg p\left(r/r_{\max }\right)$ curve was drawn to calculate the fractional dimension of the particle size distribution, D, of samples after the compaction tests. The graded crushed stone samples after cyclic compaction and the sieved tests are shown in Figure 4.

Figure 4. Graded crushed stone samples after repeated compaction and screening.

3. Results and Analysis

3.1. Maximum Dry Density and Optimized Water Content

Figure 5 illustrates the obtained results from the repeated compaction tests. It is observed that the dry density of graded crushed stone increases first then starts to drop as water content keeps increasing. It was found that the compaction curves have convex distributions. The dry density of graded crushed stone had a similar variation law after repeated compaction, and the compaction curve continued to shift upwards as the repeated compaction time increased. Water content is an important factor affecting the dry density of graded crushed stone. When the water content reaches a certain suitable value, the dry density of graded crushed stone can reach the maximum value. With the increase in the repeated compaction time, graded crushed stone will have better compaction effect.

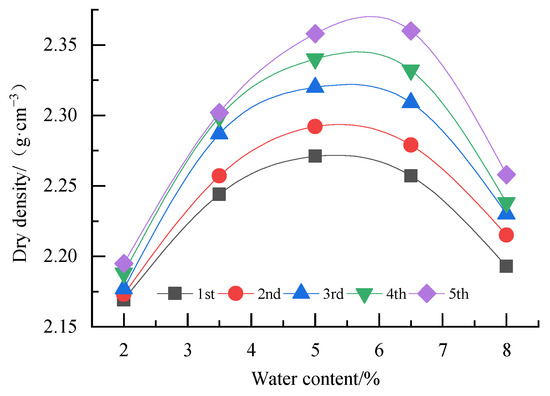
Figure 5. Test curves of repeated compaction.

After fitting, the water content and dry density corresponding to the peak point of the compaction curve are defined as the optimal water content and optimal dry density. The maximum dry density and optimized water content corresponding to different repeated compaction times were obtained and the results are summarized in Table 4.

Table 4. Test results of repeated compaction.

Repeated Compaction Times	Maximum Dry Density/(g·cm−3)	Optimized Water Content/%
1st	2.272	5.25
2nd	2.293	5.35
3rd	2.321	5.40
4th	2.343	5.57
5th	2.368	5.84

Table 4 indicates that as the repeated compaction time increases, the corresponding maximum dry density and optimized water content of the graded crushed stone increases.

Figure 6 shows the correlation between the maximum dry density of the graded crushed stone and repeated compaction times. It is observed that within the studied range of repeated compaction times, there is a linear correlation between the maximum dry density of the graded crushed stone and repeated compaction times. This correlation can be mathematically expressed as follows:

$${\rho }_{dm}=2.247+0.024n (n=1, 2, 3, \dots )$$

(5)

where ${\rho }_{dm}$ is the maximum dry density of the graded crushed stone at nth repeated compaction.

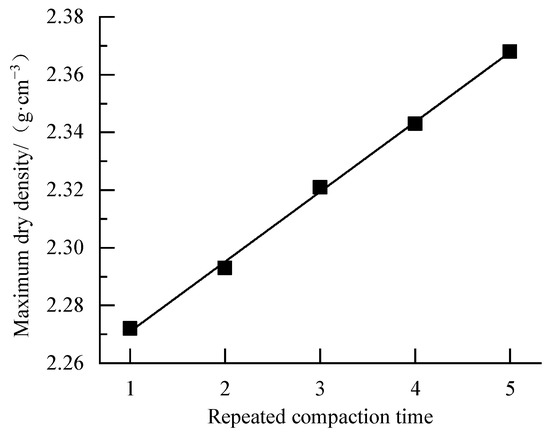
Figure 6. Distribution of the maximum dry density against the repeated compaction times.

When the stone is broken, there must be voids between the formed particles. In general, the voids will not completely disappear after the graded crushed stone is compacted again. This shows that although the maximum dry density of graded crushed stone had a linear correlation with repeated compaction times, this linear law will not apply when the repeated compaction time is greater. Therefore, there is an upper limit for the maximum dry density, which will not increase infinitely with the increase in repeated compaction times. The measured apparent density of the graded crushed stone was 2.70 g·cm⁻³, and in general, the upper limit of the maximum dry density will not exceed this value.

Figure 7 shows the distribution of the graded crushed stone’s optimized water content against the repeated compaction times.

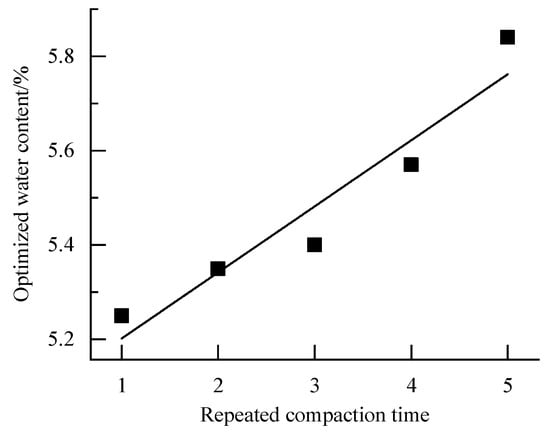
Figure 7. Distribution of optimized water content against the repeated compaction times.

It is observed that as the repeated compaction times increases, the corresponding optimized water content of the graded crushed stone increases linearly, which can be expressed in the following form:

$${\omega }_0=5.062+0.14n (n=1, 2, 3, \dots )$$

(6)

where ${\omega }_0$ is the optimized water content of graded crushed stone at nth repeated compaction.

According to the change rules mentioned above, the optimal water content of graded crushed stone will encounter the same problem as the maximum dry density. The optimum water content of graded crushed stone cannot increase infinitely with the increase in repeated compaction times. The rules of Equations (5) and (6) are accurate for instances where the repeated compaction time is small.

3.2. Correlation between the Fractal Dimension of Particle Size Distribution and Repeated Compaction Times

When the graded crushed stone was compacted under different water content conditions, the crushed stone particles in each size range were broken to different degrees, thereby changing the gradation of the graded crushed stone. After repeated compaction, the graded crushed stone samples were sieved to obtain the gradation distribution curve corresponding to each compaction state, and the fractal dimension of particle size distribution under each condition was fitted using Equation (3). Figure 8 shows the distribution of the fractal dimension of the particle size distribution against repeated compaction times under different water contents.

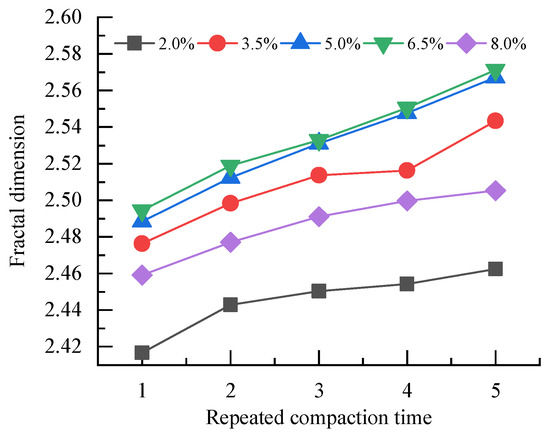
Figure 8. Distribution of fractal dimension against the repeated compaction time.

It is observed that at a constant water content, the fractal dimension of graded crushed stone has a good linear relationship with repeated compaction time. The fractal dimension of particle size distribution increases with the increase in the repeated compaction time. The particle breakage caused by repeated compaction can make the graded crushed stone more compact. Moreover, when the water content of the graded crushed stone is close to the optimal water content, the linear relationship between the fractal dimension and repeated compaction time will be more stable. For example, as repeated compaction time increased, the increment of fractal dimension was in the range of 0.0165~0.0239 at the water content of 5%, and the increment of fractal dimensions was between 0.0074~0.0261 at the water content of 2.0%.

3.3. Correlation between the Fractal Dimension of Particle Size Distribution and the Water Content

According to different repeated compaction times, the fractal dimension of particle size distribution and water content were analyzed, and the obtained results are shown in Figure 9. It is observed that as the water content increases, the fractal dimension of the particle size distribution first increases and then decreases, which is consistent with the distribution of dry density and water content.

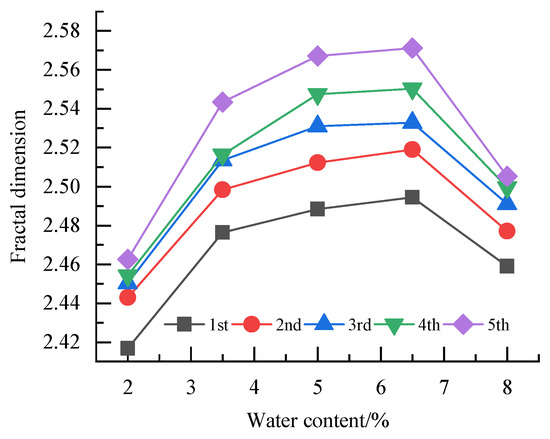
Figure 9. Distribution of the fractal dimension against the water content.

It was observed that at a constant repeated compaction time, the water content of graded crushed stone has a greater influence on the fractal dimension. Using the repeated compaction time of three as an example, when the water content increased from 2.0% to 3.5%, the fractal dimension increased by 0.11 g/cm⁻³; when the water content increased from 5.0% to 6.5%, the fractal dimension increased by 0.011 g/cm⁻³. It can be seen that the closer the water content of the graded crushed stone is to the optimal water content, the smaller the influence of water content on the change of the fractal dimension, and the more easily the graded crushed stone is compacted. When the water content of the graded crushed stone is too low or too high, it is difficult for the graded crushed stone to achieve a better compact state.

Figure 9 indicates that there is a strong correlation between the fractal dimension of particle size distribution and water content. In this regard, a quadratic function D = aω² + bω + c was used to fit the data. The correlation coefficients of the fitting results are above 0.97, indicating the accuracy of the curve fitting. The obtained list for different items is provided in Table 5.

Table 5. Fitting results of fractal dimension and water content.

Repeated Compaction Times	a	b	c	R2
1	−0.0062	0.0690	2.3053	0.9774
2	−0.0064	0.0701	2.3287	0.9771
3	−0.0072	0.0785	2.3231	0.9897
4	−0.0081	0.0891	2.3065	0.9900
5	−0.0100	0.1071	2.2880	0.9849

3.4. Correlation of Fractal Dimension of Particle Size Distribution with Dry Density

Figure 10 shows the obtained results for 25 groups of different size distributions and dry densities.

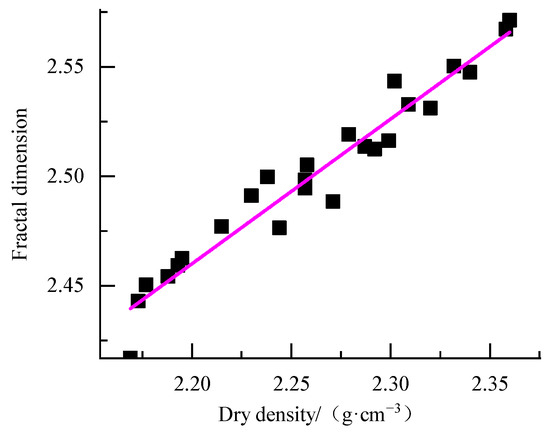
Figure 10. Correlation curve of fractal dimension and dry density.

It is observed that there is a linear correlation between the fractal dimension of particle size distribution and dry density, which can be fitted using the following expression:

$$D=0.6617{\rho }_d+1.0044 (R=0.9438)$$

(7)

As demonstrated by the fitting results, there must be a certain internal relationship between the fractal dimension D and dry density ${\rho }_d$ of graded crushed stone. The larger the fractal dimension of the graded crushed stone, the greater the dry density it can achieve. The fractal dimension of graded crushed stone can well reflect the compaction effect.

3.5. Correlation Validation of the Fractal Dimension of Particle Size Distribution with Dry Density

Based on the requirements of different highway grades, five graded crushed stone samples (the material source is the same as that used in the above tests) were prepared for the validation tests. Through compaction and sieving tests, the measured values of dry density and the fractal dimension of graded crushed stone samples were obtained, respectively. According to Formula (6), the theoretical value of the fractal dimension of the graded crushed stone sample is calculated and used for comparative analysis with the measured value. The validation results are shown in Table 6.

Table 6. Correlation validation results of fractal dimension with dry density.

Sample No.	Measured Water Content/%	Measured DRY Density/(g·cm−3)	Theoretical Fractal Dimension	Measured Fractal Dimension	Deviation of Fractal Dimension
6	1.82	2.153	2.4290	2.4024	−0.0066
7	3.68	2.219	2.4727	2.4831	0.0154
8	5.44	2.267	2.5045	2.5103	0.0158
9	6.32	2.242	2.4879	2.4805	−0.0114
10	7.66	2.207	2.4648	2.4616	−0.0032

Table 6 indicates that the maximum deviation between the theoretical fractal dimension and the measured fractal dimension of the five graded crushed stone samples is only 0.0158, and the theoretical fractal dimension is very close to the measured fractal dimension. The test results show that the linear relationship between the fractal dimension of particle size distribution and dry density is universal when the sources of graded crushed stone are the same.

4. Correlation between The Fractal Dimension and Compaction Characteristics

Graded crushed stone is a special mixture of crushed grains and its fractal dimension is related to the degree of crushing. Perfect [35] proposed the following expression between the fractal dimension of particle breakage and the degree of breakage:

$$D=3-\frac{\log f}{\log d}$$

(8)

where $f=N{\alpha }^3$ is the probability of particle breakage; N is the number of particles after breakage; α is the reciprocal of the ratio of the particle size before and after particle breakage; d is the particle size after breakage.

Equation (8) indicates that as the fragmentation probability of the particles increases, the fractal dimension of the particle distribution after fragmentation also increases. When parameters are set to $f={\alpha }^3$ and $D=0$, the whole particle is void so these values are not physical. When $f=1$ and $D=3$, there is no void in the whole particle and the parameters are not physical again. Accordingly, the fractal dimension of the particle size distribution of the graded crushed stone varies in the range of 0 to 3.

When the solid particles are completely broken, the fractional dimension of particle size distribution approaches a constant value, which is generally 2.6. Moreover, the index of stone grading could be evaluated using the fractal dimension. The corresponding fractal dimension in an appropriate gradation varies in the range of 2.22~2.63, and the fractal dimension corresponding to the optimal grading is generally 2.55~2.60. In this study, the fractal dimension of the particle size distribution of graded crushed stone was 2.33~2.57, and the fractal dimension increased with an increase in repeated compaction times, which was consistent with the foregoing analyses.

Based on the performed experimental analyses, the maximum fractal dimension of the particle size distribution of graded crushed stone was 2.60. The theoretical maximum dry density of graded crushed stone samples was 2.411 g·cm⁻³ and the corresponding optimized water content was 6.02%. When the graded crushed stone reaches the theoretical maximum dry density, the ratio of the particle size of crushed stone can be calculated using Equation (3).

In summary, the fractal dimension of particle size distribution effectively reflects the compaction characteristics of graded crushed stone. As the fractal dimension of particle size distribution increases, the theoretical maximum dry density of graded crushed stone increases, and graded crushed stone becomes more compact under optimized water content, thereby improving the working conditions.

5. Conclusions

Aiming at the problem of the reuse of recycled graded crushed stone, this paper studied the change law of the fractal dimension, the repeated compaction time, the water content and the dry density by performing repeated compaction tests of graded crushed stone; furthermore, a linear function relationship between the fractal dimension of graded crushed stone and dry density was established. The main achievements can be summarized as follows:

(1)

After five repeated compactions, graded crushed stone maintained reasonable compaction characteristics and the compaction curve was convex. At a constant repeated compaction time, the dry density of graded crushed stone increases first then starts to drop as water content continues to increase. As the repeated compaction times increased, both the maximum dry density and the optimized water content increased, and the average increments after each repeated compaction were 0.024 g·cm⁻³ and 0.14%, respectively.

(2)

At a constant water content, the fractal dimension of particle size distribution increased with the increase in the repeated compaction time. When the water content of the graded crushed stone is close to the optimal water content, the linear relationship between the fractal dimension and repeated compaction time is more stable. At a constant repeated compaction time, the fractal dimension of the particle size distribution of graded crushed stone increased and then decreased as the water content increased. Water content and repeated compaction times are important factors affecting the fractal dimension of graded crushed stone.

(3)

There is a linear correlation between the fractal dimension of the particle size distribution of the graded crushed stone and the dry density, and the linear correlation coefficient is as high as 0.9438. The fractal dimension of particle size distribution after repeated compaction effectively reflects the compactness of the graded crushed stone. It is found that the maximum dry density is proportional to the fractal dimension.

(4)

Recycled graded crushed stone is an important source of materials for future highway construction. The optimized gradation material could be blended according to the fractal dimension to achieve the optimized working performance of the recycled pavement structural layer material. It can not only solve the problem of material shortage, but can also reduce environmental pollution caused by material waste.