Abstract
Vapor-liquid separation during condensation enables the enhancement of heat transfer coefficient and reduction in pressure drop simultaneously. The vapor-liquid separator is vital to the performance of such a liquid-separation condenser (LSC). It should fulfill the functions of allowing the condensate to drain away as much as possible from the separator and leaving only vapor to continue condensing afterwards. However, due to the intensive interactions between the liquid and vapor, it is really hard to achieve perfect vapor-liquid separation, adding new uncertainties to the maldistributions in the branch outlets of a parallel condenser. To discover more insights of the flow conditions in the header and phase distributions, the characteristics of the orifice-baffle header are studied by using CFD and the mechanistic model for the droplet analysis is established by means of force balance in this paper. A parametrical analysis is carried out to discover the effects of operating conditions. It is found that the maximum vapor-liquid separation efficiency (η) is 51.94% as the inlet mass flow rate (ṁin) is 12 g/s. The vapor leakage from the orifice because of the liquid impact is one of the main reasons that deteriorate the vapor-liquid separation performance. Moreover, the vortex in the header increases the local mass flux, thereafter decreasing the droplet diameter. With the increasing of ṁin, the dominant force of the droplet in the vertical direction switches from FG to FD2.
1. Introduction
The vapor phase is generally converted into the liquid phase during condensation. The condensate accumulates on the heat transfer surface and the liquid film becomes thicker and thicker, leading to the increasing of thermal resistance and flow resistance. Peng et al. [1] proposed the concept of “liquid-separation condensation” to enhance the condenser performance. The configuration of a liquid-separation condenser (LSC) is shown in Figure 1a. The condensate can be promptly removed by the vapor-liquid separator in the headers. To deal with the alleviated mass flow rate due to the liquid drainage, the flow area should be shrunk accordingly to keep the pace of variations in mass flux. In this way, the thickness of the liquid film is largely reduced and the vapor quality is significantly improved, which finally enhances the heat transfer coefficient (HTC), as shown in Figure 1b.
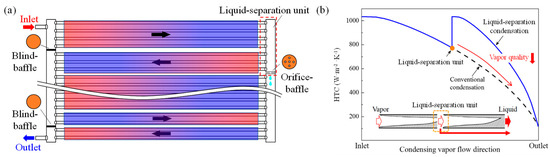
Figure 1.
(a) Scheme of LSC; (b) HTC enhancement in LSC, modified from [2].
Researchers have verified the superiorities of LSC. Hua [3] theoretically found that HTC of LSC can be 34.6% higher and the pressure drop can be 74.4% lower than the conventional condenser. Zhong et al. [4] experimentally confirmed that when the mass flux is higher than 590 km/(m2∙s), LSC has a higher heat transfer coefficient and 30.5–52.6% lower pressure drop, simultaneously. They further pinpointed that LSC has superior comprehensive performance in terms of penalty factor and minimum entropy generation number [5]. Li et al. [6] discovered that the condenser inserted with a T-junction unit can improve the heat transfer capacity by approximately 5.1%. At the level of the thermal systems, LSC also exhibits its advances in air conditioning systems, heat pump, and organic Rankine cycle (ORC). Chen et al. [7] found that the Energy Efficiency Ratio (EER) at cooling mode and Coefficient of Performance (COP) at heating mode in an air conditioning with LSC are 9.8% and 7.3% higher than these in baseline system, respectively. They further pointed out that using LSC can reduce avoidable exergy destruction of the compressor by 45.5% [8]. Li et al. [6] found that the refrigeration system with LSC results in a higher COP by 6.6% compared to a conventional condenser. Chen et al. [9] revealed that the heat pump with LSC has a higher COP and lower power consumption. Lu et al. [10] concluded that the ORC with LSC achieves a 21.43% lower average electricity production cost than conventional ORC. In short, liquid-separation condensation is a promising technology that enables the improvement of both the condenser performance and thermal system efficiency.
As one of the essential parameters, the vapor quality (x) largely determines HTC during condensation. The higher the vapor quality is, the higher the HTC becomes. In principle, for a superior HTC in LSC, it is preferable to have a high vapor quality that is close to one after the vapor-liquid separation. Therefore, the performance of the liquid-separation unit that dominates the redistributions of vapor quality and mass flow rate is vital to LSC. More attention should be paid to the liquid-separation unit.
Up to now, only two kinds, namely the T-junction header and the orifice-baffle header, are extensively employed in LSC.
LSC with a T-junction header is based on the differential inertia force of the liquid and vapor. It was proposed by Oh et al. [11]. Li et al. carried out a comprehensive study on this T-junction header, including a visualization experiment [12], theoretical model [13] and the CFD model [14]. They found that the liquid drainage ratio (FL) can be 100% at low inlet mass flux, and it reduces with the increasing of the inlet mass flux or inlet quality. However, in the T-junction header, the liquid and vapor can only be separated one, which limited the improvement of HTC in LSC.
Alternatively, the vapor-liquid separation in the orifice-baffle header is on the basis of gravitation force. As shown in Figure 1, the two-phase flow from the branch inlets enters into the header where the vapor-liquid separation occurs on the orifice-baffle due to their distinct physical properties and the pressure difference across the orifices. Ideally, the liquid is accumulated on the orifice-baffle and drained out from the orifices, whereas the vapor flows out via the branch outlets. Hence, the phase separation is achieved. However, in practice, due to the intensive interactions between liquid and vapor, incomplete vapor-liquid separation occurs in the liquid-separation unit, thus limiting the potential release of liquid-separation condensation. Mo et al. [15] pointed out that in the orifice-baffle header of LSC, the vapor-liquid separation efficiencies of annular flow and slug flow at the inlet are 45% and 80%, respectively. Li et al. [16] established a numerical simulation model of the orifice-baffle header based on the Volume of Fluid (VOF) method. The results showed that when the diameter of the orifice is larger than 2 mm, the liquid drainage by the orifice is almost the same, and the vapor leakage rate of the orifice increases as well. The available studies on the orifice-baffle header have been simplified as one branch inlet and one branch outlet as well as only a single orifice in the center of the baffle. However, the branches and the orifices are multiple in the actual LSC [7]. Furthermore, the mass flow rate in the header is 2–5 g/s in Li et al. [16], which is substantially differentiated from that in LSC. The interactions between the liquid and vapor are more intensive in LSC and there exists fluid maldistribution in multiple branches. In short, the vapor-liquid separation performance and the flow characteristic in the orifice-baffle header with multiple branches and orifices under various inlet operating conditions are quite different from the existing findings. Mechanics of vapor-liquid separation and flow maldistribution in the branch are still to be unveiled, and this is in great need of further exploration.
In this paper, a numerical simulation model for an orifice-baffle header with multiple branches and orifices is established and validated. The vapor-liquid separation features and the flow characteristics at various operating conditions are analyzed. This paper is of great importance to reveal the mechanisms of vapor-liquid separation and flow maldistribution.
2. Model Description
2.1. Computational Domain and Boundary Condition
Based on the previous LSC structure [17], the branch parameters of the orifice-baffle header are shown in Figure 2. The liquid-separation unit consists of four branch inlets and three branch outlets, namely I1, I2, I3, I4, B1, B2, and B3 from top to bottom. Furthermore, the orifice is not assigned on the right side of the baffle to avoid the direct liquid impact. The boundary condition at the inlets and outlets are set as velocity inlet and pressure outlet, respectively. The velocity of each phase is calculated using the void fraction model proposed by EI Hajal et al. [18] and compiled by a user-defined function (UDF). The pressure difference between the branch outlet PB and the orifice PO approximately equals to the pressure drop in the next two paths of the LSC [17].
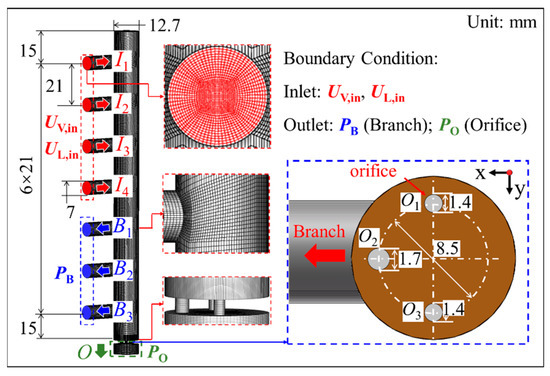
Figure 2.
Scheme of the header and the boundary conditions.
2.2. Methematical Method
In this paper, the volume of fluid (VOF) multiphase model is used to simulate the two-phase flow owing to its special geo-reconstruction interpolation. Moreover, due to the intense interaction between liquid and vapor, the RNG k-ε turbulence model is also used. The Standard Wall Function is chosen to simulate the near-wall flow. The following assumptions are made for the simulation: (1) the fluid properties are constants. (2) two-phase fluid flows in the header are adiabatic and the mass transfer between vapor-liquid interface is not considered. The governing equation is shown in Table 1.

Table 1.
Governing equations.
A segregated solver is employed for the transient-state process. The time step is set as 10−5 s. The governing equations are discretized by the Finite Volume Method (FVM). Furthermore, the residuals through every time step iterations are all lower than 10−4. The discrete scheme and the under-relaxation factor as well as other details are found in our previous research [16].
2.3. Mesh-Sensitive Test and Model Validation
The geometry of the header is discrete by the hexahedral mesh (Figure 2) and the first layer of the mesh is set in the sub-layer region, in which y+ is larger than 11.225. Moreover, four sets of cases with different mesh numbers are simulated for the mesh-sensitive test. Figure 3a shows that when the mesh number is more than 2.03 million, the liquid drainage rate by the orifice (ṁL,O) changes insignificantly. Hence, to balance the calculation consumption and the accuracy of the numerical model, the mesh number of 2.03 million is selected, in which the minimum orthogonal quality, the maximum ortho skew and the aspect ratio are 0.54, 0.43 and 2.53, respectively.
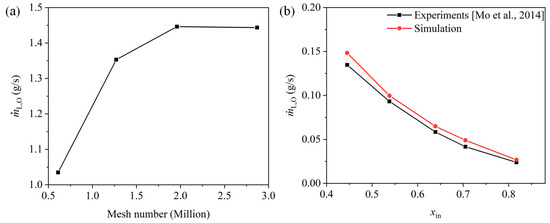
Figure 3.
(a) Mesh-sensitive test; (b) model validation [15].
The numerical model is also validated based on the experiments [15]. It is seen from Figure 3b that when the inlet vapor quality xin changes from 0.45 to 0.82, the average deviation between simulation data and experimental results is less than 10%, indicating good validity.
2.4. Evaluation Indicator
To evaluate the vapor-liquid separation performance, the vapor-liquid separation efficiency (η) is proposed (Equation (10)). It consists of two parts: the liquid drainage ratio (FL) and the vapor leakage ratio (FV). FL is defined as the ratio of the liquid drainage from the orifice to the inlet, as shown in Equation (11). Similarly, FV is defined as Equation (12).
3. Results and Discussion
In this paper, the two-phase flow characteristics in the branch outlets and orifices are comprehensively studied. The vapor-liquid separation performance and the phase distributions in the orifice are firstly investigated to obtain the vapor-liquid separation features. Then, the phase maldistributions in the branch outlet are discussed. Finally, the mechanistic model based on the force balance is established with a concern on the “droplet entrainment”.
R134a is used as the working fluid and its properties are calculated by REFPROP [19]. The inlet operating conditions including temperature and vapor quality (xin) are 45 °C and 0.5, respectively. To investigate its features under various conditions, the inlet mass flow rate (ṁin) is set in the range of 9–21 g/s based on scenarios in the air conditioning.
3.1. Performance of the Header and Flow Characteristics in the Orifices
The variation of η under different ṁin is depicted in Figure 4. It can be observed that with the increasing of ṁin, η increases firstly to the maximum value of 51.94% at ṁin = 12 g/s and then decreases. When ṁin is larger than 15 g/s, the degradation of η becomes severer. It becomes 29.99% at ṁin = 21 g/s. This will be discussed in the following section. The pressure difference (ΔP) crossing the orifice-baffle, which is one of the main driving forces for the liquid drainage [16], increases with the increasing of ṁin. This is because more liquid flows towards the right side of the orifice-baffle, leading to an increase in the height of the liquid film above the orifice-baffle. Thereafter, the static pressure above the orifice-baffle increases.
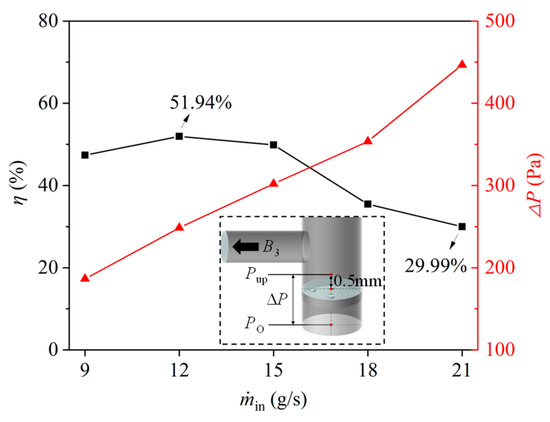
Figure 4.
Vapor-liquid separation efficiency and the pressure difference across the orifice-baffle.
To obtain a deep understanding of the flow characteristic and discover the causes of deteriorated vapor-liquid separation performance, the mass flow rates of the liquid drainage and vapor leakage through the orifices, i.e., ṁL,O and ṁV,O, are analyzed, as shown in Figure 5. As mentioned above, there exists a strong liquid impact at the right side of the baffle, O2, being the furthest away from the liquid impact, has a higher ṁL,O than O1 and O3. Different from η that is peaked at ṁin = 12 g/s, the peak of ṁL,O = 3.75 g/s appears at ṁin = 15 g/s. This is explained as: compared to ṁin = 12 g/s, ṁin = 15 g/s has a higher ṁL,O because of a larger driving force, but its FL is much smaller owing to the more liquid within ṁin, leading to a lower η given that FV in these two cases are negligible (see Figure 5b). ṁL,O maintains at around 3.30 g/s when ṁin is 18 g/s and 21 g/s. Meanwhile, ṁV,O weakens the vapor-liquid separation performance, derived from Equations (11) and (12). As seen in Figure 5b, ṁV,O has an opposite trend to ṁL,O. It decreases at first when ṁin is smaller than 15 g/s and then increases to 0.15 g/s at ṁin = 21 g/s. The vapor only leakage about 0.02 g/s and 0.01 g/s as ṁin equals to 12 g/s and 15 g/s, respectively. This is due to the liquid film above the orifice-baffle in these two cases being able to resist the impact of the liquid flow from the wall, in which the orifices are rarely affected by the fluid impact and only a small amount of vapor leakage. Conversely, much vapor leakage out from the orifice under the other three ṁin because of the unstable liquid film above the orifice-baffle. Moreover, the vapor is escaped out from O2 is less than that from O1 and O3 owing to its farthest distance away from the liquid impact.
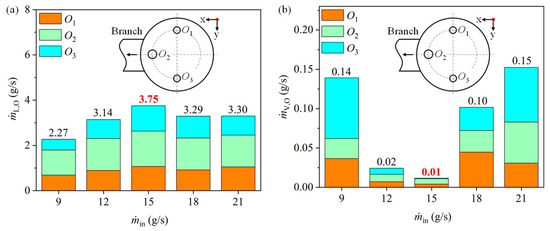
Figure 5.
Mass flow rate of (a) liquid; (b) vapor at each orifice.
Figure 6 displays the distributions of vector and density at the central section of the orifices. Clearly, the flow characteristics in O2 are significantly different from those in O1 and O3. When ṁin is between 9–15 g/s, the vapor velocity in O2 is normally lower than 1.5 m/s and it mostly exists near the wall of the orifice. As ṁin increases, the vapor with high velocity begins to appear in O2, which indicates more vapor leakage. This phenomenon is mainly due to the induced stronger liquid impact on the orifice-baffle at higher ṁin. As a result, the liquid film above the orifice-baffle is unable to resist the liquid impact and meanwhile the interactions between the liquid and vapor becomes intensive, leading to the increasing of ṁV,O. As for O1 and O3 that are closer to the liquid impact region, they are more likely to have a higher vapor velocity. As shown in Figure 6b, the velocity of the vapor in O1 and O3 can be up to 3 m/s as ṁin = 9 g/s. However, with more liquid accumulated on the orifice-baffle (Figure 6c,d), the effect of the fluid impact on these two orifices weakens, with only a little vapor leakage out from the orifices. Further increasing ṁin (Figure 6e,f), the liquid impact is enhanced again, contributing to a higher vapor velocity in O1 and O3. Summarily, the effects of the liquid impact on the orifice are the competitions between the liquid film on the orifice-baffle and ṁin. At the lower ṁin, the liquid film is too thin to resist the liquid impact and, consequently, the vapor escapes from the orifices, whereas at the higher ṁin, the interactions of the liquid and vapor are upgraded and the vapor is carried to the orifices by the liquid.
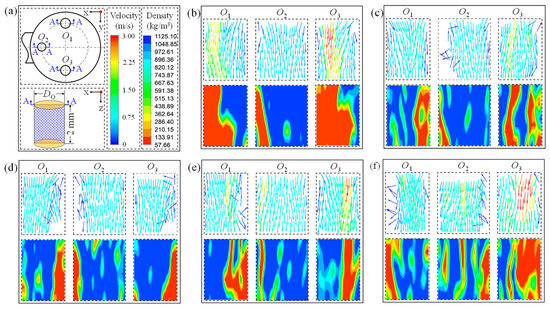
Figure 6.
(a) Instructions and distributions of velocity and density in each orifice at (b) 9 g/s, (c) 12 g/s, (d) 15 g/s, (e) 18 g/s and (f) 21 g/s.
3.2. Flow Characteristics in the Branch Outlet
As shown in Figure 7, the maldistributions of ṁB and xB in the branch outlets are rather significant. The liquid mass flow rate in each branch outlet (ṁL,B) increases with the increasing of ṁin. Moreover, the liquid flows into the header and jets on the header wall of the header. A part of the liquid breaks up into droplets that are thereafter dragged into the branch outlets by the vapor, which is termed as “droplet entrainment”. A similar phenomenon was also found by Li [12] and Zheng [20]. Obviously, ṁL,B in B3 is remarkably higher than that in B1 and B2. This is because the liquid flows to B3 is not only by droplet entrainment, but also comes from the overflowing liquid from the orifice-baffle that cannot be drained promptly. However, the vapor in the branch outlet is more uniform than liquid owing to its lower inertia force. ṁV,B in B1 is slightly lower than B2 and B3 for the considered ṁin.
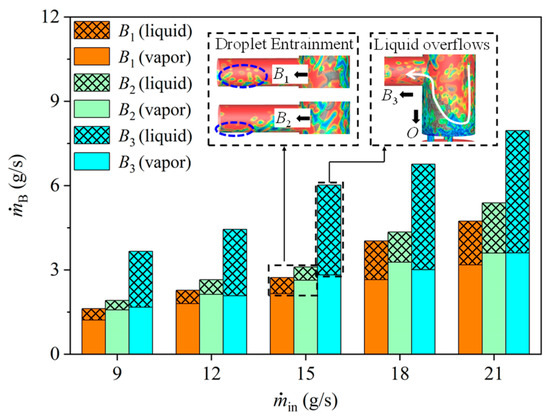
Figure 7.
Mass flow rate in each branch outlet.
The droplets which enter the branch outlet is mostly due to the drag of the vapor. Hence, the vapor velocity is essential. To further explore the vapor flow characteristic, the vapor velocity distribution along each branch outlet and the specific header planes are plotted in Figure 8. The two-phase fluid flows from the branch inlet I4 and mixes in S10. Due to the inertia, the fluid gathers on the right side of the header and a vortex is generated on the left side, resulting in the vapor velocity on the left side being lower than that on the right side. After S10, the fluid continues to flow downwardly, and then a part of it is divided into the B1 because of the suction of the branch outlet. The fluid is more accumulated at the lower part of B1 due to the inertia (S7), in which the vortex exists above the B1 and shows a vapor velocity non-uniform distribution. The other part of the fluid from I4 that cannot enter B1 in time will keep flowing in the header. In this way, the fluid also flows on the left side, resulting in a lower non-uniformity at S11. Similarly, the vapor velocity distribution in the next branch outlet (S8) and header (S12) are close to the S7 and S11 respectively. However, due to the diversion of the fluid, the vapor velocity decreases correspondingly. On the other hand, in the B3, the distribution of the vapor velocity is more uniform. This is mainly due to the fact that B3 has a maximum mass flow rate than B1 and B2, in which case the fluid can be fully fill at the B3, where there is no vortex generated. With the increase in ṁin, not only does the velocity increase but it also improves the non-uniformity of the velocity distributions.
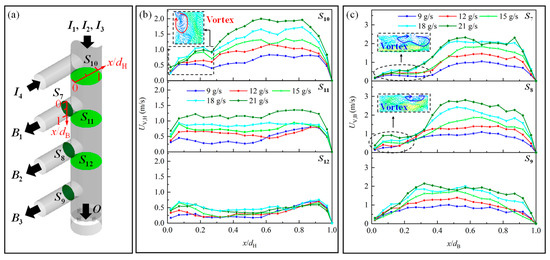
Figure 8.
(a) Instructions and the vapor velocity distribution in (b) header and (c) branch outlet.
3.3. Mechanism Model of Droplet
As described above, the droplets in the branch outlets are dragged by the vapor. Meanwhile there exist vortexes in the header and the branch outlets, resulting in the mainstream area being smaller than the actual cross-section area, which substantially increases the local mass flux. According to the droplet model proposed by Tan [21] that is listed in Appendix A, the droplet diameter (d) is mainly affected by the mass flux that is relevant to the vortexes. Hence, the vortex has a great influence on the droplet entrainments. However, the vortexes are sometimes neglected when analyzing droplet [13]. In order to reveal the effect of the vortex on droplet characteristics, the force on the droplets is analyzed. Moveover, a critical vapor velocity for “droplet entrainment” (UV,C) is also proposed. The following assumptions are made for the droplets: (1) they are spherical; (2) they have the same diameter in the same branch outlet.
Taking B1 as an example, Figure 9 demonstrates d in the header and the vapor velocity in B1 with and without vortex. It is observed that an increase in ṁin leads to an enlarged droplet diameter and decreased vapor velocity simultaneously. In addition, the existence of the vortex decreases the droplet diameter by up to 1.76 times and increases the vapor velocity in the branch outlet by 35.10%, which significantly affects the forces of the droplet.
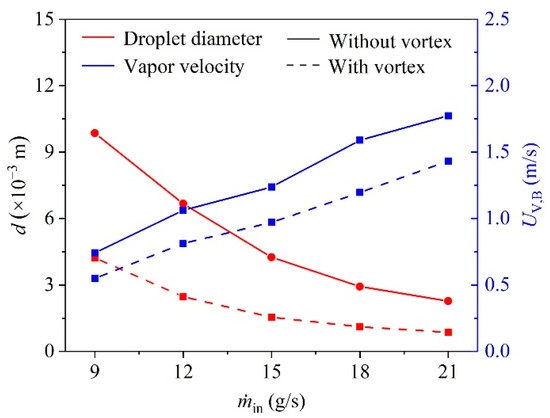
Figure 9.
Droplet diameter and the vapor velocity in the branch outlet under various ṁin.
The force balance of the droplet is further established and analyzed. The droplet in the header is generally subjected to four forces (Figure 10), they are the gravitation force (FG), the drag force (FD2) and the buoyancy force (FB) in the vertical direction as well as the drag force (FD1) in the axial direction. The details of these four forces are described in Appendix B. In these four forces, FG and FB are only dominated by d. Moreover d, the drag force (FD1 and FD2) is also depended on the velocity. The higher mass flux represents the smaller droplet diameter. The drag force under different ṁin is a result of the vapor velocity competing with d. As shown in Figure 11, the sum of forces in the vertical direction shows fluctuation with the increasing of ṁin and the minimum value is 2.04 × 10−4 N at ṁin = 12 g/s, while the force in the axial increases monotonously. FD1 and FD2 increases with the increasing of ṁin, which indicates the increasing rate of the velocity is larger than the decreasing rate of d. Meanwhile, FG and FB both decrease due to the droplet being smaller when increasing of ṁin. FG at ṁin = 21 g/s is only 1.02% to that at ṁin = 12 g/s. Since FG and FB are only related to the density difference, FG is constantly 20.14 times higher than FB, which represents that in general, the force in the vertical upward is relatively small compared to the downward. Interestingly, the dominant force in the vertical direction switches from FG to FD2 when ṁin is higher than 12 g/s.
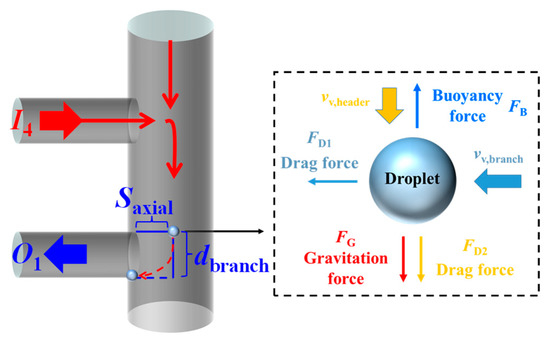
Figure 10.
Forces on droplet in the header.
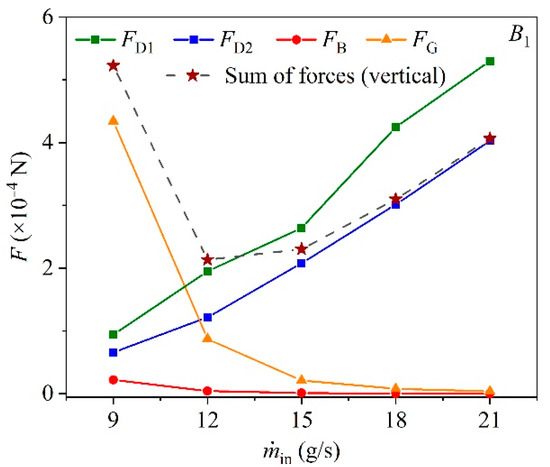
Figure 11.
Forces on droplet under various ṁin.
When the droplets flow into the intersection of the header and the branch outlet, the axial distance for droplets to be entrained to the branch outlet is Saxial and the vertical distance is the diameter of the branch outlet (dB), as shown in Figure 10. If the flowing time of droplet in the vertical direction tvertical is longer than that in the axial direction taxial, the droplet will be entrained to the branch outlet. Therefore, the critical point for the droplet entrainment is defined at tvertical = taxial. In this way, the critical vapor velocity (UV,C) required to entrain the droplet can be obtained when the droplet in the branch outlets is located in Saxial, as calculated as in Equations (13)–(15).
It can be observed that UV,C is highly correlated to the velocity of both phases in the header, the vapor velocity in the branch and d UV,C at the different axial locations under various ṁin is plotted in Figure 12. Clearly, the larger Saxial requires a higher UV,C to entrain the droplet and the growth rate of the UV,C decreases as the Saxial increases. Moreover, under the same axial location, for the droplet to be dragged to the branch outlet needs a higher UV,C when ṁin is increased. This is mainly due to the smaller d at higher ṁin, causing the larger acceleration and the shorter flow time tvertical in the vertical direction.
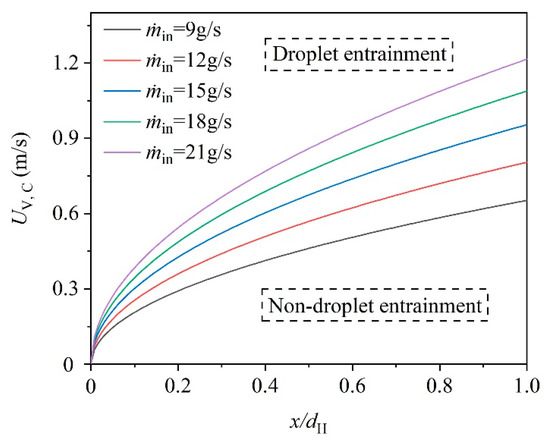
Figure 12.
The critical vapor velocity with and without vortex under various ṁin.
It is worth mentioning that in this study, the velocity in the header and the branch outlets are simplified to be averaged from each plane. The distributions of the droplet are assumed to be uniform in the header. Nevertheless, for the actual flow, the distributions of velocity and the volume fraction are non-uniform and extremely complex. In future work, the distribution characteristics of these parameters are of great interest to be quantified by a refined the model to improve the model accuracy.
4. Conclusions
Based on the VOF model and k-ε turbulence model, the flow characteristic of the fluid in the orifice-baffle header at various inlet operating conditions is simulated by CFD with attentions to the vortexes and droplets. Under the considered conditions, the conclusions are addressed as follows:
- (1)
- The vapor-liquid separation efficiency maintains superior at the inlet mass flow rate of 9–15 g/s and then deteriorated as beyond 15 g/s. The maximum η are 51.94% at the inlet mass flow rate of 12 g/s;
- (2)
- The liquid impact on the orifice-baffle results in the vapor leakage from the orifice. It becomes more intensive and is the main reason that deteriorates the separation performance when the inlet mass flow rate is higher than 15 g/s;
- (3)
- The liquid maldistribution in the branch outlets is mainly because of the overflowing in B3 that can be up to 4.36 g/s at the inlet mass flow rate of 21 g/s, whereas the vapor is more uniform distribution in the branch outlets owing to its lower inertia;
- (4)
- The vortex in the header causes a decrease in the droplet diameter and an increase in the vapor velocity significantly in the branch outlet. The dominant force of the droplet in the vertical direction changes from FG to FD2 as ṁin increases.
Author Contributions
Conceptualization, J.C.; methodology, K.H.; software, K.H.; visualization, K.H. and Z.Y.; formal analysis, X.L.; investigation, J.C.; data curation, K.H.; writing—original draft preparation, K.H.; writing—review and editing, Y.L. and J.H.; supervision, J.C.; project administration, J.C.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (51736005), Guangdong Basic and Applied Basic Research Foundation (2022A1515012035) and Innovation Leadership of Sciences and Technologies Program in Guangdong Special Support Plan (2017TX04N371).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbol | |
| avertical | Acceleration in the vertical direction, m/s2 |
| Cd | Drag force coefficient |
| C1ε | Empirical constants, 1.42 |
| C2ε | Empirical constants, 1.68 |
| Cμ | Empirical constants, 0.0845 |
| d | Diameter, mm |
| F | Drainage (leakage) rate ratio |
| FB | Buoyancy force, N |
| FD1 | Drag force (axial), N |
| FD2 | Drag force (vertical), N |
| FG | Gravitational force, N |
| f | The friction factor of the vapor |
| Gk | Generation of turbulent kinetic energy |
| g | Gravitational acceleration, m/s2 |
| ṁ | Mass flow rate, kg/s |
| ΔP | Pressure difference, Pa |
| Re | Reynold number |
| Saxial | Axial distance, m |
| t | Time, s |
| tvertical | Droplet flow time in the vertical direction, s |
| taxial | Droplet flow time in the axial direction, s |
| U | Velocity, m/s |
| Greek Symbol | |
| α | Volume fraction |
| ε | Turbulence kinetic dissipation, m2/s3 |
| η | Vapor-liquid separation efficiency |
| μ | Dynamic viscosity, kg/(m2·s2) |
| μt | Turbulence kinetic viscosity, kg/(m2·s2) |
| ρ | Density, kg/m3 |
| σ | Surface tension coefficient N/m |
| σk | Empirical constants, 1.0 |
| σε | Empirical constants, 1.2 |
| Subscript | |
| B | Branch outlet |
| C | Critical |
| H | Header |
| in | Inlet |
| L | Liquid |
| O | Orifice outlet |
| S | Supercritical |
| V | Vapor |
Appendix A
The droplet diameter is calculated based on Tan et al. [21], as shown in Equations (A1)–(A4).
where the σ, UL,S, UV,S, ρV, f represents the surface tension surface tension, the supercritical velocity of liquid, the supercritical velocity of vapor, vapor density and the friction factor of the vapor.
Appendix B
The droplet in the header is generally subjected to drag force in the axial direction (FD1), the gravitation force (FG), the buoyancy force (FB) and the drag force in the vertical direction (FD2). They are evaluated as follow:
where UV,H, UL,H and UV,B represent the vapor velocity and the droplet velocity in the header and the vapor velocity in the branch outlet, respectively. d is the droplet diameter. Cd is the drag force coefficient for the droplet, which is calculated by the classical model proposed by Schiller and Naumann [22], as shown in Equation (A9).
References
- Peng, X.; Wu, D.; Lu, G.; Wang, Z.; Huang, M. Liquid-Vapor Separation Air Condenser. China Patent No. 200610113304.4, 22 September 2006. [Google Scholar]
- Li, J.; Yang, Z.; Hu, S.; Yang, F.; Duan, Y. Thermo-Economic Performance Improvement of Butane/Isopentane Mixtures in Organic Rankine Cycles by Liquid-Separated Condensation Method. Appl. Therm. Eng. 2020, 181, 115941. [Google Scholar] [CrossRef]
- Hua, N.; Xi, H.; Xu, R.J.; Chen, Y.; Wang, H.S. Numerical Simulation of Multi-Pass Parallel Flow Condensers with Liquid-Vapor Separation. Int. J. Heat Mass Transf. 2019, 142, 118469. [Google Scholar] [CrossRef]
- Zhong, T.M.; Chen, Y.; Zheng, W.X.; Hua, N.; Luo, X.L.; Yang, Q.C.; Mo, S.P.; Jia, L.S. Experimental Investigation on Microchannel Condensers with and without Liquid-Vapor Separation Headers. Appl. Therm. Eng. 2014, 73, 1510–1518. [Google Scholar] [CrossRef]
- Zhong, T.; Chen, Y.; Hua, N.; Zheng, W.; Luo, X.; Mo, S. In-Tube Performance Evaluation of an Air-Cooled Condenser with Liquid-Vapor Separator. Appl. Energy 2014, 136, 968–978. [Google Scholar] [CrossRef]
- Li, J.; Hrnjak, P. Improvement of Condenser Performance by Phase Separation Confirmed Experimentally and by Modeling. Int. J. Refrig. 2017, 78, 60–69. [Google Scholar] [CrossRef]
- Chen, J.; Ding, R.; Li, Y.; Lin, X.; Chen, Y.; Luo, X.; Yang, Z. Application of a Vapor–Liquid Separation Heat Exchanger to the Air Conditioning System at Cooling and Heating Modes. Int. J. Refrig. 2019, 100, 27–36. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Lin, X.; Yang, Z.; Chen, Y.; Luo, X. Quantification on the Effects of Liquid-Vapor Separation in Air-Conditioning System by Using Advanced Exergy Analysis. J. Therm. Sci. 2020, 29, 597–608. [Google Scholar] [CrossRef]
- Chen, J.; Chen, L.; Lin, X.; Chen, Y.; Luo, X.; Yang, Z.; Liang, Y. Performance of Heat Pump Water Heater (HPWH) with and without Liquid-Separation: Detailed Experimental Comparisons. Appl. Therm. Eng. 2020, 179, 115713. [Google Scholar] [CrossRef]
- Lu, P.; Luo, X.; Wang, J.; Chen, J.; Liang, Y.; Yang, Z.; Wang, C.; Chen, Y. Thermo-Economic Design, Optimization, and Evaluation of a Novel Zeotropic ORC with Mixture Composition Adjustment during Operation. Energy Convers. Manag. 2021, 230, 113771. [Google Scholar] [CrossRef]
- Oh, K.; Lee, S.; Park, T.; Kim, Y. Multistage Gas and Liquid Phase Separation Condenser. U.S. Patent 10/444,486, 23 May 2003. [Google Scholar]
- Li, J.; Hrnjak, P. Visualization and Quantification of Separation of Liquid-Vapor Two-Phase Flow in a Vertical Header at Low Inlet Quality. Int. J. Refrig. 2018, 85, 144–156. [Google Scholar] [CrossRef]
- Li, J.; Hrnjak, P. Parametric Study and Improvement of Phase Separation in Intermediate Headers of Microchannel Condensers. J. Fluids Eng. Trans. ASME 2020, 142, 2–12. [Google Scholar] [CrossRef]
- Li, J.; Hrnjak, P. Numerical Study of R134a Liquid-Vapor Flow in a Vertical Header for Phase Separation with Low Inlet Quality. Int. J. Refrig. 2021, 129, 11–21. [Google Scholar] [CrossRef]
- Mo, S.; Chen, X.; Chen, Y.; Yang, Z. Passive Control of Gas-Liquid Flow in a Separator Unit Using an Apertured Baffle in a Parallel-Flow Condenser. Exp. Therm. Fluid Sci. 2014, 53, 127–135. [Google Scholar] [CrossRef]
- Li, Y.; Luo, X.; Wang, Z.; Yang, Z.; Chen, J.; Liang, Y.; Wang, C.; Chen, Y. Numerical Simulation on the Header-Orifice Structure-Based Liquid-Vapor Separator Used in Liquid-Separation Condenser. Chem. Eng. Sci. 2021, 235, 116475. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Ding, R.; Lin, X.; Chen, Y.; Luo, X.; Yang, Z. Comparative Performance of Air-Conditioning Systems with Different Refrigerant Circuitries in Liquid-Separation Condenser. Int. J. Refrig. 2018, 92, 154–164. [Google Scholar] [CrossRef]
- EI Hajal, J.; Thome, J.R. Condensation in Horizontal Tubes, Part 1: Two-Phase Flow Pattern Map. Int. J. Heat Mass Transf. 2003, 46, 3349–3363. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP; Version 10; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Su, W.; Hwang, Y.; Deng, S.; Zheng, N.; Zhao, L.; Lu, P. Experimental Study on Phase Separation of Refrigerant at Horizontal T-Junction. Int. J. Multiph. Flow 2018, 105, 217–233. [Google Scholar] [CrossRef]
- Tan, X.H.; Li, X.P.; Liu, J.Y. Model of Continuous Liquid Removal from Gas Wells by Droplet Diameter Estimation. J. Nat. Gas Sci. Eng. 2013, 15, 8–13. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, Z. A Drag Coefficient Correlation. Z. Ver. Deutsch. Ing. 1935, 77, 318–320. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).