Enhanced Search-and-Rescue Optimization-Enabled Secure Route Planning Scheme for Internet of Drones Environment

Abstract

The Internet of Drones (IoD) is greatly developed and promotes many civil applications. However, it can still be prone to several security problems which threaten public safety. The issue of security poses further problems upon linking the IoD to the Internet, as its data stream is exposed to attack. For secure communication between drones, an effective route planning scheme with a major intention of accomplishing security is needed. With this aim, this study develops an enhanced search-and-rescue optimization-enabled secure route planning (ESRO-SRP) scheme for the IoD environment. The presented ESRO-SRP technique mainly aims to derive a set of optimal routes to the destination. In addition, the ESRO-SRP algorithm is derived by the integration of the quasi-oppositional-based learning (QOBL) concept with the conventional SRO algorithm. Moreover, the presented ESRO-SRP technique derived a fitness function encompassing different input parameters such as residual energy, distance, and degree of trust. The experimental validation of the ESRO-SRP technique is carried out under several aspects, and the results demonstrated the enhancements of the ESRO-SRP model over recent approaches. The ESRO-SRP model has provided an increased packet delivery ratio (PDR) of 86%, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm approaches have accomplished a minimal PDR of 79.60%, 73.60%, 67.60%, and 63.20%, respectively.

1. Introduction

The use of unmanned aerial vehicles (UAVs), also termed drones, is anticipated to incline at exceptional rates because of growing curiosity from investors, hobbyists, and researchers; the quantity of drones is quickly rising, and the Internet of Drones (IoD) environment and number of related applications are expanding rapidly, in which an infinite number of multi-sized drones flawlessly communicate with one another via area service providers whose objective it is to understand and align the accessibility of drones to a controlled airspace and operate a navigation service [1]. The economic development of drone industries in the United States, involving military scouting, traffic, wildlife surveillance, urban safety scrutiny of infrastructure, on-demand package supply, aerial photography, etc., is reported to be substantial for industries or business operations [2,3]. Figure 1 depicts the procedure of IoD.

Figure 1. Application areas of IoD.

Even though the IoD network offers numerous benefits, it also carries numerous susceptibilities which should be handled, the most important criteria of which are privacy and security problems [4]. However, the IoD network system is commonly placed for real-time application zones where end users need to obtain real-time information from UAVs which are connected to a particular area. So, there are high chances of security assaults occurring, leading to the colossal ruin of the data exchange functions inside the network [5,6,7]. An attacker can gain access to the keys and block transmissions. For the accessibility of keys, the intruder can abuse a susceptibility in the IoD network and its application zones. The intruder might alter this information, resulting in the misguidance of the receivers. However, IoD access management is a significant variable, and security problems regarding authorization and accessibilities must be emphasized [8,9]. This applies to the data in transfer, which should be protected for confidentiality, authenticity, and integrity.

Most of the privacy and security methods advanced by authors were intended to ensure security measures on the IoD network [10,11]. The approaches focused on mitigating problems which influence the secure localization of drones or privacy and security necessities linked with the IoD network system. Localization fault assaults impede the reliability position of UAVs, leading to distressing costs for the overall functionality of the IoD network [12]. Additionally, privacy and security necessities are the objectives that decide the functions and capacities of the IoD network attained in justifying certain privacy and security measures [13]. The privacy and security needs of the IoD network involve authenticity, integrity, availability, privacy preservation, and confidentiality [14].

Tian et al. [15] suggested a powerful privacy-preserving validation architecture. With the help of a lightweight online/offline signature model, this architecture guarantees verification effectiveness while placing resource constraints on small-scale UAVs. Considering the high mobility of UAVs, a prediction validation model is explored by using mobile edge computing (MEC) in this architecture for reducing the verification expenses for possible verification activity. Allouch et al. [16] developed an Unmanned Traffic Management (UTM)-Chain, a light-weight blockchain-related security model with hyper ledger fabric for UTM of lower-altitude UAV that fits the storage and computation resource constraints of UAV. Furthermore, UTM-Chain offers secured and unchangeable traffic information among their ground control stations and the UAVs. In [8], a blockchain-related security model for cyber-physical systems is introduced for ensuring secured transmission of datasets amongst drones. In this model, the miner node is chosen by deep learning (DL)-based technique, that is, a deep Boltzmann machine, with features such as flight time of the drone, computation resource, and the available battery power.

The authors in [17] developed a lightweight user verification system where the client in the IoD environments needs to directly access information from a drone to show that the client is authorized for accessing the dataset from that drone. The formal security validation with the generally recognized automatic confirmation of Internet security protocol and application tool alongside informal security investigation shows that the suggested technique is secured against well-known attacks. In [18], the authors developed a Drone-map organizer, viz., a service-related fog-based drone managing scheme that monitors, communicates, and controls with drones through the networks. The suggested technique enables interaction with various drones through the internet that allows drones to be controlled anyplace and anywhere, with no long-distance restrictions. This model offers drones access to fog computational resources for drones to perform heavyweight load computation. Though existing works have focused on the IoD environment, it is still necessary to design energy-efficient and security-based solutions for the IoD environment with the inclusion of multiple input parameters of the drones.

This study develops an enhanced search-and-rescue optimization-enabled secure route planning (ESRO-SRP) scheme for the IoD environment. The presented ESRO-SRP technique mainly aims to derive a set of optimal routes to the destination. In addition, the ESRO-SRP algorithm is derived by the integration of the quasi-oppositional-based learning (QOBL) concept with the conventional SRO algorithm. Moreover, the presented ESRO-SRP technique derived a fitness function encompassing different input parameters such as residual energy (RE), distance, and trust degree. The experimental validation of the ESRO-SRP technique is carried out under several aspects. In short, the major contributions are summarized as follows.

• To the best of our knowledge, the ESRO-SRP technique for the IoD environment does not exist in the literature.
• Develop a new ESRO-SRP technique for a secure route selection process in the IoD environment.
• Derive an ESRO-SRP algorithm using the combination of QOBL with the traditional SRO algorithm and derive a fitness function involving multiple input parameters.
• Simulate the performance of the ESRO-SRP technique under varying levels of energy consumption in the IoD environment.

The rest of the paper is organized as follows. Section 2 offers a detailed discussion of the proposed model and Section 3 validates the experimental results of the proposed model. Finally, Section 4 concludes the study with key findings and possible future enhancements.

2. Materials and Methods

In this study, a novel ESRO-SRP technique has been developed for secure communication among drones in the IoD environment. The presented ESRO-SRP technique mainly aims to derive a set of optimal routes to the destination. In addition, the ESRO-SRP algorithm is derived by the integration of the QOBL concept with the conventional SRO algorithm. Moreover, the presented ESRO-SRP technique derived a fitness function encompassing different input parameters such as RE, distance, and trust degree.

2.1. Overview of ESRO-SRO Algorithm

In the SRO approach, the human position is equal to the resolution of the optimization issues, and the clue quantity accomplished in the location characterizes the objective function. The group members gather clue information in the search. Few clues are absent in the event of gaining optimal clues in another position, but the dataset is exploited for optimizing the searching technique [19]. Here, the position of the left clue can be stored in the ($M$ memory matrix), where the position of the human is stored in the ($X$ position matrix). The $M$ matrix dimension is the same as $X$. They are $N\times D$ matrices, whereas $D$ symbolizes problem dimension and $N$ embodies human count. The clue matrixes have the attained clue position. The $M$ and $C$ matrixes are upgraded in all human searching processes [19]:

$$C=\left\{\begin{array}{l}X\hfill \\ M\hfill \end{array}\right\}=\left\{\begin{array}{lll}{X}_{11}\hfill & \cdots \hfill & X_{1D}\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill \\ X_{N1}\hfill & \cdots \hfill & X_{ND}\hfill \\ M_{11}\hfill & \cdots \hfill & M_{1D}\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill \\ M_{N1}\hfill & \cdots \hfill & M_{ND}\hfill \end{array}\right\},$$

(1)

In Equation (1), $X$ and $M$ represent the position of human and memory matrixes; correspondingly, $X_{N1}$ embodies the position of initialized dimension for $N^{\mathrm{th}}$ human, and $M_{1D}$ characterizes $D^{\mathrm{th}}$ dimensional position for the preliminary memory. Given the description presented in the previous section, in addition to an arbitrary clue amid accomplished clues, the search path is described as follows:

$${\mathrm{SD}}_i=\left(X_i-C_k\right) , k\ne i,$$

(2)

In Equation (2), $X_i,$ $C_k$, and ${\mathrm{SD}}_i$ correspondingly symbolize $j^{\mathrm{th}}$ human location, the $k^{\mathrm{th}}$ clue location, and $j^{\mathrm{th}}$ human searching direction; $k$ suggests arbitrary numbers within 1 and $2N$ and appropriately chosen $k\ne i.$ It is important to emphasize that human usually seeks accordingly, and some repetitious positions could not be searched another time. Henceforth, the search should be generated if the group member is restrained. Therefore, $X_j$ dimension could not be rehabilitated.

For applying this constraint, the binomial crossover operator has been exploited when the clue is larger than that of the clue associated with the present position, an ${\mathrm{SD}}_j$ direction and the position of that search clue; next, the searching method undergoes the present location beside the ${\mathrm{SD}}_i$ direction [16].

$$\begin{gathered} X_{i,j=}^{\prime } \{\begin{array}{c}\{\begin{array}{l}{C}_{k,j}+r\mathrm{l}\times \left(X_{i,j}-C_{k,j}\right),if f\left(C_k\right)>,f\left(X_i\right)\hfill \\ X_{\mathrm{i},j}+r\mathrm{l}\times \left(X_{i,j}-C_{k,j}\right),otherwise\hfill \end{array}\\ X_{i,j}\end{array}\begin{array}{c}if r2<\mathrm{SEor} j=j_{rand},\\ otherwise,\end{array} \\ \left(j=1, \dots , D\right), \end{gathered}$$

(3)

where the following are defined: $X_{i,j}^{\prime }$ symbolizes the novel place of $j^{\mathrm{th}}$ parameters of $i^{\mathrm{th}}$ humans; $C_{k, j}$ specifies place of $j^{\mathrm{th}}$ parameter for the $k^{\mathrm{th}}$ accomplished clues; $f\left(C_k\right)$ and $f\left(X_i\right)$ correspondingly imply an objective function for the $C_k$ and $X_i$ solution; $r\mathrm{l}$ and $r2$ epitomize arbitrary value; $j_{\mathrm{rand}}$ symbolizes arbitrary value within 1 and $D$ that assures that 1D of $X_{i,j}^{\prime }$ is varied from $X_{i,j}^{ }$. Equation (3) is applied to accomplish a new place of $j^{\mathrm{th}}$ human in all dimensions.

Next, humans search nearby the current place, and the concept of related discrete clues applied in the social phase is exploited for searching. In conflict with the social phase, $X_i$ dimension is attuned in the separation phase. The novel place of $j^{\mathrm{th}}$ human can be accomplished as follows [16]:

$$X_i^{\prime }=X_j+r3\times \left(C_k-C_m\right) , i\ne k\ne m,$$

(4)

In Equation (4), $k$ and $m$ characterize arbitrary numbers within 1 and $2N$. To evade motion besides another clue, $k$ and $m$ are designated in this manner, such that $i\ne k\ne m.$ $r3$ symbolizes an arbitrary value between zero and one. In the metaheuristic method, each solution should be positioned in the solution region, and when they are farther from the permitted solution region, they should be altered. If the novel place of a human is farther from the solution region, the succeeding equation is exploited for altering the novel place:

$$X_{i,j=}^{\prime }\left\{\begin{array}{l}\frac{\left(X_{i,j}+X_j^{ max }\right)}{2},if X_{i,j}^{\prime }>x_j^{max},\hfill \\ \frac{\left(X_{i,j}+X_j^{ min }\right)}{2},if X_{i,j}^{\prime }<x_j^{min},\hfill \end{array}\right. \left(\begin{array}{c}j\\ =1,\dots , D\end{array}\right)$$

(5)

The process involved in the SRO algorithm is given in Algorithm 1.

Algorithm 1: Pseudo-code of the SRO algorithm

Begin $\mathrm{Initialize} \mathrm{parameters}: \mathrm{Arbitrary} \mathrm{population} \mathrm{initialization} \mathrm{of} 2\mathrm{N} \mathrm{solutions}, \left[X_j^{min}, X_j^{max}\right]$$, j=1,\dots , D$ $\mathrm{Organize} \mathrm{the} \mathrm{solution} \mathrm{in} \mathrm{a} \mathrm{decreasing} \mathrm{manner} \mathrm{and} \mathrm{decide} \mathrm{the} \mathrm{optimal} \mathrm{location} \left(\mathrm{Xbest}\right)$ $\mathrm{Exploit} \mathrm{the} 1\mathrm{st} \mathrm{half} \mathrm{of} \mathrm{the} \mathrm{organized} \mathrm{outcome} \mathrm{for} X$$\mathrm{and} \mathrm{the} \mathrm{remaining} \mathrm{for} M$ $\mathrm{Represent} \mathrm{variables} (\mathrm{SE}, \mathrm{MU}) \mathrm{and} \mathrm{set} \mathrm{the} {\mathrm{USN}}_i=0$$\mathrm{where} i=1,\dots , N$ $\mathbf{While} \mathrm{end} \mathrm{criteria} \mathrm{are} \mathrm{not} \mathrm{met} \mathbf{do}$  $\mathbf{For} i=1$$\mathrm{to} N \mathbf{do}$   $\mathrm{C}= \left\{\begin{array}{l}X\hfill \\ M\hfill \end{array}\right\}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}//\mathrm{Social} \mathrm{Phase}$    ${\mathrm{SD}}_j=$$\left(X_j-{\mathrm{C}}_k\right),$$k$$\mathrm{was} \mathrm{chosen} \mathrm{arbitrarily} \mathrm{that} i\ne k$   $j_{\mathrm{rand}}=$$\mathrm{rand} \mathrm{int}$$[1, D]$    $r1$$=$ rand [−1, 1]    $\mathbf{For} j=1$ $\mathrm{to} D$ do     $X_{i,j}^{\prime }=\left\{\begin{array}{cc}\left\{\begin{array}{cc}{C}_{k,j}+r1\times S{D}_{i,j}, & if f\left(C_k\right)>f\left(X_i\right),\\ X_{i,j}+r1\times S{D}_{i,j},& otherwise\end{array}\right.& \\ & \end{array}\right.$      $X_{i,j}^{\prime }=\left\{\begin{array}{cc}\left(X_{i,j}+X_j^{max}\right)/2,& \mathrm{if} X_{i,j}^{\prime }>X_j^{max}\\ \left(X_{i,j}+X_j^{min}\right)/2,& \mathrm{if} X_{i,j}^{\prime }<X_j^{min}\end{array}\right.$   End For   $M_n=\left\{\begin{array}{cc}{X}_i,& \mathrm{if} f\left(X_i^{\prime }\right)>f\left(X_i\right),\\ M_n,& otherwise\end{array}\right.$    $X_i=\left\{\begin{array}{l}{X}_i^{\prime }, \mathrm{if} f\left(X_i^{\prime }\right)>f\left(X_i\right)\hfill \\ X_i, otherwise\hfill \end{array}\right.$    ${\mathrm{USN}}_i=\left\{\begin{array}{l}{\mathrm{USN}}_i+1, \mathrm{if}f\left(X_i^{\prime }\right)<f\left(X_i\right)\hfill \\ 0, otherwise\hfill \end{array}\right.$    $\mathrm{C}= \left\{\begin{array}{l}X\hfill \\ M\hfill \end{array}\right\}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}//\mathrm{Individual} \mathrm{Stage}$    $X_i^{\prime }=X_i+$$\mathrm{rand} \left[0, 1\right]\times$$\left({\mathrm{C}}_k-{\mathrm{C}}_m\right),$    $\mathbf{For} j=l$ $\mathrm{to} D$ do     $X_{i,j}^{\prime }=\left\{\begin{array}{cc}\left(X_{i,j}+X_j^{max}\right)/2,& \mathrm{if} X_{i,j}^{\prime }>X_j^{max}\\ \left(X_{i,j}+X_j^{min}\right)/2,& \mathrm{if} X_{i,j}^{\prime }>X_j^{min}\end{array}\right.$   End For   $M_n=\left\{\begin{array}{cc}{X}_i,& \mathrm{if} f\left(X_i^{\prime }\right)>f\left(X_i\right),\\ M_n,& otherwise\end{array}\right.n randomly chosen$    $X_i=\left\{\begin{array}{l}{X}_i \mathrm{if} f\left(X_j^{\prime }\right)>f\left(X_i\right)\hfill \\ X_i \mathrm{otherwise}\hfill \end{array}\right.$    ${\mathrm{USN}}_i=\left\{\begin{array}{l}{\mathrm{USN}}_i+1, \mathrm{if} f\left(X_i^{\prime }\right)<f\left(X_i\right)\hfill \\ 0,otherwise\hfill \end{array}\right.$    $\mathbf{If} \mathrm{the} {\mathrm{USN}}_i> \mathrm{MU} \mathbf{do}$     $\mathbf{For} j=l$ $\mathrm{to} D$ do      $X_{i,j}=X_j^{mini}+$$\mathrm{rand} \left[0, 1\right]\times$$\left(X_j^{maxi}-X_j^{mini}\right)$    End for     ${\mathrm{USN}}_i=0$     End If   End for   Decide the existing finest place and upgrade Xbest End while Return Xbest End

Next, in all iterations, the member of the group searched according to the two phases, and after each stage, once the value of the main function is in position, $X_i^{\prime }\left(f\left(X_i^{\prime }\right)\right)$ is greater than that of the preceding one ($f \left(X_i\right)),$ thus the earlier position $\left(X_i\right)$ would be stored in an arbitrary place of the M memory matrix and it would be adopted as a novel place. If not, the position is left and memory is not improved:

$$M_n=\left\{\begin{array}{c}{X}_i,if f \left(X_i^{\prime }\right)>,f\left(X_i\right) \\ M_n, \mathrm{otherwise} \end{array}\right.$$

(6)

$$X_i=\left\{\begin{array}{c}{X}_i^{\prime },if f \left(X_i^{\prime }\right)>,f\left(X_i\right) \\ X_i, \mathrm{otherwise},\end{array}\right.$$

(7)

where $M_n$ indicates the location of $n^{\mathrm{th}}$ clue saved in the $M$, and $n$ represents arbitrary numbers within 1 and $N$. With that memory, upgrading increases the different kinds of techniques and the ability of methods for detecting a globally optimum solution. Firstly, the unsuccessful search number (USN) is fixed as zero for all human beings. Once the human discovers an optimal clue in the first and second stages of the searching technique, the USN is fixed as zero for that human; if not, it raises it by one point as follows [16]:

$${\mathrm{USN}}_i=\left\{\begin{array}{c}{\mathrm{USN}}_i+\mathrm{l},if f\left(X_i^{\prime }\right)<,f\left(X_j\right)\\ 0,or else\end{array}\right.$$

(8)

The arbitrary place from the search region is represented in the following equation and ${\mathrm{USN}}_i$ is fixed as zero for that human:

$$X_{i,j}=X_j^{\min }+r4\times \left(X_j^{\max }-X_j^{ \min }\right)j=1, \dots , D,$$

(9)

In Equation (9), $r4$ designates an arbitrary value and is discrete for each dimension. Tizhoosh proposed the concept of oppositional-based learning (OBL) that includes opposite numbers having the highest possibility of accomplishing a solution compared to arbitrary numbers. The incorporation of OBL with the SRO method leads to an improved convergence rate and effective result of the presented ESRO-SRP algorithm. The QOBL method applies quasi-opposite value efficiently through the opposite number in the global optimal outcome. Assume $\chi$ represents a real number in $I$-dimensional region. The $x^o$ and $x^{qo}\left(\mathrm{of} x\right)$ opposite and quasi-opposite numbers are shown in the following [20]:

$$x^0=a+b-x$$

(10)

In which $x\in ℝ$ and $\in$ $b$].

$$x^{qo}=rand\left(\frac{a+b}{2}, x^0\right)$$

(11)

Let $X\left(x_1, x_2, \dots , x_n\right)$ be a point from the $n$-dimensional region. The opposite point, $X^o\left(x_1^o, x_2^o, \dots , x_n^0\right)$ and quasi-opposite point, $X^{qo}\left(x_1^{qo}, x_2^{qo}, \dots , x_n^{qo}\right)$ are shown in the following.

$$x_i^o=a_i+b_i-x_i$$

(12)

Here, $x_i\in ℝ$ and $x_i\in \left[a_i, b_i\right]\forall i\in 1, 2, \dots , n.$

$$x_i^{qo}=rand\left(\frac{a_i+b_i}{2}, x_i^o\right)$$

(13)

In QOBL is exploited to the SRO algorithm to initialize the population as well as creation jumping. It generates a group of optimum outcomes for population initialization [8]. Algorithm 2 defines the QOBL pseudo-code to the novel population.

Algorithm 2: Pseudo-code of QOBL

$\mathbf{for} i=1: Eco\_size$   $\mathbf{for} j=1: D$     $X_{i,j}^o=l{b}_j+u{p}_j-X_{i,j};$     $C_{i,j}=\left(l{b}_j+u{p}_j\right)/2;$     $\mathbf{if} (X_{i,j}<C_{i,j})$        $X_{i,j}^{qo}=C_{i,j}+\left(X_{i,j}^o-C_{i,j}\right)\times rand;$     else        $X_{i,j}^{qo}=X_{i,j}^o+\left(C_{i,j}-X_{i,j}^o\right)\times rand;$     end if   end for end for

2.2. Process Involved in ESRO-SRP Technique

To define an optimum group of routes, an offered function was employed to determine the following hop to destination and is represented by:

$$f\left(x\right)=\{i, for which\left|\left(\frac{i}{k}-X_{i_{f}j}\right)\right| is minimum, {\forall }_{i}1\le i\le k$$

(14)

The drive is to determine an optimum group of routes from the cluster heads (CHs) to the base station (BS), employing a fitness function (FF) comprising 2 parameters such as energy and distance. Primarily, the RE of the next-hop node is determined, and a node with higher energy was provided as a relay node. To transfer data, the source node sends it to the relay node, which is further forwarded to BS utilizing inter CHs. Thus, the node with higher RE is provided as the next-hop node. A primary sub-objective $f1$ was offered as:

$$f1=E_{CH}$$

(15)

In addition, the Euclidean distance was executed to define the distance from CH to BS. The minimized energy dissipation was frequently dependent on the broadcast distances. With a lesser distance, the energy was retained significantly [21]. Once the distance is improved, a further count of energy is spent. Hence, the node with lesser distances is chosen to relay nodes. So, the next sub-objective using distance is $f2$ which is formulated as:

$$f2=\frac{1}{{{\displaystyle \sum }}_{i=1}^{\mathrm{m}}d is\left(C{H}_i, NH\right)+dis\left(NH, BS\right)}$$

(16)

The present research work utilized direct trust values (TVs) amongst drones, and their mathematical process was signified as:

$$f3=Trust$$

(17)

$$T{r}_{i,j}=\left(T{r}_{ij}^{Dir}+T{r}_{ij}^{Indir}\right)/2.$$

(18)

Here, $T{r}_{ij}^{dir}$ and $T{r}_{ij}^{indir}$ denotes the direct as well as indirect TVs of one node to another node correspondingly. The count of trust nodes from the cluster is attained in the group with maximal TVs, and their state value was provided by the level of confidence values suggested in one node to another node. The TV of BS was computed as:

$$T{r}_C={\displaystyle \sum }_{j=1}^{S-1}T{r}_{C\left(i,j\right)}/\left(S-1\right).$$

(19)

In the above formula, $T{r}_C$ refers to the trusted value and $S$ represents the amount of drones. If the path trust was smaller than the trust requirement value, the path trust alert occurrence was triggered.

The above-mentioned sub-objective was revised as to FF as offered in that ${\alpha }_1$ and ${\alpha }_2$ denotes the weight assigned to every sub-objective.

$$Fitness={\alpha }_1\left(f1\right)+{\alpha }_2\left(f2\right)+{\alpha }_1\left(f3\right), where{\displaystyle \sum }_{i=1}^3{\alpha }_i=1{\alpha }_i\epsilon \left(0,1\right);$$

(20)

3. Results and Discussion

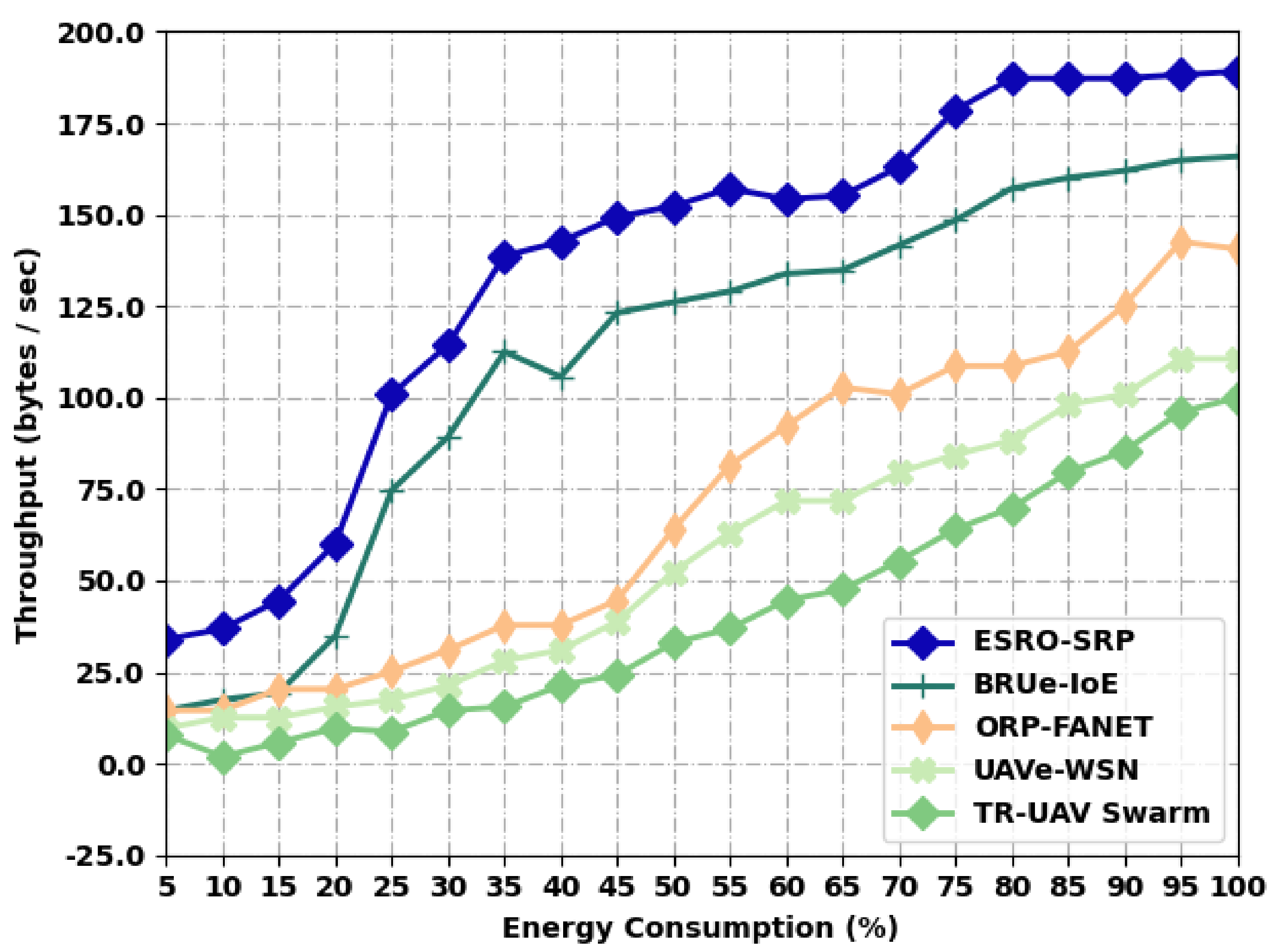
In this section, the performance validation of the ESRO-SRP model is examined under distinct levels of energy consumption (EC). The EC is varied from 5% to 100% with a step size of 5%. Table 1 and Figure 2 report a comparative throughput (THRP) inspection of the ESRO-SRP model with recent models under distinct levels of energy [22,23,24,25]. The results portrayed that the ESRO-SRP model has accomplished maximum values of THRP under all energy levels. For instance, with an EC of 5%, the ESRO-SRP model has provided an increased THRP of 33.95 bytes/s, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm models have accomplished a reduced THRP of 14.54 bytes/s, 14.54 bytes/s, 9.69 bytes/s, and 7.75 bytes/s, respectively. Moreover, with an EC of 100%, the ESRO-SRP system has offered a maximal THRP of 189.20 bytes/s, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm techniques have accomplished a lower THRP of 165.91 bytes/s, 140.68 bytes/s, 110.60 bytes/s, and 99.93 bytes/s, respectively.

Table 1. Throughput analysis of ESRO-SRP technique with existing algorithms under distinct levels of energy.

Throughput (bytes/s)
EC (%)	ESRO-SRP	BRUe-IoE	ORP-FANET	UAVe-WSN	TR-UAV Swarm
5	33.95	14.54	14.54	9.69	7.75
10	36.86	17.45	14.54	12.60	1.93
15	44.62	19.39	20.36	12.60	5.81
20	60.15	34.92	20.36	15.51	9.69
25	100.90	74.70	25.21	17.45	8.72
30	114.48	89.26	31.04	21.33	14.54
35	138.74	112.54	37.83	28.12	15.51
40	142.62	105.75	37.83	31.04	21.33
45	149.42	123.22	44.62	38.80	24.24
50	152.33	126.13	64.03	52.38	32.98
55	157.18	129.04	81.49	63.06	36.86
60	154.27	133.89	92.17	71.79	44.62
65	155.24	134.86	102.84	71.79	47.53
70	163.00	141.65	100.90	79.55	55.29
75	178.53	148.45	108.66	84.40	64.03
80	187.26	157.18	108.66	88.28	69.85
85	187.26	160.09	112.54	97.99	79.55
90	187.26	162.03	125.16	100.90	85.37
95	188.23	164.94	142.62	110.60	96.05
100	189.20	165.91	140.68	110.60	99.93

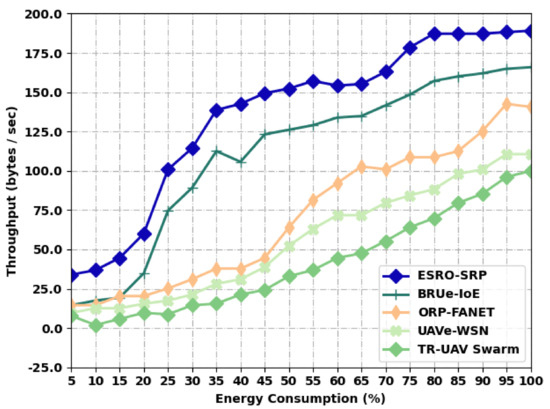
Figure 2. Throughput analysis of ESRO-SRP technique under distinct levels of energy.

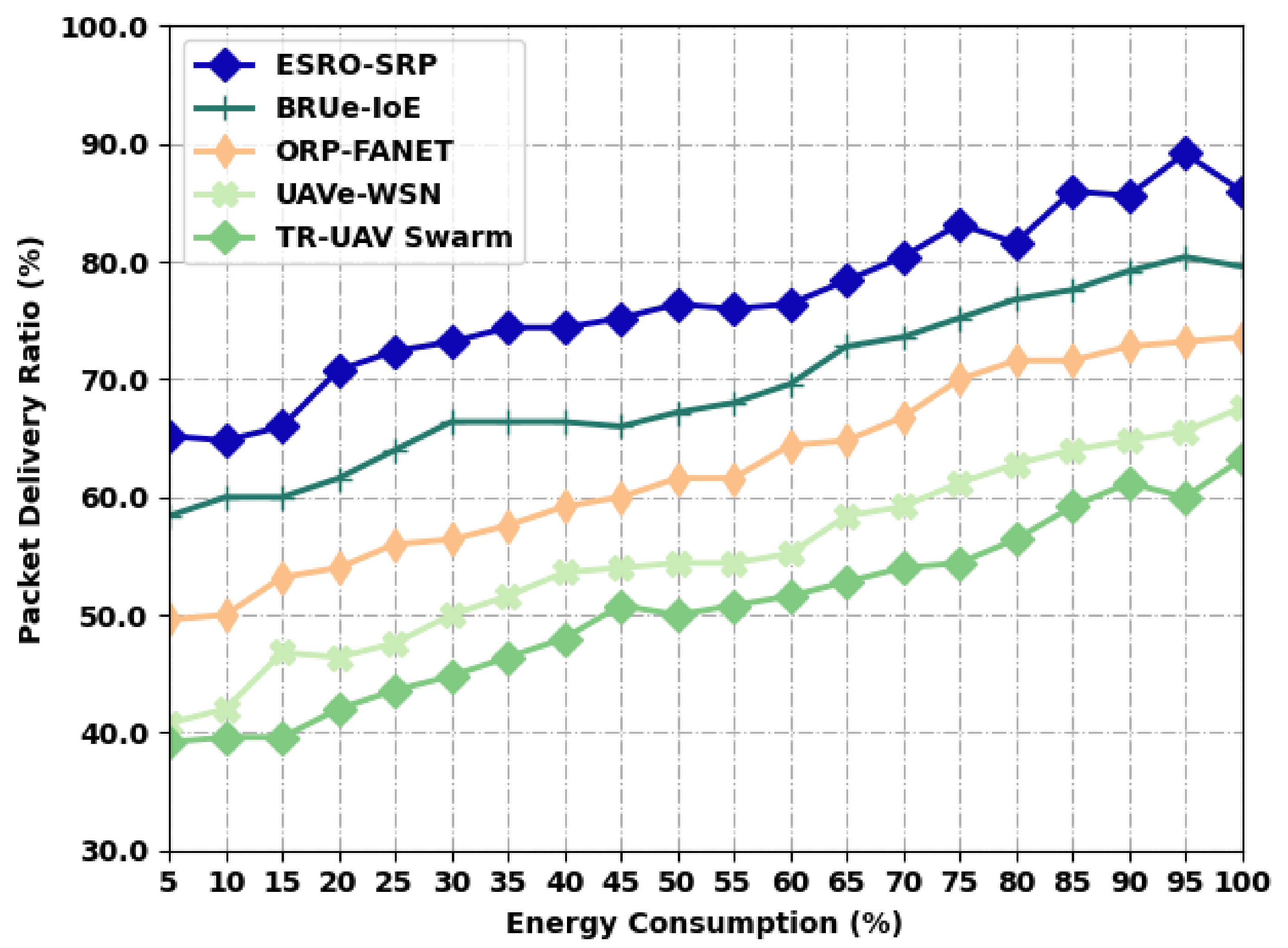
Table 2 and Figure 3 define a comparative PDR examination of the ESRO-SRP approach with recent models under distinct levels of energy. The results exposed that the ESRO-SRP model has accomplished maximal values of PDR under all energy levels. For example, with an EC of 5%, the ESRO-SRP model has provided an increased PDR of 65.20%, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm systems have accomplished a decreased PDR of 58.40%, 49.60%, 40.80%, and 39.20%, respectively. Additionally, with an EC of 100%, the ESRO-SRP model has provided an increased PDR of 86%, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm approaches have accomplished a minimal PDR of 79.60%, 73.60%, 67.60%, and 63.20%, respectively.

Table 2. PDR analysis of ESRO-SRP technique with existing algorithms under distinct levels of energy.

Packet Delivery Ratio (%)
EC (%)	ESRO-SRP	BRUe-IoE	ORP-FANET	UAVe-WSN	TR-UAV Swarm
5	65.20	58.40	49.60	40.80	39.20
10	64.80	60.00	50.00	42.00	39.60
15	66.00	60.00	53.20	46.80	39.60
20	70.80	61.60	54.00	46.40	42.00
25	72.40	64.00	56.00	47.60	43.60
30	73.20	66.40	56.40	50.00	44.80
35	74.40	66.40	57.60	51.60	46.40
40	74.40	66.40	59.20	53.60	48.00
45	75.20	66.00	60.00	54.00	50.80
50	76.40	67.20	61.60	54.40	50.00
55	76.00	68.00	61.60	54.40	50.80
60	76.40	69.60	64.40	55.20	51.60
65	78.40	72.80	64.80	58.40	52.80
70	80.40	73.60	66.80	59.20	54.00
75	83.20	75.20	70.00	61.20	54.40
80	81.60	76.80	71.60	62.80	56.40
85	86.00	77.60	71.60	64.00	59.20
90	85.60	79.20	72.80	64.80	61.20
95	89.20	80.40	73.20	65.60	60.00
100	86.00	79.60	73.60	67.60	63.20

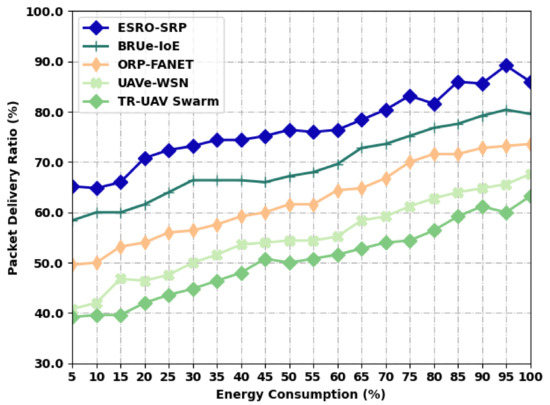
Figure 3. PDR analysis of ESRO-SRP technique under distinct levels of energy.

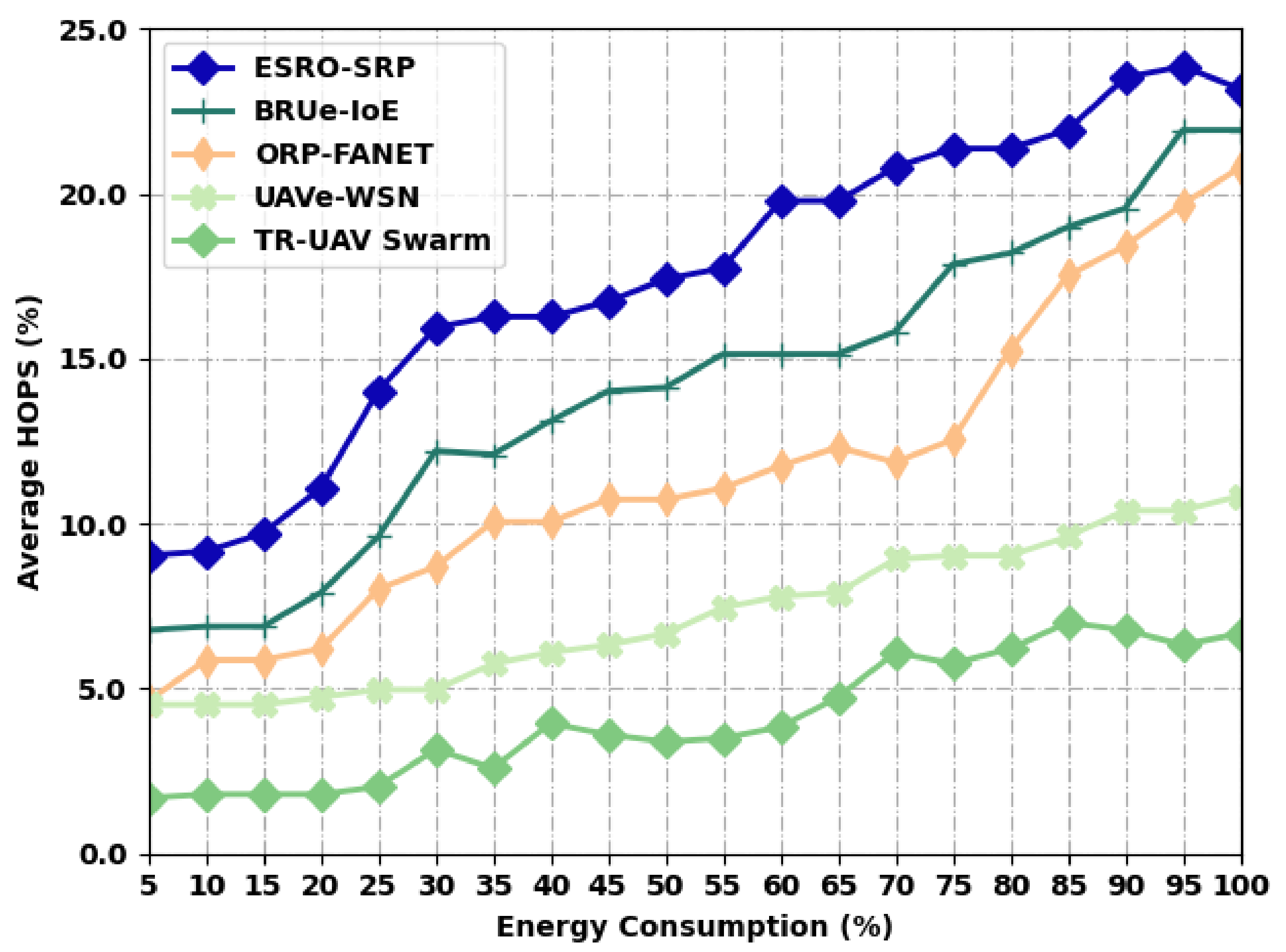
Table 3 and Figure 4 demonstrate a comparative average HOPS (AHOPS) analysis of the ESRO-SRP system with recent models under distinct levels of energy. The results depicted that the ESRO-SRP approach has accomplished higher AHOPS values under all energy levels. For instance, with an EC of 5%, the ESRO-SRP model has provided an increased AHOPS of 9%, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm algorithms have accomplished a minimal AHOPS of 7%, 5%, 5%, and 2%, respectively. Finally, with an EC of 100%, the ESRO-SRP model has offered superior AHOPS of 23%, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm methodologies have accomplished a lower AHOPS of 22%, 21%, 11%, and 7% correspondingly.

Table 3. Average HOPS analysis of ESRO-SRP technique with existing algorithms under distinct levels of energy.

Average HOPS (%)
EC (%)	ESRO-SRP	BRUe-IoE	ORP-FANET	UAVe-WSN	TR-UAV Swarm
5	9	7	5	5	2
10	9	7	6	5	2
15	10	7	6	5	2
20	11	8	6	5	2
25	14	10	8	5	2
30	16	12	9	5	3
35	16	12	10	6	3
40	16	13	10	6	4
45	17	14	11	6	4
50	17	14	11	7	3
55	18	15	11	7	4
60	20	15	12	8	4
65	20	15	12	8	5
70	21	16	12	9	6
75	21	18	13	9	6
80	21	18	15	9	6
85	22	19	18	10	7
90	24	20	18	10	7
95	24	22	20	10	6
100	23	22	21	11	7

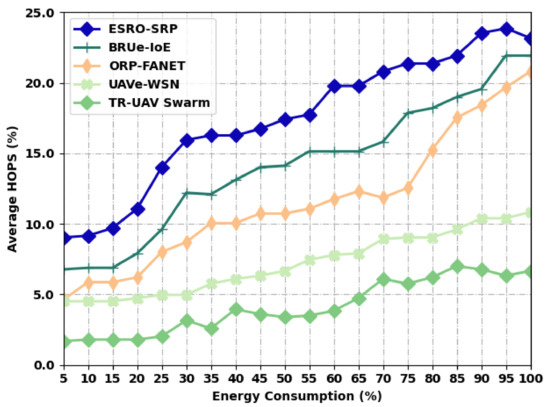
Figure 4. AHOPS analysis of ESRO-SRP technique under distinct levels of energy.

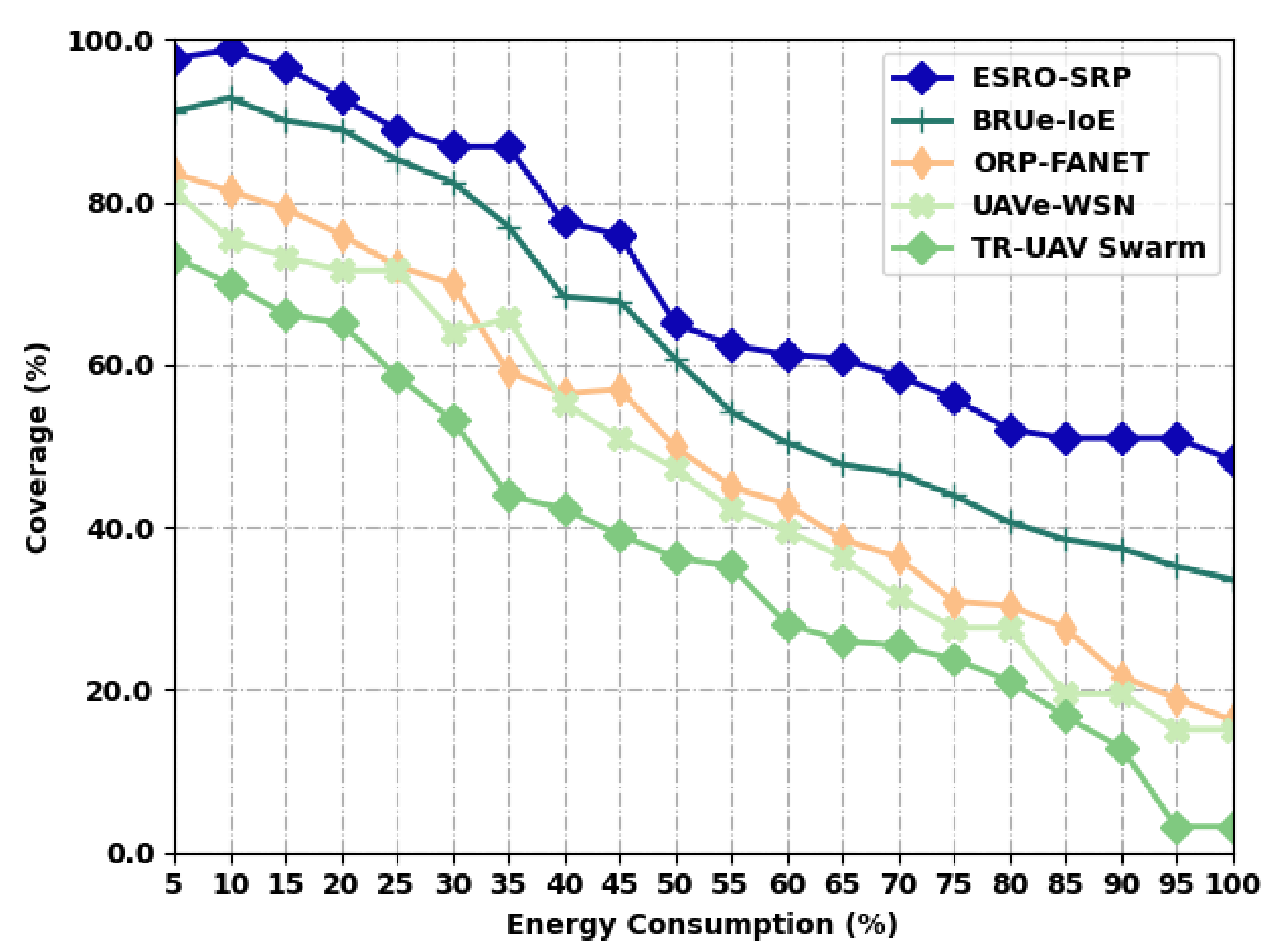
Table 4 and Figure 5 illustrate a comparative coverage inspection of the ESRO-SRP approach with recent models under distinct levels of energy. The outcomes represented that the ESRO-SRP model has accomplished improved values of coverage under all energy levels. For instance, with an EC of 5%, the ESRO-SRP model has provided a maximal coverage of 97.69%, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm methods have accomplished a decreased coverage of 91.18%, 83.58%, 81.41%, and 73.26%, respectively. Finally, with an EC of 100%, the ESRO-SRP model has provided an enhanced coverage of 48.29%, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm models have accomplished minimal coverage of 33.63%, 16.26%, 15.18%, and 3.24%, respectively.

Table 4. Coverage analysis of ESRO-SRP technique with existing algorithms under distinct levels of energy.

Coverage (%)
EC (%)	ESRO-SRP	BRUe-IoE	ORP-FANET	UAVe-WSN	TR-UAV Swarm
5	97.69	91.18	83.58	81.41	73.26
10	98.78	92.81	81.41	75.43	70.01
15	96.61	90.09	79.23	73.26	66.21
20	92.81	89.01	75.98	71.63	65.12
25	89.01	85.21	72.18	71.63	58.61
30	86.83	82.49	70.01	64.03	53.18
35	86.83	77.06	59.15	65.66	43.95
40	77.61	68.38	56.43	55.35	42.32
45	75.98	67.83	56.98	51.01	39.06
50	65.12	60.78	49.92	47.21	36.35
55	62.41	54.26	45.03	42.32	35.26
60	61.32	50.46	42.86	39.61	28.21
65	60.78	47.75	38.52	36.35	26.03
70	58.61	46.66	36.35	31.46	25.49
75	55.89	43.95	30.92	27.66	23.86
80	52.09	40.69	30.38	27.66	21.15
85	51.01	38.52	27.66	19.52	16.81
90	51.01	37.43	21.69	19.52	13.01
95	51.01	35.26	18.98	15.18	3.24
100	48.29	33.63	16.26	15.18	3.24

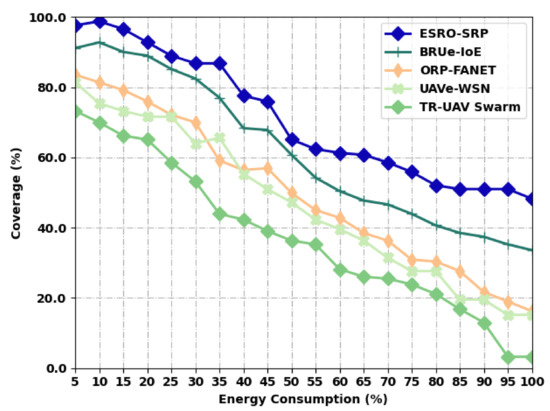
Figure 5. Coverage analysis of ESRO-SRP technique under distinct levels of energy.

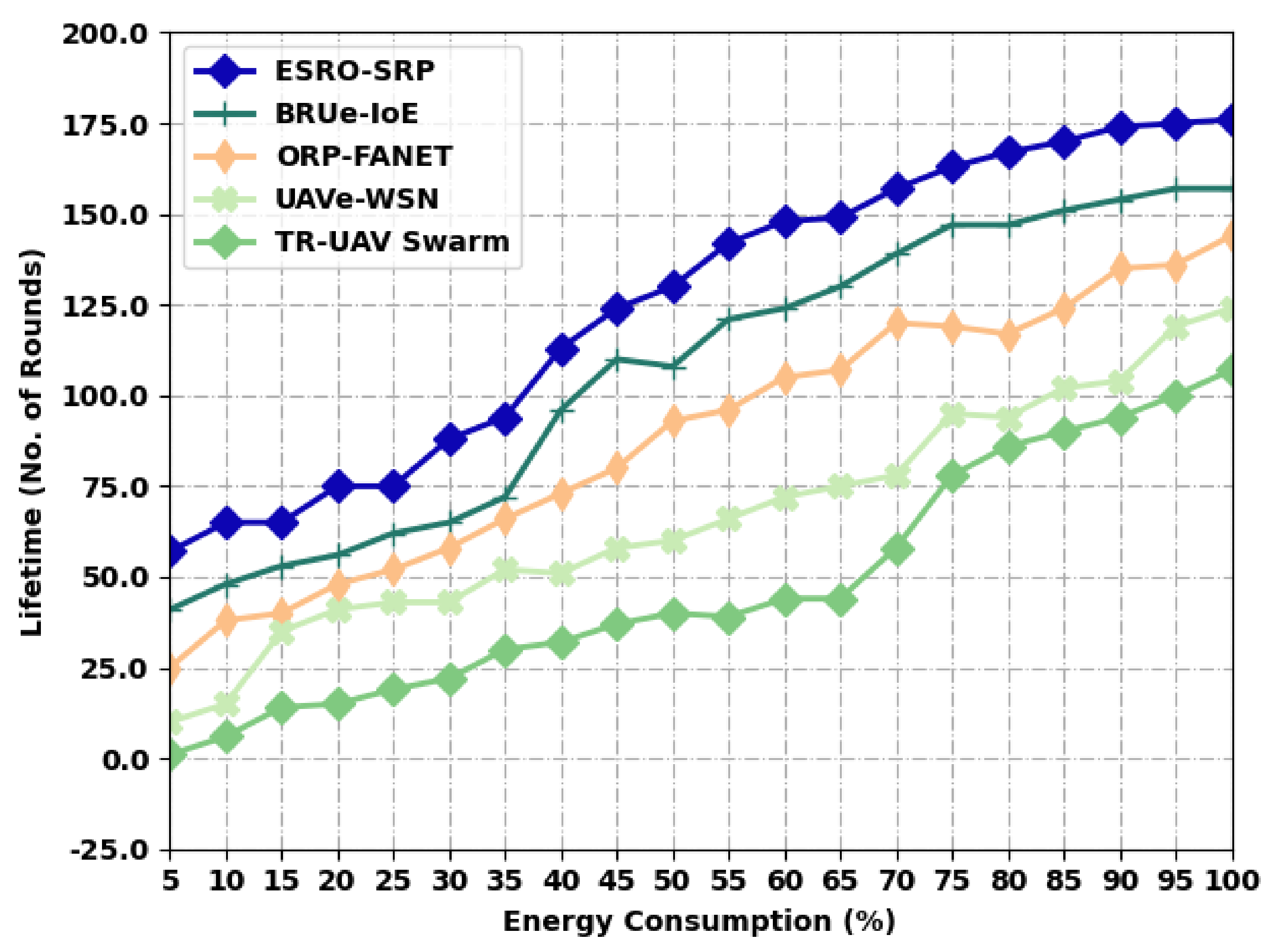
Table 5 and Figure 6 depict a comparative lifetime analysis of the ESRO-SRP algorithm with recent methodologies under distinct levels of energy. The results outperformed in that the ESRO-SRP model has accomplished maximum values of a lifetime under all energy levels. For instance, with an EC of 5, the ESRO-SRP system has provided a higher lifetime of 57 rounds, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm algorithms have accomplished a minimal lifetime of 41, 25, 10, and 1 round, respectively. Moreover, with an EC of 100, the ESRO-SRP model has an obtainable increased lifetime of 176 rounds, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm approaches have accomplished a decreased lifetime of 157, 144, 124, and 107 rounds, respectively.

Table 5. Lifetime analysis of ESRO-SRP technique with existing algorithms under distinct levels of energy.

Lifetime (No. of Rounds)
EC (%)	ESRO-SRP	BRUe-IoE	ORP-FANET	UAVe-WSN	TR-UAV Swarm
5	57	41	25	10	1
10	65	48	38	15	6
15	65	53	40	35	14
20	75	56	48	41	15
25	75	62	52	43	19
30	88	65	58	43	22
35	94	72	66	52	30
40	113	96	73	51	32
45	124	110	80	58	37
50	130	108	93	60	40
55	142	121	96	66	39
60	148	124	105	72	44
65	149	130	107	75	44
70	157	139	120	78	58
75	163	147	119	95	78
80	167	147	117	94	86
85	170	151	124	102	90
90	174	154	135	104	94
95	175	157	136	119	100
100	176	157	144	124	107

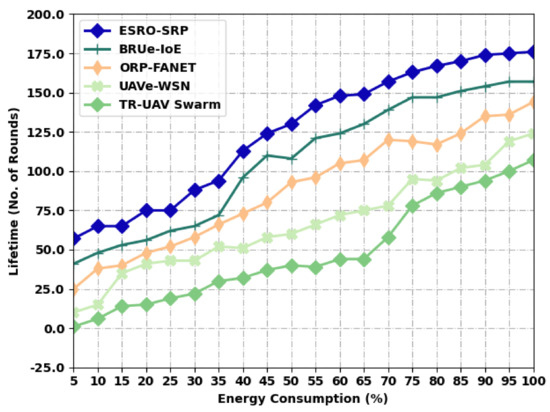
Figure 6. Lifetime analysis of ESRO-SRP technique under distinct levels of energy.

The experimental results ensured the superior outcomes of the proposed model over other models in the IoD environment.

4. Conclusions

In this study, a novel ESRO-SRP technique was established for secure communication among the drones in the IoD environment. The presented ESRO-SRP technique mainly aims to derive a set of optimal routes to the destination. In addition, the ESRO-SRP algorithm is derived by the integration of the QOBL concept with the conventional SRO algorithm. Moreover, the presented ESRO-SRP technique derived a fitness function encompassing different input parameters such as RE, distance, and trust degree. The experimental validation of the ESRO-SRP technique is carried out under several aspects, and the results demonstrated the enhancements of the ESRO-SRP model over recent approaches. The ESRO-SRP model has provided an increased PDR of 86%, whereas the BRUe-IoE, ORP-FANET, UAVe-WSN, and TR-UAV Swarm approaches have accomplished a minimal PDR of 79.60%, 73.60%, 67.60%, and 63.20%, respectively. Therefore, the ESRO-SRP technique can be exploited as an effective tool to improve security and network efficiency. In the future, the performance of the ESRO-SRP algorithm will be extended to the integration of lightweight cryptographic techniques.