Sign Language Gesture Recognition with Convolutional-Type Features on Ensemble Classifiers and Hybrid Artificial Neural Network

Abstract

The proposed research deals with constructing a sign gesture recognition system to enable improved interaction between sign and non-sign users. With respect to this goal, five types of features are utilized—hand coordinates, convolutional features, convolutional features with finger angles, convolutional features on hand edges and convolutional features on binary robust invariant scalable keypoints—and trained on ensemble classifiers to accurately predict the label of the sign image provided as input. In addition, a hybrid artificial neural network is also fabricated that takes two of the aforementioned features, namely convolutional features and convolutional features on hand edges to precisely locate the hand region of the sign gesture under consideration in an attempt for classification. Experiments are also performed with convolutional neural networks on those benchmark datasets which are not accurately classified by the previous two methods. Overall, the proposed methodologies are able to handle a diverse variety of images that include labyrinthine backgrounds, user-specific distinctions, minuscule discrepancies between classes and image alterations. As a result, they are able to produce accuracies comparable with state-of-the-art literature.

1. Introduction

Sign Language is the mode of communication employed by specially abled people who are unable to hear or speak or both. It comprises a series of hand gestures mainly concentrated around the upper portion of the body, including occasionally the face, to convey sentences and emotions. There are various sign language systems based on the diverse alphabet systems as well as regional variants. For instance, Indian Sign Language addresses both the Hindi alphabet and the English alphabet, varying with respect to the number of hands utilized compared to American Sign Language. Despite the contrasts exhibited by such systems, their main goal is to facilitate human interaction. However, not everyone is well versed with sign language which can a be real hassle when a normal speaker is trying to understand a sign user. Hence, it is necessary to devise a system capable of recognizing sign language to foster better communication with maximum possible accuracy. With regards to this, the proposed system aims to tackle a small subset of sign language recognition known as static sign image classification by extracting features most representative of the input image.

The proposed system makes use of ensemble methods such as random forest [1] and XGBoost [2] to augment overall classification accuracy at the expense of an initial feature extraction phase which reduces the input of the system to numerical features. The extracted features are mostly derived from a convolutional neural network [3] on the original images, images with edge detection [4] for the hand and non-hand region and images infused with keypoints that define spatial regions of interest, as well as hand coordinates. In addition to the ensemble methods, artificial neural networks [5] are also employed alongside the genesis of a hybrid artificial neural network that takes both original image and edge image as input. Due to the complexity of some benchmark datasets, they are trained directly on a convolutional neural network without a feature extraction stage.

Overall, the experiments performed in this paper have led to the following research contributions:

• The usage of numerical image features obtainable from a convolutional neural network, with classifiers other than artificial neural networks for acquiring stellar accuracy values, in this case, ensemble models such as random forest and XGBoost.
• A neoteric method to obtain features from an image with binary robust invariant scalable keypoints on hand edges.
• The inception of a hybrid artificial neural network architecture that exploits both original image data and edge image data to augment classification performance on sign gestures compared to a single artificial neural network.

With the objective of the research now adequately defined, the following section discusses some notable works for the problem domain under consideration. Next, Section 3 elaborates on the dataset and implementation details followed by Section 4 that displays the results with the significant inferences. Lastly, a conclusion is drawn on the entire research and any scope for future improvement is also highlighted.

2. Related Work

First and foremost, for an image classification task such as sign gesture recognition, a standard approach in practice is to apply a convolutional neural network (CNN) to segregate the distinct image classes. For instance, Sagayam, K.M. et al. [6] feed RGB images of the Cambridge hand gesture dataset directly to a CNN comprising a convolutional layer of 16 filters of size 4 × 4 followed by a rectified linear unit (ReLU) activation, cross-channel normalization and max pooling. The pooled output when passed through a fully-connected layer equipped with softmax classification gives an accuracy of 96.66% when trained using stochastic gradient descent for 100 epochs. Similarly, Hurroo, M. et al. [7] also use a CNN but it feeds the RGB images in gray scale in which the white hand is retained against the black background. Compared to Sagayam, in K.M. et al. [6], the convolutional layers comprise 32 filters of size 3 × 3. When trained on 10 American Sign Language (ASL) alphabets—A, B, C, D, H, K, N, O, T, Y—it achieves an overall accuracy of 98%. On the other hand, Aly, W. et al. [8] utilize depth information of RGB images from the ASL finger-spelling dataset for hand segregation. These depth images are fed to a special type of CNN known as the principal component analysis network (PCANet) for feature extraction rather than classification. It consists of two convolutional layers. The first one contains L1 filters to learn low-level features, and the second one contains L2 filters to learn high-level features. When these features are passed through a support vector machine (SVM) classifier, the leave-one-out accuracies thus obtained are 88.70% and 84.50%, respectively, for the single PCANet model and the user-specific PCANet model.

Secondly, instead of a CNN, artificial neural networks (ANNs) are also used for classifying hand gestures. However, to train them, numerical features are required. Gattupalli, S. et al. [9], for example, make use of seven annotated upper body joint locations as numerical inputs to two types of ANNs with transfer learning weights from pose estimation. The first one uses the context of body joints by solving a regression equation to increase accuracy via a cascade of pose regressors, while the second method utilizes heatmap regression for pose estimation. Thalange, A. et al. [10] also employ an ANN, but it needs to extract numerical features before it can be passed as input. The features extracted include an orientation histogram (OH); six statistical parameters (ST), namely mean, standard deviation, variance, coefficient of variation, range and root mean square of successive difference; a combination of the previous two (COHST); and a 2D discrete wavelet transform (DWT) using a Haar wavelet. When the ANN is trained on the ASL digits, COHST gives an accuracy of 87.94%, outperforming its individual components, and the Wavelet features acquire an accuracy of 98.17%.

The former two types of neural networks deal with sign images, but to handle sign language videos that consist of sequential images, a recurrent neural network (RNN) such as long short-term memory (LSTM) is necessary. One example is the hierarchical attention network with latent space (LS-HAN), as described by Huang, J. et al. [11], which comprises three components: a two-stream CNN which maps one-hot encoded words in a sentence to semantic space along with video features, a latent space (LS) that uses the dynamic time warping (DTW) algorithm for semantic bridging, and a HAN that computes log-probability of the sentences using bidirectional LSTM equipped with a softmax function. Another example that elaborates the usage of LSTM for classifying sign videos is in Cui, R. et al. [12] which maps sign video sequences to gloss labels with the assistance of bidirectional LSTM by representing the input as a spatio-temporal feature via a recurrent neural network. A detection net employing stacked temporal convolution then selects those video segments that aligned maximally with the predicted gloss labels. This is followed by a three-stage optimization–connectionist temporal classification (CTC) for alignments between input and target, feature learning for building more training samples and sieving out unnecessary segments.

Apart from using neural networks, Sign Language images can also be classified using simple machine learning algorithms. Gangrade, J. et al. [13], for instance, extract keypoint-related features such as SIFT (scale invariance feature transform), SURF (speed up robust features), ORB (oriented fast and rotated BRIEF) from gray scale depth images and then learns a new representative feature vector obtained from K-means clustering using na SVM and a K-nearest neighbors (KNN) classifier. Testing the system on the Indian Sign Language (ISL) digits, NUS I and II datasets give maximum accuracy of 93.26%, 80.6% and 85.6%, respectively. Raheja, J.L. et al. [14] train an SVM as well but with hand-segmented binary images as input and Hu moments, fingertip detection and hand trajectory as features, giving a recognition rate of 97.5% on four hand signs. IN contrast, Thang, P.Q. et al. [15] compare two variations of an SVM, namely simplification of SVM (SimpSVM) and relevance vector machine (RVM) on the Auslan dataset and the American Sign Language Image Dataset (ASLID). When sign classification is carried out using 5-fold cross validation, the SimpSVM outperformed the RVM for both datasets. Kumara, B.M. et al. [16], on the other hand, perform feature vector similarity using the nearest-neighbors classification on spatial features such as centroids of the face, manual hand and non-manual hand (C1,C2,C3) and the global centroid (GC) extracted from the UoM-ISL sign language dataset with an overall recognition rate in terms of F-measure being 58.82.

Last but not the least, hand gestures can also be recognized by devising features that vary for each sign. This is demonstrated in Shivashankara, S. et al. [17] where the roundness of the image and the peak offset are formulated from the gray scale sign images of ASL alphabets and digits for classification purposes without the usage of any machine-learning or deep-learning algorithm. Pansare, J.R. et al. [18] also make use of a feature known as edge orientation histogram (EOH) extracted from regions of interest (ROI) of gray scale images of the ASL alphabet. When classification is performed based on similarity between the feature vectors formed from EOH coefficients, it gives a recognition rate of 88.26%.

Based on the majority of works performed in this problem domain, it can be observed that the sign images are always reduced to numerical features which simplifies the classification process. This also means that the extracted features need to be perfectly representative of the hand gestures and hence complex. Keeping this in mind, the proposed system attempts to surpass the accuracy of the following literature in Table 1. To highlight the effectiveness of numerical features over a technique devoid of feature extraction, the papers that use a CNN are taken for comparison in Table 1. In addition, other state-of-the-art techniques that utilize numerical features also need to be compared. For this reason, a paper using keypoints is also taken for comparison in Table 1:

Table 1. Base papers for comparison.

Paper	Problem Statement	Dataset	ML/DL Models Used	Results
Sagayam, K.M. et al. [6]	Devise a hand-gesture recognition model using a well-tuned deep CNN without using hybrid processes such as image pre-processing, segmentation and classification	Cambridge Hand Gesture Dataset	Methodology Convolutional Neural Network Stochastic Gradient Descent with momentum	Accuracy—96.66% Sensitivity—85% Specificity—98.12%
Aly, W. et al. [8]	Devise a user-independent recognition system that exploits depth information of RGB images to learn features using PCA for classifying the sign gestures	ASL Finger Spelling dataset	Methodology Depth thresholding and median filter Principal Component Analysis (PCA) network Support Vector Machine (SVM)	Accuracy Single PCANet—88.70% User-specific PCANet—84.50%
Gangrade, J. et al. [13]	Devise a system to recognize signs in a cluttered environment invariant of scaling, rotation and lighting	Self-generated ISL digits 0–9, NUS Dataset I and II	Methodology Adaptive Thresholding and Gaussian blur 7Hu Moments, SIFT (Scale Invariant Feature Transform), SURF (Speed Up Robust Features), ORB (Oriented FAST and Rotated BRIEF) K-means clustering SVC and KNN classifier	Accuracy-ISL digits ORB + Nu-SVC = 90.4% ORB + KNN = 93.26% Accuracy-NUS I ORB + Nu-SVC = 76.9% ORB + KNN = 80.6% Accuracy-NUS II ORB + Nu-SVC = 81.25% ORB + KNN = 85.6%

3. Datasets and Methods

The proposed system differentiates between various static hand gestures, i.e., images, with the help of representative features with the core objective of maximizing the accuracy on the testing dataset.

3.1. Datasets

The proposed methodology is applied on the ASL alphabet dataset with 80% training data and 20% testing data. In addition, the methodology is also demonstrated on datasets associated with state-of-the-art techniques to draw a comparative analysis on the results obtained and any significant improvement observed. These datasets include the Cambridge hand gesture dataset, the ASL finger-spelling dataset, the NUS dataset I and II and ISL digits. A glimpse of these datasets is shown in Figure 1 whereas Table 2 outlines the details of the datasets used in this methodology.

Figure 1. Datasets–ASL alphabet, ASL finger-spelling dataset, Cambridge dataset, NUS I and II, ISL digits.

Table 2. Dataset details–ASL alphabet, ASL finger-spelling dataset, Cambridge dataset, NUS I and II, ISL digits.

	Size	No. of Classes	Samples per Class	Test Size
ASL alphabet	72,000	24	3000	20%
ASL finger-spelling dataset	65,774	24	>2600	20%
Cambridge hand gesture dataset	63,188	9	>6000	20%
NUS I dataset	240	10	24	10.4%
NUS II dataset	2000	10	200	12.5%
ISL digits	2000	10	200	12.5%

3.2. Methodology

The task of sign recognition from a given hand gesture is essentially an image classification problem. Table 3 represents the operations involved in sign recognition. The proposed system takes as input an annotated dataset of sign images/hand gestures from which it extracts five features followed by dimensionality reduction on the convolutional-related features. Lastly, it trains these features on supervised classifiers in an attempt to achieve maximum recognition accuracy which is a crucial metric in evaluating the performance of the trained models.

Table 3. Methodology for sign image classification.

Input:	Sign Images Annotated with Labels
1:	Extract numerical features from sign images:
	Hand coordinates–3D coordinates of hand joints;
	Convolutional features–features obtained from a CNN after convolution and pooling operations;
	Convolutional features + finger angles–convolutional features from a CNN along with cosine of angles between the fingers;
	CNN features on hand edges–convolutional features on sign images whose background is removed and only hand edges are retained;
	CNN features on BRISK–convolutional features on hand edges retained sign images that are infused with BRISK keypoints;
2:	Perform dimensionality reduction on convolutional-related features:
	PCA–dimensionality reduction through orthogonal transformation;
3:	Apply random forest and XGBoost on hand coordinates and all PCA-applied convolutional-type features;
4:	Apply neural networks on the features:
	Hybrid ANN–applied on convolutional features and CNN features on hand edges;
	CNN–applied directly on NUS I and II datasets;
	ANN–applied on hand coordinates extracted from ASL finger-spelling dataset for testing leave-on-out-accuracy.
Output:	Predicted label of sign images.

3.2.1. Feature Extraction

In this subsection, two types of features are extracted from the sign images-hand coordinates which are a non-convolutional feature and four convolutional-related features that are obtained from the CNN architecture described in Table 4.

Table 4. Architecture for convolutional-related features.

Operation	Kernel	Stride	Filters	Pool	Activation
Conv2D	3 × 3	1 × 1	64
Conv2D	3 × 3	1 × 1	64
MaxPooling2D		1 × 1		2 × 2
Conv2D	3 × 3	1 × 1	128		ReLU
Conv2D	3 × 3	1 × 1	128		ReLU
MaxPooling2D		1 × 1		19 × 19
Flatten

The hand coordinates extracted in Table 5 are robust because even if the depth or orientation of the hand varies, the relative distance between the joints will be equal for the same sign. However, this procedure is constrained by the quality of the sign images and in certain scenarios may not detect the hand due to lighting conditions as well as image noise. Overall, it gives a feature vector of size 63.

Table 5. Features extracted.

Feature	Extraction Steps
Hand coordinates	1: Initialize Mediapipe [19] hands object; 2: Pass the hand gesture image to the object; 3: The location of 21 hand joints in a 3D coordinate space are returned with each of them in the form of a 3-tuple as follows: $$(x_i,y_i,z_i)$$ (1) where (i = 0) to (20).
Convolutional features	1: Feed the sign gesture image to the CNN described in Table 4; 2: The convolutional features are obtained as a flattened 1D feature vector after passing through convolutional layers and pooling layers.
Convolutional features + finger angles	1: Obtain the hand coordinates 0, 3, 5, 8, 12, 16 and 20 using Mediapipe [19] as shown in Figure 2 to calculate the finger angles; 2: The Euclidean distances [20] $a_i,b_i,c_i$, where i = 1 to 4 are calculated in three dimensions; 3: The four finger angles as depicted in Figure 2 are calculated using the law of cosines for triangles which is as follows: $$\cos {\theta }_1=\frac{a_1^2+b_1^2-c_1^2}{2a_1{b}_1}$$ (2) $$\cos {\theta }_2=\frac{a_2^2+b_2^2-c_2^2}{2a_2{b}_2}$$ (3) $$\cos {\theta }_3=\frac{a_3^2+b_3^2-c_3^2}{2a_3{b}_3}$$ (4) $$\cos {\theta }_4=\frac{a_4^2+b_4^2-c_4^2}{2a_4{b}_4}$$ (5) 4: These finger angles are combined with Convolutional features to give a hybrid feature.
CNN features on hand edges	1: Initialize a skin-mask with the real skin tone color scheme [21] but decrease the lower bound to capture darker skin tones as well as skin tones under insufficient lighting; 2: Perform a bitwise AND between the skin mask and the input image to segment the hand region from the background; 3: Denoise the hand-segmented image using median blur; 4: Apply Canny filter [22] on the denoised image to retain only the hand edges; 5: The CNN described in Table 4 is used to extract features from the edge image.
CNN features on BRISK image	1: Initialize a BRISK object; 2: Using the object, detect BRISK keypoints in the edge image obtained in the previous feature; 3: Pass this keypoint-infused image through the CNN described in Table 4.

Figure 2. Finger angles.

Coming to the convolutional features, the convolutional neural network (CNN) described in Table 5 is able to extract 2D feature maps using the convolutional filters, and the pooling layers scoop these features in a summarised form from specific windows/regions of the image along with reducing dimensionality. In the context of sign images, these features can indicate the position of fingers, hand orientation, etc.

Moving on to finger angles, these are proposed to capture the variations between signs of the same language such as the letters ‘a’ and ‘e’ in the American Sign Language as depicted through the two images in Figure 3. These variations are captured in terms of the relative position of the fingers with respect to each other. Similar to hand coordinates, finger angles also remain constant despite hand depth or orientation in the input image for the same class label.

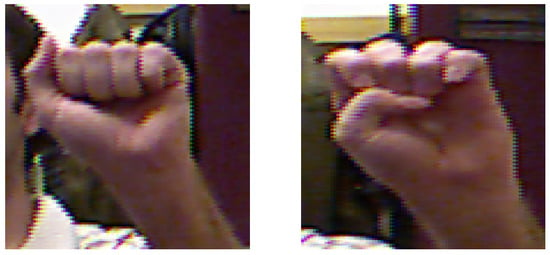
Figure 3. Similarity between sign images: ‘a’ (left) and ‘e’ (right).

For a sign image taken in a cluttered environment, the resulting convolution process may be unable to extract features specific to the sign. CNN features on hand edges alleviate this problem by segmenting the hand region in the original input image with the help of an approximate skin mask so that the neighboring regions become black. A skin mask indicates a range of RGB values that encompasses the majority of skin tones that can be observed in sign images. This is followed by obtaining the edges in the hand-segmented image. For edge detection, a Canny filter is preferred over a Sobel filter [23] because the edges retained are smooth in nature. Figure 4 outlines the images obtained during the extraction of this feature. This feature extraction method is applied on the original input image without calculating the finger angles. Once the edge image has been obtained, the CNN described in Table 4 would be able to extract features corresponding to only the hand region without including any of the complex background since it has been removed when finding hand edges.

Figure 4. Original image (left); masked image (middle); edge image (right).

Keypoints describe regions of interest of an image where each keypoint is calculated by taking a neighborhood of pixels into consideration with specific intensities. For the last feature, binary robust invariant scalable keypoint (BRISK) [24] is chosen which returns these keypoints as a vector of size 64, representing the bins of an image histogram. When dealing with sign images, however, BRISK may compute keypoints catering to objects in the background of the sign user if the images have not been taken in a clutter-free environment. So, to retain the keypoints of only the hand region, BRISK is applied on the edge image as shown in Figure 5. Each of the concentric circles in Figure 5 represents a keypoint, and the radius of the circle indicates the span of pixels it considers. One thing to note while using these keypoints is the fact that their count can vary across images. Applying the CNN described in Table 4 on the BRISK image keeps the number of features for each image consistent. BRISK, similar to other keypoint algorithms, is invariant to scale and rotation, i.e., any kind of transformation that preserves lines and features across diverse geometric variations of the same image, and it is also computationally less expensive.

Figure 5. BRISK keypoints on hand edges.

3.2.2. Dimensionality Reduction-Principal Component Analysis

Since all the convolutional-related features of an image that are extracted in Section 3.2.1 can be extensive in number, dimensionality reduction is applied on these features. This is performed to retain only the most significant features so that the model does not learn from insignificant features that reduce accuracy. It also helps to lessen storage space and multicollinearity [25].

PCA utilizes orthogonal transformation [26] to reduce a covariance matrix of features into a set of uncorrelated features, which correspond to the maximum eigenvalues and at the same time retaining trends and patterns such as patterns that are capable of identifying different hand gestures.

The set of uncorrelated features obtained after applying PCA are referred to as principal components which are linear combinations of the original data containing as much compressed information as possible in decreasing order, i.e., the first component has maximum information, the second component has the second maximum information and so on.

3.2.3. Classification-Ensemble Methods

When the results from multiple machine-learning models are combined, an ensemble is obtained. An ensemble is capable of minimizing the variance of the predictions or the amount of error incurred. This ability is leveraged by the proposed system to augment classification accuracy for the sign images. This section trains the hand coordinates feature and the PCA-applied convolutional-related features on the ensemble techniques outlined in Table 6.

Table 6. Ensemble techniques.

Ensemble Technique	Implementation Steps
Random Forest, XGBoost	1: Split the dataset into training and testing sets; 2: Initialize Random Forest classifier with 100 decision trees and XGBoost classifier with default parameterization of xgboost [27] library in python; 3: Fit the classifiers on the training sets; 4: Evaluate accuracy on the testing set using the trained classifiers.

Random Forest

An ensemble method where all the individual models are decision trees is referred to as a random forest. Random forest uses bagging or bootstrap aggregating where it takes multiple decision trees, each trained on a random subset of features. to obtain a final prediction which is a mean of the results from all the trees. This ebbs away the variance of a single decision tree thus reducing overfitting [28].

XGBoost

XGBoost or extreme gradient boosting is an ensemble algorithm that uses regression trees as the base learners. XGBoost’s boosting nature gives more preference to misclassified instances during the next iteration of the algorithm and is hence robust on unbalanced datasets. The model uses gradient boosting, with each tree improving upon the errors of the previous tree in a sequential manner.

3.2.4. Classification-Neural Networks

This section trains the features extracted in Section 3.2.1 on a standard ANN and a hybrid ANN. Classification is also performed using a CNN on the NUS I and II datasets. Table 7 highlights the steps followed for the neural networks.

Table 7. Deep-learning techniques.

Neural Network

Implementation Steps

ANN, hybrid ANN, CNN

1: Construct the neural network as per the architectures specified in Section 3.2.4; 2: Split the dataset into training and testing sets; 3: Compile the neural network using a categorical cross entropy loss function and an Adam optimizer [29]; 4: Perform one-hot encoding on the dependent variable of the training and testing sets 5: Train the neural network on the training set with the testing set as the validation data.

Artificial Neural Network(ANN)

ANNs are comprised of neurons or nodes arranged in layers, starting from the input layer followed by some hidden layers and ending at an output layer, all of which are interconnected with each node assigned an initial weight. After each step or epoch of the training phase, ANN is capable of learning hidden patterns in the data (in this case, patterns distinguishing various sign gestures) and adjust its weights accordingly to generalize better on unseen data.

ANN is applied on the ASL finger-spelling dataset for leave-one-out-accuracies discussed in Section 4.4 with a corresponding architecture having four fully-connected or Dense layers of 64 neurons each and ReLU activation alongside he-uniform [30] initialization and a softmax classification layer with 24 neurons.

Hybrid ANN

The CNN features on hand edges as described in Section 3.2.1 rely on an approximate masking operation to segment the hand edges. However, this technique is prone to retaining background edges as well, most specifically if the background encompasses hues within the skin mask used in this operation. To mitigate this issue, a hybrid ANN is proposed which is illustrated in Figure 6.

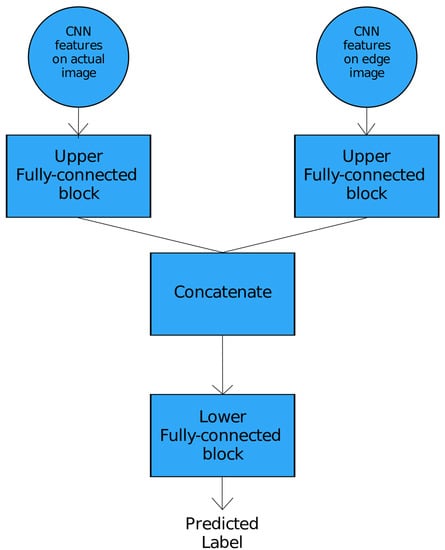
Figure 6. Illustration for hybrid ANN.

The hybrid ANN takes two sets of inputs—convolutional features on the original image at the left of the neural network and CNN features on the edge image, i.e., one containing hand edges at the right of the neural network—both of which are explained in detail in Section 3.2.1. Both of these inputs are passed through fully connected blocks followed by a concatenation operation and a final fully connected block at the end of which the predicted class label is obtained.

The fully connected blocks correspond to a series of dense layers, whereas the concatenate block gives a concatenated feature vector obtained by passing both the inputs through the fully connected blocks. The inception of this hybrid ANN stems from the hypothesis that if the original image is passed in parallel along with the edge image, the neural network would be able to differentiate between the hand edges and the background edges, if any, because the original image features provide additional information to the ANN to capture the location of both the background and the hand region.

Table 8 outlines the architecture of the hybrid ANN for the ISL digits, the Cambridge hand gesture dataset, the ASL alphabet and the ASL finger-spelling dataset.

Table 8. Hybrid ANN architecture–ISL digits, Cambridge hand gesture dataset, ASL alphabet and ASL finger-spelling dataset.

	Upper Fully-Connected Block
Neural Network Layer	No. of Neurons	Activation Function
Dense	64	ReLU
Dense	64	ReLU
Dense	No. of CNN features after PCA	Linear
	Lower Fully-Connected Block
Neural Network Layer	No. of Neurons	Activation Function
Dense	64	ReLU
Dense	64	ReLU
Dense	No. of classes	Softmax

The hybrid ANN utilizes he-uniform [30] as an initialization scheme for the ReLU layers.

Convolutional Neural Network (CNN)

Since the NUS I and II datasets are among the most complex datasets in terms of background variations, image transformations such as zooming and minimal separability between classes and thus did not produce higher accuracies with ensemble technqiues as illustrated in Section 4.2, standard CNNs are applied to them to see if they can achieve appreciable accuracies in comparison to the ensemble techniques discussed in Section 3.2.3. The CNNs are illustrated in Figure 7 and Figure 8.

Figure 7. CNN architecture—NUS I dataset.

Figure 8. CNN architecture—NUS II dataset.

In both Figure 7 and Figure 8, the convolutional block comprises a convolutional layer with 32 filters, a kernel size of 3 × 3 and ReLU activation function, and a max pooling layer of stride size 2 × 2 and pooling size 2 × 2. The fully-connected block is a dense layer with 32 and 128 neurons for NUS I and NUS II datasets, respectively. Each of the layers incorporating ReLU activation has he-uniform initialization [30].

4. Results

The first subsection displays the ideal number of PCA components for the convolutional-related features, whereas the remaining subsections exhibit recognition accuracies for the datasets when tested with different classifiers mentioned in Section 3.2.3 and Section 3.2.4. In addition, the last subsection also examines an accuracy comparison with the literature outlined in Table 1.

4.1. Principal Component Analysis (PCA)

For a total of six datasets, PCA is applied on the four convolutional-related features to retain only the principal components of the extensive number of features. To decide on the ideal number of components, a scree graph is used. It is a line graph between variance and number of components. By observing the scree graph, the elbow value corresponding to the X-axis beyond which there is negligible decrease in variance is chosen as the ideal value. Figure 9, for instance, shows the scree graph for the ASL alphabet on convolutional features.

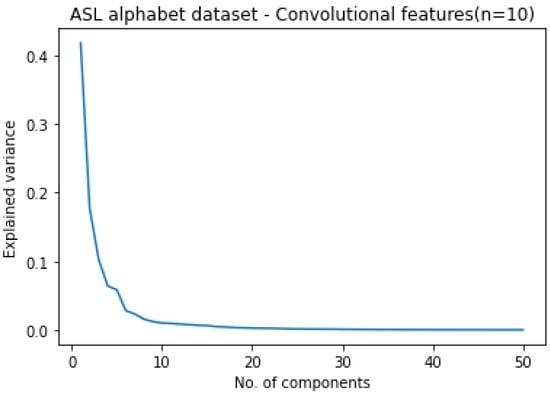
Figure 9. Scree graph on convolutional features-ASL alphabet.

In Figure 9, the X-axis indicates the number of PCA components, whereas the Y-axis indicates the decrease in variance for that specific count of PCA components. It is evident from Figure 9 that 10 is the ideal number of PCA components since beyond this value there is negligible decrease in variance. In the presence of multiple elbows, however, an approximate value is taken as the ideal count. Table 9 outlines the ideal number of components for all the datasets.

Table 9. Ideal number of PCA components.

	ASL Alphabet	ASL Finger-Spelling Dataset	Cambridge Hand Gesture Dataset	NUS I Dataset	NUS II Dataset	ISL Digits
Convolutional features	10	10	10	10	10	5
Convolutional features + finger angles	10	10	10	10	10	5
CNN features on hand edges	15	5	15	10	20	5
CNN features on BRISK	15	15	15	10	15	15

4.2. Sign Recognition Accuracies: Ensemble Methods

Two ensemble techniques, namely random forest and XGBoost, are applied on the features extracted in Section 3.2.1. Table 10 highlights the highest accuracies obtained when the ensemble methods are used with the hand coordinates and convolutional related features using different number of PCA components mentioned alongside the corresponding accuracies. In some cases, an ideal number of PCA components as described in Section 4.1 give better accuracies, whereas in other scenarios, an increased number of PCA components yields better results.

Table 10. Ensemble accuracies for different numbers of PCA components in convolutional-related features, and hand coordinates.

	ASL Alphabet	ASL Finger-Spelling Dataset	Cambridge Hand Gesture Dataset	NUS I Dataset	NUS II Dataset	ISL Digits
Hand coordinates + Random Forest	98.063%	98.967%	98.626%	80.000%	97.200%	100.000%
Hand coordinates + XGBoost	98.647%	99.136%	98.789%	80.000%	97.200%	99.602%
Convolutional features + PCA + Random Forest	97.188% (n = 10)	96.663% (n = 60)	99.549% (n = 10)	56.000% (n = 20)	68.000% (n = 50)	98.000% (n = 5)
Convolutional features + PCA + XGBoost	93.847% (n = 10)	96.556% (n = 60)	96.669% (n = 10)	52.000% (n = 10)	68.800% (n = 50)	96.000% (n = 5)
Convolutional features + finger angles + PCA + Random Forest	96.806% (n = 10)	96.391% (n = 60)	99.243% (n = 10)	60.000% (n = 20)	71.200% (n = 40)	96.016% (n = 5)
Convolutional features + finger angles + PCA + XGBoost	93.901% (n = 10)	96.121% (n = 60)	96.711% (n = 10)	52.000% (n = 20)	64.000% (n = 40)	95.219% (n = 5)
CNN features on hand edges + PCA + Random Forest	95.306% (n = 60)	90.901% (n = 60)	99.565% (n = 15)	52.000% (n = 20)	65.600% (n = 50)	98.800% (n = 5)
CNN features on hand edges + PCA + XGBoost	93.729% (n = 60)	90.422% (n = 60)	99.391% (n = 15)	56.000% (n = 20)	66.400% (n = 50)	98.800% (n = 5)
CNN features on BRISK + PCA + Random Forest	88.993% (n = 60)	79.506% (n = 15)	98.093% (n = 15)	64.000 (n = 20)	49.200% (n = 15)	96.400% (n = 15)
CNN features on BRISK + PCA + XGBoost	86.229% (n = 60)	78.449% (n = 60)	92.807% (n = 15)	60.000% (n = 10)	40.400% (n = 50)	96.000% (n = 15)

From Table 10, it is evident that ‘Hand coordinates’ when trained on Random Forest and XGBoost outperform on all datasets compared to other features since they capture specific positions of the hand region in a 3D space such that the relative distance between each coordinate remains unchanged despite rotation or scaling, something which is not accounted for by convolutional-related features because image augmentation is not applied to the images before extracting the convolutional-related features. Hence, two signs of the same class in different conditions retain the same pattern in terms of coordinates. The only exception is the Cambridge hand gesture dataset because it comprises sequential data which means that the coordinates change within the same class.

Secondly, for convolutional-related features, XGBoost performs less than or equal to random forest. This is because random forest uses the bagging technique to train multiple subsets of the dataset on various decision trees to improve overall accuracy, whereas XGBoost uses the boosting technique to iteratively improve prediction for misclassified instances. However, since PCA is performed on the convolutional-related features, there seems to be a loss of information for XGBoost to make any further improvement. This does not seem to be true for the NUS I and II datasets using ‘CNN features on hand edges’ and the NUS II dataset using ‘Convolutional features’ for XGBoost, where the number of principal components seem to be sufficient enough to rectify itself on the misclassified sign gestures and consequently surpass random forest.

Moving on to the next inference, ‘CNN features on hand edges’ gives better accuracy compared to ‘Convolutional features’ alone since the system has segmented the hand region and retained only the outline in the form of edges. This has made the resultant image free from any background complexity and hence easier to learn by the ensemble models. However, it does have the following exceptions—the ASL finger-spelling dataset and the NUS II dataset (due to retention of background edges within the range of the skin mask thus adding background complexity), and the ASL alphabet dataset (due to deletion of hand edges falling outside of the skin mask which gives an incorrect hand outline not generalized by the ensemble models).

It can also be observed that the NUS I and II datasets give the lowest accuracies when tested with the proposed features on the ensemble models. This is because the classes in the NUS I dataset appear to be similar, and there is a variety of different backgrounds even within the same class for the NUS II dataset. These factors add complex non-linear patterns in the data which the ensemble models are unable to learn. On the other hand, the Cambridge hand gesture dataset records the highest accuracies among all the datasets due to the simplistic background of the input images, uniform and distinguishable hand gestures for each sign and the hand region in all the images falling within the skin-mask.

It can be noted from Table 10 that the NUS I and II datasets give the highest accuracies with hand coordinates due to their perfect pinpointing of the hand region despite complicated backgrounds or minute differences between sign image classes. Moreover, convolutional features give better accuracy than CNN features on BRISK. This is because the latter extracts features from keypoints computed over an approximate hand outline due to the application of an approximate skin mask. Due to the absence of parts of the hand region over the various datasets and thus an absence of keypoints, there is some information loss for CNN features on BRISK and hence lesser accuracy.

4.3. Sign Recognition Accuracies: Neural Networks

This section applies all the neural network architectures discussed in Section 3.2.4 on the datasets to see how much accuracy is obtained on the testing data. In addition, two types of diagnostic plots—the accuracy curve (which ideally should increase with time) and the loss curve (which ideally should decrease with time)—are also visualized to study the behavior of the neural models over the training epochs.

4.3.1. Hybrid ANN

Table 11 lists the accuracies obtained when using the hybrid ANN structure as described in Section 3.2.4—“Hybrid ANN”—with a batch size of 5 for ISL digits and a batch size of 16 for the Cambridge dataset, the ASL alphabet and the ASL finger-spelling dataset. On the other hand, Figure 10 displays the corresponding accuracy graphs. and Figure 11 displays the corresponding loss graphs. All the accuracies are computed with the best weights over the training epochs.

Table 11. Hybrid ANN accuracies.

ISL Digits	Cambridge Hand Gesture Dataset	ASL Alphabet	ASL Finger-Spelling Dataset
100.000%	99.533%	95.368%	96.883%

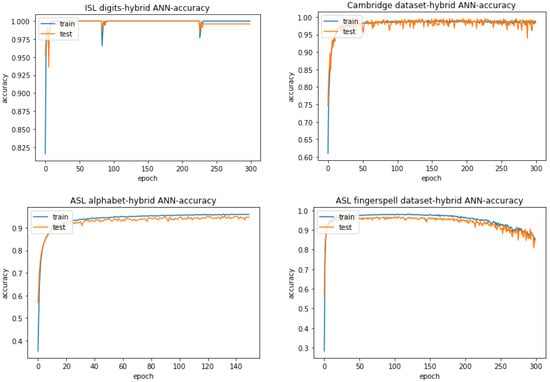
Figure 10. Hybrid ANN accuracy curves.

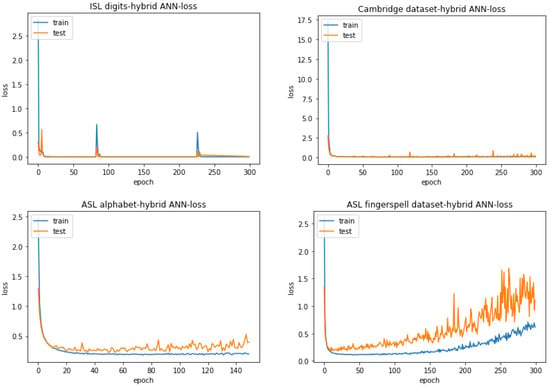
Figure 11. Hybrid ANN loss curves.

From Figure 10 and Figure 11, it can be seen that for ISL digits and the Cambridge dataset, the diagnostic curves indicate a perfect fit with each of them attaining maximum possible accuracy as indicated in Table 11. This is because in the accuracy and loss graphs, the curves for the training and testing sets overlap over the training epochs, indicating a point of stability for the deep-learning model. The curves for the ASL alphabet, however, show a little bit of overfitting judging from the small gap between the training and testing plots in both the accuracy and loss curves. Despite this, the small loss and a constant trend in the accuracy and loss curves are indicative of a representative feature set fed to the hybrid ANN as it is properly able to learn in the training stage. On the other hand, the curves for the ASL finger-spelling dataset show degradation after a certain point in its training, i.e., decrease in accuracy and increase in loss. This can be attributed to the particular mini-batch being trained. The ASL finger-spelling dataset contains variations among the same sign gestures owing to user-specific usage. There may be a possibility that for a given mini-batch sample, the current network weights are not able to generalize properly due to these variations. The large gap between the training and testing plots in the loss curve of the ASL finger-spelling dataset also indicate significant overfitting, i.e., a large generalization error on the testing set.

If one takes a closer look at Table 11, the ISL digits have the highest accuracy since the sign images are taken in a simple backdrop that makes the hand segmentation process much easier and hence able to retain an accurate hand outline in the form of edges for the hybrid ANN. In contrast, the ASL alphabet has the lowest accuracy due to the presence of sign images taken in different lighting conditions which is why the skin mask is unable to retain the entire hand region in certain cases, causing information loss for the hybrid ANN.

4.3.2. Convolutional Neural Networks (CNN)

In this subsection, the CNNs described in Section 3.2.4—“Convolutional Neural Network (CNN)”—are applied on the complex NUS I and NUS II datasets to see if they can obtain comparable or even better accuracy than the convolutional-related features in Section 4.2. The results are highlighted in Table 12, and the diagnostic curves for the NUS I and the NUS II datasets are shown in Figure 12 and Figure 13, respectively.

Table 12. CNN accuracies.

NUS I Dataset (Batch Size = 5)	NUS II Dataset (Batch Size = 16)
80.000%	90.800%

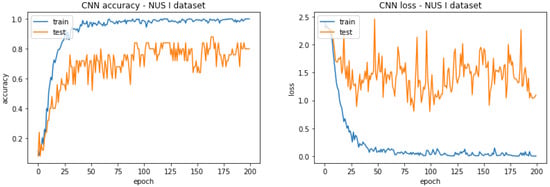
Figure 12. Diagnostic curves for CNN-NUS I dataset.

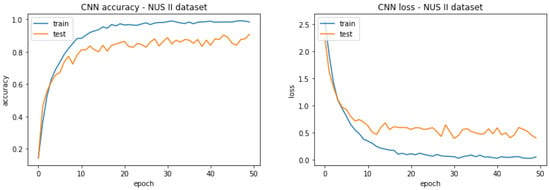
Figure 13. Diagnostic curves for CNN-NUS II dataset.

From Figure 12, it is evident that the curves for the NUS I dataset indicate overfitting due to the large gap between training and testing plots. Therefore, although the CNN is complex enough to capture the variations in the images of this dataset in terms of scaling, which is why it is able to obtain a decent accuracy of 80% in Table 12, the dataset is too small to learn all the parameters of the model.

Moving on to the NUS II dataset in Figure 13, the gap between the training and testing curves shrinks, indicating less overfitting. So, despite having an intricate architecture to capture background complexity in this dataset, the dataset is large enough to learn the model parameters and alleviate the overfitting problem compared to the NUS I dataset. This alleviation is also the reason why the NUS II dataset acquires a greater accuracy of 90.8% in Table 12.

Overall, for these two datasets, the CNN outperforms the ensemble methods when compared with convolutional-related features since all the convolutional features are being utilized to learn the complex patterns in the aforementioned datasets rather than applying PCA on said features which leads to information loss.

4.4. Leave-One-Out-Accuracy

This is applied only to the ASL finger-spelling dataset which comprises user-specific implementations of sign gestures. It works in the following manner:

• Consider User A. To find the leave-one-out-accuracy for this user, the model under consideration is trained on the remaining users and tested on User A.
• This process is repeated for all users. The mean accuracy for all the users gives the leave-one-out-accuracy for the entire dataset.

This user-specificity can be accurately captured with the aid of ‘Hand coordinates’ which are used to find the leave-one-out-accuracies as shown in Table 13. For the ANN results in Table 13, the batch size is 16, the neural network is run for 10 epochs and the best weights are used for evaluation.

Table 13. Leave-one-out-accuracies.

	User A	User B	User C	User D	User E	Average Accuracy
Hand coordinates + Random Forest	85.472%	85.695%	93.436%	85.588%	92.222%	88.483%
Hand coordinates + XGBoost	87.916%	88.780%	94.789%	87.276%	92.387%	90.230%
Hand coordinates + ANN	92.611%	90.687%	95.028%	91.689%	92.676%	92.538%

It is evident from Table 13 that ANN is effective in capturing the complex non-linear patterns in user-specific variations compared to simple ensemble techniques which is why its mean accuracy is greater than the mean accuracies of the ensemble methods.

4.5. Comparison with Base Paper Results

It is evident from Table 14 that in the case of the Cambridge dataset, whose hand gestures are devoid of any cluttered backdrop, using a convolutional-related feature such as CNN features on hand edges with an ensemble classifier such asXGBoost, gives increased accuracy compared to a CNN with softmax classification as described in Sagayam, K.M. et al. [6]. This is because by nature ensembles bolster the predictive performance by decreasing variance of the predictive process with the aid of multiple classifiers each of which adds bias. A single CNN, on the other hand, is limited by its specific architecture and count of epochs to achieve only a certain level of accuracy. Sagayam, K.M. et al. [6] could have obtained better results with an ensemble of CNNs. Secondly, the usage of hand coordinates pinpoints exact locations of the regions of interest of the hand gesture for better mapping between input features and target label compared to a CNN which requires meticulous hyperparameter tuning to capture the exact same features. It can also be seen that the hybrid ANN outperforms the base paper CNN since it takes into consideration both the actual image and the edge information of the gestures to categorize the sign images.

Table 14. Results comparison.

Paper	Dataset	Test Size	Paper Technique	Proposed Technique
Sagayam, K.M. et al. [6]	Cambridge hand gesture dataset	20%	96.66% (CNN Classification)	- 98.789% (Hand coordinates + XGBoost)
				- 99.565% (CNN features on hand edges + PCA + Random Forest)
				- 99.533% (Hybrid ANN)
Aly, W. et al. [8]	ASL finger-spelling dataset	leave-one-out-accuracy	- 88.70% (Single PCANet model + SVM)	- 90.230% (Hand coordinates + XGBoost)
			- 84.50% (User-specific PCANet model + SVM)	- 92.538% (Hand coordinates + ANN)
Gangrade, J. [13]	Self-generated ISL digits	250	- 90.4% (ORB + Nu-SVC)	- 100.000% (Hand coordinates + Random Forest)
			- 93.26% (ORB + KNN)	- 98.800% (CNN features on hand edges + PCA + Random Forest)
				- 98.800% (CNN features on hand edges + PCA + XGBoost)
				- 100.000% (Hybrid ANN)
	NUS I dataset	25	- 76.9% (ORB + Nu-SVC)	- 80.000% (Hand coordinates + Random Forest)
			- 80.6% (ORB + KNN)	- 80.000% (Hand coordinates + XGBoost)
				- 80.000% (CNN)
	NUS II dataset	250	- 81.25% (ORB + Nu-SVC)	- 97.200% (Hand coordinates + Random Forest)
			- 85.6% (ORB + KNN)	- 97.200% (Hand coordinates + XGBoost)
				- 90.800% (CNN)

In the proposed technique, the ISL digits mentioned in the data availability statement have been used instead of a self-generated dataset.

Table 14 also highlights the fact that for the ASL finger-spelling dataset, to test leave-one-out-accuracy, hand coordinates transcend the convolutional features from a PCANet model as specified in Aly, W. et al. [8]. This is because despite user-specificity, when using hand coordinates, the relative distance between the hand joints for the same sign remain consistent across all users, whereas in Aly, W. et al. [8], some of this information is lost since the PCANet model uses PCA to select its convolutional filters. Moreover, in Aly, W. et al. [8], the PCANet seems to be generating features greater than the number of instances in the dataset. This causes the SVM to get stuck in a particular hyperplane without advancing any further which could have given better separation between image classes. Ensemble classifiers and ANN do not suffer from this problem.

For the ISL digits in Table 14, the usage of depth images as mentioned in Gangrade, J. [13] is causing the hand gesture to be a white region amidst a black environment. This is leading to some information loss in terms of sign-specific hand features for the ORB algorithm to detect valuable keypoints. The proposed technique, however, gets rid of depth images in favour of hand coordinates which provides exact location of hand region and convolutional features on the original image as well as the edge image so that the exact hand outline can be learned by the ensemble classifiers and the hybrid ANN. These factors assist in better separation between the digits.

Since the NUS I dataset (having minimal segregation between individual classes) and the NUS II dataset (having highly intricate backgrounds) are complex in type, it is clear from Table 14 that hand coordinates are the ideal feature to classify the images contained within it as they deal with hand region location in a 3D space. Moreover, the utilization of a CNN is ideal in this scenario compared to ORB as specified in Gangrade, J. [13] because with the help of convolutional filters, a CNN is able to identify both the low-level and high-level features necessary for distinguishing labels of such complicated datasets, whereas a representative ORB keypoint of the same features can be the same for multiple classes.

5. Conclusions

In conclusion, the proposed features give astounding results with ensemble classifiers on datasets free from any background complexity and ones containing distinguishable and uniform hand gestures, given that the right count of principal components is chosen for the features employing convolutional layers. The two datasets which deviate from obtaining appreciable accuracies from the majority of these features are the NUS I and II datasets comprising inter-class similarities and complicated environments, respectively. In this case, only the hand coordinates feature is able to maximally represent the sign images. The aforementioned anomalous datasets also perform well when trained with a standard CNN. In addition, the hybrid ANN has proved to be highly effective for sign gesture recognition by taking a combination of features from both the actual image and the image with the hand edges. In short, the research has been successful in constructing a hand gesture recognition system with the constraint that only with the help of hand coordinates alone can user-specificity be enforced which refers to the application of this system beyond the scope of the training data provided. This can be observed in the case of the ASL finger-spelling dataset which contains different user implementations for the same alphabet. Improvement can be made in this scenario by training a multitude of different sign image datasets captured under different conditions on a deep-tuned CNN. Currently, the entire system can operate on static sign gestures, i.e. images, so changes need to be made in this regard to capture real-time sign language usage that includes natural language rules.