Human Activity Recognition Based on Non-Contact Radar Data and Improved PCA Method

Abstract

Human activity recognition (HAR) can effectively improve the safety of the elderly at home. However, non-contact millimeter-wave radar data on the activities of the elderly is often challenging to collect, making it difficult to effectively improve the accuracy of neural networks for HAR. We addressed this problem by proposing a method that combines the improved principal component analysis (PCA) and the improved VGG16 model (a pre-trained 16-layer neural network model) to enhance the accuracy of HAR under small-scale datasets. This method used the improved PCA to enhance features of the extracted components and reduce the dimensionality of the data. The VGG16 model was improved by deleting the complex Fully-Connected layers and adding a Dropout layer between them to prevent the loss of useful information. The experimental results show that the accuracy of our proposed method on HAR is 96.34%, which is 4.27% higher after improvement, and the training time of each round is 10.88 s, which is 12.8% shorter than before.

1. Introduction

The World Health Organization reports that 42% of people over 70 might fall at least once a year [1]. By 2050, the proportion of the world’s population aged over 65 is expected to increase to 21.64% [2]. As the world’s most populous country, China has accelerated its urbanization process in recent years and its original family structure has changed. A large number of empty nesters have appeared in both urban and rural areas of the country. Empty nesters are vulnerable to safety hazards at home due to old age and limited mobility. Especially for those empty nesters living alone, an unexpected fall can result in death in the worst-case scenario. Research shows that timely help can save the lives of those who fall [3]. However, existing medical resources are infeasible to meet the massive demand for elderly home care due to the significant number of older adults. In this circumstance, various sensors and technologies have been applied to monitor and recognize the activities of the elderly at home to improve their home safety through technical means. Among these technologies, human activity recognition (HAR) is a key technology for home safety monitoring of the elderly. Although HAR is promising, it still faces many challenges. For example, its recognition accuracy is unsatisfactory and not convenient enough for users [4].

2. Related Work

Many researchers have studied HAR from different aspects, such as sensors and algorithms. HAR methods can be divided into the following three categories based on the types of sensors: wearable devices, cameras, and millimeter-wave radars. The advantages and disadvantages of different sensors are shown in Table 1. In addition to the reasons listed in the table, cost is also an important and realistic factor influencing users’ choice. For example, the camera-based method is usually cheaper than the millimeter-wave radar-based method, but the millimeter-wave radar-based method can better protect user privacy. The cost of a wearable device is usually more than the cost of a single camera, but users may need multiple cameras to monitor different rooms while one wearable device can fulfill a user’s needs. Therefore, in the se-lection of monitoring methods, it is often necessary to consider the actual situation and needs of users.

Table 1. Advantages and disadvantages of different sensors.

Types of Sensors	Advantages	Disadvantages
Methods based on cameras	♦ High accuracy and robustness ♦ Non-contact and comfortable ♦ Avoid manual use	♦ Limited application scenarios ♦ Difficult to use in a dark environment ♦ Privacy issues
Methods based on wearable devices	♦ Privacy protection ♦ Easy to collect data ♦ Various types of sensors can be chosen	♦ Inconvenient ♦ Uncomfortable ♦ Limited battery capacity ♦ Difficult for the elderly to use
Methods based on millimeter-wave radars	♦ Privacy protection ♦ Non-contact and comfortable ♦ Avoid manual use ♦ Not affected by the light condition	♦ Difficult to collect data ♦ Easily affected by noise ♦ Limited location of installation

HAR based on cameras has been popular in the past. Some researchers separated the image background from the human and then used machine learning or deep learning to extract features [5,6]. Espinosa et al. [7] separated the person in the picture from the background and extracted the ratio of length to width of the human body to recognize standing and falling. In addition, some researchers extracted human contour features and recognized activities through changes in contour [8,9,10]. Rougier et al. [11] used an ellipse rather than a bounding box on HAR. They suggested that the direction standard deviation and ratio standard deviation of the ellipse can better recognize the fall. Meanwhile, Lai et al. [12] improved this method by extracting the picture’s features and using three points to represent people instead of using the bounding box. In this way, the changed information of the upper and lower parts of the human body can be easily analyzed. With the development of computer technology and deep learning, Nunez-Marcos et al. [13] proposed an approach that used convolutional neural networks (CNN) to recognize the activities in a video sequence. Khraief et al. [14] used four independent CNNs to obtain multiple types of data and then combined the data with 4D-CNN for HAR. Compared with other methods, visual methods have better recognition accuracy and robustness, but the performance of cameras will decline rapidly in the dark environment. Having the camera based in certain places, such as bedrooms and bathrooms, will significantly violate personal privacy and bring moral and legal problems [15]. As a result, the usage of traditional cameras as sensors for HAR has been abandoned in recent years. Although researchers including Xu and Zhou [16] have promoted 3D cameras, they have a limit on the use distance and can only be used within 0.4–3 m, which is not suitable for daily use.

Wearable devices are also widely used for HAR, based on the principle that acceleration changes rapidly when the human body moves. There are many methods to measure the change of acceleration, such as accelerometer [17,18], barometer [17], gyroscope [19,20], and other sensors. In 2009, Le et al. [21] designed a fall recognition system with wearable and acceleration sensors to meet the needs of comprehensive care for the elderly. In 2015, Pierleoni et al. [22] designed an algorithm to analyze the tri-axial accelerometer, gyroscope, and magnetometer data features. The results showed that the method had a better performance on the recognition of falls than similar methods. In 2018, Mao et al. [23] extracted information and direction by combining different sensors, and then used thresholds and machine learning to recognize falls with 91.1% accuracy. Unlike visual methods, wearable devices pay more attention to privacy protection and will not be disturbed in a dark environment. However, wearable devices need to be worn, which reduces comfort and usability and is challenging to apply to older adults. In addition, the limitations of the battery capacity of wearable devices makes it difficult for them to work for an extended period. To address these disadvantages, Tsinganos and Skodras [24] used sensors in smartphones for HAR. However, this method still has some limitations for the elderly who are either not familiar with or do not have smartphones.

With the development of radar sensors, there has been an emergence of HAR using millimeter-wave radar data [25]. Compared with other methods, radar data can better protect personal privacy and is more comfortable for users. The key to using radar to recognize human activities is to extract and identify the features of the micro-Doppler signal generated when the elderly move. In 2011, Liu et al. [26] extracted time–frequency features of activities through the mel frequency cepstrum coefficient (MFCC) and used support vector machine (SVM) and k-nearest neighbor (KNN) to recognize activities with 78.25% accuracy for SVM and 77.15% accuracy for KNN. However, the limit of supervised learning is that it can only extract features artificially and cannot transfer learning. Deep learning does not require complex feature extraction and has good learning and recognition ability for high-dimensional data. Sadreazami et al. [27] and Tsuchiyama et al. [28] used distance spectrums and time series of radar data combined with CNN for HAR. In 2020, Bhattacharya and Vaughan [29] used spectrograms as input of CNN to distinguish falling and non-falling. In the same year, Maitre et al. [30] and Erol et al. [31] used multiple radar sensors for HAR to solve the problem that a single radar sensor could only be used in a small range. Hochreiter et al. [32] proposed a long short-term memory network (LSTM)) to solve the problem of gradient vanishing and gradient explosion. Wang et al. [33] used an improved LSTM model based on a recurrent neutral network (RNN) combined with deep CNN. Their work recognized radar Doppler images of six human activities with an accuracy of 82.33%. Garcia et al. [34] also used the CNN-LSTM model to recognize human activities. The authors proposed an approach to collect data on volunteer activity by placing a non-invasive tri-axial accelerometer device. Their innovation lies in two aspects: they used LSTM to classify time series and they proposed a new data enhancement method. The results show that their model is more robust. Bouchard et al. [35] used IR-UWB radar combined with CNN for binary classification to recognize falling and normal activities with an accuracy of 96.35%. Cao et al. [36] applied a five-layer convolutional neural network AlexNet with fewer layers on HAR. They believed that features could be better extracted by using fewer convolution layers.

Although deep learning has a strong learning ability and high accuracy in HAR, it needs a large volume of data for training purposes. Due to the particularity of the elderly, it is difficult for them to generate some high-risk activities for data collection. In order to solve this problem, we proposed a method that combines improved principal component analysis (PCA) with an improved VGG16 model (a 16-layer neural network model pre-trained by the Visual Geometry Group) for HAR. This method enhances feature dimensions with high-value information while preserving the basic features of the raw data. Moreover, it speeds up the convergence rate and reduces over-fitting.

3. Methodology

3.1. Improved VGG16

VGG is a model proposed by the Visual Geometry Group at the University of Ox-ford. It obtained excellent results in the 2014 ImageNet Large Scale Visual Recognition Challenge (ILSVRC-2014), which ranked second in classification task and first in localization task. The outstanding contribution of VGG is proving that small convolution can effectively improve performance by increasing network depth. VGG retains the characteristics of AlexNet and also of a deeper network layer.

The improvement of the VGG16 model has two aspects: the improvement of the model structure and the optimization of the model training parameter. Firstly, we adjusted the number of layers to fit the sample features of spectrograms and added a Dropout layer between Fully-Connected layers to prevent over-fitting. Then, in relation to convergence rate, we converted the constant learning rate to a dynamic learning rate to ensure convergence.

3.1.1. Improvement of the Model Structure

In our experiments, we chose to train a VGG16 model to recognize human activities, not only because it excels at image feature extraction but also because it uses fewer convolutional layers, making it more suitable for the task of the small-scale millimeter-wave radar dataset. The traditional VGG16 model has 16 layers, including 13 Convolutional layers and 3 Fully-Connected layers. The initial input size of the VGG16 model is 224 × 224 × 3. After multiple convolutions and 2 Fully-Connected layers, the output of the Fully-Connected layer is 4096 and the final output dimension is 1000. The VGG16 model was originally trained on the ImageNet dataset with 1000 classifications [37]. In this work, the implemented VGG16 model does not need as many complex layers as the original VGG16 model. Therefore, we reduced the 3-layer Full-Connected layer to 2-layer and used Relu as the activation function. In addition, a Dropout layer was added between Fully-Connected layers in the improved VGG16 model, as the high-dimensional features of the spectrogram of radar data account for the most amount of information. Doing this could reduce ineffective features, improve the recognition speed of single images, and prevent over-fitting. The results of HAR are obtained after a Softmax layer. In the improved VGG16 model, we not only reduced the number of network parameters but also accelerated the convergence rate. Figure 1 shows the improved VGG16 model.

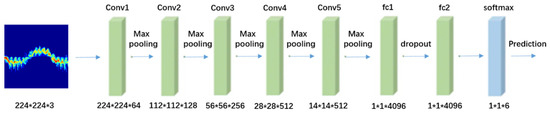
Figure 1. The improved VGG16 Model.

3.1.2. Optimization of the Parameter

In the training of the VGG16 model, the learning rate controls the error used to update the parameters during the back propagation, so that the parameters gradually fit the output of the sample and tend to the optimal result. If the learning rate is high, the influence of output error on the parameters is more significant and the parameters are updated faster but, at the same time, the influence of abnormal data is greater. For small-scale datasets, the ideal learning rate is not fixed but is a value that changes with the training rounds. In other words, the learning rate should be set to a larger value at the beginning of training, and then the learning rate will decrease in the training model until convergence.

In this paper, we halve each round’s learning rate. We then increase the learning rate according to the number of training rounds, and decrease it with the exponential interpolation. The value of the learning rate can be derived as below.

$$l_{r_t}=l_{r_0}\times k^{\frac{t}{T}}$$

(1)

$$l_{r_t}=l_{r_{t-1}}\times k^{\frac{1}{T}}$$

(2)

$l_{r_t}$ denotes the learning rate after the change, $l_{r_{t-1}}$ denotes the learning rate of the last round (they are recursive), $l_{r_0}$ denotes the initial learning rate, $k$ controls the speed at which the learning rate decreases, $t$ denotes the number of training rounds, and $T$ denotes the number of rounds to finish the learning rate decay.

3.2. Improved PCA

Traditional principal component analysis (PCA) is a linear dimension reduction method which uses orthogonal transformation as the mapping matrix. PCA uses the orthogonal matrix $\mathit{A}\in {\mathit{R}}^{k \ast n}$ to map samples to lower dimensional spaces $\mathit{A}m\in {\mathit{R}}^k$ for data samples in high-dimensional spaces. $k\ll n$ plays a role in dimensionality reduction, which can solve the problem of too many parameters due to poor data and also speeds up the rate of convergence.

Equation (3) shows a $m\times n$ matrix created from $m$ samples of $n$ dimensions.

$$\mathit{X}=\left[\begin{array}{ccc}{x}_{11}& \cdots & x_{1n}\\ ⋮& \ddots & ⋮\\ x_{m1}& \cdots & x_{mn}\end{array}\right]$$

(3)

${\mathit{X}}_{\mathrm{pre}}$ is given by zero-mean normalization and standardization, as shown in Equation (4).

$${\mathit{X}}_{\mathit{p}\mathit{r}\mathit{e}}=\left[\begin{array}{ccc}\frac{X_{11}-\overline{X_1}}{S_1}& \cdots & \frac{X_{1n}-\overline{X_n}}{S_n}\\ ⋮& \ddots & ⋮\\ \frac{X_{m1}-\overline{X_1}}{S_1}& \cdots & \frac{X_{mn}-\overline{X_n}}{S_n}\end{array}\right]$$

(4)

$$\overline{X_n}=\frac{1}{n}{\displaystyle \sum }_{i=1}^m{x}_{mn}$$

(5)

In Equation (5), $\overline{X_n}$ denotes the mean value of each dimension and

$S_n$ denotes the standard deviation of each dimension.

$$S_n=\frac{1}{m}\sqrt{\sum _{i=1}^m(x_{mn}-\overline{X_n})}$$

(6)

The covariance matrix ${\mathit{X}}_{\mathrm{cov}}$ is given by Equation (7).

$${\mathit{X}}_{\mathrm{cov}}=\frac{1}{n-1}\overline{X_{pre}{X}^T}$$

(7)

The value $\mathit{\lambda }=\left[{\mathit{\lambda }}_1,\dots {\mathit{\lambda }}_{\mathit{n}}\right]$ of the covariance matrix and the orthonormal vector $\mathit{V}=\left[{\mathit{v}}_1,\dots ,{\mathit{v}}_{\mathit{n}}\right]$ are obtained by diagonalizing ${\mathit{X}}_{\mathrm{cov}}$.

Traditional PCA extracts orthonormal vectors and sorts the values to obtain the top principal components with the highest contribution. When the principal component matrix is given, it is compressed from $n$ dimension to $k$ dimension by multiplying with ${\mathit{X}}_{\mathrm{pre}}$. However, when the data dimension is greatly compressed for small-scale datasets, it can lead to a decrease in accuracy and over-fitting. This effect also pays the price, that is, at the expense of freedom. The loss of information caused by data compression can be offset by increasing the number of principal components retained for final analysis with an associated cost of a loss of degrees of freedom. The impact is more significant in smaller datasets than in larger datasets.

Therefore, our work used an improved PCA to arrange the contribution of principal components and enhance values. Firstly, we selected $k$ eigenvectors from the $n$ dimensions, which accounted for most (>70%) of the valuable information of the spectrograms and then enhanced these $k$ values by making them normally distributed. The abnormal values that are not on the interval of $(\overline{x}-2\sigma ,\overline{x}+2\sigma )$ were replaced by the mean of the $n-k$ dimensions. The substituted values were then added with a deviation to prevent over-fitting, while the values of the $n-k$ eigenvectors left did not change. Finally, the $k$ eigenvectors were combined into a new principal component matrix ${\mathit{V}}^{\prime }$ after enhancement, with ${\mathit{V}}^{\prime }$ given by Equation (8).

$${\mathit{V}}^{\prime }=\left[\begin{array}{c}{v}_1^{\prime }\\ \begin{array}{l}{v}_2^{\prime }\\ v_p^{\prime }\end{array}\\ \dots \\ v_k\end{array}\right]$$

(8)

$v_1^{\prime },v_2^{\prime }\dots v_k^{\prime }$ are eigenvectors whose values are processed by the algorithm and ${\mathit{V}}^{\prime }$ is an enhanced matrix that combines these values with the rest of the unchanged values. Finally, the compressed matrix of $k$ dimensions is given by ${\mathit{V}}^{\prime }\times {\mathit{X}}_{\mathrm{pre}}$. The data preprocessing process based on PCA is shown in Figure 2.

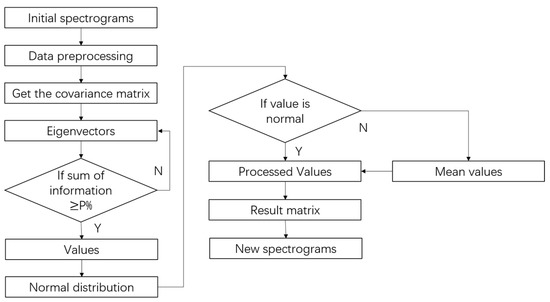
Figure 2. Data preprocessing process based on PCA.

4. Experiments and Results

Comparative experiments were conducted to evaluate the performance of our proposed method against traditional methods. For comparisons, we processed radar spectrograms with the improved PCA algorithm and the traditional PCA algorithm, respectively. Moreover, the wanted HAR model was trained with the improved VGG16 model and the original VGG 16 model.

4.1. Dataset

The dataset [38] that we used in the experiments was downloaded from http://researchdata.gla.ac.uk/848/ accessed on 5 September 2019. It was contributed by Shah et al. from the University of Glasgow. They collected data using FMCW radar, which operated in C-band (5.8 GHz) with a bandwidth of 400 MHz, chirp duration of 1 ms, and output power of about 18 dBm. The radar can record the micro-Doppler signals of moving people in the region of interest, and the format of each collected original radar data is a long 1D complex array. This dataset includes six activity types and the data format is binary. These data files can be used to generate 224 × 224 PNG images using MATLAB code provided by the authors.

The dataset contains radar signatures of six types of indoor human activities—walking, sitting, standing up, picking up items, drinking, and falling—collected from 99 older people in nine different places. Table 2 shows the number of samples of each activity type in the dataset. Figure 3 shows the examples of radar spectrograms (Time–Velocity pattern) of six activities from 20-to-100-year-old female/male subjects. Among these volunteers, people over 60 years old make up the majority.

Table 2. Number of samples per activity type.

Types of Activities	Number
Walking	286
Sitting	289
Standing	287
Picking up things	287
Drinking	286
Falling	198
Total	1633

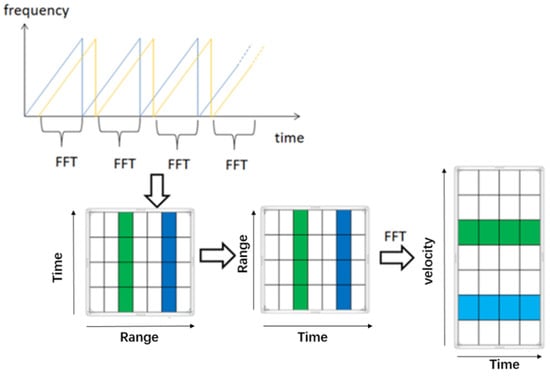
Figure 3. Radar data process showing Time–Velocity patterns.

4.2. Signal Preprocess: Improved PCA

To convert the 1D raw radar data into 2D spectrograms, we first performed FFT (Fast Fourier transform) on the raw radar data and obtained the Range-Time images. Range FFT is used to derive the distance information of the target. The sampling data on each chirp is FFT and stored as a row vector of the matrix. We then transposed the X-axis with the Y-axis of the Range-Time images to obtain the Time-Velocity pattern of spectrograms which can better represent the characteristics of the movement. After the transposition, the X-axis represents Time and the Y-axis represents Range. Finally, we performed a second FFT on each range dimension using the Doppler FFT to obtain target speed information from the spectrogram (Time-Velocity pattern). The data conversion process is demonstrated in Figure 3. The typical spectrogram of each activity type is shown in Figure 4.

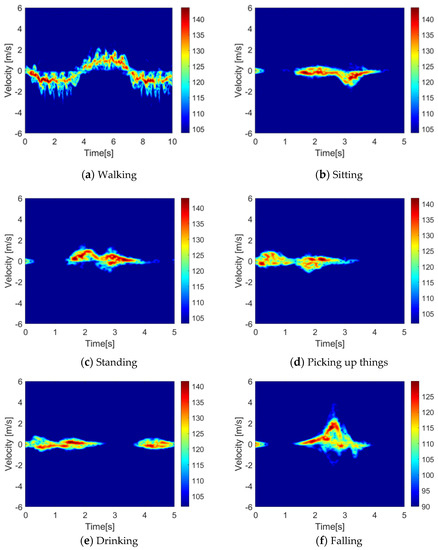
Figure 4. Radar spectrograms of six activities.

To extract the features of the obtained 2D spectrograms, we processed the data using the PCA algorithm. Figure 5 shows the contribution rate of the first 10 components extracted from six types of radar spectrograms.

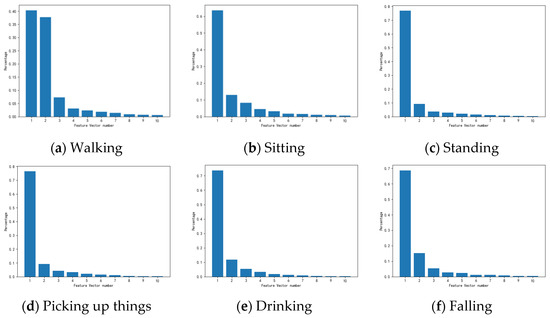
Figure 5. Contribution rates of the first 10 components of different activities.

As shown in Figure 5, the first two eigenvectors account for 70–80% of the sample information. Therefore, we set the parameter $p=2$ in the improved PCA method and select these two eigenvectors for value enhancement. The other eigenvectors do not change their values. Figure 6 shows the spectrogram reconstructed from the principal components k = 1 to k = 6.

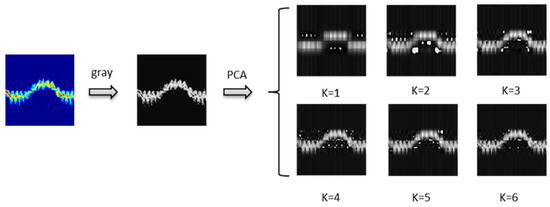
Figure 6. Image Reconstruction in PCA method.

Figure 6 highlights that the first two principal components have reconstructed the main contours of the original spectrogram. After that, as the principal components increase, the information of the image gradually increases and the noise becomes smaller but still exists. Therefore, we only enhanced the first two values of the dimensions that contain most of the spectrogram information.

In value enhancement, the size of the original radar spectrograms was $256\times 256$ and the number of values in each dimension was 256. We selected the values of the first two dimensions for enhancement which accounted for most of the image information, with the number of selected values being $2\times 256$. Each type of activity contained Q images. We calculated the mean value of data in these two dimensions of spectrograms. These values with the size of $Q\times 1$ are normally distributed and the abnormal values were then selected and replaced with the mean values while the remaining normal values remained unchanged. The process of selecting and enhancing values is shown in Figure 7.

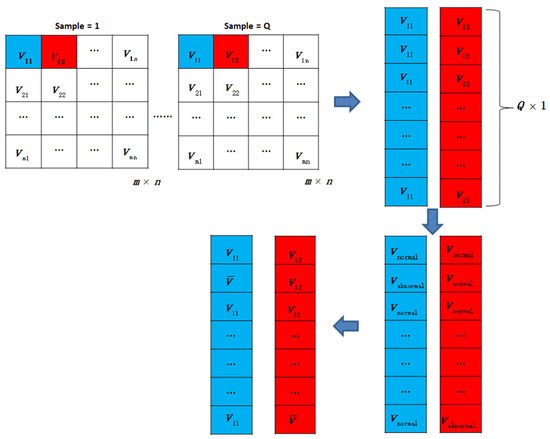
Figure 7. Values’ selection and enhancement process.

In Figure 7, ${\mathit{v}}_{\mathrm{normal}}$ denotes the normal values, ${\mathit{v}}_{\mathrm{abnormal}}$ denotes the abnormal values, and $\overline{\mathit{V}}$ represents the mean values. The mean is not global. There are six activities in the dataset and Q samples in each activity. The mean value is obtained according to each value of the enhanced eigenvector. The mean number of the enhanced eigenvectors is the sequence length of the eigenvectors.

As can be seen in Figure 8, before the normal distribution, some of the values of the first two dimensions did not follow the 2 σ principle of normal distribution and were outside the $(\overline{\mathit{x}}-2\sigma ,\overline{\mathit{x}}+2\sigma )$ range. Therefore, to enhance the values, we assigned these outlier values to the mean of the values. In order to avoid over-fitting in training, the assigned values were added to a random constant of the range of $({10}^{-3}$,${10}^{-4})$. By doing so, all values within these two dimensions were following the 2$\sigma$ principle of normal distribution.

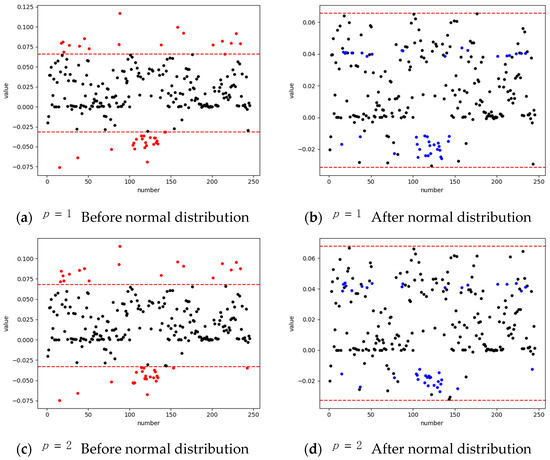
Figure 8. Distribution of values in the first two dimensions. Black represents normal points; Red represents the abnormal point before processing; Blue represents the normal point from the abnormal point after processing.

Figure 9 shows the comparisons of spectrograms processed by the improved and traditional PCA methods. Both methods preserved 90% of the information in the raw radar spectrograms.

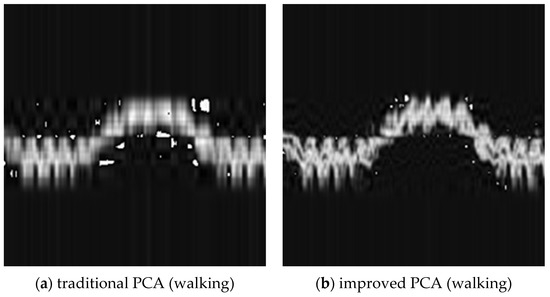
Figure 9. Comparison of spectrograms processed by the improved PCA and the traditional PCA.

While traditional PCA preserves the most valuable information, the spectrograms of walking and sitting in Figure 9a,c still had large areas of blur and noise. Spectrograms processed by using the improved PCA method were significantly better. Although there was still noise in Figure 9b,d, the overall spectrograms were smoother and clearer, proving that the improved PCA had a better performance in processing the radar spectrograms than did the traditional PCA.

4.3. Test and Evaluation

In order to verify the effectiveness of the proposed algorithm and network structure, the parameters of accuracy, precision, recall, F1-score, and training time were used as the evaluation index of the experiments.

$$Accuracy=\frac{TP+TN}{TP+FN+FP+TN}$$

(9)

$$Precision=\frac{TP}{TP+FP}$$

(10)

$$Recall=\frac{TP}{TP+FN}$$

(11)

$$F1-score=2 \ast \frac{Precision \ast Recall}{Precision+Recall}$$

(12)

TP means true positive, TN means true negative, FN means false negative, and FP means false positive.

Comparative experiments were conducted to evaluate the performance of our proposed method with traditional methods. The spectrograms in the dataset were divided into the training set and test set by a ratio of 8:2. The initial learning rate is 1 $\times {10}^{-4}$, batch size is 32, and the epoch is 300. The optimizer adopted Adam and the loss function was the cross-entropy loss function.

The following methods were trained respectively:

• Method 1: Training raw radar spectrograms through VGG16;
• Method 2: Training raw radar spectrograms through improved VGG16;
• Method 3: Training the data processed by traditional PCA through improved VGG16;
• Proposed Method: Training the data processed by improved PCA through improved VGG16.

The training accuracy of these four methods with epochs based on the training set is shown in Figure 10.

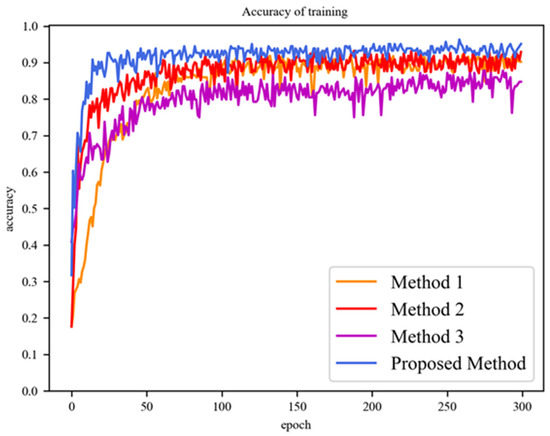
Figure 10. Accuracy of training for the four methods.

The accuracy, precision, recall, and training time of each round of the four methods based on the test set are shown in Table 3.

Table 3. Performance of different methods.

Methods	Accuracy/%	Precision	Recall	F1-Score	Training Time (/epoch/s)
Method 1	92.07	0.93	0.91	0.92	12.47
Method 2	93.47	0.94	0.93	0.93	11.39
Method 3	87.84	0.90	0.87	0.89	10.14
Proposed Method	96.34	0.96	0.96	0.96	10.88

As shown in Table 3, method 1 used raw radar spectrograms to train the VGG16 model with 90% accuracy after 100 rounds of training; At this point, the parameters had converged in a smaller range. However, the curve appeared to oscillate after 100 rounds and there was over-fitting as the dataset is small-scale. Method 2 used raw radar spectrograms to train the improved VGG16 model, achieving 90% accuracy after 50 rounds, 1.4% higher than method 1. Although method 2 is faster, there was still over-fitting in the later training phase. Method 3 used samples processed by traditional PCA to train the improved VGG16 model. These reconstructed samples removed surplus information from the raw radar spectrograms and compressed the data dimensions. The results of method 3 showed that although the model can converge in less than 50 rounds, its accuracy and precision are the lowest among the four methods. Its accuracy-epoch curve also had a severe oscillation later in training, which usually indicates serious over-fitting. The proposed method used processed images which were given by the improved PCA to train the improved VGG16 model, with the results showing that it had the best performance among the four methods in terms of accuracy, precision, recall, and F1-score. The proposed method converged faster than methods 1 and 2. Although it did not converge as fast as method 3, its accuracy-epoch curve was the most stable, with no significant oscillations in the later training phase. According to the results, the proposed method had the best performance compared with other methods, and the improved PCA combined with the improved VGG16 model significantly improved the performance of HAR and reduced the training time.

4.3.1. Performance Comparison

We used the Skimage Python package to convert image files into pixel information and stored the data in a python array. The shape of the image data array is [224,224,3], representing a PNG file with a width of 224 pixels and height of 224 pixels, with 3 representing the pixel values of red, green and blue (RGB). We then converted the image to a grayscale image, removed the color, and changed the array shape to [224,224,1]. This data array was saved in CSV format for machine learning processing. We then compared the proposed method with some commonly used machine learning methods, with the results shown in Table 4.

Table 4. Comparison of different methods with the proposed method.

Methods	Accuracy/%	Precision	Recall	F1-Score	Training Time (/epoch/s)
Random Forest	84.75	0.86	0.85	0.85	16.49
SVM	74.46	0.76	0.74	0.70	13.76
KNN	90.85	0.91	0.91	0.91	14.28
Bi-LSTM	83.53	0.87	0.84	0.85	23.17
Proposed Method	96.34	0.96	0.96	0.96	10.88

According to the results shown in Table 4, our proposed method had the best performance in terms of accuracy, precision, recall, F1-score, and training time. In addition to our proposed method, KNN had better performance than the other machine learning algorithms when using original radar spectrograms, mainly due to its simple logic and insensitivity to abnormal values. SVM had a shorter training time than the other methods due to its advantages in processing small-scale datasets. However, the traditional SVM only gave the binary classification algorithm, so the results of SVM were not ideal when dealing with the problem of six classifications. The overall performance of Bi-LSTM was acceptable, but the training time was too long because of its complex network structure. Overall, the results of traditional machine learning methods in radar data classification were not satisfactory. Our proposed method based on improved PCA and an improved VGG16 model is more suitable for processing small-scale radar data, which is superior to other methods in terms of results and training time reduction.

4.3.2. Performance Study in Fall Detection

Among the six typical activities, walking, sitting, standing, picking up things, drinking, and falling, falling is the most harmful to the elderly. Older adults may suffer severe injuries after falling, or even endanger their life. For this reason, recognizing falls was critical in the HAR field. We separated the other five daily activities from falls and used binary classification to recognize the fall.

As can be seen from Figure 11, our proposed method had a significant advantage in detection accuracy, with a fall detection of 96% and non-fall detection of 95.5% compared with the other three methods. It can also be seen that method 2 was slightly higher than method 1 in the accuracy of fall detection, but there was no difference in identifying normal activities. The reason might be that the improved VGG16 model used in method 2 can better identify differences between falls and other activities. The performance of method 3 was the worst, mainly because the spectrograms processed by the traditional PCA algorithm not only reduced the dimension of the samples but also discarded a large amount of information, resulting in method 3 having difficulty identifying the fall. The proposed method achieved the best performance in fall detection, mainly because the improved PAC algorithm enhanced the values of the retained dimension while reducing the redundant dimension, thereby improving the training speed and recognition of the spectrograms.

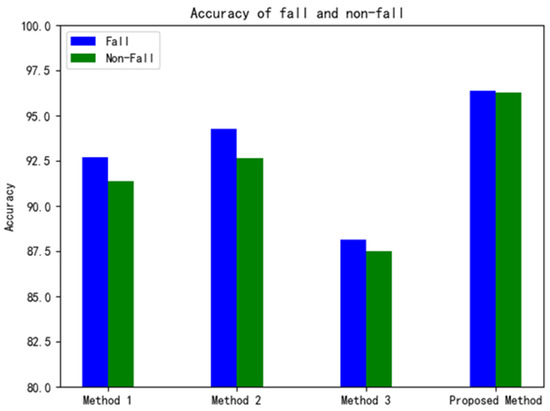
Figure 11. Comparison of accuracy of fall and non-fall for the four methods.

5. Conclusions

This paper used a convolutional neural network to recognize the human activities of the elderly. To solve the problem of over-fitting caused by the small-scale dataset and improve the training speed of the model, we proposed an improved PCA method to process the raw radar spectrograms and then used them to train an improved VGG16 model to develop an efficient human activity recognition model. Our proposed method determined the number of principal components by preserving 90% of information. The values of the extracted dimensions were normally distributed to obtain the normal and abnormal values. The abnormal values were then replaced with the mean value of its dimension to enhance values. In this way, the meaningless and unimportant dimensions in the image can be removed by the PCA algorithm, and dimensions that can represent the image can be enhanced. This is beneficial to improve the rate of convergence in model training and reduce over-fitting when using small-scale datasets. In conclusion, we used a radar-based non-contact method to recognize human activities. This ensured the recognition accuracy and did not infringe on the home privacy of the elderly, nor did it require the elderly to carry out complex installation and wearing, which can effectively alleviate the pressure on the medical care industry.

However, there are also certain limitations to our work. First, the dataset we used in this study is balanced and contained only six types of activities, so it is worth testing our method with some unbalanced data and extreme types of activities in future work. In addition, this future work will also apply our methods to areas such as object recognition in autonomous driving technology. Since millimeter-wave radar has some defects, such as poor penetration ability in automatic driving applications [39], the object activity recognition algorithm that combines millimeter-wave radar data and ultrasonic radar data is also worth further investigation and research.