Abstract
In this paper, we study the characteristics of the supercontinuum (SC) induced by the filamentation of two typical vortex beams (i.e., Laguerre-Gaussian (LG) and Bessel-Gaussian (BG) beams) in water. By moving the cuvette filled with water along the laser propagation path, we measure the SC induced by the filamentation of the two vortex beams at different positions in water. The results show that the degree of spectral broadening induced by the filamentation of LG beams hardly changes with the change of position, while for BG beams, the spectral broadening induced by filamentation is weak on both sides and strong in the middle. The value of topological charge (TC) affects the length of the filament formed by BG beams; however, its effect on the spectral broadening induced by the filamentation of LG and BG beams is negligible.
1. Introduction
In 1992, Allen et al. theoretically predicted that apart from spin angular momentum, photons can also carry another form of angular momentum: orbital angular momentum []. It comes from the helical phase of light waves, i.e., a light beam with a phase term (l is an orbital angular quantum number, which is also called topological charge (TC) and is the azimuth angle), and each photon carries an orbital angular momentum (OAM) of . Theoretically, l can be any integer or a fraction [,,]. Laguerre-Gaussian (LG) and Bessel-Gaussian (BG) beams are two typical kinds of vortex beams. Another obvious feature of the vortex beam is that the spatial distribution of its intensity presents a ‘donut’ structure, i.e., its intensity at the center is zero, and the radius of the hollow center increases gradually with the increase of l. The OAM carried by the vortex beams can be transferred to matters during the interaction of vortex beams and matters [,].
These special properties make vortex beams widely applied in optical tweezers [,,,,,,], optical imaging [,,], information transmission and cryptography [,,,,,] and micro-processing [,,,] and other fields. For example, Bessel beams have propagation invariance compared with Gaussian ones; that is, they have the ability to maintain their shape and peak power at the extended focal region (Bessel region), which makes them have promising application prospects in many fields, especially for micro-processing. Using the Bessel beams, the length, plasma density and laser intensity of the femtosecond filament can be well controlled [,,,], see Table 1. For example, Wang et al. tailored the profile of the annular Bessel beams by placing an amplitude mask and iris diaphragm, respectively, before the axicon, and thus the onset and terminal positions of femtosecond laser filament in the fused silica can be arbitrarily controlled []. Once the parameters of femtosecond filament are controlled, they are accompanied by several nonlinear phenomena such as photoionization and supercontinuum (SC) generation; fluorescence emission is also affected [,,]. For example, Dota et al. studied the filamentation of Bessel beams in BaF2 by measuring the side emitted fluorescence and transmitted SC []. They observed the transition from a stable state to a nonlinear unstable state for Bessel beams by changing the incident laser pulse energy and found that SC generation depends on the size of the incident beam and the distance from the sample to the tip of the axicon. However, these studies are limited to 0-order vortex beams. For higher-order vortex beams, they carry OAM, which will increase the complexity of the filamentation process. As they propagate in a transparent medium, they have a great chance to split into multiple filaments [,,,], thus affecting the filamentation dynamics. In addition, the filamentation threshold of the higher-order LG filament increases with TC, which can be roughly described by , where is the critical power of self-focusing for Gaussian beams [,]. Miller et al. found that by using coherent conjugate asymmetric higher-order BG beams to control the far-field intensity distribution, the filamentation process can be spatiotemporally controlled []. Jukna et al. experimentally and numerically studied the nonlinear propagation of higher-order BG light in transparent solids [] and found that higher-order BG beams retain all the properties of 0-order BG beams, while the TC provides additional parameters which can control the filamentation of BG beams. They also found that the radius and plasma density increase with the increase of TC value and top angle []. Zhang et al. studied the coherence of the SC generated by LG beams with different TC values in water [] and found that spectral broadening is not related to the TC value; however, they did not study the SC induced by filamentation at different locations in water.

Table 1.
Recent works in vortex beam.
Due to the different geometries (i.e., focal spot shape and size, etc.) of BG and LG beams, the filaments generated by BG and LG beams exhibit different shapes. As a result, the laser fluence, intensity as well as plasma density inside the filament generated by the two kinds of vortex beams differ much from each other, which further affects SC generation. In this paper, by analyzing the changes of the SC induced by the filamentation of BG and LG beams at different locations in a cuvette filled with water, we discuss the characteristics of the SC induced by these two vortex beams.
2. Femtosecond Laser Filamentation and SC Generation in Water
Femtosecond laser filamentation is an important nonlinear process in a nonlinear medium. As femtosecond laser pulses propagate in transparent media, say air, glass and water, etc., the laser intensity keeps increasing due to the Kerr self-focusing effect, and as it increases to a certain value (1013–1014 W/cm2), the medium will be ionized by the high-intensity beam, generating a large number of plasmas which play a defocusing role. A self-induced plasma channel will be formed when the Kerr self-focusing effect and the plasma defocusing effect reach a dynamical balance [,], which is called filamentation. During femtosecond filamentation, nonlinear effects such as Kerr self-focusing, multiphoton/tunnelling ionization, plasma formation and recombination lead to the change of refractive index, making the laser field undergo self-phase modulation (SPM) []. According to the self-phase modulation effect, the variation of the spectrum induced by SPM can be described by [,]:
where is the variation of the phase of the laser pulse, , z, n2, and are the central wavelength of the laser pulse, the propagation distance in media, second-order nonlinear refractive index, plasma density and the critical plasma density (), , e and me are permittivity of vacuum, electron charge and electron mass), respectively. As a result, the spectral broadening results from the SPM. It can be seen from Equation (1) that the spectral broadening is affected by several factors, such as the temporal evolution of laser intensity and plasma density, nonlinear refractive index of the medium and filament length, etc.
Obviously, the degree of spectral broadening is positively related to the filament length. The span of laser spectra after spectral broadening ranges from ultraviolet to infrared wavelength covering the entire visible range [], and therefore it is also called white light or SC [,]. SC has a wide range of applications, such as time-resolved excitation and absorption spectroscopy [], optical pulse compression [] and the characterization of laser-induced structural transitions [], etc. The SC generation induced by femtosecond laser in water has been extensively studied in the past few decades, both experimentally and theoretically [,,,,,,,,,]. Quite a few approaches are used to study the property of the SC and to control the SC generation [,,,,,,,,,]. For example, the coherence of the SC can be studied by the interference method [,]. By manipulating the parameters of femtosecond laser pulses (such as spatial distribution of intensity [,], polarization [] and pulse energy [], etc.), doping the water with other matters [,], adopting a two-color scheme [], the SC generation can be enhanced. However, these works mainly dealt with Gaussian pulses. In this paper, we mainly focus on the characteristics of the SC generated by higher-order vortex beams in water.
3. Experimental Setup
To explore the characteristics of the SC induced by filamentation of BG and LG beams at different locations in water, we design an experimental setup shown in Figure 1. The laser pulses are generated by an amplified Ti: Sapphire laser system. The central wavelength, duration and repetition rate of the laser pulses are 800 nm, 50 fs and 1 kHz, respectively. The maximum pulse energy is 3.0 mJ, and the pulse energy is adjusted by an energy attenuator composed of a half-wave plate H and a Glan prism G to the desired value. The beam spot size is adjusted by an iris (which is 10 mm in the experiment), and consequently, the light beam can perfectly enter the liquid crystal screen of a spatial light modulator (SLM, Hamamatsu LCOS-SLM, X13138). The SLM can generate LG beams by loading the phase diagram (see Figure 2a′–c′ in Ref. []). In this experiment, we attempt to compare the characteristics of the SC generated by higher-order BG and LG beams, and thus two kinds of optical lenses are used to focus the vortex beams: One is a focusing (plano-convex) lens (fused silica), whose focal length is f = 75 mm, and the other one is an axicon lens, whose top angle is 170 degrees. As the generated LG beams with different TC values pass through the axicon lens, higher-order BG beams can be generated. The dashed rectangle suggests the axicon lens can be replaced by a focusing lens. The vortex beams are focused into a quartz cuvette C (with dimensions: 50 mm × 10 mm × 40 mm) filled with water and form filament generating the SC. The transmitted spectrum (i.e., the SC) is firstly collected by an integrating sphere IS and then guided to a spectrometer (Avantes, avaspec-uls2048l), and thus the transmitted spectral data are obtained. Both the cuvette and integrating sphere are fixed on an electric translation stage, and by moving the electric translation stage, the SC induced by femtosecond laser filamentation at different locations in water is recorded. This method is somewhat similar to the Z-scan technology [,,]. The propagation of laser beams in water is affected by the water attenuation and water-induced turbulence (e.g., bubble generation), which affect the stability of supercontinuum. To reduce the error, each spectrum is obtained by an average of a hundred measurements.
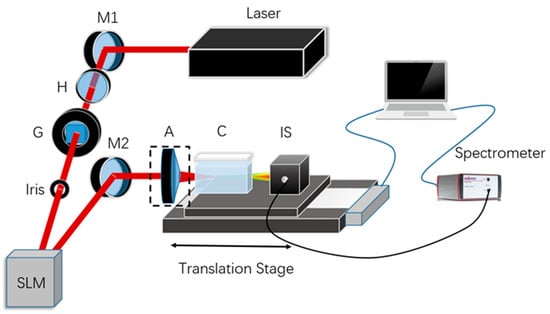
Figure 1.
Schematic diagram of the experimental setup to explore the SC induced by the filamentation of BG and LG beams at different locations in water. M1, M2: plane mirror, H: half-wave plate, G: Glan prism, SLM: spatial light modulator, A: axicon lens, the dashed rectangle indicates it can be replaced by a focusing (plano-convex) lens, C: cuvette filled with water, IS: integrating sphere. The black and blue lines are the optical fiber and data cable, respectively.
4. Results and Discussion
First of all, by measuring the transmitted spectrum, we obtain the SC induced by the filamentation of 0-order LG and BG beams (i.e., l = 0) at different locations in water, as shown in Figure 2. It should be noted that the intensity of the transmitted spectrum around 800 nm (central wavelength) is beyond the measuring range of the spectrometer and the dark red area indicates that the spectral intensity is saturated. In the paper, we mainly focus on the degree of spectral broadening, and thus we do not discuss the saturation of the spectral signal. To facilitate the discussion of the experimental results, we define the position where the front wall of the cuvette is 3 mm (35 mm) away from the axicon lens (focusing lens) as the ‘zero position’, i.e., D = 0 mm, as shown in Figure 3a,b. It can be clearly seen from Figure 2 that the variation of the SC induced by the filamentation of 0-order LG and BG beams in water with D shows different tendencies. As the filament formed by LG beams gradually moves toward the front wall of the cuvette, it could be seen that when D is between 0 mm and 35 mm, the degree of spectral broadening remains almost unchanged, and thus the transmitted spectrum exhibits a plateau, as shown in Figure 2a. As we further increase D, the degree of spectral broadening becomes smaller, and the transmitted spectrum becomes very weak at D = 40 mm, showing a ‘dip’. As D is larger than 40 mm, the transmitted spectrum remains almost unchanged. In contrast, the SC generated by the filamentation of BG beams shows entirely different behaviors: as D increases, the degree of spectral broadening firstly becomes larger, reaches its maximum at a certain position and gradually becomes smaller, as shown in Figure 2b.
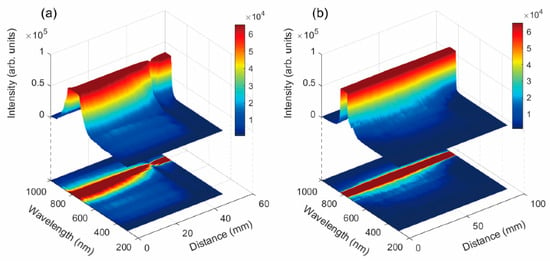
Figure 2.
Variation of the SC induced by the filamentation of (a) LG and (b) BG beams with D in the case of l = 0. The incident pulse energy of LG and BG beams are 104 μJ and 188 μJ, respectively.
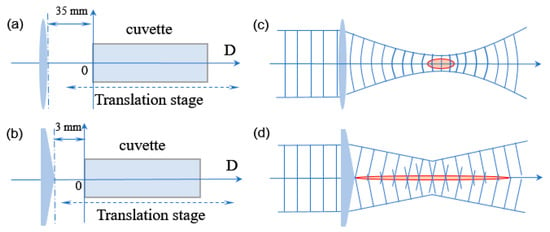
Figure 3.
Definition of the ‘zero position’ in the experiment (i.e., D = 0 mm) in the case of using the (a) focusing and (b) axicon lenses. Schematic diagram for Gaussian beam which passes the (c) focusing and (d) axicon lenses. The red areas in (c,d) denote the focal region.
Usually, Bessel beams are produced by an axicon lens whose focus is linear, resulting in a longer focal region (see Figure 3d), and it has non-diffraction property in the Bessel region; therefore, the filament generated by Bessel beams is longer than that generated by Gaussian beams with the same energy. In the process of changing the distance between the cuvette and the axicon lens, the length of the Bessel beam filament located in water firstly increases and then decreases, as schematically shown in Figure 4e–h. Consequently, the degree of spectral broadening induced by the BG beams firstly becomes larger, reaches its maximum at a certain position and becomes smaller gradually. In contrast, the filament generated by LG beams is relatively short, which is much shorter than the length of the cuvette. As we move the cuvette, the filament is almost located in water (see Figure 4a,b). Consequently, when D is between 0 mm and 35 mm, the SC changes little in both intensity and the degree of spectral broadening. As D is between 35 mm and 40 mm, part of the filament enters into the back wall of the cuvette, leading to the decrease in the length of filament in water, and thus the degree of spectral broadening becomes smaller. As D is larger than 40 mm, the focal region of LG beams moves out of the cuvette and enters the air (see Figure 4d). Since the critical power of self-focusing Pcr in the air [] is much higher than that in water [], no filament is formed, and the spectrum is hardly broadened.
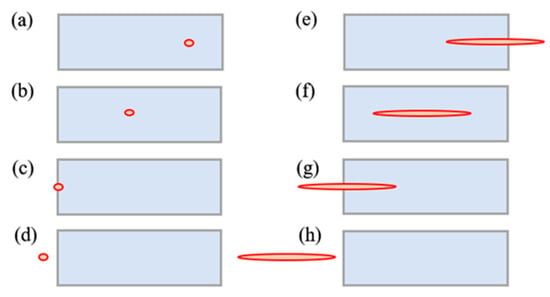
Figure 4.
Spatial relationship between the focal region of (a–d) LG, (e–h) BG beams and cuvette. The red areas denote the focal region, and light blue rectangles denote the cuvette filled with water.
In the process of moving the cuvette, both the focal regions of LG and BG beams pass through the cuvette wall; however, the spatial distribution of the transmitted spectrum only shows a ‘dip’ in the case of LG beams (at D = 40 mm). This is caused by the different spatial distribution of the laser intensity of the two beams. The focus region of LG beams is very small, which results in higher intensity of LG beams in the focal region. In contrast, due to the existence of the Bessel region, the focal region of BG beams is very long, resulting in a lower intensity of BG beams in the focal region, which is lower than the damage threshold of the cuvette wall. As a result, the laser pulse energy will not be absorbed by the cuvette wall when the focal region of BG beams covers the cuvette wall, and the transmitted spectrum is similar to that measured when the focal region is located in the air, as shown in Figure 2b. It should be noted that the thickness of the cuvette wall is 1 mm, which is comparable with the length of the LG beam filament in water. Since the focal length of the focusing lens is f = 75 mm, at D = 40 mm, the focal region of LG beams covers the front wall of the cuvette (see Figure 4c). The laser intensity of the focal region of LG beams is higher than the damage threshold of the cuvette wall, resulting in the ablation of the cuvette wall. As a result, part of the laser signal is reflected, and part of the laser energy is absorbed by the cuvette wall, resulting in a weak transmitted spectrum. Figure 2 show the SC induced by filamentation of LG and BG beams only in the case of l = 0. In the following part, we will study the SC produced by higher-order LG and BG beams (i.e., l > 0). Table 2 show the pulse energy and TC value of these vortex beams selected in our experiment.

Table 2.
Parameters of the LG and BG beams used in our experiment.
The laser pulse energy also affects SC generation. By changing the pulse energy (10, 52 and 104 μJ), we study the variation of the SC induced by filamentation of LG beams with D in the case of l = 0 and l = 2, as shown in Figure 5. It can be seen from Figure 5a,d that when the pulse energy is 10 μJ, the transmitted laser spectrum shows no obvious broadening, indicating that no filament is formed, for the SC generation is an obvious feature of femtosecond filamentation. It should be noted that due to the low pulse energy (10 μJ), the laser intensity in the focal region is relatively low, which is lower than the damage threshold of the cuvette wall, and thus little energy is absorbed or reflected by the cuvette wall. As a result, though the focal region of LG beams covers the cuvette wall at D = 40 mm, the transmitted spectrum changes little, which confirms the previous speculation of spectral ‘dip’. As the pulse energy is 52 and 104 μJ, filaments can be formed by LG beams, and the transmitted spectrum shows obvious broadening. Due to the high laser intensity in the focal region, as the cuvette wall overlaps with the focal region, it is ablated, part of the laser energy is absorbed or reflected, and thus the spatial distribution of transmitted spectrum shows a ‘dip’, as shown by Figure 5b,c,e,f. Figure 6 show the variation of the SC generated by LG beams with D when the value of TC is 0, 1, 2, 3, 4 and 5. For higher-order LG beams, the variation of the degree of spectral broadening with D is similar to that shown in Figure 6a (i.e., 0-order LG beam), which also exhibits plateau regions, as shown in Figure 6c–f. It can also be seen from the figure that along with the increase of TC value, the degree of spectral broadening changes little, i.e., it is not related to the TC value of LG beams, which is consistent with the work of Zhang et al. [].
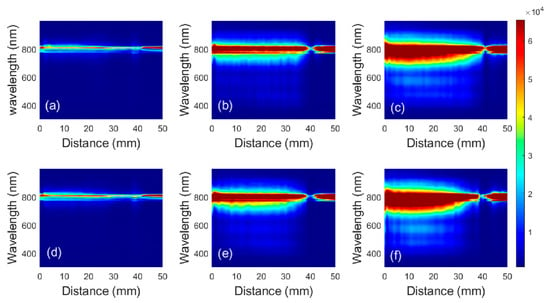
Figure 5.
Variation of the SC induced by the filamentation of LG beams with D when the incident pulse energy is (a,d) 10, (b,e) 52 and (c,f) 104 μJ. (a–c) and (d–f) refers to the cases of l = 0 and l = 2.
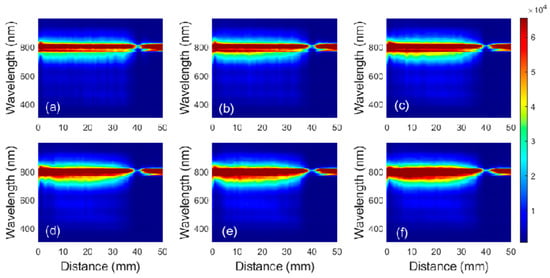
Figure 6.
Variation of the SC induced by the filamentation of LG beams with D when the value of TC is (a) 0, (b) 1, (c) 2, (d) 3, (e) 4 and (f) 5. The incident pulse energy is 52 μJ.
The SC generated by the filamentation of higher-order BG beams shows entirely different behaviors compared with that generated by higher-order LG beams. As D increases, the degree of spectral broadening firstly becomes larger, reaches its maximum at a certain position and becomes smaller gradually, as shown in Figure 7b–f. The cause for this phenomenon is actually the same as the case of the 0-order BG beam, i.e., the degree of spectral broadening is closely related to the filament length. At first, only part of the focal region of higher-order BG beams is located in water in the cuvette. As we move the cuvette (increase D), the length of the focal region of higher-order BG beams in water becomes larger, resulting in the enlargement of spectral broadening. As the focal region of higher-order BG beams is completely located in water, the degree of spectral broadening reaches its maximum, and as it gradually moves away from the cuvette, the filament length in water becomes shorter, leading to the decrease in the degree of spectral broadening. When the focal region of higher-order BG beams moves out of the cuvette (D > 60 mm), the transmitted spectrum shows little change, as shown in Figure 7. Figure 8 show the SC generated by different-order BG beams at the position where the spectral broadening reaches its maximum. According to the previous analysis, the focal region of BG beams is completely located in water at this time. It can be seen from the figure that the TC value also has little effect on the degree of the spectral broadening induced by the filament of higher-order BG beams, which is similar to the case of higher-order LG beams []. Both LG and BG beams belong to the vortex beam; in condensed media, the SC induced by filamentation of these beams will lose the orbital angular momentum, and therefore the spectral broadening is hardly affected by the TC value of the vortex beam.
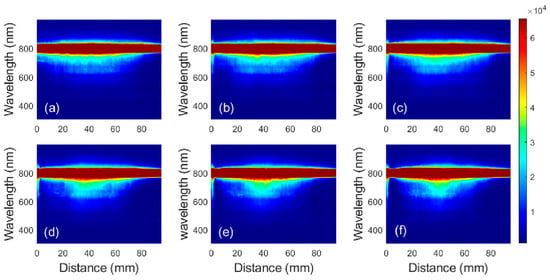
Figure 7.
Variation of the SC induced by the filamentation of BG beams with D when the value of TC is (a) 0, (b) 1, (c) 2, (d) 3, (e) 4 and (f) 5. The incident pulse energy is 188 μJ.
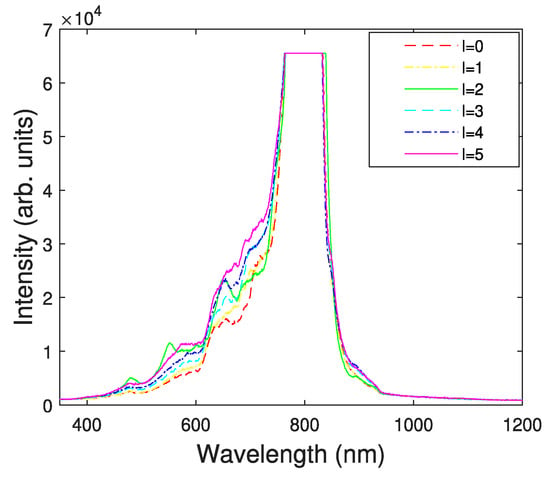
Figure 8.
SC induced by the filamentation of BG beams with TC different values. The incident pulse energy is 188 μJ.
It can also be seen from Figure 7 that there also exists a platform region with a constant spectral range during the filamentation of higher-order BG beams in water at different positions (spectral broadening changes little with increasing D). For example, in Figure 7b, when D is from 30 mm to 50 mm, the transmitted spectrum remains almost unchanged. It is easy to be understood since the filament formed by higher-order BG beams is shorter than the length of the cuvette. In the process of changing D, there exists a distance at which the filament formed by BG beams is completely located in water. However, the increase of TC value reduces the platform region, as shown in Figure 7a–d, which can be attributed to the fact that with the increase of TC value, the length of the Bessel region also increases, making the distance that the Bessel region is completely located in water becomes shorter. The phenomena suggest that the length of the filament generated by the BG beams is positively related to the TC value. However, as stated previously, the filament length also affects the degree of spectral broadening. Therefore, it seems that our conclusion is contradictory. In effect, it can be seen from Equation (1) that, apart from the filament length, other factors such as plasma density and laser intensity also affect the degree of spectral broadening. Since the incident pulse energy is the same for all the TC values (Figure 7 and Figure 8), with the increase of TC value, though the filament length is larger, the plasma density and laser intensity are lower, whose contribution to the degree of spectral broadening becomes lower. Comprehensively considering these factors, the degree of spectral broadening is hardly affected by the TC value of BG beams. It should be noted that temporal coherence is one key feature of SC generation, which is not explored in this paper. In future work, we will conduct systematic research on the temporal coherence of the SC generated by different vortex beams, which can provide a deeper understanding of the unique characteristics of SC generated by vortex beams.
5. Conclusions
In this paper, the characteristics of the SC generated by BG and LG beams are studied experimentally. The different focal regions of LG and BG beams lead to different variation tendencies of white light produced by them at different positions in water. The spectral broadening degree is proportional to the filament length. Due to the shorter focal region of LG beams, there is a long distance at which the focal region of LG beams is completely located in water in the process of changing the distance between the cuvette and the focusing lens, and the generated SC remains unchanged, presenting a long plateau structure. In contrast, the focal region of BG beams is comparable with the length of the cuvette. By changing the distance between the cuvette and the axicon lens, the length of filament formed by BG beams in water firstly increases and then decreases; as a result, the degree of spectral broadening first increases and then decreases. Though there also exists a plateau structure, the length of the plateau is shorter compared with the case of LG beams. In addition, with the increase in TC value, the length of the plateau decreases, indicating that the length of the filament generated by the BG beams is positively related to the TC value. In addition, we also found that the degree of spectral broadening induced by the filamentation of LG and BG beams is hardly dependent on TC value.
Author Contributions
Conceptualization, methodology and theory, J.W.; data analysis, J.W. and S.L.; experiments, J.W. and S.L.; writing—original draft, J.W.; writing—review and editing, J.W., L.H., Y.N., Z.W., T.C., S.G. and S.L.; funding, supervision and project administration, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting reported results can be obtained from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef]
- Leach, J.; Yao, E.; Padgett, M.J. Observation of the vortex structure of a non-integer vortex beam. New J. Phys. 2004, 6, 71. [Google Scholar] [CrossRef]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259. [Google Scholar] [CrossRef]
- Oemrawsingh, S.S.R.; Ma, X.; Voigt, D.; Aiello, A.; Eliel, E.T.; Woerdman, J.P. Experimental demonstration of fractional orbital angular momentum entanglement of two photons. Phys. Rev. Lett. 2005, 95, 240501. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Friese, M.E.J.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett. 1995, 75, 826. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Li, N.; Su, H.; Li, W.; Hu, H. A review of optically induced rotation. Front. Inform. Technol. Electron. Eng. 2022, 23, 171–185. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810. [Google Scholar] [CrossRef]
- Paterson, L.; MacDonald, M.P.; Arlt, J.; Sibbett, W.; Bryant, P.E.; Dholakia, K. Controlled rotation of optically trapped microscopic particles. Science 2001, 292, 912. [Google Scholar] [CrossRef]
- Tao, S.H.; Yuan, X.C.; Lin, J.; Peng, X.; Niu, H.B. Fractional optical vortex beam induced rotation of particles. Opt. Express 2005, 13, 7726–7731. [Google Scholar] [CrossRef]
- Li, M.; Yan, S.; Yao, B.; Liang, Y.; Lei, M.; Yang, Y. Optically induced rotation of Rayleigh particles by vortex beams with different states of polarization. Phys. Lett. A 2016, 380, 311–315. [Google Scholar] [CrossRef]
- Lehmuskero, A.; Li, Y.; Johansson, P.; Käll, M. Plasmonic particles set into fast orbital motion by an optical vortex beam. Opt. Express 2014, 22, 4349–4356. [Google Scholar] [CrossRef] [Green Version]
- Andrade, U.M.S.; Garcia, A.M.; Rocha, M.S. Bessel beam optical tweezers for manipulating superparamagnetic beads. Appl. Opt. 2021, 60, 3422–3429. [Google Scholar] [CrossRef]
- Tsarukyan, L.; Badalyan, A.; Hovsepyan, R.; Drampyan, R. Bessel beam approach for photovoltaic trapping of micro- and nanoparticles on Fe-doped lithium niobate crystal. Opt. Laser Technol. 2021, 139, 106949. [Google Scholar] [CrossRef]
- Torner, L.; Torres, J.P.; Carrasco, S. Digital spiral imaging. Opt. Express 2005, 13, 873–881. [Google Scholar] [CrossRef] [Green Version]
- Dong, M.; Zhao, C.; Cai, Y.; Yang, Y. Partially coherent vortex beams: Fundamentals and applications. Sci. China Phys. Mech. Astron. 2021, 64, 224201. [Google Scholar] [CrossRef]
- Balasubramaniam, G.M.; Biton, N.; Arnon, S. Imaging through diffuse media using multi-mode vortex beams and deep learning. Sci. Rep. 2022, 12, 1561. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.X.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [Green Version]
- Vallone, G.; D’Ambrosio, V.; Sponselli, A.; Slussarenko, S.; Marrucci, L.; Sciarrino, F.; Villoresi, P. Free-space quantum key distribution by rotation invariant twisted photons. Phys. Rev. Lett. 2014, 113, 060503. [Google Scholar] [CrossRef] [Green Version]
- Molina-Terriza, G.; Vaziri, A.; Řeháček, J.; Hradil, Z.; Zeilinger, A. Triggered qutrits for quantum communication protocols. Phys. Rev. Lett. 2004, 92, 167903. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.K.; Wang, F.X.; Liu, J.; Chen, W.; Han, Z.F.; Forbes, A.; Wang, J. High-Dimensional Quantum Cryptography with Hybrid Orbital-Angular-Momentum States through 25 km of Ring-Core Fiber: A Proof-of-Concept Demonstration. Phys. Rev. Appl. 2021, 15, 064034. [Google Scholar] [CrossRef]
- Chen, B.; Wei, Y.; Zhao, T.; Liu, S.; Su, R.; Yao, B.; Yu, Y.; Liu, J.; Wang, X. Bright solid-state sources for single photons with orbital angular momentum. Nat. Nanotechnol. 2021, 16, 302–307. [Google Scholar] [CrossRef]
- Oosterbeek, R.N.; Ashforth, S.; Bodley, O.; Simpson, M.C. Measuring the ablation threshold fluence in femtosecond laser micromachining with vortex and Bessel pulses. Opt. Express 2018, 26, 34558–34568. [Google Scholar] [CrossRef]
- Yu, X.; Trallero-Herrero, C.A.; Lei, S. Materials processing with superposed Bessel beams. Appl. Surf. Sci. 2016, 360, 833–839. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.D.; Moreno, E.; Rudenko, A.; Faure, N.; Sedao, X.; Mauclair, C.; Colombier, J.P.; Stoian, R. Super-efficient drilling of metals with ultrafast non diffractive laser beams. Sci. Rep. 2022, 12, 2074. [Google Scholar] [CrossRef]
- Šlevas, P.; Orlov, S.; Nacius, E.; Ulčinas, O. Azimuthally modulated axicon vortical beams for laser microprocessing. Opt. Commun. 2022, 505, 127509. [Google Scholar] [CrossRef]
- Panagiotopoulos, P.; Kolesik, M.; Tochitsky, S.; Moloney, J.V. Generation of long homogeneous plasma channels with high power long-wave IR pulsed Bessel beams. Opt. Lett. 2021, 46, 5457–5460. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y.; Song, X.; Lin, J. Flexible manipulation of the onset and terminal positions of femtosecond laser filamentation in fused silica via controlling beam profile before axicon. Opt. Commun. 2022, 516, 128262. [Google Scholar] [CrossRef]
- Lü, J.Q.; Cheng, T.Y.; Wang, W.Y.; Guo, J.X.; Li, J.S.; Liu, S. Analysis of the extension of optical filament in air based on phase-nested laser beam. Opt. Commun. 2022, 519, 128244. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y.; Song, X.; Guo, K.; Lin, J. Multi-dimensional control of femtosecond laser filaments by inserting a wedge plate in the forced focusing region. Phys. Plasmas 2022, 29, 012301. [Google Scholar] [CrossRef]
- Davino, M.; Summers, A.; Saule, T.; Tross, J.; McManus, E.; Davis, B.; Trallero-Herrero, C. Higher-order harmonic generation and strong field ionization with Bessel–Gauss beams in a thin jet geometry. J. Opt. Soc. Am. B 2021, 38, 2194. [Google Scholar] [CrossRef]
- Dota, K.; Pathak, A.; Dharmadhikari, J.A.; Mathur, D.; Dharmadhikari, A.K. Femtosecond laser filamentation in condensed media with Bessel beams. Phys. Rev. A 2012, 86, 023808. [Google Scholar] [CrossRef]
- Ju, L.B.; Huang, T.W.; Xiao, K.D.; Wu, G.Z.; Yang, S.L.; Li, R.; Yang, Y.C.; Long, T.Y.; Zhang, H.; Wu, S.Z. Controlling multiple filaments by relativistic optical vortex beams in plasmas. Phys. Rev. E 2016, 94, 033202. [Google Scholar] [CrossRef] [PubMed]
- Fibich, G.; Gavish, N. Theory of singular vortex solutions of the nonlinear Schrödinger equation. Phys. D 2008, 237, 2696–2730. [Google Scholar] [CrossRef] [Green Version]
- Fibich, G.; Gavish, N. Critical power of collapsing vortices. Phys. Rev. A 2008, 77, 045803. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Li, D.; Chang, J.; Xi, T.; Hao, Z. Helical filaments array generated by femtosecond vortex beams with lens array in air. Results Phys. 2021, 26, 104334. [Google Scholar] [CrossRef]
- Miller, J.K.; Tsvetkov, D.; Terekhov, P.; Litchinitser, N.M.; Dai, K.; Free, J.; Johnson, E.G. Spatio-temporal controlled filamentation using higher order Bessel-Gaussian beams integrated in time. Opt. Express 2021, 29, 19362. [Google Scholar] [CrossRef]
- Jukna, V.; Milián, C.; Xie, C.; Itina, T.; Dudley, J.; Courvoisier, F.; Couairon, A. Filamentation with nonlinear Bessel vortices. Opt. Express 2014, 22, 25410–25425. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhang, Y.; Lin, S.; Chang, M.; Yu, M.; Wang, Y.; Chen, A.; Jiang, Y.; Li, S.; Jin, M. Testing the coherence of supercontinuum generated by optical vortex beam in water. J. Phys. B 2021, 54, 165401. [Google Scholar] [CrossRef]
- Couairon, A.; Mysyrowicz, A. Femtosecond filamentation in transparent media. Phys. Rep. 2007, 441, 47. [Google Scholar] [CrossRef]
- Braun, A.; Korn, G.; Liu, X.; Du, D.; Squier, J.; Mourou, G. Self-channeling of high-peak-power femtosecond laser pulses in air. Opt. Lett. 1995, 20, 73–75. [Google Scholar] [CrossRef] [PubMed]
- Kasparian, J.; Sauerbrey, R.; Mondelain, D.; Niedermeier, S.; Yu, J.; Wolf, J.P.; Andre, Y.B.; Franco, M.; Mysyrowicz, A.; Rodriguez, M.; et al. Infrared extension of the supercontinuum generated by femtosecond terawatt laser pulses propagating in the atmosphere. Opt. Lett. 2000, 25, 1397–1399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brodeur, A.; Chin, S.L. Band-gap dependence of the ultrafast white-light continuum. Phys. Rev. Lett. 1998, 80, 4406. [Google Scholar] [CrossRef]
- Liu, X.L.; Lu, X.; Liu, X.; Feng, L.B.; Ma, J.L.; Li, Y.T.; Chen, M.; Dong, Q.L.; Wang, W.M.; Wang, Z.H.; et al. Broadband supercontinuum generation in air using tightly focused femtosecond laser pulses. Opt. Lett. 2011, 36, 3900. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.M.; Shi, K.; Liu, Z.; Philbrick, C.R. Long-path supercontinuum absorption spectroscopy for measurement of atmospheric constituents. Opt. Express 2008, 16, 8457. [Google Scholar] [CrossRef]
- Husakou, A.V.; Herrmann, J. Supercontinuum generation of higher-order solitons by fission in photonic crystal fibers. Phys. Rev. Lett. 2001, 87, 203901. [Google Scholar] [CrossRef] [Green Version]
- Glezer, E.N.; Siegal, Y.; Huang, L.; Mazur, E. Laser-induced band-gap collapse in GaAs. Phys. Rev. B 1995, 51, 6959. [Google Scholar] [CrossRef]
- Potemkin, F.V.; Mareev, E.I.; Smetanina, E.O. Influence of wave-front curvature on supercontinuum energy during filamentation of femtosecond laser pulses in water. Phys. Rev. A 2018, 97, 033801. [Google Scholar] [CrossRef]
- Polynkin, P.; Kolesik, M.; Moloney, J. Filamentation of femtosecond laser Airy beams in water. Phys. Rev. Lett. 2009, 103, 123902. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Tan, W.J.; Si, J.H.; Tang, S.Y.; Yang, Y.; Hou, X. Depolarization of the supercontinuum induced by linearly and circularly polarized femtosecond laser pulses in water. Phys. Rev. A 2021, 104, 053535. [Google Scholar] [CrossRef]
- Melnik, M.; Vorontsova, I.; Putilin, S.; Tcypkin, A. The dependence of the supercontinuum coherence time in water jet on the input radiation intensity. Appl. Phys. B 2020, 126, 60. [Google Scholar] [CrossRef]
- Cook, K.; Kar, A.K.; Lamb, R.A. White-light supercontinuum interference of self-focused filaments in water. Appl. Phys. Lett. 2003, 83, 3861. [Google Scholar] [CrossRef]
- Vasa, P.; Singh, M.; Bernard, R.; Dharmadhikari, A.K.; Dharmadhikari, J.A.; Mathur, D. Supercontinuum generation in water doped with gold nanoparticles. Appl. Phys. Lett. 2013, 103, 111109. [Google Scholar]
- Li, H.; Shi, Z.; Wang, X.; Sui, L.; Li, S.; Jin, M. Influence of dopants on supercontinuum generation during the femtosecond laser filamentation in water. Chem. Phys. Lett. 2017, 681, 86. [Google Scholar] [CrossRef]
- Tcypkin, A.N.; Putilin, S.E.; Melnik, M.V.; Makarov, E.A.; Bespalov, V.G.; Kozlov, S.A. Generation of high-intensity spectral super continuum of more than two octaves in a water jet. Appl. Opt. 2016, 55, 8390. [Google Scholar] [CrossRef]
- Vengris, M.; Garejev, N.; Tamošauskas, G.; Čepėnas, A.; Rimkus, L.; Varanavičius, A.; Jukna, V.; Dubietis, A. Supercontinuum generation by co-filamentation of two color femtosecond laser pulses. Sci. Rep. 2019, 9, 9011. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.A.; Van Stryland, E.W. High-sensitivity, single-beam n2 measurements. Opt. Lett. 1989, 14, 955–957. [Google Scholar] [CrossRef]
- Wu, K.; Wang, Z.; Yang, J.; Ye, H. Large optical nonlinearity of ITO/Ag/ITO sandwiches based on Z-scan measurement. Opt. Lett. 2019, 44, 2490–2493. [Google Scholar] [CrossRef]
- Zhang, Y.; Sui, L.; Chen, A.; Zhang, D.; Wang, Q.; Xu, W.; Li, S.; Jin, M. Spectral resolved study of filamentation effect on the nonlinear absorption in carbon disulfide. Opt. Express 2019, 27, 20980–20989. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).