Abstract
Suction bucket foundation is a novel and cheaper foundation used in marine structures, such as offshore wind turbines, breakwater and oil platforms. Compared with a single bucket foundation, tetrapod bucket foundations can bear larger loads because of the group effects. However, the vertical, horizontal and moment capacity factors of tetrapod bucket foundations have not been presented in existing specifications. A series of three-dimensional finite-element analyses were conducted to investigate the group effects on uniaxial capacities and failure mechanisms of tetrapod bucket foundations in undrained clay considering various foundation separation distance ratios, embedment depth ratios, soil-strength heterogeneity indices and load direction angles. Generalized formulas for undrained uniaxial capacities of tetrapod bucket foundations were proposed in order to establish a bridge connecting the capacities of tetrapod bucket foundations and those of the single bucket foundation, which can provide a reference for industrial designs of capacities of tetrapod bucket foundations. The results show that the vertical group effect factor of tetrapod bucket foundations is basically not affected by the foundation separation distance ratio, embedment depth ratio, soil-strength heterogeneity index and load direction angle, which can adopted 0.9 based on a conservative estimation. The normalized horizontal and moment group effect factors of tetrapod bucket foundations are both affected by the separation distance ratio, embedment depth ratio and soil-strength heterogeneity index, but the moment group effect factor is also obviously affected by the load direction angle. The value of the horizontal and moment capacity factors of tetrapod bucket foundations are about 2.3 and 13.8 times that of a single bucket foundation, respectively, when the separation distance ratio is 3.5, embedment depth ratio is 1.0 and soil-strength heterogeneity index is 10, which have both been significantly enhanced. A value of 3.5 is suggested for the separation distance ratio to attain good capacities and a relatively high global stiffness for the tetrapod bucket foundations.
1. Introduction
For marine structures in undrained clay, their foundation is a significant component to ensure their safety, which is designed to sustain self-weight and environmental loads that can be decomposed into the vertical load, horizontal load and moment. Suction bucket foundation is considered as a novel foundation with advantages of wider adaptability, easy transportation, fast installation and low cost [1]. Compared with a single bucket foundation, a multipod bucket foundation can provide greater resistances against vertical, horizontal and moment loadings. A multipod bucket foundation mainly includes tripod bucket foundations and tetrapod bucket foundations. As shown in Figure 1, the tetrapod bucket foundation consists of four single-suction bucket foundations in a square shape, which is better suited for deeper water.

Figure 1.
Photograph of tetrapod bucket foundations (courtesy of Statoil ASA).
The penetration of the tetrapod bucket foundation into the seabed mainly includes two steps. In the first step, the skirts of the four buckets are simultaneously penetrated into the seabed by self-weight, providing a seal between the buckets and soils. Then, water is pumped out of the buckets, creating differential pressure at the tops of the buckets referred to as ‘suction’, to allow for further penetration. In the second step, water discharge from each bucket can be adjusted, respectively, to ensure good verticality of the tetrapod bucket foundation. The penetration stops when the tops of the buckets touch the seabed and the suction pressure confines the soils in the skirts.
The undrained capacities of a single-suction foundation in clay have been studied by means of theoretical analyses [2,3,4,5,6,7], physical investigations [8,9,10,11,12,13,14,15], finite-element analysis [16,17,18,19,20,21,22,23,24] and artificial intelligence methods [25,26,27]. Aubeny and Murff (2005) [2] established a plastic limit solution for the capacity of a single-suction anchor in undrained clay. Plasticity theory proved by the results of centrifuge experiments was used to evaluate the influence of linearly increasing undrained shear strength with depth on the bearing capacity of shallow foundations with a skirt system underneath their base in clay [3]. A limit analysis method is used to determine the updated rotation center position and horizontal bearing capacity of a single bucket foundation in soft ground [4]. The bearing capacity of the single skirted foundation was studied using an h-adaptive finite-element method (FEM) and extended upper-bound method [5]. A series of plane-strain finite-element analyses were conducted to investigate how the skirt geometry directly affects the undrained strip-foundation capacity under combined horizontal–moment loading and the mechanisms occurring at failure [6]. Skau and Jostad (2014) [7] introduced the application of the NGI procedure for the design of bucket foundations for offshore wind farms. A series of tests were conducted in a drum centrifuge with the aim of investigating the performance of a single bucket foundation on soft normally consolidated clay [8]. Laboratory tests were conducted to study the behavior of suction caisson when loaded horizontally below the mudline in normally consolidated kaolinite clay [9]. A program of testing of caisson foundations in clay at the Bothkennar test site relevant to the design of foundations for offshore wind turbines is described [10]. The partial removal, adjusting and re-penetrating tests for a mooring dolphin platform with three-bucket foundations after a seven-year service were introduced [11]. The suction caisson was pulled out at a certain loading angle to obtain the failure modes and corresponding capacities after applying many one-way cyclic loadings in the model tests [12]. The response of suction caissons to long-term lateral cyclic loading in single-layer and layered seabeds was introduced [13]. The lateral bearing behaviors of suction bucket foundations for offshore wind turbines were investigated by centrifuge modeling [14]. Undrained response of bucket foundation to moment loading was investigated by model tests and FEM [15]. The ultimate response of the shallow foundations calculated by FEM was compared to other available theoretical predictions [16]. The effect of strength non-homogeneity on the shape of failure envelopes for the combined loading of shallow foundations on clay was investigated by FEM [17]. The failure loci of suction caisson foundations in clay under combined loading conditions was presented [18]. Optimal skirt spacing for subsea mudmats under loading in six degrees of freedom was studied using FEM [19]. The vertical and horizontal bearing capacities of bucket foundations in clay were evaluated by FEM [20]. The shape and size of the failure envelopes of the skirted circular foundations were compared to those of solid embedded circular foundations and skirted strip foundations using FEM [21]. The undrained pullout capacity of cylindrical suction caissons was calculated by finite-element limit analysis [22]. The effect of strength anisotropy on the failure envelope of offshore shallow foundations in clay under combined loading was investigated by FEM [23]. The capacities and failure modes of the suction bucket foundation with internal bulkheads in clay were studied using FEM [24]. A hybrid intelligence method (GMDH-HS) was used to predict the uplift capacity of suction caisson in clay [25]. Fuzzy modeling of the holding capacity of offshore suction caisson anchors was conducted [26]. The fuzzy sets theory was used to predict the uplift capacity of suction caissons in clay [27]. These existing studies have primarily taken account of the effects of foundation shape (e.g., strip, rectangle, square and circular), foundation embedment (e.g., surface, solid and skirted), soil-strength heterogeneity (e.g., homogeneous or non-homogeneous) and soil–foundation interaction (e.g., smooth or rough) on the capacities of a single suction foundation. However, only a few studies focused on the capacities of the multipod bucket foundation in clay, which were mainly related to tripod bucket foundation [28,29,30,31]. The studies on the undrained capacities of tetrapod bucket foundations in clay remain scarce. Zhu et al. (2020) [32] investigated the uplift response of tetrapod bucket foundations in soft clay using centrifuge modeling. The vertical, horizontal and moment capacity factors of tetrapod bucket foundations have not been given in existing specifications, such as API [33] and DNVGL design codes [34].
Systematic studies in this study were performed by using 3D finite-element analyses to provide insights into the group effects of tetrapod bucket foundations on its capacities and failure modes with various foundation separation distances, embedment depths, soil-strength heterogeneities and load direction angles. The purpose of this study is to establish a bridge connecting the capacities of tetrapod bucket foundations and those of a single bucket foundation. Generalized formulas proposed in this study can conveniently evaluate the uniaxial capacities of tetrapod bucket foundations in clay through multiplying the uniaxial capacities of a single bucket foundation by the corresponding group effect factors, which can be used as a reference for the industrial designs of capacities of tetrapod bucket foundations. This provides a useful tool for engineers who are not good at finite-element methods to quickly design the foundation.
2. Finite-Element Model
All 3D finite-element models were programmed using commercial finite-element package ABAQUS with small-strain analyses [35]. The geometric dimensions of tetrapod bucket foundations are illustrated in Figure 2. The diameter of the individual bucket and the width of tetrapod bucket foundations are denoted as D and B, respectively. The wall thickness is adopted as 25 mm, while the diameter D of a single bucket is 10 m, which are common values for steel bucket foundations. The cross-sectional area of a single bucket foundation and tetrapod bucket foundations are denoted as As and A (A = 4 × As), respectively. The foundation separation distance between the center of each bucket and that of the tetrapod bucket foundations, and foundation embedment depth are defined as s and d, which are normalized as s/D and d/D, respectively. The foundation separation distance ratios (s/D) were taken as 0.75, 1.0, 1.25, 1.5, 2.0, 2.5, 3.0 and 3.5, while the foundation embedment depth ratios (d/D) were taken as 0.25, 0.5, 0.75 and 1.0. The width of the tetrapod bucket foundations (B) is equal to . Finite-element results in this study show that the undrained capacities of the tetrapod bucket foundations are dependent on the dimensionless quantities s/D and d/D, regardless of D.
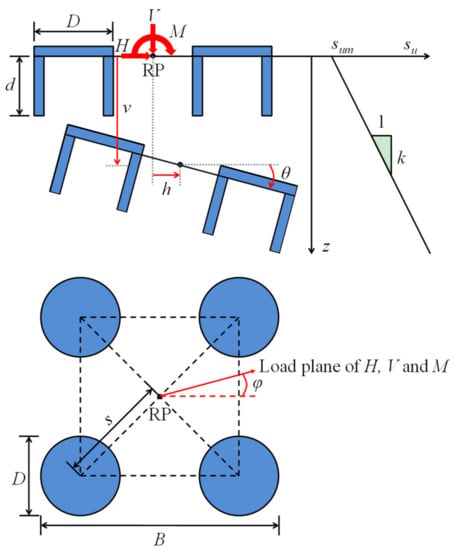
Figure 2.
The geometric dimensions of tetrapod bucket foundations, common conventions of loadings and displacements and spatial distribution of undrained soil shear strength.
2.1. Property
The undrained clay was modeled as a linear elastic-perfectly plastic material with Tresca yield criterion, which is a widespread assumption when evaluating the undrained capacities of various offshore structures [21,29,36,37,38,39]. The undrained shear strength (su) of the offshore seabed was assumed to increase linearly with depth, as plotted in Figure 2, and expressed as
where sum is the undrained soil shear strength on the mud’s surface and k is the gradient of su with depth z. The degree of soil-strength heterogeneity can be described by a dimensionless index
It was demonstrated that the undrained capacities of the suction bucket foundation were influenced by the soil-strength heterogeneity index (κ), regardless of sum or k [21]. The values of κ = 0 (homogenous clay), 1, 2, 6, 10 and 20 (inhomogeneous clay) were considered. The effective unit weight (γ’) of the clay was taken as 6 kN/m3, which is a realistic value for marine clay. The Young’s modulus (E) was adopted as E = 500 su, which was considered irrelevant to the undrained capacities of offshore foundation [29,40]. The undrained shear strength (su) and Young’s modulus (E) at different depths for inhomogeneous clay are calculated according to Equation (1) and E = 500 su implemented in a user subroutine VUSDFLD in this study. Poisson’s ratio (ν’) was adopted as 0.499 to simulate the undrained conditions of no volume change while ensuring numerical stability [41].
2.2. Interaction
Both tetrapod bucket foundations and the single bucket foundation were modeled as rigid bodies with a reference point (RP) located at its geometric center on the mud’s surface, as marked in Figure 2. The interface between the soil and foundations was simulated as fully bonded to simulate the undrained response due to the effect of the passive suction force and cohesion of undrained clay, which has also been adopted in the literature [6,15,20,26,40] to evaluate the bearing capacities of bucket foundations in undrained clay. The effect of suction on undrained behavior tends to keep the clay attached to the caisson, while failure occurs within the clay. Barari and Ibsen (2012) [15] pointed out that the suction generated during installation prevents the detachment of the foundation from the soil. The interface between the soil and foundation was allowed to behave as though fully bonded (fully rough), which is an appropriate assumption for offshore foundations.
2.3. Load
The common conventions of loads (V, H and M) and the corresponding displacements (v, h and θ) are illustrated in Figure 2. The intersection angle between the load and symmetry planes of the tetrapod bucket foundations is defined as φ, as marked in Figure 2. Due to the symmetry of tetrapod bucket foundations, the load direction angles (φ) were taken as 0°, 15°, 30° and 45° to represent a full circle.
The displacement controlled method was adopted to obtain the uniaxial capacities of the tetrapod bucket foundations. The uniaxial displacements (v, h and θ) were exerted on the reference point (RP), respectively, until a plastic plateau was observed in the counter-force and displacement curve. At this point, the counter-force induced by the exerted uniaxial displacement reached an ultimate load.
2.4. Mesh
First-order fully integrated hexahedral hybrid element C3D8H was adopted in this study. The hybrid element, mixing displacements and stress variables, is recommended for simulating the response of nearly incompressible materials, including undrained clay, considering its advantages of clearly identifying the plastic yield point and ensuring numerical stability [41].
Examples of 3D finite-element models for tetrapod bucket foundations at φ = 0° and φ ≠ 0° are illustrated in Figure 3a,b, respectively. Considering the symmetry of tetrapod bucket foundations at φ = 0°, only half of the foundations were modeled in a cuboid soil domain, while the complete foundations were modeled in a cylindrical soil domain when φ ≠ 0°. The vertical depth and horizontal distance (from RP to boundary) of the soil domain were equal to 5B when φ = 0°, while the vertical depth and radius (from RP to boundary) of that were equal to 5B when φ ≠ 0°, confirming that the soil domain was sufficient to ensure no boundary effects. To improve calculation accuracy, finer mesh was used in the region close to the foundations. The lateral and bottom boundaries were fully constrained, while symmetrical constraint was applied on the symmetry planes. The total number of elements varied from 45,000 to 90,000 for the half models (φ = 0°) and from 90,000 to 180,000 for the complete models (φ ≠ 0°).
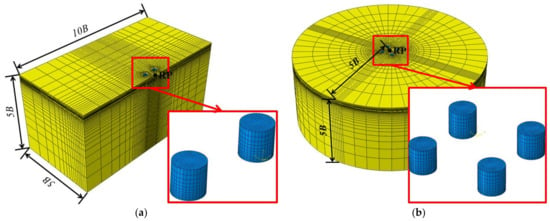
Figure 3.
Example of 3D finite-element models for tetrapod bucket foundations when (a) φ = 0° (b) φ ≠ 0°.
3. Validation
In this section, the validities of finite-element models in terms of capturing the capacities of a single bucket foundation and tetrapod bucket foundations in undrained clay were demonstrated and discussed.
When s = 0, the tetrapod bucket foundations become equivalent to a single bucket foundation. The uniaxial vertical, horizontal and moment capacity factors of a single bucket foundation are defined as NV,s = Vult,s/Assu0, NH,s = Hult,s/Assu0 and NM,s = Mult,s/AsDsu0, respectively. Vult,s, Hult,s and Mult,s are the uniaxial vertical, horizontal and moment capacities of the single bucket foundation, respectively. su0 is taken as the soil undrained shear strength at the skirt tip level in this section. The values of NV,s, NH,s and NM,s with rough contact conditions and d = 0 obtained from the finite-element results in this study are validated, and they are basically coincident with the existing solutions [17,42], as listed in Table 1.

Table 1.
Comparisons between finite-element results in this study and existing theoretical solutions for uniaxial capacities of single circular footing.
The differences of NV,s between the results presented in this study and exact solutions reported by Houlsby and Wroth [42] are within 2.4%. For NH,s, the differences between the results presented in this study and exact solutions NH,s = 1.0 were within 7.5%. Ideally, for a single circular footing under horizontal loading, a sliding failure occurred in a very thin layer of soil along the soil–foundation interface. When its thickness is assumed 0, NH,s is equal to 1.0. However, in finite-element models in this study, the thickness of this thin layer was meshed as 0.003 D, which inhibited soil sliding and induced a slightly higher value for NH,s. NM,s in this study was no more than 10.5% higher compared to that given by the solution based on plastic theory [17]. The slight overprediction of NM,s was caused by representing a circular-scoop failure mechanism with hexahedron elements [21].
For the single bucket foundation with d/D = 0.2, the finite-element results in this study were compared to lower-bound (LB) solutions reported by Tani and Craig [3] and UB solutions presented by Hu et al. [5], as shown in Figure 4a. The comparison showed that the finite-element results are situated between the upper- and lower-bound solutions.
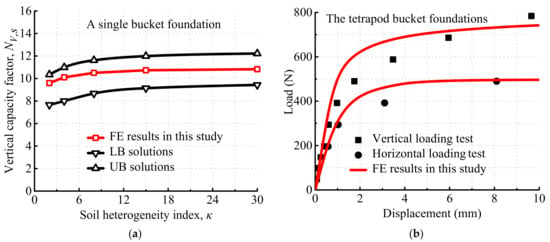
Figure 4.
Comparisons between finite-element results in this study and (a) analytic solutions of a single bucket foundation or (b) model tests of the tetrapod bucket foundations.
Wang [43] used the Dagang drilling rigs based on the tetrapod bucket foundation as prototypes and conducted a 1:40 model test in the mud pool. The main physical and mechanical indexes of the indoor soil model were as follows: effective unit weight γ’ = 6 kN/m3, undrained shear strength su = 1.2 + 0.157 z kPa and Young’s modulus Eu = 1000 su. The vertical and horizontal load tests were conducted, respectively. The vertical load point passed through the geometric center of the tetrapod bucket foundation and the height of the horizontal load point was 75 mm above the mud’s surface. In this paper, the finite-element model was established according to the same foundation dimension and soil parameters as the model test. The displacement controlled method was adopted to obtain the uniaxial capacities of the tetrapod bucket foundation. The comparison between the finite-element results and model test is shown in Figure 4b. It can be observed that the deviation between the vertical and horizontal capacities and that of the model test is less than 1% and 3.5%, respectively.
The validations in this section indicate that the finite-element models for this study are acceptably accurate.
4. Capacities of the Single Bucket Foundation
Before establishing the bridge connecting the tetrapod bucket foundations and the single bucket foundation, the vertical, maximum horizontal and moment capacity factors of single bucket foundation should be expressed. In existing studies, due to the different locations of RP (e.g., on the mud’s surface [20] or at the foundation base [21,44]) and different definitions of undrained soil shear strength at a specific depth (su0) used to non-dimensionalize the capacity (e.g., at the foundation base [21] or at a specific depth below the foundation’s base [8,20]), the capacities of the single bucket foundation can be expressed in different formulas. In addition, the formula for the maximum horizontal capacity of the single bucket foundation remains scarce. In this study, the location of RP was set at the center of the single bucket foundation on the mud’s surface and su0 was adopted at depth D/4 below the skirt tip level, as suggested by Byrne and Cassidy [8]. Then, the vertical, maximum horizontal and moment capacity factors of single bucket foundations (NV,s, NHmax,s and NM,s) with different foundation embedment depth ratios (d/D) and soil-strength heterogeneity indices (κ) can be deduced from the finite-element results in this study, as expressed in Equations (3)–(5), respectively.
where a1 = 12.8 − 9.14 × 0.32d/D, b1 = 2.18 + 0.27 × 4.05d/D, c1 = −0.83 + 0.83 × 0.24d/D, 0.25 ≤ d/D ≤ 1.0, 0 ≤ κ ≤20;
where a2 = −15.2 + 15.38 × 1.35d/D, b2 = −7.24 + 7.94 × 1.74d/D, c2 = −1.54 + 1.31 × 0.55d/D, 0.25 ≤ d/D ≤ 1.0, 0 ≤ κ≤20;
where a3 = −0.68 + 0.9 × 2.75d/D, b3 = 0.21 + 0.23 × 6.98d/D, c3 = −0.09 − 0.67d/D, 0.25 ≤ d/D ≤ 1.0, 0 ≤ κ≤20.
The good agreement between the finite-element results and the fitted curves plotted according to Equations (3)–(5), as shown in Figure 5, validates the fact that the formulas established in this study are suitable to evaluate the capacity factors of the single bucket foundation.
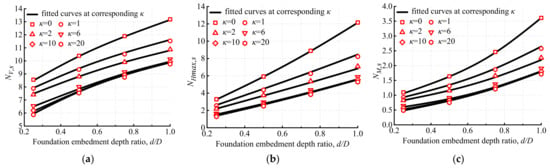
Figure 5.
Comparisons of capacity factors for the single bucket foundation between finite-element results and fitted curves: (a) vertical capacity factor, (b) maximum horizontal capacity factor and (c) moment capacity factor.
5. Capacities of Tetrapod Bucket Foundations
5.1. Vertical Capacities
5.1.1. Effects of Foundation Separation Distance Ratio on Vertical Capacities
If the uniaxial vertical capacity of tetrapod bucket foundations is denoted as Vult, the vertical capacity factor of tetrapod bucket foundations can be defined as NV = Vult/Asu0. su0 is adopted at depth D/4 below the skirt tip level in this section. The vertical capacities of tetrapod bucket foundations with various foundation separation distance ratios (s/D) at κ = 10 are presented in Figure 6. The results indicate that NV almost equals the vertical capacity factor of the single bucket foundation (NV,s = Vult,s/Assu0).
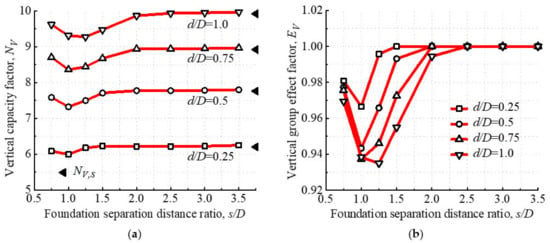
Figure 6.
Vertical capacities of tetrapod bucket foundations at κ = 10: (a) vertical capacity factor and (b) vertical group effect factor.
At short separation distances (about s/D ≤ 1.0), an obvious decrease in NV is observed with the increase in s/D. Furthermore, the maximum decrease in NV is approximately 6.5%, in comparison to NV,s. After decreasing with s/D, NV enhances and finally converges into NV,s.
The vector fields of the displacement of the single bucket foundation and tetrapod bucket foundations under ultimate vertical loading at κ = 10 when d/D = 0.25 and 1.0 are shown in Figure 7. The horizontal line is the mudline.
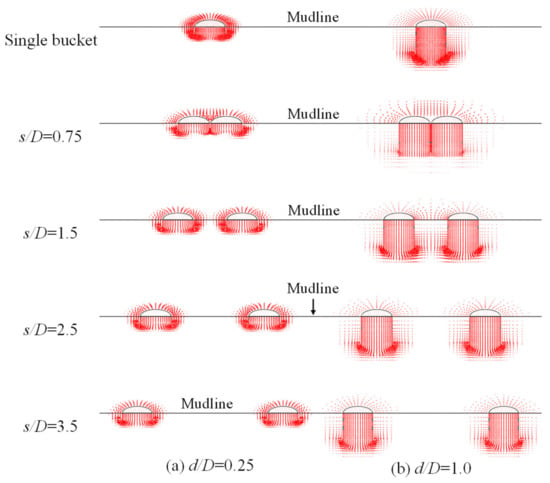
Figure 7.
The vector fields of the displacement of the single bucket foundation and tetrapod bucket foundations under ultimate vertical loading at κ = 10 when (a) d/D = 0.25 and (b) d/D = 1.0.
Driven by the buckets, the soils among them flow downwards at a very small foundation separation distance ratio (s/D = 0.75). In this case, buckets and the soils surrounded by them can be regarded as a whole to resist vertical loading, so NV is close to NV,s. The soil failure mechanism at this time is a Prandtl failure mechanism, which is the soil failure mechanism of a single bucket foundation under uniaxial vertical loading. As s/D increases, the soil failure mechanism of each bucket is an insufficiently developed Prandtl failure mechanism. At this time, NV is less than NV,s. When s/D is large enough, there is no discernible interaction of soils surrounding each bucket, and a Prandtl failure mechanism is observed for each bucket, explaining that the vertical group effect factors of tetrapod bucket foundations (EV = NV/NV,s) are equal to 1.0 in the end, as shown in Figure 6b.
5.1.2. Effects of Foundation Embedment Depth Ratio on Vertical Capacities
The vertical capacities of tetrapod bucket foundations (NV) with various foundation embedment depth ratios (d/D) at κ = 10 are also shown in Figure 6. An evident enhancement for NV was observed because of increased soil resistances on increased foundation embedment, and there was a lower and steeper trend in the curves of the vertical group effect factor (EV) with the increase in d/D, which indicates that the interaction of soils surrounding each bucket gradually increases as d/D increases. The magnitude of displacement contours of tetrapod bucket foundations and soils under ultimate vertical loading with various d/D at s/D = 1.5 and κ = 10 are plotted in Figure 8. At a smaller d/D, there was no obvious interaction of soils surrounding each bucket. While d/D was larger, the soil flow zone of each bucket tended to be deeper and wider with the increase in d/D, resulting in a more noticeably overlapped soil flow zone surrounding each bucket and lower values of EV.
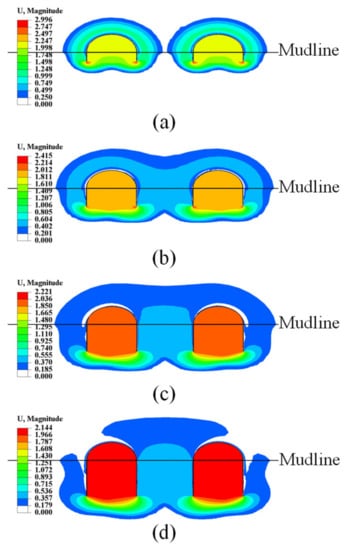
Figure 8.
The magnitude of displacement contours of tetrapod bucket foundations and soils under ultimate vertical loading at s/D = 1.5 and κ = 10 when (a) d/D = 0.25, (b) d/D = 0.5, (c) d/D = 0.75 and (d) d/D = 1.0.
5.1.3. Effects of the Soil-Strength Heterogeneity Index on Vertical Capacities
Vertical group effect factors of tetrapod bucket foundations (EV) under various soil-strength heterogeneity indices (κ) are demonstrated in Figure 9. The changing curves of EV show an upper and flatter trend with the increase in κ, manifesting that the interaction of soils surrounding each bucket decreases with the increase in κ. The magnitude of displacement contours of tetrapod bucket foundations and soils under ultimate vertical loading with various κ at s/D = 1.5 and d/D = 0.25 are illustrated in Figure 10, respectively. At a larger κ, there is no obvious interaction of soils surrounding each bucket. While κ is smaller, the soil flow zone of each bucket tends to be deeper and wider with the decrease in κ, resulting in a more significantly overlapped soil flow zone among individual buckets and lower values of EV.
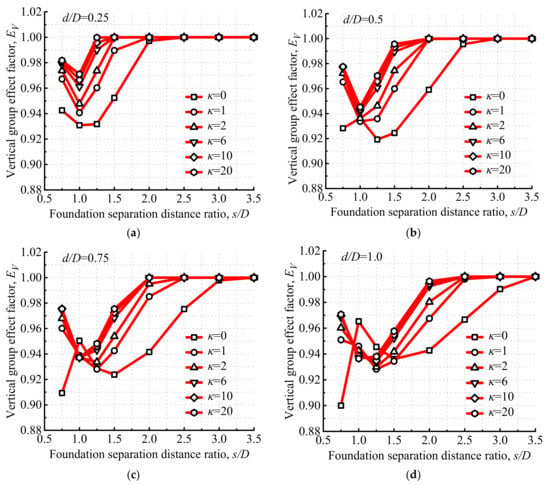
Figure 9.
Vertical group effect factors of tetrapod bucket foundations under various κ: (a) d/D = 0.25, (b) d/D = 0.5, (c) d/D = 0.75 and (d) d/D = 1.0.
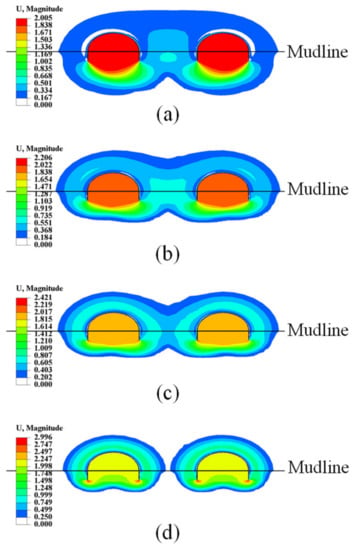
Figure 10.
The magnitude of displacement contours of tetrapod bucket foundations and soils under ultimate vertical loading at s/D = 1.5 and d/D = 0.25 when (a) κ = 0, (b) κ = 1, (c) κ = 2 and (d) κ = 10.
5.1.4. Formula for Vertical Capacities
By parametric studies, it can be concluded that the vertical capacity factors for tetrapod bucket foundations (NV) are prominently determined by the foundation embedment depth ratio (d/D) and soil-strength heterogeneity index (κ). The vertical group effect factor (EV) is located among 0.9–1.0 for all cases, so a simplified formula to evaluate the uniaxial vertical capacity of tetrapod bucket foundations (Vult) is given based on the following conservative estimation:
where EV = 0.9 and NV,s are calculated by Equation (3). For all cases, EV = 1.0 when s/D ≥ 3.5, which indicates that there is no group effect. At this time, the tetrapod bucket foundation has the largest vertical bearing capacity.
5.2. Horizontal Capacities
5.2.1. Effects of Foundation Separation Distance Ratio on Horizontal Capacities
If the uniaxial horizontal capacity of tetrapod bucket foundations is denoted as Hult, the horizontal capacity factor of tetrapod bucket foundations can be defined as NH = Hult/Asu0. Take φ = 0 as an example: the horizontal capacities of tetrapod bucket foundations at κ = 10 are shown in Figure 11.
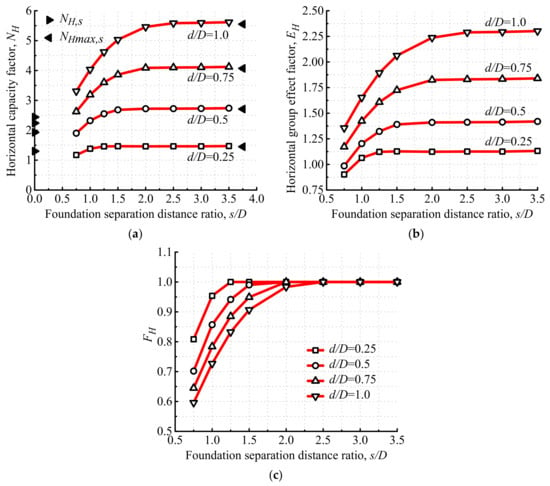
Figure 11.
Horizontal capacities of tetrapod bucket foundations at κ = 10: (a) horizontal capacity factor, (b) horizontal group effect factor and (c) normalized horizontal group effect factor.
It can be observed from Figure 11a that NH is visibly dependent on the foundation separation distance ratio (s/D). With the increase in s/D, NH shows an enhancement trend at first and finally converges into the maximum horizontal capacity factor of the single bucket foundation (NHmax,s = Hmax,s/Assu0) corresponding to the motion mode of pure horizontal displacement without a rotation angle. Hmax,s is the maximum horizontal capacity of the single bucket foundation. Take φ = 0 for instance: the rotation angles of tetrapod bucket foundations (θ) under uniaxial horizontal loading are listed in Table 2. The results show that θ decreases with the increase in s/D because of the increase in the anti-tipping moment, which is mainly caused by the increase in the moment arm. When s/D is large enough, θ is close to 0. Therefore, NH becomes closer to NHmax,s as s/D increases. The horizontal group effect factor of tetrapod bucket foundations (EH = NH/NH,s) is shown in Figure 11b. It indicates that EH increases notably with the increase in s/D and most of EH are greater than 1.0. Meanwhile, it can be observed from Figure 11b that the maximum value of NH is about 2.3 times of NH,s, manifesting that the horizontal capacity of tetrapod bucket foundations greatly enhances with large s/D, compared to that of the single bucket foundation. In order to produce simplified formulas to evaluate the horizontal capacity of tetrapod bucket foundations, the normalized horizontal group effect factor of tetrapod bucket foundations (FH = NH/NHmax,s) is defined, as shown in Figure 11c. FH firstly increases with the increase in s/D, and finally converges into 1.0.

Table 2.
Rotation angles of tetrapod bucket foundations under uniaxial horizontal loading.
5.2.2. Effects of the Foundation Embedment Depth Ratio on Horizontal Capacities
The horizontal capacities of tetrapod bucket foundations with various foundation embedment depth ratios (d/D) at κ = 10 are also shown in Figure 11. From Figure 11a, we can observe that greater d/D results in greater NH, owing to the increased horizontal soil pressure difference on the increased foundation embedment. As shown in Figure 11b, EH increases with the increase in d/D, indicating that the horizontal capacity of the tetrapod bucket foundation with a larger d/D enhances more significantly, compared to that of the single bucket foundation. From Figure 11c, we can observe that the changing curves of FH show a lower and steeper trend with the increase in d/D, which indicates that the rotation angles of tetrapod bucket foundations (θ) under uniaxial horizontal loading increase with the increase in d/D, which is in agreement with the results in Table 2.
5.2.3. Effects of the Soil-Strength Heterogeneity Index on Horizontal Capacities
Take φ = 0 as an example: the normalized horizontal group effect factors of tetrapod bucket foundations (FH) under various soil-strength heterogeneity indices (κ) are plotted in Figure 12, respectively. As shown in Figure 12, the changing curves of FH show an upper and flatter trend with the increase in κ, indicating that the rotation angle of tetrapod bucket foundations (θ) under uniaxial horizontal loading decreases with the increase in κ. It is in agreement with the results presented in Table 2.
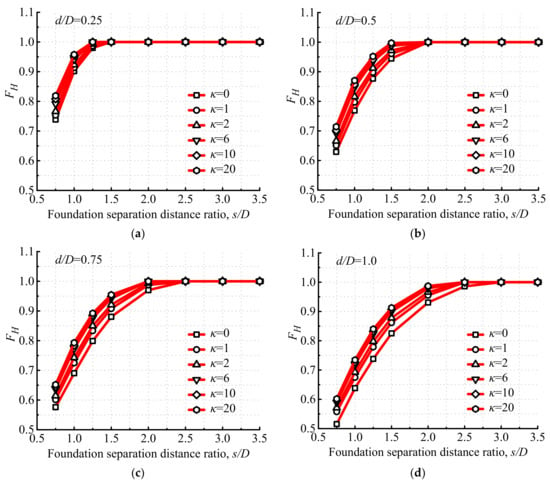
Figure 12.
Normalized horizontal group effect factors of tetrapod bucket foundations under various κ: (a) d/D = 0.25, (b) d/D = 0.5, (c) d/D = 0.75 and (d) d/D = 1.0.
5.2.4. Effects of the Load Direction Angle on Horizontal Capacities
The horizontal capacity factors of tetrapod bucket foundations with various load direction angles (φ) at κ = 10 are shown in Figure 13. It indicates that NH slightly increases with the increase in φ, but negligibly. Hence, it is reasonable that the effect of the load direction angle on horizontal capacities is neglected.
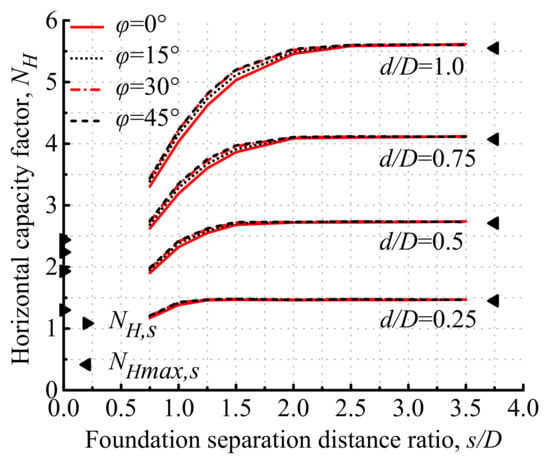
Figure 13.
Horizontal capacity factors of tetrapod bucket foundations with various φ at κ = 10.
5.2.5. Formulas for Horizontal Capacities
The results show that the foundation separation distance ratio (s/D), embedment depth ratio (d/D) and soil-strength heterogeneity index (κ) have obvious effects on the normalized horizontal group effect factor of tetrapod bucket foundations (FH), whose values are among 0.5–1.0 for all cases. The proposed equations evaluating the horizontal capacity of tetrapod bucket foundations, including s/D, d/D and κ, are described as following Equations (7) and (8).
where a4 = 0.4 × 0.83κ − (11.09 κ + 40.22) × e−8.34 d/D − 1.89, b4 = 0.36 × 0.65κ − (0.28 κ + 8.97) × e−(1.03 × 0.82κ + 3.51) (d/D) − 1.73, and NHmax,s is calculated by Equation (4).
As shown in Figure 14, a good agreement between the finite-element results and fitted curves plotted according to Equations (7) and (8) indicates that the proposed equations can accurately calculate the horizontal capacities of tetrapod bucket foundations. For all cases, FH = 1.0 when s/D ≥ 3.0, which indicates that the tetrapod bucket foundation has the maximum horizontal capacity with the motion mode of pure horizontal displacement.
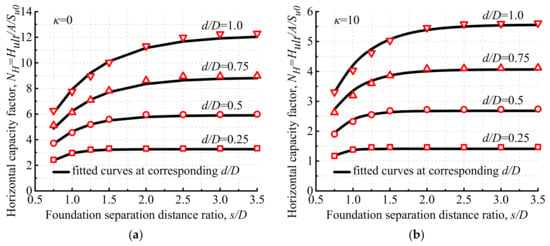
Figure 14.
Comparisons of horizontal capacity factors for tetrapod bucket foundations between finite-element results and fitted curves when (a) κ = 0 and (b) κ = 10.
5.3. Moment Capacities
5.3.1. Effects of the Foundation Separation Distance Ratio on Moment Capacities
If the uniaxial moment capacity of tetrapod bucket foundations is denoted as Mult, the moment capacity factors can be defined as NM = Mult/ADsu0. Take φ = 0 as an example: the moment capacities of tetrapod bucket foundations with various foundation separation distance ratios (s/D) at κ = 10 are shown in Figure 15. The results indicate that NM and the group effect factor of the tetrapod bucket foundations (EM = NM/NM,s) both increase remarkably with the increase in s/D, because of the increase in the moment arm. EM is greater than 1.0 and its enhancement is up to 27-fold when s/D = 3.5 and d/D = 0.25, manifesting that the moment capacity of the tetrapod bucket foundation greatly enhances at large s/D, compared to that of the single bucket foundation.
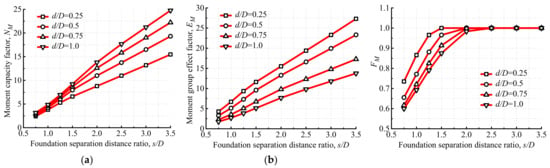
Figure 15.
Moment capacities of tetrapod bucket foundations at κ = 10: (a) moment capacity factor, (b) moment group effect factor and (c) normalized moment group effect factor.
Take φ = 0 as an example: the vector fields of the displacement of the single bucket foundation and tetrapod bucket foundations under ultimate moment loading at κ = 10 when d/D = 0.25 and 1.0 are presented in Figure 16. When s/D =0.75, the tetrapod bucket foundations and soils among the buckets can be regarded as a single foundation and rotate around a point under ultimate moment loading. When s/D increases to 3.5, the failure mode of the tetrapod bucket foundations evolves into a push–pull failure mode, which means that some buckets are pushed downwards while some buckets are pulled upwards under ultimate moment loading as shown in Figure 16.
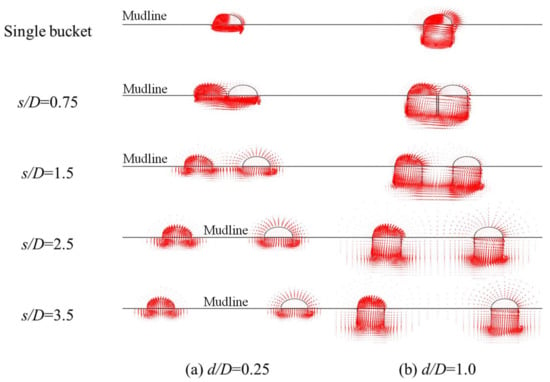
Figure 16.
The vector fields of the displacement of the single bucket foundation and tetrapod bucket foundations under ultimate moment loading at κ = 10 when (a) d/D = 0.25 and (b) d/D = 1.0.
The moment capacity of tetrapod bucket foundations in the push–pull failure mode (Mmax,pp) can be calculated by the vertical tensile and compressive resistances of individual buckets (Vult,s) as shown in Figure 17 and Equations (9) and (10).
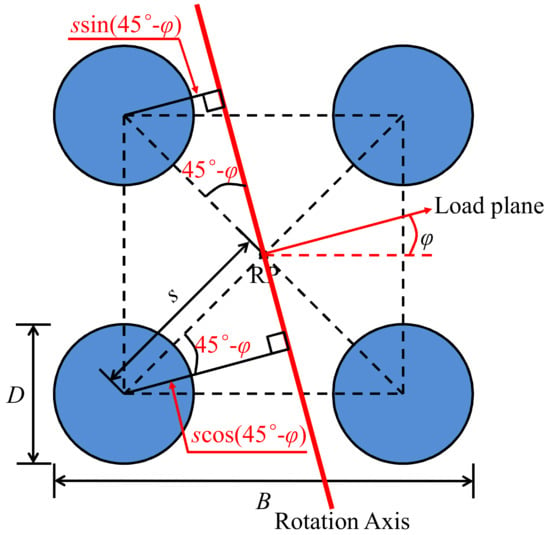
Figure 17.
Diagram of tetrapod bucket foundations illustrating calculation of moment capacities in push–pull failure mode.
In order to produce simplified formulas to evaluate the moment capacity of tetrapod bucket foundations, the normalized moment group effect factor of tetrapod bucket foundations (FM = Mult/Mmax,pp) is defined, as shown in Figure 15c. The interactions of soils surrounding each bucket gradually vanish and the failure mode of tetrapod bucket foundations gradually evolves into a push–pull failure mode with the increase in s/D, so Mult gradually increases to Mmax,pp and FM finally converges into 1.0.
5.3.2. Effects of the Foundation Embedment Depth Ratio on Moment Capacities
The moment capacities of tetrapod bucket foundations with various foundation embedment depth ratios (d/D) at κ = 10 are also shown in Figure 15. From Figure 15a, we can observe that a greater foundation embedment depth ratio (d/D) results in a greater moment capacity factor of tetrapod bucket foundations (NM), mainly caused by increased soil resistances on increased foundation embedment. As shown in Figure 15b, the moment group effect factor of tetrapod bucket foundations (EM) decrease with the increase in d/D, indicating that the enhancement of the moment capacity of tetrapod bucket foundations with a larger d/D is smaller. From Figure 15c, we can observe that the changing curves of FM show a lower and steeper tendency as d/D increases, which indicates that the interaction of soils surrounding each bucket under ultimate moment loading increases with the increase in d/D. It is consistent with the magnitude of displacement contours of tetrapod bucket foundations under ultimate moment loading at various d/D, as shown in Figure 18.
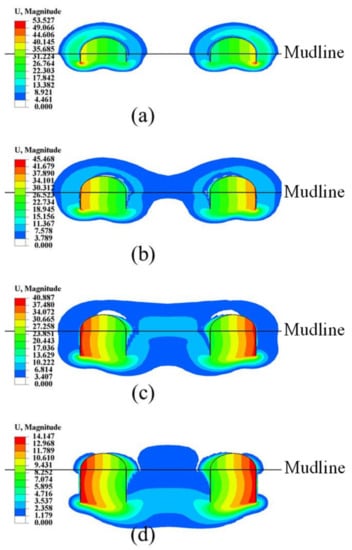
Figure 18.
The magnitude of displacement contours of tetrapod bucket foundations and soils under ultimate moment loading at s/D = 2.0 and κ = 10 when (a) d/D = 0.25, (b) d/D = 0.5, (c) d/D = 0.75 and (d) d/D = 1.0.
5.3.3. Effects of the Soil-Strength Heterogeneity Index on Moment Capacities
Take φ = 0 as an example: moment normalized group effect factors of tetrapod bucket foundations (FM) under various soil-strength heterogeneity indices (κ) are plotted in Figure 19. The changing curves of FM show an upper and flatter trend with the increase in κ, indicating that the interaction of soils surrounding each bucket under ultimate moment loading decreases with the increase in κ, which is in agreement with the magnitude of displacement contours of tetrapod bucket foundations under ultimate moment loading at various κ, as shown in Figure 20. When κ ≥ 6, there is little change for the moment capacity.
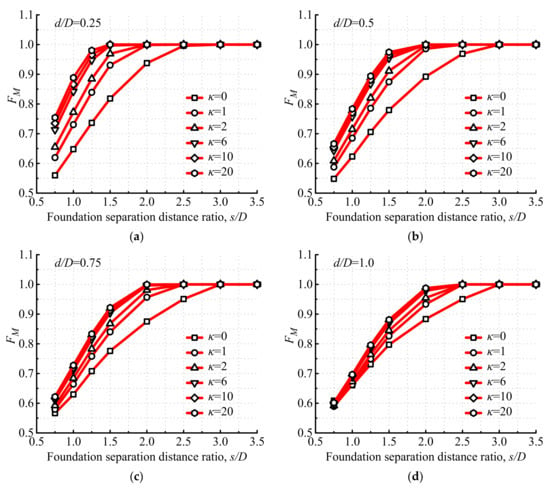
Figure 19.
Normalized moment group effect factors of tetrapod bucket foundations under various κ: (a) d/D = 0.25, (b) d/D = 0.5, (c) d/D = 0.75 and (d) d/D = 1.0.
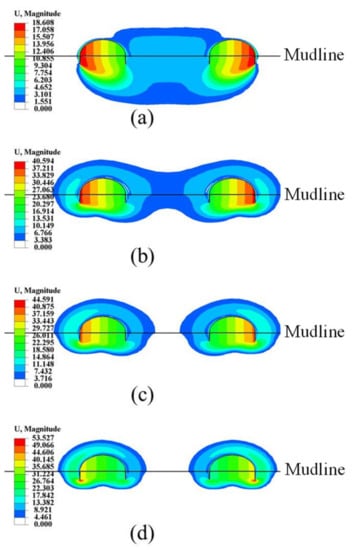
Figure 20.
The magnitude of displacement contours of tetrapod bucket foundations and soils under ultimate moment loading at s/D = 2.0 and d/D = 0.25 when (a) κ = 0, (b) κ = 1, (c) κ = 2 and (d) κ = 10.
5.3.4. Effects of the Load Direction Angle on Moment Capacities
The moment capacities of tetrapod bucket foundations are influenced by the load direction angles (φ), mainly because of the difference of the moment arm for each bucket with different φ, which can be observed in Figure 17 and Equations (9) and (10).
5.3.5. Formulas for Moment Capacities
The proposed equations evaluating the moment capacities of tetrapod bucket foundations, including s/D, d/D, κ and φ, are described as following Equations (11)–(13).
where a5 = 1.02 × 0.48κ − (0.68 κ + 1.36) × e(5.24 × 0.83κ − 6.01)(d/D) − 1.4, b5 = 0.48 × 0.74κ + (5.76 × 0.89 − 6.63) × e(1.87 × 0.85κ − 3.8)(d/D) − 1.52, NV,s and NM,s are calculated by Equations (3) and (5), respectively.
As shown in Figure 21, a good agreement between the finite-element results and fitted curves plotted according to Equations (11)–(13) indicates that the proposed equations can accurately calculate the moment capacities of tetrapod bucket foundations. For all cases, FH = 1.0 when s/D ≥ 3.0, which indicates that interactions of soils surrounding each bucket gradually vanish and the failure mode of tetrapod bucket foundations evolves into a push–pull failure mode.
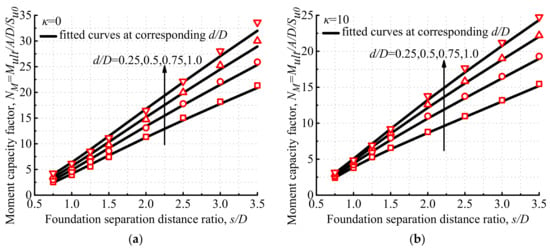
Figure 21.
Comparisons of moment capacity factors for tetrapod bucket foundations between finite-element results and fitted curves with various d/D when (a) κ = 0 and φ= 0, and (b) κ = 10 and φ = 0.
6. Conclusions
A considerable number of 3D finite-element analyses have been performed to investigate the uniaxial capacities and failure mechanisms of tetrapod bucket foundations in undrained clay. Systematic parametric studies were conducted to provide insights into the group effects of tetrapod bucket foundations considering the foundation separation distance ratio (s/D), embedment depth ratio (d/D), soil-strength heterogeneity index (κ) and load direction angle (φ). Generalized formulas for the uniaxial capacities of tetrapod bucket foundations considering group effects in undrained clay were proposed based on the finite-element results to provide a fast designing method for engineering designers.
- (1)
- The vertical capacity factor of the tetrapod bucket foundations (NV) increases as d/D increases, decreases as κ increases and changes quite insignificantly as s/D increases. NV almost equals NV,s, and the vertical group effect factor (EV) is among 0.9–1.0 for all cases in this study. Buckets and soils surrounded by them can be regarded as a whole when resisting vertical loading at a small s/D, while a Prandtl failure mechanism is observed for each bucket at a large enough s/D. The uniaxial vertical capacity of the tetrapod bucket foundations can be calculated through multiplying 4 times of that of a single bucket foundation by EV, which is taken as 0.9 based on conservative estimation.
- (2)
- As s/D increases, the horizontal capacity factor of tetrapod bucket foundations (NH) firstly enhances perceptibly and finally converges into the maximum horizontal capacity factor of the single bucket foundation (NHmax,s) corresponding to the motion mode of pure horizontal displacement. Meanwhile, NH increases with the increase in d/D and decreases with the increase in κ. NH with higher d/D or κ increases more visibly, compared to that of the single bucket foundation. The effect of the load direction angle (φ) on NH can be neglected. A tetrapod bucket foundation is more likely to move horizontally than to rotate, and its rotation angle (θ) gradually decreases with the increase in s/D and κ, as well as the decrease in d/D under the ultimate horizontal load. The uniaxial horizontal capacity of the tetrapod bucket foundations can be calculated through multiplying 4 times that of Hmax,s by the normalized horizontal group effect factor (FH), which is among 0.5–1.0 and is influenced by s/D, d/D and κ.
- (3)
- The moment capacity factor of the tetrapod bucket foundations (NM) increases quite remarkably as s/D increases, and its enhancement is up to 27 fold when s/D = 3.5 and d/D = 0.25, compared to NM,s. Meanwhile, NM increases with the increase in d/D and decreases with the increase in κ. NM with a smaller d/D or larger κ enhances more significantly, compared to that of the single bucket foundation. The tetrapod bucket foundations and soils surrounded by them can be regarded as one foundation, which rotate around a point under ultimate moment loading when s/D is small, while its failure mode evolves into a push–pull failure mode at a large enough s/D. The uniaxial moment capacity of the tetrapod bucket foundations is influenced by s/D, d/D, κ and φ, and can be calculated through multiplying the moment capacity of the tetrapod bucket foundations in the push–pull failure mode (Mmax,pp) by the normalized moment group effect factor (FM).
- (4)
- The tetrapod bucket foundation has the largest vertical bearing capacity when s/D ≥ 3.5, while it has the maximum horizontal capacity when s/D ≥ 3.0. Failure mode of tetrapod bucket foundations evolves into a push–pull failure mode when s/D ≥ 3.0 to provide a good moment capacity. s/D = 3.5 is suggested to gain good capacities and a relatively high global stiffness for the tetrapod bucket foundations.
- (5)
- Systematic parametric studies are suggested to investigate the bearing-capacity envelopes and failure mechanisms of tetrapod bucket foundations under combined loadings in further studies.
Author Contributions
Conceptualization, Z.X.; data, Z.X. and Y.W.; curation, Z.X. and Y.W.; formal analysis, Z.X. and Y.W.; funding acquisition, Z.X., Y.T., R.W., R.T. and X.W.; investigation, Z.X., Y.W. and Y.L.; methodology, Z.X. and Y.W.; project administration, Z.X., Y.T., R.W., R.T. and X.W.; resources, Z.X., Y.T., R.W., R.T. and X.W.; software, Z.X. and Y.W.; supervision, Z.X.; validation, Z.X., Y.W. and Y.L.; visualization, Z.X., Y.W. and Y.L.; writing—original draft, Z.X., Y.W. and Y.L.; writing—review & editing, Z.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (No. 2021YFB2600200), the National Natural Science Foundation of China (No. 51879187; No. 51890915) and the CCCC Research & Development Project (2018-ZJKJ-01).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Notation List
| A | Cross-sectional area of tetrapod bucket foundations |
| As | Cross-sectional area of a single bucket foundation |
| B | Width of tetrapod bucket foundations |
| d | Foundation embedment depth |
| D | Diameter of a single bucket foundation |
| E | Young’s modulus |
| EH | Horizontal group effect factor of tetrapod bucket foundations = NH/NH,s |
| EM | Moment group effect factor of tetrapod bucket foundations = NM/NM,s |
| EV | Vertical group effect factor of tetrapod bucket foundations = NV/NV,s |
| FH | Normalized horizontal group effect factor of tetrapod bucket foundations = NH/NHmax,s |
| FM | Normalized moment group effect factor of tetrapod bucket foundations = Mult/Mmax,pp |
| h | Horizontal displacement |
| H | Horizontal load |
| Hmax,s | Maximum horizontal capacity of a single bucket foundation |
| Hult | Uniaxial horizontal capacity of tetrapod bucket foundations |
| Hult,s | Uniaxial horizontal capacity of a single bucket foundation |
| k | Undrained soil shear strength gradient with depth |
| M | Moment |
| Mmax.pp | Moment capacity of tetrapod bucket foundations in push–pull failure mode |
| Mult | Uniaxial moment capacity of tetrapod bucket foundations |
| Mult,s | Uniaxial moment capacity of a single bucket foundation |
| NH | Horizontal capacity factor of tetrapod bucket foundations = Hult/Asu0 |
| NH,s | Horizontal capacity factor of a single bucket foundation = Hult,s/Assu0 |
| NHmax,s | Maximum horizontal capacity factor of a single bucket foundation = Hmax,s/Assu0 |
| NM | Moment capacity factor of tetrapod bucket foundations = Mult/ADsu0 |
| NM,s | Moment capacity factor of a single bucket foundation = Mult,s/AsDsu0 |
| NV | Vertical capacity factor of tetrapod bucket foundations = Vult/Asu0 |
| NV,s | Vertical capacity factor of a single bucket foundation = Vult,s/Assu0 |
| s | Separation distance between the center of each bucket and that of the tetrapod bucket foundation |
| su | Undrained shear strength of clay |
| sum | Undrained shear strength of clay at the ground surface |
| su0 | Undrained shear strength of clay at a specific depth (at depth D/4 below skirt tip level for tetrapod bucket foundations in this study) |
| v | Vertical displacement |
| V | Vertical load |
| Vult | Uniaxial vertical capacity of tetrapod bucket foundations |
| Vult,s | Uniaxial vertical capacity of a single bucket foundation |
| γ’ | Effective unit weight |
| θ | Rotation angle |
| κ | Soil-strength heterogeneity index |
| φ | The intersection angle between the load plane and symmetry plane of the tetrapod bucket foundations |
References
- Wang, X.; Zeng, X.; Li, J.; Yang, X.; Wang, H. A review on recent advancements of substructures for offshore wind turbines. Energy Convers. Manag. 2018, 158, 103–119. [Google Scholar] [CrossRef]
- Aubeny, C.; Murff, J.D. Simplified limit solutions for the capacity of suction anchors under undrained conditions. Ocean Eng. 2005, 32, 864–877. [Google Scholar] [CrossRef]
- Tani, K.; Craig, W.H. Bearing capacity of circular foundation on soft clay of strength increasing with depth. Soils Found. 1995, 35, 21–35. [Google Scholar]
- Tang, X.; Zhang, X.; Shao, Q.; Li, Z. Rotation center and horizontal bearing capacity of the bucket foundation in soft ground. Mar. Georesourc. Geotechnol. 2016, 34, 594–601. [Google Scholar] [CrossRef]
- Hu, Y.; Randolph, M.F.; Watson, P.G. Bearing response of skirted foundation on nonhomogeneous soil. J. Geotech. Geoenviron. 1999, 125, 924–935. [Google Scholar] [CrossRef]
- Bransby, M.F.; Yun, G. The undrained capacity of skirted strip foundations under combined loading. Géotechnique 2009, 59, 115–125. [Google Scholar] [CrossRef]
- Skau, K.S.; Jostad, H.P. Application of the NGI-procedure for design of bucket foundations for offshore wind farms. In Proceedings of the 24th International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014. [Google Scholar]
- Byrne, B.W.; Cassidy, M.J. Investigating the response of offshore foundations in soft clay soils. In Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering, Oslo, Norway, 23–28 June 2002. [Google Scholar]
- Coffman, R.R.; El-Sherbiny, R.M.; Rauch, A.F. Measured horizontal capacity of suction caissons. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 2004. [Google Scholar]
- Houlsby, G.T.; Kelly, R.B.; Huxtable, J.; Byrne, B.W. Field trials of suction caissons in clay for offshore wind turbine foundations. Géotechnique 2005, 55, 287–296. [Google Scholar] [CrossRef]
- Le, C.; Ding, H.; Zhang, P. Prototype testing for the partial removal and re-penetration of the mooring dolphin platform with multi-bucket foundations. Mar. Struct. 2018, 59, 80–93. [Google Scholar] [CrossRef]
- Guo, Z.; Jeng, D.; Guo, W.; Wang, L. Failure mode and capacity of suction caisson under inclined short-term static and one-way cyclic loadings. Mar. Georesourc. Geotechnol. 2018, 36, 52–63. [Google Scholar] [CrossRef]
- Zhu, F.Y.; O’Loughlin, C.D.; Bienen, B.; Cassidy, M.J.; Morgan, N. The response of suction caissons to long-term lateral cyclic loading in single-layer and layered seabeds. Géotechnique 2018, 68, 729–741. [Google Scholar] [CrossRef]
- Wang, X.; Yang, X.; Zeng, X. Lateral capacity assessment of offshore wind suction bucket foundation in clay via centrifuge modelling. J. Renew. Sustain. Energy 2017, 9, 033308. [Google Scholar] [CrossRef]
- Barari, A.; Ibsen, L.B. Undrained response of bucket foundations to moment loading. Appl. Ocean. Res. 2012, 36, 12–21. [Google Scholar] [CrossRef]
- Taiebat, H.A.; Carter, J.P. Numerical studies of the bearing capacity of shallow foundations on cohesive soil subjected to combined loading. Géotechnique 2000, 50, 409–418. [Google Scholar] [CrossRef]
- Gourvenec, S.; Randolph, M.F. Effect of strength non-homogeneity on the shape of failure envelopes for combined loading of strip and circular foundations on clay. Géotechnique 2003, 53, 575–586. [Google Scholar] [CrossRef]
- Wang, D.; Jin, X. Failure loci of suction caisson foundations under combined loading conditions. China Ocean Eng. 2008, 22, 455–464. [Google Scholar]
- Feng, X.; Gourvenec, S.; Randolph, M.F. Optimal skirt spacing for subsea mudmats under loading in six degrees of freedom. Appl. Ocean. Res. 2014, 48, 10–20. [Google Scholar] [CrossRef][Green Version]
- Hung, L.C.; Kim, S.R. Evaluation of vertical and horizontal bearing capacities of bucket foundations in clay. Ocean Eng. 2012, 52, 75–82. [Google Scholar] [CrossRef]
- Vulpe, C. Design method for the undrained capacity of skirted circular foundations under combined loading: Effect of deformable soil plug. Géotechnique 2015, 65, 669–683. [Google Scholar] [CrossRef]
- Ukritchon, B.; Keawsawasvong, S. Undrained pullout capacity of cylindrical suction caissons by finite element limit analysis. Comput. Geotech. 2016, 80, 301–311. [Google Scholar] [CrossRef]
- Wu, K.; Fan, Q.; Zheng, J. Effect of strength anisotropy on failure envelope of offshore shallow foundations under combined loading. J. Coastal Res. 2015, 73, 521–526. [Google Scholar] [CrossRef]
- Xiao, Z.; Ge, B.; Wang, Y. Capacities and failure modes of suction bucket foundation with internal bulkheads. J. Ocean Univ. China 2017, 16, 627–634. [Google Scholar] [CrossRef]
- Masoumi Shahr-Babak, M.; Khanjani, M.J.; Qaderi, K. Uplift capacity prediction of suction caisson in clay using a hybrid intelligence method (GMDH-HS). Appl. Ocean Res. 2016, 59, 408–416. [Google Scholar] [CrossRef]
- Kim, Y.; Ahn, J.; Jung, J. Fuzzy modeling of holding capacity of offshore suction caisson anchors. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1038–1054. [Google Scholar] [CrossRef]
- Derakhshani, A. On the uncertainty analysis of uplift capacity of suction caissons in clay based on the fuzzy sets theory. Ocean Eng. 2018, 170, 416–425. [Google Scholar] [CrossRef]
- Stergiou, T.; Terzis, D.; Georgiadis, K. Undrained bearing capacity of tripod skirted foundations under eccentric loading. Geotechnik 2015, 38, 17–27. [Google Scholar] [CrossRef]
- Kim, S.R.; Hung, L.C.; Oh, M. Group effect on bearing capacities of tripod bucket foundations in undrained clay. Ocean Eng. 2014, 79, 1–9. [Google Scholar] [CrossRef]
- Hung, L.C.; Kim, S.R. Evaluation of combined horizontal-moment bearing capacities of tripod bucket foundations in undrained clay. Ocean Eng. 2014, 85, 100–109. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Y.; Ma, Z.; Andersen, K.H.; Jostad, H.P.; Liu, D.; Pei, A. Design considerations of suction caisson foundations for offshore wind turbines in Southern China. Appl. Ocean Res. 2020, 104, 102358. [Google Scholar] [CrossRef]
- Zhu, B.; Dai, J.; Kong, D.; Feng, L.; Chen, Y. Centrifuge modelling of uplift response of suction caisson groups in soft clay. Can. Geotech. J. 2020, 57, 1294–1303. [Google Scholar] [CrossRef]
- API. RP 2GEO Geotchnical and Foundation Design Considerations, 1st ed.; Americal Petroleum Institute: Washington, DC, USA, 2011. [Google Scholar]
- DNVGL. RP E303, Geotechnical Design and Installation of Suction Anchors in Clay; DNVGL: Oslo, Norway, 2017. [Google Scholar]
- Dassault Systemes. Abaqus User’s Manual, Version 6.13; Simula Corp: Providence, RI, USA, 2013. [Google Scholar]
- Gao, F.; Wang, N.; Zhao, B. Ultimate bearing capacity of a pipeline on clayey soils: Slip-line field solution and FEM simulation. Ocean Eng. 2013, 73, 159–167. [Google Scholar] [CrossRef]
- Feng, X.; Randolph, M.F.; Gourvenec, S.; Wallerand, R. Design approach for rectangular mudmats under fully three dimensional loading. Geotechnique 2014, 64, 51–63. [Google Scholar] [CrossRef]
- Fu, D.; Bienen, B.; Gaudin, C.; Cassidy, M. Undrained capacity of a hybrid subsea skirted mat with caissons under combined loading. Can. Geotech. J. 2014, 51, 934–949. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Y.; Zhang, L.; Tian, Y.; Cassidy, M.; Zhang, L. Random finite element method for spudcan foundations in spatially variable soils. Eng. Geol. 2016, 205, 146–155. [Google Scholar] [CrossRef]
- Vulpe, C.; Gourvenec, S.; Power, M. A generalised failure envelope for undrained capacity of circular shallow foundations under general loading. Géotech. Lett. 2014, 4, 187–196. [Google Scholar] [CrossRef]
- Xiao, Z.; Tian, Y.; Gourvenec, S. A practical method to evaluate failure envelopes of shallow foundations considering soil strain softening and rate effects. Appl. Ocean Res. 2016, 59, 395–407. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Wroth, C.P. Calculation of stresses on shallow penetrometers and footings. In Proceedings of the IUTAM/IUGG Symposium on Seabed Mechanics, Tyne, UK, 5–9 September 1983; Springer: Dordrecht, The Netherlands; Newcastle, UK, 1983. [Google Scholar]
- Wang, J. A Study on Bearing Capacity Behaviour of Bucket Foundations under Combined Loading in Soft Clay; Tianjin University Press: Tianjin, China, 2012. (In Chinese) [Google Scholar]
- Hung, L.C.; Kim, S.R. Evaluation of undrained bearing capacities of bucket foundations under combined loads. Mar. Georesourc. Geotechnol. 2014, 32, 76–92. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).