Densities, Viscosities and Excess Properties for Dimethyl Sulfoxide with Diethylene Glycol and Methyldiethanolamine at Different Temperatures
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Measurements and Method Analysis
3. Results
3.1. Density and Viscosity
3.2. Excess Properties
3.2.1. Excess Molar Volume
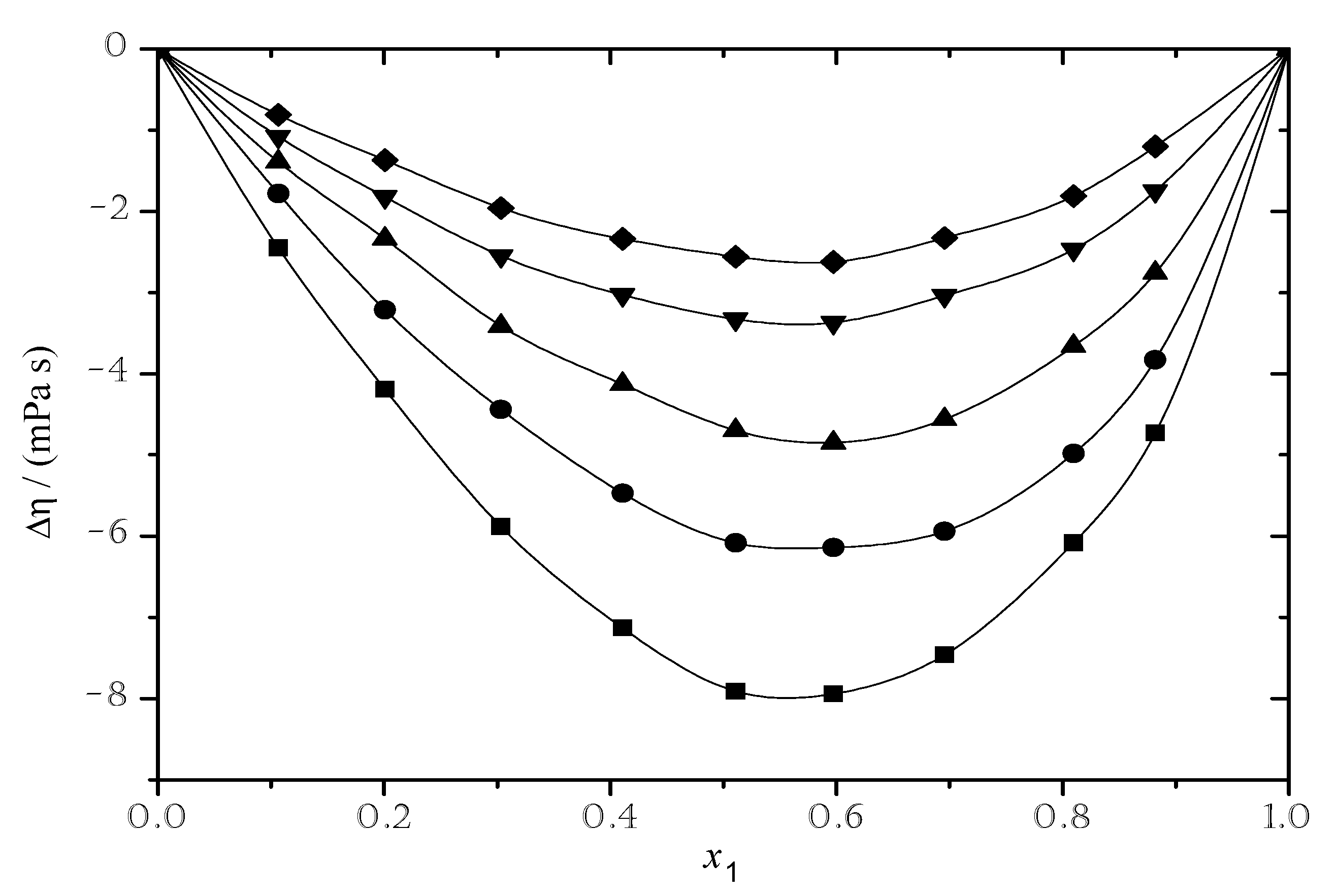
3.2.2. Viscosity Deviation
3.2.3. Apparent Molar Volume
3.2.4. Partial Molar Volumes
3.3. Thermodynamic Functions of Activation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameters and σ/(g·cm−3) | T/(K) | |||||
|---|---|---|---|---|---|---|
| Model | 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| DEG (1) + DMSO (2) | ||||||
| Belda | m1 m2 104.σ | 0.0732 −0.5208 1.49 | 0.0781 −0.4861 1.94 | 0.0914 −0.4518 1.81 | 0.1248 −0.4087 1.97 | 0.0734 −0.4267 2.12 |
| Herraez | A B C 105·σ | 0.8147 −1.0314 0.7901 7.84 | 0.8549 −1.1068 0.8852 7.49 | 0.8652 −1.0394 0.8077 4.70 | 0.8883 −1.0627 0.8238 4.95 | 0.8994 −1.0737 0.8712 2.80 |
| MDEA (1) + DMSO (2) | ||||||
| Belda | m1 m2 104·σ | 0.3401 −0.2987 1.13 | 0.3454 −0.2827 1.24 | 0.3586 −0.2690 1.53 | 0.3935 −0.2366 1.77 | 0.4319 −0.2016 2.09 |
| Herraez | A B C 104·σ | 0.8238 −0.7358 0.3382 1.17 | 0.8289 −0.7382 0.3382 0.99 | 0.8346 −0.7492 0.3481 1.13 | 0.8448 −0.7638 0.3557 1.27 | 0.8576 −0.7930 0.3788 1.20 |
| DEG (1) + DMSO (2) A1 = 1.0860 A2 = 1.4180 P1 = −0.0368 P4 = −0.3664 P7 = 0.4773 A00 = 1.4584 A10 = −0.4239 A20 = 0.0383 MDEA (1) + DMSO (2) A1 = 1.6658 A2 = 1.4324 P1 = 0.1702 P4 = −0.2610 P7 = 0.3710 A00 = 1.4621 A10 = 0.3647 A20 = −0.1692 | Emmerling et al. B1 = 9.7611 × 10−4 B2 = −0.0012 P2 = 3.6037 × 10−4 P5 = 0.0023 P8 = −0.0030 104·σ = 1.09 Gonzalez-Olmos-Iglesias A01 = −0.0014 A11 = 0.0028 A21= −3.6947 × 10−4 104·σ = 3.14 Emmerling et al. B1 = −0.0034 B2 = −0.0013 P2 = −0.0016 P5 = 0.0019 P8 = −0.0026 104·σ = 1.52 Gonzalez-Olmos-Iglesias A01 = −0.0015 A11 = −0.0035 A21 = 0.0016 104·σ = 3.87 | C1 = −2.9500 × 10−6 C2 = 2.9207 × 10−7 P3 = −6.2313 × 10−7 P6 = −3.6487 × 10−6 P9 = 4.6316 × 10−6 A02 = 6.9155 × 10−7 A12 = −4.4132 × 10−6 A22 = 6.3730 × 10−7 C1 = 4.2989 × 10−6 C2 = 4.4600 × 10−7 P3 = 3.0708 × 10−6 P6 = −3.4634 × 10−6 P9 = 4.5659 × 10−6 A02 = 8.2965 × 10−7 A12 = 6.4086 × 10−6 A22 = −3.0582 × 10−6 |
Model | Parameters and ADD% | T/(K) | ||||
|---|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | ||
| DEG (1) + DMSO (2) | ||||||
| Grunberg- Nissan | d ADD% | 0.528 1.03 | 0.533 1.91 | 0.426 2.00 | 0.520 0.84 | 0.531 0.96 |
| Heric-Brewer | α12 α21 ADD% | 0.575 −0.122 0.75 | 0.582 −0.357 0.41 | 0.475 −0.350 0.69 | 0.568 −0.130 1.45 | 0.579 −0.164 0.51 |
| Wilson | λ12 λ21 ADD% | −481.19 −681.61 0.82 | 1985.47 −1986.45 0.86 | 1754.04 −1754.39 1.23 | −287.47 −868.51 0.56 | 724.45 −1501.24 0.50 |
| Noda and Ishida | w12 w21 ADD% | −30.23 30.42 1.02 | −31.10 −31.28 1.90 | −28.29 28.43 1.97 | −30.77 30.96 0.85 | −31.31 31.50 0.93 |
| Eyring-NRTL a | τ12 τ12 ADD% | −0.455 1.172 0.80 | −1.227 2.586 0.58 | −1.380 2.753 0.66 | −0.544 1.297 0.54 | −0.780 1.681 0.50 |
| MDEA (1) + DMSO (2) | ||||||
| Grunberg- Nissan | d ADD% | 1.627 10.41 | 1.517 10.68 | 1.383 9.60 | 1.224 8.84 | 1.250 8.47 |
| Heric-Brewer | α12 α21 ADD% | 1.719 −1.889 5.82 | 1.610 −1.965 5.02 | 1.474 −1.762 4.82 | 1.316 −1.609 4.90 | 1.342 −1.574 3.68 |
| Wilson | λ12 λ21 ADD% | 3811.93 −3812.09 6.33 | 3720.99 −3727.36 6.68 | 3538.15 −3555.24 6.37 | 3393.73 −3399.01 6.50 | 3422.86 −3425.11 5.46 |
| Noda and Ishida | w12 w21 ADD% | −53.26 53.84 10.43 | −52.00 52.55 10.68 | −50.55 51.04 9.62 | −48.21 48.65 8.88 | −48.71 49.17 8.49 |
| Eyring-NRTL a | τ12 τ12 ADD% | 0.014 14.593 2.18 | −0.136 14.381 1.61 | −0.049 15.552 1.74 | −1.329 8.453 3.30 | −1.362 7.5085 3.30 |
Model | Parameters and σ | T/(K) | ||||
|---|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | ||
| VE/(cm3·mol−1) DEG (1) + DMSO (2) | ||||||
| Redlich-Kister | a0 a1 a2 a3 103·σ | −0.736 0.420 0.157 −0.384 3.0 | −0.726 0.411 0.296 −0.422 3.5 | −0.701 0.339 0.319 −0.328 2.7 | −0.679 0.287 0.379 −0.307 3.7 | −0.668 0.280 0.453 −0.198 2.4 |
| Hwang | A0 A1 A2 103·σ | −0.785 0.545 −0.139 7.4 | −0.821 0.703 0.071 8.0 | −0.805 0.689 0.150 6.3 | −0.803 0.717 0.285 6.3 | −0.817 0.853 0.348 4.4 |
| Myers and Scott | B0 B1 B2 C0 C1 103·σ | −0.730 −0.391 −0.240 1.122 1.001 2.9 | −0.720 −0.343 0.105 1.060 0.693 3.3 | −0.708 −0.003 −0.394 0.556 1.488 2.0 | −0.680 −0.141 0.137 0.654 0.680 3.9 | −0.666 0.004 0.518 0.410 0.018 2.6 |
| MDEA (1) + DMSO (2) | ||||||
| Redlich-Kister | a0 a1 a2 a3 103·σ | 1.436 0.164 −0.274 0.208 5.1 | 1.403 0.188 −0.307 0.250 5.3 | 1.364 0.211 −0.359 0.240 8.4 | 1.307 0.268 −0.411 0.264 10.0 | 1.259 0.315 −0.520 0.281 10.4 |
| Hwang | A0 A1 A2 103·σ | 1.527 −0.084 −0.647 5.2 | 1.505 −0.083 −0.737 5.6 | 1.483 −0.129 −0.830 8.2 | 1.444 −0.120 −0.977 9.7 | 1.432 −0.202 −1.186 10.1 |
| Myers and Scott | B0 B1 B2 C0 C1 103·σ | 1.428 −0.387 −1.759 −0.394 −1.078 3.8 | 1.389 −0.586 −1.874 −0.573 −1.152 5.4 | 1.348 −0.466 −1.742 −0.522 −1.073 8.4 | 1.287 −0.425 −1.836 −0.545 −1.162 7.9 | 1.234 −0.313 −1.788 −0.519 −1.125 8.2 |
| Δη/(mPa·s) DEG (1) + DMSO (2) | ||||||
| Redlich-Kister | a0 a1 a2 a3 σ | −30.94 −8.67 −6.08 −6.46 0.11 | −23.81 −7.84 −6.20 6.31 0.05 | −18.47 −7.25 −2.65 −0.60 0.06 | −13.15 −3.29 −1.35 −0.65 0.04 | −10.22 −2.78 0.31 1.15 0.03 |
| Hwang | A0 A1 A2 σ | −28.89 −21.19 4.89 0.11 | −21.73 −20.30 3.67 0.07 | −17.60 −12.42 5.41 0.06 | −12.70 −6.00 2.40 0.03 | −10.34 −2.39 3.29 0.04 |
| MDEA (1) + DMSO (2) | ||||||
| Redlich-Kister | a0 a1 a2 a3 σ | −119.76 −45.73 −19.54 −54.82 0.63 | −85.34 −35.93 −20.99 −43.35 0.39 | −62.82 −22.03 −15.89 −42.66 0.37 | −48.12 −17.44 −7.35 −27.20 0.26 | −34.08 −11.65 −8.74 −23.83 0.19 |
| Hwang | A0 A1 A2 σ | −113.24 −103.14 51.24 0.80 | −78.34 −88.66 32.85 0.56 | −57.52 −64.94 22.75 0.59 | −45.67 −41.77 22.27 0.38 | −31.17 −35.30 12.10 0.32 |
x1 | T/(K) | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| DEG (1) + DMSO (2) | |||||
| 0.0000 0.1062 0.2007 | - 94.499 94.759 | - 94.922 95.157 | - 95.293 95.560 | - 95.770 95.983 | - 96.147 96.366 |
| 0.3034 0.4110 0.5108 0.5972 0.6955 0.8096 0.8819 1.0000 | 95.077 95.391 95.645 95.837 96.023 96.203 96.306 96.455 | 95.445 95.775 96.035 96.236 96.433 96.626 96.736 96.895 | 95.861 96.172 96.440 96.648 96.853 97.055 97.171 97.340 | 96.287 96.591 96.858 97.068 97.280 97.486 97.605 97.779 | 96.679 96.994 97.270 97.487 97.707 97.925 98.049 98.232 |
| MDEA (1) + DMSO (2) | |||||
| 0.0000 0.1003 0.1967 0.2997 0.4006 0.5001 0.6020 0.6937 0.7983 0.8967 1.0000 | - 114.274 113.424 112.488 111.671 110.936 110.265 109.730 109.186 108.731 108.310 | - 114.764 113.859 112.975 112.167 111.429 110.760 110.226 109.682 109.226 108.805 | - 115.141 114.243 113.405 112.618 111.886 111.229 110.706 110.169 109.719 109.304 | - 115.450 114.619 113.843 113.053 112.343 111.700 111.183 110.654 110.208 109.797 | - 115.770 115.008 114.263 113.511 112.815 112.182 111.671 111.151 110.711 110.305 |
x1 | T/(K) | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| DEG (1) + DMSO (2) | |||||
| 0.0000 0.1062 0.2007 0.3034 0.4110 0.5108 0.5972 0.6955 0.8096 0.8819 1.0000 | 71.014 70.966 70.899 70.832 70.780 70.752 70.752 70.765 70.725 70.792 - | 71.339 71.304 71.244 71.166 71.124 71.090 71.095 71.120 71.111 71.195 - | 71.656 71.633 71.585 71.522 71.462 71.432 71.438 71.466 71.467 71.533 - | 71.989 71.968 71.917 71.862 71.801 71.767 71.764 71.808 71.799 71.899 - | 72.322 72.304 72.254 72.201 72.145 72.114 72.111 72.158 72.211 72.327 - |
| MDEA (1) + DMSO (2) | |||||
| 0.0000 0.1003 0.1967 0.2997 0.4006 0.5001 0.6020 0.6937 0.7983 0.8967 1.0000 | 71.014 71.004 71.080 71.188 71.337 71.485 71.634 71.794 72.003 72.066 - | 71.339 71.332 71.389 71.514 71.670 71.807 71.959 72.121 72.333 72.397 - | 71.666 71.660 71.709 71.842 72.004 72.126 72.273 72.455 72.655 72.666 - | 71.989 71.972 72.018 72.167 72.302 72.434 72.597 72.765 72.986 72.944 - | 72.322 72.295 72.340 72.482 72.632 72.764 72.923 73.076 73.320 73.224 - |
x1 | T/(K) | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| DEG (1) + DMSO (2) | |||||
| 0.0000 0.1062 0.2007 0.3034 0.4110 0.5108 0.5972 0.6955 0.8096 0.8819 1.0000 | 94.262 94.243 94.286 94.375 94.490 94.600 94.687 94.770 94.837 94.862 94.877 | 94.773 94.679 94.675 94.728 94.820 94.918 95.001 95.082 95.150 95.176 95.192 | 95.142 95.067 95.067 95.115 95.197 95.284 95.358 95.431 95.494 95.519 95.535 | 95.635 95.533 95.513 95.541 95.606 95.681 95.748 95.816 95.875 95.900 95.915 | 95.966 95.888 95.876 95.904 95.964 96.033 96.096 96.161 96.221 96.246 96.263 |
| MDEA (1) + DMSO (2) | |||||
| 0.0000 0.1003 0.1967 0.2997 0.4006 0.5001 0.6020 0.6937 0.7983 0.8967 1.0000 | 115.271 115.225 115.145 115.034 114.915 114.799 114.690 114.607 114.536 114.495 114.481 | 115.647 115.644 115.593 115.505 115.400 115.292 115.190 115.110 115.042 115.003 114.989 | 115.955 115.978 115.947 115.877 115.786 115.689 115.594 115.519 115.453 115.415 115.401 | 116.191 116.266 116.274 116.235 116.167 116.087 116.003 115.936 115.876 115.840 115.827 | 116.400 116.539 116.595 116.595 116.555 116.492 116.421 116.360 116.303 116.269 116.257 |
x1 | T/(K) | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| DEG (1) + DMSO (2) | |||||
| 0.0000 0.1062 0.2007 0.3034 0.4110 0.5108 0.5972 0.6955 0.8096 0.8819 1.0000 | 71.014 71.007 70.992 70.974 70.954 70.933 70.907 70.863 70.774 70.688 70.471 | 71.338 71.329 71.313 71.293 71.274 71.258 71.241 71.211 71.146 71.078 70.897 | 71.666 71.656 71.639 71.616 71.593 71.573 71.554 71.527 71.475 71.425 71.295 | 71.989 71.979 71.960 71.935 71.910 71.889 71.871 71.849 71.809 71.770 71.669 | 72.322 72.313 72.293 72.267 72.242 72.224 72.213 72.206 72.202 72.200 72.189 |
| MDEA (1) + DMSO (2) | |||||
| 0.0000 0.1003 0.1967 0.2997 0.4006 0.5001 0.6020 0.6937 0.7983 0.8967 1.0000 | 71.014 71.034 71.086 71.171 71.281 71.414 71.577 71.748 71.977 72.231 72.548 | 71.338 71.359 71.411 71.496 71.605 71.736 71.896 72.065 72.292 72.548 72.872 | 71.666 71.686 71.738 71.823 71.931 72.060 72.214 72.374 72.587 72.825 73.122 | 71.989 72.010 72.064 72.149 72.257 72.383 72.534 72.690 72.897 73.127 73.417 | 72.322 72.344 72.400 72.487 72.593 72.716 72.859 73.003 73.192 73.399 73.657 |
References
- Wang, X.; Yang, F.; Gao, Y.; Liu, Z. Volumetric properties of binary mixtures of dimethyl sulfoxide with amines from (293.15 to 363.15) K. J. Chem. Thermodyn. 2013, 57, 145–151. [Google Scholar] [CrossRef]
- Kohl, A.L.; Nielsen, R. Gas Purification, 5th ed.; Gulf Publishing Co.: Houston, TX, USA, 1997. [Google Scholar]
- Zhao, T.; Zhang, J.; Guo, B.; Zhang, F.; Sha, F.; Xie, X.; Wei, X. Density, viscosity and spectroscopic studies of the binary systems of ethylene glycol + dimethyl sulfoxide at T = (298.15 to 323.15) K. J. Mol. Liq. 2015, 207, 315–322. [Google Scholar] [CrossRef]
- Huang, K.; Chen, Y.L.; Zhang, X.M.; Xia, S.; Wu, Y.T.; Hu, X.B. SO2 absorption in acid salt ionic liquids/sulfolane binary mixtures: Experimental study and thermodynamic analysis, Chem. Eng. J. 2014, 237, 478–486. [Google Scholar] [CrossRef]
- Xu, Y.M.; Schutte, R.P.; Hepler, L.G. Solubilities of carbon dioxide, hydrogen sulfide and sulfur dioxide in physical solvents. Can. J. Chem. Eng. 1992, 70, 569–573. [Google Scholar] [CrossRef]
- Tsierkezos, N.G.; Palaiologou, M.M. Ultrasonic studies of liquid mixtures of either water or dimethylsulfoxide with ethylene glycol, diethylene glycol, triethylene glycol, tetraethylene glycol, 1,2-propylene glycol and 1,4-buthylene glycol at 298.15 K. Phys. Chem. Liq. 2009, 47, 447–459. [Google Scholar] [CrossRef]
- Yue, X.; Zhao, L.; Ma, L.; Shi, H.; Yang, T.; Zhang, J. Density, dynamic viscosity, excess property and intermolecular interplay studies for 1,4-butanediol + dimethyl sulfoxide binary mixture. J. Mol. Liq. 2018, 263, 40–48. [Google Scholar] [CrossRef]
- Kumar Naidu, B.V.; Rao, C.K.; Subha, M.C.S. Densities and Viscosities of Mixtures of Some Glycols and Polyglycols in Dimethyl Sulfoxide at 308.15 K. J. Chem. Eng. Data 2002, 47, 379–382. [Google Scholar] [CrossRef]
- Wang, W.; Li, C.; Zhang, N.; Li, M. Excess Molar Volumes and Kinematic Viscosities of Diethylene Glycol + Dimethyl Sulfoxide at T = (298.15, 303.15, 308.15, 313.15 and 318.15) K. Asian J. Chem. 2013, 25, 5087–5091. [Google Scholar] [CrossRef]
- Aznarez, S.B.; Mussari, L.; Postigo, M.A. Temperature dependence of molar volumes for the domethyl sulfoxide + thiophene system and thermal expansion coefficients between 293.15 and 313.15 K. J. Chem. Eng. Data 1993, 38, 270–273. [Google Scholar] [CrossRef]
- Tsierkezos, N.G.; Kelarakis, A.E.; Palaiologou, M.M. Densities, Viscosities, Refractive Indices, and Surface Tensions of Dimethyl Sulfoxide + Butyl Acetate Mixtures at (293.15, 303.15, and 313.15) K. J. Chem. Eng. Data 2000, 45, 395–398. [Google Scholar] [CrossRef]
- Qiao, X.; Zhao, T.; Guo, B.; Sha, F.; Zhang, F.; Xie, X.; Zhang, J.; Wei, X. Excess properties and spectral studies for binary system tri-ethylene glycol + dimethyl sulfoxide. J. Mol. Liq. 2015, 212, 187–195. [Google Scholar] [CrossRef]
- Baragi, J.G.; Aralaguppi, M.I.; Aminabhavi, T.M.; Kariduraganavar, M.Y.; Kittur, A.S. Density, Viscosity, Refractive Index, and Apeed of Sound for Binary Mixtures of Anisole with 2-Chloroethanol, 1,4-Dioxane, Tetrachloroethylene, Tetrachloroethane, DMF, DMSO, and Diethyl Oxalate at (298.15, 303.15 and 308.15) K. J. Chem. Eng. Data 2005, 50, 910–916. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, J.; Yu, X.; Zhang, J.; Wei, X. Densities and viscosities for binary mixtures of poly(ethylene glycol) 400 + dimethyl sulfoxide and poly(ethylene glycol) 600 + water at different temperatures. J. Chem. Eng. Data 2011, 56, 3083–3088. [Google Scholar] [CrossRef]
- Ali, A.; Ansari, S.; Nain, A.K. Densities, refractive indices and excess properties of binary mixtures of dimethylsulfoxide with some poly(ethylene glycol)s at different temperatures. J. Mol. Liq. 2013, 178, 178–184. [Google Scholar] [CrossRef]
- Ciocirlan, O.; Iulian, O. Density, viscosity and refractive index of the dimethyl sulfoxide + o-xylene system. J. Serb. Chem. Soc. 2009, 74, 317–329. [Google Scholar] [CrossRef]
- Shi, H.; Ma, L.; Zhao, B.; Pang, Y.; Wu, Z. Density, viscosity and molecular interaction of binary system tetraethylene glycol + dimethyl sulfoxide at T = (293,15 to 318,15) K. J. Mol. Liq. 2018, 250, 182–191. [Google Scholar] [CrossRef]
- Omota, L.M.; Iulian, O.; Ciocirlan, O.; Nita, I. Viscosity of water, 1,1-dioxane and dimethyl sulfoxide binary and ternary systens at temperatures from 293.15 K to 313.15 K. Rev. Roum.Chim. 2008, 53, 977–988. [Google Scholar]
- Yasmeen, S.; Riyazuddeen, A.N. Interaction of 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)-imide with methanol/dimethyl sulfoxide at (298.15, 303.15, 308.15, 313.15, 318.15 and 323.15)K: Measurements and correlations of thermophysical properties. J. Mol. Liq. 2016, 221, 1207–1217. [Google Scholar] [CrossRef]
- Ciocirlan, O.; Croitoru, O.; Iulian, O. Densities and Viscosities for Binary Mixtures of 1-Butyl-3-Methylimidazolium Tetrafluoroborate Ionic Liquid with Molecular Solvents. J. Chem. Eng. Data 2011, 56, 1526–1534. [Google Scholar] [CrossRef]
- Grande, M.C.; Juliá, J.A.; Garcí, M.; Marschoff, C.M. On the density and viscosity of (water + dimethylsulphoxide) binary mixtures. J. Chem. Thermodyn. 2007, 39, 1049–1056. [Google Scholar] [CrossRef]
- Bernal-García, J.M.; Guzmán-López, A.; Cabrales-Torres, A.; Rico-Ramírez, V.; Iglesias-Silva, G.A. Supplementary densities and viscosities of aqueous solutions of diethylene glycol from (283.15 to 353.15) K. J. Chem. Eng. Data 2008, 53, 1028–1031. [Google Scholar] [CrossRef]
- Klimaszewski, K.; Stronka-Lewkowska, E.; Soliwoda, K.; Bald, A. Acustic and volumetric studies on water + diethylene glycol mixtures in a wide temperature range. Comparison with mixtures of water with tri- and tetraethylene glycol. J. Mol. Liq. 2016, 215, 520–533. [Google Scholar] [CrossRef]
- Kinart, C.M.; Klimczak, M.; Kinart, W.J. Volumetric and dielectric characterization and analysis of internal structure of binary mixtures of 2-ethoxyethanol with ethylene glycol, diethylene glycol, triethylene glycol, and tetraethylene glycol at T = (293.15, 298.15 and 303.15) K. J. Mol. Liq. 2009, 145, 8–13. [Google Scholar] [CrossRef]
- Sastry, N.V.; Patel, M.C. Densities, Excess Molar Volumes, Viscosities, Speeds of Sound, Excess Isentropic Compressibilities, and Relative Permittivities for Alkyl (Methyl, Ethyl, Buthyl, and Isoamyl) Acetates + Glycols at Different Temperatures. J. Chem. Eng. Data 2003, 48, 1019–1027. [Google Scholar] [CrossRef]
- Almasi, M. Densities and Viscosities of Binary Mixtures Containing Diethylene Glycol and 2-Alkanol. J. Chem. Eng. Data 2012, 57, 2992–2998. [Google Scholar] [CrossRef]
- Begum, S.K.; Clarke, R.J.; Ahmed, M.S.; Begum, S.; Saleh, M.A. Densities, viscosities, and surface tensions of the system water + diethylene glycol. J. Chem. Eng. Data 2011, 56, 303–306. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.; Li, Q.; Guo, B.; Zhao, T.; Sha, F. Density, viscosity, surface tension, and spectroscopic properties for binary system of 1,2-ethanediamine + diethylene glycol. Thermochim. Acta 2014, 590, 91–99. [Google Scholar] [CrossRef]
- Karunarathane, S.S.; Eimer, D.A.; Øi, L.E. Density, Viscosity, and Excess Properties of MDEA + H2O, DMEA + H2O, and DEEA + H2O Mixtures. Appl. Sci. 2020, 10, 3196. [Google Scholar] [CrossRef]
- Yin, Y.; Fu, T.; Zhu, C.; Ma, Y. Volumetric and viscometric study and FT-IR analysis of binary and ternary mixtures of 1-butyl-3-methylimidazolium tetrafluoroborate, methyldiethanolamine and water. J. Mol. Liq. 2017, 243, 664–676. [Google Scholar] [CrossRef]
- DiGuilio, R.M.; Lee, R.J.; Schaffer, S.T.; Brasher, L.L.; Teja, A.S. Densities and viscosities of the ethanolamines. J. Chem. Eng. Data 1992, 37, 239–242. [Google Scholar] [CrossRef]
- Bernal-Garcia, J.M.; Ramos-Estrada, M.; Iglesias-Silva, A.; Hall, K.R. Densities and excess molar volumes of aqueous solutions of n-Methyldiethanolamine (MDEA) at temperatures from (283.15 to 363.15) K. J. Chem. Eng. Data 2003, 48, 1442–1445. [Google Scholar] [CrossRef]
- Vahidi, M.; Moshtari, B. Dielectric data, densities, refractive indices, and their deviations of the binary mixtures of N-methyldiethanolamine with sulfolane at temperatures 293.15–328.15 K and atmospheric pressure. Thermochim. Acta 2013, 551, 1–6. [Google Scholar] [CrossRef]
- Rebolledo-Libreros, M.E.; Trejo, A. Density and Viscosity of Aqueous Blends of Three Alkanolamines: N-Methyldiethanolamine, Diethanolamine, and 2-Amino-2-methyl-1-propanol in the range of (303 to 343) K. J. Chem. Eng. Data 2006, 51, 702–707. [Google Scholar] [CrossRef]
- Zhang, Q.; Cai, S.; Zhang, W.; Lan, Y.; Zhang, X. Density, viscosity, conductivity, refractive index and interaction study of binary mixtures of the ionic liquid 1-ethyl-3-methylimidazolium acetate with methyldiethanolamine. J. Mol. Liq. 2017, 233, 471–478. [Google Scholar] [CrossRef]
- Al-Ghawas, H.A.; Hagewiesche, D.P.; Ruiz-Ibanez, G.; Sandall, O.C. Physicochemical properties important for carbon dioxide absorption in aqueous methyldiethanolamine. J. Chem. Eng. Data 1989, 34, 385–391. [Google Scholar] [CrossRef]
- Akbar, M.M.; Murugesan, T. Thermophysical properties of 1-hexyl-3-methylimidazolium tetrafluoroborate [hmim][BF4] + N-methyldiethanolamine (MDEA) at temperatures (303.15 to 323.15) K. J. Mol. Liq. 2013, 177, 54–59. [Google Scholar] [CrossRef]
- Belda, R. A proposed equation of correlation for the study of thermodynamic properties (density, viscosity, surface tension and refractive index) of liquid binary mixtures. Fluid Phase Equilib. 2009, 282, 88–99. [Google Scholar] [CrossRef]
- Herraez, J.V.; Belda, R.; Diez, O.; Herraez, M. An equation for the correlation of viscosities of binary mixtures. J. Sol. Chem. 2008, 37, 233–248. [Google Scholar] [CrossRef]
- Emmerling, U.; Figurski, G.; Rasmussen, P. Densities and kinematic viscosities for the systems benzene + methyl formate, benzene + ethyl formate, benzene + propyl formate, and benzene + butyl formate. J. Chem. Eng. Data 1998, 43, 289–292. [Google Scholar] [CrossRef]
- Gonzales-Olmos, R.; Iglesias, M. Influence of temperature on thermodynamics of ethers + xylenes. Fluid Phase Equilib. 2008, 267, 133–139. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Grunberg, L.; Nissan, A.H. Mixture law for viscosity. Nature 1949, 164, 799–800. [Google Scholar] [CrossRef]
- Heric, E.L.; Brewer, J.G. Viscosity of some binary liquid nonelectrolyte mixtures. J. Chem. Eng. Data 1967, 12, 574–583. [Google Scholar] [CrossRef]
- Wilson, G.M. Vapor—Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing. J. Am. Chem. Soc. 1964, 86, 127–130. [Google Scholar] [CrossRef]
- Noda, K.; Ishida, K. Correlation and prediction of the viscosity of liquid mixtures. J. Chem. Eng. Jpn. 1977, 10, 478–480. [Google Scholar] [CrossRef][Green Version]
- Novak, L.T. Relationship between the Intrinsic Viscosity and Eyring-NRTL Viscosity Model Parameters. Ind. Eng. Chem. Res. 2004, 43, 2602–2604. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenhalter, R.N.; De Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Ciocirlan, O.; Croitoru, O.; Iulian, O. Viscosity of binary mixtures of 1-ethyl-3-methylimidazolium tetrafluoroborate ionic liquid with four organic solvents. J. Chem. Thermodyn. 2016, 101, 285–292. [Google Scholar] [CrossRef]
- Zivkovic, N.V.; Serbanovic, S.S.; Kijevcanin, M.L.; Zivkovic, E.M. Volumetric and Viscometric Behavior of Binary Systems 2-Butanol + PEG 200, + PEG 400, + Tetraethylene Glycol Dimethyl Ether, and + N-Methyl-2-pyrrolidone. J. Chem. Eng. Data 2013, 58, 3332–3341. [Google Scholar] [CrossRef]
- Egorov, G.I.; Makarov, D.M.; Kolker, A.M. Densities and Volumetric Properties of Ethylene Glycol + Dimethylsulfoxide Mixtures at Temperatures of (278.15 to 323.15) K and Pressures of (0.1 to 100) MPa. J. Chem. Eng. Data 2010, 55, 3481–3488. [Google Scholar] [CrossRef]
- Carey, F.A. Organic Chemistry, 4th ed.; McGraw-Hill College: New York, NY, USA, 2000. [Google Scholar]
- Fernandez, J.E. Organic Chemistry: An Introduction; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1982. [Google Scholar]
- Comelli, F.; Francesconi, R.; Bigi, A.; Rubini, K. Excess Molar Enthalpies, Molar Heat Capacities, Densities, Viscosities, and Refractive Indices of Dimethyl Sulfoxide + 1-Propanol at (288.15, 298.15, and 308.15) K and at Normal Pressure. J. Chem. Eng. Data 2006, 51, 1711–1716. [Google Scholar] [CrossRef]
- Dubey, G.P.; Sharma, M.; Dubey, N. Study of densities, viscosities, and speeds of sound of binary liquid mixtures of butan-1-ol with n-alkanes (C6, C8, and C10) at T = (298.15, 303.15, and 308.15) K. J. Chem. Thermodyn. 2008, 40, 309–320. [Google Scholar] [CrossRef]
- Mahajan, A.R.; Mirgane, S.R. Excess Molar Volumes and Viscosities for the Binary Mixtures of n-Octane, n-Decane, n-Dodecane, and n-Tetradecane with Octan-2-ol at 298.15 K. J. Thermodyn. 2013, 2013. [Google Scholar] [CrossRef]
- Pal, A.; Kumar, A. Excess molar volumes and viscosities of binary mixtures of some polyethers with 1-propanol at 288.15, 298.15, and 308.15 K. J. Chem. Sci. 2004, 116, 39–47. [Google Scholar] [CrossRef]
- Hoga, H.E.; Torres, R.B. Volumetric and viscometric properties of binary mixtures of {methyl tert-butyl ether (MTBE) + alcohol} at several temperatures and p = 0.1 MPa: Experimental results and application of the ERAS model. J. Chem. Thermodyn. 2011, 43, 1104–1134. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A.T. Algebraic Representation of Thermodynamic Properties and the Classification of Solutions. Ing. Eng. Chem. 1948, 40, 345–348. [Google Scholar] [CrossRef]
- Hwang, C.A.; Holste, J.C.; Hall, K.R.; Mansoori, G.A. A simple relation to predict or to correlate the excess functions of multicomponent mixtures. Fluid Phase Equilib. 1991, 62, 173–189. [Google Scholar] [CrossRef]
- Myers, D.B.; Scott, R.L. Thermodynamic functions for nonelectrolyte solutions. Ind. Eng. Chem. 1963, 55, 43–46. [Google Scholar] [CrossRef]
- Kinart, C.M.; Bald, A.; Kinart, W.J.; Kolasinski, A. Dimethylsulfoxide—N,N-Dimethylformamide Binary Mixtures and Their Physicochemical Properties. Phys. Chem. Liq. 1998, 36, 245–256. [Google Scholar] [CrossRef]
- Eyring, H.; Jhon, M.S. Significant Liquid Structures; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]



| Chemical Name | Chemical Formula | Source | Mass Fraction Purity | Isolation Method |
|---|---|---|---|---|
| DMSO DEG MDEA | C2H6OS C4H10O3 C5H13NO2 | Merck Chemical Company Chemical Company | 99.5% ≥99.3% ≥99.3% | None Desiccation a and Degasification b Desiccation a and Degasification b |
| Component | T/(K) | ρ/(g·cm−3) | η/(mPa·s) | ||
|---|---|---|---|---|---|
| This Work | Lit. Value | This Work | Lit. Value | ||
| DMSO | 293.15 298.15 303.15 308.15 313.15 | 1.1002 1.0952 1.0902 1.0853 1.0803 | 1.1002 [10] 1.10053 [11] 1.100865 [1] 1.0955 [12] 1.0954 [13] 1.09530 [6] 1.0946 [9] 1.0904 [12] 1.0900 [14] 1.0888 [9] 1.090812 [1] 1.0854 [12] 1.08573 [15] 1.0831 [9] 1.0807 [12] 1.08024 [16] 1.0785 [9] 1.080770 [1] | 2.271 2.021 1.843 1.710 1.525 | 2.245 [17] 2.2255 [18] 2.00 [12] 2.025 [19] 1.40 [9] 1.84 [12] 1.843 [20] 1.21 [9] 1.69 [3] 1.6689 [21] 1.12 [9] 1.5351 [21] 1.52 [12] 1.00 [9] |
| DEG | 293.15 298.15 303.15 308.15 313.15 | 1.1185 1.1148 1.1108 1.1064 1.1024 | 1.11705 [22] 1.116583 [23] 1.11303 [24] 1.11351 [25] 1.1128 [9] 1.11260 [1] 1.1098 [26] 1.10948 [27] 1.1093 [9] 1.1056 [26] 1.10629 [22] 1.1052 [9] 1.1023 [28] 1.102274 [23] 1.0998 [9] | 33.270 26.865 21.280 17.291 14.117 | - 27.15 [26] 27.5 [28] 17.00 [9] 21.7 [28] 21.754 [26] 12.4 [9] 17.26 [26] 16.9 [28] 10.4 [9] 14.2 [28] 8.19 [9] |
| MDEA | 293.15 298.15 303.15 308.15 313.15 | 1.0409 1.0363 1.0326 1.0288 1.0250 | 1.0406 [29] 1.03966 [30] 1.0406 [1] 1.03556 [31] 1.037863 [32] 1.0331 [29] 1.03213 [30] 1.033017 [1] 1.02834 [31] 1.0303 [33] 1.0255 [29] 1.0250 [34] 1.025401 [1] | 100.614 74.927 57.582 45.129 34.833 | 102.7 [31] 100.72 [29] 74.81 [35] 57.57 [36] 57.615 [30] 44.21 [37] 44.62 [29] 34.78 [36] 35.00 [37] 34.89 [29] |
| T/(K) | |||||
|---|---|---|---|---|---|
| x1 | 293.15 | 298.15 | 303.15 | 308.15 | 313.15 |
| DEG (1) + DMSO (2) | |||||
| 0.1062 0.2007 0.3034 0.4110 0.5108 0.5972 0.6955 0.8096 0.8819 | 1.1038 1.1068 1.1095 1.1117 1.1133 1.1144 1.1155 1.1168 1.1174 | 1.0988 1.1019 1.1049 1.1072 1.1090 1.1102 1.1114 1.1128 1.1135 | 1.0939 1.0970 1.1000 1.1026 1.1045 1.1058 1.1071 1.1086 1.1094 | 1.0889 1.0921 1.0951 1.0978 1.0998 1.1012 1.1025 1.1041 1.1049 | 1.0840 1.0873 1.0904 1.0932 1.0953 1.0968 1.0982 1.0998 1.1007 |
| MDEA (1) + DMSO (2) | |||||
| 0.1003 0.1967 0.2997 0.4006 0.5001 0.6020 0.6937 0.7983 0.8967 | 1.0899 1.0808 1.0725 1.0654 1.0595 1.0544 1.0504 1.0465 1.0436 | 1.0850 1.0762 1.0678 1.0607 1.0549 1.0498 1.0458 1.0419 1.0390 | 1.0803 1.0718 1.0635 1.0565 1.0509 1.0459 1.0419 1.0381 1.0353 | 1.0758 1.0675 1.0592 1.0525 1.0469 1.0419 1.0380 1.0342 1.0315 | 1.0712 1.0631 1.0550 1.0483 1.0428 1.0379 1.0341 1.0303 1.0277 |
| T/(K) | |||||
|---|---|---|---|---|---|
| x1 | 293.15 | 298.15 | 303.15 | 308.15 | 313.15 |
| DEG (1) + DMSO (2) | |||||
| 0.1062 0.2007 0.3034 0.4110 0.5108 0.5972 0.6955 0.8096 0.8819 | 3.110 4.306 5.792 7.884 10.198 12.843 16.372 21.286 24.874 | 2.877 3.799 5.115 6.762 8.630 10.717 13.356 17.154 20.097 | 2.520 3.404 4.334 5.702 7.072 8.605 10.796 13.923 16.220 | 2.281 3.012 3.883 5.082 6.337 7.647 9.502 11.854 13.703 | 2.049 2.677 3.383 4.361 5.394 6.428 7.951 9.912 11.431 |
| MDEA (1) + DMSO (2) | |||||
| 0.1003 0.1967 0.2997 0.4006 0.5001 0.6020 0.6937 0.7983 0.8967 | 5.745 7.771 10.987 15.147 21.152 29.452 40.462 54.870 71.350 | 4.859 6.572 9.100 12.513 16.806 23.184 30.372 40.971 53.015 | 4.170 5.595 7.542 10.120 13.775 18.668 24.585 32.239 40.925 | 3.680 4.837 6.364 8.490 11.189 15.024 19.888 25.861 32.869 | 3.173 4.084 5.508 7.188 9.673 12.455 15.955 20.465 25.494 |
x1 | ΔH≠ (kJ/mol) | ΔS≠ (J/mol·K) | ΔG≠ (kJ/mol) T/(K) | ||||
|---|---|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |||
| DEG (1) + DMSO (2) | |||||||
| 0.0000 0.1062 0.2007 0.3034 0.4110 0.5108 0.5972 0.6955 0.8096 0.8819 1.0000 | 14.02 15.59 17.40 19.96 21.80 23.55 25.69 26.68 28.41 29.02 32.34 | −2.01 0.26 3.49 9.58 13.10 16.72 21.91 23.06 26.52 27.12 35.69 | 14.61 15.51 16.34 17.15 17.96 18.65 19.27 19.91 20.64 21.07 21.88 | 14.62 15.51 16.33 17.10 17.80 18.57 19.16 19.80 20.50 20.93 21.71 | 14.63 15.51 16.31 17.05 17.83 18.48 19.05 19.68 20.37 20.80 21.53 | 14.64 15.50 16.29 17.01 17.77 18.40 18.94 19.57 20.24 20.66 21.35 | 14.65 15.50 16.27 16.96 17.70 18.32 18.83 19.45 20.11 20.53 21.17 |
| MDEA (1) + DMSO (2) | |||||||
| 0.0000 0.1003 0.1967 0.2997 0.4006 0.5001 0.6020 0.6937 0.7983 0.8967 1.0000 | 14.02 21.72 23.69 25.93 28.08 29.52 32.32 34.31 36.57 38.16 39.56 | −2.01 16.02 19.72 24.08 28.27 30.13 36.46 40.39 45.18 48.10 49.62 | 14.61 17.02 17.91 18.87 19.79 20.69 21.63 22.47 23.32 24.06 25.01 | 14.62 16.94 17.81 18.75 19.65 20.54 21.45 22.26 23.10 23.82 24.76 | 14.63 16.86 17.71 18.63 19.51 20.39 21.26 22.06 22.87 23.58 24.51 | 14.64 16.78 17.61 18.51 19.37 20.24 21.08 21.86 22.64 23.34 24.27 | 14.65 16.70 17.52 18.39 19.23 20.09 20.90 21.66 22.42 23.10 24.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Budeanu, M.M.; Dumitrescu, V. Densities, Viscosities and Excess Properties for Dimethyl Sulfoxide with Diethylene Glycol and Methyldiethanolamine at Different Temperatures. Appl. Sci. 2022, 12, 116. https://doi.org/10.3390/app12010116
Budeanu MM, Dumitrescu V. Densities, Viscosities and Excess Properties for Dimethyl Sulfoxide with Diethylene Glycol and Methyldiethanolamine at Different Temperatures. Applied Sciences. 2022; 12(1):116. https://doi.org/10.3390/app12010116
Chicago/Turabian StyleBudeanu, Maria Magdalena, and Vasile Dumitrescu. 2022. "Densities, Viscosities and Excess Properties for Dimethyl Sulfoxide with Diethylene Glycol and Methyldiethanolamine at Different Temperatures" Applied Sciences 12, no. 1: 116. https://doi.org/10.3390/app12010116
APA StyleBudeanu, M. M., & Dumitrescu, V. (2022). Densities, Viscosities and Excess Properties for Dimethyl Sulfoxide with Diethylene Glycol and Methyldiethanolamine at Different Temperatures. Applied Sciences, 12(1), 116. https://doi.org/10.3390/app12010116





