An ANN Model for Predicting the Compressive Strength of Concrete

Abstract

An artificial neural network (ANN) model for predicting the compressive strength of concrete is established in this study. The Back Propagation (BP) network with one hidden layer is chosen as the structure of the ANN. The database of real concrete mix proportioning listed in earlier research by another author is used for training and testing the ANN. The proper number of neurons in the hidden layer is determined by checking the features of over-fitting while the synaptic weights and the thresholds are finalized by checking the features of over-training. After that, we use experimental data from other papers to verify and validate our ANN model. The final result of the synaptic weights and the thresholds in the ANN are all listed. Therefore, with them, and using the formulae expressed in this article, anyone can predict the compressive strength of concrete according to the mix proportioning on his/her own.

1. Introduction

Due to the high compressive strength and the capability of being casted into any shape and size, concrete is the most used construction material in the world. The compressive strength is related to the proportioning of its ingredients, such as water, cement, coarse aggregates, sand, and other admixtures. How to predict the compressive strength according to the proportioning design is a very practical topic. For example, with a prediction model one can estimate the compressive strengths of dozens of mix designs and just choose those that achieve the required strength for further physical tests. This can reduce the number of trials for a specific compressive strength requirement and can save a lot of money and time. Furthermore, one can determine the most inexpensive choice among those that required compressive strength for economical consideration.

Conventionally, statistics are a useful tool for evaluating the results of strength tests. For instance, one can obtain a regression equation using data of water–cement ratio versus the compressive strengths [1]. However, there are not just one or two factors that affect compressive strength. The predicted results by just using the water–cement ratio could be very poor in many cases.

In recent decades, the artificial neural networks (ANNs) have drawn more and more attention because of the capability of dealing with multivariable analysis. Several authors have used the ANNs to determine the compressive strength of concrete [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. An ANN is like a black box. After training the ANN, one can input several numerical values and the ANN will prompt another numerical value which represents the predicted compressive strength of the concrete. The components for the input can be factors such as the proportioning of water, cement, sand, etc. Recently, more and more new types of ANN structures, such as the Support Vector Machines [17,18], Deep Learning Neural Network [19,20,21,22,23], Radial Basis Function Network [24,25,26,27,28,29] for various research areas have popped out, as well as other algorithms like tabu and genetic [15,19,26,28,29,30] are newly applied for training the ANN.

In [16], data of real concrete mix proportioning listed in [12] were used to establish a database. With that database, the ANN of back-propagation type (BP) with single hidden layer was employed to establish the prediction models of strength and slump of concrete. Cylindrical test samples of 12 additional mix designs were also casted and their compressive strengths were examined in the laboratory to verify the established ANN model. In this study, we use the same database for establishing our new ANN model. However, we think data for establishing a concrete slump prediction model are insufficient due to 39% of slump records being missing from the database. Therefore, we just focus on establishing a prediction model for the compressive strength of concrete in this study.

Typically, the database has to be divided into two parts, one for training and the other for testing. This is for the sake of avoiding over-training and over-fitting. In [16], most of the data were used for training the ANN while only 20 pieces of data were used in the testing process. There are 482 pieces of data in the database, so data for testing were about 4% of the whole. In our opinion, that is inadequate, though the results of verification were still acceptable. Consequently, we contrive an improvement by using fewer data for training and more data for testing, for the reason that the over-fitting can be alleviated.

There are so many choices for establishing the ANN model but for comparison with [16], we still use the BP-ANN with single hidden layer. The final result of the synaptic weights and the thresholds in the ANN are all listed in this paper. Therefore, anyone can use them accompanied with the formulae expressed in the article to predict the concrete compressive strength according to the mix proportioning on his/her own.

Our new ANN model outperforms the ANN model of [16] as we check the result of verification. Further validation is implemented by using the data of [15]. A good agreement is also found. This implies our ANN model really works for practical uses.

2. The Concrete Mix Proportioning

According to [16], the 28-day compressive strength is related to seven factors. They are the mass of water, cement, fine aggregate (or sand), coarse aggregate, blast furnace slag, fly ash, and superplasticizer mixed in 1 m³ concrete. Therefore, the compressive strength of concrete can be expressed as a mathematical function with seven variables:

$$y=f(\mathit{x})$$

(1)

in which;

$$\mathit{x}={\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_7\end{array}\right]}^{\mathbf{T}}$$

(2)

where $x_1$ to $x_7$ are those just mentioned proportioning factors while $y$ is the compressive strength of concrete. For the input and output of the ANN, all the data have to be normalized into the range of 0 to 1. The linear transformation is applied. The ranges from $x_1$ to $x_7$ are listed in Table 1.

$${\xi }_i=\frac{x_i-x_{i,}{}_{\min }}{x_{i,}{}_{\max }-x_{i,}{}_{\min }}$$

(3)

$$\eta =\frac{y-y_{\min }}{y_{\max }-y_{\min }}$$

(4)

Table 1. The ranges of the inputs and the output in the raw data [12].

	Inputs							Output
	x1	x2	x3	x4	x5	x6	x7	y
Maximum	255	599	1293	1226	375	330	27.17	95.3
Minimum	116.5	74	30	436	0	0	0	5.66

Printing out all the data might make this paper redundant. Those who need the digital file of the raw data of the database may contact the authors of [16]. Listed data can also be found in the tables of [12] which has been openly published and is downloadable from NCTU library website (https://ir.nctu.edu.tw/handle/11536/71533 (accessed on 12 March 2021)). For implementing this research, we downloaded [12], and copied the data from the tables in that thesis. The normalized data are listed in Appendix A. One can use them accompanied by those listed in Table 1 to retrieve their original values.

3. The Artificial Neural Network

The artificial neural network used in this study is the Back Propagation (BP) which was proposed in [31]. Following [16], we also use the single hidden layer network. According to the database of the real concrete mix proportioning, we have 7 neurons in the input layer and only 1 neuron in the output layer. The structure of the BP-ANN employed in this study is shown in Figure 1.

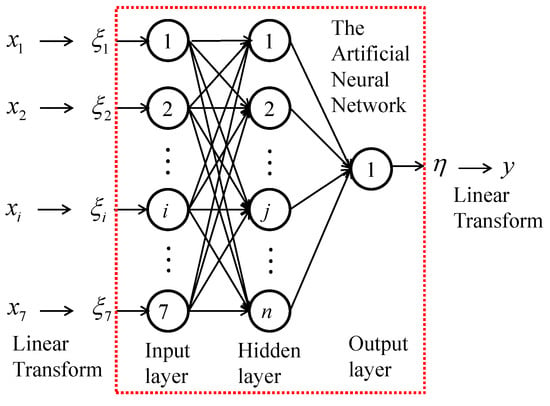
Figure 1. The input-output relation for predicting the compressive strength of concrete and the structure of the ANN model.

The formula for the normalized input-output relation can be expressed mathematically:

$$\eta =w_0^{(2)}+{\displaystyle \sum _{j=1}^n\left(\frac{w_j^{(2)}}{1+\exp (-\alpha v_j)}\right)}$$

(5)

in which;

$$v_j=w_{0,j}^{(1)}+{\displaystyle \sum _{i=1}^7\left(w_{i,j}^{(1)} {\xi }_i\right)}$$

(6)

where, in Equations (5) and (6), $w_{0,j}^{(1)}$ and $w_0^{(2)}$ are so-called thresholds, $w_{i,j}^{(1)}$ and $w_j^{(2)}$ are the synaptic weights, $\alpha$ is the shape parameter of the activating function, $i$ represents the index of a neuron in the input layer, $j$ represents the index of a neuron in the hidden layer, and $n$ represents the total number of neurons in the hidden layer. The suitable number of neurons in the hidden layer is to be determined.

From the database, $N$ records are randomly chosen for training the ANN. The error residual is defined as:

$$E={\displaystyle \sum _{\underset{\_}{k}=1}^N{\left({\eta }_{\underset{\_}{k}}^{(o)}-{\eta }_{\underset{\_}{k}}^{(d)}\right)}^2}$$

(7)

where ${\eta }_{\underset{\_}{k}}^{(d)}$ is the desired value which represents the normalized compressive strength in the data, ${\eta }_{\underset{\_}{k}}^{(o)}$ is the output of the ANN, and $k$ is the sequential number. We use the underline for $k$ to remind that the samples have been re-numbered because we randomly picked them up from the database. The training process is to find a set of suitable values for the thresholds and the synaptic weights. In the beginning, all the values of the thresholds and the synaptic weights are set up with small random numbers.

Now the error residual $E$ is a function of the thresholds and the synaptic weights. We can use the steepest descendent method to update their guess values and make them move toward a better solution:

$$w_{i,j}^{(1),\mathrm{new}}=w_{i,j}^{(1),old}-\mu \frac{\partial E}{\partial w_{i,j}^{(1)}}$$

(8)

$$w_j^{(2),\mathrm{new}}=w_j^{(2),old}-\mu \frac{\partial E}{\partial w_j^{(2)}}$$

(9)

where $\mu$ is the step parameter of the correction. The basic/standard backpropagation algorithm is employed for training. The detailed training procedure can be found in [32] (in Section 3.3 of this book) or traced back in [31]. We coded the programs by ourselves. The computer language is VBA which is embedded in Microsoft Excel^®.

In this study, the value of $\alpha$ is chosen as 1. The constant step parameter is employed. The value of $\mu$ is chosen as 0.02. It should be kept in mind that in Equations (5) and (6) the beginning numbers of $i$ and $j$ are both 1, but in Equations (8) and (9) the beginning numbers of $i$ and $j$ are both 0. Random numbers in the range of −1 to 1 are chosen as the initial values of the thresholds and the synaptic weights. Accordingly, the results will not be exactly the same in each training process. Even so, the tendency of convergence will be very similar.

4. The Results

There are 482 data in the database. We separate the database into two sets, the training set and the testing set, respectively. The training set includes 85% of the data. Therefore, the training set comprises 410 samples and the testing set comprises 72 samples. Samples included in the testing set are marked in the Appendix A.

Artificial neural networks with 3–12 neurons in the hidden layer are tested. More neurons in the hidden layer mean the ANN is more complicated so it can memorize more detailed features. However, it also means the result of the ANN has a tendency towards over-fitting. Furthermore, too many repetitions of the training iteration will also make the ANN memorize too many detailed features and perform poorly when it is in practical use. A time of iteration indicates all the synaptic weights and the thresholds are updated according to the error residual in the training set.

To help us detect whether over-fitting or over-training happens, both the root-mean-square errors of the training set and the testing are calculated after finishing each iteration. The values of the thresholds and the synaptic weights are also temporarily saved so we can come back to use them when we have selected a suitable ANN structure and have determined the proper iteration times. The root-mean-square error is defined as:

$$E_{r.m.s.}=\sqrt{ \overline{{\left({\eta }^{(d)}-{\eta }^{(o)}\right)}^2}}$$

(10)

where the overbar represents the average in the data set. Note that the numbers of samples in the two data sets are different.

Among all the training results, we chose the results of 3, 7, and 12 neurons in the hidden layer to demonstrate the features of over-fitting and over-training. They are shown in Figure 2. It can be observed that the root-mean-square error of the training set decreases as more iterations are processed, but it does not happen to the testing set. This demonstrates the effect of over-training. One can also find that setting more neurons in the ANN can help reduce the root-mean-square error of the training set. But the root-mean-square error of the testing set seems to not go the same way as more and more neurons in the hidden layer are comprised. This indicates that setting more neurons in the hidden layer tends to cause over-fitting. With the results shown in Figure 2, we suggest that setting 7 neurons in the hidden layer is sufficient for the ANN in this study. It is worth noting that the ANN in [16] has 14 neurons in the hidden layer.

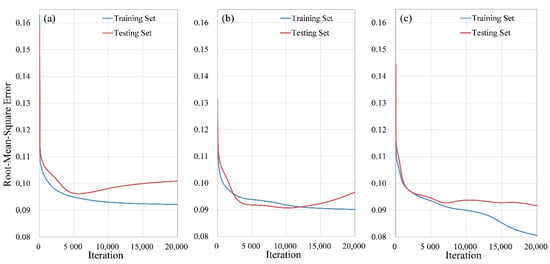
Figure 2. The result of the training: (a) 3 neurons in the hidden layer, (b) 7 neurons in the hidden layer, (c) 12 neurons in the hidden layer.

The thresholds and the synaptic weights of the 7-hidden-neuron ANN with 12,040 times of training iteration are used for further investigations. This is chosen for the reason that the root-mean-square errors of the training set and the testing set are equivalent to each other. The synaptic weights from the input layer to the hidden layer and the thresholds of the hidden neurons are listed in Table 2. The synaptic weights from the hidden layer to the output neuron and the threshold of the output neuron are shown in Table 3. With these thresholds and synaptic weights, the predicted outputs are calculated and compared with their desired values. The comparison is shown in Figure 3. It can be found that the results of the two data sets have similar divergence. That is because the root-mean-square errors of the two sets are very close. It is also worth noting that in [16] the result of such comparison looks very close to a central inclined line which represents the predicted are exact to their targets.

Table 2. The thresholds of the hidden neurons and the synaptic weights from the input layer to the hidden layer ($w_{i,j}^{(1)}$ ).

		i
		0	1	2	3	4	5	6	7
j	1	0.6144	0.8055	0.1110	0.8372	1.7008	−0.3427	0.6209	0.5749
	2	1.3936	1.0523	1.4664	0.1982	−0.4601	−0.5712	0.5264	3.1878
	3	0.5066	−1.7844	0.0736	−1.7298	−1.0940	0.0095	−0.9082	1.1462
	4	−1.3016	0.8221	1.3503	0.2557	0.0471	2.0145	−1.1131	1.5552
	5	−0.4564	0.0257	−1.7657	2.7258	−1.7268	−1.9379	0.2811	1.4361
	6	−0.0404	0.1909	1.1077	2.3484	−0.5073	2.2264	−0.1963	1.4299
	7	0.7199	−0.0957	0.2010	−0.1656	2.5119	−0.2500	0.0705	−0.1386

Table 3. The threshold of the output neuron and the synaptic weights from the hidden layer to the output neuron ($w_j^{(2)}$ ).

j
0	1	2	3	4	5	6	7
−1.0706	−0.2102	2.0741	2.3526	−1.2642	−1.3384	2.2950	−1.5356

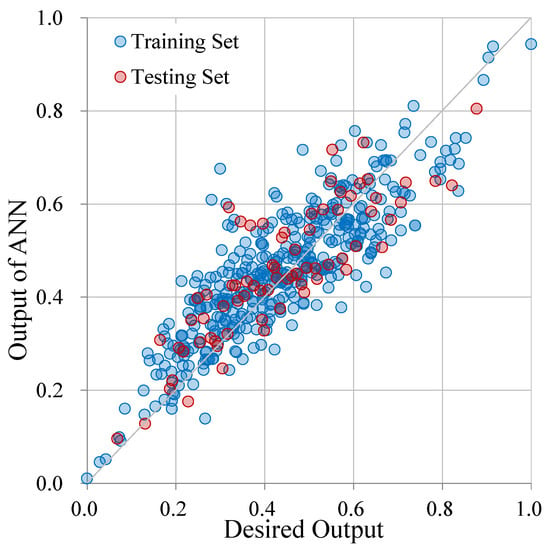
Figure 3. The comparison of the outputs of ANN with their target values in which the ANN has seven neurons in the hidden layer and is trained after 12,040 times of iteration.

After the number of neurons in the hidden layer and all the thresholds and synaptic weights are determined, we use our ANN to predict the compressive strengths of the 12 mix designs in [16] and compare the results with the data observed in their laboratory. The results are listed in Table 4. The predicted compressive strengths in [16] are also listed in the same table. The comparisons of the predicted and the actual compressive strengths are plotted in Figure 4. Note that the range shown in this figure is from 0 to 100 due to the range of the compressive strength in the database is from 5.66 to 95.3 MPa. It is found in Figure 4 that the circular dots are more focused to the central inclined line. This implies that our ANN model outperforms the ANN model of [16] in the verification.

Table 4. The predicted and actual compressive strengths of the experimental concrete mixtures in [16].

Ingredients (kg/m3)							Compressive Strength (MPa)
Water	Cement	Fine Aggregate	Coarse Aggregate	Blast Furnace Slag	Fly Ash	Super-Plasticizer	Actual	Predicted in Ref. [16]	Predicted by Present Model
194	223	669	1040	76	72	0.74	44.10	34.43	40.20
184	244	649	1104	105	19	0.79	47.99	32.26	42.87
187	194	650	1072	171	22	0.81	49.75	34.85	42.60
189	272	670	1040	121	14	0.70	52.87	35.60	47.14
191	346	549	1136	38	41	0.73	46.70	45.96	43.99
189	261	619	1072	93	57	0.88	47.06	39.04	45.78
204	331	457	1136	99	54	0.77	54.52	54.55	44.53
191	280	555	1104	121	46	0.68	47.61	50.16	46.91
210	300	535	1040	131	51	0.54	46.06	52.05	47.60
207	430	604	960	20	61	0.76	54.30	40.08	52.32
190	329	516	1104	112	52	0.87	54.98	55.07	50.83
208	351	554	960	52	121	0.72	55.13	40.91	52.00

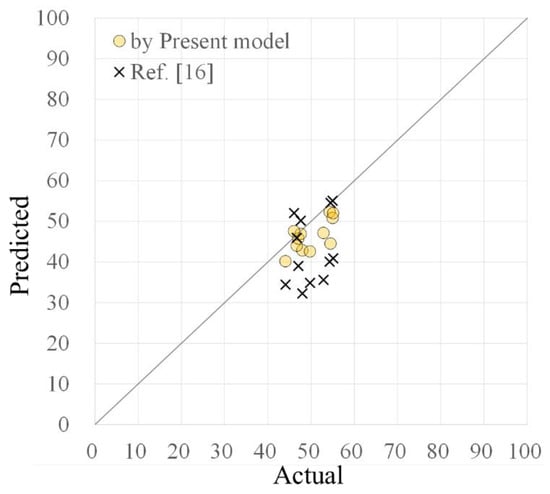
Figure 4. Comparison of predicted compressive strength with the actual strength of the 12 experimental concrete mixtures in [16] (Unit: MPa).

Now the results are no longer in the range of 0 to 1. We use the coefficient of efficiency ($C.E.$) to evaluate performance:

$$C.E.=1-E_{r.r.m.s.}^2$$

(11)

in which

$$E_{r.r.m.s.}=\sqrt{ {\displaystyle \sum {\left(y^{(p)}-y^{(a)}\right)}^2}/{\displaystyle \sum {\left(y^{(a)}\right)}^2}}$$

(12)

where $y^{(a)}$ is the actual compressive strength, $y^{(p)}$ is the predicted compressive strength, and $E_{r.r.m.s.}$ is the relative root-mean-square error. The $C.E.$ of the predicted results in [16] is 0.955. The high $C.E.$ means the predicted results in [2] are quite acceptable indeed. However, the $C.E.$ of the results predicted by the present model is 0.991. The improvement is significant for the relative root-mean-square error is reduced by 21.2% to 9.49%.

In [15], the artificial neural network and genetic programming were employed to predict the 28-day, 56-day, and 91-day compressive strengths of concrete admixing with fly ash or without fly ash. The proportions of 76 concrete mixes were listed as well as their compressive strengths. Forty-nine of them are admixed without fly ash while the other 27 are admixed with fly ash. Blast furnace slag and superplasticizer are not admixed in all of them. These data are good for further validation of our prediction model. The predicted results of [15] were not listed in their paper so a further comparison is unavailable.

With our model, the predicted compressive strengths of concrete are calculated and listed in Table 5. The comparisons of the predicted and the actual compressive strengths are plotted in Figure 5. In this figure, it can be found that the predicted compressive strengths of those without fly ash are rather close to the actual values. The $C.E.$ is 0.975. The relative root-mean-square error is 15.8%. Those mixes with fly ash are all slightly overpredicted. The $C.E.$ is 0.940. The relative root-mean-square error is 24.5%. The high $C.E.$ in both sets indicates that our prediction model really works at a good level. The predictions of non-fly ash mixes are more credible. We could expand the database for further improvement in the future.

Table 5. The predicted and actual compressive strengths of the experimental concrete mixtures in [15].

Ingredients (kg/m3)					Compressive Strength (MPa)		Ingredients (kg/m3)					Compressive Strength (MPa)
Water	Cement	Fine Aggregate	Coarse Aggregate	Fly Ash	Actual	Predicted	Water	Cement	Fine Aggregate	Coarse Aggregate	Fly Ash	Actual	Predicted
198.75	375.00	592.50	1143.75	0.00	36.84	37.51	191.25	425.00	463.25	1139.00	0.00	50.35	42.83
200.00	400.00	572.00	1128.00	0.00	43.13	39.88	189.00	450.00	441.00	1102.50	0.00	54.11	47.58
212.00	400.00	616.00	1196.00	0.00	38.58	34.23	198.75	375.00	551.25	903.75	0.00	37.3	50.61
199.75	425.00	544.00	1096.50	0.00	47.16	43.36	200.00	400.00	528.00	884.00	0.00	44.04	54.08
208.25	425.00	590.75	1177.25	0.00	45.05	37.44	212.00	400.00	576.00	944.00	0.00	39.61	45.73
198.00	450.00	513.00	1057.50	0.00	49.63	47.81	199.75	425.00	505.75	862.75	0.00	47.37	58.13
211.50	450.00	562.50	1143.00	0.00	47.42	39.59	208.25	425.00	548.25	926.50	0.00	44.69	50.23
199.50	475.00	498.75	1040.25	0.00	54.01	50.01	198.00	450.00	481.50	837.00	0.00	50.93	63.16
209.00	475.00	565.25	1168.50	0.00	50.05	40.59	211.50	450.00	526.50	900.00	0.00	48.08	52.86
198.75	375.00	592.50	1143.75	0.00	37.81	37.51	199.50	475.00	451.25	798.00	0.00	54.14	68.13
200.00	400.00	572.00	1128.00	0.00	44.11	39.88	209.00	475.00	503.50	874.00	0.00	51.31	57.50
212.00	400.00	616.00	1196.00	0.00	40.9	34.23	180.00	400.00	440.00	1080.00	60.00	39.04	48.88
199.75	425.00	544.00	1096.50	0.00	47.51	43.36	178.50	425.00	416.50	1045.50	63.75	45.09	53.70
208.25	425.00	590.75	1177.25	0.00	45.3	37.44	191.25	425.00	463.25	1139.00	63.75	41.14	44.16
216.75	425.00	641.75	1253.75	0.00	42.54	33.08	199.75	425.00	544.00	1096.50	63.75	38.35	45.00
198.00	450.00	513.00	1057.50	0.00	52.03	47.81	189.00	450.00	441.00	1102.50	67.50	46.13	48.59
211.50	450.00	562.50	1143.00	0.00	48.74	39.59	198.00	450.00	513.00	1057.50	67.50	42.5	49.15
220.50	450.00	616.50	1228.50	0.00	46.59	34.47	211.50	450.00	562.50	1143.00	67.50	39.58	41.91
199.50	475.00	498.75	1040.25	0.00	54.49	50.01	199.50	475.00	498.75	1040.25	71.25	47.34	51.29
209.00	475.00	565.25	1168.50	0.00	53.06	40.59	209.00	475.00	565.25	1168.50	71.25	43.55	43.09
218.50	475.00	584.25	1192.25	0.00	49.18	37.41	191.25	425.00	463.25	1139.00	63.75	42.01	44.16
221.00	425.00	607.75	858.50	0.00	40.02	48.94	199.75	425.00	544.00	1096.50	63.75	38.85	45.00
220.50	450.00	580.50	837.00	0.00	45.25	52.77	189.00	450.00	441.00	1102.50	67.50	47.25	48.59
229.50	450.00	175.95	855.00	0.00	42.68	49.07	198.00	450.00	513.00	1057.50	67.50	43.09	49.15
218.50	475.00	555.75	817.00	0.00	48.67	56.97	211.50	450.00	562.50	1143.00	67.50	40.26	41.91
228.00	475.00	598.50	869.25	0.00	45.52	49.91	220.50	450.00	616.50	1228.50	67.50	37.15	37.48
178.50	350.00	486.50	1141.00	0.00	39.52	40.43	199.50	475.00	498.75	1040.25	71.25	48.41	51.29
189.00	350.00	521.50	1197.00	0.00	31.66	34.46	209.00	475.00	565.25	1168.50	71.25	44.02	43.09
180.00	375.00	468.75	1121.25	0.00	42.73	43.49	218.50	475.00	584.25	1192.25	71.25	40.73	40.26
191.25	375.00	506.25	1196.25	0.00	40.69	35.95	199.75	425.00	505.75	862.75	63.75	38.9	58.24
180.00	400.00	440.00	1080.00	0.00	47.99	48.40	198.00	450.00	481.50	837.00	67.50	43.22	62.94
192.00	400.00	484.00	1168.00	0.00	44.89	39.14	211.50	450.00	526.50	900.00	67.50	39.85	53.71
178.50	425.00	416.50	1049.75	0.00	51.25	53.24	220.50	450.00	580.50	837.00	67.50	36.87	53.69
191.25	425.00	463.25	1139.00	0.00	49.05	42.83	229.50	450.00	625.50	891.00	67.50	35.23	47.81
189.00	450.00	441.00	1102.50	0.00	53.69	47.58	199.50	475.00	451.25	798.00	71.25	47.94	67.52
189.00	350.00	521.50	1197.00	0.00	36.64	34.46	209.00	475.00	503.50	874.00	71.25	43.87	58.03
191.25	375.00	506.25	1196.25	0.00	41.57	35.95	218.50	475.00	555.75	817.00	71.25	40.34	57.64
192.00	400.00	484.00	1168.00	0.00	46.22	39.14	228.00	475.00	598.50	869.25	71.25	37.65	51.32

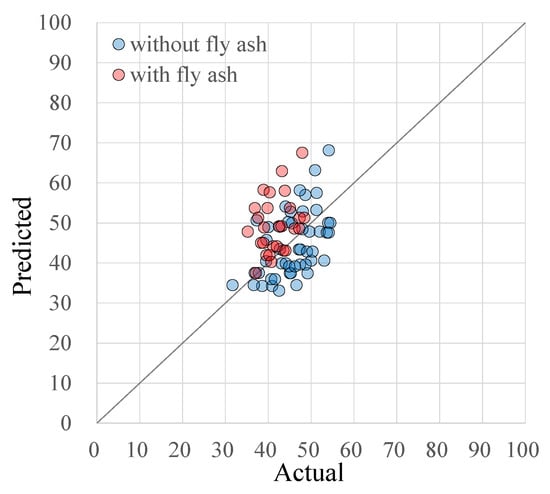
Figure 5. Comparison of predicted compressive strength with the actual strength of the 76 experimental concrete mixtures in [15] (Unit: MPa).

5. Conclusions

In this study, the database of real concrete mix proportioning listed in [12] is used to establish an ANN prediction model for the concrete compressive strength. The ANN structure chosen in this study is the Back Propagation network with 1 hidden layer. The same database was also used in [16], and the number of hidden layers in the ANN is also the same. The database is divided into two sets, the training set and the testing set, respectively. In comparison with [16], we use fewer data for testing and more data for testing. The testing set comprises 15% of the data while in [16] it was just 4%. Considering the possible effect of over-fitting, the number of neurons in the hidden layer is finally chosen as 7, which is half the number used in [16]. The present ANN model outperforms the model in [16] in the verification in which we compare the predicted results with the experimental data. For corroborating that our model performs well in further practical use, we use experimental data from [15] for validation. A good agreement has also been found.

The synaptic weights and the thresholds are all listed in this article. With these numbers and using Equations (1)–(6), anyone can predict the compressive strength of concrete according to the concrete mix proportioning on his/her own.