Fast Calculation of Transient Thermal Stress in Surge Lines with Thermal Stratification Region

Abstract

Nuclear power plants applying for license renewal are required to undertake a fatigue assessment of various components, which demands the fast calculation of transient thermal stress of the fatigue-sensitive components such as surge lines. In this study, the strategy of Green’s function database construction for the thermal stratification region was investigated, and the thermal stress calculation was shown to be more accurate by dividing the flow cases and thermal zones. Furthermore, a method to determine the fluid temperature for the thermal zones of the thermal stratification region was studied. In addition to the temperature of the hot leg fluid and the outlet fluid from the pressurizer, seven thermocouples installed on the outside wall in the thermal stratification region were used to determine the fluid temperature of thermal zones with stratification, and the calculation result of the fluid temperature was verified with the temperature Green’s functions.

1. Introduction

Nuclear power has many advantages such as strong power generation capacity, mature technology and cleanliness. According to the report of the International Atomic Energy Agency, by the end of 2018, there were 450 nuclear reactors in service worldwide. For nuclear power plants that have already reached the end of their service lives, the Member States of the International Atomic Energy Agency are likely to give priority to license renewal projects.

Thermal fatigue is regarded as an important damage mechanism in nuclear power plants [1], and the fast calculation of transient thermal stress is a key part of the process of license renewal for nuclear power plants. In order to perform fatigue assessment on nuclear power plants, several fatigue monitoring systems have been developed. In 1986, the Electric Power Research Institute (EPRI, U.S.) developed FatiguePro software. Electricite De France (EDF) has many years of experience in the development of FatigueMeter, which is an online fatigue monitoring system [2,3]. In 1995, EDF designed the SYSFAC (System de Surveillance en Fatigue de la Chaudiere) fatigue monitoring system [4]. In South Korea, the KFAMS project, developed by KAERI, was installed in the YGN-1 nuclear power plant in order to monitor the fatigue of the pressurizer surge line caused by thermal stratification. A FAMS fatigue monitoring system was also developed in Japan. This monitoring system is based on measuring temperatures by thermocouples at seven dangerous locations, applying the Green’s function method, and assuming the convective heat transfer coefficient in order to achieve fast calculation of thermal stress [5].

An extensive investigation performed for the Paks Nuclear Power Plant resulted in a list of the primary pipes that might be affected. These are as follows: the primary loops, the pressurizer surge line, the pressurizer spray system, the feed water pipe of the steam generator and the auxiliary emergency feed water connection into the steam generator [6]. The surge line studied in this paper, connects the lower head of the pressurizer and the hot leg, which enables the fluid in the primary circuit to exchange with the fluid in the pressurizer. The thermal stratification phenomenon is obvious in surges line. When two fluids with different densities flow in the pipeline, a stratified flow phenomenon may occur. If the density difference is caused by the fluid temperature, thermal stratification may occur, which can cause huge bending stress. The causes of thermal fatigue in the surge line are thermal stratification and thermal shock oscillation. The temperature of the fluid from the pressurizer is high, and the temperature of the fluid from the hot leg is low. Because of the difference in density of the cold and hot fluid, stratification occurs in the surge line when the surge flow is relatively low [7]. In May 1988, researchers discovered that the pressurizer surge line of the power plant had shifted and deformed beyond design at the Troy Power Station of the Portland Power Company in the United States. After investigation and research, it was proved that this was caused by thermal stratification in the surge line. Then, the Nuclear Regulatory Commission issued Bulletin No.88-11, which decreed that all pressurized water reactor (PWR) nuclear plants owners should verify the integrity of the surge line of the pressurizer [8]. More than 12 cracks have been identified since 1979, as a result of thermal stratification, and cracks due to thermal stratification were found in French nuclear power plants as well. Hungary installed a large-scale program at its only nuclear power plant, the Paks Nuclear Power Plant. Boros and Aszódi conducted a finite element simulation analysis on the surge line, and the result showed that the phenomenon of thermal stratification existed symmetrically in the surge line [9], and the maximum temperature difference of the measuring points can reach 130–140 °C.

In order to avoid the occurrence of thermal stratification, French experts optimized the surge line’s structure. In CATTENOM Nuclear Power Plant Unit 1, the inclination angle of the surge line and the hot section joint of the hot leg was designed to be 45° to reduce the stratification of cold and hot fluids in the radial direction, caused by the density difference between hot and cold fluids [9].

For nuclear power plants that have already been built, fatigue monitoring of the surge line is required. As a key part of fatigue monitoring project, fast calculation of thermal stress has been studied for many years and there are many methods for doing this. For example, the BOSSES system in India uses the online finite element method, but this method requires a lot of computing resources [10]. At present, Green’s function method is the most widely used and generally recognized method. In order to evaluate the fatigue life of the pressurizer, Chang established the overall three-dimensional complex geometric model of the pressurizer, using Green’s function method, and compared the results of Green’s Function Method (GFM) to the results of 3D finite element analysis to illustrate the effectiveness of this method [11]. Song used the Green’s function method in the fatigue analysis calculation of the turbine rotor [12]. The calculation of thermal stress by Green’s function method is based on the calculation results of the temperature field, which is highly dependent on thermal boundaries for thermal zones. Boo used the method of Green’s function to calculate the fluid temperature in the pipe according to the change in the temperature of the fluid at the inlet of the branch pipe, but if the surge line is much longer and the stratification region is very large, this method is not very suitable [13]. There is no clear solution for determining the thermal zone boundary to obtain the reality of the temperature field. In this paper, we focus on a methodology to solve the thermal zone boundary problem when we calculate the transient thermal stress of the surge line with Green’s function method.

2. Theoretical Background

Green’s function method is a method used to solve in-homogeneous differential equations with boundary conditions or initial conditions. The sub-equation can be regarded as the mathematical relationship between the specific “field” and the “source” that causes the specific field. In the fast calculation of the thermal stress of the surge line, the temperature field of the fluid in the surge line causes the thermal stress change in the surge line, so the temperature field of the fluid in the surge line is the “source”, and the thermal stress is the “field”. When the overall temperature on the thermal boundary area of any plant components and equipment changes with time, the temperature distribution depends on the temperature distribution state of the previous time. Additionally, the temperature distributions on them are determined by the state of the temperature distribution of a previous time.

The thermal stress at any point in time can be obtained through the temperature distribution. The heat transfer equation in a component under the boundary conditions of heat convection and heat conduction is:

$$K\frac{\partial }{\partial n}T\left(n\right)+CT\left(t\right)=\phi (t)$$

(1)

where T(t) and φ(t) are the component temperature and the fluid temperature at time t, respectively, n is the normal direction at the boundary, and K and C are the functions of heat conduction and heat convection.

Using Green’s function, the transient temperature distribution can be expressed in the form of Duhamel integral as

$$T\left(t\right)={\displaystyle {\int }_0^{t}X(t-\tau )}\frac{\partial }{\tau }\phi (\tau )d\tau$$

(2)

where X(t − τ) is the temperature Green’s function.

For the temperature change history at any time, it can be discretized into a series of temperature change points. Each temperature change point causes the response of thermal stress. According to the principle of linear elastic stress superposition, the stress change with time can be calculated. The Green’s function method calculates the thermal stress through volume integral operation. The thermal stress at time t is as follows:

$$\sigma (t)={\displaystyle {\int }_0^{t}g(t}-\tau )\frac{\partial }{\partial \tau }\phi (\tau )d\tau$$

(3)

$$\sigma \left(t\right)=g_0(\phi (t)-T_{ref})+{\displaystyle \sum _{t-t_d}^{t}g(t)\Delta \phi (\tau )}$$

(4)

where $g_0=\underset{t\to \infty }{\lim }g(t)$ s the steady-state value during transient changes, t_d is the decay period of Green’s function, which is required for the steady state of the transient process area, T_ref is the reference temperature for structural stress calculation at which the structure is in a state of zero thermal stress, g(t) is the thermal stress at time t, g(t) is the unit Green’s function value at the elapsed time t, φ(t) and Δφ(t) are the fluid temperature and temperature change value at time t, respectively.

3. Fast Calculation of Thermal Stress Based on Green’s Function Method

3.1. Finite Model

The model of the surge line is shown in Figure 1. The length of the hot leg in the model is 736.6 mm (much longer than the edge stress decay length). The inner and outer diameter of the hot leg are 736.6 mm and 870.6 mm, respectively. The inner and outer diameter of the surge line are 284.2 mm and 355.6 mm, respectively. The length of the surge line is about 21.70 m.

Figure 1. The 3-D model of the surge line.

Solid 185 element was used to mesh the surge line and there were 302,880 elements in the finite element model as shown in Figure 2.

Figure 2. The finite element model of the surge line. (a) Ends of the hot leg. (b) The pressurizer end.

The two ends of the pressurizer surge line were connected to the hot leg and the bottom nozzle of the pressurizer, respectively. So, one end of the hot leg was limited in the axial and circumferential direction, another end was only limited in the circumferential direction. The end-to-connect pressurizer bottom nozzle was limited in both the axial and circumferential direction. The constraints are also illustrated in Figure 3. The establishment of Green’s function is the same as the constraints imposed by finite element verification, and the constraints are applicable to all working conditions.

Figure 3. The finite element model of the surge line and the constraints. (a) Ends of the hot leg. (b) The pressurizer end.

3.2. Division of Thermal Zones and Working Conditions

In order to divide thermal zones, computational fluid dynamics (CFD) simulation was performed for a start-up condition of the surge line with transient analysis by using Ansys Fluent. The flow rate in the hot leg is 15.5 m/s, and the temperature of the fluid in the hot leg is 290 °C. The flow rate from the pressurizer is 0.05 m/s, and the temperature of the fluid in the pressurizer is 330 °C. After the calculation result reaches stable, the thermal stratification is very significant in the horizontal pipe section, as shown in Figure 4. The turbulent penetration phenomenon exists in the hot leg end. In this region, the streamline presents swirling flow, and there is no significant difference between the temperature of the top and bottom fluids. Figure 5 shows the temperature of the top and bottom fluid at different positions of the straight pipe section near the hot leg. When the distance from the inlet of the branch pipe is less than 1200 mm, the temperature difference is small, which indicates swirling flow with penetration. When the distance is more than 1200 mm, the temperature difference quickly gets larger, which indicates that the turbulent penetration phenomenon disappears. So the length of the turbulent penetration is about 1200 mm. As for the vertical pipe section, there is little difference in the temperature of the fluid in the pipe.

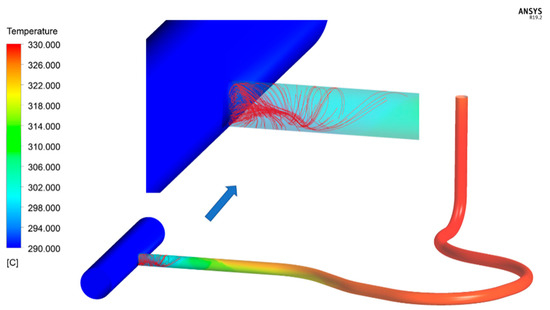
Figure 4. The streamline of the turbulent penetration region.

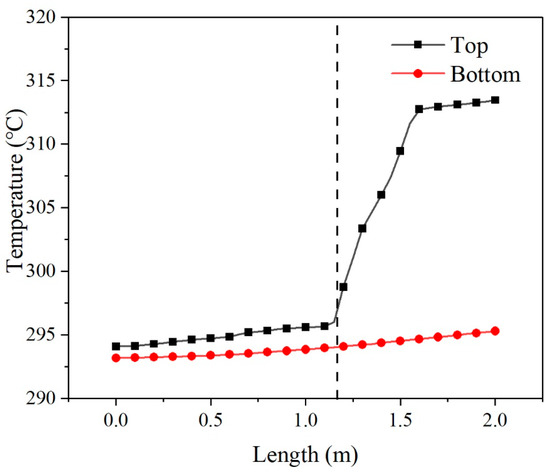
Figure 5. The temperature of the top and bottom fluid changes with the distance from the hot leg.

According to the CFD simulation results, the entire flow field can be divided into the following parts: the hot leg, the turbulent penetration region, the thermal stratification region, and the vertical pipe region.

As the fluid temperature in the hot leg and vertical pipe stays almost constant, one thermal zone can be assigned for each region, namely, zone 1 for hot leg and zone 10 for the vertical pipe section. The turbulent penetration region and the nozzle are divided into two zones, named zone 2 and 3. They generally have the same heat transfer boundary, but thermal zone 2 (the upper half) and thermal zone 3 (the lower half) can employ different heat transfer boundaries for large surge flow rates, in which turbulent penetration may be suppressed. The turbulent penetration length can also be calculated by Equation (5), and the empirical Equations (6) and (7) are based on the test data [14].

$$\frac{{\overline{x}}_m}{D}=\frac{L_{\mathsf{\Omega }}}{D}\left[{\left(\frac{\frac{{\mathsf{\Omega }}_{0}D}{2U}}{\xi \frac{U_{srg}}{U}}\right)}^{1/\beta }-1\right]\pm 1$$

(5)

$$\frac{{\mathsf{\Omega }}_{0}D}{2U}=0.63\left(\frac{D}{D_R}\right)$$

(6)

$$\frac{L_{\mathsf{\Omega }}}{D}=3.2$$

(7)

where ${\overline{x}}_m$ is the length of turbulent flow penetration, Ω₀ is the entry swirl, D is the inner diameter of the surge line, U is the average velocity, D_R is the inner diameter of the hot leg, U_srg is the average flow velocity of the surge line, ξ is taken as 6 for the horizontal pipe section, and β is taken as 1.4 by experience. The term “±1” in Equation (5) accounts for the uncertainty in model predictions that is ±1 diameter corresponding, to a 95% confidence limit. The calculated turbulent penetration length ranges from 1095–1665 mm (about 10D_srg), which is similar to the CFD result.

When the thermal stratification phenomenon exists, the fluid temperature difference in different locations is very large. In dividing the thermal zone of the thermal stratification region, some experts divide the thermal stratification region into two thermal zones, and the temperature of the upper zone is taken as the temperature of the fluid from the pressurizer, and the temperature of the lower zone is taken as the temperature of the fluid from the hot leg.

However, this kind of division of thermal zones is too simple to describe the temperature field of thermal stratification, and the error in the temperature field will cause large errors in the calculation of thermal stress. Therefore, a much more accurate description of the thermal zone is needed. Referring to the thermal stratification monitoring work for the surge line of the Paks Nuclear Power Plant [9], seven thermocouples were installed on the outer wall of the surge line. In order to accurately describe the fluid temperature in the thermal stratification region, all temperatures at the seven measuring points were used to divide the thermal stratification region into six thermal zones, which were named zone 4–9. The division of the thermal zone of the surge line is shown in Figure 6.

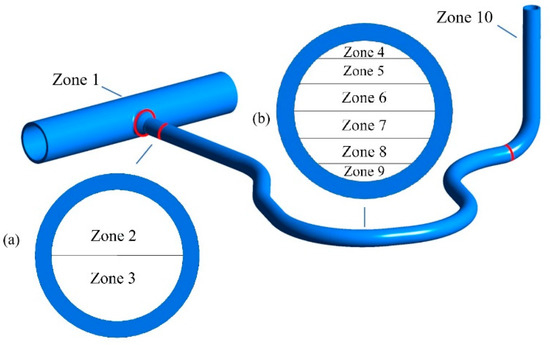
Figure 6. The division of thermal zones of the surge line. (a) Turbulent penetration region. (b) Thermal stratification region.

During the operation of a nuclear power plant, the working conditions are very complicated. The stratification state and thermal hydraulic parameters in the surge line are different under different working conditions. Based on the power plant operation experience, seven flow cases were set according to the presence or absence of thermal stratification, the flow rates of the hot leg and the outlet of the pressurizer. Among the seven flow cases, case 3 is a start-up condition, and the thermal stratification phenomenon is most obvious under this flow case. Cases 6 and 7 are accident conditions, which correspond to the power off of the main pump and the low flow rate in the hot leg. Generally, such an accident occurs when the hot leg flow rate drops below one-tenth of the rated rate Q_n. The judgments and description of every flow cases is shown in Table 1.

Table 1. Typical flow cases of the pressurizer surge line.

Flow Case	Judgments	Description
Case 1	Qhl = 100%Qn Abs(Qsrg) ≥ Q1 *	Main pump running at full power Surge out with large flow Without thermal stratification
Case 2	Qhl = 100%Qn Abs(Qsrg) < Q1 Thl > T1	Main pump running at full power Surge in (out) with small flow With thermal stratification
Case 3	Qhl = 100%Qn Abs(Qsrg) < Q1 Thl < T1 *	Main pump running at full power Surge in (out) with small flow With thermal stratification
Case 4	Qhl = 100%Qn Abs(Qsrg) >Q1	Main pump running at full power Surge in with large flow Without thermal stratification
Case 5	Qhl = 100%Qn Abs(Qsrg) > Q2 *	Main pump running at full power Surge in with very large flow Without thermal stratification
Case 6	Qhl < 10%Qn Abs(Qsrg) > Q1	No flow in the hot leg Surge in with large flow Without thermal stratification
Case 7	Qhl < 10%Qn Abs(Qsrg) < Q1	No flow in the hot leg Surge in with small flow Without thermal stratification

* Q₁ is the critical flow rate for thermal stratification. When the flow rate is less than Q₁, thermal stratification phenomenon occurs. Q₂ is the critical value of large surge flow and super surge flow. When the flow rate is greater than Q₁, the convection heat transfer method is forced convection heat transfer. T₁ is the critical temperature of the fluid in the hot leg when the reactor reaches normal operation.

When determining the wall–fluid convective heat transfer coefficient of each thermal zone, the fluid temperature and flow rate should be considered. When the flow rate is low, it is natural convective heat transfer controlled. When the flow rate is high enough, it is forced convective heat transfer controlled. In the turbulent penetration region, spiral convective heat transfer should be more suitable. So, convective heat transfer coefficients should be determined carefully with suitable empirical equations and thermal hydraulic parameters [15].

In this paper, the start-up condition (case 3) is taken as an example, and the calculation results of the convective heat transfer coefficient of each hot zone under this condition is shown in Table 2.

Table 2. The heat transfer coefficient of flow case 3.

Thermal Zone	Heat Transfer Type	Heat Transfer Coefficient (W/m2·°C)
Zone 1	forced convective heat transfer	38,617
Zone 2, 3	spiral convective heat transfer	4700
Zone 4–9	natural convective heat transfer	1000
Zone 10	forced convective heat transfer	35,303

3.3. The Establishment of Thermal Stress Green’s Function

3.3.1. Material Properties

Thermal stress Green’s function is generally obtained by applying a certain step temperature on each thermal zone. However, the physical parameters of metal materials are greatly affected by temperature. Koo and Kwon [16] confirmed that the temperature characteristics of materials have a significant influence on the maximum peak stress, and the temperature dependence of material properties affects the maximum stress range for fatigue evaluation; they used the weighting function method to make the Green’s function method more accurate. Therefore, it is necessary to consider this effect when using the Green’s function method to monitor the fatigue damage of the actual operating conditions of nuclear power plants. Therefore the temperature-dependent material properties were defined in the current study. The surge line and the connected hot leg are Z3CND20.09M and Z2CND17.12, respectively, and the material properties were taken from RCC-M specifications, as shown in Figure 7. The Poisson’s ratio is taken as a constant of 0.3, and the density is taken as a constant of 7930 kg/m³, and the fluid physical parameters change with temperature, as shown in Figure 8.

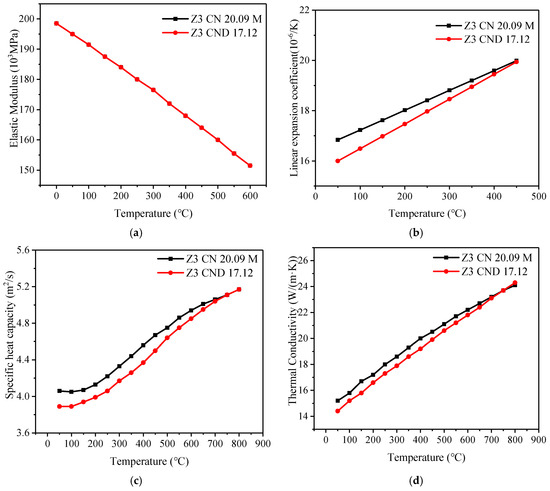
Figure 7. Material parameters at different temperatures. (a) Elastic modulus. (b) Linear expansion coefficient. (c) Thermal conductivity, (d) Specific heat capacity.

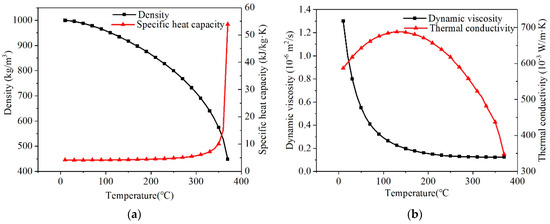
Figure 8. Material parameters of water at different temperatures. (a) Density. (b) Dynamic viscosity.

3.3.2. Selection of Fatigue Evaluation Sections and Paths

FRAMATOME’s research on the surge line of a 900 MW pressurized water reactor nuclear power plant revealed that the elbow of the vertical pipe section is the position most prone to thermal fatigue [10]. In addition, large thermal stress is likely to occur at the butt-weld of the hot leg nozzle. So, these two sections were set as monitoring sections, as shown in Figure 9, and named Section A and Section B, respectively.

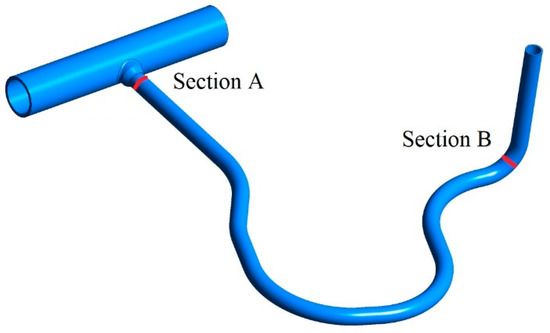
Figure 9. The location of the fatigue evaluation sections.

In order to determine the analysis path, 36 paths are set every 10° in the monitoring sections, as shown in Figure 10, and named Path 0 to Path 350.

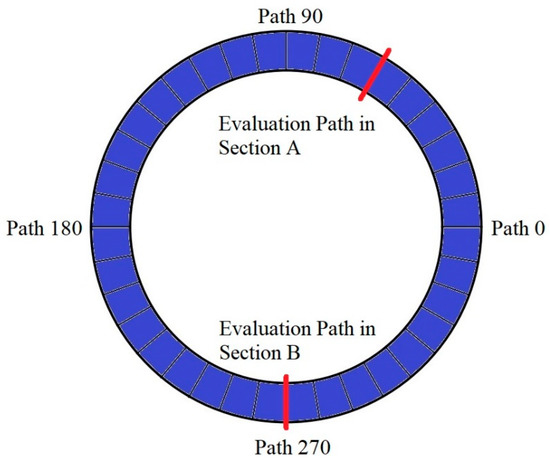
Figure 10. The paths in the monitoring sections.

In monitoring Section A, the maximum stress occurs in Path 60, and in Section B, the maximum stress occurs in Path 270, as shown in Figure 11. So, Path A-60 was set as the evaluation path of Section A, and Path B-270 was set as the evaluation path of Section B.

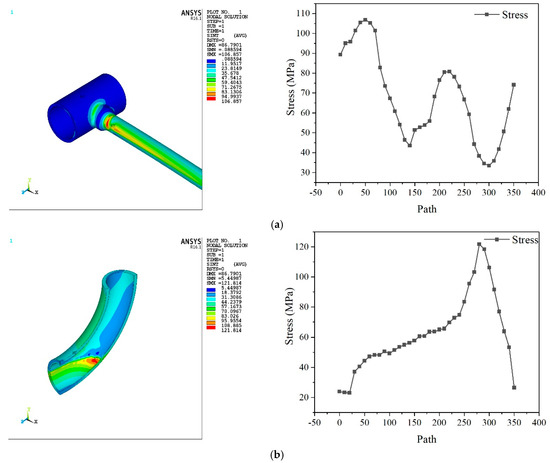
Figure 11. Stress distribution in Section A and B. (a) Section A. (b) Section B.

3.3.3. Strategy to Construct Thermal Stress Green’s Functions

Thermal stress Green’s functions should be worked out for every fatigue evaluation section and path with respect to the step temperature loading and convective heat transfer coefficient of every thermal zone. Thermal stress Green’s functions may be shared if convective heat transfer coefficients are identical for different flow cases. Generally, thermal stress Green’s functions have a huge database, covering every flow case.

For example, we assumed 20 °C as the zero-thermal stress temperature of the structure and a uniform temperature of 20 °C in all thermal zones as the beginning of the transient thermal analysis. A step temperature of 320 °C was applied as the fluid bulk temperature only in the appointed thermal zone 4 with a specified convective heat transfer coefficient corresponding to flow case 3. Then, 6000 s was used to obtain a stable state for the temperature response, which is illustrated in Figure 12, for the outside point of the evaluation paths in the two sections. The temperature response data is the temperature Green’s function of each thermal zone under each working condition.

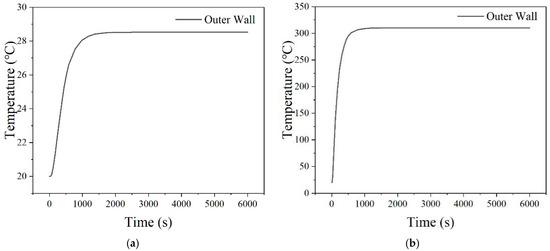
Figure 12. Temperature response of the outside point of the evaluation paths. (a) Section A. (b) Section B.

Then, elastic thermal stress can be calculated by reading the transient thermal analysis results. The time length of Green’s function is 6000 s, and the Green’s functions of the evaluation paths are shown in Figure 13. It is clear that all directional stresses and S_int remain stable after 2000 s. This reveals that 6000 s is quite enough to obtain the stable state of the step response. So the time length of Green’s functions, which is the set decay time, is much larger than the actual decay period, and this means the time length of Green’s function is reasonable.

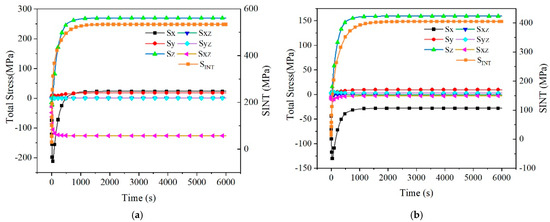
Figure 13. Transient thermal stress (total stress and S_int) response of evaluation paths based on FEM. (a) Section A-60 (b) Section B-270.

The obtained stress response needs to be normalized to get Green’s function datum. The Green’s function of each thermal zone is denoted as G_ij, where the subscript i varies from 1 to 10, corresponding to 10 thermal zones, and j varies from 1 to 7, corresponding to seven different flow cases. The steady-state value of each Green’s function is recorded as G_0,ij, and the transient-state value is G_ij − G_0,ij, where i and j have the same meaning as the subscript of Green’s function, and g_0,ij and g_ij represent the steady-state and transient values of Green’s function after normalization, respectively

$$g_{0,ij}=G_{0,ij}/\Delta T$$

(8)

$$g_{ij}=(G_{ij}-G_{0,ij})/\Delta T$$

(9)

The equation for calculating the thermal stress of the evaluation path using Green’s function is as follows. φ_i(t) is the fluid temperature of thermal zone i, and T_ref is the fluid temperature at time 0, n is the number of thermal zones, and S is the thermal stress of the evaluation path.

$$S={\displaystyle \sum _{i=1}^n(g_{0,ij}·({\phi }_i(t)-T_{ref})+{\displaystyle \sum _{t-t_d}^t{g}_{ij}\Delta \phi (t))}}$$

(10)

3.3.4. Verification of the Green’s Function

In this paper, a working condition was designed in order to verify the accuracy of the Green’s function. The temperature change in each thermal zone with time in the designed condition is shown in Figure 14.

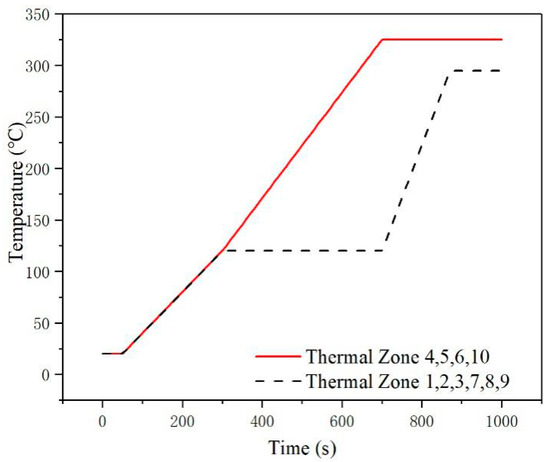
Figure 14. Temperature of each thermal zone in the designed condition.

We used the established Green’s function of each thermal zone to perform convolution calculation with the temperature–time change of each thermal zone, and added the stress calculation results for each thermal zone to obtain the stress change with time under this working condition. The stress calculation result of Green’s function method was compared with the stress result calculated by finite element calculation software, and the results are shown in Figure 15. Comparing the calculation result of Green’s function method with the calculation result of finite element method, the error of the maximum stress value was 3.451%.

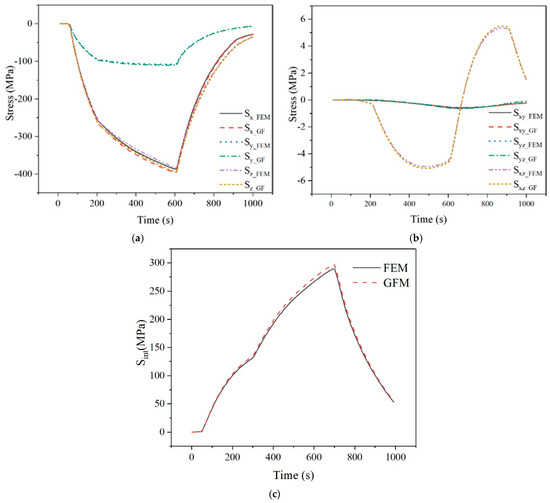
Figure 15. The comparison between Green’s function method(GFM) and Finite element method(FEM). (a) Normal stress. (b) Shear stress. (c) Stress intensity.

The difference in the step temperature load applied to the thermal zone will cause fluctuations in the results after the normalization of the Green’s function. In order to reduce the relative error of the comparison between the Green’s function and the finite element calculation result, it is necessary to adjust the step temperature load applied to the different thermal zones. The step temperature was set to 100 °C, 200 °C, 300 °C, 400 °C, 500 °C and 1000 °C, respectively, to find the optimal one.

The S_int curves of the Green’s function method and the finite element result at different step temperatures are compared in Figure 16. The relative errors of the maximum stress between the Green’s function method calculation result and the finite element calculation result at different step temperatures are shown in Figure 17.

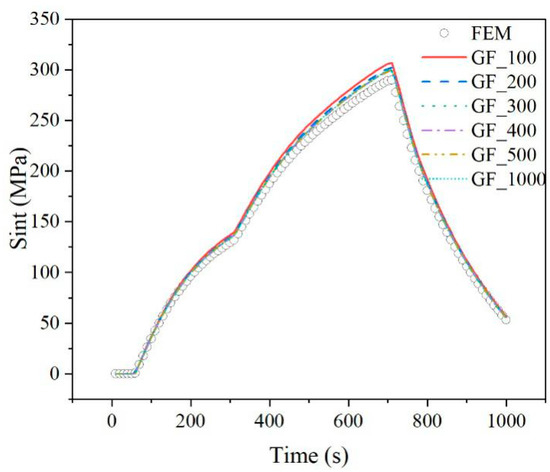
Figure 16. Comparison of Green’s function and finite element calculation results.

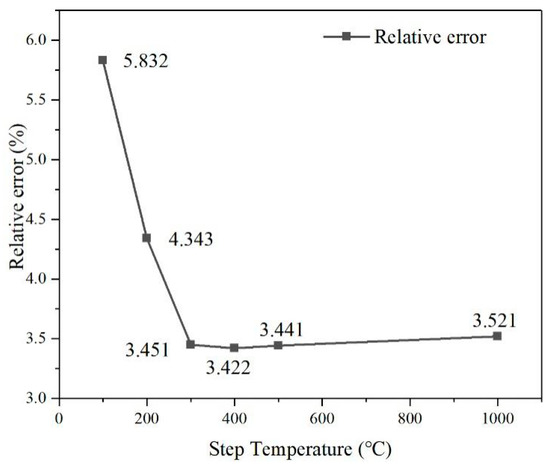
Figure 17. Relative error as a function of step temperature.

It can be seen from Figure 17 that step temperatures above 300 °C yield small relative error. A step temperature of 400 °C gives the smallest relative error of 3.422%.

From the above analysis, it was found that the Green’s functions can yield transient thermal stress in quite good agreement with that calculated directly by FEM. However, we cannot say for sure that the method provides the real transient thermal stress. The shortcoming is the assuming fluid temperatures for thermal zones especially in stratification region, which has not given any evidence to close the problem. As factory datum are generally available for hot leg fluid and outlet fluid from the pressurizer, temperatures for thermal zones 1, 2, 3, and 10 may be easily determined. With large surge out or in flow case, temperatures in zone 4–9 can also be taken as the temperature of the fluid from the hot leg or outlet fluid from the pressurizer. So, we focused on the determination of the fluid temperature for thermal zones 4–9 when stratification occurs.

4. Determination of Fluid Temperatures of Thermal Zones in Stratification Region

Green’s function method to calculate thermal stress is based on the temperature field solution, both of which are unique and dependent upon the particular initial and boundary conditions of the problem. The accuracy of the fluid temperature field calculation is directly related to the accuracy of the rapid thermal stress calculation. However, it is difficult to directly measure the temperature field of the fluid in the pipe with stratification. A practical method is to monitor the outer wall temperature in the stratification region. If we can develop a methodology to determine the fluid temperature for each thermal zone in the stratification region with the measured data, and the responses of the determined fluid temperatures agree with the measured outer wall temperatures, this can, to some extent, solve the problem of calculating transient thermal stress with Green’s function method.

4.1. Monitoring Temperature Analysis

Based on previous installation experience, thermocouples were installed at four locations in a power plant in order to monitor thermal stratification. The installation positions are shown in Figure 18. There are four thermocouples with an interval of 90° for monitoring Section 1, as shown in Figure 18a, named as monitoring point 11 to monitoring point 14. Seven temperature monitoring points are set on the remaining monitoring sections, and the distribution of the monitoring points is shown in Figure 18b. The monitoring points on monitoring Section 2 are named as monitoring point 21 to 27 from top to bottom. Similarly, the monitoring points on monitoring Section 3 and 4 are named as monitoring point 31 to 37 and monitoring point 41 to 47, respectively.

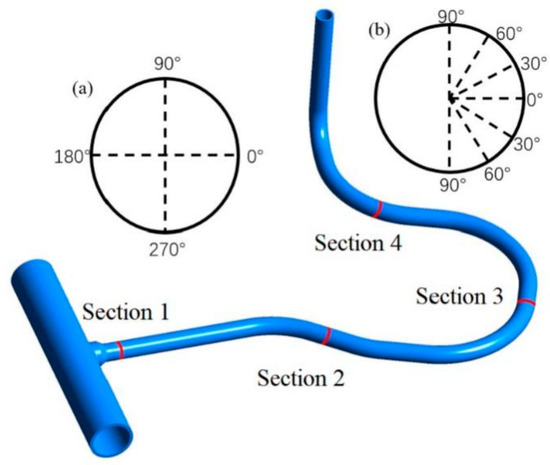
Figure 18. Position of the monitoring points. (a) Section 1. (b) Sections 2–4.

The most obvious thermal stratification exists in the start-up conditions, so the start-up condition was selected as the analysis condition in this paper. The temperature changes in the fluid in the pressurizer and the fluid in the hot leg in this working condition are shown in Figure 19. This working condition was divided into three time spans called span A, span B, and span C, which are 0–70,000 s, 70,000–13,000 s and 130,000–280,000 s, respectively. There is no temperature difference between the fluids in the two parts in time span A. Time span B corresponds to the process of establishing the gas cavity in the pressurizer. During this time span, the temperature of the fluid in the hot leg gradually increases, and the temperature gap of the fluid in the two different components begins to occur and gradually increase. In time span C, the temperature of the fluid from the pressurizer and the hot leg is stable, which indicates that the reactor has entered a stage of stable operation.

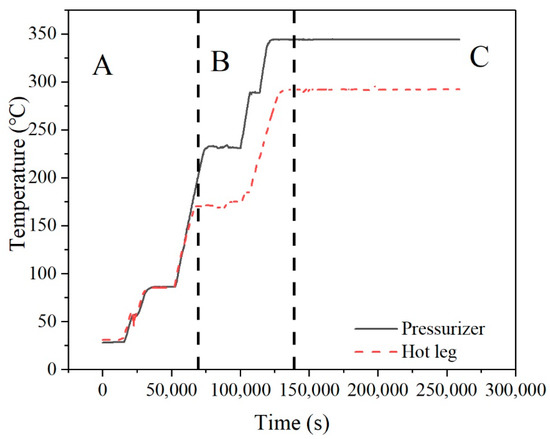
Figure 19. The temperature of the fluid in the pressurizer and hot leg.

The data for the four monitoring sections under the starting condition are shown in Figure 20, and three time spans are divided, named A, B, C respectively. It is obvious that the temperatures of the upper and lower fluid are different during time span B and C for monitoring Section 2 to 4, which revels that thermal stratification exists. However, in monitoring Section 1, the value of the top temperature monitoring point is almost the same as that of the bottom monitoring point, which indicates that the phenomenon of thermal stratification does not exist in this monitoring section. The temperature differences between the top and the bottom monitoring points in monitoring Section 2 to 4 are over 100 °C, which indicates that significant thermal stratification exists in monitoring Section 2 to 4. The distance between monitoring Section 2 and monitoring Section 4 is 10.12 m. Thus, the length of the thermal stratification phenomenon is greater than 10.12 m, and exceeds 50% of the overall horizontal pipeline length, which is 19.25 m.

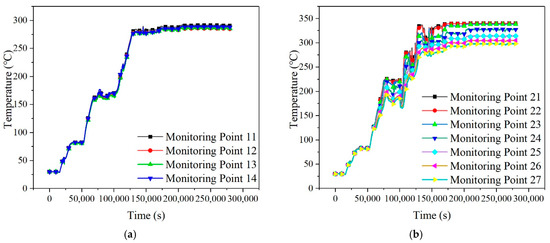
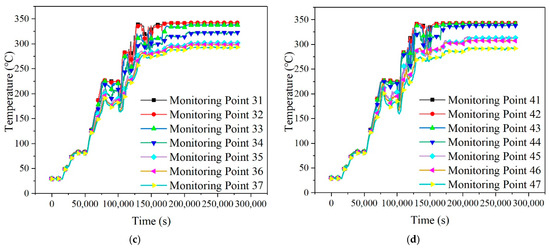
Figure 20. Temperature at each monitoring point under start-up conditions. (a) Monitoring Section 1. (b) Monitoring Section 2. (c) Monitoring Section 3. (d) Monitoring Section 4.

4.2. Determination of Fluid Temperatures of Thermal Zone 4–9

We assumed the temperature of the outer wall at the monitoring point is T_O1, T_O2, T_O3, T_O4, T_O5, T_O6, T_O7 from top to bottom in order, and the corresponding fluid temperature of each layer is T_f12, T_f23, T_f34, T_f45, T_f56, T_f67.

The temperature data was selected from the stable section after 20,000 s, as shown in Figure 21, the top measured temperature decreases a little from the pressurizer side to the hot leg side, and the bottom measured temperature decreases a little from the hot leg side to the pressurizer side. This is due to the heat loss of the fluid along the flow direction. However, with the help of pipe insulation, the heat loss effect can be neglected. Thus, the difference of temperature in the axial direction is ignored, and the fluid temperature of one zone is constant.

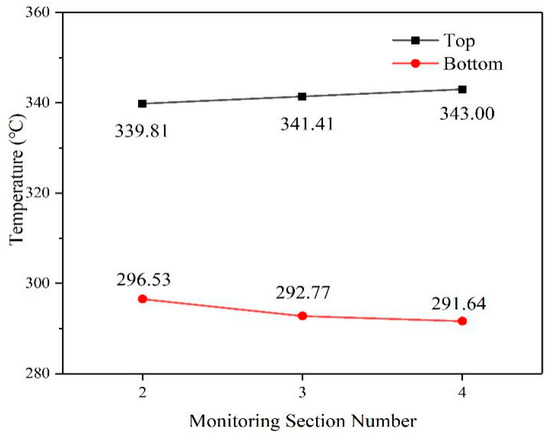
Figure 21. Comparison of the temperature at the top and bottom monitoring points in different monitoring sections.

The top and bottom measured temperatures in each monitoring section were compared with the temperature of the outlet fluid from pressurizer T_hot and the temperature of the hot leg fluid T_cold, respectively, as shown in Figure 22.

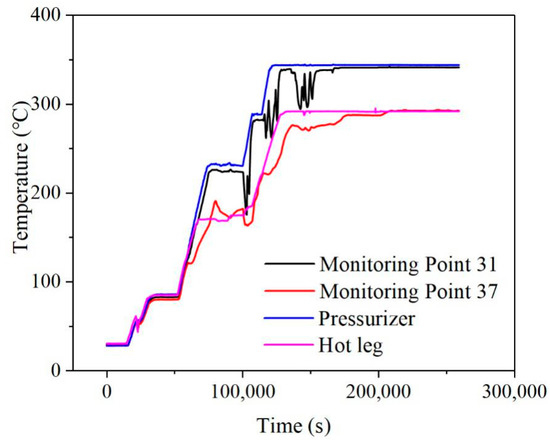
Figure 22. The temperature of the fluid from the pressurizer and hot leg.

In time span B (70,000–130,000 s) and time span C (130,000–280,000 s) before stable operation, the measured temperatures fluctuate sharply due to changes in surge flow, which strongly disturbs the fluid temperature field. During stable operation, the top and bottom measured temperatures are roughly the same as the temperature of the fluid from pressurizer and hot leg, respectively. It can be seen that at the time of stable operation, the top measured temperature is slightly lower than T_hot, and the bottom measured temperature is slightly lower than T_cold. Taking into account slight thermal diffusion through the pipe insulation, it is reasonable that the outside wall temperatures are slightly lower than that of the fluid temperature. So, it is reasonable to assume that during stable operation, the temperature of the top zone fluid is equal to T_hot, and the temperature of the bottom zone is equal to T_cold, which is

$$T_{f1}=T_{hot}$$

(11)

$$T_{f7}=T_{cold}$$

(12)

Then, from the radial heat transfer Equations (13) and (14), the heat flux densities at the top and bottom can be obtained,

$$q_1=\frac{T_{f1}-T_{o1}}{\frac{1}{{\alpha }_1}+\frac{\delta }{\lambda }}$$

(13)

$$q_7=\frac{T_{f7}-T_{o7}}{\frac{1}{{\alpha }_7}+\frac{\delta }{\lambda }}$$

(14)

where α₁ and α₇ are the convective heat transfer coefficient of thermal stratified flow used in the calculation of Green’s functions, λ is the thermal conductivity of the surge line metal material, and δ is the thickness of the surge line.

As for other monitoring points, heat flux may be assumed with the obtained q₁ and q₇. Two kinds of heat flux distribution are suggested. One is uniform heat flux as the maximum of q₁ and q₇ as shown by Equation (15). Another is linear heat flux distribution as shown by Equation (16).

$$q_i=\max (q_1,q_7)$$

(15)

$$q_i=q_1+\frac{q_7-q_1}{6}(i-1),i=2,3,\dots ,6$$

(16)

The obtained heat flux is used to calculate the fluid temperature at the corresponding position of the monitoring points:

$$T_{fi}=T_{oi}+q_i(\frac{1}{{\alpha }_1}+\frac{\delta }{\lambda }),i=2,3,\dots ,6$$

(17)

The fluid temperature in the uppermost thermal zone is taken as T_hot, and the fluid temperature in the lowermost thermal zone is taken as T_cold. The fluid temperature in other fluid areas is taken as the average of the fluid temperatures corresponding to two adjacent monitoring points.

4.3. Verification of Suggested Fluid Temperature Determination Method

In this section, the temperature Green’s function is used to verify the suggested fluid temperature determination method. The temperature responses of the monitoring points on the outer wall were also obtained by applying temperature step loads to thermal zones separately, that is, the same method of establishing the Green’s function of stress in Section 3.3. The difference is that g in the Equation (18) is Green’s function of temperature and T_out is the temperature of the outer wall in the location of the monitoring point.

$$T_{out}={\displaystyle \sum _{i=1}^n(g_{0,ij}·({\phi }_i(t)-T_{ref})+{\displaystyle \sum _{t-t_d}^t{g}_{ij}\Delta \phi (t))}}$$

(18)

4.4. Result and Verification of the Fluid Temperature

4.4.1. Uniform Heat Flux Assumption

For the uniform heat flux assumption, the measured temperature and calculated temperature, which is the convolution result of the assumed fluid temperature and temperature Green’s functions are compared in Figure 23 for the seven monitoring points of monitoring Section 3. It can be seen from Figure 23 that there are large errors at the top monitoring point 31 and the middle monitoring point 34, which are about 5.03% and 3.79%, respectively. The error of the bottom monitoring point 37 is relatively small, about 0.91%. The reason for this kind of error may be that all seven monitoring points use the same heat flux. The calculation results of the heat flux at the top and bottom show that there are certain differences in the heat flux at different locations.

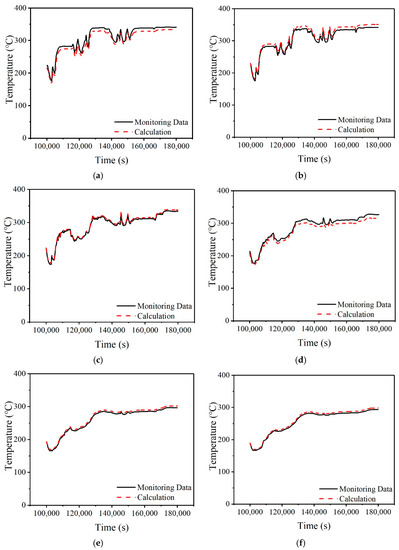
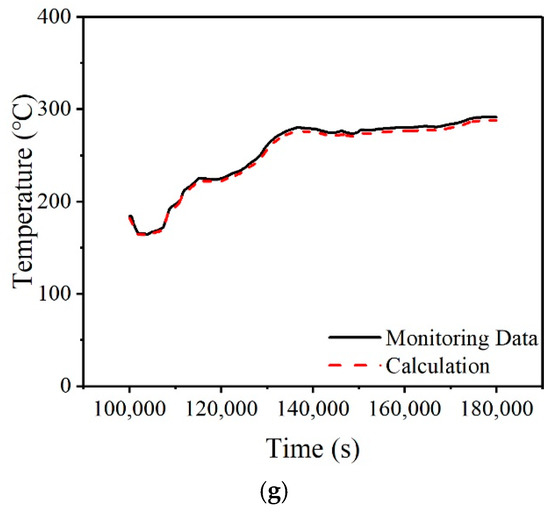
Figure 23. The comparison of calculation result for fixed heat flux and temperature of monitoring points. (a) Monitoring Point 31. (b) Monitoring Point 32. (c) Monitoring Point 33. (d) Monitoring Point 34. (e) Monitoring Point 35. (f) Monitoring Point 36. (g) Monitoring Point 37.

4.4.2. Linear Heat Flux Distribution Assumption

For the linear heat flux distribution assumption, the measured temperature and calculated temperature, which is the convolution result of the assumed fluid temperature and temperature Green’s functions are compared in Figure 24 for the seven monitoring points of Section 3. It can be seen that all measured temperatures agree quite well with the calculated ones. The maximum error at the top monitoring point is 2.03%, the maximum error of the calculation result at the middle monitoring point is 1.07%, and the maximum error of the calculation result at the bottom monitoring point is 0.04%.

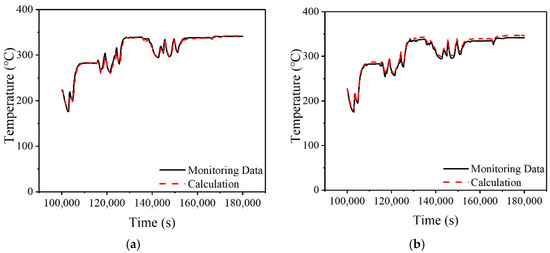
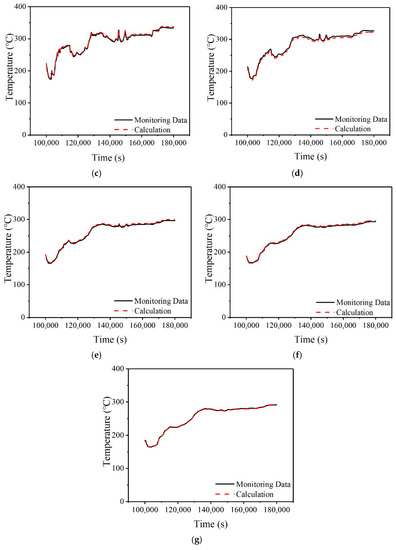
Figure 24. The comparison of the calculation result for the heat flux of the linear distribution law with the temperature of the monitoring points. (a) Monitoring Point 31. (b) Monitoring Point 32. (c) Monitoring Point 33. (d) Monitoring Point 34. (e) Monitoring Point 35. (f) Monitoring Point 36. (g) Monitoring Point 37.

4.5. Comparison of Thermal Stress Calculation Results with Different Number of Thermal Zones in Stratification Region

In order to study the effect of the number of dividing thermal zone in the stratification region on the calculation result of thermal stress, the stable conditions after 20,000 s were used for comparison. When the thermal stratification region is divided into two zones, the bulk temperature of fluid in the upper zone is taken as the temperature of the fluid from the pressurizer, and the bulk temperature of the fluid in the lower zone is taken as that from the hot leg. The stress intensity contour is shown in Figure 25, the maximum stress intensity in Section A is 119 MPa, and the maximum stress intensity in Section B is 137 MPa.

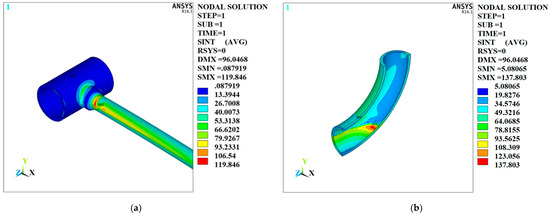
Figure 25. Stress intensity contour of two zones in stratification region. (a) Section A. (b) Section B.

When the thermal stratification region is divided into six zones, the bulk temperature of the fluid in each thermal zone is taken as the calculation results in Section 4.2. The stress intensity contour is shown in Figure 26. The maximum stress intensity in Section A is 98 MPa, and the maximum stress intensity in Section B is 67 MPa. It can be seen that when the thermal stratification region is divided into two zones, the stress calculation result is too conservative, and the six thermal zones division yields more accurate results for the evaluation of thermal fatigue.

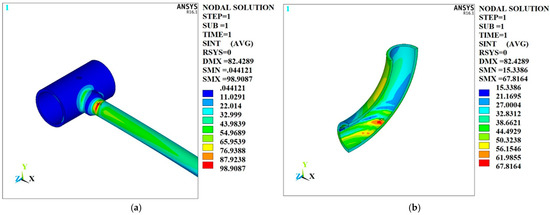
Figure 26. Stress intensity contour of six zones in stratification region. (a) Section A. (b) Section B.

5. Conclusions

Detailed analysis of the fast calculation of the transient thermal stress by Green’s function for surge lines revealed the following conclusions.

In order to calculate the transient thermal stress of the surge line fast by Green’s function method, both the flow cases and thermal zones should be considered for the construction of Green’s function. Using more thermal zones in the stratification region is helpful to obtain more accurate thermal stress results for thermal fatigue evaluation. Higher step temperature (more than 300 °C) should be preferred for higher accuracy of the Green’s function.

Using the temperature data from the thermocouples installed on the outer wall can improve the calculation results of the fluid temperature in each thermal zone in the stratification region. It was found that the linear heat flux distribution assumption is more appropriate for calculating the fluid temperature of thermal zones. In order to verify the accuracy of the fluid temperature calculation results obtained by the method described in this paper, the temperature Green’s function was used to verify the calculation results. Based on the above work, the transient stress calculated by Green’s function method is much more reasonable which is very critical to the safety monitoring and life extension of nuclear power plants.