Seismic Response of Skewed Integral Abutment Bridges under Near-Fault Ground Motions, Including Soil–Structure Interaction

Abstract

Studies on the seismic response of skewed integral abutment bridges have mainly focused on response under far-field non-pulse-type ground motions, yet the large amplitude and long-period velocity pulses in near-fault ground motions might have significant impacts on bridge seismic response. In this study, the nonlinear dynamic response of an skewed integral abutment bridge (SIAB) under near-fault pulse and far-fault non-pulse type ground motions are analyzed considering the soil–structure interaction, along with parametric studies on bridge skew angle and compactness of abutment backfill. For the analyses, three sets of near-fault pulse ground motion records are selected based on the bridge site conditions, and three corresponding far-field non-pulse artificial records are fitted by their acceleration response spectra. The results show that the near-fault pulse type ground motions are generally more destructive than the non-pulse motions on the nonlinear dynamic response of SIABs, but the presence of abutment backfill will mitigate the pulse effects to some extent. Coupling of the longitudinal and transverse displacements as well as rotation of the bridge deck would increase with the skew angle, and so do the internal forces of steel H piles. The influence of the skew angle would be most obvious when the abutment backfill is densely compacted.

1. Introduction

Seismic safety of bridge structures has always been a major concern. In the last few decades, several major earthquakes had occurred and caused serious damage to infrastructure including bridges across the world, such as the Northridge (USA) earthquake in 1994, the Kobe (Japan) earthquake in 1995, the Kocaeli (Turkey) and the Chi-Chi (Taiwan) earthquake in 1999, the Bam (Iran) earthquake in 2003, the Wenchuan (China) earthquake in 2008 and the Haiti earthquake (Haiti) in 2010, etc. The damage will not only threaten the life-safety of people on or near the infrastructure, but also cause dis-functioning of the transportation lines, inducing secondary disasters that aggravates the earthquake influence, especially for densely populated areas and the main traffic arteries [1,2].

Studies on the seismic response of bridge structures have largely focused on response and damage under far-field ground motions, while response and damage under near-fault ground motions have gained more and more attention in recent years [3]. In general, seismic regions within 20 km distance from the fault rupture are defined as the near-fault field [4,5,6], in which the ground motions are quite different from the far-field ground motions and depend heavily on the mechanism of the fault rupture [7,8,9,10,11,12,13,14]. Long-period displacements and velocity pulses, along with permanent ground displacement, are often generated in the near-fault ground motions with unique forward-directivity and fling-step effects, which introduce high seismic energy into structures, and induce large structural deformations and damages [15].

Research has been carried out on the seismic response of various bridge types under near-fault pulse type ground motions. Li et al. [16] studied the seismic response of a typical three-span continuous highway girder bridge under near-fault strong ground motions, and found that the seismic design spectrum considering near-fault effects significantly intensified bridge seismic response. Zhang et al. [17] evaluated the seismic response of a simply supported girder bridge under six sets of near-fault ground motions, considering contact and separation between the girder and abutment in the longitudinal direction, and concluded that the peak bridge response increased as the amplitude and period of the ground motion pulse increased. Zheng et al. [18] investigated the seismic response of a long-span asymmetrical suspension bridge subjected to four levels of near-fault ground motions. The results showed that compared to far-field ground motions, the response and power spectrum values were several times higher in the long-period range, and the seismic response of the bridge tower increased significantly under the near-fault ground motions, especially in soft soil. Xin et al. [19] investigated the seismic behavior of a long-span concrete-filled steel tubular arch bridge subjected to near-fault ground motions, and found that the forward-directivity and fling-step effects might induce significantly higher seismic demands and damage to the bridge structure. Li et al. [20] investigated the seismic behavior of a long-span cable-stayed bridge under near-fault ground motions, which generated larger internal forces and displacements in the bridge.

However, until now, almost no research has been published on the seismic response of integral abutment bridges under near-fault pulse-type ground motions. Integral abutment bridges are bridges in which the super-structure is cast monolithically with the abutment, typically supported by a single row of piles to provide the required flexibility for thermal movements [21,22,23]. In the United Kingdom the trend is to have the flexible abutment with a double row of piles [24,25,26]. Compared to expansion joints and abutment bearings, the integral abutments would facilitate faster and simpler construction, minimum joint corrosion or damage, reduced maintenance costs and increased structural integrity [27,28,29]. However, during an earthquake the abutments would move together with the superstructure, which induces a complex soil–structure interaction between the abutment-backfill and the pile-foundation [30,31], and plastic hinges tend to form at the top of the abutment piles under severe seismic events [32,33]. Some researchers have also studied the possibility to put EPS Geofoam between the abutment walls and the backfill, in order to avoid the complex soil–structure interaction during earthquakes [24]. Currently, seismic design and analyses of integral abutment bridges only involve the far-field non-pulse type ground motions [21,22,30,31], while the large amplitude and long-period velocity pulses of the near-fault pulse type ground motions might have quite different influences on bridge seismic response, especially considering the complex soil–structure interaction.

Therefore, this paper presents a study on the nonlinear seismic response of skewed integral abutment bridges (SIABs) under near-fault pulse and far-field non-pulse type ground motions, with parametric studies on bridge skew angles and the compactness of abutment backfill. Three-dimensional numerical models of SIABs were built using the analysis and design software SAP2000 [34], with nonlinear soil springs around the piles and behind the abutments. Three near-fault pulse ground motion records were selected based on the bridge site condition, and three corresponding far-field non-pulse artificial ground motions were fitted by the response spectra of the near-fault records. Nonlinear time-history analyses were conducted on the SIABs model, and a seismic response was obtained including abutment and deck displacement, soil pressure behind the abutment, deflection and internal forces of the piles, and internal forces of the main girder, etc. This study could provide a reference for future studies on the seismic behavior and design of SIABs in near-fault regions.

2. Modeling of Skewed Integral Abutment Bridges

2.1. Three Dimensional Bridge Model

The prototype bridge was a one-span SIAB with a span of 37.0 m from bearing to bearing and a skew angle of 15°, which is the angle between the longitudinal direction of the bridge and the normal direction of the abutment. The bridge superstructure consisted of five steel girders with a center to center spacing of 3 m, supporting a concrete deck with a thickness of 0.22 m and a width of 14.2 m. The bridge substructure consisted of two abutments, each of which was 0.9 m thick and 3.9 m high, and supported by five HP 310 × 125 steel piles with the strong axis parallel to the bridge longitudinal direction. Figure 1 shows the elevation view, plan view and details of the skewed integral abutment bridge.

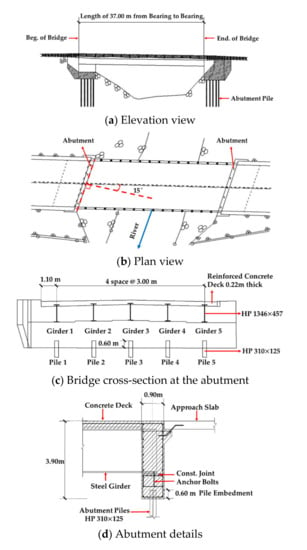
Figure 1. A skewed integral abutment bridge.

A three-dimensional finite element model of the bridge was established using the design and analysis software SAP2000, as shown in Figure 2. In addition to the prototype bridge, bridge models with a skew angle of 0°, 30° and 45° were also established to study the effects of skew angle on bridge seismic behavior. The bridge deck and abutments were modeled using four-node thin shell elements and the girders and piles were modeled using two-node beam elements. In order to consider the composite action, rigid link elements were used to connect the nodes on the deck and the steel girders, and rigid connections were assumed between the abutment-girders and abutment-piles. The bridge deck and abutments were constructed with concrete with a nominal compressive strength of 27.6 MPa, and the girders and piles were constructed with Grade 345 steel with a nominal yield strength of 345 MPa. The girders were assumed to be elastic, since there was no report of superstructure damage in integral abutment bridges in previous seismic events. The maximum stress in the girder during the time-history analyses was checked, and there was no sign of yielding in the girders. Plastic hinges were placed at the top of the piles to consider material nonlinearity, and vertical displacements were constrained at the bottom of the piles. The damping coefficient of the model was taken as 0.05.

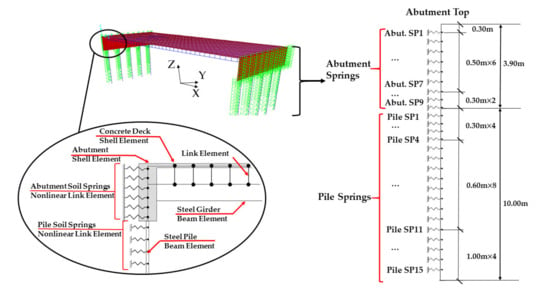
Figure 2. Finite element model of a skewed integral abutment bridge.

2.2. Nonlinear Soil Springs

In order to simulate the soil–structure interaction, nonlinear discrete Winkler spring elements were placed behind and perpendicular to the abutments as well as around the piles, as shown in Figure 2. In the prototype bridge, the abutment backfill was densely compacted cohesionless sand. For the parametric study, loosely, medium-densely and densely compacted sandy backfill were modeled with soil properties from reference [35], as shown in Table 1 below, and a no backfill (soil-free) case was also included.

Table 1. Backfill soil properties.

Case	Abutment Backfill
1	Loosely compacted sand ($\varphi =37°,c=0,\gamma =16.5 \mathrm{kN}/{\mathrm{m}}^3$)
2	Medium-densely compacted sand ($\varphi =40.5°,c=0,\gamma =18.3 \mathrm{kN}/{\mathrm{m}}^3$)
3	Densely compacted sand ($\varphi =45°,c=0,\gamma =23.2 \mathrm{kN}/{\mathrm{m}}^3$)

Notes: $\gamma$ = effective soil density, $\varphi$ = friction angle.

2.2.1. Soil Springs behind the Abutment

The force-displacement relationship from Shamsabadi et al. [36] was used for the soil springs behind the abutment, as shown in Equation (1) below.

$$F\left(y\right)=\frac{F_{ult}\left(2K{y}_{\max }-F_{ult}\right)y}{F_{ult}{y}_{\max }+2\left(K{y}_{\max }-F_{ult}\right)y}$$

(1)

where $y$ represents the lateral displacement of the abutment; $y_{\max }$ represents the abutment displacement when the soil pressure reaches the maximum passive soil pressure; $K$ represents the average stiffness of soil behind the abutment; $F_{ult}$ represents the ultimate abutment force (per unit length of the wall) developed at a maximum displacement of $y_{\max }$. For cohesionless soil $F_{ult}$ can be obtained by

$$F_{ult}=0.5K_{\mathrm{pe}}\gamma h^2$$

(2)

where $K_{\mathrm{pe}}$ represents the seismic passive earth pressure coefficient; $\gamma$ represents the soil density; $h$ represents the abutment height.

Based on site testing results, $y_{\max }$ was taken as $0.024l$, $0.03l$ and $0.05l$ for loosely, medium-densely and densely compacted cases respectively [36], where $l$ is the height of the pile cap. For an abutment with a height of 3.9 m, $K$ was taken as $279 \mathrm{kN}/\mathrm{cm}/m$, $418 \mathrm{kN}/\mathrm{cm}/m$ and $666 \mathrm{kN}/\mathrm{cm}/m$ for loosely, medium-densely and densely compacted cases respectively [36,37]. Figure 3a shows the force–displacement relationship of the soil springs along the height of the abutment for the prototype bridge, where the abutment backfill was densely compacted.

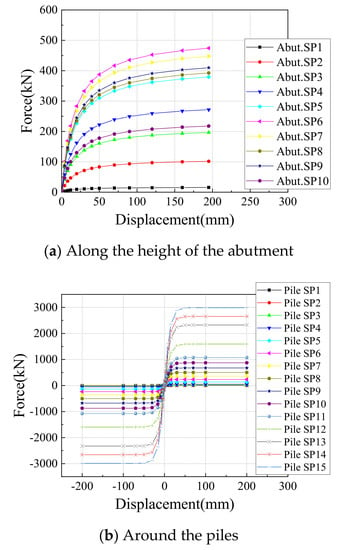
Figure 3. Force–displacement relationship of the soil springs.

2.2.2. Soil Springs around the Piles

The force–displacement relationship from the American petroleum institute (API) [38] was used for the soil springs around the piles, as shown in Equation (3) below.

$$P=0.9p_u\tanh \left(\frac{kH{y}^{\prime }}{0.9p_u}\right)$$

(3)

where $y^{\prime }$ represents the horizontal pile deflection; $k$ represents the initial modulus of soil around the piles; $H$ represents the depth from top of soil layer to the specified node; $p_u$ represents the estimated ultimate lateral resistance of soil around piles at depth $H$.

For the prototype bridge, the soil around the piles was densely compacted sand with properties from test data obtained by Cummins [39]. Since the prototype bridge was skewed and there would be longitudinal and transverse displacements of the abutment and piles, soil springs were placed in two orthogonal directions to simulate the lateral soil resistance along the piles. Figure 3b shows the force–displacement relationship of the soil springs along the pile length for the prototype bridge, where soil was densely compacted sand.

2.3. Modal Analysis and Sensitivity Studies

Model analyses were performed on 16 SIAB models, in which the skew angle varied from 0°, 15°, 30° to 45°, and the abutment backfill varied from no-backfill (soil-free) to loosely, medium-densely and densely compacted sand. The first six mode shapes for Model 10, the prototype bridge model with a 15° skew and densely compacted backfill, are shown in Figure 4. As shown in the figure, when there is a skew angle, the major vibration modes of integral abutment bridge include transverse translation, vertical bending, in-plane rotation, longitudinal translation, rotation about the longitudinal axis (X), and rotation about the transverse axis (Y) etc., and the first vibration mode is transverse translation.

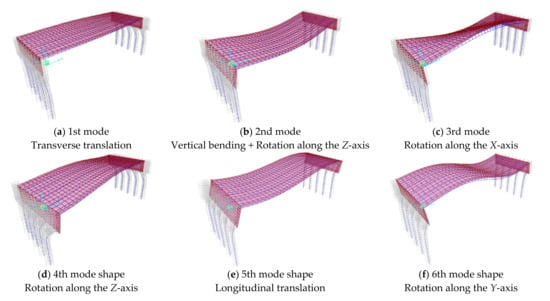
Figure 4. Mode shapes of Model 10.

Table 2 shows the period, mode shape and mass participation ratio in the longitudinal (X) and transverse (Y) direction for the first longitudinal mode of the 16 SIAB models. Note that the longitudinal mode means that the mass participation ratio in the X direction is generally higher than the Y direction. Although the longitudinal modes were not necessarily the first mode, they were chosen to be presented because backfill stiffness is one of the main parameters, and the longitudinal modes will better reflect the influence of this parameter.

Table 2. Dynamic properties of SIAB models.

Model	Abutment Backfill	Skew Angle (°)	Period (s)	Mode Shape	X Dir	Y Dir
					Mass (%)
1	Loosely compacted sand	0	0.351	LT	92.0	0.0
2	Loosely compacted sand	15	0.338	LT	87.0	6.7
3	Loosely compacted sand	30	0.326	LT + TT	69.0	24.0
4	Loosely compacted sand	45	0.308	LT + TT	47.0	46.0
5	Medium-densely compacted sand	0	0.311	LT	88.0	0.0
6	Medium-densely compacted sand	15	0.298	LT	85.0	6.1
7	Medium-densely compacted sand	30	0.287	LT + TT	69.0	23.0
8	Medium-densely compacted sand	45	0.271	LT + TT	45.0	40.0
9	Densely compacted sand	0	0.272	LT	77.0	0.0
10 (Prototype)	Densely compacted sand	15	0.256	LT	80.0	5.4
11	Densely compacted sand	30	0.248	LT + TT	67.0	21.0
12	Densely compacted sand	45	0.234	LT + TT	43.0	40.0
13	Soil-free	0	0.606	LT	97.0	0.0
14	Soil-free	15	0.593	LT	97.0	0.0
15	Soil-free	30	0.587	LT	95.0	2.0
16	Soil-free	45	0.589	LT	89.0	8.4

Notes: LT—longitudinal translation; TT—transverse translation.

As shown in Table 2, when the skew angle increases, the mass participation ratio in the X direction decreases, and the mass participation ratio in the Y direction as well as the period of the first longitudinal mode increases. In addition, the mode shape changes from longitudinal translation (LT) to a combination of longitudinal and transverse translation (LT + TT). This is mainly because when the skew angle increases, the longitudinal lateral stiffness of the bridge provided by the abutment backfill decreases, and there is more obvious coupling between the longitudinal and transverse displacements.

As is also shown in Table 2, when the backfill compactness increases, the mass participation ratio of the first longitudinal mode in the X direction as well as the period, decreases, since the longitudinal lateral stiffness of the bridge provided by the abutment backfill increases. When the backfill changes from soil-free to densely compacted sand, the period decreases over 50%. The backfill condition also affects the influence of the skew angle. When there is no backfill (soil-free), the mode shape is mainly the longitudinal translation with a mass participation ratio over 89% in the X direction, and the skew angle has an almost negligible influence on the period or the mass participation ratio.

3. Nonlinear Time-History Analyses on Skewed Integral Abutment Bridges

3.1. Selection of Near-Fault Ground Motions

A design response spectrum was generated for the prototype bridge, based on a site category of class II, a seismic fortification intensity of degree VIII, a design seismic group of class C, a design seismic acceleration of 0.2 g, as well as the bed rock conditions of the region. The response spectrum of the near-fault seismic ground motion records from the strong ground motion database in PEER [40] were then matched with the design response spectrum above, and three records with the best fitting accuracy were chosen, which were the ground motion records from the Yarimaca Test Site station in the Kocaeli earthquake (EQ1), the Newhall-W_Pico_Canyon_Rd Test Site station in the Northridge earthquake (EQ2), and the Takatori Test Site station in the Kobe earthquake(EQ3). Magnitudes of the chosen earthquake records varied from M6.7 to M7.9, the distances from the Test Site stations to the rupture sources were all less than 10 km, the peak ground velocities (PGV) were significantly higher than 20 cm/s, and the PGV to peak ground acceleration (PGA) ratios were larger than 0.2 s. Parameters of the three selected near-fault ground motions are listed in Table 3.

Table 3. Characteristic parameters of pulse and non-pulse type ground motions.

Parameters	EQ1		EQ2		EQ3
	GM1	GM2	GM3	GM4	GM5	GM6
Ground motion type	Pulse	Non-pulse	Pulse	Non-pulse	Pulse	Non-pulse
Fault Type	Strike-Slip		Reverse		Strike-Slip
Earthquake event	Kocaeli		Northridge		Kobe
Station name	Yarimca		Newhall-W_Pico_Canyon_Rd.		Takatori
Earthquake magnitude	7.5		6.7		6.9
${\mathrm{R}}_{\mathrm{jb}}$ (km)	1.4		2.1		1.5
Duration (s)	35.00	35.00	24.98	24.98	40.95	40.95
${\mathrm{T}}_{\mathrm{p}}$ (s)	4.6	0	2.2	0	1.6	0
PGA (g)	0.2	0.2	0.2	0.2	0.2	0.2
PGV (cm/s)	47.66	21.75	54.57	20.48	50.69	22.11
PGV/PGA (s)	0.238	0.109	0.273	0.102	0.253	0.110

Note: ${\mathrm{R}}_{\mathrm{jb}}$ denotes the Joyner-Boore distance, which is the shortest distance to the surface projection of the fault plane [41]; ${\mathrm{T}}_{\mathrm{p}}$ denotes the pulse period of pulse type ground motions.

Three corresponding non-pulse artificial seismic records (GM2, GM4, GM6) were produced using the SIMQKE_GR software, which were consistent with the response spectra of the near-fault seismic records (GM1, GM3, GM5). The acceleration, velocity, and displacement time-histories of both the pulse and non-pulse type ground motions are shown in Figure 5, where it is clear that there are distinctive two-side or one-side pulses in the velocity time-histories of pulse type ground motions with rupture forward-directivity effect or reverse-directivity effect. The acceleration response spectra of all ground motions are shown in Figure 6, where it is clear that the acceleration response spectra of the pulse type ground motions fit well with the non-pulse ones. The PGV/PGA ratios of non-pulse type ground motions are generally small, and less than 0.11 in this paper. Table 3 presents the characteristic parameters of the pulse type and non-pulse type ground motions, and PGA of the six ground motions was uniformly adjusted to 0.2 g.

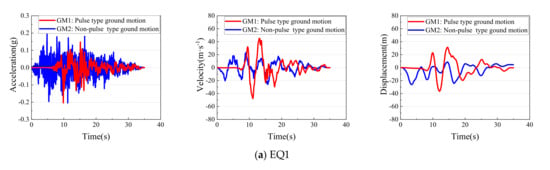
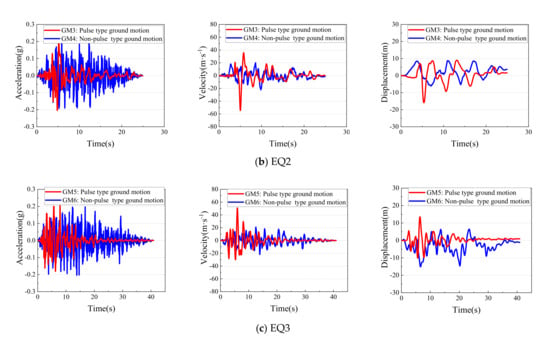
Figure 5. Acceleration, velocity, and displacement time-histories of pulse and non-pulse type ground motions.

Figure 6. Acceleration response spectra of pulse and non-pulse type ground motions.

3.2. Nonlinear Time History Analyses

Six nonlinear time history analyses were performed on the 16 SIAB models under the six ground motions in Table 2 along the longitudinal direction of the bridge. Therefore, a total of 96 nonlinear time history analyses were performed.

4. Results and Discussion

4.1. Displacement of Abutments

From the time-history analyses on all SIAB models, it was found that the maximum longitudinal and transverse displacements of the abutment were always located at the abutment top. Therefore, only the abutment top displacement is discussed in this section. Table 4 shows the maximum abutment displacements from the time-history analyses on the prototype bridge model (Model 10) with a skew angle of 15° and densely compacted abutment backfill.

Table 4. Maximum abutment displacement for Model 10.

Abutment	Lateral Displacement	Location	Pulse Ground Motion (mm)			Non-Pulse Motion (mm)
			GM1	GM3	GM5	GM2	GM4	GM6
Abutment 1	Longitudinal	Acute	9.1	9.3	8.7	8.5	8.9	11.2
		Obtuse	4.6	6.8	6.1	6.0	6.3	8.8
	Transverse	Acute	15.5	21.8	15.5	12.9	14.1	15.4
		Obtuse	13.9	20.0	14.0	11.4	12.5	13.7
Abutment 2	Longitudinal	Acute	7.4	9.6	8.9	8.6	8.9	11.3
		Obtuse	6.3	6.7	5.9	5.8	6.1	8.4
	Transverse	Acute	14.3	15.0	14.5	12.8	15.0	14.1
		Obtuse	12.6	13.3	12.9	11.2	13.4	12.4

From Table 4, it is clear that there are longitudinal as well as transverse displacements of the abutment under earthquake ground motions inputted in the longitudinal direction of the bridge, which reflected an in-plane rotation of the bridge superstructure, as shown in Figure 7 below. This is mainly because when there is a skew angle between the longitudinal direction of the bridge and the normal direction of the abutment, the rigid center of the bridge deck does not coincide with the mass center, so there will be coupling between the longitudinal and the transverse displacements of the bridge deck, which is directly reflected in the abutment displacements. Furthermore, abutment displacement at the acute corners is always higher than the obtuse corners, especially for Abutment 1, for which the longitudinal displacement at the acute corner is about twice as much as that of the obtuse corner under GM1. Therefore, only the abutment displacement at the lower left acute corner of Abutment 1 is discussed in the following sections.

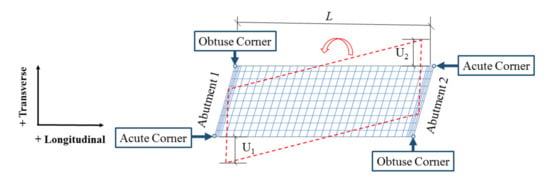
Figure 7. Abutment displacement and bridge deck in-plane rotation.

In order to quantify the rotation angle of the bridge deck, Equation (4) below was used with orientation and sign conventions defined in Figure 7.

$$\omega =\arctan \left(\left|U_2-U_1\right|/L\right)$$

(4)

where $U_1$ represents transverse displacement of abutment 1 at obtuse corner, $U_2$ represents transverse displacement of abutment 2 at acute corner, and $L$ is the bearing to bearing distance of the skewed integral abutment bridge.

Time-history curves of the longitudinal and transverse displacement of the abutment are shown in Figure 8 and Figure 9 below for Model 12 (skew angle is 45°, densely compacted backfill) and Model 16 (skew angle is 45°, no backfill), respectively. As shown in the Figures, the abutment displacement time-history under the pulse and non-pulse type ground motions are quite different, although the PGA was the same, and the pulse type ground motions obviously induced much higher abutment displacements, which is more destructive for the bridge. In addition, when there was backfill behind the abutment, the longitudinal displacement of the abutment was significantly decreased, especially under pulse-type ground motions.

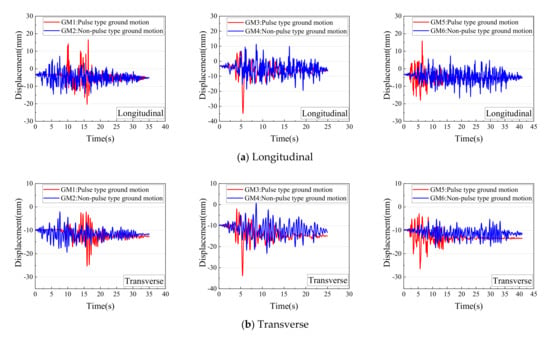
Figure 8. Displacement time-history of the abutment under pulse and non-pulse type ground motions (Model 12).

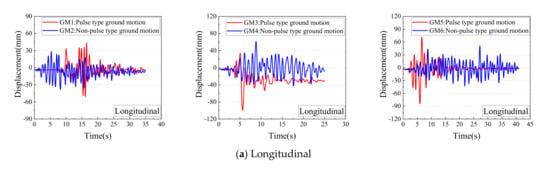
Figure 9. Displacement time-history of the abutment under pulse and non-pulse type ground motions (Model 16).

The maximum longitudinal displacement of the abutment from time-history analyses on all SIAB models with varying skew angles and backfill compactness are shown in Figure 10a below. It is shown in Figure 10a that the abutment longitudinal displacement generally increases with the skew angle. For example, when the abutment backfill is densely compacted, the ratio between the abutment longitudinal displacement with a 45° skew angle and the abutment displacement with no skew is 2.5 under non-pulse type ground motions, and 7.1 under pulse type ground motions, respectively. This is mainly because when the skew angle increases, the angle between the earth pressure behind the abutment and the longitudinal direction of the bridge increases, and the constraint effects of the abutment backfill on abutment longitudinal displacement decreases. However, the influence of skew angle diminishes for loosely compacted backfill under non-pulse type ground motions. It is also shown that the abutment longitudinal displacement decreases as the abutment backfill compactness increases, since the constraint effects of the abutment backfill increases.

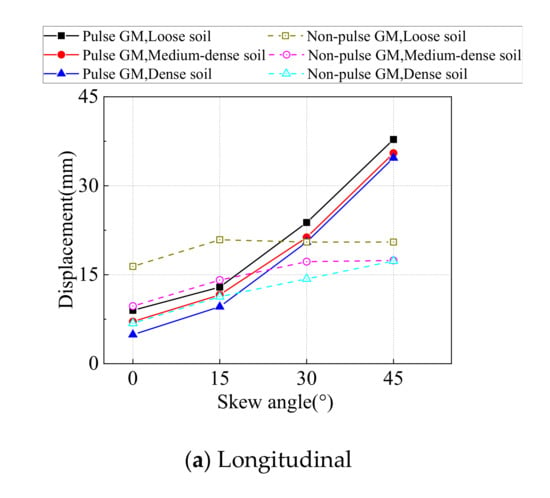
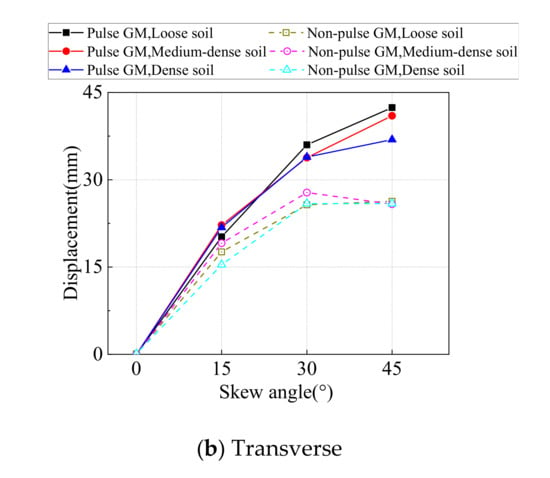
Figure 10. Maximum displacement of the abutment.

The maximum transverse displacement of the abutment from time-history analyses on all SIAB models with varying skew angles and backfill compactness are shown in Figure 10b below. As shown in Figure 10b, the abutment transverse displacement increases with the skew angle, mainly due to the coupling between the longitudinal and transverse displacements of the bridge deck. For example, when the abutment backfill is densely compacted, the ratio between the abutment transverse displacement with a 45° skew angle and the abutment displacement with a 15° skew angle is about 1.7 under non-pulse or pulse type ground motions. The abutment transverse displacement generally decreases with the abutment backfill compactness, but to a much less extent compared to the longitudinal displacement.

It is also shown in Figure 10 that the longitudinal and transverse abutment displacements under pulse type ground motions are generally higher than the non-pulse type ground motions, and the difference increases with the skew angle. When the skew angle reaches 45°, the longitudinal and the transverse abutment displacement under pulse type ground motions is about 100% and 30–60% higher than the displacement under non-pulse type ground motions, respectively.

The maximum rotation angle of the bridge deck from time-history analysis on all SIAB models with varying skew angles and backfill compactness are shown in Figure 11. As shown in Figure 11, similar to the abutment transverse displacement, the bridge deck rotation increases with the skew angle, mainly due to the coupling between the longitudinal and transverse displacements. When the abutment backfill is densely compacted, the ratio between the bridge deck rotation with a 45° skew angle and the bridge deck rotation with a 15° skew angle is about 1.96 under non-pulse type ground motions, and 1.74 under pulse type ground motions, respectively. The deck rotation decreases with the abutment backfill compactness, except for the case with a skew angle of 45° and non-pulse type ground motions, in which the bridge with densely compacted backfill has the highest rotation.

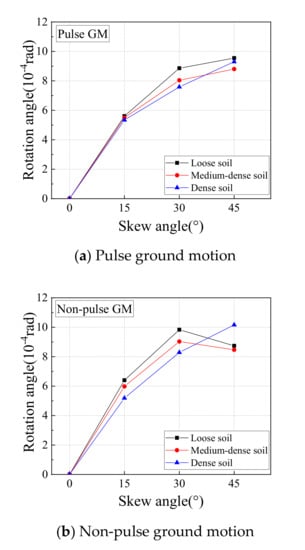
Figure 11. Maximum rotation of bridge deck.

4.2. Soil Pressure Distribution of Abutment Backfill

When the earthquake ground motion is inputted along the longitudinal direction of a bridge with a skew angle, the resultant force of soil pressure behind the abutment does not pass through the mass center of the bridge, which makes the superstructure twist and lead to the non-uniform distribution of soil pressure behind the abutment. The development of soil pressure behind the abutment during one typical cycle in a time-history analysis is shown in Figure 12 below. At first, the bottom left portion of the abutment at the obtuse corner gets in contact with the soil, and creates soil pressure as shown as the shaded area in stage (I) in Figure 12. The soil pressure gradually develops until it covers the whole abutment, as shown in stage (III). Then the top right portion of the abutment at the acute corner starts to move away from the soil, and the soil pressure there becomes zero, as shown in stage (IV). More top right portions of the abutment move away from the soil, and finally the soil pressure distribution in stage (IV) will be similar to stage (I). During this process, the soil pressure behind the abutment at the obtuse corner is always greater than the soil pressure at the acute corner.

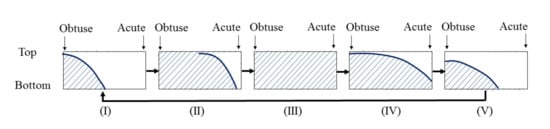
Figure 12. Development of soil pressure behind abutment.

The maximum soil pressure behind abutment from time-history analyses on all SIAB models with varying skew angles and backfill compactness are shown in Figure 13 below. It is shown in Figure 13 that when the skew angle is 0°, the soil pressure behind the abutment at the obtuse corner is equal to that at the acute corner. As the skew angle increases, the soil pressure behind the abutment decreases, but the pressure at the acute corner decreases much faster, so the soil pressure at the obtuse corner is always higher than the acute corner, and the ratio between them (O/A ratio) increases with the skew angle. As the backfill compactness increases, the soil pressure behind the abutment at the obtuse corner increases, but the pressure at the acute corner changes little, so the O/A ratio increases with the backfill compactness.

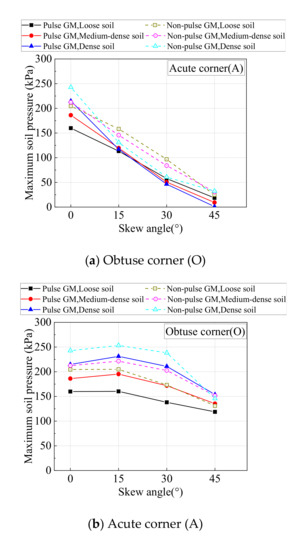
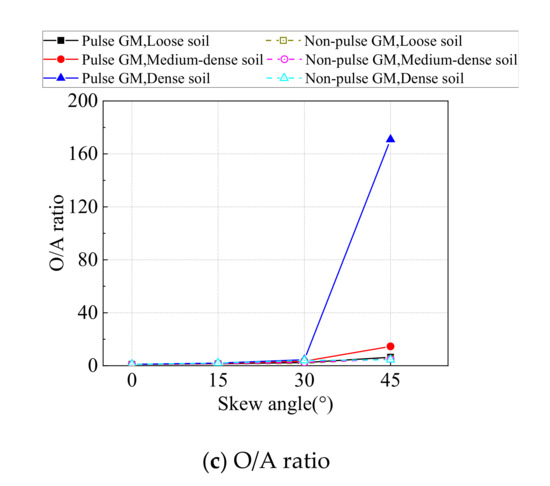
Figure 13. Maximum soil pressure behind abutment.

It is also shown in Figure 13 that although the soil pressure behind the abutment under pulse type ground motions is generally smaller than non-pulse type ground motions, the O/A ratio is higher. When the skew angle is 45° and the backfill is densely compacted, the O/A ratio is 4.5 under non-pulse type ground motions and as high as 170 under pulse type ground motions. Therefore, the distribution of the soil pressure behind a skewed abutment is non-uniform, which is more obvious under pulse type ground motions, with the increase of the skew angle and soil compactness.

4.3. Deflection of Steel H Piles

Distribution of the pile deflection along the pile height are shown in Figure 14 and Figure 15 for the bridge longitudinal and transverse direction, respectively. The pile was chosen as the one below Abutment 1 at the acute corner. From the Figures, it is obvious that the maximum deflection always locates at the pile top, i.e., pile-abutment interface, and then decrease sharply along the depth, until it approaches zero at a depth of 3–5 m. Only the maximum deflection at the pile top is discussed in the following section.

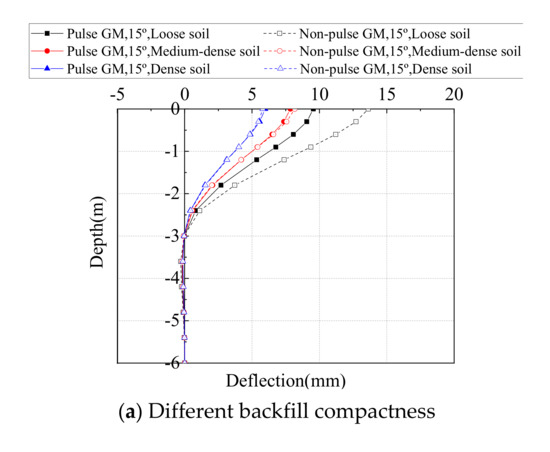
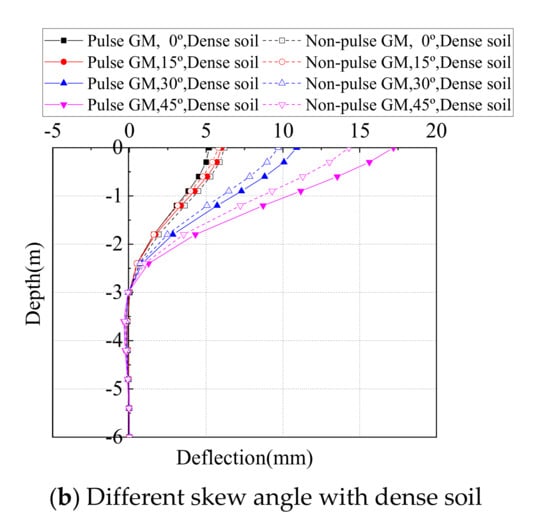
Figure 14. Distribution of pile deflections along the depth in the longitudinal direction.

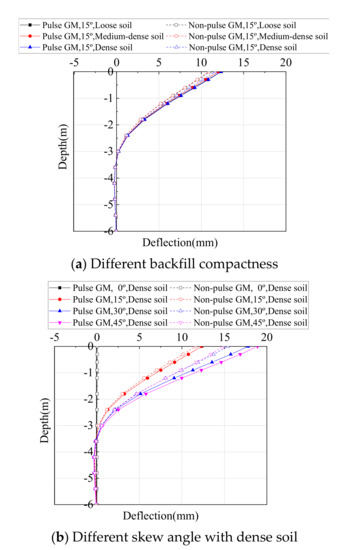
Figure 15. Distribution of pile deflections along the depth in the transverse direction.

The maximum longitudinal and transverse deflection at the top of Steel H piles from time-history analyses on all SIAB models with varying skew angles and backfill compactness are shown in Figure 16. As shown in Figure 16, the longitudinal deflection of the pile top first decreases and then increases with the skew angle, while the transverse deflection of the pile top always increases with the skew angle. The longitudinal deflection decreases with the abutment backfill compactness, and so does the transverse deflection, but to a lesser extent.

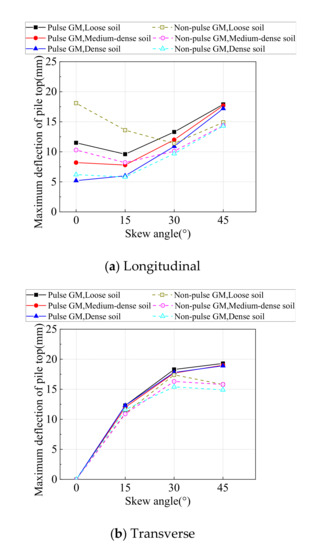
Figure 16. Maximum deflection of the pile top.

It is also shown in Figure 15 that when the skew angle is small, the longitudinal deflection at the pile top is lower under pulse type ground motions, especially for loosely compacted backfill and the transverse deflection is close. But when the skew angle is more than 15°, both the longitudinal and the transverse deflection of the pile is higher under pulse type ground motions.

4.4. Moment and Yield Surface Function of Steel H Piles

4.4.1. Moment in Steel Piles

The piles are oriented such that it will bend about the weak axis when moving in the longitudinal direction of the bridge. Distribution of the pile moment along the pile height are shown in Figure 17 and Figure 18 for moment about the strong and the weak-axis of the section, respectively. The pile was chosen as the one below Abutment 1 at the acute corner. From the Figures, it is obvious that a peak moment will always appear at the pile top, i.e., the pile–abutment interface, and then decrease sharply along the depth, until it approaches zero the first time around a depth of 0.7–1.2 m, i.e., the first inflection point. Then the pile moment will increase in the opposite direction and reach the second peak around a depth of 2.0–2.5 m, and approaches zero when the depth goes beyond 3–5 m. The two peaks of the pile moment are directly related, therefore only the maximum moment at the pile top is discussed in the following section.

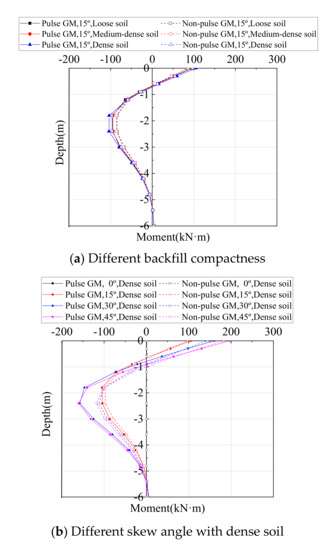
Figure 17. Distribution of pile moment around strong axis.

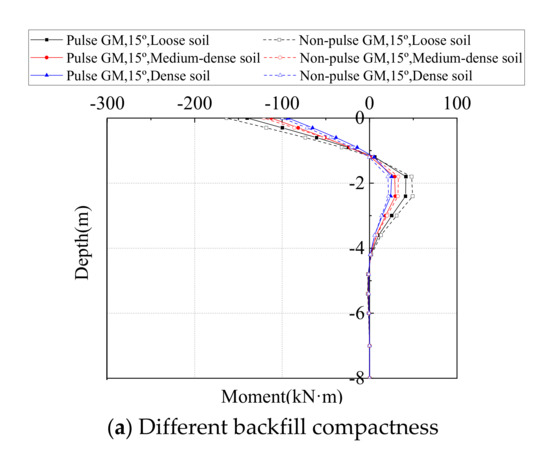
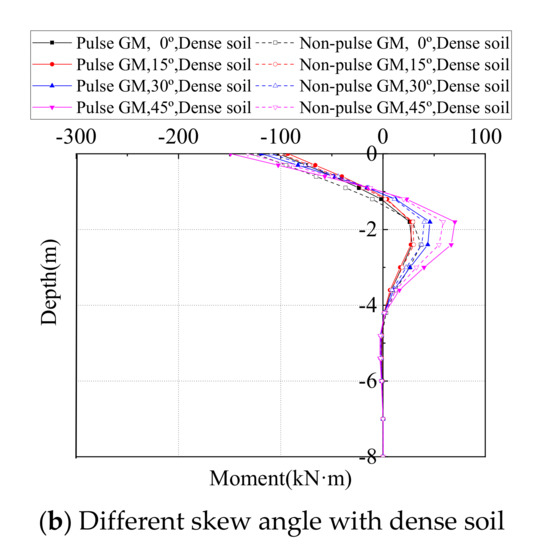
Figure 18. Distribution of pile moment around the weak axis.

The maximum moment at the pile top around weak-axis and the strong-axis from time-history analyses on all SIAB models with varying skew angles and backfill compactness are shown in Figure 19. As shown in Figure 19, the variation of the pile moment is much more similar to the pile deflections. The moment around the weak-axis first decreases and then increases with the skew angle, while the moment around the strong-axis always increases with the skew angle. The moment around the weak-axis decreases with the abutment backfill compactness, and so does the moment around the strong-axis, but to a lesser extent. It is also shown that when the skew angle is small, the moment at the pile top is lower under pulse type ground motions, but when the skew angle is more than 15°, the moment at the pile top is higher under pulse type ground motions, especially with densely compacted backfill.

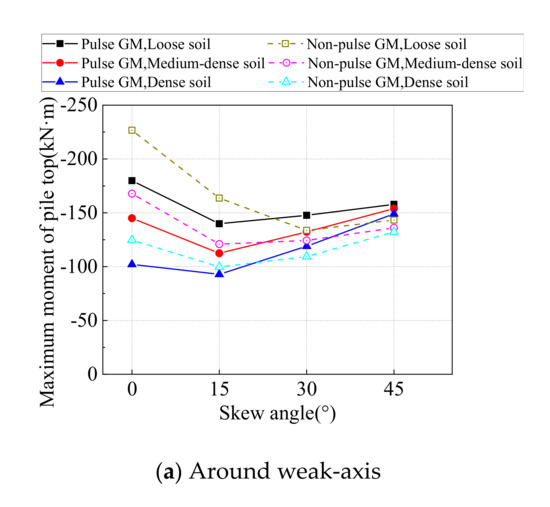
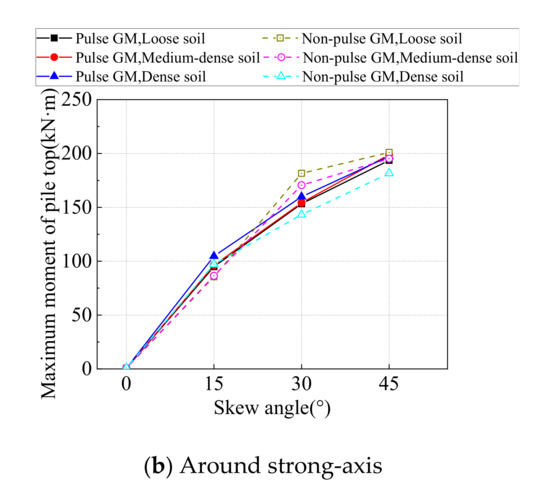
Figure 19. Maximum moment of pile top.

4.4.2. Yield Surface Function Value of Steel Piles

Since the steel H piles are under axial load as well as bi-axial bending, it is necessary to consider the P–M–M interaction on the pile cross-section. Therefore, a yield surface function $\phi$ is defined in this paper to characterize the internal force response of the steel H piles, as shown in Equations (5) and (6) below, based on the strength interaction equation from the literature [31,32]. When $\phi \ge 1$, the steel pile reaches a full-section yielding and a plastic hinge is formed.

$$\phi \left(N, M_x,M_y\right)={\left(\frac{M_x}{M_{pcx}}\right)}^{\alpha }+{\left(\frac{M_y}{M_{pcy}}\right)}^{\alpha }$$

(5)

$$\alpha =1.6-\frac{N/N_p}{2\ln \left(N/N_p\right)}$$

(6)

where $M_x$ represents bending moment about the strong-axis, $M_y$ represents bending moment about the weak-axis, $M_{pcx}$ represents the plastic flexural strength about the strong-axis under axial force N, $M_{pcy}$ represents the plastic flexural strength about the weak-axis under axial force N, $N$ represents the axial force, $N_p$ represents the axial compressive strength without considering bending moment and $\alpha$ represents the influence parameter of the axial force.

From the time-history analyses, it was found that the maximum bending moment was always located at the top. Therefore, only the $\varphi$ value at the pile top is discussed in this section, and the maximum $\varphi$ value at the pile top from time-history analyses on all SIAB models with varying skew angles and backfill compactness are shown in Figure 20. As shown in Figure 20, $\varphi <1$ for all cases, meaning that no plastic-hinge was formed at the pile top during the nonlinear time-history analyses. It is clear from the figure that under non-pulse type ground motions, the $\varphi$ value decreases with the backfill compactness, indicating that when the backfill is densely compacted, it decreases the normal stress in steel piles. For densely compacted backfill, the $\varphi$ value increases with the skew angle, but it is the opposite trend for loosely compacted backfill.

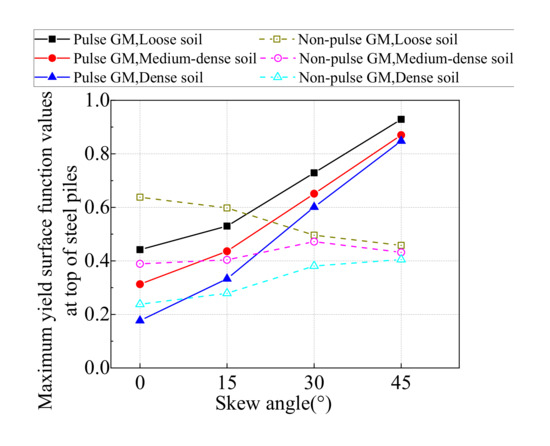
Figure 20. Maximum yield surface function value of the pile top.

Under pulse type ground motions, the $\varphi$ value still decreases with the backfill compactness, but it consistently increases with the skew angle for all types of backfill. For the densely compacted backfill, the $\varphi$ value with a 45° skew angle can be 4.8 times the value with no skew. In addition, when there is no skew, the $\varphi$ values are smaller under pulse-type ground motions than non-pulse type ground motions, but as the skew angle increases, the $\varphi$ values under pulse-type ground motions increases so sharply that they are about 2 times the value under non-pulse type ground motions, when the skew angle is 45° for all types of backfill. Therefore, the near-fault effects significantly increase the normal stress in steel piles, and amplify the influence of the skew angle.

5. Conclusions

Nonlinear dynamic response and seismic performance of skewed integral abutment bridges under near-fault pulse and far-field non-pulse type ground motions were investigated, and parametric studies were conducted on the bridge skew angle and the backfill compactness. The conclusions are as follows:

(1)

The longitudinal and transverse displacement of the abutment generally increases with the skew angle, mainly due to the decreased constraints of the backfill on abutment longitudinal displacements and the increased coupling between the longitudinal and transverse displacements of the bridge deck. The longitudinal and transverse displacement of the abutment generally decreases with the abutment backfill compactness. Under pulse type ground motions, the longitudinal and the transverse abutment displacement are obviously higher than the abutment displacements under non-pulse type ground motions, and the differences increase with the skew angle.

(2)

The bridge deck rotation generally increases with the skew angle due to the coupling between the longitudinal and transverse displacements, especially with densely compacted backfill. The deck rotation generally decreases with the abutment backfill compactness. Under pulse type ground motions, the bridge deck rotations are close and sometimes lower than the deck rotations under non-pulse type ground motions, except when the skew angle is 45° and with medium densely and loosely compacted backfill.

(3)

For SIAB, the resultant force from soil pressure does not pass through the mass center of the bridge, so the superstructure twists and leads to a non-uniform distribution of soil pressure behind the abutments. The pressure at the obtuse corner is always higher than the acute corner, and the ratio increases with the skew angle as well as the backfill compactness. The ratio is even higher under the pulse type ground motions.

(4)

The longitudinal deflection of the pile top first decreases and then increases with the skew angle, while the transverse deflection of the pile top always increases with the skew angle. The longitudinal deflection decreases with the abutment backfill compactness, and so does the transverse deflection, but to a lesser extent. When the skew angle is larger than 15°, both the longitudinal and the transverse deflection of the pile is higher under pulse type ground motions.

(5)

The moment around the weak-axis first decreases and then increases with the skew angle, while moment around the strong-axis always increases with the skew angle. The moment around the weak-axis and the strong-axis decrease with the abutment backfill compactness. When the skew angle is larger than 15°, the moment at the pile top is higher under pulse type ground motions, especially with densely compacted backfill.

(6)

Under non-pulse type ground motions, the yield surface function $\varphi$ value as well as the maximum normal stress on the steel pile cross-section decrease with the backfill compactness, and increase with the skew angle for densely compacted backfill. Under pulse type ground motions, the $\varphi$ value still decreases with the backfill compactness, but it consistently and sharply increases with the skew angle for all types of backfill. The near-fault effects significantly increase the yield surface function $\varphi$ value as well as maximum normal stress in steel piles, and amplify the influence of the skew angle.