Metamaterial Based Design of Compact UWB/MIMO Monopoles Antenna with Characteristic Mode Analysis

Abstract

In this article, a novel metamaterial inspired UWB/multiple-input-multiple-output (MIMO) antenna is presented. The proposed antenna consists of a circular metallic part which formed the patch and a partial ground plane. Metamaterial structure is loaded at the top side of the patches for bandwidth improvement and mutual coupling reduction. The proposed antenna provides UWB mode of operation from 2.6–12 GHz. The characteristic mode theory is applied to examine each physical mode of the antenna aperture and access its many physical parameters without exciting the antenna. Mode 2 was the dominant mode among the three modes used. Considering the almost inevitable presence of mutual coupling effects within compact multiport antennas, we developed an additional decoupling technique in the form of perturbed stubs, which leads to a mutual coupling reduction of less than 20 dB. Finally, different performance parameters of the system, such as envelope correlation coefficient (ECC), channel capacity loss (CCL), diversity gain, total active reflection coefficient (TARC), mean effective gain (MEG), surface current, and radiation pattern, are presented. A prototype antenna is fabricated and measured for validation.

1. Introduction

The multiple input multiple output system is all about the channel capacity, and it depends on bandwidth and signal to noise ratio. The low power requirements of the UWB system have earned significant attention in wireless high data rate [1]. The Federal communication commission has dispensed an unlicensed frequency spectrum of 3.1–10.6 GHz for ultra-wideband (UWB) frameworks [2]. One of the factors that affect the output of the UWB system is the limited channel capacity. To serve more users with better performance within the limited available frequency: bandwidth and transmission power are critical topics in the wireless communication industry [3]. To have a better performance, some have sought to allocate the operable spectrum dynamically, called spectrum collaboration [4], or increase the operable scope by operating at a millimeter frequency range proposed for a future fifth-generation (5G) [5]. Examples of these technologies are multiple-input-multiple-output (MIMO) methods [6,7] and full-duplex radio [8]. MIMO system is a more popular choice because multiplexing efficiency can be vastly raised without offering more frequency spectrum channel capacity [9]. MIMO techniques present a solution to overcome the channel capacity, antenna physical limits, and mutual coupling challenges [10]. Deployment of multiple antennas increases channel capacity and transmission range [11]. MIMO systems promise an increase in channel capacity without offering an additional spectrum of frequency and transmitted power. Many factors could undermine the system performance, especially in compact devices, because of many constraints imposed on MIMO antenna design due to some limitation in terms of area and electromagnetic interaction between the MIMO elements termed as mutual coupling. When several radiating pieces are situated close to each other, the fields generated by one antenna changes the current distribution on the different radiating elements. Therefore, each MIMO element’s impedance matching and radiation pattern are assigned based on the presence of other components [12]. This electromagnetic interaction between the antenna elements subverts the performance of the MIMO system. All the radiating features must be in a single aperture, making it a single multiport antenna design problem. The traditional array design concept that a single antenna element can be designed and then assembled into an array topology does not apply to compact devices. Some researchers use a multiport decoupling or matching network to reduce the antennas’ mutual coupling effect [13]. It is clearly shown that MIMO radiating elements should have more than one port, and it is desirable to have those ports being isolated and well-paired (for the fact that no matching network is connected). However, different applications will have other properties when it comes to design, like the base stations where the antenna’s size is not a problem in terms of the space. This implementation will be more comfortable. But for a much spacelimited application, this is not practical. For reduction the electromagnetic interactions and ample space between the radiating elements, some researchers used various innovative techniques known as defected ground structure [14,15,16], parasitic elements [17], neutralization line [18], and electromagnetic bandgap (EBG) configurations [19].

The modal analysis of the MIMO antenna helps to see some good thoughts regarding antenna arrays. The MIMO antenna designers cannot avail from this understanding without seeing how the modes influence the antenna’s performance parameters [20]. The use of modal analysis for antenna design and analysis was investigated in recent literature [21,22]. All this research work has significantly advanced the capability and application of characteristic mode theory. The linearity and orthogonality of the characteristic mode are potentially useful for MIMO system design. Different modes can be sorted differently, in which each mode can be excited as a MIMO channel resulting in the very low mutual coupling between other ports. This accounted for our employment of characteristic mode theory for the MIMO antenna design. Some impressive design has been presented in recent literature on modal analysis for MIMO antennas [23,24,25]. Some of them used chassis mode, and it relies on quite an amount of cuts and tries before reaching an optimal design. Recently, the metamaterial transmission lines have been used for various applications, such as antenna designs, filters, absorbers, couplers, mutual coupling reduction for multiple MIMO antennas, etc., in the microwave, millimeter-waves, and terahertz bands due to their interesting electromagnetic properties [26,27].

In this work, we use metamaterial in the form of a rectangular loop resonator and a slotted stub for mutual coupling reduction; we also look at MIMO antenna design from a modal perspective, that is, using the characteristic mode theory to get a physical insight regarding antenna operating principle without a particular feeding considered. The isolation level is improved below −20 dB with a notch behavior from 4 to 6 GHz and 10 to 11 GHz. The antenna is created on an accessible and generally utilized substrate. The MIMO system is designed using both time-domain analysis and multilayer solver analysis in commercial software computer simulation technology (CST). A detailed topology and analysis of the design are presented. A model is created to validate the simulated results. The comparison between the measured and simulated results is given, and it is discovered that they are in acceptable agreement.

2. UWB-MIMO with Characteristic Modes Theory and Metamaterial Structure

2.1. Characteristic Mode Theory

Modal analysis saw its initiation in the mid-1970s when Garbacz built up a generalized approach to enlarge the field transmitted from a conducting structure [28]. Nonetheless, the reformulation refined by Harrington and Mautz [29] considered the mode’s functional calculation utilizing the method of moments. This formulation is the reason for a large majority of the work, which uses mode analysis. As per Harrington, the part of an incident electric field tangential to the surface of at least one impeccably conducting body characterized by surface S is related to the current through a linear operator is explained in the following equation:

$$Z\left(J\right)=E_{itan},$$

(1)

where $Z\left(J\right)$ represents the symmetric operator of the induced current on the conductor surface S due to the incident E-field, and $E_{itan}$ is the incident E-field in the scatter problems or input power.

This linear operator can be gotten from Maxwell’s equations utilizing the magnetic vector potential A and the electric scalar potential $\varphi$ of the current flow from each point on a superficial level S and incorporating the appropriate free-space Green’s function the whole surface. The characterizing of two vector functions’ inner product on the surface S is given in the following equation:

$$\left(BC\right)={\int \int }_{t}B.Cds,$$

(2)

where $BC$ is the inner product over complex space, and $ds$ is the surface integral function.

If the Z operator is consider to be symmetric, then we have following equation:

$$\left(Z\right(B),C)=(B,Z(d\left)\right),$$

(3)

where $Z\left(d\right)$ is the Z operator over complex space This property is a result of the reciprocity of Maxwell’s equations in free space. By setting $Z=R+J_x,$ the following weighted eigenvalue problem is defined as in equation:

$$Z\left(I_n\right)=V_{n}R\left(I_n\right).$$

(4)

$V_n$ is the eigenvalues, the $I_n$ is the modal current, and R is a weight operator. By using $V_n=1+j$ and canceling the common terms $R\left(I_n\right)$ in (4), then the Equation (4) will be in the following form:

$$X\left(I_n\right)={\lambda }_{n}R\left(I_n\right).$$

(5)

Since X and R are a real symmetric operator, ${\lambda }_n$ is the eigenvalue, and the resultant eigenvalues and eigenvectors will be purely real. Therefore, we consider the eigenvectors [$I_n$] to be the modal surface current for the perfectly conducting surface S defined by the operator Z. For an electrically small radiator, a couple of modes are needed to describe the antenna’s behavior. Modes with small ${\lambda }_n$ are good radiators. Those with large ${\lambda }_n$ are poor radiators, while mode with ${\lambda }_n$ = 0, it is resonance [30,31]. The extend of eigenvalues, thus, tells how well a specific mode transmits. The modal significance is defined as in the following equation:

$$MS=|\frac{1}{1+j{\lambda }_n}|,$$

(6)

where $MS$ is the modal significance which is related to the conducting body’s shape, dimension, and frequency. But, it is port independent. The characteristic angle is defined in References [32,33] as:

$$\theta =180-ta{n}^{-1}\left({\lambda }_n\right).$$

(7)

Equation (7) above gives a clear explanation of how energy is stored in the 2 × 2 MIMO antenna. When the angle is at 180 degrees, the mode resonates when it is less than 180 degrees; the mode stores magnetic energy, and, when it is more significant than 180 degrees, the mode stores electric energy.

2.2. Metamaterial Structure

Figure 1 illustrates geometry of novel rectangular loop resonator designed on FR4 substrate with a relative permittivity of 4.3, thickness 1.6 mm. The unit cell metamaterial geometry posses an overall size of 3 mm × 4.8 mm. The structure is designed based on the analysis called floquet mode [34].

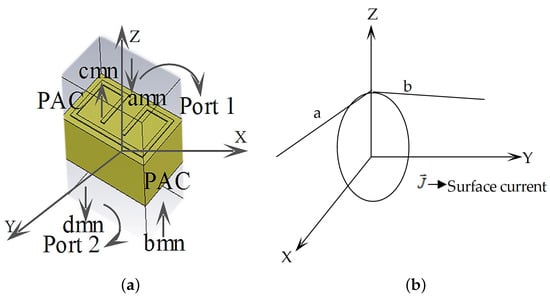
Figure 1. (a) Unit cell metamaterial. (b) Decomposition of surface current.

In Figure 1b above, the surface current $\overrightarrow{J}$ is mathematically defined as in the following equation:

$$\overrightarrow{J}\to f(x,y).$$

(8)

Therefore, the x components of the surface current can be represented as [35]:

$$\overrightarrow{J_x}(x,y)=\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }f(x-m_a,y-n_b),$$

(9)

where m is the number of unit cell on x-axis, and a is the dimension, while n is the number of unit cell on y-axis, and b is the dimension. Equation (9) can also be presented in phase radians as:

$$\overrightarrow{J_x}(x,y)=\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }f(x-m_a,y-n_b)e^{(-jk{x}_o{m}_a-jk{y}_o{n}_b)}.$$

(10)

$K_{xo}$ and $k_{yo}$ are the phase radians of x and y axis and can be defined as in Equations (11) and (12):

$$k{x}_o=k_{o}sin{\theta }_{o}cos{\theta }_o,$$

(11)

$$k{y}_o=k_{o}sin{\theta }_{o}sin{\theta }_o.$$

(12)

The unit cell will form a beam in a direction of (${\theta }_o$,${\varphi }_o$), considering the phase radians along the infinite array. Taking the Fourier transform of the surface current of Equation (10), we have:

$$\overrightarrow{J_x}(x,y)=\frac{4{\pi }^2}{ab}\overrightarrow{f}(k_x,k_y)\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }\delta (k_x-k_{xmn})\delta (k_y-k_{ymn}),$$

(13)

$$k_{xmn}=k_{xo}+\frac{2m\pi }{a},$$

(14)

$$k_{ymn}=k_{yo}+\frac{2n\pi }{b},$$

(15)

where $k_x$,$k_y$ represent the phase radians on x and y axis, $K_{ymn}$, $K_{xmn}$ shows the phase radians for the incident wave is from port 1 and port 2, and a, b is the dimension of the unit cell.

Transforming the Equation (13) in to time domain, we have:

$$\overrightarrow{J_x}(x,y)=\frac{4{\pi }^2}{ab}\overrightarrow{f}\left(x_y{k}_y\right)\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }{e}^{-}(-j{k}_{xmn}x-j{k}_{yny}),$$

(16)

where $\overrightarrow{J_x}(x,y)$ is the Fourier transform in time domain, and a and b remain the dimensions of the unit cell. From port 1 to port 2, as indicated in Figure 1a, we inject floquet mode and determine a general scattering metric (GSM) for the system:

$$\left[\begin{array}{c}{c}_{mn}^{TE}\\ c_{mn}^{TM}\\ d_{mn}^{TE}\\ d_{mn}^{TM}\end{array}\right]=\left[\begin{array}{c}GSM\\ GSM\\ GSM\\ GSM\end{array}\right]\left[\begin{array}{c}{a}_{mn}^{TE}\\ a_{mn}^{TM}\\ b_{mn}^{TE}\\ b_{mn}^{TM}\\ \end{array}\right],$$

(17)

where $a_{mn}^{TE}$ is the incident wave for transverse electric mode from port 1, $a_{mn}^{TM}$ is the incident wave for transverse magnetic mode from port 1, $b_{mn}^{TE}$ is the incident wave for transverse electric mode from port 2, $b_{mn}^{TM}$ is the incident wave for transverse magnetic mode from port 2, $c_{mn}^{TE}$ is the scattered transverse electric mode from port 1, $c_{mn}^{TM}$ is the scattered transverse magnetic mode from port 1, $d_{mn}^{TE}$ is the scattered transverse electric mode from port 2, and $d_{mn}^{TM}$ is the scattered transverse magnetic mode from port 2.

$$\left[\begin{array}{c}{c}_{mn}^{TE}\\ c_{mn}^{TM}\\ d_{mn}^{TE}\\ d_{mn}^{TM}\end{array}\right]=\left[\begin{array}{cccc}{S}_{11}^{TE}{,}^{TE}& S_{11}^{TE}{,}^{TM}& S_{12}^{TE}{,}^{TE}& S_{12}^{TE}{,}^{TM}\\ S_{11}^{TM}{,}^{TE}& S_{11}^{TM}{,}^{TM}& S_{12}^{TM}{,}^{TE}& S_{12}^{TM}{,}^{TM}\\ S_{21}^{TE}{,}^{TE}& S_{21}^{TE}{,}^{TM}& S_{22}^{TE}{,}^{TE}& S_{22}^{TE}{,}^{TM}\\ S_{21}^{TM}{,}^{TE}& S_{21}^{TM}{,}^{TM}& S_{22}^{TM}{,}^{TE}& S_{22}^{TM}{,}^{TM}\end{array}\right]\left[\begin{array}{c}{a}_{mn}^{TE}\\ a_{mn}^{TM}\\ b_{mn}^{TE}\\ b_{mn}^{TM}\\ \end{array}\right],$$

(18)

where $a_{mn}$ is the incident wave from port 1, $b_{mn}$ is the incident wave from port 2, $c_{mn}$ is the scattered wave from port 1, and $d_{mn}$ is the scattered wave from port 2. After placing the ground plane on port two, we will have only port one, and Equation (18) will be as in [36]:

$$\left[\begin{array}{c}{c}_{mn}^{TE}\\ c_{mn}^{TE}\end{array}\right]=\left[\begin{array}{cc}{S}_{11}^{TE}{,}^{TE}& S_{11}^{TE}{,}^{TM}\\ S_{11}^{TM}{,}^{TE}& S_{11}^{TM}{,}^{TM}\end{array}\right]\left[\begin{array}{c}{a}_{mn}^{TE}\\ a_{mn}^{TE}\\ \end{array}\right],$$

(19)

where $TE$ is the transverse electric mode; $TM$ is the transverse magnetic mode; $S_{11}^{TE}{,}^{TE}$ is the general scattering matrix for transverse electric mode; and $S_{11}^{TE}{,}^{TM}$ is the general scattering matrix for transverse magnetic mode

3. Topology and Analysis

The basic concept of the antenna designed methodology has been presented in Reference [37]. The layout and fabricated models of the proposed UWB/MIMO antenna are presented in Figure 2. The framework consists of two printed circular patches on top of the plane, and, at a ground plane, four slots were employed in both the upper and bottom layers to achieve wideband matching. Four rows of metamaterial structures were set around the two antenna components, which fill in as a decoupling network to combat the surface waves. Each row has three metamaterial components, which are adequate for perfect inductance. The total design space was 30 mm × 60 mm${}^2$. Two perturbed stubs were also utilized in the middle of the ground plane, which likewise fills in as a decoupling structure for isolation improvement. The decoupling network acts as a band-stop filter that generates transmission zeros within the transmitting components that upset the flow of current, surface waves, and near fields. Equivalent circuit model of the proposed antenna structure. Series left-handed capacitance ($C_L$), shunt left-handed inductance ($L_L$), shunt right-handed capacitance ($C_R$) and series right-handed inductance($L_R$) are realized by slots, unit-cells, gap distances between the ground-plane and top surface, and unwanted currents flowing on the surface, respectively. The circuit model is shown in Figure 3. The dimension of the MIMO antenna and associated parameters are shown in Table 1.

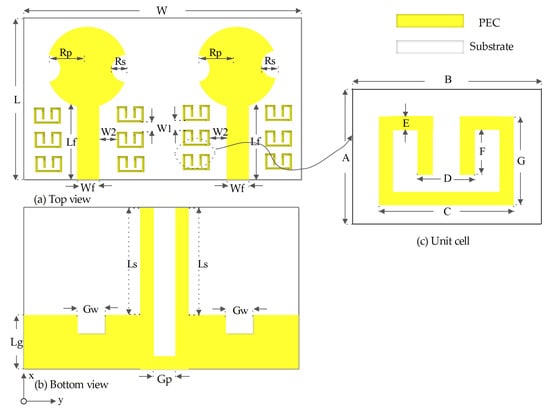
Figure 2. System model; (a) Top view, (b) bottom view, (c) unit cell.

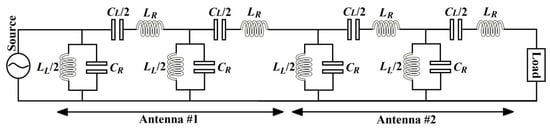
Figure 3. Equivalent circuit model of the proposed UWB/multiple-input-multiple-output (MIMO) antenna.

Table 1. Different parameters and size of the antenna.

Parameter	Size (mm)	Parameter	Size (mm)	Parameter	Size (mm)
L	30	W	60	$W_1$	$0.4$
A	3	B	$4.8$	C	$4.2$
$L_f$	$11.05$	$L_g$	10	$L_s$	20
$R_p$	$9.35$	$R_s$	$2.6$	$W_2$	5
$W_f$	$2.5$	$G_w$	3	$G_p$	$2.5$
D	1	E	$0.2$	F	$1.75$
G	$2.4$	H	$1.6$	D	10

3.1. Design Procedure for Single Element

An itemized evolution technique for the proposed set up is presented in Figure 4. In step 1, a round molded single component with an opened and partial ground plane is designed. The ground plane covers the region between the lower edge and the feed line. In step-2, two radiating patches with a common ground is made. In step three, six metamaterial segments were set around every radiator at the upper plane with two perturbed stubs at the ground plane to lessen the electromagnetic interaction between the MIMO components. The metamaterial structure and perturbed stubs suppress the surface waves reducing the electromagnetic interaction between the antenna components keeping it below −20 dB. The parametric analysis was also carried out to have an optimal value for the radius of the slots ($R_S$) as shown in Figure 5.

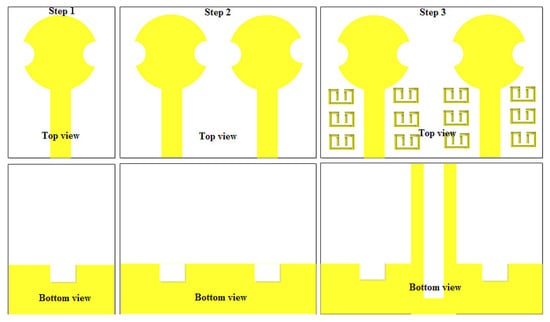
Figure 4. Evolution stages of the proposed UWB/MIMO antenna.

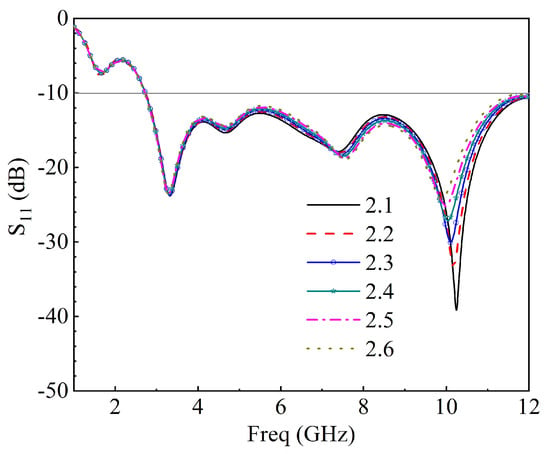
Figure 5. Effect of slot radius on the resonant frequency, $R_s$ (mm).

3.2. Modal Analysis of the MIMO Antenna

Characteristic mode analysis was employed to the 2 × 2 MIMO antenna without a feeding structure using a multilayer solver in CST version 2017. It conforms to the standardized amplitude of the current modes. This normalized amplitude does not depend on the feeding port but only on the conducting object’s shape and size. The first three modes’ modal significance at 5.2 GHz is presented in Figure 6; only mode 2 has an exactly modal significance of up to 1.0. The remaining mode has been shifted slightly; only mode 2 will dominate at this frequency response. At 10.6 GHz, only mode 2 has an exactly modal significance of nearly 1.0, mode 1 and mode 3 is not at 10.6 GHz; therefore, mode 2 will also dominate at this frequency as depicted in Figure 7. The characteristics angle for the MIMO antenna at mode 1, 2, and 3 is shown in Figure 6. A mode resonates when ${\lambda }_n=0$ that is when the characteristic curve is 180${}^{\circ }$. Figure 8 shows that mode 2 is almost at 5.2 GHz and remains the frequency of interest; from Figure 9, mode 2 is at 10.6 GHz or virtually at the resonance frequency of interest. It was clearly shown that, for all the two frequencies of interest, the characteristic angle is closer to 180${}^{\circ }$, which signifies that the mode is a good radiator. Figure 10 and Figure 11 present the eigenvalues for the three modes at the resonant frequency of interest. The results clearly showed that the three modes are resonant ${\lambda }_n=0$, but mode 2 is more dominant. For a more physical insight into the MIMO antenna design, Figure 12 shows the modal significance of three modes at 5.5 GHz, mode 2 being the dominant mode is at precisely 1.0. The characteristic angle of three modes at 5.5 GHz is also shown in Figure 13, and the eigenvalues for the three modes at 5.5 GHz is also presented in Figure 14.

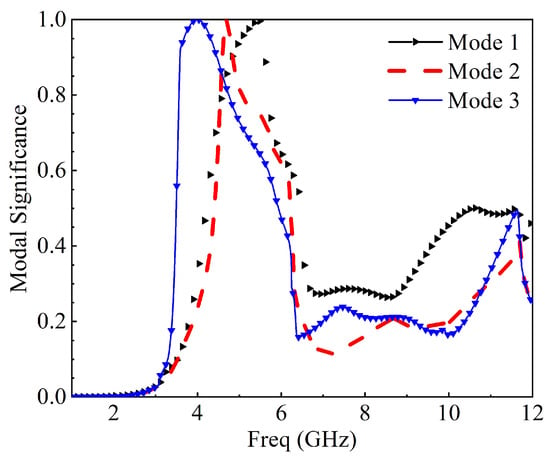
Figure 6. Modal significance at 5.2 GHz.

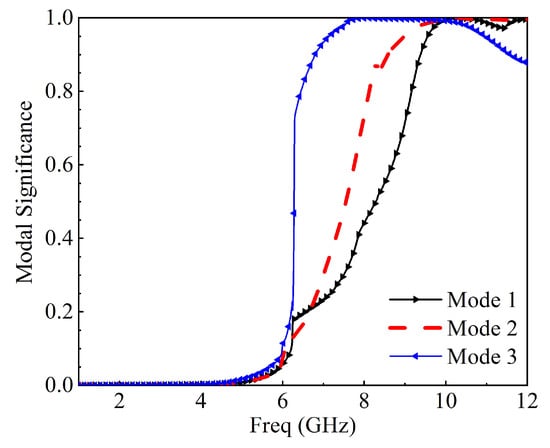
Figure 7. Modal significance at 10.6 GHz.

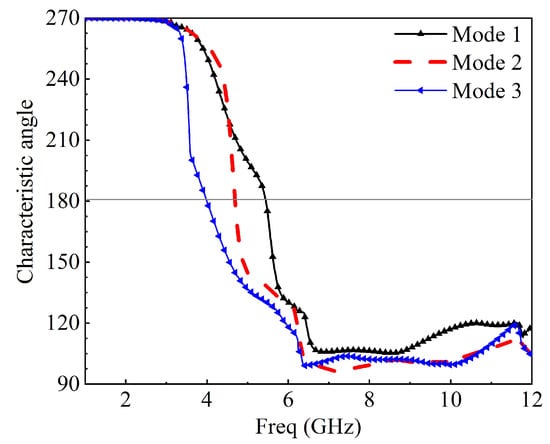
Figure 8. Characteristic angle curve of three modes at 5.2 GHz.

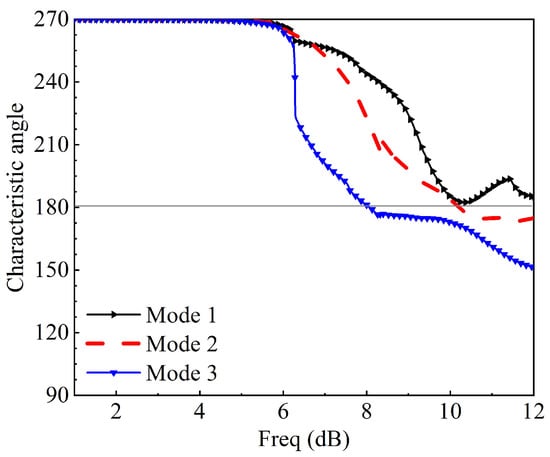
Figure 9. Characteristic angle curve of three modes at 10.6 GHz.

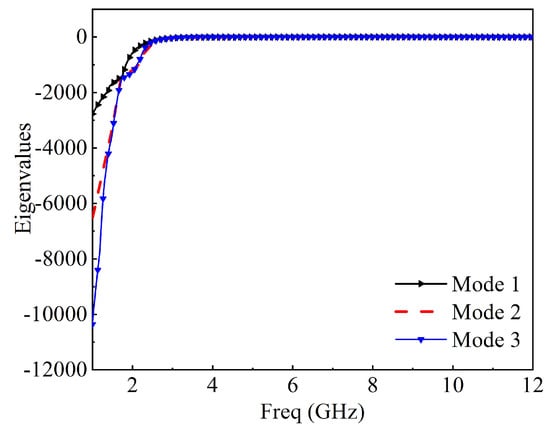
Figure 10. Eigenvalues of three modes at 5.2 GHz.

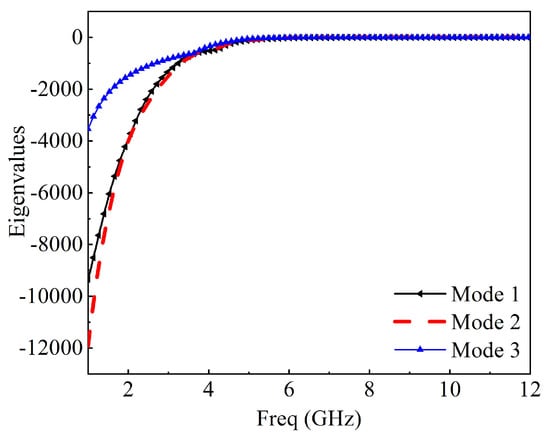
Figure 11. Eigenvalues of three modes at 10.6 GHz.

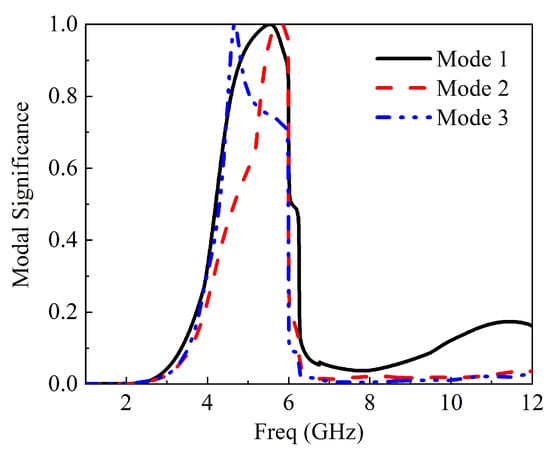
Figure 12. Modal significance at 5.5 GHz.

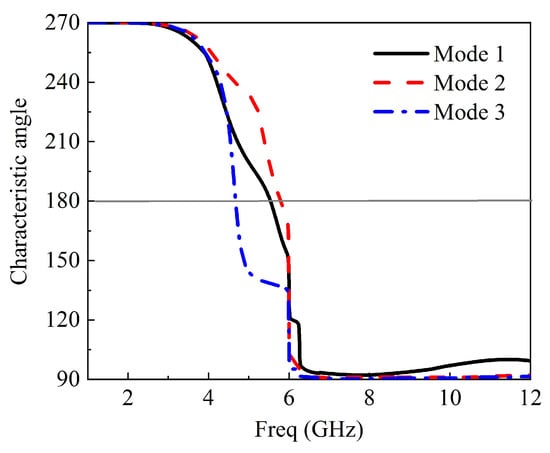
Figure 13. The characteristic angle of three modes at 5.5 GHz.

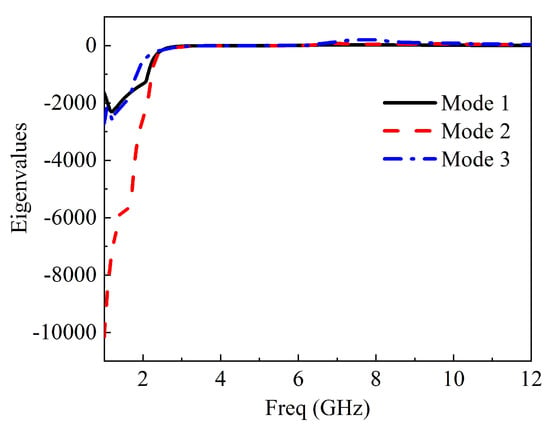
Figure 14. Eigenvalues of three modes at 5.5 GHz.

At 7 GHz, mode 2 has an exactly modal significance of 1.0, as depicted in Figure 15. The characteristic angle at 7 GHz for the three modes is shown in Figure 16. With mode 2 being the dominant mode, the value of 180${}^{\circ }$ is significantly closer compared to other modes. Figure 17 presented the eigenvalues of three modes at 7 GHz; all three modes are resonant.

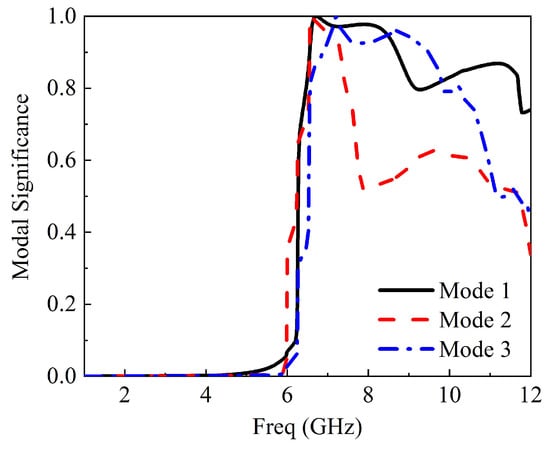
Figure 15. Modal significance at 7 GHz.

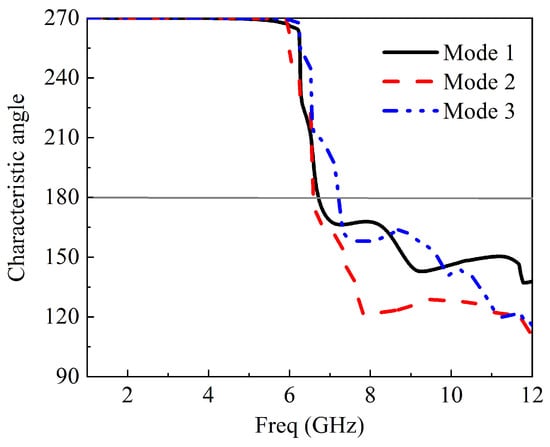
Figure 16. Characteristic angle for three modes at 7 GHz.

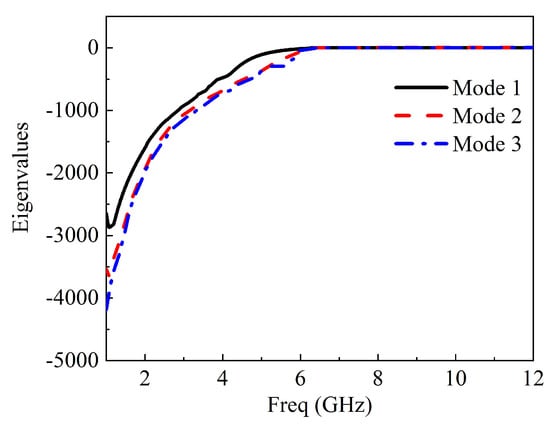
Figure 17. Eigenvalues for three modes at 7 GHz.

Figure 18 presents the normalized modal 3D radiation pattern of different modes at 5.2 GHz. Figure 19 illustrates the normalized 3D radiation pattern of three different modes at 10.6 GHz. We can see that mode 2, being the dominant mode, had more gain in all the two frequency responses than other modes.

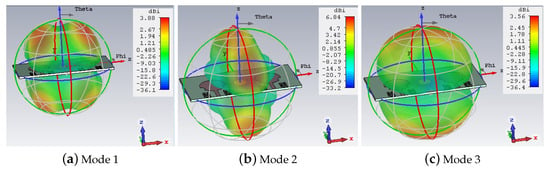
Figure 18. Normalized 3D radiation pattern of three modes at 5.2 GHz.

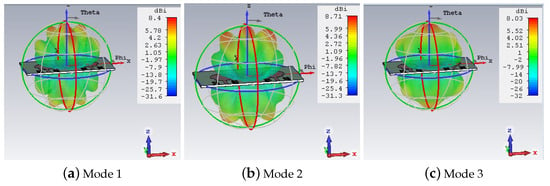
Figure 19. Normalized 3D radiation pattern of three modes at 10.6 GHz.

4. Experimental Results

The proposed MIMO antenna with a decoupling network was fabricated and measured utilizing a two-port vector network analyzer. The unit cell of the proposed metamaterial structure, shown in Figure 20, is used as a decoupling structure between the antennas for adequate isolation between them. The $S_{11}$ and $S_{21}$ of the unit cell are also presented in Figure 20. The measured and simulated S-parameter results for the proposed MIMO antenna appear in Figure 21 and Figure 22. The results were in good agreement. The isolation between the two radiating elements was below −20 dB. Together with the perturbed stubs, the metamaterial structure helps concentrate the surface waves within the decoupling frame, bringing about high isolation between the MIMO components. The $S_{21}$ with and without decoupling network can be seen in Figure 23. The current distribution with and without the metamaterial and perturbed stubs at 10.6 GHz is depicted in Figure 24. Gain is one of the basic parameters of the antenna. The MIMO antenna’s gain and total efficiency appear in Figure 25, and the efficiency is calculated as gain divided by directivity, as shown in Table 2. The maximum value of 5.5 dBi is at 5.5 GHz and a total efficiency of 89%. The measured and simulated far-field patterns have emerged for two different frequencies, i.e., 5.2 GHz and 10.6 GHz. The xz-plane and yz-plane radiation characteristics for 5.2 GHz are shown in Figure 26, while 10.6 GHz is also shown in Figure 27, respectively. The discrepancies between the measured and simulated are due to environmental factors and fabrication tolerance.

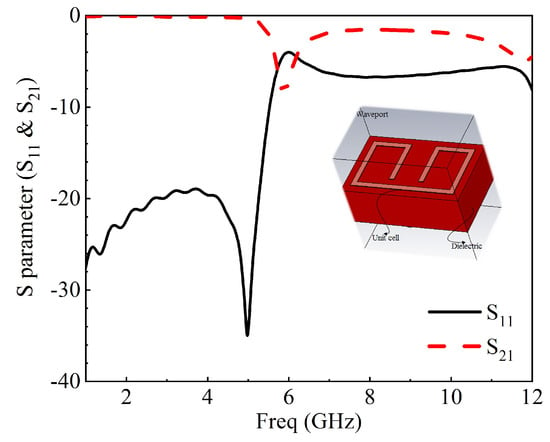
Figure 20. $S_{11}$ and $S_{21}$ of metamaterial unit cell.

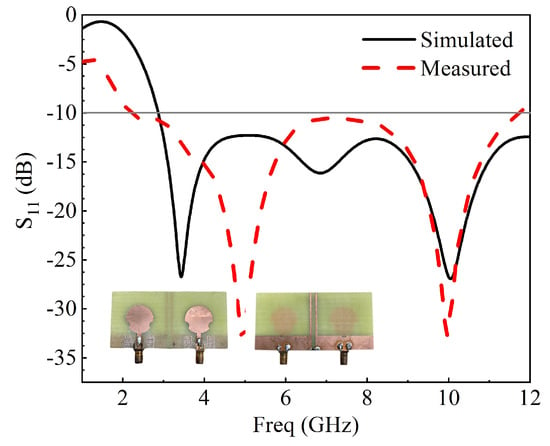
Figure 21. Measured and simulated $S_{11}$ of the designed antenna.

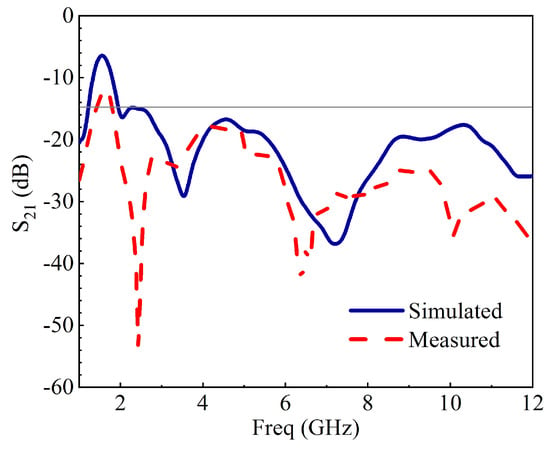
Figure 22. Measured and simulated $S_{21}$ of the designed antenna.

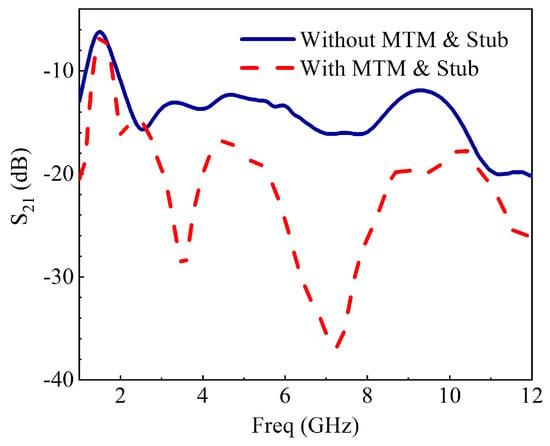
Figure 23. Simulated S-parameter with and without metamaterial.

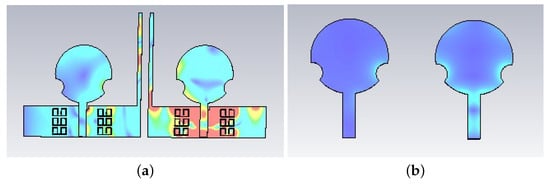
Figure 24. (a) Surface current distribution with metamaterial and stub. (b) Surface current distribution without metamaterial and stub.

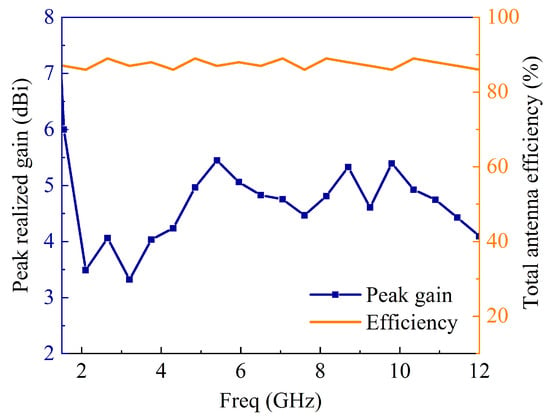
Figure 25. Antenna peak gain and efficiency.

Table 2. Calculation of total efficiency of the MIMO antenna.

Freq (GHz)	Gain (dBi)	Directivity	Efficiency
1.0	2.345364	2.650531	88.48657
1.5	2.234537	2.542113	87.90077
2.1	2.235137	2.571639	86.91488
2.6	2.544508	2.849149	89.30765
3.2	2.048274	2.331656	87.84632
3.7	2.281293	2.571777	88.70517
4.3	2.517722	2.921468	86.18003
4.8	3.103329	3.450808	89.74138
5.4	3.384417	3.888636	87.03352
5.9	2.876688	3.263257	88.15389
6.5	2.825989	3.353426	88.49395
7.1	2.700976	3.006092	89.85007
7.6	2.587078	3.002546	86.16281
8.2	2.982342	3.328644	89.59630
8.7	3.483621	3.781620	88.94656
9.3	2.890328	3.356058	87.69202
9.8	3.460307	3.992106	86.67873
10.4	3.460211	3.882106	89.13231
10.9	2.983070	3.355766	88.89386
11.5	2.733849	3.138083	87.118441
12	2.565467	2.917081	87.946405

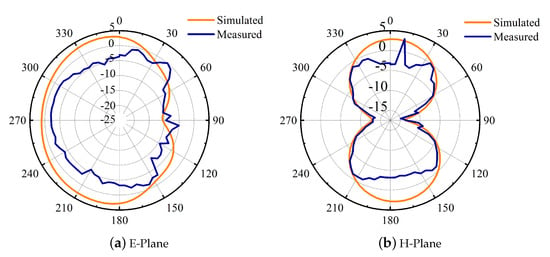
Figure 26. The measured and simulated far-field pattern for E and H plane at 5.2 GHz.

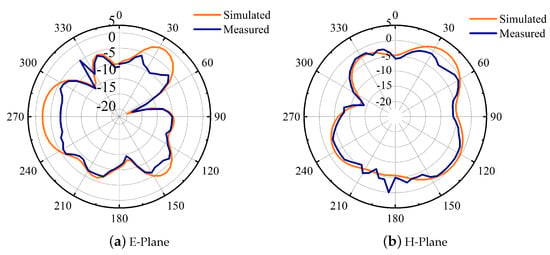
Figure 27. The measured and simulated far-field pattern for E and H plane at 10.6 GHz.

5. Diversity Analysis of the MIMO Antenna

In this section, some merits are used to evaluate the performance of the proposed MIMO antenna. These are the envelope correlation coefficient, total active reflection coefficient, channel capacity loss, mean effective gain, and diversity gain. They are evaluated using the S-parameters extracted from either the electromagnetic solver or the vector network analyzer. The envelope correlation coefficient (ECC) and total active reflection coefficient (TARC) are essential parameters to quantify signal interference between MIMO channels [38,39] to secure the MIMO antenna’s capability. TARC can be computed for a 2 × 2 MIMO antenna using the following equation:

$${\Gamma }_a^t=\sqrt{\frac{{\displaystyle \sum _{i=1}^N}|b_i{|}^2}{{\displaystyle \sum _{i=1}^N}|a_i{|}^2,}}$$

(20)

where $\Gamma$ is the symbol of reflection coefficient, t is the total, a is the active, $a_i$ is the incident signal, and $b_i$ is the reflected signal.

$$TARC=\sqrt{\frac{{|S_{11}+S_{12}{e}^j\theta |}^2+{|S_{22}+S_{21}{e}^j\theta |}^2}{2}},$$

(21)

where $\theta$ is the phase difference between the excitation difference of our MIMO antenna. The MIMO antenna’s TARC plot is given in Figure 28, with a difference of $\theta$ from 0${}^{\circ }$ to 180${}^{\circ }$ with an interval of 30${}^{\circ }$. The plot reveals that $0\le {\Gamma }_a^t\le 1$. The ECC $\left(\rho e\right)$ is computed from the far-field radiation pattern as in Equation (22) [40].

$$\rho e=\frac{|{\int \int }_{4\pi }[\overrightarrow{F_1}(\theta ,\varphi )\times \overrightarrow{F_2}(\theta ,\pi )d\Omega ]{|}^2}{|{\int \int }_{4\pi }\left[\overrightarrow{F_1}(\theta ,\varphi )\right]{|}^{2}d\Omega |\int \int 4\pi \left[\overrightarrow{F_2}(\theta ,\pi )\right]{|}^{2}d\Omega },$$

(22)

where $\overrightarrow{F_1}(\theta ,\varphi )$ is the farfield property of the MIMO array when port i is excited. The proposed MIMO antenna ECC was calculated from 1 to 12 GHz, as shown in Figure 29; it can be observed that ECC’s value is less than 0.002 through the UWB bandwidth and fulfills good diversity standard for a MIMO system [41].

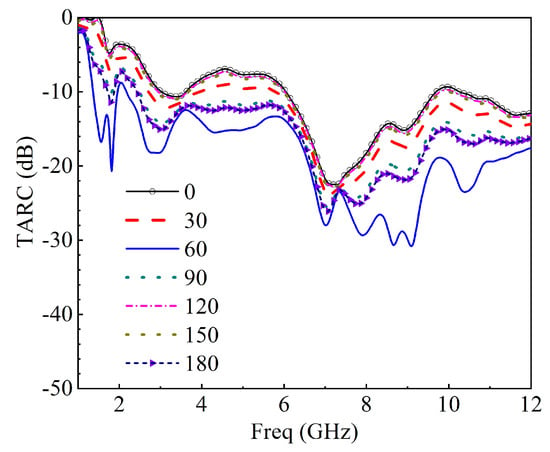
Figure 28. Total active reflection coefficient (TARC) of MIMO antenna system when $\theta$ changed from 0 to 180 degrees.

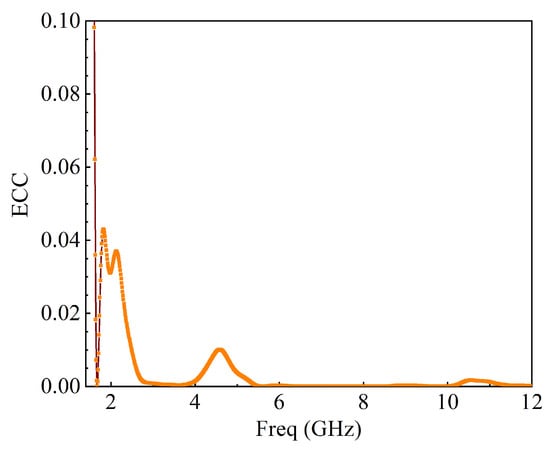
Figure 29. Envelope correlation coefficient (ECC) of MIMO antenna system.

Channel capacity can be defined as a data rate supported in a particular channel, and that channel is a fading environment [42,43]. Considering a high signal to noise ratio value, CCL can be evaluated from either measured or simulated S-parameters [44,45]. The CCL graph is shown in Figure 30; the plot uncovers that the channel capacity loss is less than $0.35$ over the whole UWB span because, in practical terms, $CCL<0.4$ bps/Hz. The capacity loss is given in the following equation:

$$C_{Loss=-}{log}_{2}det\left({\alpha }^R\right),$$

(23)

$${\alpha }^R=\left[\begin{array}{cc}{\alpha }_{11}& {\alpha }_{12}\\ {\alpha }_{21}& {\alpha }_{22}\end{array}\right],$$

(24)

$${\alpha }_{ii}=1-(\sum _{j=1}^N|S_{ij}{|}^2),$$

(25)

$${\alpha }_{ij}=-(S_{ii}^{*}{S}_{ij}+S_{ji}^{*}{S}_{ij}),$$

(26)

where ${\alpha }^R$ shows the S-Parameter matrix, and $S_{ii}$$S_{ij}$ represent $S_{11}$S11, $S_{12}$, $S_{21}$, and $S_{22}$, respectively.

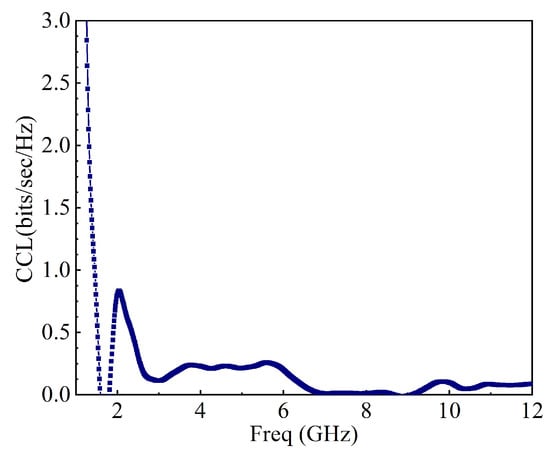
Figure 30. Channel capacity loss (CCL) of the MIMO antenna system.

The diversity gain of MIMO antennas can be computed from ECC using the relation [46]:

$$DG=10\sqrt{1-EC{C}^2},$$

(27)

where $DG$ is the diversity gain. In Figure 31, the diversity gain of nearly 10 dB is depicted; this signifies that the antenna has low polarization diversity that can give low mutual coupling.

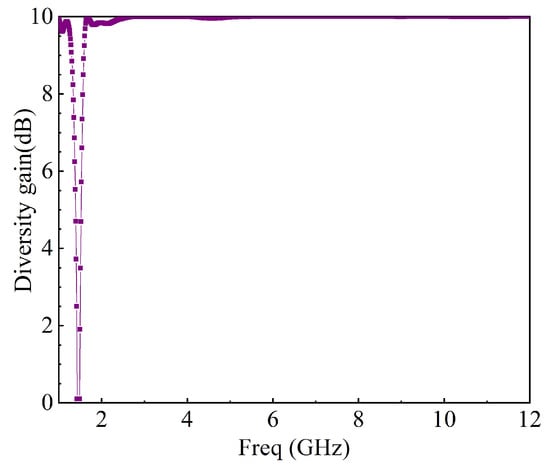
Figure 31. Diversity gain of the MIMO antenna.

The antenna mean effective gain (MEG) is defined as the ratio of the average power received at the microwave circuit to the sum of the average power of the vertically and horizontally polarized waves received by an isotropic antenna [47]. Figure 32 shows the MEG, which is less than −3 dB. It can be calculated as in following equation:

$$MEG=0.5[1-\sum _{j=1}^N|S_{ij}|].$$

(28)

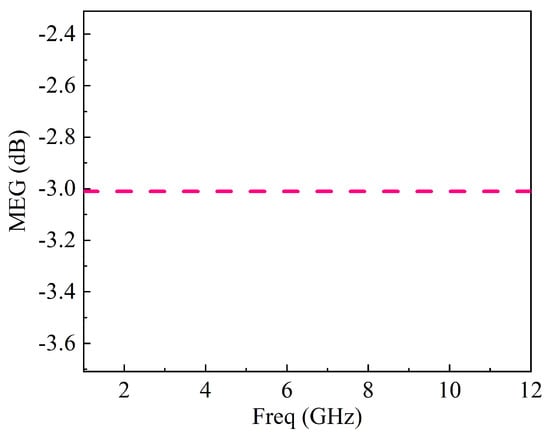
Figure 32. Mean effective gain (MEG) of the MIMO system.

The N is the number of antenna elements. A comparison between the proposed and the UWB-MIMO antennas presented in the literature regarding isolation approach/structure, size, frequency range, antenna spacing, envelope correlation coefficient (ECC), peak gain, and total efficiency is classified in Table 3. It is perceptible that the proposed MIMO antenna has high gain, high efficiency, and high isolation. Moreover, we extracted characteristic mode analysis at 5.2 and 10.6 GHz to gain more physical insight into antenna operating principles.

Table 3. Performance comparison with other antennas presented in the literature.

Ref.	Size (mm${}^2$)	Publ Year	Spacing (mm)	Freq (GHz)	Isolation (dB)	ECC	Gain (dBi)	Efficiency (%)
[3]	24 × 42	2020	NG *	3.5	NG *	NG *	4.9	86.4
[5]	33 × 48	2020	3	2–13.7	20	0.15	4.3	NG *
[20]	39 × 44	2018	7	NG *	24.5	0.1	4	NG *
[31]	32 × 64	2020	NG *	2.7–10.5	22.5	0.025	8.4	50
[32]	55 × 55	2019	NG *	5–6	32	0.0001	5.3	84
[33]	23 × 29	2016	NG *	3–12	15	0.15	4.7	82
[40]	70 × 150	2019	NG *	2.5–3.6	15	0.02	NG *	NG *
[41]	37 × 44	2020	5.82	NG *	23	0.1	4.25	82.4
[45]	26 × 26	2020	NG *	NG *	25	0.02	2.4	77
[46]	40 × 40	2020	NG *	2.4–2.48	25	0.21	2.36	NG *
This Work	30 × 30	2021	10	2.6–12	20	0.01	5.5	89

NG * = Not Given.

6. Conclusions

This paper presents a UWB-MIMO antenna with the isolation of −20 dB. The UWB response is achieved by designing a slotted shaped circular antenna. Simultaneously, the isolation is improved by using metamaterial structure on the upper plane and perturbed stub in the ground plane. Characteristic mode analysis is introduced to gain physical insight into antenna operating principles. The simulated design is fabricated, and performance parameters are calculated and measured. The simulated and measured results are in good agreement. The ECC, DG, TARC, CCL and MEG are $0.01$, 9.99 dBi less than 0 dB, less than 0.35 bps/Hz, and less than −3 dB, respectively.