Featured Application
The research results highlight a way to effectively combine the solution of elastohydrodynamics and the commercial multibody dynamics program.
Abstract
Currently, multibody dynamics simulations are moving away from issues exclusive to dynamics to more multiphysical problems. Most mechanical systems contain contact pairs that influence the dynamics of the entire mechanism, such as friction loss, wear, vibration and noise. In addition, deformation often affects the interaction between the contact bodies. If that is the case, this effect must be considered. However, a major disadvantage arises in that it leads to an increase in the number of degrees of freedom and the computational time. Often, the general-purpose multibody dynamics software does not take into account advanced phenomena, such as a lubricated contact pair. This paper can serve as a guide to implementing the elastohydrodynamic lubrication of rough surfaces into general-purpose multibody dynamics software (in this case MSC Adams), which remains challenging. In this paper, the deformation shape reconstruction of the reduced flexible bodies is described, as well as a solution to the increase in the computational speed issues thereby caused. To alleviate this burden, advanced sensitivity analysis techniques are used. In this paper, parallel computing has been employed. The proposed method leads to reasonable computational times for the multibody dynamics simulations, including elastohydrodynamic lubrication. The proposed method is applied to the multibody dynamics simulation of the piston–liner interaction of an internal combustion engine.
1. Introduction
Generally, mechanisms in the mechanical engineering industry consist of components in contact with one another. If a suitable combination of relative surface contact speed, load and viscosity is achieved, hydrodynamic lubrication occurs. Hydrodynamic forces differ from dry contact forces [1]. The magnitude of hydrodynamic forces depends not only on the relative speed of the contact surfaces and the load, but also on the properties of the lubricant and the shape of the gap between the contact surfaces.
There are applications where the hydrodynamic forces are small enough to cause significant deformation to the contact bodies; thus, affecting the hydrodynamic effect. Such cases include high-speed journal bearings and pad bearings. Contrarily, there are applications where the hydrodynamic forces are so great that they significantly affect the shape of the contact bodies, thereby affecting the distribution of the hydrodynamic pressure. This case of hydrodynamic lubrication is called elastohydrodynamic lubrication (EHL). Typical examples of EHL include rolling bearings, low-speed journal bearings and gear wheels. In some cases, deformation of the contact bodies is required to create a hydrodynamic phenomenon, thereby allowing for the correct function of the component, e.g., lip seals, piston rings and pistons of an internal combustion engine.
The dynamics of mechanical systems are typically solved using the theory of multibody dynamics (MBD). Industrial companies tend to use commercial MBD solvers rather than their in-house programs. Over decades of use of MBD systems, these companies have built proven solutions to solve specific issues they encounter. However, at present, to maintain their existence, they are pressured to push their products to the limits of possibility (companies operating in the automotive industry are a typical example). This also relates to the improvement of the development cycle, which is often based on computational modelling and subsequent experimental testing. When dealing with the dynamics of mechanical systems, companies are forced to expand their MBD simulations to include additional physical phenomena, creating multiphysical problems. In other words, the MBD models that use the basic solution of hydrodynamic lubrication must be extended with a more detailed EHL to uncover a gap in the design.
Linking an EHL and an MBD simulation is a typical coupled simulation problem. A detailed classification and historical overview of coupled simulations has been presented by Vaculín et al. [2]. One way to create an MBD model with EHL is to use a separate integrator for each subsystem. This is a weak-coupled co-simulation between the MBD software and another fluid dynamics program. During co-simulation, each subsystem solver conducts the integration of its states interacting with its environment only at communication points in which coupling variables are exchanged. This may be the root cause of unstable integration. Rahikainen et al. [3] presented a methodology to determine a stable configuration for computationally efficient non-iterative co-simulations, which are often found in real-time applications. Their work addresses multiphysical issues in the context of the simulation of machinery. Schweizer et al. [4] used a combination of higher-order approximation for interpolation/extrapolation of the coupling variables. They used relaxation techniques to avoid artificial oscillations in the Lagrange multipliers of the kinematic differential equations. Jäger and Vogel [5] applied co-simulation to calculate a squeeze-film damper designed to dampen the outer ring of the ball bearing of the jet engine. In this scenario, the dynamics were solved in MSC Adams, while the damper lubrication was calculated in MATLAB/Simulink. Similarly, Liao and Du [6] co-simulated an electric power steering control system and a full-vehicle dynamic model in an MBD system. Schörgenhumer et al. [7] combined the MBD solution and smoothed particle hydrodynamics solution to calculate the fluid–structure interaction.
Moreover, another way to generate an MBD model with EHL is through monolithic modelling. Monolithic modelling, sometimes called uniform, is based on the representation of all subsystems of a multiphysical problem using the same time integrator [8]. González et al. [9] investigated two coupling techniques: those in which only one tool performs integration (function evaluation), and those where each tool uses its own integrator (co-simulation). Function evaluation means that one software is performing numerical integration, while the other software returns values on request, as per the states passed to the integrator tool. This type of coupled simulation cannot be classified as co-simulation since only a single integrator performs the integration. This technique is popular in expanding the original simulation code with additional phenomena, which is originally not included.
The MBD software with a prepared EHL solution is commercially available. Often, the software is designed to be used in a specific industry, e.g., internal combustion engines [1,10,11,12,13]. These types of software offer fast computational time, though they are unable to solve problems of dynamics in other industries. Commercial general-purpose MBD software often do not include a solution to EHL. Therefore, it is necessary to create a coupled simulation in one of the above-mentioned ways. Another large group of MBD software with EHL are scientific software that have been developed at universities or research organizations. Generally, this type of software is intended for a specific group of users, as often there is no user-friendly interface or user manual [14].
The aforementioned MBD programs extended by EHL differ in their approaches to solving this phenomenon. The simplest approach is to use empirical approximation relationships that are designed for a given application. Tian et al. [15] applied such a simplified solution to the elastohydrodynamic contact of the teeth in a geared multibody system. A more advanced lubrication solution considers the premise of an infinitely short or infinitely long bearing. As per this assumption, it is possible to derive an analytic expression for the hydrodynamic pressure of a bearing [16]. Nevertheless, in the real world, the bearings have finite dimensions. Therefore, there is a more complex numerical solution to EHL that requires that the Reynolds equation to be solved either directly or iteratively. The Reynolds equation is numerically discretized, such as by the finite difference method [17], the finite volume method [18] or the finite element method [19].
Available MBD models with EHL differ according to the method of calculation of elastic deformation. Tian et al. [15] calculated the tooth deflection of the geared multibody system as the superposition of bending deflection (nonuniform cantilever beam), the deflection of the fillet and foundation, and the local contact and compression deflection (linearized Hertzian contact model with constant stiffness). At this point, it is worth noting that the Hertz contact theory [20] is adequate for the concentrated contact between two ellipsoids. For concentrated line contacts, as between two cylinders, the Hertz theory does not afford such a relationship, and the formulae for ellipsoids are invalid [21]. Li et al. [17] calculated the bearing deformation using a simplified Winkler model [22], where the deformable body is modelled as a set of spring elements neglecting the shearing action. The actual deformation at a point is only dependent on the contact pressure at that point, the material and the geometric parameters of contact bodies. The component mode synthesis is a universal and efficient method for calculating deformation in the MBD system. Krinner and Rixen [19] presented a comparison of three different reduction methods for elastic structures with lubricated interfaces (Craig–Bampton method, Craig–Bampton two-step method and the load dependent reduction strategy), which they applied to the slider-crank mechanism. The most complex and demanding way to calculate the body deformation in the MBD model is done by using the finite element method in co-simulation [23].
As can be determined from the literature, there are several techniques for solving EHL in the MBD system. These methods differ in complexity, universality and computational cost. However, there remain few articles describing a universal and effective solution to this multidisciplinary problem. This paper aims to offer a guide to implementing EHL into general-purpose MBD software using monolithic modelling. The advantage of monolithic modelling is that no additional licenses of other software are required, and the issue of weak-coupled co-simulation instabilities is eliminated. During the process of implementation of EHL into MBD software, there are several pitfalls. The existence of which and the solutions thereof are described in this paper. The novelty of this paper is, that it describes these problems in detail and it shows efficient ways of how to solve them. Some of the presented solutions can be further customized according to the industry of interest.
This paper is organized as follows: Section 2 describes the mathematical models of elastohydrodynamic lubrication and their numerical solution. In Section 3, these techniques are implemented in commercial multibody dynamics software. At this stage there is a problem with the computational speed, which in this case is solved by a parallel solution. Section 4 offers a summary of the main findings and suggestions for further improvements.
2. Computational Model
There are many commercially available general-purpose MBD software, e.g., MSC Adams, Recurdyn, and Simpack, among others. The software mentioned initially, MSC Adams, is used in this paper. The multibody dynamics software share the basic idea of dynamics modelling, so the procedures and principles in this paper may be applied to other MBD software as well. The chosen MBD software uses the Euler–Lagrange method to generate equations of motion in the form of:
where represents the generalized mass matrix, is the reaction force to the action force acting on the generalized coordinates of size , reflects the Lagrange multiplier, and indicates time. The generalized coordinates used here are Cartesian coordinates for position and Euler angles for the orientation of the body centroidal reference frames. If flexible bodies are present, the set of generalized position coordinates is augmented with the deformation modes. The solution must satisfy a set of kinematic constraint equations :
A total number of dynamic degrees of freedom is:
Equations (1) and (2) yield a system of differential algebraic equations that are solved for unknowns and . The solution can be found using numerical techniques, e.g., the backward differentiation formulas or the HHT integrator [24], which is based on the α-method proposed by Hilber, Hughes and Taylor [25]. The HHT integrator is second-order accurate, unconditionally stable, and presents high-frequency numerical damping to avoid numerical oscillations in the Lagrange multipliers. Therefore, the HHT integrator is favored in the integration of large finite element systems [26].
2.1. Elastic Deformation
The most commonly used method for calculating elastic deformation in the MBD system is through modal superposition, where the total body deformation is estimated as a linear combination of its mode shapes. In other words, the physical deformation is depicted by a small number of eigenvectors:
where represents the vector of linear deformations, and the modal matrix stores the vector of the modal coordinates of the mode shapes . Notably, the vector of modal coordinates is a subset of generalized coordinates. This means that the number of mode shapes used for the deformation calculus increases the number of degrees of freedom in the MBD model.
To correctly estimate the deformation, one must have a proper database of the mode shapes. To respect the boundary conditions, the component mode synthesis (in this case, the Craig–Bampton method [27]) is employed, as it enables the exclusion of the specific degree of freedom from modal superposition. The Craig–Bampton method belongs to a group of reduction methods that reduce the number of degrees of freedom of the finite element model. Krinner and Rixen [19] presented improved reduction methods for calculating the elastic deformation of a lubricated body in the MBD system and compared them with the original Craig–Bampton method [27]. These methods are applied in the finite element software so that the user must create their script or use the default script of the application of the reduction method. The result of the finite element software is a reduced body, called the modal neutral file, which represents an input to the MBD model.
The expensive projection of the load in physical form to the modal coordinates is used only once when creating the modal neutral file. This way is more advantageous than repeatedly calculating the projection during the simulation, because the MBD solver requires only the modal form of the load :
Equation (5) represents the most general way of estimating the modal force vector. Since this paper focuses on monolithic modelling of EHL in the MBD system (solution within one numerical integrator), the modal force is calculated within the user-written subroutine. The subroutine is called by the MBD solver whenever it must estimate the contact forces. Nevertheless, the use of Equation (5) in the subroutine bears the burden of high computational cost, as presented by Dlugoš et al. [28].
The magnitude of the modal force depends on the lubrication conditions of the contact pair. Moreover, the contact forces between the lubricated surfaces are carried by the lubricant or by the surface asperities, according to the distance of the contact surfaces. Based on the size of the ratio between these two contributors, the lubrication regime is identified as a boundary lubrication regime, a partial (mixed) lubrication regime or a hydrodynamic lubrication regime.
2.2. Regime of Hydrodynamic Lubrication
If the fluid film thickness is strong enough, it fully separates the contact surfaces. In addition to that, the lubricant flow is not significantly affected by the contact asperities. This is the case of the hydrodynamic lubrication regime and it occurs when the ratio between the nominal lubricant thickness and the composite surface roughness is significantly greater than three [29]:
The pressure distribution in the hydrodynamic lubrication regime can be described by the Reynolds equation [30], which is derived from the Navier–Stokes equations and the continuity equation, or from the equilibrium of the fluid element. The Reynolds equation is valid for Newtonian fluids and requires the fulfillment of several key assumptions, which can be found in [31]. The Reynolds equation in its universal form is:
where and are the coordinates in the circumferential and axial direction, reflects the hydrodynamic pressure, indicates the lubricant dynamic viscosity, reflects the lubricant density, and represent the velocities for body No. 1 and No. 2 in direction, and U1 and are the velocities for body No. 1 and No. 2 in direction. The hydrodynamic lubrication causes the shear stress:
where and indicate the shear stress in the and direction, respectively.
2.3. Regime of Partial Lubrication
The partial lubrication regime occurs when the lubricant film thickness respects the following inequations [29]:
In this case, the surface asperities have a strong influence on the lubricant flow. The universal Reynolds Equation (7) does not consider this effect. Therefore, the Average Reynolds equation developed by Patir and Cheng [29] has to be employed:
where represents the mean hydrodynamic pressure, and are the pressure flow factors, is the shear flow factor, and represents the average film thickness [32].
Similar to the mean hydrodynamic pressure, the shear stress formula takes into account the effect of the surface asperities:
where and indicate the shear stress factors, and represents the averaging factor. The numerical solution to Equation (11) is presented in the Numerical Solution Section. In addition to hydrodynamic lubrication, in a partial lubrication regime, some of the contact forces are carried by the surface asperities. The calculation of this phenomenon is identical to that of the boundary lubrication regime, and it is described in the following section.
2.4. Regime of Boundary Lubrication
When the nominal film thickness is less than or equal to the combined surface roughness:
the contact forces are carried predominantly by the surface asperities. This is the case of the boundary lubrication regime. Several computational models have been developed to capture the effect of asperity contact [20,33,34]. However, the most popular theory of the rough surface contact remains to be that conceived by Greenwood and Tripp [35] (or Greenwood and Williamson [36]). According to their work, the formula for the asperity contact pressure takes the form:
where indicates the surface density of roughness peaks, reflects the average radius of the curvature of the rough surface asperities, and represents the function describing the increase in the contact pressure dependent on the thickness ratio [35]. Parameter is:
where indicates the combined elastic modulus:
where and represent the elastic modules of each of the contact surfaces, and v1 and represent their Poisson’s ratios. Coulomb’s law of friction is valid for the asperity contact:
where indicates the asperity contact frictional force, represents the contact area, and indicates the dry friction coefficient.
From a vibration point of view, contact asperities can lead to a random excitation of resonances—a phenomenon called the Tribofilm–Asperity Interaction. The vibrations then affect the pressure distribution in the lubricant layer. It is a stochastic process and is not considered in the case of this manuscript. More details can be found in Ref. [37].
2.5. Numerical Solution
When dealing with EHL, it is crucial to adequately load the contact surfaces, as the distribution of hydrodynamic pressure, shear stress, contact pressure and friction of the asperity contact have a significant influence on the elastic deformation of the contact bodies and vice versa. Due to this, the force interaction between the contact bodies is simulated by the modal force of Equation (5), where the forces are applied to the boundary nodes on the contact surfaces.
Depending on the lubrication regime, two solutions to hydrodynamic lubrication, the universal Reynolds Equation (7) and Average Reynolds Equation (11), were presented in the previous section. The Average Reynolds equation is simply the universal Reynolds equation augmented by the flow factors. Since the flow factors compare the flow in a rough bearing with that of a smooth bearing, their effect disappears with the thick film thickness. This effect can be observed in the dependence of the flow factors on the oil film thickness available in Ref. [32]. Therefore, the Average Reynolds equation is more general and can be used in both partial lubrication regime and hydrodynamic lubrication regime.
In this paper, only the Average Reynolds equation is used. In practical terms, flow factor data may not be available for a contact pair of interest. In this case, it is more suitable to begin with the universal Reynolds equation. A simpler model imitates the crawl–walk–run approach and is easier to debug. Then the model should be refined using the Average Reynolds equation.
The Reynolds equation (in both forms) can be further simplified for a specific application of interest. First, the lubricant density can be considered constant with a certain level of simplification [37,38]. In this way, the hydrodynamic pressure does not depend on the lubricant density value. In addition, further simplification can be achieved if some surfaces move in one direction, and the surface velocity in other directions are neglected. If one of the bearing dimensions is significantly smaller than the other, the pressure gradient (the Poiseuille term) in the large dimension direction is negligible. This is the essence of the solution of an infinitely short and infinitely long bearing. In this case, it is possible to derive an analytic expression of the hydrodynamic pressure for these simplified bearings.
If a finite length bearing is investigated, the Reynolds equation is solved numerically. It is classified as a nonlinear partial differential equation. These types of equations may be discretized by either the finite difference method, the finite volume method or the finite element method. In the case of this manuscript, the finite difference method is used—each derivative is replaced with an approximate difference formula at each nodal point, and the new set of equations is generated. There are three approaches to the solution of this new set of equations: the relaxation (iterative) methods, the direct matrix methods and the rapid methods (Fourier methods, for example) [39]. In the case of this manuscript, the Gauss–Seidel iteration method with the overrelaxation parameter is used. The solution of the discrete node is as follows:
where indicates the dimensionless pressure of the previous iteration , reflects the residuum, and represents the Jacobian. Moreover, the Chebyshev acceleration can be used for the overrelaxation parameter estimation [39]. The Gauss–Seidel method uses updated values of the solution as they become available, which is observable from the residuum calculus:
The iteration converges when:
where is the criterion, and is estimated as:
where and represent the grid sizes in the and direction. The established value of the criterion is .
2.6. Deformation Reconstruction
The nominal film thickness determines the magnitude of the hydrodynamic forces and asperity contact forces. Among others, these forces depend on the exact position of the contact surfaces, as well as on the actual load applied, or the operational deformation. Thus, the subroutine (calculating the force effects) must estimate the actual deformation response of the contact bodies to be able to yield adequate force values.
In general, the MBD solver has no variables as the deformation of each nodal point. Instead, it stores the information about the deformation in the variables termed modal coordinates. To estimate the deformation of each node, the subroutine asks the MBD solver for the modal coordinates of all active mode shapes and then reconstructs the deformed shape according to Equation (4).
In addition to deformation, the calculation of the lubricant squeeze effect, which is the last term of the Average Reynolds Equation (11), requires the time derivative of the deformation. Therefore, the MBD solver returns the time derivation of the modal coordinates as well. Considering deformation, one active mode shape is represented by two system variables in the subroutine. This is essential for the improvement of the computational speed, as described in the Results and Discussion Sections.
2.7. Deformation and Force Mapping
During the MBD simulation, the computational grids of contact surfaces overlap. The ideal shape of contact bodies such as a ball, cylinder or plane, is a myth. In fact, the contact bodies have a true shape determined by the manufacturing process. In addition, operational steady-state temperature deformation can also be a contributor to the true shape. The solution to elastohydrodynamics requires knowledge of the deformation and the true shape of the contact bodies. Therefore, mapping algorithms are inevitable. The Cubic Hermite spline is sufficient for this task. After the evaluation of hydrodynamic and asperity contact forces, they must be mapped to the structural grids (used for the evaluation of the deformation) of the contact bodies. If a cubic spline is used for the force effects mapping, the MBD solver struggles to find a converged solution and unacceptable computational time occurs. This is the result of not guaranteeing that the pressure distribution of the source field is statically equivalent to the pressure distribution of the target mapped field.
Thus, the force effects are mapped using analytic integration, and the discrete field of the pressures is replaced by the continuous function p, defined by shape functions N:
The shape functions are bilinear:
The function is then integrated for each half grid element of the structural grid:
Numerical integration is trivial, since the function p(v,w) is analytically defined as bilinear. This way, the pressure distribution of the source field is statically equivalent to the pressure distribution of the target mapped field. Mapping through analytical integration is advantageous for different structural and hydrodynamic grid sizes. The deformation of the contact body is well represented by the coarse mesh. Nevertheless, the hydrodynamic grid requires a fine mesh. For simulations where the same fine mesh is used for the structural and hydrodynamic grid, the computational time becomes excessive. Therefore, it is effective to use different structural and hydrodynamic grid sizes and map data between them.
3. Results and Discussion
To demonstrate the functionality and pitfalls of the above-described computational model, it has been applied to solve the MBD of the interaction between the piston and the liner of an internal combustion engine. In this case, the consideration of the deformation is crucial, since it affects the piston dynamics, thereby dramatically affecting the overall engine performance. As already mentioned, MSC Adams is used as the MBD software. The EHL is implemented by the user-written subroutine, which consists of all features described in the previous sections, such as the hydrodynamic lubrication, the asperity contact, the iterative solution of contact forces, the deformation reconstruction, etc.
The process of solving the MBD simulation is shown in Figure 1. First, the MBD model (Figure 2) is constructed, which consists of rigid bodies, flexible bodies and boundary conditions. Subsequently, the equation of motion is created and it is sent to the solver. As soon as the solver needs to quantify the forces in the contact interface, it sends the necessary inputs to the subroutine in the form of modal coordinates (deformation) and other generalized coordinates, e.g., current piston position. The subroutine processes these data along with other user inputs, calculates forces based on the current piston–liner lubrication regime, and provides the solver with the modal force acting. The force action affects the current deformation and the position of the force interaction, and therefore it is an iterative process.
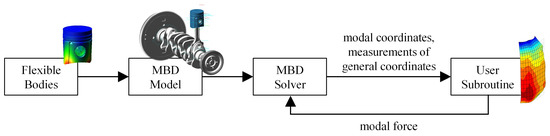
Figure 1.
The MBD modeling procedure.
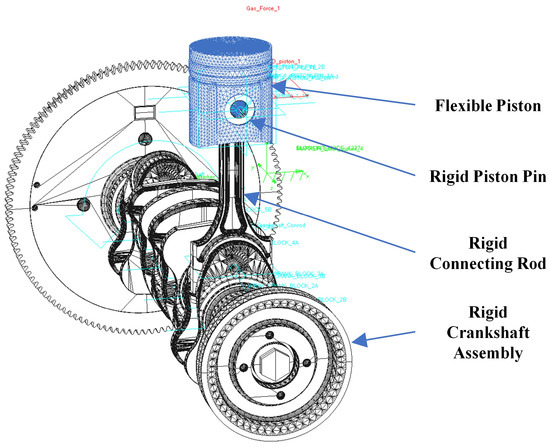
Figure 2.
The MBD model of piston–liner interaction. Crankshaft assembly is connected to the engine block via revolute joint with motion applied. Other revolute joints are between the crankshaft asembly-connecting rod and the connecting rod–piston pin. The piston pin is connected to the piston via joint primitives. The gas force is applied at the center of the piston bowl and the modal force is applied on the entire piston flexible body. The engine block is represented as a ground.
The first trials of this computational model required unacceptable computational time due to the excessive number of degrees of freedom within the subroutine. To resolve this issue, one must investigate the design sensitivity analysis performed by the MBD solver, which is described in the following section.
3.1. Design Sensitivity Analysis
The Jacobian matrix of the system of equations quantifies the trends in the MBD system. This matrix is crucial for estimating the solution during the predictor phase. Thus, it heavily influences the convergence rate of the solution. To find a converged solution as quickly as possible, the MBD solver must track the behavior of the subroutine, which is the relationship between inputs and outputs. This is a typical task for sensitivity analysis. In the case of the modal force subroutine, the sensitivity analysis consists of the evaluation of the partial derivatives:
where indicates the modal force components for the mode shape of number . Not all generalized coordinates of the whole MBD system affect the subroutine directly. Usually, the subroutine uses only selected subset of generalized coordinates which are available through the measurements of the system state provided by a functional interface:
f(L(q)).
Thus, the term (26) takes the following form:
The analytical relationship between the generalized coordinates and the measurements is known, so the partial derivative can be calculated analytically. The other partial derivative can be calculated using either the finite forward difference method, the automatic differentiation method, the direct differentiation method or the adjoint variable method.
The finite forward difference method approximates the partial derivative by the finite difference. This method is the most broadly used technique, as it is easily implemented and treats the derived function as a black box. However, it has two major disadvantages. First, the subroutine must be evaluated times to estimate the partial derivatives. Second, the accuracy of this method is strongly related to the perturbation step size used.
The analytical methods, namely, the automatic differentiation method, the adjoint variable method or the direct differentiation method, offer other approaches to acquire the solution to the design sensitivity analysis. The automatic differentiation method is comprised of a set of techniques that can decompose the complex algorithm into elementary operations (subtraction, addition, division, multiplication, etc.) and elementary functions (sin, cos, exp, log, etc.). This decomposition enables the chain rule to be applied so that the derivative of a composite function (two or more elementary functions) may be computed. This process is applicable even on very complex functions [40].
The adjoint variable method introduces an additional set of differential equations that comprise the adjoint variables. These equations are derived according to the variational theory, and they can be solved using numerical integration [41]. Solving a sequence of adjoint relationships yields the design sensitivity vector, which directly corresponds to the sensitivity of the performance measures in terms of design variable variations [42].
Moreover, the direct differentiation method is another analytical technique to determine the gradient information. Compared with the adjoint variable method, the direct differentiation method is more advantageous for a smaller number of design variables (a detailed comparison of these two methods is given in Refs. [43,44]). The direct differentiation method is based on the differentiation of the equations of motion with respect to the design parameters, thereby producing differential equations for the sensitivity functions [43]. The advantage of direct differentiation is that the dynamic and sensitivity equations are simultaneously integrated in time, resulting in effective control of the time integration errors [45].
The MBD solver in this paper uses the finite forward difference method for the sensitivity analysis as the default setting. The reference modal force is perturbated by step in the direction of measurement so the approximate value of the partial derivative may be calculated:
where
This approach is time-consuming, especially if it is serially computed as it is in the case of the MBD solver MSC Adams. Nevertheless, the modal force calculus for each measurement in the subroutine is independent and may be parallelized. For the ability to parallelize the solution to Equation (29), one must know the size of the perturbation step . It must be estimated appropriately so that the calculated sensitivity analysis, hence Jacobian, will be as accurate as possible. The optimal perturbation step size depends on individual measurements. Therefore, the perturbation step calculation is demonstrated in the MBD simulation of the piston–liner interaction in the following section.
3.2. Perturbation Step
The first eight measurements in the piston–liner subroutine are piston lateral displacement, piston tilt angle, piston lateral velocity, piston tilt angular velocity, piston axial position, piston reciprocating velocity, crank angle and cylinder pressure (Figure 3). The perturbation step sizes for these eight measurements (not related to the deformation of bodies), which were estimated using the default serial finite forward differencing method, were recorded during one operational cycle of the crankshaft mechanism. The evolution of the relative perturbation steps (the ratio between the actual and initial perturbation step) is depicted in Figure 4.
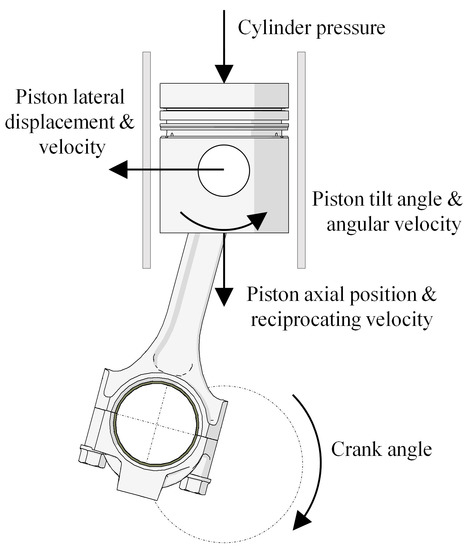
Figure 3.
Subroutine’s measurements not related to the deformation for the multibody dynamics model of the piston–liner interaction.
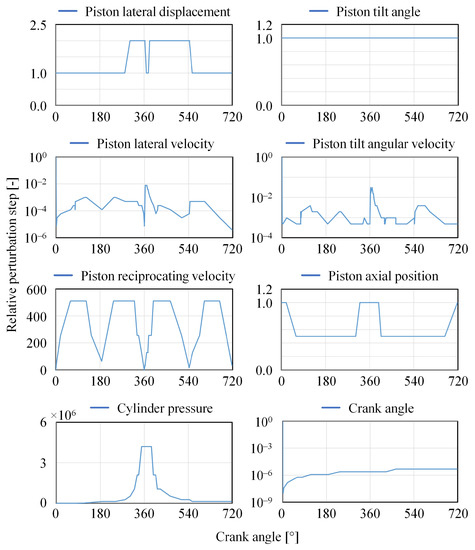
Figure 4.
Relative perturbation steps of subroutine’s measurements not related to deformation. The values are plotted depending on the crankshaft angular position.
The relative perturbation steps of the measurements piston lateral displacement, piston axial position and piston tilt angle do not significantly change their sizes during the simulation. This does not hold for other measurements, such as the piston reciprocating velocity and the cylinder pressure, which change their perturbation steps, sometimes quite rapidly—the piston lateral velocity, piston tilt angular velocity and crank angle are depicted in Figure 4 by the scale logarithmic scale. Figure 4 illustrates the perturbation step size adjusted as per the current simulation conditions so that the optimal value may be estimated. For instance, the trend of relative perturbation steps of the measurements of the piston axial position and piston reciprocating velocity represents the typical piston primary motion of the crankshaft mechanism. This also applies to the measurement of cylinder pressure when the related perturbation step adapts according to the pressure in the combustion chamber of a four-stroke internal combustion engine.
As previously mentioned, the MBD solver is able to adapt the perturbation step size to the actual simulation conditions (change in the measurement). This way, the Jacobian is estimated effectively, and small number of iterations is necessary to find the converged solution. Unfortunately, some MBD solvers are unable to pass these effectively estimated perturbation steps to the subroutine (the case of the MBD solver used in this paper). However, most of the measurements in the subroutine of EHL are related to the deformation (the modal coordinates and their time derivatives), and their perturbation steps tend to remain nearly constant throughout the simulation.
3.3. User-Calculated Sensitivity Analysis of a Subroutine
The following algorithm is proposed to calculate the sensitivity analysis of the subroutine within the subroutine: record the perturbation steps of all measurements in the subroutine during the first Jacobian evaluation. Let the partial derivatives for the first eight measurements (those not related to the deformation) be calculated by the MBD solver using the default serial finite forward difference method. Let the rest of the partial derivatives of the sensitivity analysis be calculated by the subroutine using the same serial finite forward difference method with the use of the perturbation steps estimated during the first Jacobian evaluation. If the solution struggles to converge, update the perturbation steps. The scheme of the algorithm is depicted in Figure 5, and it is used by the user finite forward difference (User) method.
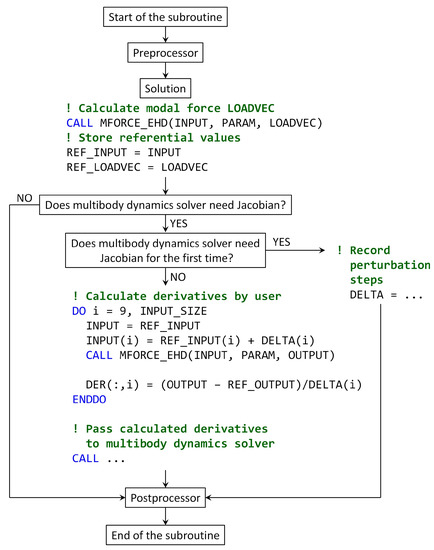
Figure 5.
Scheme of sensitivity analysis of the subroutine using the User finite forward difference method for deformation-related measurements in Fortran. The modal force LOADVEC is calculated using function MFORCE_EHD based on measurements INPUT and parameters PARAM. If the multibody dynamics solver is calculating the Jacobian for the first time, the subroutine records the perturbation steps DELTA. Otherwise, the subroutine calculates the partial derivatives of Equation (29), stores them in DER, and passes them to the multibody dynamics solver.
The User method was applied to the MBD model of the piston–liner interaction (20 mode shapes of the flexible piston only—first six modes are depicted in Figure 6) and compared with the default finite forward difference (Default) method. For numerical solution, the HHT integrator was employed with the following settings: integrator tolerance 10−6, step size 8.3 × 10−5 s, a maximum number of iterations of 10 and the original corrector. The Intel® Core™ i7-4770S 3.1 GHz processor with four physical cores and eight virtual cores was used.
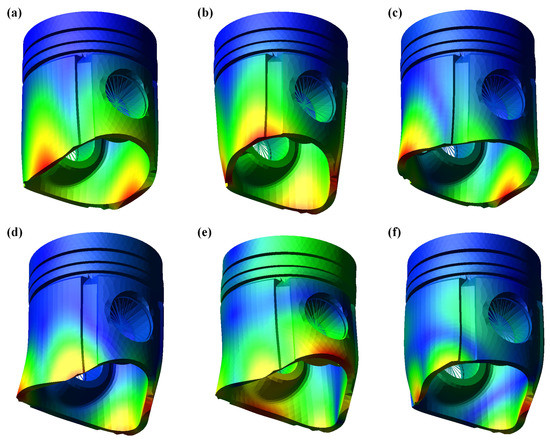
Figure 6.
First six mode shapes of flexible piston: (a) 5,4883 Hz; (b) 6320 Hz; (c) 9597 Hz; (d) 10,434 Hz; (e) 11,370 Hz; (f) 13,458 Hz.
A comparison of the results using the Default method and the User method is indicated in Table 1. Both simulations led to very similar elapsed times. The Default method required 25 min and 10.4 s while the User method was slower with elapsed time of 25 min and 20.2 s. The Default method also needed fewer iterations to converge of 7877 compared to 8311 of the User method. According to these results, the Jacobian quality is not degraded by the user serial finite forward difference method (for the measurements related to the deformation) and it merits further investigation. From the perspective of maximum CPU usage, the complexity of a particular MBD simulation (only 48 measurements in the subroutine) and a serial sensitivity analysis solution cannot sufficiently utilize the hardware capabilities.

Table 1.
Computational speed of the simulation using the Default and with the User method for a reduced number of mode shapes.
3.4. Parallel Solution
A DO loop of the User method in the previous section (Figure 5) consists of the calls that are independent. Therefore, this loop can be effectively parallelized (Figure 7)—the parallel user finite forward difference (Parallel) method. In this case, Open MP is employed in order to parallelize the subroutine coded in the Fortran programming language.

Figure 7.
Scheme of Parallel user finite forward difference method, illustrating the parallelization of the sensitivity analysis of the subroutine for deformation-related measurements.
The Parallel method was used in the same MBD simulation of the piston–liner interaction with reduced number of flexible piston mode shapes. Table 2 presents the results. As expected, the maximum CPU utilization increased, in this case, from 18.5 to 46.5%. This resulted in an acceleration of the computation time from 25 min and 10.4 s to 17 min and 38.7 s (acceleration 1.43 times). The use of the Parallel method required 5.51% more iterations compared to the Default method, the results of which are presented in Table 1. These results show that the Parallel method significantly accelerated the simulation, even if only a low number of the flexible body mode shapes were used. The larger the number of the mode shapes included, the greater the acceleration of the parallel solution.

Table 2.
Computational speed of the simulation with the Parallel method for a reduced number of mode shapes.
Until now, the parallel solution to the sensitivity analysis of the subroutine has only been applied to a simplified analysis with a flexible body with 20 mode shapes. To properly include elastic deformation of the bearing surface, all nodes on that surface should be the boundary nodes in the component mode synthesis. If each boundary node has three degrees of freedom in the finite element model, the number of degrees of freedom in the MBD simulation is increased by three times the number of boundary nodes. Fortunately, the dominant load of a journal bearing is radial, meaning that only the radial degree of freedom of each boundary node of the computational grid can be excluded from the modal superposition during the modal neutral file creation. This leads to a significant reduction in the number of degrees of freedom in the MBD model. However, there are still many boundary nodes on the bearing surfaces that significantly increase computational time.
In the demonstrative case of this paper, the MBD model of the piston–liner interaction consisted of a box-type flexible piston with two piston skirts, each containing 29 circumferential and 17 axial nodes. This led to an increase in the mode shape count by 986. The subroutine had measurements related to the modal coordinate as per each mode shape as well as the time derivative of the modal coordinates. Therefore, the parallel DO loop for the Parallel method ran 1972 times. In each of these runs, the iterative solution of hydrodynamics is computed. Therefore, the parallel solution should rapidly decrease the computational time.
To confirm these assumptions, two MBD simulations were computed, and both used all 992 piston mode shapes enabled. The first simulation utilized the Default method. The other simulation utilized the Parallel method, which led to promising results in the previous simulation with a much lower mode shape count.
The presented results (Table 3) were obtained by the 2 × processor Intel® Xeon® E5 2640 0 2.5 GHz with twelve virtual cores (six physical cores), and the integrator settings were the same as in the previous simulations. The elapsed time above 78 h of simulation with the Default method was caused by very low CPU usage (maximum of 5.6%). On the contrary, the Parallel method led to the maximum CPU usage of 100%, resulting in a reduction in the elapsed time, by almost ten times, to a value of approximately 8 h. In addition, the Parallel method required fewer iterations to find the converged solution: 9987 versus 11597 iterations. The Default method used perturbation steps, which were periodically updated as per a certain number of iterations. As previously mentioned, the Parallel method used perturbation steps estimated during the first call for the Jacobian unless the MBD solver struggled to converge. In this case, the perturbation steps used by the parallel solution seem to lead to a more accurate Jacobian matrix. However, this cannot be regarded as a general rule, as it is likely to be a characteristic of the current simulation and solver settings. According to several study cases it can be concluded that the Parallel method reduces the elapsed time by an order of magnitude as per the above-specified hardware and the DO loop size around 2000 runs.

Table 3.
Computational speed of the simulation with the Default and the Parallel method for the full number of mode shapes.
By analyzing the simulation results, when the piston reached the expansion mid-stroke (an approximately 450° crank angle), the MBD solver struggled to find the converged solution. Although the simulation with the Parallel method led to a similar number of iterations (Figure 8), the design sensitivity analysis was solved much quicker, as was the simulation (Figure 9). Convergence issues during the lower expansion stroke occur due to the small oil film thickness between the piston and the liner at the anti-thrust side. The solver struggles to balance between the deformation and the pressure distribution due to the boundary or mixed lubrication regime.
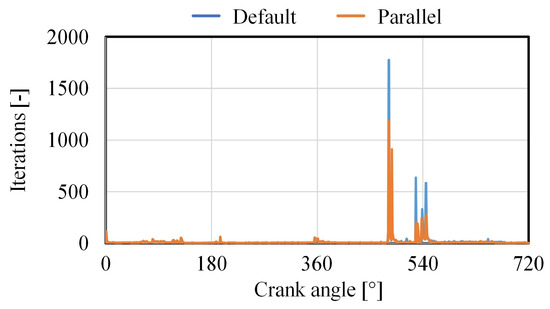
Figure 8.
The number of iterations of the piston–liner multibody dynamics simulation with elastohydrodynamic lubrication. The values are plotted depending on the crankshaft angular position.
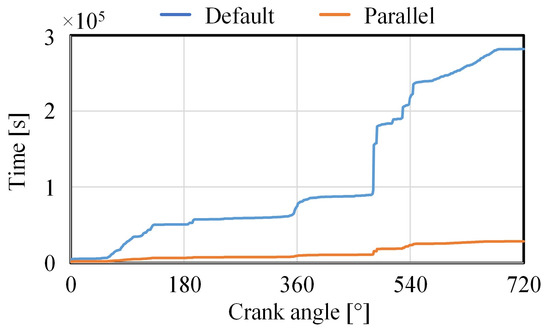
Figure 9.
Cumulative elapsed time of the piston–liner multibody dynamics simulation with elastohydrodynamic lubrication. The values are plotted depending on the crankshaft angular position.
3.5. Hydrodynamic and Elastohydrodynamic Solution to the Piston–Liner Interaction
The purpose of this paper is to present a guide to implementing EHL into the general-purpose MBD software utilizing monolithic modelling. The MBD model of the piston–liner interaction of a small spark-ignition engine was used as a demonstration example, and therefore, not all details were given as they were not relevant. For the sake of completeness, the following text focuses on pertinent results of this particular computational model, which could be applicable to other simulations.
The differences between the hydrodynamic solution (omitting the deformation) and the elastohydrodynamic solution were studied. The piston secondary motion is one of the key elements when investigating the design of the piston and liner. It consists of the piston lateral displacement and the piston tilt angle. Figure 10 depicts the change in the piston lateral displacement when the deformation of the piston skirt is neglected (the positive direction is towards the piston thrust side). The most significant difference between the hydrodynamic and the elastohydrodynamic solution occurs in the expansion stroke when the driving force of the piston secondary motion—the side force—reaches its highest values. The high deformation of the piston skirt allows the piston to travel further in a lateral direction.
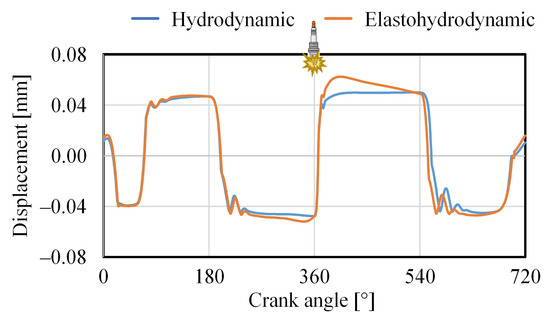
Figure 10.
Piston lateral displacement dependent on the crankshaft angular position. The firing occurs near a crank angle of 360°.
The specific height ratio is a parameter that represents the asperity contact and wear of the contact pair surfaces. It is the ratio between the surface distance and the composite surface roughness. Figure 11 indicates this ratio on the thrust side of the piston for the hydrodynamic and the elastohydrodynamic solution. If the piston is considered as a rigid, the minimal value of the specific height ratio is 3.15 at a 439° crank angle. Enabling the piston to deform, the minimum value is increased to 4.76 at a 542.5° crank angle. If the limit value of the specific height ratio is set to three [29,32], the hydrodynamic solution might limit the piston–liner design while there is still room for improvement. This may be crucial for the optimization of internal combustion engines restricted by emission directives and regulations.
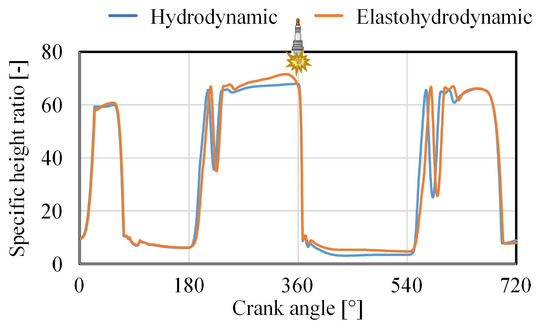
Figure 11.
Piston thrust side minimum oil film thickness dependent on the crankshaft angular position.
4. Conclusions
In some cases, the solution to EHL is required to properly assess the functionality and performance of the design of the mechanism, and examples are not hard to find. An internal combustion engine has several components, such as a piston group, cam followers, gears, etc., where EHL plays a critical role. To analyze these components, general-purpose MBD software is often used. However, not every general-purpose MBD software has a prepared option to solve the advanced lubricated contact pair. Therefore, it must be augmented with these physical effects. To keep the simulation within one software, monolithic modelling is advantageous. In this case, the EHL is implemented in the MBD solver using the user-written subroutine. This brings challenges that may be solved as follows.
During the solution to the MBD simulation, the overlapping of structural and hydrodynamic grids occurs. Thus, data from one grid must be mapped onto another grid. To transfer the deformation and true shape data, a cubic Hermite spline is a precise option.
A cubic spline is not sufficient to map the force effects and leads to solution instabilities. On the contrary, mapping by analytical integration respects the equivalence between the source and target mapped field and is suited for mapping force effects. This type of mapping is recommended when different structural and hydrodynamic grid sizes are used. This is advantageous as the size requirements of these grids differ heavily. The deformation is well represented by the coarse mesh. However, the hydrodynamic solution requires a fine mesh. In this case, where the same fine mesh is used for the structural grid, the computational time becomes excessive.
The introduction of EHL in the MBD model causes an increase in the number of degrees of freedom, thereby causing an increase in the computational time. If the sensitivity analysis is solved serially by the finite forward difference method, the computational time may be unacceptable. If the MBD solver allows for the use of a more advanced method, such as the adjoint variable method, the direct differentiation method or the automatic differentiation method, it is highly recommended to do so. The Parallel method proposed and verified in this paper reduces the computational time by an order of magnitude.
The parallelization of the design sensitivity analysis requires minor changes to the subroutine’s code. The accuracy of this method is determined as per the perturbation step size used. In general, the optimal perturbation step size changes during the MBD simulation. Nevertheless, it does not change significantly for the measurements related to the deformation. Therefore, in this case, the perturbation step sizes estimated at the beginning of the simulation can be used for the rest of the simulation without significantly reducing the accuracy of the Jacobian.
Author Contributions
Conceptualization, J.D.; methodology, J.D.; software, J.D.; validation, P.N.; writing—original draft preparation, J.D.; writing—review and editing, P.N. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results has received support from Specific research of Brno University of Technology, project No. FSI-S-20-6267.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Offner, G.; Herbst, H.M.; Priebsch, H.H. A Methodology to Simulate Piston Secondary Movement under Lubricated Contact Conditions; Society of Automotive Engineers, Inc.: San Marcos, TX, USA, 2001. [Google Scholar]
- Vaculín, O.; Krüger, W.R.; Valášek, M. Overview of coupling of multibody and control engineering tools. Veh. Syst. Dyn. 2004, 41, 415–429. [Google Scholar] [CrossRef]
- Rahikainen, J.; González, F.; Naya, M.Á. An automated methodology to select functional co-simulation configurations. Multibody Syst. Dyn. 2020, 48, 79–103. [Google Scholar] [CrossRef]
- Schweizer, B.; Lu, D.; Li, P. Co-simulation method for solver coupling with algebraic constraints incorporating relaxation techniques. Multibody Syst. Dyn. 2016, 36, 1–36. [Google Scholar] [CrossRef]
- Jäger, S.; Vogel, S. Validation of a squeeze-film-damper test rig by using multibody cosimulation. Multibody Syst. Dyn. 2015, 34, 243–257. [Google Scholar] [CrossRef]
- Liao, Y.G.; Du, H.I. Cosimulation of multi-body-based vehicle dynamics and an electric power steering control system. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 2005, 215, 141–151. [Google Scholar] [CrossRef]
- Schörgenhumer, M.; Gruber, P.G.; Gerstmayr, J. Interaction of flexible multibody systems with fluids analyzed by means of smoothed particle hydrodynamics. Multibody Syst. Dyn. 2013, 30, 53–76. [Google Scholar] [CrossRef]
- Samin, J.C.; Brüls, O.; Collard, J.F.; Sass, L.; Fisette, P. Multiphysics modeling and optimization of mechatronic multibody systems. Multibody Syst. Dyn. 2007, 18, 345–373. [Google Scholar] [CrossRef]
- González, F.; González, M.; Mikkola, A. Efficient coupling of multibody software with numerical computing environments and block diagram simulators. Multibody Syst. Dyn. 2010, 24, 237–253. [Google Scholar] [CrossRef]
- Back, A. Elasto-hydrodynamic bearing model in powertrain multi-body simulation. SAE Int. J. Engines 2018, 11, 215–227. [Google Scholar] [CrossRef]
- Knoll, G.; Bargende, M.; Lang, J.; Philipp, U.; Lazzara, M. Piston pin in mixed friction contact. MTZ Worldw. 2009, 70, 54–60. [Google Scholar] [CrossRef]
- Berberich, N.; Knoll, G.; Groß, T.; Fischersworring-Bunk, A.; Kornprobst, W.; Spitznagel, T. Functional optimization of the piston-cylinder system. MTZ Worldw. 2009, 70, 42–48. [Google Scholar] [CrossRef]
- Perchanok, M. Modeling of Piston-Cylinder Lubrication with a Flexible Skirt and Cylinder Wall. 2000. Available online: https://www.sae.org/publications/technical-papers/content/2000-01-2804/ (accessed on 6 February 2021).
- Meng, F.M.; Zhang, Y.Y.; Hu, Y.Z.; Wang, H. Thermo-elasto-hydrodynamic lubrication analysis of piston skirt considering oil film inertia effect. Tribol. Int. 2007, 40, 1089–1099. [Google Scholar] [CrossRef]
- Tian, Q.; Xiao, Q.; Sun, Y.; Hu, H.; Liu, H.; Flores, P. Coupling dynamics of a geared multibody system supported by ElastoHydroDynamic lubricated cylindrical joints. Multibody Syst. Dyn. 2015, 33, 259–284. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J.; Claro, J.P. Dynamic analysis for planar multibody mechanical systems with lubricated joints. Multibody Syst. Dyn. 2004, 12, 47–74. [Google Scholar] [CrossRef]
- Li, P.; Chen, W.; Li, D.; Yu, R. A novel transition model for lubricated revolute joints in planar multibody systems. Multibody Syst. Dyn. 2016, 36, 279–294. [Google Scholar] [CrossRef]
- Duyar, M.; Bell, D.; Perchanok, M. A Comprehensive Piston Skirt Lubrication Model Using a Mass Conserving EHL Algorithm. 2005. Available online: https://www.researchgate.net/publication/326319550_Piston_dynamics_lubrication_and_tribological_performance_evaluation_A_review (accessed on 6 February 2021).
- Krinner, A.; Rixen, D.J. Interface reduction methods for mechanical systems with elastohydrodynamic lubricated revolute joints. Multibody Syst. Dyn. 2018, 42, 79–96. [Google Scholar] [CrossRef]
- Hertz, H. Ueber die Berührung fester elastischer Körper. J. Reine Angew. Math. 1881, 92, 156–171. [Google Scholar]
- Gummer, A.; Sauer, B. Modeling planar slider-crank mechanisms with clearance joints in RecurDyn. Multibody Syst. Dyn. 2014, 31, 127–145. [Google Scholar] [CrossRef]
- Põdra, P.; Andersson, S. Wear simulation with the Winkler surface model. Wear 1997, 207, 79–85. [Google Scholar] [CrossRef]
- Antunes, P.; Magalhães, H.; Ambrósio, J.; Pombo, J.; Costa, J. A co-simulation approach to the wheel–rail contact with flexible railway track. Multibody Syst. Dyn. 2019, 45, 245–272. [Google Scholar] [CrossRef]
- Negrut, D.; Rampalli, R.; Ottarsson, G.; Sajdak, A. On an Implementation of the Hilber-Hughes-Taylor method in the context of index 3 differential-algebraic equations of multibody dynamics (DETC2005-85096). J. Comput. Nonlinear Dyn. 2007, 2, 73–85. [Google Scholar] [CrossRef]
- Hilber, H.M.; Hughes, T.J.R.; Taylor, R.L. Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq. Eng. and Struct. Dyn. 1977, 5, 283–292. [Google Scholar] [CrossRef]
- Bauchau, O.A. Flexible Multibody Dynamics, 1st ed.; Solid Mechanics and Its Applications; Springer: New York, NY, USA, 2011; ISBN 978-94-007-0334-6. [Google Scholar]
- Craig, R.R.; Bampton, M.C.C. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
- Dlugoš, J.; Novotný, P.; Raffai, P. Difficulties in computational modelling of piston/liner interaction. Vibroeng. Procedia 2016, 7, 134–137. [Google Scholar]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Reynolds, O. On the Theory of lubrication and its application to Mr. Beauchamp Tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Stachowiak, G.W.; Batchelor, A.W. Engineering Tribology, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2014; ISBN 978-012-3977-762. [Google Scholar]
- Patir, N.; Cheng, H.S. Application of average flow model to lubrication between rough sliding surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Pasaribu, H.R.; Schipper, D.J. Application of a deterministic contact model to analyze the contact of a rough surface against a flat layered surface. J. Tribol. 2005, 127, 451–455. [Google Scholar] [CrossRef][Green Version]
- Lagemann, V. Numerische Verfahren zur tribologischen Charakterisierung bearbeitungsbedingter rauher Oberflächen bei Mikrohydrodynamik und Mischreibung. Dissertation, Kassel. 2000. Available online: https://www.tib.eu/en/search/id/TIBKAT%3A322166365/Numerische-Verfahren-zur-tribologischen-Charakterisierung/ (accessed on 6 February 2021).
- Greenwood, J.A.; Tripp, J.H. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. A Math. Phys. Eng. Sci. 1966, 295, 300–319. [Google Scholar]
- Ma, J.; Zhang, H.; Lou, S.; Chu, F.; Shi, Z.; Gu, F.; Ball, A.D. Analytical and experimental investigation of vibration characteristics induced by tribofilm-asperity interactions in hydrodynamic journal bearings. Mech. Syst. Signal Process. 2021, 150. [Google Scholar] [CrossRef]
- Forero, J.D.; Ochoa, G.V.; Alvarado, W.P. Study of the piston secondary movement on the tribological performance of a single cylinder low-displacement diesel engine. Lubricants 2020, 8, 97. [Google Scholar] [CrossRef]
- Press, W.H. FORTRAN Numerical Recipes: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992; ISBN 05-214-3064-X. [Google Scholar]
- Bischof, C.; Carle, A.; Corliss, G.; Griewank, A.; Hovland, P. ADIFOR–Generating derivative codes from Fortran programs. Sci. Program. 1992, 1, 11–29. [Google Scholar] [CrossRef]
- Bestle, D.; Eberhard, P. Analyzing and optimizing multibody systems. Mech. Struct. Mach. 2018, 20, 67–92. [Google Scholar] [CrossRef]
- Hsu, Y.; Anderson, K.S. Low operational order analytic sensitivity analysis for tree-type multibody dynamic systems. J. Guid. Control Dyn. 2001, 24, 1133–1143. [Google Scholar] [CrossRef]
- Haug, E.J. Design sensitivity analysis of dynamic systems. Comput. Aided Optim. Des. Struct. Mech. Syst. 1987, 27, 705–755. [Google Scholar]
- Schaffer, A.S. On the Adjoint Formulation of Design Sensitivity Analysis of Multibody Dynamics. Dissertation, Iowa. 2005. Available online: https://ir.uiowa.edu/cgi/viewcontent.cgi?article=1278&context=etd (accessed on 6 February 2021).
- Dias, J.M.P.; Pereira, M.S. Sensitivity analysis of rigid-flexible multibody systems. Multibody Syst. Dyn. 1997, 1, 303–322. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).