Abstract
Natural weathering is known as one of the key mechanisms causing degradation in building materials. Great efforts have been made to develop new materials and new processes for protecting those that already exist. Natural stones are an example of a natural material that has been extensively used for building construction since ancient times. In addition, they fit durability, aesthetic, and mechanical requirements. Thus, they still have great importance in the construction business nowadays. Though chemical interactions in natural stones, such as oxidation or hydrolyses, have been widely studied, in the last few decades, the physical weathering due to daily temperature variations has begun to be considered as a key mechanism of degradation and has been incorporated in international standards. This process is particularly important in calcitic marble slabs, where it can cause extensive damages to facades. Consequently, there are restrictive rules for the use of marble as an external coating material in many countries. In this paper, the thermal stresses induced by daily variations in temperature are calculated using geographic and meteorological information. The concept of sol-air temperature is used to estimate the temperatures of the hidden and exposed surfaces of a slab, and Fourier’s law and the theory of elasticity are used to calculate the temperature and stress distribution, respectively. The proposed methodology allows for a detailed reconstruction of the stress induced inside marble slabs using parameters commonly acquired in meteorological stations as input data. The developed methodology was validated by comparing in-situ measurements of the temperature of a building in Pescara (Central Italy). A good correlation between the theoretical and real temperatures was found; in particular, the peak tensile stresses inside the slabs were estimated at 75 kPa.
1. Introduction
Durability against natural weathering has been considered one of the greatest challenges that building materials must face when they are used in external environments. Artificial materials, such as polymers and glasses, have been developed to overcome this problem [1,2,3,4]. Many studies have been conducted on rock-like materials to develop new processes and technologies for increasing their performance (in terms of durability and mechanical properties), as well as their competitiveness with other construction technologies. Natural stones just partially fit these requirements, but due to their unique aesthetic features and the low CO2 emissions in their exploitation chain (which is very important nowadays), they still have great importance as building materials.
Nonetheless, the durability of natural stones may be reduced by natural weathering. Staining, detachment, oxidation, and efflorescence are the pathologies most commonly found in building-covering systems, but, in the last two decades, a phenomenon known as bowing, already studied in the last century, has become the object of numerous studies [5,6,7,8,9,10,11,12,13].
Bowing affects carbonate rocks, mainly calcitic marbles, and it is characterized by plastic deformation that might be easily visually noticed. In some cases, the warping is imperceptible, but the internal damage can be even greater. This key feature might help to distinguish this pathology from the others. The causes of this process are still debated: Some researchers consider the mineralogical influence as basically responsible for leading to this deformation [12,13,14,15]. Others also take into account the humidity and the anchorage system [16,17]. However, one of the most accepted hypotheses is the anisotropic thermal expansion of grains. One of the most known cases occurred at the Finland Hall’s facade, in which Carrara marble was used as an external coating; after some years, the deformation was so evident that renewal of the whole facade was demanded. However, after a few months, the same problem affected the building again. The testing and assessment of marble and limestone [18] have verified that the occurrence of this pathology is spread throughout many countries.
Thermal action has been demonstrated to be an important factor that leads to accelerated degradation in many carbonate rocks, such as marbles [19,20,21,22,23]. For this reason, it is considered in European standards that are focused on the applicability of natural stones in external environments. In marble, the relationship between thermal action and weathering depends on its mineralogical composition. Calcite belongs to the trigonal–hexagonal mineralogical system, which means that the and optical axes are perpendicular to each other. This orthotropic behavior has also been verified in the thermal expansion coefficients of this mineral. During heating–cooling cycles, the grain tends to expand in one direction, but it contracts in the direction perpendicular to that, which leads to internal stresses.
The main goal of this paper is to propose a methodology for the evaluation of thermal stresses induced by insolation on natural stones used as an external coating material. Meteorological and geographical data were used for forecasting the thermal strain generated within marble slabs. The proposed methodology has the advantage of using parameters that are commonly measured in meteorological stations; consequently, it is promising as a cost- and time-saving procedure. Data coming from the monitoring of the facade of the Pescara Justice Court were used for the validation of the proposed methodology. Therefore, Carrara marble’s parameters were used in the calculation. It is worthwhile to note that this methodology’s application is not limited to the evaluation of the stress state in facades, but it could be applied to any structures used in external environments that are subject to natural thermal weathering.
2. Fundamentals and Methodology
The variation of temperature on a slab in an external environment presents a periodic behavior, as demonstrated by several authors [24,25,26,27]. Consequently, daily temperature variation can be assumed as a periodic function. The sunlight acting on a surface tends to increase when the sun is rising, and, in general, the peak of the temperature is reached in the afternoon. Then, the temperature decreases and the cycle repeats again.
The temperature of the internal face of this structure also presents cyclic behavior, but it is delayed, and two possible conditions can occur: The first one is defined as the slow-cooling mode, in which the internal and external temperatures are almost the same (red line in Figure 1), and the second one is named the fast-cooling mode. The latter one can occur due to rain, wind, or the combination of any other external factor acting on the external surface, in which the temperature at the external face is lower than the internal one and the heat flux through the slab comes from the inner to the external side.
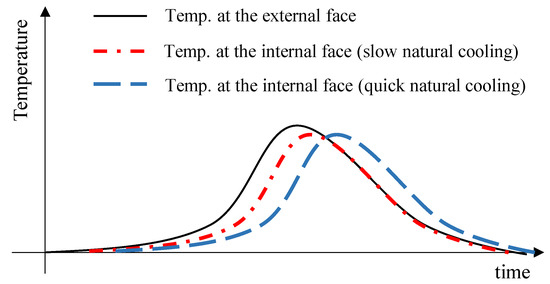
Figure 1.
Daily variation of temperature in a ventilated structure.
In the following sections, some concepts of thermal comfort in building environments are presented [28], which are coupled with the theoretical formulation of thermal stresses in continuum media in order to calculate the induced thermal stresses in ventilated slabs. Firstly, the sol-air temperature is calculated. After that, the temperature at the non-exposed surface of the slab (internal surface) is calculated considering the sol-air temperature and the internal temperature. Finally, the temperature inside the slab and the respective stresses are calculated using the Fourier law and its integral over the width.
2.1. Solar Radiation
The total solar radiation for a clear sky can be estimated as:
where is the direct solar radiation, is the diffuse solar radiation, and is the reflected solar radiation.
In this study, the reflected solar radiation flux and the direct solar radiation were considered to be equal to zero because the measurements on the marble slab were made in the shading area. For a vertical surface (wall) and clear-sky conditions, the diffuse solar radiation can be calculated using Equations (2)–(5) [29,30]:
where is the diffuse horizontal irradiance, Y is the correction factor of the direct solar radiation, and is the angle of incidence.
The diffuse horizontal irradiance is [31]:
where is the extraterrestrial radiant flux, is the diffuse optical depth, m is the air mass, is the diffuse air mass, and is the beam optical depth. The values of and for the month of August in 2009 in the city of Pescara were 0.494 and 1.935, respectively [32].
According to the American Society of Heating, Refrigerating, and Air-Conditioning Engineers [31], the extraterrestrial radiant flux can be approximated by:
where is the solar constant and n is the day of the year. As stated by Iqbal (1983) [33], the solar constant assumes the value of 1367 .
Air mass and solar altitude can be expressed as [34]:
where l is the latitude, h is the hour angle, and d is the declination angle.
The hour angle and declination angle are expressed as follows:
where is the local solar time (h), and it is calculated according to Equation (11):
where is the clock time (h), is the standard meridian for the local time zone, is the longitude, is the equation of time, is the correction for daylight savings time, and is the universal coordinated time.
The equation of time , in minutes, can be approximated by [33]:
where is the angular correction.
The angle of incidence , the surface–solar azimuth angle , and the azimuth angle can be computed using the following equations:
where is the surface–solar azimuth angle, is the surface tilt angle (90° for vertical surfaces), and is the surface azimuth.
2.2. Heat Flux
Solar radiation flux is expressed as:
where is the solar absorptivity.
Gray-body radiation flux is defined by the Sfetan–Boltzmann law as:
where is the Stefan–Boltzmann constant (5.67 ), is the surface emissivity, and is the wall surface temperature.
The superficial heat exchange due to convection flux can be calculated by Newton’s law of cooling:
where is the convection heat-transfer coefficient for the outside or inside surface and is the outdoor or indoor dry-bulb temperature.
The convection heat-transfer coefficients for the outside and the inside surfaces are defined as:
where is the Nusselt number, is the air thermal conductivity (0.025 W/m·K ), is the equivalent length, B is the building plan width, is the building plan length, and is the wind direction.
The influence of forced air velocity on the Nusselt number can be represented by [35]:
where is the Prandtl number and is the Reynolds number. However, the correction of the viscosity in Equation (23) could be neglected for gases [36].
For the natural condition in which the wind velocity is set as zero, the Nusselt number is calculated considering natural convection [37]:
where is the Grashof number, c is a constant, and n depends on the flow regime ( for laminar flow and for turbulent flow).
Finally, the sol-air temperature can be expressed as:
where is the outdoor dry-bulb temperature, is the surface emissivity, and is the infrared radiation correction factor. For vertical surfaces, .
2.3. Inner Temperature
The internal temperature was calculated assuming a simplified formulation in which the heat flux inside the slab occurs due to conduction only, as shown in Figure 2. Convective and thermal radiation are considered on the external side; on the internal side, just convective heat transfer is considered.
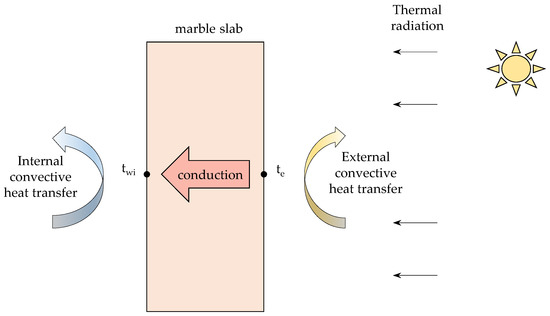
Figure 2.
Simplified model of heat flux in a ventilated facade.
In this formulation, the temperature at the internal face of the slab is given by the harmonics of the Fourier series and natural frequencies [28]:
where is the inside wall surface temperature, is the inside dry-bulb temperature, is the combined convective and thermal radiation heat-transfer coefficient for the inside surface, U is the heat transmission coefficient, is a factor, is the mean value of sol-air temperature, is the harmonic coefficient, is the angular velocity, is the time, is the angle, and is the lag angle.
where is the combined convective and thermal radiation heat-transfer coefficient for the inside surface, k is the thermal conductivity, L is the thickness of the material, , , and are factors, and and are the Fourier coefficients.
and are defined as:
where T is the period of the periodic function.
The temperature at each point of the slab is calculated by interpolation of internal and external temperatures with respect to Fourier’s law of heat conduction.
2.4. Induced Thermal Stresses
The variation of temperature causes changes in the volume of materials, which might be positive or negative depending on the thermal expansion coefficient. When these deformations do not occur homogeneously along the whole body, differential strains appear. Moreover, to balance these body deformations, internal stresses, known as thermal stresses, are induced.
2D Formulation
In this study, the slabs are considered as thick structures, and the gradient of the temperature varies through the width from the external to the internal side. A unidirectional heat flux means that sunlight exposure and environmental heat exchanges occur homogeneously along the external face of each slab. According to BS 8298 [38], fixing systems should allow thermal deformation without any restriction; therefore, the support condition could be assumed to be isostatic, as well as the plane strain state.
The thermal expansion of an infinitesimal fiber normal to the gradient of temperature in isostatic conditions should be counterpoised in order to maintain the self-equilibration of the internal stresses. According to Johns [39], in 2D analysis, the thermal stresses are given by Equation (36), where the y-axis is perpendicular to the gradient of the temperature. In this equation, the first integral eliminates unbalanced axial forces caused by thermal strains, while the second integral balances the linear momentum.
where is the normal stress in the y direction, E is the Young modulus, is the thermal expansion coefficient, is Poisson’s ratio, and is the temperature.
The previous equation could be rewritten in dimensionless form, as presented in Equation (37). This solution could be applied to any temperature distribution or any sum of temperature distributions. Moreover, considering the particular solution for the linear distribution of temperatures, it would result in null stress, since the first integral eliminates the second, whilst the last term returns a null integral. Hence, thermal stresses in a slab could be determined by integrating the temperature calculated in the previous section along the width via Fourier’s series.
where is the temperature function and is the dimensionless thickness.
3. Results and Discussion
The southern facade of the Pescara Justice Court (Latitude: 4227, Longitude: 1413) was monitored by Ferrero et al. [40] in 2007 to evaluate bowing problems, and the results of that study were used to validate the theoretical model. The temperature of the external facade, made of 3 cm thick Carrara marble slabs, was measured every 15 min during 8–13 August; however, meteorological data were not acquired. For this reason, we used the data recorded in that year at the Pescara airport (in Appendix A), which were provided by the Division of Meteorological Services of the Italian Air Force. It is known that meteorological measures can vary from one place to another, but the errors were reduced by choosing the closest weather station in the study area (approximately 3 km away), and the measurements were performed in a flat area.

Table 1.
Properties of the Carrara marble used in this study.

Table 2.
Properties of Pescara’s Justice Court used in this study.
3.1. Temperature
Figure 3 presents the comparison between the theoretical temperature at the exposed surface and the in situ measurements observed on 10 August. Both the peak and trend of the temperature are well simulated by the model. The detachment between the curves (around 14:30) is probably due to the occurrence of wind gusts and the sudden decrease in dry-bulb temperature measured at the Pescara airport, which was probably not so perceptible at the Pescara Justice Court. This difference could be minimized if the data of other meteorological stations were available; then, the Thiessen polygon method would be used to improve the input data. Nonetheless, it is important to highlight that the gradient of temperature between the external and internal sides is less relevant than the rate at which temperature changes in the thermoelastic analysis of isostatic plates, in which heat flux occurs through the width, because the latter can induce great amounts of stresses, even for small gradients, due to the differential strain, as verified by Ito et al. [11]. Therefore, the difference between the absolute values of the theoretical and the measured temperatures would not affect the stress calculation in the same proportions.
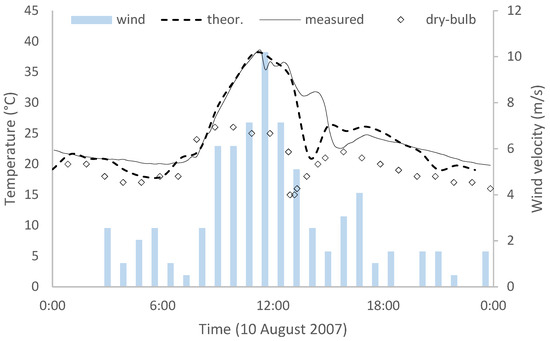
Figure 3.
Comparison between the theoretical temperatures on the external surface and in situ measurements.
3.2. Stresses Due to Daily Variation of Temperature
The current temperature at each point inside the slab was calculated using the Fourier law, and these differences in temperature were used to evaluate the thermal stresses according to the procedure described in Section 2.4. During the heating stage, compressive stresses were acting at the boundaries, while the tensile stresses were rose in the cooling stages, as presented in Figure 4. The major absolute values of stresses were achieved between the sunrise and the sunset, as already expected. However, the peak of the thermal stresses was developed around 14:00 on 10 August, and not at 11:15, when the highest temperature was measured. The highest stresses occurred due to the rapid decrease in temperature on the external face, which corroborates the study presented by Ito et al. (2020), in which the parametric analysis showed that transient heat flux can cause more damage than just considering the values of thermal variation in steady-state conditions.
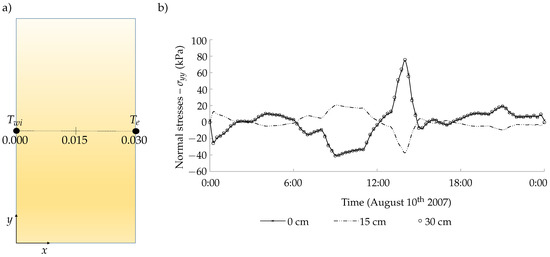
Figure 4.
Variation of thermal stresses along the width on 10 August 2007: (a) Axis orientation where the 0.000 position represents the internal (hidden) surface and the 0.030 position represents the external (exposed) surface; (b) distribution of thermal stress throughout the cycle.
The physical meaning of the highest stress due to the rapid decrease in temperature can be understood by the non-gradual deformation from the external to the internal surface of the slab. Internal stresses are induced to counterpoise these unbalanced deformations in order to maintain the integrity of the body. In this case, the differential strains produced tensile stresses at the boundaries and compressive stresses in the inner part of the slab, as indicated in Figure 5.
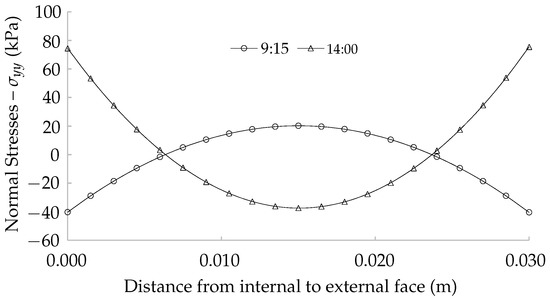
Figure 5.
Thermal stresses calculated at 09:15 and at 14:00 on 10 August.
The parabolic distribution of stress is in line with the increase in porosity along the width, which was verified in naturally weathered marble slabs via the total optical porosity method proposed by Bellopede et al. [44], in which one can verify that the decohesion of grains (or the increase in porosity) is greater at the boundaries than in the inner part of the slab. Moreover, the faster changes in temperature during the winter and the random orientation of the calcite grains (hypothesis not considered in this formulation) could help to explain the higher decohesion between calcite grains on the exposed surface rather than the other one as verified by those authors.
4. Conclusions
Natural thermal weathering has challenged engineers to develop resistant materials for application in external environments and to provide models for predicting their long-term behavior. In this paper, we proposed a new methodology by coupling the evaluation of thermal exchanges in building-covering systems to compute the thermal stresses due to daily variations in temperature. The sol-air temperature, which was calculated with parameters measured at the Pescara airport, presented a good correlation with the temperature, which was measured on the external face of a slab at the Pescara Justice Court, even knowing that these two concepts are related, but have different meanings.
The peak of the tensile stresses occurred on 10 August at 14:30, and it was of the same order of magnitude as the one proposed by Ferrero et al. [40], who considered in situ measurements of temperature; however, in our methodology, the stress along the slab presents an almost symmetrical distribution. For gradual changes in temperature, the induced thermal stresses approach those found in almost-steady-state conditions. A non-symmetrical distribution of stress would occur if the temperature changed suddenly. The type of stress (compressive or tensile) and its magnitude depend on the rate with which the gradient of temperature changes between the two sides.
The thermal load acting on the facade of the Pescara Justice Court on 8–13 August 2007 was small in comparison with the failure stress of Carrara marble, but it was sufficient to cause the decohesion of calcite grains and deformation, as the bowing phenomenon was verified by previous authors. It must be highlighted that the peak of stress presented in this work was calculated for a specific time, which means that the thermal load floats continuously according to the daily variations in temperature, which would result in continuous loading and unloading cycles throughout the day.
In short, the methodology proposed in this paper was efficiently applied for external facades using Carrara marble as the building material, but it can also be applied to evaluate stresses in other structures, such as pavements or roofs, if corrections of the heat exchanges are made.
Author Contributions
Conceptualization, W.H.I. and T.S.; Methodology, W.H.I., T.S., J.R., and P.I.B.d.Q.; Validation, W.H.I., T.S., and P.I.B.d.Q.; Formal analysis, W.H.I., T.S., and J.R.; Investigation, A.M.F. and M.R.M.; Data curation, W.H.I., T.S., and J.R.; Funding acquisition, A.M.F.; Writing—original draft preparation, W.H.I. and T.S.; Writing—review and editing, F.V., A.M.F., M.R.M., and P.I.B.d.Q.; Supervision, A.M.F. and P.I.B.d.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of these data. Data was obtained from the Division of Meteorological Services of the Italian Air Force and are available http://clima.meteoam.it/RicercaDati.php with the permission of the Division of Meteorological Services of the Italian Air Force.
Acknowledgments
The authors are indebted to the Division of Meteorological Services of the Italian Air Force, which provided the meteorological data measured at the Pescara airport in August 2007 used in this paper. Additionally, the corresponding author would like to thank the University of Turin for the financial support during this research.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| diffuse air mass | - | |
| B | building plan width | (m) |
| c | constant | - |
| clock time | (h) | |
| d | declination angle | (C) |
| correction for daylight savings time | (h) | |
| E | Young’s modulus | (GPa) |
| equation of time | (minutes) | |
| Grashof number | - | |
| h | hour angle | () |
| convection heat-transfer coefficient for inside surface | (W/m·K) | |
| convection heat-transfer coefficient for outside surface | (W/m·K) | |
| extraterrestrial radiant flux | (W/m) | |
| diffuse horizontal irradiance | (W/m) | |
| solar constant | (W/m) | |
| diffuse solar radiation | (W/m) | |
| direct solar radiation | (W/m) | |
| reflected solar radiation | (W/m) | |
| total solar radiation | (W/m) | |
| k | thermal conductivity | (K/m·K) |
| air thermal conductivity | (K/m·K) | |
| l | latitude | () |
| building plan length | (m) | |
| L | thickness of material | (m) |
| equivalent length | (m) | |
| longitude | () | |
| standard meridian for the local time zone | (W/m) | |
| local solar time | (h) | |
| m | air mass | - |
| Fourier coefficient | (C) | |
| n | day of the year | - |
| n | constant | - |
| Fourier coefficient | (C) | |
| Nusselt number | - | |
| Prandtl number | - | |
| convection flux | (W/m) | |
| solar radiation flux | (W/m) | |
| gray body radiation flux | (W/m) | |
| Reynolds number | - | |
| T | period of a periodic function | (h) |
| outside dry-bulb temperature | (C) | |
| sol-air temperature | (C) | |
| harmonic coefficient | (C) | |
| mean value of sol-air temperature | (C) | |
| indoor dry-bulb temperature | (C) | |
| wall surface temperature | (C) | |
| inside wall surface temperature | (C) | |
| U | heat transmission coefficient | (W/m·C) |
| universal coordinated time | (h) | |
| factor | (W/m·C) | |
| Y | correction factor of the direct solar radiation | - |
| factor | - | |
| factor | - | |
| dimensionless thickness | - | |
| thermal expansion coefficient | (m/s) | |
| solar absorptivity | - | |
| angle of incidence | () | |
| time | (h) | |
| temperature | () | |
| wind direction | (m/s) | |
| beam optical depths | - | |
| diffuse optical depths | - | |
| solar altitude | () | |
| surface–solar azimuth angle | () | |
| angular correction | () | |
| azimuth angle | () | |
| surface azimuth | () | |
| angle | () | |
| viscosity | (Pa·s) | |
| surface emissivity | - | |
| angular velocity | (rad/h) | |
| Stefan–Boltzmann constant | (W/m·K) | |
| factor | (m) | |
| normal stress in y direction | (kPa) | |
| infrared radiation correction factor | (W/m) | |
| surface tilt angle | () | |
| temperature function | - | |
| lag angle | () | |
| Poisson’s ratio | - |
Appendix A
In Table A1, the meteorological data used to calculate the temperature on the external facade in the Pescara Justice Court are presented.

Table A1.
Meteorological data for Pescara, 10 August.
Table A1.
Meteorological data for Pescara, 10 August.
| Time | Wind Velocity (m/s) | Wind Direction | Relative Humidity (%) |
|---|---|---|---|
| 23:50 | 2.04 | SSW | 82 |
| 0:50 | 1.53 | Variable | 82 |
| 1:50 | 0 | - | 82 |
| 2:50 | 0 | - | 82 |
| 3:50 | 0 | - | 77 |
| 4:50 | 2.55 | S | 82 |
| 5:50 | 1.02 | Variable | 82 |
| 6:50 | 2.04 | SSW | 82 |
| 7:50 | 2.55 | SSW | 82 |
| 8:50 | 1.02 | Variable | 56 |
| 9:50 | 0.51 | Variable | 46 |
| 10:50 | 2.55 | NE | 50 |
| 11:50 | 6.12 | NE | 60 |
| 12:50 | 6.12 | NNE | 64 |
| 12:55 | 7.14 | N | 63 |
| 13:10 | 10.2 | W | 67 |
| 13:18 | 7.14 | NNW | 87 |
| 13:50 | 5.1 | N | 93 |
| 14:26 | 2.55 | SSW | 87 |
| 14:50 | 1.53 | Variable | 82 |
| 15:50 | 3.06 | NNW | 72 |
| 16:50 | 4.08 | NNW | 59 |
| 17:50 | 1.02 | Variable | 59 |
| 18:50 | 1.53 | Variable | 63 |
| 19:50 | 0 | - | 67 |
| 20:50 | 1.53 | Variable | 72 |
| 21:50 | 1.53 | Variable | 77 |
| 22:50 | 0.51 | Variable | 82 |
| 23:50 | 0 | - | 82 |
References
- Bedon, C.; Zhang, X.; Santos, F.; Honfi, D.; Kozłowski, M.; Arrigoni, M.; Figuli, L.; Lange, D. Performance of structural glass facades under extreme loads—Design methods, existing research, current issues and trends. Constr. Build. Mater. 2018, 163, 921–937. [Google Scholar] [CrossRef]
- Friedrich, D. Effects from natural weathering on long-term structural performance of wood-polymer composite cladding in the building envelope. J. Build. Eng. 2019, 23, 68–76. [Google Scholar] [CrossRef]
- Hawila, A.A.W.; Merabtine, A.; Troussier, N.; Bennacer, R. Combined use of dynamic building simulation and metamodeling to optimize glass facades for thermal comfort. Build. Environ. 2019, 157, 47–63. [Google Scholar] [CrossRef]
- Hua, L.; Shen, J.; Chena, Y.; Lan, Q.; Liu, J. Wipe-on and durable self-cleaning coating for glass facade. Thin Solid Film. 2020, 697. [Google Scholar] [CrossRef]
- Alenka, M.; Tadeja, M.; Ana, M. 3D visualization and quantification of bowing marble microstructure. Constr. Build. Mater. 2009, 23, 2380–2385. [Google Scholar] [CrossRef]
- Marini, P.; Bellopede, R. Bowing of marble slabs: Evolution and correlation with mechanical decay. Constr. Build. Mater. 2009, 23, 2599–2605. [Google Scholar] [CrossRef]
- Tschegg, E.K. Environmental influences on damage and destruction of the structure of marble. Int. J. Rock Mech. Min. Sci. 2016, 89, 250–258. [Google Scholar] [CrossRef]
- Grelk, B.; Christiansen, C.; Schouenborg, B.; Malaga, K. Durability of Marble Cladding—A Comprehensive Literature Review. J. ASTM Int. 2007, 4, 19. [Google Scholar] [CrossRef]
- Schouenborg, B.; Grelk, B.; Malaga, K. Testing and Assessment of Marble and Limestone (TEAM)—Important Results from a Large European Research Project on Cladding Panels. J. ASTM Int. 2007, 4, 1–14. [Google Scholar] [CrossRef]
- Ito, W.H.; Ferrero, A.M.; Vagnon, F.; Migliazza, M.R.; de Queiroz, P.I.B. Thermomechanical numerical analysis of bowing in marble slabs. In Proceedings of the 14th International Congress on Rock Mechanics and Rock Engineering, Foz Do Iguassu, Brazil, 13–18 September 2019; pp. 2649–2657. [Google Scholar]
- Ito, W.H.; Ferrero, A.M.; de Queiroz, P.I.B. Numerical analysis of bowing phenomenon due to thermal stresses in marble slabs. Materials 2020, 13, 4367. [Google Scholar] [CrossRef]
- Weiss, T.; Siegesmund, S.; Fuller, E.R., Jr. Thermal degradation of marble: Indications from finite-element modelling. Build. Environ. 2003, 38, 1251–1260. [Google Scholar] [CrossRef]
- Ferrero, A.M.; Migliazza, M.; Spagnoli, A.; Zucali, M. Micromechanics of intergranular cracking due to anisotropic thermal expansion in calcite marbles. Eng. Fract. Mech. 2014, 130, 42–52. [Google Scholar] [CrossRef]
- Weiss, T.; Siegesmund, S.; Fuller, E.R., Jr. Thermal stresses and microcracking in calcite and dolomite marbles via finite element modelling. Geol. Soc. 2002, 205. [Google Scholar]
- Royer-Carfagni, G.F. On the thermal degradation of marble. Int. J. Rock Mech. Min. Sci. 1999, 36, 119–126. [Google Scholar] [CrossRef]
- Scherer, G. Internal stress and cracking in stone and masonry. In Measuring Monitoring and Modeling Concrete Properties; Springer: Berlin/Heidelberg, Germany, 2006; pp. 633–641. [Google Scholar]
- Hudson, J.A.; Cosgrove, J.W. Deterioration of building stones and stone buildings. In Understanding Building Stones and Stone Buildings; CRC Press: London, UK, 2019; pp. 328–332. [Google Scholar]
- European Commission. Testing and Assessment of Marble and Limestone; Final Technical Report; EC-Project: TEAM—G5RD-CT-2000-00233; European Commission: Brussels, Belgium, 2005. [Google Scholar]
- Vagnon, F.; Colombero, C.; Colombo, F.; Comina, C.; Ferrero, A.M.; Mandrone, G.; Vinciguerra, S.C. Effects of thermal treatment on physical and mechanical properties of Valdieri Marble—NW Italy. Int. J. Rock Mech. Min. Sci. 2019, 116, 75–86. [Google Scholar] [CrossRef]
- Weydt, L.M.; Bar, K.; Colombero, C.; Comina, C.; Deb, P.; Lepillier, B.; Mandrone, G.; Milsch, H.; Rochelle, C.A.; Vagnon, F.; et al. Outcrop analogue study to determine reservoir properties of the Los Humeros and Acoculco geothermal fields, Mexico. Adv. Geosci. 2018, 45, 281–287. [Google Scholar] [CrossRef]
- Comite Europeen de Normalisation. Natural Stone Test Methods. Determination of Resistance of Marble to Thermal and Moisture Cycles; EN 16306; Comite Europeen de Normalisation: Brussels, Belgium, 2013. [Google Scholar]
- Malaga, K.; Shouernborg, B.; Grelk, B. Bowing and expansion of natural stone panels: Marble and limestone testing and assessment. Mater. Constr. 2008, 58, 97–112. [Google Scholar] [CrossRef]
- Siegesmund, S.; Ullemeyer, K.; Weiss, T.; Tschegg, E.K. Physical weathering of marbles caused by anisotropic thermal expansion. Int. J. Earth Sci. 2000, 89, 170–182. [Google Scholar] [CrossRef]
- Li, C.; Wei, J.; Li, C. Influence of foliage thickness on thermal performance of green façades in hot and humid climate. Energy Build. 2019, 199, 72–87. [Google Scholar] [CrossRef]
- Mackiewicz, P. Thermal stress analysis of jointed plane in concrete pavements. Appl. Therm. Eng. 2014, 73, 1169–1176. [Google Scholar] [CrossRef]
- Naboni, E.; Milella, A.; Vadalà, R.; Fiorito, F. On the localised climate change mitigation potential of building facades. Energy Build. 2020, 224, 110284. [Google Scholar] [CrossRef]
- Stazi, F.; Ulpiani, G.; Pergolini, M.; Perna, C.; D’Orazio, M. The role of wall layers properties on the thermal performance of ventilated facades: Experimental investigation on narrow-cavity design. Energy Build. 2020, 209, 109622. [Google Scholar] [CrossRef]
- Kuehn, T.H.; Ramsey, J.W.; Threlkeld, J.I. Thermal Environmental Engineering, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1998; pp. 381–414. [Google Scholar]
- Stephenson, D.G. Equations for solar heat gain through windows. Sol. Energy 1965, 9, 81–86. [Google Scholar] [CrossRef][Green Version]
- Threlkeld, J.L. Solar irradiation of surfaces on clear days. ASHRAE Trans. 1963, 69, 24. [Google Scholar]
- ASHRAE. Fundamentals; I-P Edition; ASHRAE: Atlanta, GA, USA, 2017. [Google Scholar]
- ASHRAE Climatic Design Conditions. Available online: http://ashrae-meteo.info/v2.0/index.php?lat=42.43&lng=14.20&place=%27%27&wmo=162300&ashrae_version=2009 (accessed on 7 December 2020).
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: Montreal, QC, Canada, 1983. [Google Scholar]
- Kasten, F.; Young, T. Revised optical air mass tables and approximation formula. Appl. Opt. 1989, 28, 4735–4738. [Google Scholar] [CrossRef]
- Whitaker, S. Elementary Heat Transfer Analysis; Pergamon: New York, NY, USA, 1976. [Google Scholar]
- Ozisik, M.N. Heat Transfer: A Basic Approach; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- McAdams, W.H. Hear Transmission, 3rd ed.; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- BSI. BS 8298: Code of Practice for Design and Installation of Natural Stone Cladding and Lining; BSI: London, UK, 2010. [Google Scholar]
- Johns, D.J. Two-dimension formulations and solutions. In Thermal Stress Analyses; Pergamon Press: London, UK, 1965; pp. 21–32. [Google Scholar]
- Ferrero, A.M.; Migliazza, M.; Spagnoli, A. Theoretical modelling of bowing in cracked marble slabs under cyclic thermal loading. Constr. Build. Mater. 2009, 23, 2151–2159. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavigne, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Rosso, F.; Pisello, A.L.; Jin, W.; Ghandehari, M.; Cotana, F.; Ferrero, M. Cool Marble Building Envelopes: The Effect of Aging on Energy Performance and Aesthetics. Sustainability 2016, 8, 753. [Google Scholar] [CrossRef]
- Costa, A.A.M.N. Study on the Contribution of Thermal Mass Indoors Placed on Windowsills and Jambs. Master’s Thesis, Faculty of Engineering of the University of Porto, Porto, Portugal, 2017. [Google Scholar]
- Bellopede, R.; Zichella, L.; Marini, P. Marble durability assessment by means of total optical porosity and adjacent grain analysis. Key Eng. Mater. 2020, 848, 35–47. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).