Abstract
Initially, Anticipatory Classifier Systems (ACS) were designed to address both single and multistep decision problems. In the latter case, the objective was to maximize the total discounted rewards, usually based on Q-learning algorithms. Studies on other Learning Classifier Systems (LCS) revealed many real-world sequential decision problems where the preferred objective is the maximization of the average of successive rewards. This paper proposes a relevant modification toward the learning component, allowing us to address such problems. The modified system is called AACS2 (Averaged ACS2) and is tested on three multistep benchmark problems.
1. Introduction
Learning Classifier Systems (LCS) [1] comprise a family of flexible, evolutionary, rule-based machine learning systems that involve a unique tandem of local learning and global evolutionary optimization of the collective model localities. They provide a generic framework combining the discovery and learning components. Despite the misleading name, LCSs are not only suitable for classification problems but may instead be viewed as a very general, distributed optimization technique. Due to representing knowledge locally as IF-THEN rules with additional parameters (such as predicted payoff), they have high potential to be applied in any problem domain that is best solved or approximated through a distributed set of local approximations or predictions. The main feature of LCS is the employment of two learning components. The discovery mechanism uses the evolutionary approach to optimize the individual structure of each classifier. On the other side, there is a credit assignment component approximating the classifier fitness estimation. Because those two interact bidirectionally, LCSs are often perceived as being hard to understand.
Nowadays, LCS research is moving in multiple directions. For instance, BioHEL [2] and ExSTraCS [3] algorithms are designed to handle large amounts of data. They extend the basic idea by adding expert-knowledge-guided learning, attribute tracking for heterogeneous subgroup identification, and a number of other heuristics to handle complex and noisy data mining. On the other side, there are some advances made towards combining LCS with artificial neural networks [4]. Liang et al. [5] took the approach of combining the feature selection of Convolutional Neural Networks with LCSs. Tadokoro et al. [6] have a similar goal—they want to use Deep Neural Networks for preprocessing in order to be able to use LCSs for high-dimensional data while preserving their inherent interpretability. An overview of recent LCS advancements is published yearly as a part of the International Workshop on Learning Classifier Systems (IWLCS) [7].
In the most popular LCS modification-XCS [8], where the classifier fitness is based on the accuracy of a classifier’s payoff prediction instead of the prediction itself, the learning component responsible for local optimization follows the Q-learning [9] pattern. Classifier predictions are updated using the immediate reward and the discounted maximum payoff anticipated in the next time step. The difference is that, in XCS, it is the prediction of a general rule that is updated, whereas, in Q-learning, it is the prediction associated with an environmental state–action pair. In this case, both algorithms are suitable for multistep (sequential) decision problems in which the objective is to maximize the discounted sum of rewards received in successive steps.
However, in many real-world situations, the discounted sum of rewards is not the appropriate option. This choice is right when the rewards received in all decision instances are equally important. The criterion applied in this situation is called the average reward criterion and was introduced by Puterman [10]. He stated that the decision maker might prefer it when the decisions are made frequently (so that the discount rate is very close to 1) or other terms cannot easily describe the performance criterion. Possible areas of an application might include situations where system performance is assessed based on the throughput rate (like making frequent decisions when controlling the flow of communication networks).
The averaged reward criterion was first implemented in XCS by Tharakunnel and Goldberg [11]. They called their modification AXCS and showed that it performed similarly to the standard XCS in the Woods2 environment. Later, Zang et al. [12] formally introduced the R-learning [13,14] technique to XCS and called it XCSAR. They compared it with XCSG (where the prediction parameters are modified by applying the idea of gradient descent) and ACXS (maximizing the average of successive rewards) in large multistep problems (Woods1, Maze6, and Woods14).
In this paper, we introduce the average reward criterion to yet another family of LCSs-anticipatory learning classifier systems (ALCS). They differentiate from others so that a predictive schema model of the environment is learned rather than reward prediction maps. In contrast to the usual classifier structure, classifiers in ALCS have a state prediction or an anticipatory part that predicts the environmental changes caused when executing the specified action in the specified context. Similarly, as in the XCS, ALCSs derive classifier fitness estimates from the accuracy of their predictions; however, anticipatory state predictions’ accuracy is considered rather than the reward prediction accuracy. Popular ALCSs use the discounted criterion in the original form, optimizing the performance in the infinite horizon.
Section 2 starts by briefly describing the psychological insights from the concepts of imprinting and anticipations and the most popular ALCS architecture-ACS2. Then, the RL and the ACS2 learning components are described. The default discounted reward criterion is formally defined, and two versions of undiscounted (averaged) criterion integration are introduced. The created system is called AACS2, which stands for Averaged ACS2. Finally, three testing sequential environments with increasing difficulty are presented: the Corridor, Finite State Worlds, and Woods. Section 3 examines and describes the results of testing ACS2, AACS2, Q-learning, and R-learning in all environments. Finally, the conclusions are drawn in Section 4.
2. Materials and Methods
2.1. Anticipatory Learning Classifier Systems
In 1993, Hoffman proposed a theory of “Anticipatory Behavioral Control” that was further refined in [15]. It states that higher animals form an internal environmental representation and adapt their behavior through learning anticipations. The following points (visualized in Figure 1) can be distinguished:
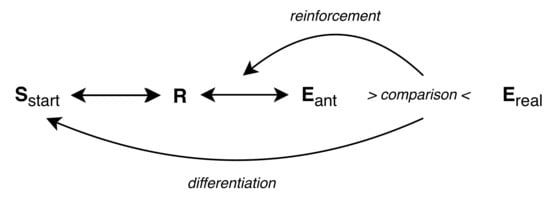
Figure 1.
The theory of anticipatory behavioral control; the figure was adapted from [16], p. 4.
- Any behavioral act or response (R) is accompanied by anticipation of its effects.
- The anticipations of the effects are compared with the real effects .
- The bond between response and anticipation is strengthened when the anticipations were correct and weakened otherwise.
- Behavioral stimuli further differentiate the relations.
This insight into the presence and importance of anticipations in animals and man leads to the conclusion that it would be beneficial to represent and utilize them in animals.
Stolzmann took the first approach in 1997 [17]. He presented a system called ACS (“Anticipatory Classifier System”), enhancing the classifier structure with an anticipatory (or effect) part that anticipates the effects of an action in a given situation. A dedicated component realizing Hoffmann’s theory was proposed—Anticipatory Learning Process (ALP), introducing new classifiers into the system.
The ACS starts with a population of most general classifiers (‘#’ in a condition part) for each available action. To ensure that there is always a classifier handling every consecutive situation, those cannot be removed. During each behavioral act, the current perception of environment is captured. Then, a match set is formed, consisting of all classifiers from where the condition matches the perception . Next, one classifier is drawn from using some exploration policy. Usually, an epsilon-greedy technique is used, but [18] describes other options as well. Then, the classifier’s action is executed in the environment, and a new perception and reward values are presented to the agent. Knowing the classifiers’ anticipation and current state, the ALP module can adjust the classifier ’s condition and effect parts. Based on this comparison, certain cases might be present:
- Useless-case. After performing an action, no change in perception is perceived from the environment. The classifier’s quality decreases.
- Unexpected-case. When new state does not match the anticipation of . A new classifier with a matching effect part is generated, and the incorrect one is penalized with a quality drop.
- Expected-case. When the newly observed state matches the classifier prediction. Classifiers’ quality is increased.
After the ALP application, the Reinforcement Learning (RL) module is executed (see Section 2.3 for details).
Later, in 2002, Butz presented an extension to the described system called ACS2 [16]. Most importantly, he modified the original approach by:
- explicit representation of anticipations,
- applying learning components across the whole action set (all classifiers from advocating selected action),
- introduction of Genetic Generalization module for generating new classifier using promising offsprings,
- changing the RL module motivated by the Q-Learning algorithm.
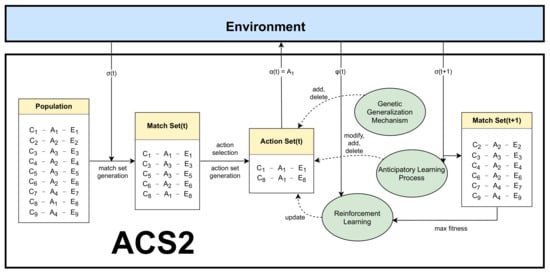
Figure 2.
A behavioral act in ACS2; the figure was adapted from [16], p. 27.
Some modifications were made later to the original ACS2 algorithm. Unold et al. integrated the action planning mechanism [21], Orhand et al. extended the classifier structure with Probability-Enhanced-Predictions introducing a system capable of handling non-deterministic environments and calling it PEPACS [22]. In the same year, they also tackled an issue of perceptual aliasing by building a Behavioral Sequences—thus creating a system called BACS [23].
2.2. Reinforcement Learning and Reward Criterion
Reinforcement Learning (RL) is a formal framework in which the agent can influence the environment by executing specific actions and receive corresponding feedback (reward) afterwards. Usually, it takes multiple steps to reach the goal, which makes the process much more complicated. In the general form, RL consists of:
- A discrete set of environment states S,
- A discrete set of available actions A,
- A mapping R between a particular state and action . The environmental payoff describes the expected reward obtained after executing an action in a given state.
In each trial, the agent perceives the environmental state s. Next, it evaluates all possible actions from A and executes action a in the environment. The environment returns a signal r and next state as intermediate feedback.
The agent’s task is to represent the knowledge, using the policy mapping states to actions, therefore optimizing a long-run measure of reinforcement. There are two popular optimality criteria used in Markov Decision Problems (MDP)—a discounted reward and an average reward [24,25].
2.2.1. Discounted Reward Criterion
In discounted RL, the future rewards are geometrically discounted according to a discount factor , where . The performance is usually optimized in the infinite horizon [26]:
The E expresses the expected value, N is the number of time steps, and is the reward received at time t starting from state s under the policy.
2.2.2. Undiscounted (Averaged) Reward Criterion
The averaged reward criterion [13], which is the undiscounted RL, is where the agent selects actions maximizing its long-run average reward per step :
If a policy maximizes the average reward over all states, it is a gain optimal policy. Usually, average reward can be denoted as , which is state-independent [27], formulated as when the resulting Markov chain with policy is ergodic (aperiodic and positive recurrent) [28].
To solve an average reward MDP problem, a stationary policy maximizing the average reward needs to be determined. To do so, the average adjusted sum of rewards earned following a policy is defined as:
The can also be called a bias or relative value. Therefore, the optimal relative value for a state–action pair can be written as:
where denotes the immediate reward of action a in state s when the next state is , is the average reward, and is the maximum relative value in state among all possible actions b. Equation (4) is also known as the Bellman equation for an average reward MDP [28].
2.3. Integrating Reward Criterions in ACS2
Despite the ACS’s latent-learning capabilities, the RL is realized using two classifier metrics-reward and immediate reward . The latter stores the immediate reward predicted to be received after acting in a particular situation and is used mainly for model exploitation where the reinforcement might be propagated internally. The reward parameter stores the reward predicted to be obtained in the long run.
For the first version of ACS, Stolzmann proposed a bucket-brigade algorithm to update the classifier’s reward [20,29]. Let be the active classifier at time t and the active classifier at time :
where is the bid-ratio. The idea is that if there is no environmental reward at time , then the currently active classifier gives a payment of to the previous active classifier . If there is an environmental reward , then is given to the previous active classifier .
Later, Butz adopted the Q-learning idea in ACS2 alongside other modifications [30]. For the agent to learn the optimal behavioral policy, both the reward and intermediate reward are continuously updated. To assure maximal Q-value, the quality of a classifier is also considered assuming that the reward converges in common with the anticipation’s accuracy. The following updates are applied to each classifier in action set during every trial:
The parameter denotes the learning rate and is the discount factor. With a higher value, the algorithm takes less care of past encountered cases. On the other hand, determines to what extent the reward prediction measure depends on future reward.
Thus, in the original ACS2, the calculation of the discounted reward estimation at a specific time t is described as , which is part of Equation (6):
The modified ACS2 implementation replacing the discounted reward with the averaged version with the formula is defined below (Equation (8)):
The definition above requires an estimate of the average reward . Equation (4) showed that the maximization of the average reward is achieved by maximizing the relative value. The next sections will propose two variants of setting it to use the average reward criterion for internal reward distribution. The altered version is named AACS2, which stands for Averaged ACS2.
As the next operation in both cases, the reward parameter of all classifiers in the current action set is updated using the following formula:
where is the learning rate and R was defined in Equation (8).
2.3.1. AACS2-v1
The first variant of the AACS2 represents parameter as the ratio of the total reward received along the path to reward and the average number of steps needed. It is initialized as , and its update is executed as the first operation in RL using the Widrow–Hoff delta rule (Equation (10)). The update is also restricted to be executed only when the agent chooses the action greedily during the explore phase:
The parameter denotes the learning rate for average reward and is typically set at a very low value. This ensures a nearly constant value of average reward for the update of the reward, which is necessary for the convergence of average reward RL algorithms [31].
2.3.2. AACS2-v2
The second version is based on the XCSAR proposition by Zang [12]. The only difference from the AACS2-v1 is that the estimate is also dependent on the maximum classifier fitness calculated from the previous and current match set:
2.4. Testing Environments
This section will describe Markovian environments chosen for evaluating the introduction of the average reward criterion. They are sorted from simple to more advanced, and each of them has different features allowing us to examine the difference between using discounted and undiscounted reward distribution.
2.4.1. Corridor
The corridor is a 1D multi-step, linear environment introduced by Lanzi to evaluate the XCSF agent [32]. In the original version, the agent location was described by a value between . When one of the two possible actions (move left or move right) was executed, a predefined step-size adjusted the agent’s current position. When the agent reaches the final state the reward is paid out.
In this experiment, the environment is discretized into n unique states (Figure 3). The agent can still move in both directions, and a single trial ends when the terminating state is reached or the maximum number of steps is exceeded.

Figure 3.
The Corridor environment. The agent (denoted by “*”) is inserted randomly and its goal is to reach the final state n by executing two actions-moving left or right.
2.4.2. Finite State World
Barry [33] introduced the Finite State World (FSW) environment to investigate the limits of XCS performance in long multi-steps environments with a delayed reward. It consists of nodes and directed edges joining the nodes. Each node represents a distinct environmental state and is labeled with a unique state identifier. Each edge represents a possible transition path from one node to another and is also labeled with the action(s) that will cause the movement. An edge can also lead back to the same node. The graph layout used in the experiments is presented in Figure 4.
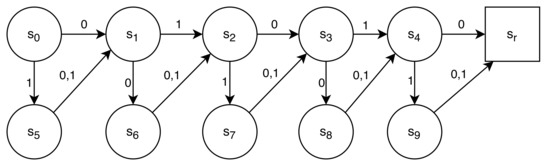
Figure 4.
A Finite State World of length 5 (FSW-5) for a delayed reward experiment.
Each trial always starts in state , and the agent’s goal is to reach the final state . After doing so, the reward is provided, and the trial ends. The environment has a couple of interesting properties. First, it can be easily scalable, just by changing the number of nodes, which will change the action chain length. It also enables the agent to choose the optimal route at each state (where the sub-optimal ones do not prevent progress toward the reward state).
2.4.3. Woods
The Woods1 [34] environment is a two-dimensional rectilinear grid containing a single configuration of objects that is repeated indefinitely in the horizontal and vertical directions (Figure 5). It is a standard testbed for classifier systems in multi-step environments. The agent’s learning task is to find the shortest path to food.
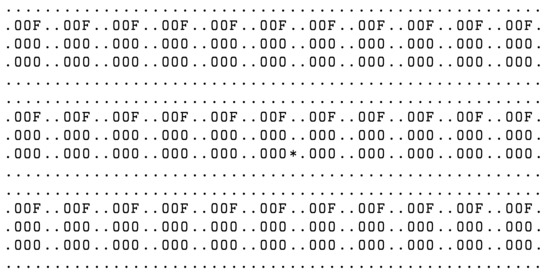
Figure 5.
Environment Woods1 with an animat “*”. Empty cells are denoted by “.”.
There are three types of objects available-food (“F”), rock (“O”), and empty cell (“.”). In each trial, the agent (“*”) is placed randomly on an empty cell and can sense the environment by analyzing the eight nearest cells. Two versions of encoding are possible. Using binary encoding, each cell type is assigned two bits, so the observation vector has the length of 16 elements. On the other hand, using an encoding with the alphabet , the observation vector is compacted to the length of 8.
In each trial, the agent can perform eight possible moves. When the resulting cell is empty, it is allowed to change the position. If its type is a block, then it stays in place, and one time-step elapses. The trial ends when the agent reaches the food providing the reward .
3. Results
The following section describes the differences observed between using the ACS2 with standard discounted reward distribution and two proposed modifications. In all cases, the experiments were performed in an explore–exploit manner, where the mode was alternating in each trial. Additionally, for better reference and benchmarking purposes, basic implementations of Q-Learning and R-Learning algorithms were also introduced and used with the same parameter settings as ACS2 and AACS2. The most important thing was to distinguish whether the new reward distribution proposition still allows the agent to successfully update the classifier’s parameter to allow the exploitation of the environment. To illustrate this, figures presenting the number of steps to the final location, estimated average change during learning, and the reward payoff-landscape across all possible state–action pairs were plotted.
For the reproduction purposes, all the experiments were performed in Python language. A PyALCS (https://github.com/ParrotPrediction/pyalcs) [35] framework was used for implementing additional AACS2-v1 and AACS2-v2 agents (https://github.com/ParrotPrediction/pyalcs) and all the environments used are implemented according to the OpenAI Gym [36] in a separate repository (https://github.com/ParrotPrediction/openai-envs). Publicly available interactive Jupyter notebooks presenting all results are available for reproduction here (https://github.com/ParrotPrediction/pyalcs-experiments).
3.1. Corridor 20
The following parameters were used: , , , . The experiments were run on 10,000 trials in total. Because there is only one state to be perceived by the agent, the genetic generalization feature was disabled. The corridor of size was tested, but similar results were also obtained for greater sizes.
The average number of steps can be calculated , which for the tested environment gives the approximate value of . It is seen that the average reward per step in this environment should be close to .
Figure 6 demonstrates that the environment is learned in all cases. The anticipatory classifier systems obtained an optimal number of steps after the same number of exploit trials, which is about 200. In addition, the AACS2-v2 updates the value more aggressively in earlier phases, but the estimate converges near the optimal reward per step.
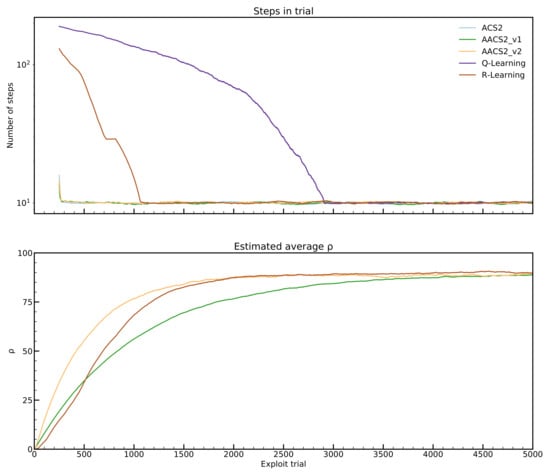
Figure 6.
Performance on Corridor 20 environment. Plots are averaged in ten experiments. For the number of steps, a logarithmic scale ordinate and a moving average with window 250 was applied.
For the payoff-landscape, all allowed state–action pairs were identified in the environment (38 in this case). The final population of learning classifiers was established after 100 trials and was the same size. Both Q-table and R-learning tables were filled in using the same parameters and number of trials.
Figure 7 depicts the differences in the payoff-landscapes. The relative distance between adjacent state–action pairs can be divided into three groups. The first one relates to the discounted reward agents (ACS2, Q-Learning). Both generate almost a similar reward payoff for each state–action. Later, there is the R-Learning algorithm, which estimates the value and separates states evenly. Furthermore, two AACS2 agents are performing very similarly. The value calculated by the R-Learning algorithm is lower than the average estimation by the AACS2 algorithm.
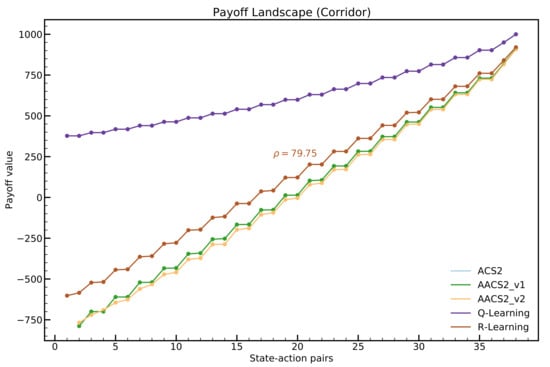
Figure 7.
Payoff Landscape for Corridor 20 environment. Payoff values were obtained after 10,000 trials. For the Q-Learning and R-Learning, the same learning parameters were applied. The ACS2 and Q-Learning generate exactly the same payoffs for each state–action pair.
3.2. Finite State Worlds 20
The following parameters were selected: , , , . The experiments were performed in 10,000 trials. Similarly as before, there is only one state observed, and the genetic generalization mechanism remains turned off. The size of the environments was chosen to be , resulting in distinct states.
Figure 8 presents that agents are capable of learning a more challenging environment without any problems. It takes about 250 trials to reach the reward state performing an optimal number of steps. Like in the corridor environment from Section 3.1, the parameter converges with the same dynamics.
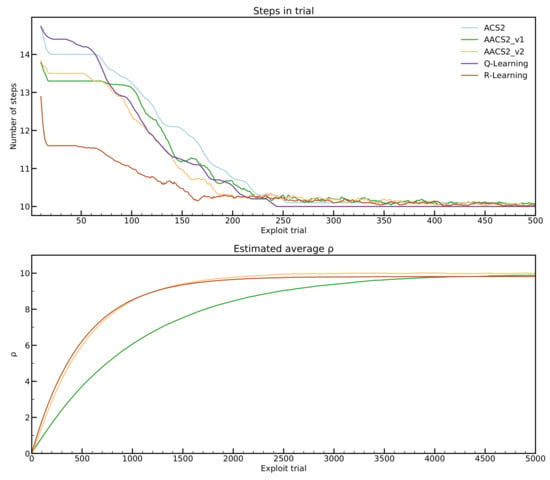
Figure 8.
Performance on the FSW-10 environment.Plots are averaged in ten experiments. For the number of steps, a moving average with window 25 was applied. Notice that the abscissa on both plots is scaled differently.
The payoff-landscape Figure 9 shows that the average value estimate is very close to the one calculated by the R-learning algorithm. The difference is mostly visible in the state–action pairs located afar from the final state. The discounted versions of the algorithms performed precisely the same.
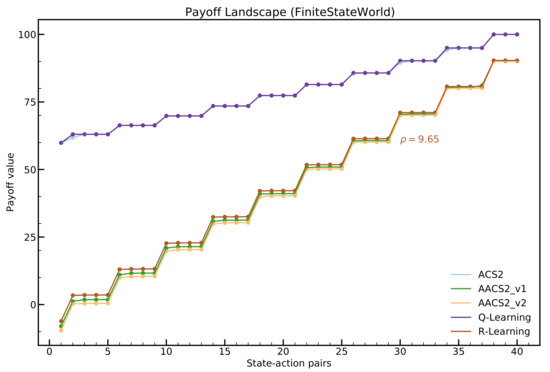
Figure 9.
Payoff Landscape for the FSW-10 environment. Payoff values were obtained after 10,000 trials. For the Q-Learning and R-Learning, the same learning parameters were applied.
3.3. Woods1
The following parameters were used: , , , . Each environmental state was encoded using three bits, so the perception vector passed to agent has the length of 24. The genetic generalization mechanism was enabled with the parameters: mutation probability , cross-over probability , genetic algorithm application threshold . The experiments were performed in 50,000 trials and repeated five times.
The optimal number of steps in the Woods1 environment is 1.68, so the maximum average reward can be calculated as , i.e., .
Figure 10 shows that the ACS2 did not manage to learn the environment successfully—the number of steps performed in the exploit trial is not stable and varies much higher than the optimal value. On the other hand, both AACS2 versions managed to function better. The AACS2-v2 stabilizes faster and with weaker fluctuations. The best performance was obtained for the Q-Learning and R-Learning algorithm that managed to learn the environment in less than 1000 trials. The average estimate value converges at the value of 385 for both cases after 50,000 trials, which is still not optimal.
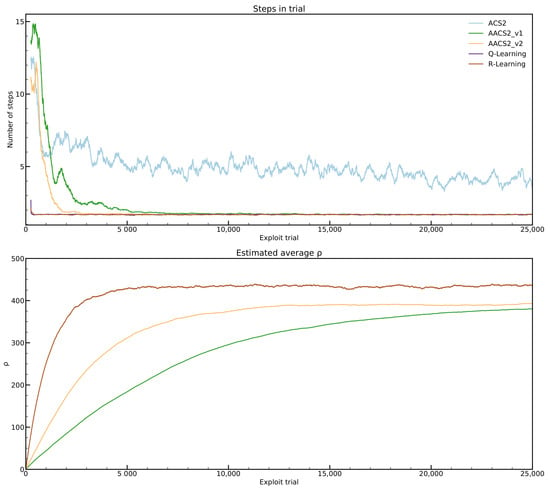
Figure 10.
Performance in the Woods1 environment. For brevity, the number of steps is averaged on 250 latest exploit trials. Both AACS2 variants managed to converge to the optimal number of steps.
What is interesting is that neither ACS2 nor AACS2 population settled to the final size. Figure 11 demonstrates the difference in size for each algorithm between total population size and the number of reliable classifiers. Even though the algorithm manages to find the shortest path for AACS2, the number of created rules is greater than all unique state–action pairs in the environment, which is 101. The experiment was also performed ten times longer (one million trials) to see if the correct rules will be discovered, but that did not happen.
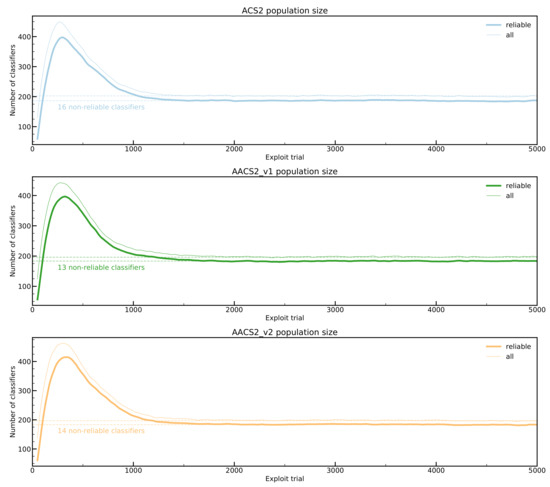
Figure 11.
Comparison of classifier populations in Woods1 environment. None of the algorithms managed to create stable population size. The number of exploit trials is narrowed to the first 5000 exploit trials, and the plots are averaged on 50 latest values for clarity.
Finally, the anticipatory classifier systems’ inability to solve the environment is depicted in payoff-landscape Figure 12. The Q-Learning and R-Learning have three spaced threshold levels, corresponding to states where the required number of steps to the reward states is 1, 2, and 3. All ALCS struggle to learn the correct behavior anticipation. The number of classifiers detected for each state–action is greater than optimal.
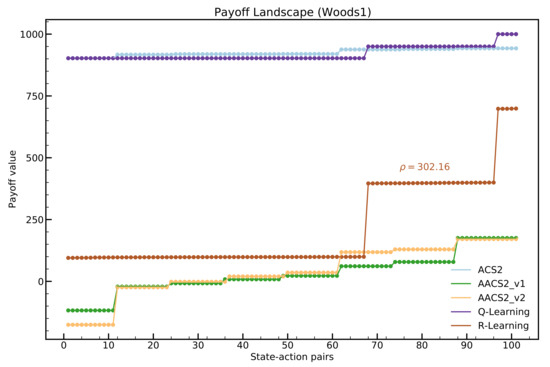
Figure 12.
Payoff-landscape in the Woods1 environment. Three threshold levels are visible for the Q-Learning and R-Learning algorithms representing states in the environment with a different number of steps to the reward state.
4. Discussion
Experiments performed indicated that anticipatory classifier systems with the averaged reward criterion can be used in multi-step environments. The new system AACS2 varies only in a way the classifier reward metric is calculated. The clear difference between the discounted criterion is visible on the payoff landscapes generated from the testing environments. The AACS2 can produce a distinct payoff-landscape with uniformly spaced payoff levels, which is very similar to the one generated by the R-learning algorithm. When taking a closer look, all algorithms generate step-like payoff-landscape plots, but each particular state–action pairs are more distinguishable when the reward-criterion is used. The explanation of why the agent moves toward the goal at all can be found in Equation (8)—it is able to find the next best action by using the best classifiers’ fitness from the next match set.
In addition, the rate at which the average estimate value converges is different for AACS2-v1 and AACS2-v2. Figure 6, Figure 8, and Figure 10 demonstrate that the AACS2-v2 settles to the final value faster, but also has greater fluctuations. That is caused by the fact that both match sets’ maximum fitness is considered when updating the values. Zang also observed this and proposed that the learning rate in Equation (11) could decay over time [12]:
where is the initial value of , and is the minimum learning rate required. The update should take place at the beginning of each exploration trial.
In addition, the fact that the optimal value was not optimal value might be caused by the exploration strategy adopted. The selected policy was -greedy. Because the estimated average reward is updated only when the greedy action is executed, the number of greedy actions to be performed during the exploration trial is uncertain. In addition, the probability distribution when the agent observes the rewarding state might be too low in order to enable the estimated average reward to reach optimal value. This was observed during the experimentation—the value was very dependent on the parameter used.
To conclude, additional research would be beneficial paying extra attention to:
- the performance on longer and more complicated environments (like containing irrelevant perception bits),
- the impact of different action selection policies, especially those used in ALCSs like the Action-Delay, Knowledge-Array or Optimistic Initial Qualities [18,37],
- fine-tuning parameter for optimal average reward estimation,
- difference between two versions of AACS2 in terms of using fitness from the match-set. The estimation is calculated differently in both cases, especially in the early phase of learning.
Author Contributions
Conceptualization, O.U. and N.K.; data curation, N.K.; formal analysis, N.K. and O.U.; funding acquisition, O.U.; investigation, N.K.; methodology, N.K. and O.U.; project administration, O.U.; resources, N.K. and O.U.; software, N.K.; supervision, O.U.; validation, O.U. and N.K., visualization, N.K.; writing—original draft preparation, N.K. and O.U.; writing—review and editing, N.K. and O.U. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AACS2 | Averaged Anticipatory Classifier System 2 |
| ACS | Anticipatory Classifier System |
| ALCS | Anticipatory Learning Classifier System |
| ALP | Anticipatory Learning Process |
| FSW | Finite State World |
| LCS | Learning Classifier System |
| MDP | Markov Decision Problem |
| RL | Reinforcement Learning |
References
- Holland, J. Escaping brittleness: The possibilities of general-purpose learning algorithms applied to parallel rule-based systems. In Machine learning: An Artificial Intelligence Approach; Morgan Kaufmann: San Francisco, CA, USA, 1986. [Google Scholar]
- Bacardit, J.; Krasnogor, N. BioHEL: Bioinformatics-Oriented Hierarchical Evolutionary Learning; University of Nottingham: Nottingham, UK, 2006. [Google Scholar]
- Urbanowicz, R.J.; Moore, J.H. ExSTraCS 2.0: Description and evaluation of a scalable learning classifier system. Evol. Intell. 2015, 8, 89–116. [Google Scholar] [CrossRef] [PubMed]
- Borna, K.; Hoseini, S.; Aghaei, M.A.M. Customer satisfaction prediction with Michigan-style learning classifier system. SN Appl. Sci. 2019, 1, 1450. [Google Scholar] [CrossRef]
- Liang, M.; Palado, G.; Browne, W.N. Identifying Simple Shapes to Classify the Big Picture. In Proceedings of the 2019 International Conference on Image and Vision Computing New Zealand (IVCNZ), Dunedin, New Zealand, 2–4 December 2019; pp. 1–6. [Google Scholar]
- Tadokoro, M.; Hasegawa, S.; Tatsumi, T.; Sato, H.; Takadama, K. Knowledge Extraction from XCSR Based on Dimensionality Reduction and Deep Generative Models. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1883–1890. [Google Scholar]
- Pätzel, D.; Stein, A.; Nakata, M. An overview of LCS research from IWLCS 2019 to 2020. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion, Cancún, Mexico, 8–12 July 2020; pp. 1782–1788. [Google Scholar]
- Wilson, S.W. Classifier fitness based on accuracy. Evol. Comput. 1995, 3, 149–175. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Tharakunnel, K.; Goldberg, D.E. XCS with Average Reward Criterion in Multi-Step Environment. 2002. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.16.3517 (accessed on 1 October 2020).
- Zang, Z.; Li, D.; Wang, J.; Xia, D. Learning classifier system with average reward reinforcement learning. Knowl. Based Syst. 2013, 40, 58–71. [Google Scholar] [CrossRef]
- Schwartz, A. A reinforcement learning method for maximizing undiscounted rewards. In Proceedings of the Tenth International Conference on Machine Learning, Amherst, MA, USA, 27–29 June 1993; Volume 298, pp. 298–305. [Google Scholar]
- Singh, S.P. Reinforcement learning algorithms for average-payoff Markovian decision processes. In AAAI-94 Proceedings; AAAI Press: Menlo Park, CA, USA, 1994; Volume 94, pp. 700–705. [Google Scholar]
- Hoffmann, J.; Sebald, A. Lernmechanismen zum Erwerb verhaltenssteuernden Wissens. Psychol. Rundsch. 2000, 51, 1–9. [Google Scholar] [CrossRef]
- Butz, M.V. Anticipatory Learning Classifier Systems; Springer Science & Business Media: New York, NY, USA, 2002; Volume 4. [Google Scholar]
- Stolzmann, W. Antizipative Classifier Systems; Shaker: Aachen, Germany, 1997. [Google Scholar]
- Kozlowski, N.; Unold, O. Investigating exploration techniques for ACS in discretized real-valued environments. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion, Cancún, Mexico, 8–12 July 2020; pp. 1765–1773. [Google Scholar]
- Butz, M.V.; Stolzmann, W. An Algorithmic Description of ACS2. In Advances in Learning Classifier Systems; Lanzi, P.L., Stolzmann, W., Wilson, S.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 211–229. [Google Scholar]
- Stolzmann, W. An introduction to anticipatory classifier systems. In International Workshop on Learning Classifier Systems; Springer: Berlin, Germany, 1999; pp. 175–194. [Google Scholar]
- Unold, O.; Rogula, E.; Kozłowski, N. Introducing Action Planning to the Anticipatory Classifier System ACS2. In International Conference on Computer Recognition Systems; Springer: Berlin, Germany, 2019; pp. 264–275. [Google Scholar]
- Orhand, R.; Jeannin-Girardon, A.; Parrend, P.; Collet, P. PEPACS: Integrating probability-enhanced predictions to ACS2. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion, Cancún, Mexico, 8–12 July 2020; pp. 1774–1781. [Google Scholar]
- Orhand, R.; Jeannin-Girardon, A.; Parrend, P.; Collet, P. BACS: A Thorough Study of Using Behavioral Sequences in ACS2. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin, Germany, 2020; pp. 524–538. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Mahadevan, S. Sensitive discount optimality: Unifying discounted and average reward reinforcement learning. In ICML; Citeseer: University Park, PA, USA, 1996; pp. 328–336. [Google Scholar]
- Andrew, A.M. Reinforcement Learning: An Introduction; Adaptive Computation and Machine Learning Series; Sutton, R.S., Barto, A.G., Eds.; MIT Press (Bradford Book): Cambridge, MA, USA, 1998; p. 322. ISBN 0-262-19398-1. [Google Scholar]
- Mahadevan, S. Average reward reinforcement learning: Foundations, algorithms, and empirical results. Mach. Learn. 1996, 22, 159–195. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov decision processes. In Handbooks in Operations Research and Management Science; Elsevier: Amsterdam, The Netherlands, 1990; Volume 2, pp. 331–434. [Google Scholar]
- Holland, J.H. Properties of the bucket brigade. In Proceedings of the 1st International Conference on Genetic Algorithms, Pittsburgh, PA, USA, 24–26 July 1985; pp. 1–7. [Google Scholar]
- Butz, M.V. ACS2. In Anticipatory Learning Classifier Systems; Springer: Berlin, Germany, 2002; pp. 23–49. [Google Scholar]
- Gosavi, A. An algorithm for solving semi-Markov decision problems using reinforcement learning: Convergence analysis and numerical results. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2000. [Google Scholar]
- Lanzi, P.L.; Loiacono, D.; Wilson, S.W.; Goldberg, D.E. XCS with computed prediction in continuous multistep environments. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Scotland, UK, 2–5 September 2005; Volume 3, pp. 2032–2039. [Google Scholar]
- Barry, A. XCS Performance and Population Structure in Multi-Step Environments. Ph.D. Thesis, Queen’s University of Belfast, Belfast, UK, 2000. [Google Scholar]
- Wilson, S.W. ZCS: A zeroth level classifier system. Evol. Comput. 1994, 2, 1–18. [Google Scholar] [CrossRef]
- Kozlowski, N.; Unold, O. Integrating anticipatory classifier systems with OpenAI gym. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; pp. 1410–1417. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Butz, M.V. Biasing exploration in an anticipatory learning classifier system. In International Workshop on Learning Classifier Systems; Springer: Berlin, Germany, 2001; pp. 3–22. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).