Improving Multi-Label Learning by Correlation Embedding

Abstract

In multi-label learning, each object is represented by a single instance and is associated with more than one class labels, where the labels might be correlated with each other. As we all know, exploiting label correlations can definitely improve the performance of a multi-label classification model. Existing methods mainly model label correlations in an indirect way, i.e., adding extra constraints on the coefficients or outputs of a model based on a pre-learned label correlation graph. Meanwhile, the high dimension of the feature space also poses great challenges to multi-label learning, such as high time and memory costs. To solve the above mentioned issues, in this paper, we propose a new approach for Multi-Label Learning by Correlation Embedding, namely MLLCE, where the feature space dimension reduction and the multi-label classification are integrated into a unified framework. Specifically, we project the original high-dimensional feature space to a low-dimensional latent space by a mapping matrix. To model label correlation, we learn an embedding matrix from the pre-defined label correlation graph by graph embedding. Then, we construct a multi-label classifier from the low-dimensional latent feature space to the label space, where the embedding matrix is utilized as the model coefficients. Finally, we extend the proposed method MLLCE to the nonlinear version, i.e., NL-MLLCE. The comparison experiment with the state-of-the-art approaches shows that the proposed method MLLCE has a competitive performance in multi-label learning.

1. Introduction

In multi-label learning, each object is represented by a single instance and is associated with multiple class label [1,2,3]. The main task of learning is to build an effective classifier based on the training data and predict the most relevant set of labels for each unseen instance. Nowadays, multi-label learning has been applied in various fields [1,4], such as music emotion classification [5], video classification [6], Internet [7], text classification [8,9], and information retrieval [10].

In recent years, multi-label learning has attracted extensive attentions from researchers. Existing research has demonstrated that exploiting label correlation can provide important information for the prediction of new instances and significantly boost classification performance. For example, if a piece of news is related to the theme of “Olympics”, it is more likely to belong to the theme of “sports” and “culture”, vice versa, “war” is unlikely. When an image was annotated with “reef”, the probability of being annotated with “waves” will be very high, and the probability of being annotated with “desert” will be very low.

Through the investigation and research of previous work on multi-label learning, a lot of methods [11,12,13,14,15] have been proposed by exploiting label correlations. For example, in CLR [14], an extra calibration label is introduced and utilized to separate the relevant and irrelevant labels for each instance. JFSC [15] learns the label-specific and shared features based on pairwise label correlation. In DLCL [12], a novel multi-label learning method is proposed, which can find the latent class labels in the training data. DLCL exploits the correlation between known and latent class labels to enhance the performance of the classifier. The Maximal Correlation Embedding Network (MCEN) uses the label similarity by embedding the maximum correlations in the label space to solve the problem of missing labels [16]. MLC-EBMD [17] introduces a multi-label classification framework based on Boolean matrix decomposition to improve the ability to predict labels in high-dimensional label space, and it also performs dimension reduction in the feature space.

The aforementioned methods definitely enhance the prediction accuracy of the multi-label algorithm by resolving and using the correlation of label. These methods on modeling label correlation mainly use either popular regular constraints, which means that any two labels with a strong relationship are assigned to similar model coefficients, or label ranking. It is noted that these methods mainly model label correlations in an indirect way, i.e., adding extra constraints on the coefficients or outputs of a multi-label classification model based on a pre-learned label correlation graph. However, in such an indirect way on modeling label correlation, the inherent correlations between different labels will not be well kept. It would be better if a direct way could be proposed. Moreover, in the environment of big data, it is convenient to collect a massive amount of data. However, the curse of dimension has brought great obstacles to multi-label learning.Therefore, it is wise to construct learning models in the low-dimensional feature and label space [18,19,20].

To solve the above mentioned issues, in this paper, we propose a new approach for Multi-Label Learning by Correlation Embedding, namely MLLCE, where the feature space dimension reduction and the multi-label classification are integrated into a unified framework. First, we project the original high-dimensional feature space to a low-dimensional latent space by a mapping matrix. To model label correlation, we learn an embedding matrix from the pre-defined label correlation graph by graph embedding. Then, we use the embedding matrix as the model coefficients to construct a multi-label classifier from the low-dimensional latent feature space to the label space. In this way, the inherent correlations between different labels will be directly kept in the model coefficients. Finally, we extend the proposed method MLLCE to the nonlinear version, i.e., NL-MLLCE. The comparison experiment with the state-of-the-art approaches shows that the proposed method MLLCE has a competitive performance in multi-label learning.

The rest of this paper is organized as follows. Section 2 reviews the previous methods of using label correlation for multi-label learning. Section 3 introduces the proposed method MLLCE in detail. Comparative experiment results and analyses are presented in Section 4. Finally, we conclude this paper in Section 5.

2. Related Works

In multi-label learning, mining the correlation among labels can provide important information, make the prediction results more accurate, and boost the performance of the model. According to the ways on modeling label correlations, existing multi-label learning algorithm can be divided into three categories, i.e., first-order, second-order, and high-order algorithms. The first-order methods [21,22] deal with multi-label classification problems without modeling the label correlations. BR [21] is a typical first-order algorithm whose basic idea is to transform a multi-label learning problem into multiple independent binary classification problems. The second-order methods exploit the pairwise relationship between labels [23,24,25]. For the high-order methods, the relationship between all class labels or a subset is modeled, such as [26,27,28]. For example, the classifier chain (CC) [29] is a chain algorithm that uses a vector of class labels as additional instance attributes to model high-order label correlation. The Probabilistic Classifier Chain (PCC) [30] is a probabilistic version of CC. LELC [31] combines label embedding and label correlation to solve multi-label text classification problems. HIDDEN [32] learns the hierarchical multi-label classification based on the joint learning of document classifier and label embedding. ELM-LMF [33] generates the latent label matrix and k-label dependency matrix based on the label matrix decomposition. CLP-RNN [34] is a multi-label classification method that allows the selection of dynamic and context-dependent label ordering based on label embedding. The MLL-FLSDR [20] algorithm is a multi-label learning method for solving the problem with many labels and features based on the label embedding, which reduces the dimension in both feature space and label space.

The second-order methods deal with the multi-label learning problem by exploring the pairwise relationship between the labels that can be divided into two types. First, the second-order methods incorporate the classification criteria ranking loss into the objective function of multi-label learning, such as Rank-SVM [23], MIMLfast [24], and LSEP [25]. Second, the second-order methods constrain the label correlations to the model coefficients or outputs, such as [11,35,36,37,38]. LLSF [35] used the correlation between the labels to learn specific label features for multi-label learning. LSF-CI [36] is a multi-label feature multi-label learning method which considered the relevant information of the label space and the feature space simultaneously. There are also some algorithms that tend to investigate global and local label correlations. ML-LOC [11] exploits local pairwise label correlation for multi-label learning. LF-LPLC [37] learns specific label features and exploits local pairwise label correlation for multi-label learning. GRRO [38] is a multi-label feature selection method that exploits the global pairwise label correlation to facilitate the selection of features. These algorithms only utilize positive label correlation between labels, while some of the label are negatively correlated or mutually exclusive with each other. To solve this problem, several algorithms have been proposed to model the negative correlation between labels. For example, the LPLC [39] is a simple and effective Bayesian model to investigate the positive correlation and negative correlation between the labels, and it finds the positive and negative relevance class labels for each label. Nan et al. [40] exploited the local positive and negative correlation between labels through kNN method. Most of these multi-label learning algorithms model label correlation with external conditions, and may not be able to maintain the correlation structure of labels well.

Dimension reduction is a fundamental pre-processing procedure for high-dimensional data, and many methods have been proposed for multi-label learning, such as MLDA [41], SSMLDA [42], and MLLS [43]. Through the overview of dimension reduction [44], dimension reduction can basically be divided into three categories, i.e, dimension reduction of the feature space, dimension reduction of the label space, and dimension reduction of the label and feature spaces simultaneously. PCA [45] is a method of dimension reduction in feature space based on label-independence. DCR [46] is a new multi-label feature selection method by combining feature relevance and label relevance. In [47], the authors propose a dimension reduction method DSE to learn the sparse weight matrix by projecting the original sample into a low-dimensional subspace. MDDM [48] is a multi-label dimension reduction approach based on maximizing the dependency between feature descriptions and relevant class labels. CLEMS [49] performs the dimension reduction of the label space through embedded instances. In addition, some methods are proposed to reduce dimension of the label space, such as [50,51]. GIMC [52] learns a nonlinear mapping of the features by reducing the instance features and labels.

In the environment of big data, the feature space of data sets becomes larger and larger, adopting dimension reduction, which can help to get rid of redundant features and obtain a more compact feature space, and further improve the performance of a model. To solve the above mentioned issues, in this paper, we propose a new approach for Multi-Label Learning by Correlation Embedding, namely MLLCE, where the feature space dimension reduction and the multi-label classification are integrated into a unified framework. We learn an embedding matrix from the pre-defined label correlation graph by graph embedding and utilize the embedding matrix as the model coefficients.

3. The Proposed Method

In multi-label learning, $\mathbf{X}={[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_n]}^T\in {\mathbb{R}}^{n\times d}$ is the feature matrix and $\mathbf{Y}\in {\{0,1\}}^{n\times q}$ is the label matrix, where n is the number of instances, d is the dimension and q is the number of class labels. The i-th example is denoted by a vector with d attribute values ${\mathbf{x}}_i=[x_{i1},x_{i2},\dots ,x_{id}]$, and ${\mathbf{y}}_i=[y_{i1},y_{i2},\dots ,y_{iq}]$ is a set of possible labels for ${\mathbf{x}}_i$, where $y_{ij}=1$ indicates the i-th instance belonging to the j-th label, otherwise, $y_{ij}=0$.

In this paper, we integrate the feature space dimension reduction and the multi-label classification into a unified framework. The learning framework of our proposed method MLLCE is shown in Figure 1. First, we project the original high-dimensional feature space to a low-dimensional latent space by a mapping matrix. To model label correlation, we learn an embedding matrix from the pre-defined label correlation graph by graph embedding. Then, we use the embedding matrix as the model coefficients to construct a multi-label classifier from the low-dimensional latent feature space to the label space. In this way, the inherent correlations between different labels will be directly kept in the model coefficients. Finally, we extend the proposed method MLLCE to the nonlinear version, i.e., NL-MLLCE.

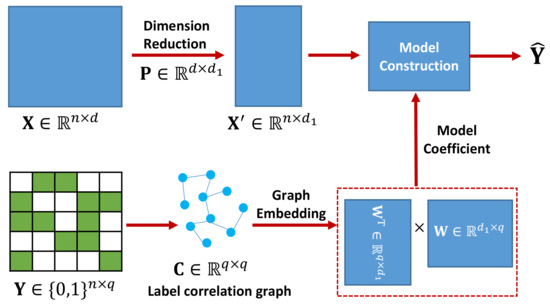
Figure 1. The learning framework of MLLCE.

3.1. Label Correlation Embedding

Exploiting the label correlation can improve the generalization ability of a model and significantly improve the accuracy of model prediction in multi-label learning [53,54]. In this paper, we model the label correlation under the second-order strategy.

First, we calculate the label correlation matrix $\mathbf{C}\in {\mathbb{R}}^{q\times q}$ by cosine similarity based on the label matrix $\mathbf{Y}\in {\{0,1\}}^{n\times q}$, where n represents the number of samples, and q indicates the number of labels. Each element $C_{ij}$ indicates the correlation between the i-th and j-th labels, and it is obtained by Equation (1).

$$C_{ij}=\sum _{h=1}^n{Y}_{hi}{Y}_{hj}/\left(\sqrt{\sum _{h=1}^n{Y}_{hi}^2}\sqrt{\sum _{h=1}^n{Y}_{hj}^2}\right)$$

(1)

where $Y_{hi}$ represents the value of the element in the h-th row and i-th column of $\mathbf{Y}$, and $Y_{hj}$ represents the value of the element in the h-th row and j-th column of $\mathbf{Y}$.

Second, we decompose the label correlation matrix $\mathbf{C}$ into a low-dimensional space by graph embedding as follows

$$\begin{array}{cc}\hfill \underset{\mathbf{W}}{min}& \frac{{\lambda }_1}{4}\left|\right|\mathbf{C}-{\mathbf{W}}^T{\mathbf{W}\parallel }_F^2.\hfill \end{array}$$

(2)

For $\mathbf{W}$, we can utilize it as the model coefficient to construct a multi-label classifier. In this paper, we first construct a linear model for multi-label classification as follows

$$\begin{array}{cc}\hfill \underset{\mathbf{W}}{min}& \frac{1}{2}{\left|\right|\mathbf{X}\mathbf{W}-\mathbf{Y}\parallel }_F^2+\frac{{\lambda }_1}{4}\left|\right|\mathbf{C}-{\mathbf{W}}^T{\mathbf{W}\parallel }_F^2+\frac{{\lambda }_2}{2}{\parallel \mathbf{W}\parallel }_{21},\hfill \end{array}$$

(3)

where $\mathbf{W}=[{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_q]\in {\mathbb{R}}^{d\times q}$, ${\lambda }_1$ and ${\lambda }_2$ are non-negative weight parameters. The ${\ell }_{21}$-norm regularization term is imposed on $\mathbf{W}$ to ensure the sparsity, which can select discriminative features. In addition, ${\ell }_{21}$ norm has been confirmed to be robust to outliers and noise [55].

Previous studies mainly constrain the correlation between labels on the model coefficient matrix or the output by manifold regularization [35,36]. Different from previous studies, we directly model the pairwise label correlations by graph embedding, and the structure of label correlation will be well kept in $\mathbf{W}$.

3.2. Dimension Reduction

During the past decades, multi-label classifiers are generally constructed from the feature space to the label space [56,57] directly. However, the high dimension of multi-label data in the feature space puts great pressure on time and memory costs. To address this issue, we explicitly introduce a feature dimension reduction stage that the data is projected from the original feature space to the low-dimensional feature space by mapping matrix.

We adopt the multiple linear regression model to build a linear classification model $f(\mathbf{X},\mathbf{P},\mathbf{W})=\mathbf{X}\mathbf{P}\mathbf{W}$ from the low-dimensional feature space to the label space, where $\mathbf{P}\in {\mathbb{R}}^{d\times d_1}$ is the feature mapping matrix, and $\mathbf{W}\in {\mathbb{R}}^{d_1\times q}$ is the model coefficient matrix. Consequently, the objective function can be rewritten as follows

$$\begin{array}{cc}\hfill \underset{\mathbf{P},\mathbf{W}}{min}& \frac{1}{2}{\left|\right|\mathbf{X}\mathbf{P}\mathbf{W}-\mathbf{Y}\parallel }_F^2+\frac{{\lambda }_1}{4}\left|\right|\mathbf{C}-{\mathbf{W}}^T{\mathbf{W}\parallel }_F^2+\frac{{\lambda }_2}{2}{\parallel \mathbf{W}\parallel }_{21}.\hfill \end{array}$$

(4)

For any matrix $\mathbf{W}\in {\mathbb{R}}^{m\times n}$, ${\parallel \mathbf{W}\parallel }_F^2={\sum }_{i=1}^m{\sum }_{j=1}^n{W}_{ij}^2=\mathrm{tr}\left({\mathbf{W}}^T\mathbf{W}\right)$, The ${\ell }_{21}$ of $\mathbf{W}$ is defined as ${\parallel \mathbf{W}\parallel }_{21}={\sum }_{i=1}^m\sqrt{{\sum }_{j=1}^n{W}_{ij}^2}$. Consequently, we can rewrite the third term ${\parallel \mathbf{W}\parallel }_{21}$ by 2$\mathrm{tr}\left({\mathbf{W}}^T\mathbf{D}\mathbf{W}\right)$, where $\mathbf{D}$ is a diagonal matrix with its diagonal element $D_{ii}=\frac{1}{2\sqrt{W_{i:}^T{W}_{i:}+\epsilon }}$ and $\epsilon$ is a small positive constant. As a result, the objective function becomes

$$\begin{array}{cc}\hfill \underset{\mathbf{P},\mathbf{W}}{min}& \frac{1}{2}{\left|\right|\mathbf{X}\mathbf{P}\mathbf{W}-\mathbf{Y}\parallel }_F^2+\frac{{\lambda }_1}{4}\left|\right|\mathbf{C}-{\mathbf{W}}^T{\mathbf{W}\parallel }_F^2+2{\lambda }_2\mathrm{tr}\left({\mathbf{W}}^T\mathbf{D}\mathbf{W}\right).\hfill \end{array}$$

(5)

3.3. Optimization

For problem (5), it is convex, and there are two parameters, i.e., $\mathbf{W}$ and $\mathbf{P}$. We adopt the effective alternate optimization strategy. Specifically, in each iteration, we update one parameter and fix the other one. We use $\mathcal{F}\left(\psi \right)$ to represent the objective function in problem (5), where $\psi =\{\mathbf{P},\mathbf{W}\}$ indicates the set of the two parameters.

3.3.1. Update $\mathbf{P}$

By fixing $\mathbf{W}$, the problem (5) is simplified as

$$\begin{array}{cc}\hfill \underset{\mathbf{P}}{min}& \frac{1}{2}{\left|\right|\mathbf{X}\mathbf{P}\mathbf{W}-\mathbf{Y}\parallel }_F^2.\hfill \end{array}$$

(6)

Then, we can obtain the gradient w.r.t $\mathbf{P}$ as

$${\nabla }_{\mathbf{P}}\mathcal{F}={\mathbf{X}}^T\mathbf{XPW}{\mathbf{W}}^T-{\mathbf{X}}^T\mathbf{Y}{\mathbf{W}}^T.$$

(7)

According the gradient descend algorithm, $\mathbf{P}$ can be updated by

$$\mathbf{P}=\mathbf{P}-{\lambda }_p{\nabla }_{\mathbf{P}}\mathcal{F},$$

(8)

where ${\lambda }_p$ is step size of $\mathbf{P}$ in the gradient descent update rules. Choosing an appropriate step size is crucial to improve the convergence rate and reduce the total running time of MLLCE. According to the literature [58], we adopt the Armijo rule to automatically determine the step size ${\lambda }_p$ in each iteration.

3.3.2. Update $\mathbf{W}$

With $\mathbf{P}$ fixed, the Equation (5) becomes:

$$\begin{array}{cc}\hfill \underset{\mathbf{W}}{min}& \frac{1}{2}{\left|\right|\mathbf{X}\mathbf{P}\mathbf{W}-\mathbf{Y}\parallel }_F^2+\frac{{\lambda }_1}{4}\left|\right|\mathbf{C}-{\mathbf{W}}^T{\mathbf{W}\parallel }_F^2+2{\lambda }_2\mathrm{tr}\left({\mathbf{W}}^T\mathbf{D}\mathbf{W}\right)\hfill \end{array}$$

(9)

Therefore, we can obtain the gradient w.r.t $\mathcal{W}$ as

$${\nabla }_{\mathbf{W}}\mathcal{F}={\mathbf{P}}^T{\mathbf{X}}^T\mathbf{XPW}-{\mathbf{P}}^T{\mathbf{X}}^T\mathbf{Y}+{\lambda }_1\left(\mathbf{W}{\mathbf{W}}^T\mathbf{W}\right)+2\mathbf{D}\mathbf{W}.$$

(10)

Consequently, $\mathbf{W}$ can be updated by

$$\mathbf{W}=\mathbf{W}-{\lambda }_w{\nabla }_{\mathbf{W}}\mathcal{F}.$$

(11)

Similarly, the step size ${\lambda }_w$ is also determined by the Armijo rule [58]. According to the above optimization process, we give the pseudo code of the proposed method MLLCE in Algorithm 1.

Algorithm 1: Improving Multi-Label Learning by Correlation Embedding

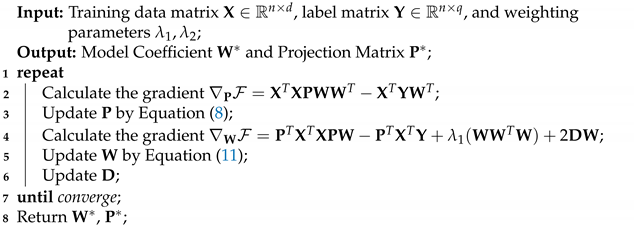3.4. Non-Linear Extension of MLLCE

In addition, by considering nuclear techniques [59], a non-linear version of the MLLCE method can be derived by introducing the kernel trick. Specifically, we adopt a nonlinear feature mapping $\mathsf{\Phi }(·):{\mathbb{R}}^d⟶{\mathbb{R}}^{\Psi }$, which maps the original feature space to the higher-dimensional Reproducing Kernel Hilbert Space (RKHS). Accordingly, the feature mapping matrix is set to be $\mathbf{P}=\mathsf{\Phi }\mathbf{H}$, where $\mathsf{\Phi }=[\mathsf{\Phi }\left({\mathbf{x}}_1\right),\mathsf{\Phi }\left({\mathbf{x}}_2\right),\dots ,\mathsf{\Phi }\left({\mathbf{x}}_n\right)]\in {\mathbb{R}}^{\mathsf{\Psi }\times n}$, $\mathbf{H}\in {\mathbb{R}}^{n\times d}$. The kernel matrix is usually given as $\mathbf{K}=\mathsf{\Phi }{\left(\mathbf{x}\right)}^T\mathsf{\Phi }\left(\mathbf{x}\right)\in {\mathbb{R}}^{n\times n}$, $\mathsf{\Phi }{\left(\mathbf{x}\right)}^T\mathbf{P}=\mathsf{\Phi }{\left(\mathbf{x}\right)}^T\mathsf{\Phi }\left(\mathbf{x}\right)\mathbf{H}=\mathbf{K}\mathbf{H}$.

Consequently, for the nonlinear version of MLLCE, the objective function of problem (5) can be rewritten as

$$\begin{array}{cc}\hfill \underset{\mathbf{H},\mathbf{W}}{min}& \frac{1}{2}{\left|\right|\mathbf{K}\mathbf{H}\mathbf{W}-\mathbf{Y}\parallel }_F^2+\frac{{\lambda }_1}{4}\left|\right|\mathbf{C}-{\mathbf{W}}^T{\mathbf{W}\parallel }_F^2+{\lambda }_2{\parallel \mathbf{W}\parallel }_{21}.\hfill \end{array}$$

(12)

Then, similar to the optimization of the linear version of MLLCE method, $\mathbf{W}$ and $\mathbf{H}$ are updated through an effective alternate optimization manner. The specific optimization process is based on Equations (7)–(11).

3.5. Complexity Analysis

For the proposed approach, data matrix $\mathbf{X}\in {\mathbb{R}}^{n\times d}$, projection matrix $\mathbf{P}\in {\mathbb{R}}^{d\times d_1}$, $\mathbf{W}\in {\mathbb{R}}^{d_1\times q}$, label matrix $\mathbf{Y}\in {\{0,1\}}^{n\times q}$, $\mathbf{D}\in {\mathbb{R}}^{d_1\times d_1}$, label correlation matrix $\mathbf{C}\in {\mathbb{R}}^{q\times q}$, which n and q are the number of instance and label respectively, d and $d_1$ are the dimension of the original and the low-dimensional feature space.

In Algorithm 1, steps 5–7 are the most time-consuming parts. For steps 5 and 6, the update needs to be calculated by steps 2 and 3, in which the calculation mainly consists of some matrix multiplications. Therefore, the total time complexity is $\mathcal{O}\left(t(n{d}^2+ndq+nd{d}_1+n{d}_{1}q+d^2{d}_1+d{d}_{1}q+d{d}_1^2+d_1^{2}q)\right)$, where t is the number of iterations. After the optimization, we only need to save $\mathbf{P}$ and $\mathbf{W}$, it can lead to a memory cost of $\mathcal{O}(d_{1}q+d{d}_1)$.

4. Experiment

4.1. Comparing Algorithms

In order to verify the performance of our proposed method, the paper selects five existing state-of-the-art multi-label classification approaches to compare with MLLCE, i.e., BR, JFSC, ML-LSS, MLL-FLSDR, and Glocal. The detailed information regarding the method of comparison and the linear and non-linear proposed in this paper are as follows:

(1)

BR [21]: The basic idea of BR is to decompose a multi-label learning problem into a set of independent binary classification sub-problems. In this paper, linear regression is adopted as the base learner for each binary classification sub-problem, where the regularization parameter is searched in $\{0.1,1,\dots ,10\}$.

(2)

JFSC [15]: JFSC is a feature selection and multi-label classification algorithm by exploiting label correlation. The search scope for parameters $\alpha ,\beta$ and $\gamma$ are $\{4^{-5},4^{-4}\dots 4^5\}$. Parameter $\eta$ is searched in $\{0.1,1,\dots ,10\}$.

(3)

ML-LSS [60]: ML-LSS is proposed for multi-label learning by modeling local similarity. Parameter ${\lambda }_1,{\lambda }_2$ are tuned in $\{2^{-5},2^{-4},\dots ,2^6\}$.

(4)

MLL-FLSDR [20]: A multi-label learning method based on label embedding that is used to solve the problem of many labels and features, where the parameter ${\lambda }_1$ is searched in $\{{10}^2,{10}^3,\dots ,{10}^6\}$, ${\lambda }_2$, and ${\lambda }_3$ and ${\lambda }_4$ are searched in $\{{10}^{-3},{10}^{-2},\dots ,{10}^1\}$.

(5)

Glocal [61]: A multi-label learning approach that utilized the global and local label correlation. The parameter $\lambda =1$ and the parameters ${\lambda }_1$ to ${\lambda }_5$ are tuned in $\{{10}^{-5},{10}^{-4}\dots {10}^1\}$, k is searched in $\{0.1l,0.2l\dots 0.6l\}$, where l is the number of labels in each data set. g is searched in $\{5,10,15,20\}$.

(6)

MLLCE and NL-MLLCE:The two versions of our proposed method in this paper. Parameter ${\lambda }_1$ and ${\lambda }_2$ are tuned in $\{{10}^{-6},{10}^{-4},\dots ,{10}^2\}$. $d_1=0.3d$ is the feature dimension in the low feature space, where d is the dimension of the original feature space.

4.2. Data Sets

In this paper, a total of 15 multi-label benchmark data sets are used to verify the effectiveness of our method. Detailed information about these data sets are summarized in Table 1. For each data set S, $\left|\mathcal{S}\right|$ denotes the number of instances, $dim\left(\mathcal{S}\right)$ denotes the number of features, and $L\left(\mathcal{S}\right)$ denotes the number of labels. In addition, $LCard\left(\mathcal{S}\right)$ is cardinality, which indicates the average number of labels belonging to instances, and $rDep\left(\mathcal{S}\right)$ denotes the ratio of unconditionally dependent label pairs.

Table 1. Description of datasets.

ID	Data Set	$\left|\mathcal{S}\right|$	$\mathit{dim}\left(\mathcal{S}\right)$	$\mathit{L}\left(\mathcal{S}\right)$	$\mathit{LCard}\left(\mathcal{S}\right)$	$\mathit{rDep}\left(\mathcal{S}\right)$
1	rcv1v2(subset1)	6000	944	101	2.88	0.202
2	rcv1v2(subset2)	6000	944	101	2.63	0.179
3	delicious	16,105	500	983	19.02	0.143
4	enron	1702	1001	53	3.38	0.141
5	recreation	5000	606	22	1.42	0.455
6	Stackex-coffee	225	1763	123	1.99	0.017
7	Stackex-chess	1675	585	227	2.41	0.030
8	Stackex-chemistry	6961	540	175	2.11	0.056
9	Stackex-philosophy	3971	842	233	2.27	0.040
10	Stackex-cs	9270	635	274	2.56	0.049
11	Stackex-cooking	10,491	577	400	2.23	0.034
12	Corel16k001	13,766	500	153	2.86	0.142
13	Corel16k002	13,761	500	164	2.88	0.128
14	Water-quality	1060	16	14	5.073	0.473
15	flags	194	19	7	3.392	0.381

4.3. Evaluation Metrics

A great many evaluation metrics have been proposed to evaluate the performance of multi-label learning algorithms. In the paper, we choose six common evaluation metrics. Define a test data $\mathcal{T}=\{({\mathbf{x}}_1,Y_1),({\mathbf{x}}_2,Y_2)\dots ({\mathbf{x}}_1,Y_{n_t})\}$, where the ground truth labels set of the instance $x_i$ is represented as $Y_i\in {\{0,1\}}^q$, $Y_i\in \mathcal{Y}$, $h\left({\mathbf{x}}_{\mathbf{i}}\right)\in {\{0,1\}}^q$ is the set of predicted class labels for the i-th instance, $f({\mathbf{x}}_i,y)$ is the the confidence score that ${\mathbf{x}}_i$ belongs to label y.

Hamming Loss evaluates the error between the predicted label of each instance obtained by the model and the true label of each instance.

$$\mathrm{Hamming}\mathrm{Loss}=\frac{1}{n_t}\sum _{i=1}^{n_t}\frac{1}{l}|h\left({\mathbf{x}}_i\right)\Delta Y_i|$$

(13)

where $\Delta$ indicates the symmetric difference between two sets.

One Error evaluates the proportion of instances whose top-ranked label is not in the ground truth label set.

$$\mathrm{One}\mathrm{Error}=\frac{1}{n_t}\sum _{i=1}^{n_t}⟦[arg\underset{y\in \mathcal{Y}}{max}f({\mathbf{x}}_i,y)]\in Y_i⟧$$

(14)

where $⟦·⟧$ represents the indication function.

Ranking Loss indicates how many irrelevant labels are ranked higher than related labels.

$$\mathrm{Ranking}\mathrm{Loss}=\frac{1}{n_t}\sum _{i=1}^{n_t}\frac{1}{|Y_i\left|\right|\widehat{Y_i}|}\left|\left\{(y^{\prime },y^{″})\right|f({\mathbf{x}}_i,y^{\prime })\le f({\mathbf{x}}_i,y^{″}),(y^{\prime },y^{″})\in Y_i\times \overline{Y_i}\}\right|$$

(15)

Average Precision evaluates the proportion of the label that is ranked before the relevant label of the instance is still the related label.

$$\mathrm{Average}\mathrm{Precision}=\frac{1}{n_t}\sum _{i=1}^{n_t}\frac{1}{|Y_i|}\sum _{y\in Y_i}\frac{\left|\right\{y^{\prime }|ran{k}_{f({\mathbf{x}}_i,y^{\prime })}\le ran{k}_{f({\mathbf{x}}_i,y)},y^{\prime }\in Y_i\}|}{ran{k}_{f({\mathbf{x}}_i,y)}}$$

(16)

Micro F1-Measure evaluates the prediction performance of the learned classifier on the label set.

$$\mathrm{MicroF}1=\frac{2{\displaystyle \sum _{i=1}^{n_t}}|h\left({\mathbf{x}}_i\right)\cap Y_i|}{{\displaystyle \sum _{i=1}^{n_t}}|Y_i|+{\displaystyle \sum _{i=1}^{n_t}}\left|h\left({\mathbf{x}}_i\right)\right|}$$

(17)

Example-based F1 is the integrated version of precision and recall for each instance.

$$\mathrm{Example}-\mathrm{based}\mathrm{F}1=\frac{1}{n_t}\sum _{i=1}^{n_t}\frac{2p_i{r}_i}{p_i+r_i}$$

(18)

where $p_i$ and $r_i$ are the precision and recall for the i-th instance.

Macro AUC evaluates the probability that a positive instance is ranked before a negative instance, averaged over all labels.

$$\mathrm{AUC}=\frac{1}{l}\sum _{i=1}^l\frac{\left|\right\{({\mathbf{x}}^{\prime },{\mathbf{x}}^{″})|f({\mathbf{x}}^{\prime },y_j)\ge f({\mathbf{x}}^{″},y_j),({\mathbf{x}}^{\prime },{\mathbf{x}}^{″})\in Z_j\times \overline{Z_j}\}|}{|Z_j\left|\right|\overline{Z_j}|}$$

(19)

where $Z_j=\left\{{\mathbf{x}}_i\right|y_j\in Y_i,1\le i\le l\}(\overline{Z_j}=\left\{{\mathbf{x}}_i\right|y_j\notin Y_i,1\le i\le l\})$ indicates that it does not belong to a set of test instances labeled $y_j$.

For the AUC and AP evaluation metrics, the larger the value, the better the classification result. Hamming loss, One Error, Ranking Loss, and Coverage value are smaller, indicating better classification performance.

4.4. Experimental Results

For each data set, 80% is used for training and 20% is used for test set. The average value as well as standard deviation of each comparison algorithm in terms of each the evaluation metric are recorded in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8 for 13 data sets. The best results in each row of the table will be emphasized in bold.

Table 2. The experimental results (mean ± standard) of all comparison methods in this paper in terms of Hamming Loss. ↓ means that the smaller the value, the better the performance is. The best results in each row are highlighted in bold face.

Data	Hamming Loss ↓
	MLLCE	NL-MLLCE	ML-LSS	JFSC	BR	Glocal	MLL-FLSDR
rcv1subset1	0.026 ± 0.000	0.026 ± 0.000	0.026 ± 0.000	0.027 ± 0.000	0.024 ± 0.000	0.027 ± 0.001	0.026 ± 0.000
rcv1subset2	0.023 ± 0.000	0.023 ± 0.000	0.023 ± 0.000	0.023 ± 0.001	0.025 ± 0.001	0.024 ± 0.001	0.024 ± 0.001
enron	0.047 ± 0.000	0.047 ± 0.002	0.047 ± 0.002	0.047 ± 0.002	0.047 ± 0.002	0.060 ± 0.004	0.044 ± 0.002
recreation	0.053 ± 0.001	0.054 ± 0.002	0.054 ± 0.001	0.054 ± 0.002	0.048 ± 0.001	0.063 ± 0.001	0.054 ± 0.001
stackex-coffee	0.015 ± 0.001	0.015 ± 0.001	0.015 ± 0.001	0.016 ± 0.001	0.016 ± 0.001	0.029 ± 0.015	0.016 ± 0.001
stackex-chess	0.009 ± 0.000	0.010 ± 0.000	0.009 ± 0.000	0.010 ± 0.000	0.010 ± 0.000	0.036 ± 0.006	0.012 ± 0.005
stackex-philosophy	0.009 ± 0.000	0.009 ± 0.000	0.009 ± 0.000	0.009 ± 0.000	0.009 ± 0.000	0.046 ± 0.007	0.009 ± 0.000
stackex-chemistry	0.011 ± 0.000	0.011 ± 0.000	0.011 ± 0.000	0.012 ± 0.000	0.011 ± 0.000	0.022 ± 0.002	0.011 ± 0.000
stackex-cs	0.008 ± 0.000	0.008 ± 0.000	0.008 ± 0.000	0.009 ± 0.000	0.008 ± 0.000	0.014 ± 0.001	0.009 ± 0.000
stackex-cooking	0.005 ± 0.000	0.005 ± 0.000	0.005 ± 0.000	0.005 ± 0.000	0.005 ± 0.000	0.009 ± 0.001	0.005 ± 0.000
corel16k001	0.019 ± 0.000	0.019 ± 0.000	0.019 ± 0.000	0.019 ± 0.000	0.019 ± 0.000	0.019 ± 0.000	0.019 ± 0.000
corel16k002	0.017 ± 0.000	0.017 ± 0.000	0.017 ± 0.000	0.017 ± 0.000	0.018 ± 0.000	0.017 ± 0.000	0.017 ± 0.000
water-quality	0.303 ± 0.007	0.305 ± 0.016	0.309 ± 0.008	0.302 ± 0.008	0.312 ± 0.008	0.314 ± 0.007	0.323 ± 0.005
flags	0.267 ± 0.044	0.281 ± 0.029	0.267 ± 0.031	0.271 ± 0.025	0.278 ± 0.025	0.286 ± 0.009	0.278 ± 0.031
delicious	0.018 ± 0.000	0.018 ± 0.000	0.018 ± 0.000	0.018 ± 0.000	0.019 ± 0.000	0.057 ± 0.002	0.018 ± 0.000

Table 3. The experimental results (mean ± standard) of all comparison methods in this paper in terms of Average Precision. ↑ means that the larger the value, the better the performance is. The best results in each row are highlighted in bold face.

Data	Average Precision ↑
	MLLCE	NL-MLLCE	ML-LSS	JFSC	BR	Glocal	MLL-FLSDR
rcv1subset1	0.620 ± 0.006	0.622 ± 0.007	0.608 ± 0.007	0.589 ± 0.002	0.637 ± 0.006	0.606 ± 0.008	0.610 ± 0.011
rcv1subset2	0.638 ± 0.003	0.635 ± 0.005	0.635 ± 0.007	0.620 ± 0.010	0.600 ± 0.011	0.629 ± 0.008	0.606 ± 0.036
enron	0.701 ± 0.007	0.699 ± 0.011	0.693 ± 0.018	0.691 ± 0.009	0.729 ± 0.006	0.674 ± 0.011	0.715 ± 0.012
recreation	0.643 ± 0.006	0.650 ± 0.012	0.640 ± 0.010	0.637 ± 0.015	0.586 ± 0.009	0.594 ± 0.019	0.630 ± 0.010
stackex-coffee	0.517 ± 0.064	0.524 ± 0.043	0.424 ± 0.031	0.450 ± 0.033	0.479 ± 0.057	0.481 ± 0.026	0.400 ± 0.040
stackex-chess	0.512 ± 0.009	0.507 ± 0.021	0.507 ± 0.009	0.479 ± 0.014	0.515 ± 0.015	0.458 ± 0.019	0.456 ± 0.083
stackex-philosophy	0.517 ± 0.013	0.510 ± 0.006	0.508 ± 0.013	0.484 ± 0.005	0.515 ± 0.013	0.466 ± 0.012	0.493 ± 0.012
stackex-chemistry	0.464 ± 0.006	0.468 ± 0.005	0.461 ± 0.008	0.437 ± 0.006	0.449 ± 0.006	0.445 ± 0.008	0.455 ± 0.009
stackex-cs	0.532 ± 0.004	0.533 ± 0.006	0.529 ± 0.008	0.495 ± 0.006	0.504 ± 0.010	0.485 ± 0.005	0.502 ± 0.005
stackex-cooking	0.519 ± 0.005	0.522 ± 0.006	0.522 ± 0.008	0.504 ± 0.008	0.502 ± 0.008	0.505 ± 0.004	0.502 ± 0.006
corel16k001	0.347 ± 0.006	0.347 ± 0.004	0.345 ± 0.004	0.344 ± 0.002	0.363 ± 0.005	0.338 ± 0.005	0.345 ± 0.002
corel16k002	0.341 ± 0.005	0.341 ± 0.003	0.341 ± 0.005	0.340 ± 0.007	0.355 ± 0.005	0.332 ± 0.003	0.339 ± 0.004
water-quality	0.669 ± 0.005	0.668 ± 0.005	0.662 ± 0.010	0.671 ± 0.014	0.650 ± 0.015	0.654 ± 0.010	0.629 ± 0.005
flags	0.816 ± 0.035	0.821 ± 0.028	0.821 ± 0.027	0.809 ± 0.028	0.815 ± 0.028	0.811 ± 0.017	0.816 ± 0.031
delicious	0.363 ± 0.002	0.389 ± 0.002	0.377 ± 0.004	0.366 ± 0.002	0.387 ± 0.002	0.355 ± 0.004	0.355 ± 0.053

Table 4. The experimental results (mean ± standard) of all comparison methods in this paper in terms of One Error. ↓ means that the smaller the value, the better the performance is. The best results in each row are highlighted in bold face.

Data	One Error ↓
	MLLCE	NL-MLLCE	ML-LSS	JFSC	BR	Glocal	MLL-FLSDR
rcv1subset1	0.415 ± 0.013	0.414 ± 0.016	0.426 ± 0.006	0.446 ± 0.008	0.450 ± 0.014	0.417 ± 0.008	0.414 ± 0.016
rcv1subset2	0.408 ± 0.005	0.416 ± 0.016	0.406 ± 0.010	0.413 ± 0.014	0.467 ± 0.014	0.411 ± 0.012	0.444 ± 0.055
enron	0.217 ± 0.009	0.219 ± 0.023	0.227 ± 0.019	0.249 ± 0.018	0.212 ± 0.018	0.246 ± 0.014	0.216 ± 0.014
recreation	0.443 ± 0.008	0.439 ± 0.018	0.452 ± 0.013	0.465 ± 0.023	0.482 ± 0.012	0.512 ± 0.026	0.456 ± 0.013
stackex-coffee	0.484 ± 0.081	0.458 ± 0.083	0.569 ± 0.043	0.573 ± 0.038	0.551 ± 0.065	0.533 ± 0.040	0.636 ± 0.041
stackex-chess	0.405 ± 0.009	0.421 ± 0.034	0.423 ± 0.018	0.463 ± 0.015	0.435 ± 0.023	0.474 ± 0.031	0.472 ± 0.100
stackex-philosophy	0.431 ± 0.015	0.446 ± 0.010	0.441 ± 0.015	0.473 ± 0.006	0.454 ± 0.024	0.479 ± 0.014	0.457 ± 0.023
stackex-chemistry	0.544 ± 0.009	0.542 ± 0.012	0.553 ± 0.014	0.579 ± 0.007	0.582 ± 0.009	0.560 ± 0.008	0.557 ± 0.009
stackex-cs	0.437 ± 0.007	0.438 ± 0.010	0.435 ± 0.013	0.474 ± 0.010	0.494 ± 0.012	0.457 ± 0.007	0.466 ± 0.008
stackex-cooking	0.412 ± 0.007	0.410 ± 0.004	0.408 ± 0.011	0.424 ± 0.012	0.451 ± 0.010	0.424 ± 0.007	0.419 ± 0.008
corel16k001	0.640 ± 0.008	0.640 ± 0.004	0.638 ± 0.006	0.640 ± 0.004	0.638 ± 0.011	0.641 ± 0.011	0.633 ± 0.006
corel16k002	0.637 ± 0.011	0.641 ± 0.006	0.639 ± 0.009	0.637 ± 0.013	0.636 ± 0.009	0.640 ± 0.009	0.636 ± 0.010
water-quality	0.309 ± 0.022	0.312 ± 0.029	0.338 ± 0.020	0.323 ± 0.040	0.337 ± 0.032	0.340 ± 0.027	0.338 ± 0.018
flags	0.203 ± 0.078	0.177 ± 0.046	0.193 ± 0.045	0.213 ± 0.069	0.198 ± 0.072	0.203 ± 0.059	0.204 ± 0.052
delicious	0.345 ± 0.004	0.310 ± 0.002	0.326 ± 0.009	0.339 ± 0.005	0.325 ± 0.002	0.369 ± 0.007	0.364 ± 0.088

Table 5. The experimental results (mean ± standard) of all comparison methods in this paper in terms of Ranking Loss. ↓ means that the smaller the value, the better the performance is. The best results in each row are highlighted in bold face.

Data	Ranking Loss ↓
	MLLCE	NL-MLLCE	ML-LSS	JFSC	BR	Glocal	MLL-FLSDR
rcv1subset1	0.044 ± 0.002	0.043 ± 0.002	0.056 ± 0.002	0.061 ± 0.003	0.040 ± 0.002	0.057 ± 0.002	0.053 ± 0.004
rcv1subset2	0.044 ± 0.002	0.043 ± 0.001	0.053 ± 0.002	0.057 ± 0.003	0.065 ± 0.005	0.056 ± 0.003	0.058 ± 0.006
enron	0.081 ± 0.004	0.078 ± 0.006	0.085 ± 0.006	0.095 ± 0.007	0.075 ± 0.002	0.110 ± 0.009	0.081 ± 0.005
recreation	0.147 ± 0.005	0.134 ± 0.008	0.137 ± 0.010	0.136 ± 0.006	0.117 ± 0.004	0.145 ± 0.005	0.148 ± 0.004
stackex-coffee	0.144 ± 0.034	0.156 ± 0.014	0.224 ± 0.038	0.307 ± 0.036	0.146 ± 0.023	0.152 ± 0.021	0.211 ± 0.037
stackex-chess	0.117 ± 0.009	0.089 ± 0.008	0.106 ± 0.004	0.130 ± 0.011	0.092 ± 0.006	0.128 ± 0.009	0.116 ± 0.035
stackex-philosophy	0.106 ± 0.008	0.098 ± 0.008	0.113 ± 0.004	0.115 ± 0.006	0.098 ± 0.004	0.144 ± 0.001	0.101 ± 0.003
stackex-chemistry	0.114 ± 0.002	0.104 ± 0.002	0.104 ± 0.004	0.100 ± 0.004	0.103 ± 0.003	0.126 ± 0.006	0.104 ± 0.006
stackex-cs	0.069 ± 0.002	0.067 ± 0.002	0.071 ± 0.003	0.076 ± 0.002	0.068 ± 0.004	0.097 ± 0.003	0.077 ± 0.003
stackex-cooking	0.084 ± 0.002	0.084 ± 0.002	0.091 ± 0.001	0.091 ± 0.003	0.084 ± 0.004	0.105 ± 0.003	0.089 ± 0.003
corel16k001	0.148 ± 0.003	0.153 ± 0.003	0.160 ± 0.003	0.160 ± 0.003	0.161 ± 0.002	0.173 ± 0.008	0.164 ± 0.002
corel16k002	0.162 ± 0.005	0.150 ± 0.003	0.154 ± 0.003	0.154 ± 0.005	0.157 ± 0.003	0.173 ± 0.003	0.163 ± 0.001
water-quality	0.268 ± 0.005	0.269 ± 0.007	0.275 ± 0.009	0.264 ± 0.010	0.282 ± 0.005	0.285 ± 0.008	0.310 ± 0.009
flags	0.211 ± 0.043	0.207 ± 0.022	0.206 ± 0.023	0.221 ± 0.024	0.214 ± 0.034	0.216 ± 0.019	0.213 ± 0.038
delicious	0.138 ± 0.002	0.118 ± 0.002	0.115 ± 0.001	0.113 ± 0.001	0.116 ± 0.001	0.149 ± 0.001	0.121 ± 0.084

Table 6. The experimental results (mean ± standard) of all comparison methods in this paper in terms of AUC. ↑ means that the larger the value, the better the performance is. The best results in each row are highlighted in bold face.

Data	AUC ↑
	MLLCE	NL-MLLCE	ML-LSS	JFSC	BR	Glocal	MLL-FLSDR
rcv1subset1	0.941 ± 0.002	0.942 ± 0.003	0.928 ± 0.002	0.921 ± 0.003	0.940 ± 0.004	0.925 ± 0.002	0.930 ± 0.004
rcv1subset2	0.936 ± 0.002	0.938 ± 0.002	0.925 ± 0.002	0.919 ± 0.004	0.910 ± 0.006	0.920 ± 0.003	0.918 ± 0.006
enron	0.911 ± 0.001	0.913 ± 0.004	0.904 ± 0.005	0.890 ± 0.009	0.908 ± 0.004	0.882 ± 0.002	0.908 ± 0.004
recreation	0.813 ± 0.009	0.826 ± 0.010	0.824 ± 0.010	0.821 ± 0.009	0.723 ± 0.005	0.820 ± 0.005	0.813 ± 0.005
stackex-coffee	0.853 ± 0.027	0.841 ± 0.019	0.763 ± 0.035	0.794 ± 0.030	0.810 ± 0.042	0.836 ± 0.022	0.781 ± 0.042
stackex-chess	0.876 ± 0.009	0.903 ± 0.009	0.884 ± 0.005	0.883 ± 0.010	0.881 ± 0.007	0.866 ± 0.011	0.877 ± 0.035
stackex-philosophy	0.881 ± 0.008	0.888 ± 0.009	0.874 ± 0.004	0.879 ± 0.003	0.870 ± 0.005	0.845 ± 0.001	0.884 ± 0.002
stackex-chemistry	0.877 ± 0.003	0.886 ± 0.002	0.888 ± 0.004	0.892 ± 0.003	0.846 ± 0.004	0.866 ± 0.004	0.887 ± 0.006
stackex-cs	0.925 ± 0.003	0.927 ± 0.002	0.923 ± 0.003	0.922 ± 0.002	0.883 ± 0.006	0.902 ± 0.003	0.917 ± 0.002
stackex-cooking	0.900 ± 0.002	0.899 ± 0.003	0.894 ± 0.005	0.892 ± 0.004	0.863 ± 0.004	0.892 ± 0.002	0.895 ± 0.002
corel16k001	0.850 ± 0.003	0.845 ± 0.003	0.838 ± 0.004	0.837 ± 0.003	0.831 ± 0.002	0.825 ± 0.007	0.834 ± 0.002
corel16k002	0.839 ± 0.004	0.851 ± 0.003	0.847 ± 0.002	0.846 ± 0.003	0.824 ± 0.003	0.828 ± 0.003	0.839 ± 0.001
water-quality	0.699 ± 0.005	0.697 ± 0.008	0.694 ± 0.007	0.702 ± 0.011	0.684 ± 0.007	0.691 ± 0.005	0.664 ± 0.012
flags	0.745 ± 0.031	0.748 ± 0.025	0.751 ± 0.017	0.736 ± 0.014	0.743 ± 0.032	0.742 ± 0.020	0.744 ± 0.037
delicious	0.859 ± 0.002	0.881 ± 0.001	0.884 ± 0.002	0.886 ± 0.001	0.882 ± 0.001	0.848 ± 0.001	0.877 ± 0.090

Table 7. The experimental results (mean ± standard) of all comparison methods in this paper in terms of Micro F1. ↑ means that the larger the value, the better the performance is. The best results in each row are highlighted in bold face.

Data	Micro F1 ↑
	MLLCE	NL-MLLCE	ML-LSS	JFSC	BR	Glocal	MLL-FLSDR
rcv1subset1	0.313 ± 0.008	0.315 ± 0.007	0.353 ± 0.005	0.316 ± 0.009	0.286 ± 0.009	0.354 ± 0.008	0.328 ± 0.011
rcv1subset2	0.302 ± 0.011	0.299 ± 0.006	0.368 ± 0.009	0.351 ± 0.012	0.333 ± 0.016	0.357 ± 0.006	0.303 ± 0.022
enron	0.525 ± 0.006	0.530 ± 0.019	0.526 ± 0.016	0.553 ± 0.018	0.573 ± 0.010	0.506 ± 0.021	0.577 ± 0.019
recreation	0.373 ± 0.007	0.348 ± 0.010	0.350 ± 0.015	0.333 ± 0.018	0.365 ± 0.010	0.053 ± 0.010	0.345 ± 0.013
stackex-coffee	0.158 ± 0.065	0.161 ± 0.031	0.155 ± 0.028	0.087 ± 0.052	0.009 ± 0.011	0.231 ± 0.060	0.066 ± 0.041
stackex-chess	0.314 ± 0.003	0.238 ± 0.023	0.274 ± 0.017	0.207 ± 0.011	0.248 ± 0.011	0.110 ± 0.014	0.251 ± 0.023
stackex-philosophy	0.271 ± 0.007	0.247 ± 0.007	0.298 ± 0.009	0.227 ± 0.007	0.256 ± 0.009	0.071 ± 0.006	0.242 ± 0.017
stackex-chemistry	0.192 ± 0.006	0.190 ± 0.011	0.190 ± 0.011	0.141 ± 0.006	0.166 ± 0.009	0.138 ± 0.009	0.157 ± 0.008
stackex-cs	0.296 ± 0.005	0.299 ± 0.005	0.301 ± 0.009	0.216 ± 0.007	0.257 ± 0.009	0.220 ± 0.014	0.256 ± 0.011
stackex-cooking	0.284 ± 0.007	0.317 ± 0.007	0.324 ± 0.006	0.247 ± 0.008	0.290 ± 0.007	0.181 ± 0.013	0.297 ± 0.004
corel16k001	0.044 ± 0.003	0.051 ± 0.002	0.064 ± 0.003	0.076 ± 0.003	0.064 ± 0.003	0.068 ± 0.001	0.057 ± 0.003
corel16k002	0.065 ± 0.002	0.053 ± 0.006	0.069 ± 0.005	0.080 ± 0.008	0.067 ± 0.003	0.076 ± 0.004	0.061 ± 0.001
water-quality	0.472 ± 0.014	0.465 ± 0.024	0.441 ± 0.016	0.460 ± 0.014	0.395 ± 0.014	0.421 ± 0.020	0.362 ± 0.016
flags	0.723 ± 0.043	0.708 ± 0.031	0.724 ± 0.046	0.709 ± 0.039	0.708 ± 0.026	0.699 ± 0.015	0.698 ± 0.031
delicious	0.182 ± 0.005	0.228 ± 0.005	0.216 ± 0.003	0.177 ± 0.004	0.220 ± 0.002	0.116 ± 0.004	0.175 ± 0.033

Table 8. The experimental results (mean ± standard) of all comparison methods in this paper in terms of Example-based F1. ↑ means that the larger the value, the better the performance is. The best results in each row are highlighted in bold face.

Data	Example-Based F1 ↑
	MLLCE	NL-MLLCE	ML-LSS	JFSC	BR	Glocal	MLL-FLSDR
rcv1subset1	0.262 ± 0.007	0.265 ± 0.008	0.306 ± 0.007	0.271 ± 0.010	0.244 ± 0.008	0.301 ± 0.007	0.279 ± 0.011
rcv1subset2	0.265 ± 0.007	0.262 ± 0.004	0.338 ± 0.013	0.323 ± 0.011	0.284 ± 0.014	0.325 ± 0.007	0.277 ± 0.020
enron	0.486 ± 0.011	0.504 ± 0.021	0.500 ± 0.020	0.534 ± 0.013	0.555 ± 0.007	0.523 ± 0.013	0.563 ± 0.018
recreation	0.299 ± 0.010	0.274 ± 0.010	0.278 ± 0.012	0.265 ± 0.013	0.243 ± 0.009	0.037 ± 0.008	0.275 ± 0.015
stackex-coffee	0.118 ± 0.059	0.119 ± 0.026	0.115 ± 0.017	0.060 ± 0.039	0.009 ± 0.011	0.239 ± 0.041	0.047 ± 0.028
stackex-chess	0.265 ± 0.004	0.196 ± 0.022	0.227 ± 0.010	0.152 ± 0.005	0.196 ± 0.008	0.216 ± 0.016	0.213 ± 0.021
stackex-philosophy	0.230 ± 0.005	0.209 ± 0.004	0.255 ± 0.013	0.175 ± 0.004	0.210 ± 0.005	0.168 ± 0.009	0.205 ± 0.015
stackex-chemistry	0.148 ± 0.005	0.147 ± 0.008	0.146 ± 0.008	0.098 ± 0.006	0.117 ± 0.007	0.160 ± 0.008	0.120 ± 0.005
stackex-cs	0.230 ± 0.005	0.233 ± 0.006	0.236 ± 0.005	0.148 ± 0.005	0.171 ± 0.006	0.239 ± 0.009	0.187 ± 0.012
stackex-cooking	0.233 ± 0.005	0.265 ± 0.007	0.270 ± 0.007	0.186 ± 0.006	0.226 ± 0.006	0.228 ± 0.007	0.247 ± 0.004
corel16k001	0.033 ± 0.002	0.039 ± 0.002	0.048 ± 0.002	0.058 ± 0.002	0.047 ± 0.002	0.052 ± 0.001	0.043 ± 0.003
corel16k002	0.046 ± 0.002	0.038 ± 0.005	0.048 ± 0.003	0.056 ± 0.005	0.046 ± 0.002	0.054 ± 0.003	0.043 ± 0.001
water-quality	0.425 ± 0.012	0.421 ± 0.023	0.401 ± 0.017	0.413 ± 0.015	0.366 ± 0.018	0.385 ± 0.021	0.338 ± 0.016
flags	0.686 ± 0.030	0.685 ± 0.039	0.694 ± 0.044	0.677 ± 0.041	0.685 ± 0.025	0.678 ± 0.023	0.679 ± 0.034
delicious	0.164 ± 0.004	0.206 ± 0.004	0.198 ± 0.003	0.155 ± 0.004	0.201 ± 0.002	0.212 ± 0.002	0.160 ± 0.029

To further understand whether MLLCE makes a significant performance difference, we adopt the Wilcoxon signed-rank test [62]. For any pair of two comparing classifiers, the test can return three probabilities between them: the probability that the first classifier has a higher score than the second (left), the probability that differences are within the region of practical equivalence (rope), or that the second classifier has a higher score (right). The sum of the probabilities of left, right, and rope is 1. The larger the value of left or right, the better the performance of the first or second classifier is. A large value of rope indicates that there is no significant difference in the performance between the two classifiers. The results of Wilcoxon signed-rank test in terms of seven metrics are reported in Table 9, Table 10, Table 11 and Table 12.

Table 9. Probabilities for the six comparisons of classifiers in terms of Hamming Loss and Average Precision. Left and right refer to the columns Classif. 1 (left) and Classif. 2 (right).

Hamming Loss					Average Precision
Classif. 1	Classif. 2	Left	Rope	Right	Classif. 1	Classif. 2	Left	Rope	Right
MLLCE	NL-MLLCE	0.006	0.994	0.000	MLLCE	NL-MLLCE	0.000	0.984	0.016
MLLCE	ML-LSS	0.000	1.000	0.000	MLLCE	ML-LSS	0.227	0.771	0.002
MLLCE	JFSC	0.000	1.000	0.000	MLLCE	JFSC	0.993	0.007	0.000
MLLCE	BR	0.003	0.997	0.000	MLLCE	BR	0.832	0.002	0.167
MLLCE	Glocal	0.995	0.005	0.000	MLLCE	Glocal	1.000	0.000	0.000
MLLCE	MLL-FLSDR	0.039	0.961	0.000	MLLCE	MLL-FLSDR	0.999	0.001	0.000

Table 10. Probabilities for the six comparisons of classifiers in terms of One Error and Ranking Loss. Left and right refer to the columns Classif. 1 (left) and Classif. 2 (right).

One Error					Ranking Loss
Classif. 1	Classif. 2	Left	Rope	Right	Classif. 1	Classif. 2	Left	Rope	Right
MLLCE	NL-MLLCE	0.081	0.626	0.293	MLLCE	NL-MLLCE	0.000	0.479	0.521
MLLCE	ML-LSS	0.628	0.362	0.010	MLLCE	ML-LSS	0.372	0.503	0.125
MLLCE	JFSC	0.999	0.001	0.000	MLLCE	JFSC	0.773	0.167	0.061
MLLCE	BR	0.999	0.000	0.000	MLLCE	BR	0.063	0.398	0.538
MLLCE	Glocal	0.998	0.002	0.000	MLLCE	Glocal	1.000	0.000	0.000
MLLCE	MLL-FLSDR	0.992	0.008	0.000	MLLCE	MLL-FLSDR	0.536	0.455	0.009

Table 11. Probabilities for the six comparisons of classifiers in terms of AUC and Micro F1. Left and right refer to the columns Classif. 1 (left) and Classif. 2 (right).

AUC					Micro F1
Classif. 1	Classif. 2	Left	Rope	Right	Classif. 1	Classif. 2	Left	Rope	Right
MLLCE	NL-MLLCE	0.000	0.555	0.445	MLLCE	NL-MLLCE	0.581	0.301	0.118
MLLCE	ML-LSS	0.395	0.470	0.135	MLLCE	ML-LSS	0.110	0.072	0.818
MLLCE	JFSC	0.729	0.148	0.123	MLLCE	JFSC	0.967	0.000	0.033
MLLCE	BR	0.999	0.001	0.001	MLLCE	BR	0.882	0.000	0.117
MLLCE	Glocal	1.000	0.000	0.000	MLLCE	Glocal	0.982	0.000	0.018
MLLCE	MLL-FLSDR	0.602	0.387	0.011	MLLCE	MLL-FLSDR	0.980	0.001	0.019

Table 12. Probabilities for the six comparisons of classifiers in terms of Example-based F1. Left and right refer to the columns Classif. 1 (left) and Classif. 2 (right).

Classif. 1	Classif. 2	Left	Rope	Right
MLLCE	NL-MLLCE	0.295	0.443	0.261
MLLCE	ML-LSS	0.053	0.007	0.939
MLLCE	JFSC	0.945	0.000	0.056
MLLCE	BR	0.945	0.001	0.055
MLLCE	Glocal	0.313	0.001	0.686
MLLCE	MLL-FLSDR	0.942	0.002	0.056

Based on the experimental results, we can observe the following conclusions.

• The linear and the nonlinear versions of the method MLLCE have comparable performance. In addition, the nonlinear MLLCE is better than the MLLCE method in terms of average precision, ranking loss, one error, and AUC, which indicates that the proposed nonlinear method can improve classification performance to some extent.
• Compared to the the five comparison methods, MLLCE achieves competitive performance in terms of ranking loss, Micro F1, AUC, one error, average precision, Example-based F1 on the 15 data sets, and these results clearly show the effectiveness of MLLCE in multi-label learning.
• In Hamming loss, the performance of all the comparing algorithms are not significantly different. However, according to Table 2, it is noted that MLLCE still achieves a relatively good performance.
• MLLCE outperforms ML-LSS and Glocal on all evaluation metrics except hamming loss, Micro F1 and Example-based F1 Since ML-LSS adds sample similarity to the model, ML-LSS has better performance in Micro F1 and Example-based F1 metrics. These results verify the feasibility of our proposed method MLLCE through graph embedding to model label correlation.

4.5. Sensitivity Analysis

There are three parameters ${\lambda }_1$, ${\lambda }_2$ and $d_1$ in our paper, where parameter ${\lambda }_1$ controls the loss of matrix embedding of label correlation $\mathbf{C}$. The parameter ${\lambda }_2$ controls the sparsity of the model coefficient matrix $\mathbf{W}$. Parameter $d_1$ indicates the reduced feature space dimension.

The search range of parameter ${\lambda }_1$ and ${\lambda }_2$ regarding the linear and nonlinear MLLCE methods proposed in the paper are both $\left\{{10}^i\right|i=-3:2\}$. The variation range value of low-dimensional feature dimension $d_1$ is $\{15\%d,19\%d\dots 15\%d\}$, d is the dimension of the original feature space on each data set. We perform the experiment on stackex-chess data set by dividing the 80% training and 20% test part of data set five times randomly. Figure 2a–d shows the average experimental results of parameters ${\lambda }_1$ and ${\lambda }_2$ with different values in terms of the evaluation metric ranking loss and AUC. Figure 2e,f shows the average experimental results of MLLCE with different values of $d_1$ in terms of the evaluation metric ranking loss and AUC. We can note that the performance of MLLCE is not so sensitive to the value of $d_1$.

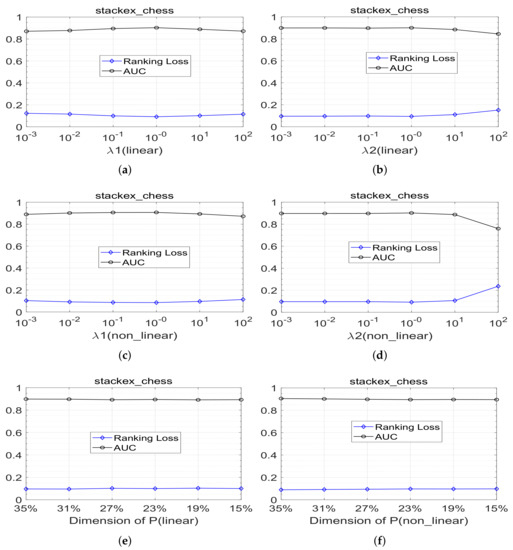
Figure 2. Parameter analysis of MLLCE and NL-MLLCE over Stackex-chess data sets. For AUC (Ranking Loss ), the bigger (smaller) the value, the better the performance of a classifier. (a) Result of MLLCE with different values of ${\lambda }_1$. (b) Result of MLLCE with different values of ${\lambda }_2$. (c) Result of NL-MLLCE with different values of ${\lambda }_1$. (d) Result of NL-MLLCE with different values of ${\lambda }_2$. (e) Result of MLLCE with different values of p. (f) Result of NL-MLLCE with different values of p.

4.6. Convergence

To illustrate the convergence of the proposed method, Figure 3 shows the change curve of the total loss of the objective function of the linear and nonlinear MLLCE as the number of iteration increases on data set corel16k001. In the experiment, we set that if the total loss of the objective function decreases less than ${10}^{-4}$ after an alternate iteration, the iterative optimization process will be terminated. As shown in Figure 3, the total loss value is rapidly reduced in the initial iteration and gradually converges with the iterative optimization process.

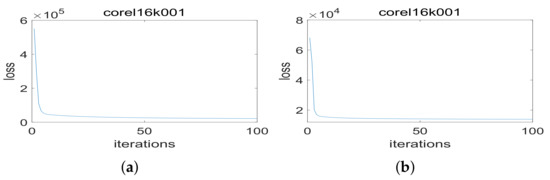
Figure 3. Convergence analysis of MLLCE and NL-MLLCE over corel16k001 data set. (a) Linear MLLCE; (b) Nonlinear MLLCE.

5. Conclusions

In this paper, we propose a new multi-label learning method by correlation embedding. First, we project the original high-dimensional feature space to a low-dimensional latent space by a mapping matrix. Then we learn an embedding matrix from the pre-defined label correlation graph by graph embedding, where the embedding matrix is utilized as the model coefficients. By learning such a classifier, the structure of the correlation matrix can be kept. In addition, the constraint of ${\ell }_{21}$ norm regularization on the $\mathbf{W}$ can further reduce the size of the model. The experimental results show the effectiveness of our proposed linear and nonlinear MLLCE. Finally, the model of our proposed method is not complicated, and future work will focus on adding some constraints to improve this model.