Hierarchical Multi-Blockchain System for Parallel Computation in Cryptocurrency Transfers and Smart Contracts

Abstract

Most of the existing smart-contract-based cryptocurrencies, such as Ethereum, use an account-based ledger. However, while the account-based model is advantageous for the efficient use of smart contracts and the increased exchangeability of cryptocurrencies, it is not well-suited to the parallel execution of smart contracts. However, unspent transaction output (UTXO)-based cryptocurrencies such as Bitcoin are advantageous for parallel cryptocurrency transfers but not well-suited to smart contracts. In this paper, we propose a hierarchical multi-blockchain system that uses multiple pairs of sidechain and dual-sidechains extended by independent block mining in their blockchain networks and a mainchain to control the branching and connection process of sidechains and dual sidechains. In the proposed method, one pair of a sidechain and dual sidechain forms one shard. The proposed method uses multiple shards to execute cryptocurrency transfers and smart contracts in parallel. In addition, the proposed model uses an accoutchain to record the resulting state changes generated by smart contract executions in each shard and securely share them with all other nodes. The proposed method uses a modifiable blockchain structure for the accountchain to obtain the database to record the smart contract execution results in each shard in as small and secure a manner as possible to ensure that all nodes trust the recorded results without executing smart contracts themselves. To examine the validity of the proposed method, we conducted a threat analysis of the proposed method by examining possible attacks in various scenarios as a thought experiment. This threat analysis concludes that the proposed blockchain system can execute smart contracts in parallel while keeping the concurrency in resulting state changes secure.

1. Introduction

Ever since the advent of Bitcoin [1] in 2009, cryptocurrency and its underlying technology, blockchain, have increased their applicability in various fields. The blockchain is a distributed ledger created by collecting all transactions that were issued into blocks and chaining them with a cryptographic hash function by ensuring that the hash value of the current block is included in the next block. This chaining structure and the collision-free cryptographic hash function makes the blockchain tamper-proof and irreversible. These properties provide enhanced security and transparent traceability in the data recorded in a blockchain, and hence enable blockchain technology to be utilized in applications that need to secure trust in a trustless environment without central control [2,3,4,5,6,7].

The field of application of blockchain technology is expanding with the advent of smart-contract-based cryptocurrencies such as Ethereum [8]. The smart contract is a program code designed to run in a virtual machine formed by distributed computers in worldwide networks. Smart contracts move blockchain technology beyond simple cryptocurrency transfers and enable its application to various business logics. The use of smart contracts is currently primarily considered in the blockchain application field, and that field is rapidly expanding [9,10,11,12]. The International Data Corporation (IDC) estimates that spending on blockchain technology will reach $6.6 billion in 2021, an increase of more than 50% compared to 2020, and will continue to see strong growth throughout the 2020–2024 forecast period, with a five-year compound annual growth rate of 48.0% [13].

1.1. Motivation of Study

As the use of smart contracts increases, concerns regarding their throughput and efficiency are also increasing. In current blockchain models, smart contracts must be executed sequentially without parallel computation, whether they are called by users or other smart contracts. In this study, the parallel computation is restricted to mean that the blockchain network executes multiple smart contracts simultaneously. In other words, it excludes the parallel computation of a smart contract by multiple nodes. This serial execution discourages the use of smart contracts in a business environment, where many smart contracts must be executed quickly. In addition, all users who want to keep their blockchain up-to-date must execute smart contracts. In other words, even if some users’ smart contract execution results are consistent and, hence, sufficient trust in the actual results is formed among all users, it is difficult for other users to accept the execution results without executing the smart contract themselves. This is also a cause of the restraint in the use of smart contracts in some business environments [14].

The previously mentioned problems in smart contracts are related to the technology called sharding. In the database, sharding is a method that partitions data into small chunks to be managed by separate database server instances for the load-spreading. In the blockchain field, sharding is the technique of dividing and allocating the work required to maintain the entire blockchain system to groups of nodes (computers that participate in the blockchain network to maintain the entire blockchain system) [15]. The sub-blockchain network allocated to this group is called a shard. It is difficult to partition the execution of smart contracts through sharding because the results of smart contract executions in one shard can affect smart contract executions in other shards. In addition, the account-based ledger model (a detailed description will be given in Section 2) used by most smart-contract-based cryptocurrencies makes sharding more difficult. However, the ledger model used in Bitcoin is UTXO (a detailed description will be given in Section 2), which makes it easy to expand cryptocurrency transfers through sharding [16]. However, it is known that the UTXO model is less convenient than the account model when applying smart contracts [17].

1.2. Key Contributions

This study proposes a method for efficiently distributing the node tasks in the network while increasing the throughput of smart contracts using sharding. Specifically, this study proposes a hierarchical multi-block system (HMBS), in which multiple sidechain and dual sidechain pairs are branched from and connected to a single blockchain (called mainchain in this work) with a prespecified rule, where each pair works as a shard. The contributions of the proposed method are as follows.

• One sidechain and dual sidechain pair form one shard, in which cryptocurrency transfers and smart contract executions are processed independently from those in other shards.
• The mainchain determines the block at which the results of cryptocurrency transfers or smart contract executions in shards are synchronized to HMBS.
• A modifiable blockchain, which we will call the accountchain, securely records the result of smart contract execution so that they are trusted by all HMBS network participants.
• When recording the state changes made by smart contract executions, the proposed method uses the accountchain to keep the database as small as possible, while existing UTXO-based blockchain models require an ever-growing database.
• The existing account-based blockchain model demands that all nodes record state changes in their local database by executing all smart contracts themselves. The proposed method allows sharded nodes to execute smart contracts and record the resulting state changes in the accountchain, to share them with all other nodes.
• The proposed method uses the mainchain to execute the smart contract that cannot be executed independently in one shard.
• Unlike existing parallelization approaches to smart contract executions, the proposed method does not require a group of privileged nodes to allocate jobs or check results in advance. Instead, it uses a predetermined rule for the parallelization of smart contract executions. Moreover, in the proposed method, all nodes can securely share execution results without resorting to the help of some privileged nodes.

1.3. Organization of the Paper

This study is outlined as follows. In Section 2, we review the backgrounds on blockchain technology and previous related works. In Section 3, we explain the proposed method. In Section 4, we test the validity of the proposed method by analyzing potential threats in various attack scenarios. Section 5 contains the discussion.

2. Backgrounds and Related Works

This section defines the terms and notations used in this paper, along with background knowledge of blockchain. In addition, we review previous research results on the main topic of this study: parallel computation in smart contracts.

2.1. Blockchain Basic

In this section, we briefly review basic blockchain theory. Readers can find a more detailed explanation in, e.g., [18]. We assume that a sufficient number of nodes try to update their blockchain copies throughout this study. We also assume that the blockchain uses an underlying cryptocurrency as a rewarding medium of incentivizing nodes to maintain the blockchain system.

Blockchain is a kind of state machine that records previous states or interactions with users. Specifically, miners (who try to compute a new block and connect it to the existing blockchain for a reward) of the blockchain network collect transactions to form a block $B^{\left[n\right]}$. Miners try to find proofs of rights (its meaning will be explained shortly) to connect $B^{\left[n\right]}$ to the blockchain ${\mathbb{BC}}^{[n-1]}$ that records all states and interactions with users up to the $n-1$-th state. Here, the block $B^{\left[n\right]}$ determines a state change that will be made to the n-th state. This process can be described as follows:

$${\mathbb{BC}}^{\left[n\right]}={\mathbb{BC}}^{[n-1]}\left|\right|B^{\left[n\right]},$$

(1)

where $\left|\right|$ means the concatenation.

Let

$$t^{\left[n\right]}=(t_1^{\left[n\right]},t_2^{\left[n\right]},\cdots ,t_{c^{\left[n\right]}}^{\left[n\right]})$$

(2)

be the collection of transactions collected in the block $B^{\left[n\right]}$ ($c^{\left[n\right]}$ is the number of transactions in $B^{\left[n\right]}$). Those $t_i^{\left[n\right]}$’s are for cryptocurrency transfers, smart contract executions/creations, etc. To prevent the block from being arbitrarily modified after it is connected to the blockchain, or the creation of a block from being monopolized by a specific miner, the blockchain includes the hash value of the last connected block in a new block and allows the miner to connect his or her block $B^{\left[n\right]}$ to ${\mathbb{BC}}^{[n-1]}$ only if the hash value $h^{\left[n\right]}$ of $B^{\left[n\right]}$ satisfies a prespecified condition. This statement is decscribed by the following equation:

$$h^{\left[n\right]}=H(h^{[n-1]}\left|\right|t^{\left[n\right]}\left|\right|r^{\left[n\right]})\in \mathcal{C},$$

(3)

where H is a cryptographic hash function, $\mathcal{C}$ is a set represeting the prespecified condition that the hash value $h^{\left[n\right]}$ of $B^{\left[n\right]}$ must satisfy, and $r^{\left[n\right]}$ is the nonce number that satisfies (3). In Bitcoin, H is SHA256 [19] and $\mathcal{C}$ is the set of 256-bitstreams that are smaller than a very small number. From now on, we shall assume that H refers to the SHA256 hash function and call that the miner who finds $r^{\left[n\right]}$ satisfying (3) has a proof of rights to connect $B^{\left[n\right]}$, which is formed by $h^{[n-1]}\left|\right|t^{\left[n\right]}\left|\right|r^{\left[n\right]}$, to ${\mathbb{BC}}^{[n-1]}$.

Bitcoin follows the UTXO ledger model. The transaction included in the Bitcoin block relates to the cryptocurrency transfer, and the main content of it is to re-allocate the cryptocurrencies allocated to the addresses in the input field to the addresses in the output field. Here, the term address is the public information used to receive cryptocurrency and is determined by the hash value of the public key associated with the private key required to use the cryptocurrency transmitted to the address. Through this process, the cryptocurrencies allocated to the addresses in the input field are spent and hence no longer usable, and the cryptocurrencies allocated to the addresses in the output field are newly created. This explains the core idea of the UTXO ledger model, and is similar to using check in everyday life. Considering this, in this study, we express the cryptocurrency assigned to the address in the UTXO-based blockchain as UTXO-Check or UC. Each UC is determined by the remittance address $addr$ and the location $loc$ in the blockchain where the transaction is recorded. We use the following notation to represent this dependency:

$$UC=UC(addr,loc).$$

(4)

We note that each UC has a unique cryptocurrency value, which is entirely determined by $addr$ and $loc$.

The complete dependency of UTXO-Check on the remittance address $addr$ and the location $loc$ in the blockchain where the transaction is recorded shows that sharding of cryptocurrencies can easily be accomplished in the UTXO model. For example, following two transactions $t_0$ and $t_1$ in the UTXO model,

$$\begin{array}{ccc}{t}_0\hfill & :& x_0\to add{r}_0:v_0,\hfill \\ t_1\hfill & :& x_1\to add{r}_1:v_1,\hfill \end{array}$$

(5)

which represent the transfer of cryptocurrencies with values $v_i,i=0,1$ from UC $x_i,i=0,1$ to $add{r}_i,i=0,1$, respectively, do not make any conflict as long as $U{C}_0\ne U{C}_1$, especially, even if $add{r}_0=add{r}_1$. Therefore, the processing of $t_0$ and $t_1$ can be preformed in different shards without any conflict, since the shard itself affects the location $loc$ in the blockchain and, hence, the outputs of $t_0$ and $t_1$ would make different UCs.

Ethereum uses an account-based ledger model. Ethereum uses an Externally Owned Account (EOA) to store the ether (the name of the cryptocurrency used in Ethereum). This EOA works like a bank account. For instance, the transaction that transfers v ether from EOA $E_0$ to EOA $E_1$,

$$t:E_0\to E_1:v,$$

(6)

instructs all nodes in the Ethereum network to subtract v ether from EOA $E_0$’s ether balance and add v ether to EOA $E_1$’s ether balance.

Smart contracts in Ethereum have their own accounts, named contract accounts or CAs, to store ether balances and the values for internal variables that need to be stored (as, being a program code, a smart contract can produce the internal variable values that are needed in the next execution). The smart contract cannot start by itself. It must be triggered by spending ether in an EOA. For instance, the transaction,

$$t:E\to C:v,d,$$

(7)

which instructs all nodes in the Ethereum network to execute the smart contract associated with the contract account C with the v ether transfer from EOA E to CA C and input data d, must be properly requested by the user with the authority to control EOA E. Once smart contracts are initiated, they can call other smart contracts in their executions by transferring ethers and input data.

The Ethereum blockchain records the transactions that instruct all nodes in the Ethereum network to compute something, not the results of computations such as ether balance changes in EOAs and CAs or values for internal variables of smart contracts. These results are to be maintained by nodes. This makes sharding difficult in Ethereum. For example, two transactions,

$$\begin{array}{ccc}{t}_0\hfill & :& E_0\to E_2:v_0,\hfill \\ t_1\hfill & :& E_1\to E_2:v_1,\hfill \end{array}$$

(8)

which instructs all nodes in Ethereum network to transfer $v_i,i=0,1$ ethers to EOA $E_2$ from EOAs $E_i,i=0,1$, respectively, cannot be processed in different shards, since the ether balance of EOA $E_2$ in each shard would not match. In general, the smart contracts that produce values for the internal variables to be used in the next execution make sharding very difficult. In addition, inter-smart contract calling makes sharding even more difficult to deployed. It is worth noting that the next Ethereum protocol is scheduled to include sharding technology [20].

2.2. Parallel Computation in Smart Contracts

Much of the existing research on parallel computation in smart contracts in blockchain systems relates to the parallel execution of multiple smart contracts on one node to increase the processing speed on individual nodes. For example, Bartoletti et al. [21] proposed a way for miners to simultaneously execute multiple smart contracts. Their method suggests that the node utilizes parallel computation after calculating how to order the smart contracts that will be executed in advance. Yu et al. [22] proposed a multi-threaded approach to execute smart contracts in parallel using a partitioning algorithm to solve the parallel-execution-related synchronization problem. Dickerson et al. [23] suggested that nodes need to classify smart contracts into those that can be processed in parallel and those that can only perform serial computation by using the software transaction memory method [24]. The advantage of these methods [21,22,23] is that they can be applied without making any changes to the blockchain system itself, but there is one disadvantage: benefits other than the speed of calculation at each node cannot be obtained. However, this disadvantage is minor in some cases.

Many researchers have studied the sharding-technique-based parallel computation in smart contracts. Luu et al. [25] explained how the sharding protocol could be applied to the public blockchain and possible problems with sharding. Ewa Syta et al. [26] proposed a protocol that randomizes the rules that determine in which shards nodes will participate. The results of their protocol are publicly verifiable, unbiased, and unpredictable in determining the node partition so that the sharding protocol can be run with Byzantine fault tolerance. Amiri et al. [27] proposed a protocol that distributes smart contract executions over multiple nodes. Their method is designed to overcome the limitations of the existing blockchain paradigm by allowing for the execution of smart contracts with concurrent contentiony. Muchhala et al. [14] proposed a new blockchain network that allows nodes in a public blockchain to deploy and execute smart contracts that provide concurrency-related functions within the framework of a smart contract. The proposed blockchain network was named ConCurrency, and was specialized for calculation using the MapReduce [28], which was developed by Google to process extensive data-based operations in a distributed system.

There was also an effort to pursue parallelizing smart contracts by combining the account ledger model with the UTXO ledger model, which is easy to shard. The cryptocurrency Qtum [29] builds on the UTXO model of Bitcoin but allows for the creation and execution of smart contracts using the account model in Ethereum. The Central Bank Digital Currency Cryptocurrency (CDBC) project proposed in [30] suggests using the account-based ledger model for frequently circulating digital currencies, especially digital assets and smart contracts with large fluctuations in value and weak liquidity, and a UTXO-based ledger model for large micropayment transactions. Chakravarty et al. [31] proposed an extension to Bitcoin’s UTXO model that supports a substantially more expressive form of validation scripts, including scripts that act like smart contracts.

Many researchers have also studied multichain-based parallel computation in smart contracts. Plasma [32] used a smart contract on the main chain to create a private blockchain (off-chain), manage all sub-chains created under it, and redesign the data in the sub-chain to be reframed for MapReduce-based parallel computation. A similar approach was also used in the aelf project [33], which was proposed to build a multi-chain parallel-computing blockchain framework. Lee et al. [34] proposed a method that can be used to handle transactions registered in the blockchain differently according to their importance, using multiple sidechains that are branched from and reconnected to the mainchain. For instance, their method can be used to make some transactions in a modifiable form, processed in a specialized protocol for fast processing, such as micropayment, or processed by a traditional method. Lee et al. [35] proposed a blockchain-based digital content service ecosystem to protect the copyright of digital content. Their method has a similar blockchain system to that in this study. Those two methods share the same name, hierarchical multi-blockchain system (HMBS). In [35] HMBS uses multiple sidechains and dual sidechains to parallel-process transactions related to the purchase and transfer of digital content rights for higher throughput.

Zhang et al. [36] proposed a blockchain-based method to verify an outsourced linear regression computation to an untrustworthy cloud server. Their approach can be helpful in the parallel execution of smart contracts that perform linear regression by outsourcing them. However, it is not clear that this kind of outsourcing is available to general smart contracts. However, it is worth noting that their method obscures computational inputs/outputs to protect the privacy of sensitive information against cloud servers.

3. Proposed Method: HMBS

The blockchain system proposed in this study, HMBS, has a structure in which multiple pairs of sidechain (SC) and dual sidechain (dSC) are attached to one mainchain (MC) and manages the state of the entire blockchain by using accountchain (AC). In HMBS, one sidechain and dual sidechain pair forms one shard. In each shard, a specific form of UTXO-model-based cryptocurrency will be used, called UTXO-Check or UC in this study. In addition, we used a specific form of UTXO model-based cryptocurrency that can only be spent in MC. We assume that users can use UC in HMBS to (1) transfer the value of UC, (2) create a new smart contract, or (3) execute a smart contract.

3.1. UTXO-Check

As in the case of Bitcoin, UC is also created as a result of block mining. As mentioned in Section 2.1, UC must have the address needed to receive the cryptocurrency. In HMBS, the address of UC x is defined by

$$add{r}_x=\left(H\right(p{k}_x\left|\right|r),r),$$

(9)

where H is the cryptographic hash function in SHA-256, $p{k}_x$ is the public key associated with the private key $s{k}_x$ that is required to spend UC x, and r is a nonce. Here, the public–private key pair $(p{k}_x,s{k}_x)$ is generated by Elliptic Curve Digital Signature Algorithm (ECDSA) [37].

HMBS uses the n tail bits of $H\left(p{k}_x\right|\left|r\right)$ (the first element of the address of UC x) to determine the shard in which UC x can be spent:

$$n \mathrm{tail} \mathrm{bits} \mathrm{of} H\left(p{k}_x\right|\left|r\right)=i \mathrm{of} \mathrm{the} \mathrm{shard}{\mathcal{S}}_i\mathrm{in} \mathrm{which} x\mathrm{can} \mathrm{be} \mathrm{spent}.$$

(10)

We shall use the UC x whose n tail bits of $H\left(p{k}_x\right|\left|r\right)$ are all zero to receive change from the smart contract and spend it only in MC. Considering this fact, we shall treat MC as a shard. In HMBS, one pair of sidechain and dual sidechain forms one shard. Therefore, HMBS has $2^n-1$ shards formed by sidechain and dual sidechain pairs and one shard formed by MC. The reason for using this nonce r when generating the address of UC is that it makes it easier to adjust $H\left(p{k}_x\right|\left|r\right)$ to the desired shard in which UC x can be spent. From now on, we use the following expression

$$x\in {\mathcal{S}}_i$$

(11)

to indicate that x is a UC that can be spent only in the shard ${\mathcal{S}}_i$.

As mentioned earlier, users in HMBS can transfer the value of HMBS cryptocurrency to others by spending their UCs. To explain this, let us consider a scenario where Alice spends her UC $x(\in Shar{d}_i)$ of value u to transfer HMBS cryptocurrency of value v to the address $add{r}_1$ of Bob’s UC and return the change to the address $add{r}_2$ of her UC:

$$t:x\to {\displaystyle \left\{\begin{array}{c}add{r}_1:v,\hfill \\ add{r}_2:u-v-ϵ\hfill \end{array}\right.} \left|\right|{\mathcal{D}S}_{s{k}_x},$$

(12)

where $ϵ>0$ represents a fee to a miner to include the transaction t in his or her block. The transaction t in (12) should be digitally signed by the private key $s{k}_x$ of UC x to spend x. The expression ${\mathcal{D}S}_{s{k}_x}$ represents the described digital signature. One thing worth noting is that in HMBS, the address of the UC that will be spent, determines the shard in which the given transaction will be recorded, not the address of the UC that will receive remittance. Another one is that addresses of the $add{r}_i(i=1,2)$ appearing in the output field of the transaction t in (12) form completely new UCs, even if some UCs with the same address have already appeared in another transaction because they are recorded in new locations in HMBS.

3.2. Smart Contracts

In this study, smart contracts are classified into the following three types according to the scope of the execution effect on the blockchain state. When given as the following functions:

• stateless smart contract uses and returns state-independent input and output, respectively,
• state-independent stateful smart contract uses a state-independent input and returns a state-dependent output, and
• state-dependent stateful smart contract uses state-dependent input and output, respectively.

We can execute the stateless smart contract independently from other smart contracts since the execution of the stateless smart contract does not affect them and is not affected by them. Thus, we can execute the stateless smart contract in any shard without updating the blockchain state. On the other hand, we can execute the state-independent stateful smart contract out of order, but we must update the execution result to the blockchain state before we execute state-dependent stateful smart contracts. This restriction also holds for the state-dependent stateful smart contract. Moreover, we must execute the state-dependent stateful smart contract with full knowledge of the blockchain state. Thus indicates that the execution of a series of state-dependent stateful smart contracts must be carried out in series.

A suggestion that derives this study on the parallelization of smart contract execution is that the user must execute the smart contract that is programmed for parallelization if he or she wishes to benefit from the parallel computation. For the execution result of a smart contract in one shard to be recognized in the entire blockchain network without updating the state, that smart contract must be programmed to be stateless. On the other hand, the state-independent stateful smart contract can be executed in one shard, but the state needs to be immediately updated according to the execution result. As mentioned earlier, state-dependent stateful smart contracts cannot benefit from parallelization through sharding. In other words, parallelizing smart contract execution must avoid using state-dependent stateful smart contracts as much as possible.

The creation of a new smart contract $sc$ is achieved by recording the following transaction on HMBS:

$$t:x\to \left\{\begin{array}{c}add{r}_{zero}:sc,id,\eta ,\hfill \\ add{r}_1:v-\eta \hfill \end{array}\right.\left|\right|{\mathcal{D}S}_{sk\left(\mathcal{X}\right)},$$

(13)

where x is the $\mathrm{UC}$, $add{r}_{zero}$ is the special address whose bits are all 0, $id$ represents which class (stateless, state-indenpendent stateful, or state-dependent stateful) $sc$ belongs to, $\eta >0$ represents the HMBS cryptocurrency value as a fee to a miner for including the transaction t in his or her block, v is the value of UC x, and $add{r}_1$ is the address of UC, which receives the change $v-\eta$. Here, we note that the transaction t in (13) must be recorded in the shard in which $x\in {\mathcal{S}}_i$.

When the smart contract $sc$ is created by the blockchain registration of the transaction t in (13), a Contract Account (CA) of $sc$ is created. CA of $sc$ has the address $add{r}_{sc}$, the cryptocurrency balance $ba{l}_{sc}$, and the internal memory $me{m}_{sc}$ to save data for its state-dependent variables. Here, $add{r}_{sc}$ is the combination of the $addr$ and $loc$ (see (4)) of the UC used to create the smart contract $sc$. Here, we note that UC used to create the smart contract $sc$ is destroyed immediately after being spent, so smart contracts with duplicated addresses cannot exist.

The execution of the stateless or state-independent stateful smart contract $sc$ is requested by registering the following transaction, which spends a UC x to send the fund to the contract account address $add{r}_{sc}$ to HMBS:

$$t:x\to \left\{\begin{array}{c}add{r}_{sc}:\theta ,ϵ,\hfill \\ add{r}_1:v-\theta -ϵ,\hfill \\ add{r}_2\hfill \end{array}\right.\left|\right|{\mathcal{D}S}_{s{k}_x},$$

(14)

where v is the value of UC x, $\theta >0$ represents a fee to a miner to include the transaction t in his or her block and execute $sc$, $add{r}_1$ is the address of the UC receiving the change $v-\theta -ϵ$, and $add{r}_2$ is the address of the UC that will receive the change after executing $sc$. Here, we note that $\theta$ is often set as higher than what is needed to execute $sc$, since the latter cannot accurately be predicted in most cases. This is the reason we need the address $add{r}_2$ in (14). We also note that the stateless or state-independent stateful smart contract $sc$ in t in (14) can be executed in any shard, but only in the shard where $x\in {\mathcal{S}}_i$.

For the parallelization of smart contracts, users should execute smart contracts that are programmed for parallelization. However, some tasks can only be programmed as state-dependent stateful smart contracts. Such contracts are to be executed on the mainchian (MC), which will be explained in Section 3.3. If a smart contract that will be executed is stateless, it is possible to reduce the load on the network by executing the smart contract in just one shard. In this case, the execution result does not need to be recognized in the entire blockchain network, because the execution of a stateless smart contract does not form a state change. If a state-independent stateful smart contract is executed, then, again, it is possible to reduce the load on the network by executing the smart contract in just one shard. However, the execution result needs to be recognized in the entire blockchain network before any state-independent stateful start contracts are executed. In HMBS, it is not expected that HMBS nodes use any method to obtain the parallelization effect by themselves. HMBS expects the acceleration effect of parallelization in smart contract execution, which can only be obtained by the efforts of smart contract creators and executors. To encourage more active efforts in the parallel computation of smart contracts, it is recommended to add a higher execution fee for stateful smart contracts.

3.3. Mainchain

The mainchain (MC) of HMBS has the same blockchain structure as explained in Section 2.1. Here, for future use, we give the following three equations with explanations:

• Miners in MC network updates MC blockchain ${\mathbb{MC}}^{[n-1]}$ to ${\mathbb{MC}}^{\left[n\right]}$ by connecting MC block $B^{\left[n\right]}$.

  $${\mathbb{MC}}^{\left[n\right]}={\mathbb{MC}}^{[n-1]}\left|\right|B^{\left[n\right]}.$$

  (15)
• The MC block $B^{\left[n\right]}$ consists of $h^{[n-1]},t_1^{\left[n\right]},\dots ,t_{c^{\left[n\right]}}^{\left[n\right]},r$, where $h^{[n-1]}$ is the hash value of the preceding MC block $B^{[n-1]}$, $t_1^{\left[n\right]},\dots ,t_{c^{\left[n\right]}}^{\left[n\right]}$ are transactions to be recorded in MC through $B^{\left[n\right]}$, and r is a nonce that proves

  $$H(h^{[n-1]}\left|\right|t_1^{\left[n\right]}\left|\right|\dots \left|\right|t_{c^{\left[n\right]}}^{\left[n\right]}\left|\right|r)\in {\mathcal{C}}_{\mathtt{MC}},$$

  (16)

  where ${\mathcal{C}}_{\mathtt{MC}}$ is a condition which every MC block must satisfy.
• The hash value of MC block is defined by

  $$h^{\left[n\right]}=H(h^{[n-1]}\left|\right|t_1^{\left[n\right]}\left|\right|\dots \left|\right|t_{c^{\left[n\right]}}^{\left[n\right]}\left|\right|r^{\left[n\right]}),$$

  (17)

  with a nonce $r^{\left[n\right]}$ which satisfies (16).

HMBS uses MC to (1) merge the blockchain state changes made in each shard, (2) impose the current blockchain state to each shard, (3) transfer the value stored in one UC to another UC, and (4) execute state-dependent stateful smart contracts. The third objective of MC follows the same approach as (12) while the fourth objective of MC follows the one in (14). The first two objectives of MC will be explained in Section 3.4.

3.4. Shard by Sidechain and Dual Sidechain

HMBS uses multiple sidechain (SC) and dual sidechain (dSC) pairs to transfer the cryptocurrency as in (12), create a smart contract as in (13), or execute an exiting smart contract as in (14) by spending UCs through multiple shards. In HMBS, we assume that one shard of HMBS consists of a sidechain and dual sidechain pair. Let ${\mathcal{S}}_{\sigma }$ be the shard formed by the sidechain ${\mathbb{S}}_{\sigma }$ and its dual sidechain ${\widehat{\mathbb{S}}}_{\sigma }$. In HMBS, each SC ${\mathbb{S}}_{\sigma }$ consists of a series of segments, each segment is formed by SC blocks, and each SC block has transactions. We denote the n-th segment of SC ${\mathbb{S}}_{\sigma }$ by ${\mathbb{S}}_{\sigma }^{\left[n\right]}$, the j-th SC block of ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ by $b_{\sigma }^{[n,j]}$, and the k-th transaction of $b_{\sigma }^{[n,j]}$ by $t_k^{[\sigma ,n,j]}$. Here, we note that $t_k^{[\sigma ,n,j]}$ is the transaction that performs (12), (13), or (14).

The proposed method uses a predetermined rule based on the block index n of $B^{\left[n\right]}$ to select one SC, in which the old segment (being mined in the SC network) is terminated and a new segment is initiated. To explain this, let us assume that the block index $n_i$ of the MC block $B^{\left[n_i\right]}$, based on the predetermined rule, initiates the n-th segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ of ${\mathbb{S}}_{\sigma }$. Let us also assume that $B^{\left[n_{i+1}\right]}$ is the next MC block, which initiates the next segment ${\mathbb{S}}_{\sigma }^{[n+1]}$ of ${\mathbb{S}}_{\sigma }$. Let

$${\mathbb{S}}_{\sigma }^{\left[n\right]}=b_{\sigma }^{[n,0]},b_{\sigma }^{[n,1]},\dots ,b_{\sigma }^{[n,k]}$$

(18)

be the SC blocks mined in the ${\mathbb{S}}_{\sigma }$ network during the time interval, which $B^{\left[n_i\right]}$ to $B^{\left[n_{i+1}\right]}$ are mined in the MC network.

In HMBS, each SC ${\mathbb{S}}_{\sigma }$ must have a dual dSC ${\widehat{\mathbb{S}}}_{\sigma }$. We will explain how these are related shortly. Just like ${\mathbb{S}}_{\sigma }$, each dSC consists of a series of segments, and each segment consist of dSC blocks. We denote the n-th segment of dSC ${\widehat{\mathbb{S}}}_{\sigma }$ by ${\widehat{\mathbb{S}}}_{\sigma }^{\left[n\right]}$ and the j-th dSC block of ${\widehat{\mathbb{S}}}_{\sigma }^{\left[n\right]}$ by ${\widehat{b}}_{\sigma }^{[n,j]}$. Let

$${\widehat{\mathbb{S}}}_{\sigma }^{\left[n\right]}={\widehat{b}}_{\sigma }^{[n,0]},{\widehat{b}}_{\sigma }^{[n,1]},\dots ,{\widehat{b}}_{\sigma }^{[n,\widehat{k}]}$$

(19)

be the dSC blocks mined in the ${\widehat{\mathbb{S}}}_{\sigma }$ network during the time interval that $B^{\left[n_i\right]}$ to $B^{\left[n_{i+1}\right]}$ are computed in the MC network.

The block chaining in the SC segment has the same structure as MC; the mining of the SC block $b_{\sigma }^{[n,i]}$ in the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ needs to find a nonce r, which proves

$$H(h_{\sigma }^{[n,i-1]}\left|\right|t_1^{[\sigma ,n,i]}\left|\right|\dots \left|\right|t_{c^{[\sigma ,n,i]}}^{[\sigma ,n,i]}\left|\right|r)\in {\mathcal{C}}_{{\mathbb{S}}_{\sigma }},$$

(20)

where $c^{[\sigma ,n,i]}$ is the number transactions to be included in $b_{\sigma }^{[n,i]}$, $h_{\sigma }^{[n,i-1]}$ is the hash value of the SC block $b_{\sigma }^{[n,i-1]}$, and ${\mathcal{C}}_{{\mathbb{S}}_{\sigma }}$ represents the condition determined by the consensus algorithm of the SC ${\mathbb{S}}_{\sigma }$. The hash value of the SC block $b_{\sigma }^{[n,i]}$ is defined by

$$h_{\sigma }^{[n,i]}=H(h_{\sigma }^{[n,i-1]}\left|\right|t_1^{[\sigma ,n,i]}\left|\right|\dots \left|\right|t_{c^{[\sigma ,n,i]}}^{[\sigma ,n,i]}\left|\right|r^{[\sigma ,n,i]})$$

(21)

with a nonce $r^{[\sigma ,n,i]}$, which satisfies (20).

The block chaining of dSC segment is almost identical to that of the SC segment. One difference is that the dSC block records only one special smart contract, which announces the state changes made by transactions in the preceding sidechain segment to HMBS, while the SC block records the multiple transactions. A detailed explanation will be given shortly.

HMBS connects the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ and the dSC segment ${\widehat{\mathbb{S}}}_{\sigma }^{\left[n\right]}$, which start from $B^{\left[n_i\right]}$ and end at $B^{\left[n_{i+1}\right]}$, to MC by making $B^{\left[n_i\right]}$ the first SC and dSC blocks in ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ and ${\widehat{\mathbb{S}}}_{\sigma }^{\left[n\right]}$ by setting

$$b_{\sigma }^{[n,0]}={\widehat{b}}_{\sigma }^{[n,0]}=B^{\left[n_i\right]}$$

(22)

and updating the hash value $h^{\left[n_{i+1}\right]}$ as

$$h^{\left[n_{i+1}\right]}\leftarrow h^{\left[n_{i+1}\right]}\left|\right|h_{\sigma }^{[n,k]}\left|\right|{\widehat{h}}_{\sigma }^{[n,\widehat{k}]},$$

(23)

where $h_{\sigma }^{[n,k]}$ and ${\widehat{h}}_{\sigma }^{[n,\widehat{k}]}$ are hash values of the last blocks in ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ and ${\widehat{\mathbb{S}}}_{\sigma }^{\left[n\right]}$, respectively.

3.5. Accounchain

HMBS records the execution results of state-independent stateful smart contracts in its on-chain database. At first glance, recording the execution results of smart contracts seems unnecessary, since HMBS records exactly how every smart contract will be or was executed. This is, however, a necessary task for the parallelization of smart contract execution in HMBS. It records the results of smart contracts that were executed in the shard formed by a SC and dSC pair in the accountchain (AC), which is a blockchain that can be modified to provide the results of smart contract execution that will be trusted by nodes operating outside the corresponding shard, without demanding that they execute the same smart contract themselves. Here, we note that HMBS demands that AC can be modified to record the frequently changing smart contract states in AC blocks.

The creation of the state-independent stateful smart contract $sc$ in the transaction $t_k^{[\sigma ,n,j]}$ of ${\mathbb{S}}_{\sigma }$ block in the segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ led to the creation of the contract account ${\mathrm{CA}}_{sc}$ in AC when ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ is connceted to the MC block $B^{\left[n_{i+1}\right]}$. Table 1 shows a list of the information stored in the contract account ${\mathrm{CA}}_{sc}$ of $sc$.

Table 1. A list of information stored in contract account associated with the smart contract $sc$.

Notation	Description
$H\left(sc\right)$	hash value of $sc$
$lo{c}_{sc}$	the location where $sc$ was created in HMBS
$w_{sc}$	target value of $sc$
$stat{e}_{sc}$	state data of $sc$
$q_{sc}$	input value of $stat{e}_{sc}$ for $sc$

In Table 1, $H\left(sc\right)$, the hash value of the smart contract $sc$, binds $sc$ to the contract account ${\mathrm{CA}}_{sc}$, and $lo{c}_{sc}$ represents the location of the transaction t where $sc$ was created in HMBS. See (13). The state data $stat{e}_{sc}$ of $sc$ represent the cryptocurrency balance $ba{l}_{sc}$ and the state-dependent variable saves internal memory $me{m}_{{\mathrm{CA}}_{sc}}$. When ${\mathrm{CA}}_{sc}$ is created for the first time, the target value $w_{sc}$ in Table 1 is computed by

$$w_{sc}=H_{\lambda }\left(H\left(sc\right)\right||lo{c}_{sc}\left)\right||0\cdots 0),$$

(24)

where $H_{\lambda }$ is the first $\lambda$-bit truncation of the SHA-256 hash function H, where $1\le \lambda \le 256$, and $0\cdots 0$ is the all zero bitstream of length 512 bits. The input value $q_{sc}$ in Table 1 is a bitstream of length 256 bits, which are designed to make

$$w_{sc}=H_{\lambda }\left(H\left(sc\right)\right||lo{c}_{sc}\left|\right|q_{sc}\left|\right|H(stat{e}_{sc}\left|\right|h\left)\right)$$

(25)

holds for $stat{e}_{sc}\left|\right|h$, where h is the hash value of the latest block at the moment when $q_{sc}$ is computed. In other words, $q_{sc}$ is said to be the input value of $stat{e}_{sc}$ for $sc$ at the moment specified by h if, and only if, $q_{sc}$ satisfies (25). The parameter $\lambda$ in (25) determines the difficulty in computing the input value $q_{sc}$.

The AC block records multiple contract accounts. Let ${\mu }_1^{\left[n\right]},\dots ,{\mu }_{{\tilde{c}}^{\left[n\right]}}^{\left[n\right]}$ be a collection of bitstreams representing the contract accounts (to be recorded in AC block $A^{\left[n\right]}$) of smart contracts $s{c}_1,\cdots ,s{c}_{{\tilde{c}}^{\left[n\right]}}$, where

$${\mu }_i^{\left[n\right]}=H\left(s{c}_i\right)\left|\right|lo{c}_{s{c}_i}\left|\right|w_{s{c}_i}$$

(26)

and ${\tilde{c}}^{\left[n\right]}$ is the number of contract accounts to be recorded in $A^{\left[n\right]}$. The process of block mining in AC is identical to that in MC. The mining of AC block $A^{\left[n\right]}$ needs to find a nonce $\rho$, which makes

$$H(g^{[n-1]}\left|\right|{\mu }_1^{\left[n\right]}\left|\right|\dots \left|\right|{\mu }_{{\tilde{c}}^{\left[n\right]}}^{\left[n\right]}\left|\right|\rho )\in {\mathcal{C}}_{\mathtt{AC}},$$

(27)

where $g^{[n-1]}$ is the hash value of the latest block $A^{[n-1]}$ in AC and ${\mathcal{C}}_{\mathtt{AC}}$ represents the condition determined by the consensus algorithm of AC. The hash value of the block $A^{\left[n\right]}$ is defined by

$$g^{\left[n\right]}=H(g^{[n-1]}\left|\right|{\mu }_1^{\left[n\right]}\left|\right|\dots \left|\right|{\mu }_{{\tilde{c}}^{\left[n\right]}}^{\left[n\right]}\left|\right|{\rho }^{\left[n\right]})$$

(28)

with a nonce ${\rho }^{\left[n\right]}$, which satisfies (27).

The modifiability of AC comes from (26). Suppose that the state data of the smart contract $sc$ need to be updated from $stat{e}_{sc}$ to ${\overline{state}}_{sc}$ as a result of the execution of $sc$. If a miner can find $q_{sc}$ that satisfies (25) with ${\overline{state}}_{sc}$ in the place of $stat{e}_{sc}$, then he or she can replace $stat{e}_{sc}$ with ${\overline{state}}_{sc}$ in ${\mathrm{CA}}_{sc}$ without destroying the chaining structure (imposed by (28)) in AC.

Before we close this subsection, it is worth mentioning why the state data of the stateless smart contract do not need to be stored in AC. This is because the cryptocurrency balance of the contract account of the stateless smart contract can be set to zero after the execution is completed, and no state-dependent variables are produced as a result of the execution of a stateless smart contract. Therefore, the state data of the stateless smart contract $sc$ need to be managed only in the shard where $sc$ is executed, and only for the duration of $sc$. HMBS serially executes the state-dependent stateful smart contract in MC. This implies that nodes in the MC network would prefer to execute the state-dependent stateful smart contract by themselves instead of waiting for the execution result from other nodes. Considering this fact, HMBS does not record the state data of the state-dependent stateful smart contract on AC.

3.6. Special Smart Contracts in Dual Sidechains

In this section, we shall explain how HMBS uses dual sidechains. For this purpose, let us assume that there is a transaction, t, which is broadcast to be recorded in a SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ in a shard, say, ${\mathcal{S}}_{\sigma }$. We first consider the case that t is the transaction that creates UCs $x_1$ and $x_2$ by spending a UC $x_0$ (See (12)). In this case, $x_0$ must be in ${\mathcal{S}}_{\sigma }$, but $x_1$ and $x_2$ can be in any other shards. If $x_1\in {\mathcal{S}}_{\tilde{\sigma }}$ and $x_2\in {\mathcal{S}}_{\sigma }$, then $x_2$ is immediately spendable after an SC block $b_{\sigma }^{[n,j]}$ containing t is mined, but $x_1$ can be spent only after the segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ is connected to MC block $B^{\left[n_{i+1}\right]}$. However, any UCs created in the segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ are spendable in their own shards after ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ ends.

We now consider that the transaction t is used to create a smart contract, $sc$. If $sc$ is stateless, then, like a newly created UC, it is executable in ${\mathcal{S}}_{\sigma }$ immediately after the SC block $b_{\sigma }^{[n,j]}$ containing t is mined, but only in the whole HMBS network after the segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ is connected to MC block $B^{\left[n_{i+1}\right]}$. Any stateless smart contracts created in the segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ are only executable after the MC block $B^{\left[n_{i+1}\right]}$ is mined. In the case when $sc$ is state-dependent stateful, $sc$ is only executable in MC and only after the MC block $B^{\left[n_{i+1}\right]}$ is mined. In the case when $sc$ is state-independent stateful, however, $sc$ is not executable in an HMBS network, even after the MC block $B^{\left[n_{i+1}\right]}$ is mined. This is because, as a state-independent stateful smart contract, $sc$ needs its contract account ${\mathrm{CA}}_{sc}$ in AC. In other words, users in the HMBS network, including users in the shard ${\mathcal{S}}_{\sigma }$, need to wait for ${\mathrm{CA}}_{sc}$ to be created in AC to execute $sc$.

In HMBS, the transaction that creates a state-independent stateful smart contract is the request signal to AC miners to create the corresponding contract account. To be specific, an AC miner create ${\mathrm{CA}}_{sc}$, with $lo{c}_{\mathrm{CA}}$ defined by

$$lo{c}_{\mathrm{CA}}=i{x}_t\left|\right|h^{\left[n_{i+1}\right]},$$

(29)

where $i{x}_t$ is the collection of indices $\sigma$ (SC), n (segment), j (block) and k (transaction) that identifies the location of the transaction t that creates $sc$ in HMBS and $h^{\left[n_{i+1}\right]}$ is the hash value of the MC block $B^{\left[n_{i+1}\right]}$. Therefore, the creation of the contract account $\mathrm{CA}$ of the smart contract $sc$ can only start after the MC block $B^{\left[n_{i+1}\right]}$ is mined. In other words, $sc$ is not immediately executable after the MC block $B^{\left[n_{i+1}\right]}$ is mined. HMBS requires that the state-independent stateful smart contract $sc$ is only executable in the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ if the contract account ${\mathrm{CA}}_{sc}$ was in AC when ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ started.

We now consider the case that transaction t is used to execute a state-independent stateful smart contract $sc$ whose contract account ${\mathrm{CA}}_{sc}$ was in AC when the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ started. See (14). In this case, the UC $x_1$ created by the address $add{r}_1$ used to receive the predetrmined change $v-\theta -ϵ$ is spendable after the SC block $b_{\sigma }^{[n,j]}$ containing t is mined if $x_1\in {\mathcal{S}}_{\sigma }$ or after the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ ends if $x_1\notin {\mathcal{S}}_{\sigma }$. The UC created by the address $add{r}_2$ is used to receive the change from the contract account ${\mathrm{CA}}_{sc}$, and is only spendable in MC.

We are now ready to explain the objective of dual sidechains. Let us begin with the scenario where $sc$ is executed in k times in the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$. When miners in ${\mathbb{S}}_{\sigma }$ first encouter the transaction that executes $sc$ in the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$, they update their local database for the state data of ${\mathrm{CA}}_{sc}$ by using the data recorded in AC. After executing $sc$, miners in ${\mathbb{S}}_{\sigma }$ update the state data of ${\mathrm{CA}}_{sc}$, not in AC, but in their local database. Miners in the dSC network update the state data of contract accounts in AC. Let Alice be the miner in ${\widehat{\mathbb{S}}}_{\sigma }$ network who tries to update the state data of ${\mathrm{CA}}_{sc}$ in AC based on $sc$ executions in ${\mathbb{S}}_{\sigma }^{\left[n\right]}$. She follows each $sc$ execution to compute correct changes and the final-state data change to be made for ${\mathrm{CA}}_{sc}$ during the time when ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ is being extended. At the moment when the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ ends, the dSC segment ${\widehat{\mathbb{S}}}_{\sigma }^{[n+1]}$ starts. During the dSC segment, ${\widehat{\mathbb{S}}}_{\sigma }^{[n+1]}$ is extended; she tries to connect the dSC block that contains only one special transaction T to ${\widehat{\mathbb{S}}}_{\sigma }^{[n+1]}$:

$$T:\left\{\begin{array}{c}add{r}_i:c_i,i=1,\cdots ,k,\hfill \\ {\overline{state}}_{sc},{\tilde{q}}_{sc},\hfill \end{array}\right.$$

(30)

where $add{r}_i,i=1,\cdots ,k$ are the addresses of the UCs that are receiving changes $c_i,i=1,\cdots ,k$ from $sc$-executions, ${\overline{state}}_{sc}$ are the state data of ${\mathrm{CA}}_{sc}$ at the moment when the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ ends, and ${\tilde{q}}_{sc}$ is the input value of ${\overline{state}}_{sc}$ for $sc$ (see Table 1). Notice that, unlike othe transactions in HMBS, the special transaction T in (30) does not require UC spending to be recorded in dSC. It is now clear that the objective of dual sidechains is to update AC based on the smart contract execution. Note that if the execution of a smart contract $sc$ in the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ is not recognized in ${\widehat{\mathbb{S}}}_{\sigma }^{[n+1]}$, then the state data change by the execution of $sc$ will be ignored in the ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ network.

Figure 1 illustrates how the state data of a state-dependent stateful smart contract $sc$ are updated. In Step 1, miners in SC ${\mathbb{S}}_{\sigma }$ and dSC ${\widehat{\mathbb{S}}}_{\sigma }$ networks compute state changes by executing $sc$ and recording them in their local database. In Step 2, state changes formed by executions of $sc$ in the ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ segment are collected to form the special transaction (see (30)) in ${\widehat{\mathbb{S}}}_{\sigma }^{[n+1]}$. Finally, in Step 3, the final state data change of $sc$ is updated in AC immediately after the dSC segment ${\widehat{\mathbb{S}}}_{\sigma }^{[n+1]}$ to MC.

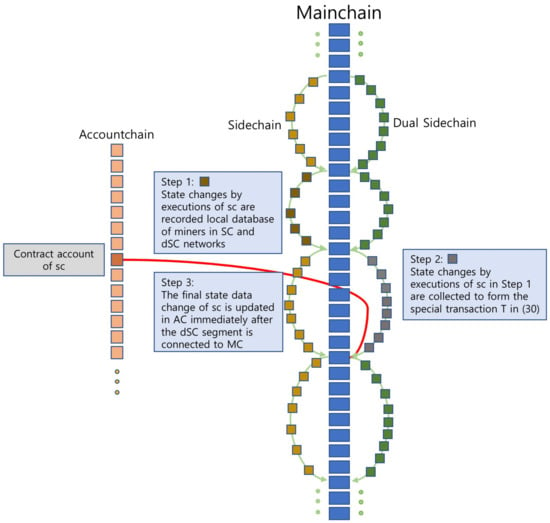
Figure 1. The process of updating the state data of a state-dependent stateful smart contract $sc$ in HMBS.

4. Results

This section shows the thought experiments that were conducted to examine the stability and feasibility of the proposed model, HMBS. We also compare HMBS with Bitcoin and Ethereum to show the benefits it can obtain.

4.1. Threat Analysis

Double UC spending in SC: Suppose that a malicious user attempts to spend or has already spent a UC x by requesting that a x-spending transaction $t_1$ is included in the SC block $b_{\sigma }^{[n,j]}$ of the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$. Let $t_0$ be the transaction that was used to spend the UC x. For each UC, the proposed method specifies the SC in which it can be spent. In other words, x-spending transactions $t_0$ and $t_1$ must be recorded in some SC blocks in ${\mathbb{S}}_{\sigma }$. Thus, the serial block-chaining structure in the SC ${\mathbb{S}}_{\sigma }$ makes nodes in the ${\mathbb{S}}_{\sigma }$ network ignore $t_1$’s request to be included in the SC block by knowing that $t_0$ was already included in ${\mathbb{S}}_{\sigma }$.

Double UC spending in MC: In HMBS, the block chaining structure in MC is identical to that in SC. Thus, no user can spend UC twice in MC.

Haste UC spending in SC: Suppose that a user attempts to spend a UC x, which was designed to be spendable in ${\mathbb{S}}_{\sigma }$ but was created in ${\mathbb{S}}_{{\sigma }^{\prime }}\ne {\mathbb{S}}_{\sigma }$. Let t, $b_{\sigma }^{[n,j]}$, and ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ be the planned transaction: to spend x in SC ${\mathbb{S}}_{\sigma }$, the SC block to which t belongs, and the SC segment in which $b_{\sigma }^{[n,j]}$ is to be recorded, respectively. Let $t^{\prime }$ and ${\mathbb{S}}_{{\sigma }^{\prime }}^{\left[n^{\prime }\right]}$ be the transaction that created the UC x in SC ${\mathbb{S}}_{{\sigma }^{\prime }}$ and the SC segment in which $t^{\prime }$ was recorded, respectively. In this case, the user can sepnd the UC x through the transaction t if, and only if, the SC segment ${\mathbb{S}}_{{\sigma }^{\prime }}^{\left[n^{\prime }\right]}$ was already connected to MC before the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ was branched out from MC. In other words, the UC x isnot spendable until its creation is reported to the MC network.

We now consider the case when the SC segment ${\mathbb{S}}_{{\sigma }^{\prime }}^{\left[n^{\prime }\right]}$ is not yet connected to MC, while blocks in the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ are being mined. We assume that the transaction $t^{\prime }$ was recorded in ${\mathbb{S}}_{{\sigma }^{\prime }}^{\left[n^{\prime }\right]}$, that is, the UC x was already created. In this case, it is possible that some miners in the ${\mathbb{S}}_{\sigma }$ network might know the creation of the UC x in SC ${\mathbb{S}}_{{\sigma }^{\prime }}$. HMBS, however, demands that miners in all SC networks determine the validity of the transaction t based on ${\mathbb{S}}_{\sigma }$ blocks preceding $b_{\sigma }^{[n,j]}$ (the SC block to which t belongs) and the MC blocks preceding the MC block $B^{\left[n_i\right]}$, from which the SC segment ${\mathbb{S}}_{\sigma }^{\left[n\right]}$ is branched out. Since the transaction $t^{\prime }$ is neither in ${\mathbb{S}}_{\sigma }$ blocks preceding $b_{\sigma }^{[n,j]}$ nor in the MC blocks preceding the MC block $B^{\left[n_i\right]}$, miners in the ${\mathbb{S}}_{\sigma }$ network would regard the UC x as not yet created, and hence not spendable. It explains why the haste UC spending (the spending of a UC not known to whole nodes in the SC network where the UC can be spent) is not possible.

Haste UC spending in MC: In HMBS, any UCs designed to be spendable in MC are only spendable after they are reported to MC and only through transactions in MC. This explains why the haste UC spending is not possible.

Replay of smart contract execution: In HMBS, any smart contract execution in SC must be triggered by spending UCs. See (14). Thus, it is impossible to replay smart contract execution in SC. The same argument and results also hold for the replay of smart contract execution in MC.

Head start block mining: Just like in Bitcoin or Ethereum, the block mining in HMBS, whether it is in MC, SC, dSC, or AC, needs the hash value of the immediately preceding block. See (16), (20), and (27). Therefore, the mining of the next block is worthless if the hash value of the current block is not computed.

Head start input value computation: Miners in dSC network compute input values for the state data of smart contracts executed in SC network. More specifically, the dSC-block in the dSC segment, say, ${\widehat{\mathbb{S}}}_{\sigma }^{[n+1]}$, is designed to record just one special transaction (see (30)), which requests that the state data are updated accroding to the change generated by the execution of a smart contract $sc$. For this purpose, when the dSC block ${\widehat{b}}_{\sigma }^{[n+1,i]}$ of ${\widehat{\mathbb{S}}}_{\sigma }^{[n+1]}$ is extended, miners in dSC network check the validity of changing state data $stat{e}_{sc}$ to ${\overline{state}}_{sc}$ for $sc$. They also check whether the updated input value ${\tilde{q}}_{s}c$ satisfies (25) with the latest dSC block hash value ${\widehat{h}}_{\sigma }^{[n+1,i-1]}$. This indicates that the head start input value computation is only useful if the latest dSC hash value is known.

4.2. Comparison with Bitcoin and Ethereum

This study’s proposed method, HMBS, uses the UTXO model in the cryptocurrency transfer, as Bitcoin does. However, it differs from Bitcoin in that it can execute smart contracts and parallelize cryptocurrency transfers and smart contract executions through sharding. In Ethereum, an externally owned account is used to receive the remaining funds back after sending enough funds to execute a smart contract. On the other hand, HMBS uses a UTXO-based cryptocurrency to execute a smart contract, and the remaining funds are returned to a UC that is only spendable in MC.

HMBS is a mixture of Bitcoin’s UTXO and Ethereum’s account models, and pursues parallelism in cryptocurrency transfers and smart contract executions using sharding techniques. In this process, to make the result of changes in the state of the blockchain system made in one shard trustable by all nodes, HMBS uses the accountchain, which has a modifiable blockchain structure.

In Ethereum, to prevent duplications in cryptocurrency transfer or smart contract execution, a number that can identify each transfer and execution (called the nonce in Ethereum) is used. However, the use of these numbers is a constraint on parallelization as it forces cryptocurrency transfers or smart contract executions to be serialized, even when the serialization is unnecessary. HMBS solved this problem by using UTXO-Check, which, once used, cannot be used again, for both cryptocurrency transfer and smart contract execution.

5. Discussion

In this study, we proposed a hierarchical multi-blockchain system (HMBS), which consists of one mainchain (MC), multiple pairs of sidechain (SC) and dual sidechain (dSC), and one accountchain (AC), to efficiently distribute the computation of cryptocurrency transfers and smart contract executions to whole nodes. In HMBS, a pair of SC and dSC forms a shard and, within a shard, some cryptocurrency transfers and smart contract executions can be processed independently, while SC or dSC segments are branched out from and reconnected to MC, according to a predetermined rule. The changes in state data generated by transactions in SC or dSC segments are synchronized in whole nodes of HMBS at the MC block to which those SC or dSC segments are terminated. This makes it possible to determine when the state changes made in SC or dSC segments are synchronized in a orderly manner. AC has a modifiable blockchain structure to ensure the state changes are not easily modifiable by a colluded mining of few nodes, and, at the same time, state changes can be modified by consensus of SC or dSC networks.

The state changes made by smart contract executions in MC are synchronized in MC block units, but those in SCs are synchronized in pair units. Therefore, for HMBS to obtain a meaningful parallelization effect through sharding, the number of shards must be increased according to the time required for block mining in SCs or dSCs. However, this might increase the possibility of a shard being monopolized by a few nodes.

In this study, we proposed an HMBS that combines the advantages of Bitcoin’s UTXO-based model and Ethereum’s account-based model. The proposed method does not use a group of privileged nodes to control parallelism in smart contract executions and can be applied to any blockchain, including public blockchains.