An Adaptive Reversible Data Hiding Scheme Using AMBTC and Quantization Level Difference

Abstract

Hiding a message in compression codes can reduce transmission costs and simultaneously make the transmission more secure. This paper presents an adaptive reversible data hiding scheme that is able to provide large embedding capacity while improving the quantity of modified images. The proposed scheme employs the quantization level difference (QLD) and interpolation technique to adaptively embed the secret information into pixels of each absolute moment block truncation coding (AMBTC)-compressed block, except for the positions of two replaced quantization levels. The values of QLD tend to be much larger in complex areas than in smooth areas. In other words, our proposed method can obtain good performance for embedding capacity and still meets the requirement for better modified image quality when the image is complex. The performance of the proposed approach was compared to previous image hiding methods. The experimental results show that our approach outperforms referenced approaches.

1. Introduction

With the rapid development of internet communication and computer technology, a large number of information is transmitted over the internet. When digital data are transmitted through the internet, some sensitive data may become vulnerable to the malicious users. Therefore, to ensure the security of the transmitted data, data owners either encrypt the transmitted data via traditional cryptographic algorithms or transfer data into an imperceptible way by using data hiding techniques [1]. In the last decade, multimedia-based transmission has become popular; as such, data hiding techniques are a secure and efficient method for such applications. Data hiding is a way to embed secret data into a digital cover media by modifying the original content, such that other users in a public network will not be aware of the existence of the embedded data. If malicious users have not noticed the transmitted data concealing confidential data, the safety of hidden data is guaranteed. Generally, a data hiding scheme can be divided into three categories, i.e., spatial domain, frequency domain, and compressed domain. The spatial domain method imparts some meaningful changes in the image pixels in order to embed information. The frequency domain method and compressed domain method embed the secret data into transformed coefficients and the compressed codes of digital images, respectively [2].

In order to transmit multimedia data efficiently on the internet, many researchers have proposed various compression methods to reduce the size of multimedia files, such as vector quantization (VQ) [3,4,5], discrete wavelet transform (DWT) [6,7,8], and discrete cosine transform (DCT) [9,10,11]. Qin et al. [3] proposed a data hiding scheme based on VQ compressed images and an index mapping mechanism. Ahmed et al. [6] proposed a data hiding method based on DWT. Their method hides a secret image inside a cover image by using two secret keys. Chang [11] et al. proposed a scheme to hide the secret information in the DCT coefficient domain. In this scheme, the image is divided into 8 × 8 blocks, where if two successive coefficients of the medium-frequency components are zero, the information is hidden in each block.

Block truncation coding (BTC) [12] is another efficient lossy block-based image compression technique. In recent years, many researchers have studied data hiding based on BTC and made improvements, such as absolute block truncation coding (AMBTC) [13], ordered dither block truncation coding (ODBTC) [14], error Diffusion Block truncation coding (EDBTC) [15], etc. BTC is characterized by low complexity and low memory, and thus it has become an ideal data hiding domain. Wu and Sun [16] presented a data hiding method in which each secret bit is embedded into the bitmap of the BTC compression codes. Kim [17] proposed a data hiding method for halftone compressed images based on ODBTC and exploiting modification direction (EMD). Guo et al. [18] introduced a data hiding scheme based on error-diffused BTC to embed an extremely large amount of watermarks without obviously damaging image quality. These methods are irreversible, and the host image is permanently altered and it cannot be recovered accurately after data extraction. However, in some applications such as medical image sharing, military image processing, remote sensing and multimedia archive management, the recovery of a host image is essential [19]. To address this problem, a reversible data hiding scheme [20] were proposed that can extract the hidden data and produce a lossless recovery of the cover image. As Zhao et al. mentioned [1], the key property of reversible data hiding is not only the secret data but also the host image can be accurately recovered in the recorder.

In 2008, Chang et al. [21] presented a reversible data hiding method aimed at BTC-compressed color images. In 2011, Li et al. [22] introduced a reversible image hiding based on the BTC-compressed approach. In this scheme, the histogram shifting and bitmap flipping technique were used to hide secret bits. In 2013, Sun et al. [23] introduced another reversible data hiding method for BTC-compressed using the joint neighbor coding technique. In 2015, Lin et al. [24] presented a reversible data hiding scheme for AMBTC-compressed images by combining secret bits with bitmap bits one by one.

In this paper, we propose an adaptive reversible data hiding scheme that is based on an AMBTC compression domain and quantization level difference. In this scheme, the cover image is compressed into corresponding quantizers and a bitmap image by absolute moment block truncation coding (AMBTC). Subsequently, a certain amount of the data bits will be embedded into this pixel according to the value of QLD. The rest of this paper consists of four sections: AMBTC’s and Lin et al.’s methods are introduced in Section 2; the proposed algorithm is illustrated in Section 3; detailed experimental description and comparative analysis are provided in Section 4; and finally, the conclusions are offered in Section 5.

2. Related Work

2.1. Absolute Moment Block Truncation Coding (AMBTC)

As a variant of BTC, AMBTC was introduced by Lema and Mitchell [13] in 1984. During the encoding procedure, the algorithm divides the original image into a set of non-overlapped blocks with a size of k $\times$ k. Assume that $x_{ij}$ is the pixel value in location $\left(i,j\right)$ of the block, the mean value u and its standard deviation $\alpha$ are computed by Equations (1) and (2), respectively.

$$u=\frac{1}{k\times k}{{\displaystyle \sum }}_{i=1}^k{{\displaystyle \sum }}_{j=1}^k{x}_{ij},$$

(1)

$$\alpha =\sqrt{\frac{{{\displaystyle \sum }}_{j=1}^{k\times k}\left|x_{ij}^2-u^2\right|}{k\times k}}.$$

(2)

Then, each block is converted to two quantizers and a bitmap image bm. The two quantizers hm and lm for the block are computed by:

$$lm=u-\alpha \sqrt{\frac{q}{k\times k-q}} ,$$

(3)

$$hm=u+\alpha \sqrt{\frac{k\times k-q}{q}} ,$$

(4)

where q is the number of pixels that are greater than or equal to the mean value u. The bitmap $bm=\left\{m_{ij}\right|m_{ij}\in \left\{0,1\right\},1\le i,j\le k\}$ is created as follows:

$$m_{ij}=\{\begin{array}{c}1, \mathrm{if} x_{ij}\ge u \\ 0, \mathrm{if} x_{ij}<u.\end{array}$$

(5)

Figure 1 shows an example to describe the procedures for the AMBTC scheme. Figure 1a shows the original image block of $4\times 4$ pixels. Then, the block mean $u$ and standard deviation $\alpha$ are computed, respectively, by using Equations (1) and (2). In this example, $u=110$ and $\alpha =10$. The bitmap generated by AMBTC is shown in Figure 1b. Finally, the quantization levels, namely $lm$ and $hm$, are calculated by using Equations (3) and (4), respectively. Figure 1c shows the reconstructed image block.

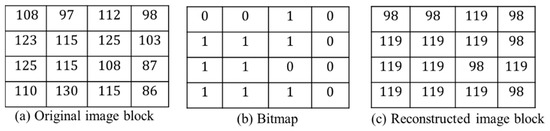
Figure 1. Example of absolute block truncation coding (AMBTC) encoding procedures.

2.2. AMBTC Scheme of Lin et al.’s Method

In 2015, Lin et al. presented a reversible data hiding scheme for AMBTC-compressed images by considering the mean value and the standard deviation to achieve a high payload and high-quality modified images. Following are details about the major steps of the embedding processing.

Step 1: Define three parameters, i.e., the bitmap $bm$, mean pixel value $u$ and standard deviation $\alpha$ using Equations (1), (2) and (5), respectively.

Step 2: Define four different scenarios for each pixel of a given $k\times k$ block. As shown in Table 1, if the secret bit is “1”, and the bit in bitmap is “0”, then the corresponding scenario is “10” by combining secret bits with bits of the bitmap.

Table 1. Four scenarios for each pixel of a given block.

Scenario	Case00	Case01	Case10	Case11
secret bit	0	0	1	1
Bit in bitmap	0	1	0	1

Step 3: Determine the cover image block is embeddable or non-embeddable. If there are only one or two different scenarios, this cover block is a non-embeddable block. If the types of scenarios are equal to three or four, the cover is an embeddable block.

Step 4: Determine the hiding strategy. The detailed Algorithm 1 for hiding strategies is shown below.

Algorithm 1. Hiding strategy of Lin’s method.

Input: current scenarios

Output: corresponding pixel value

cpv   corresponding pixel value

Switch(current scenarios){

$\begin{array}{l}\mathrm{case}00:\mathrm{c}\mathrm{p}v=u-\alpha ;break;\\ \mathrm{case}01:\mathrm{c}\mathrm{p}v=u+\alpha ;break;\\ \mathrm{case}10:\mathrm{c}\mathrm{p}v=u-\alpha -1;break;\\ \mathrm{case}11:\mathrm{c}\mathrm{p}v=u-\alpha +1;break;\end{array}$

}

returncpv;

Figure 2 shows an example of the strategy. Figure 2a shows the secret bits and the corresponding bitmap. Figure 2b shows a combination. There are four types of in this example. Figure 2c shows the result according to Algorithm 1.

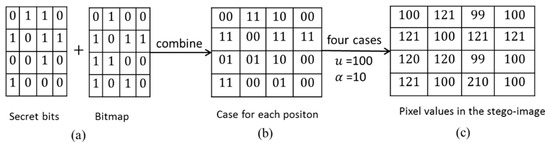
Figure 2. Example of Lin et al.’s hiding strategy.

3. The Proposed Scheme

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation as well as the experimental conclusions that can be drawn. This section describes the details of our method. Our proposal utilizes an adaptive interpolation technique and AMBTC compression technique, to improve embedding capacity and image quality. As we utilize the difference of two quantization levels to adaptively embed the secret data into the cover image, our method can obtain a high embedding capacity. Moreover, our method still meets good image quality as we exploit the middle value of two quantization levels and the values of two thresholds to limit the shifting of values. The flowcharts of embedding and extraction phases for our proposed scheme are shown in Figure 3, Figure 4, Figure 5 and Figure 6, respectively.

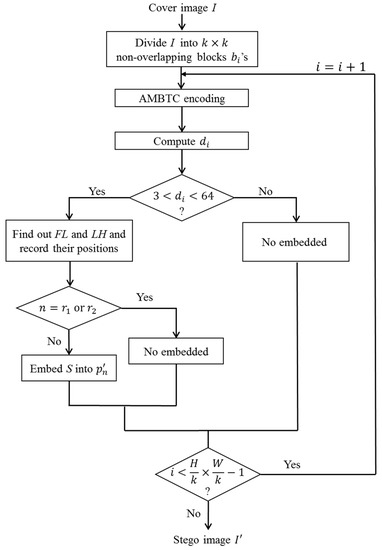
Figure 3. Flowchart of embedding phase.

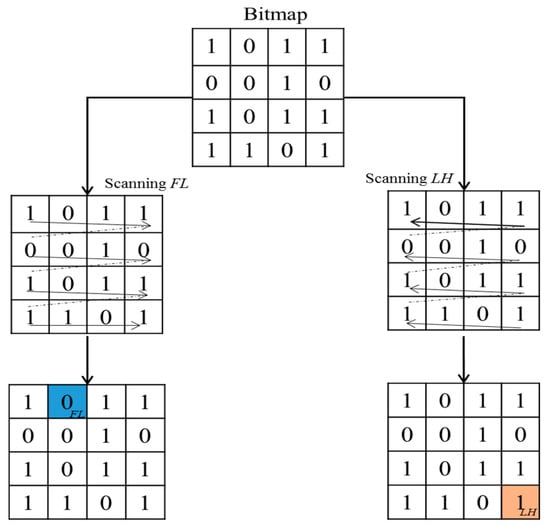
Figure 4. The example of FL and LH scanning.

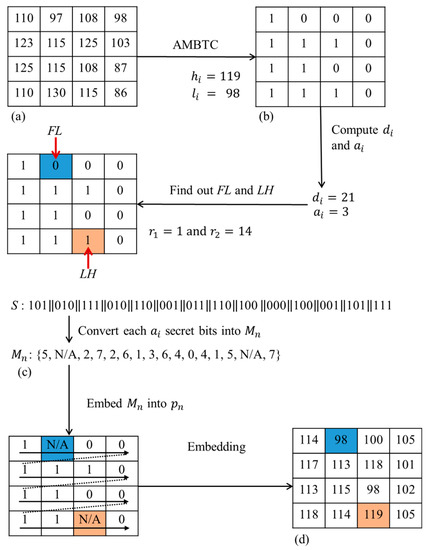
Figure 5. (a) Block $b_i \mathrm{sized} 4\times 4$, (b) The bit map of block $b_i$, (c) Secret data S and (d) The modified block $b{\prime }_i$ $\mathrm{sized} 4\times 4$.

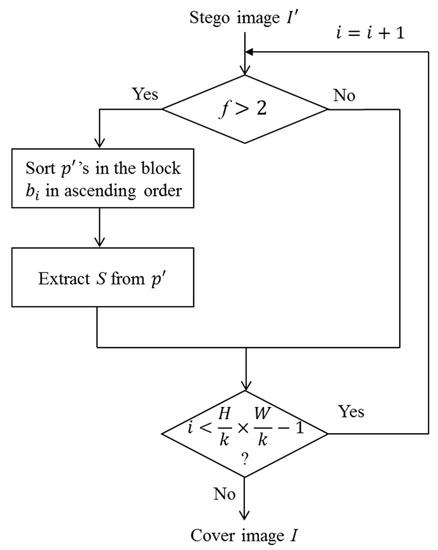
Figure 6. The flowchart of extraction and recovery phases.

3.1. Embedding Phase

The process of embedding phase is shown in Figure 3. Let I be an input cover image sized $H\times W$. Each block $b_i$ is sized $k\times k$, where $i=0, 1, \dots , \frac{H}{k}\times \frac{W}{k}-1$. Secret data S is a bit stream in binary form, and $M_n$ is the decimal value of secret bits.

Input: Cover image I and secret data S.

Output: Modified image $I^{\prime }.$

Step 1. Divide I into $k\times k$ non-overlapping blocks $b_i$’s.

Step 2. Calculate the current processing block $b_i$ using AMBTC algorithm.

Step 3. Compute $d_i$ using Equation (6).

$$d_i=h_i-l_i,$$

(6)

where $h_i$ and $l_i$ are quantization levels of high value and low value, respectively.

Step 4. Determine the value of $d_i$. If $3<d_i<64$, go to Step 5. Otherwise, go to Step 7.

Here, if $d_i$ is smaller than 3, the secret data cannot be extracted because of the middle value of two quantization levels could not be determined. For example, the values of $h_i$ and $l_{\mathrm{i}}$ are 9 and 7, respectively. We cannot know whether the modified pixel value $p_n^{\prime }$ is $h_i-1$ or $l_i+1$ while $p_n^{\prime }$ is 8. Therefore, $d_{\mathrm{i}}$ must be greater than 3. And if $d_i$ is greater than 63, it may cause a problem where the difference of the current processing block and its neighbor blocks are very large. As such, $d_i$ should be smaller than 63.

Step 5. Find out the first $b{p}_n=0$ (FL) and the last $b{p}_n=1$ (LH) in the bitmap, where $b{p}_n$ is the presented value in the bitmap and $n=0, 1, \dots , k\times k-1$. FL and LH are the first value 0 and the last value 1 in the bitmap, respectively. The locations of FL and LH are $r_1$ and $r_2$, respectively, where $r_1$ and $r_2$ are $0, 1, \dots \mathrm{or} k\times k-1$. We show an example in Figure 4 to describe in detail the process of scanning FL and LH.

Step 6. Compute the value of $a_i$ using Equation (7). Then, embed the $M_n$ into each $p_n$ using Equation (8),

$$a_i=\lfloor {\log }_2\left(\frac{d_i}{2}\right)\rfloor ,$$

(7)

$$p_n^{\prime }=\{\begin{array}{c}{h}_i , \mathrm{if} n=r_2 \\ l_i , \mathrm{if} n=r_1 \\ h_i-M_n, \mathrm{if} b{p}_n=1 \mathrm{and} n\ne r_1 \mathrm{or} r_2\\ l_i+M_n, \mathrm{if} b{p}_n=0 \mathrm{and} n\ne r_1 \mathrm{or} r_2,\end{array}$$

(8)

where $M_n$ is the decimal value of the next $a_i$ secret bits to be embedded, $p_n$ is the pixel value in the block $b_i$ and $p_n^{\prime }$ is the modified pixel value in the modified block.

Step 7. Modify the value of each $p_n$ in block $b_i$ using Equation (9) that no secret data are embedded.

$$p_n^{\prime }=\{\begin{array}{c}{h}_i, \mathrm{if} b{p}_n=1\\ l_i, \mathrm{if} b{p}_n=0.\end{array}$$

(9)

Step 8. Repeat Step 2 to Step 7 until all blocks $b_i$’s are processed.

Step 9. Obtain modified image $I^{\prime }$.

We can get modified image $I^{\prime }$ when all steps are finished. We provide an example to further clarify our embedding process in Figure 5. In Figure 5, (a) shows an example of a $4\times 4$ sized block $b_i$, (b) is the bitmap of block $b_i$, (c) presents secret data S and the decimal value $M_n$ of each $a_i$ secret bits and (d) shows the final result of modified image $I^{\prime }$. In the first step, utilize the AMBTC algorithm to compute the block $b_i$ and obtain two quantization levels $l_i$ and $h_i$. As $a_i$ is 3, S will be partitioned into multiple groups and each group contains three secret bits. Then, convert each group of $a_i$ secret bits into decimal value $M_n$. The positions of $r_1 \mathrm{and} r_2$ are utilized to substitute the values of $l_i$ and $h_i$, respectively. Moreover, no secret bits are embedded in them. As such $M_{r_1}$ and $M_{r_2}$, we use N/A to represent. In the next step, embed $M_n$ into each $p_n$ using Equation (8). And finally, S can be embedded into the block $b_i$ and obtain the modified block $b{\prime }_i$.

3.2. Extraction and Recovery Phase

The processes for the extraction and recovery phases are shown in Figure 6. S will be extracted from modified image $I^{\prime }$. When the block $b_i$ belongs to a non-embedding case, there are only two values in it. Therefore, we do not need any extra information to record whether this block has secret data or not.

Input: Modified image $I^{\prime }$.

Output: Secret data S and the cover image I.

Step 1. Divide $I^{\prime }$ into $k\times k$ non-overlapping blocks $b{\prime }_i$’s.

Step 2. Calculate the frequency f of the number of different pixels in the current processing block $b{\prime }_i$. The Algorithm 2 is described as follows.

Algorithm 2. Procedure for calculating the frequency.

Output: Frequency f

for i = 0 to k × k − 1. do

if $p{\prime }_{i+1}\ne p{\prime }_{0,1,\dots j}.$ then

f = f + 1;

endif

j++;

end for

Step 3. Determine the value of f. If $f>2$, go to step 4. Otherwise, go back to Step 2.

Step 4. Sort all $p_n^{\prime }$’s in the block $b{\prime }_i$ in ascending order. The first and last values in the sorted sequence are $l_i$ and $h_i$, respectively. And the positions of $l_i$ and $h_i$ are $r_1$ and $r_2$, respectively.

Step 5. Compute the values of $d_i$ and $a_i$ utilizing Equations (6) and (7), respectively. Extract the secret data from $p_n^{\prime }$’s using Equation (10).

$$M_n=\{\begin{array}{c}{h}_i-p_n^{\prime }, \mathrm{if} p_n^{\prime }>\frac{l_i+ h_i}{2} \mathrm{and} n\ne r_1 \mathrm{or} r_2\\ p_n^{\prime }-l_i, \mathrm{if} p_n^{\prime }<\frac{l_i+ h_i}{2} \mathrm{and} n\ne r_1 \mathrm{or} r_2\end{array}.$$

(10)

Then, convert $M_n$ into $a_i$ secret bits and add in S.

Step 6. Recover block $b{\prime }_i$ using Equation (11).

$$p_n=\{\begin{array}{c}{h}_i, \mathrm{if} p_n^{\prime }>\frac{l_i+ h_i}{2} \\ l_i, \mathrm{if} p_n^{\prime }<\frac{l_i+ h_i}{2} \end{array}.$$

(11)

Step 7. Repeat Step 2 to Step 6 until all modified blocks $b{\prime }_i$’s are processed.

Step 8. Obtain the cover image I and secret data S.

After all steps are computed, we can extract S from modified block $b{\prime }_i$ and recover each $b{\prime }_i$ using min{$p_n^{\prime }$} and max{$p_n^{\prime }$} after sorting. We used $l_i$ and $h_i$ to replace the positions of FL and LH, respectively. This allows us to know $l_i$ and $h_i$ utilizing the ascending order of all $p_n^{\prime }$’s in modified block $b{\prime }_i$ while extracting. This approach can avoid the problem when the value of $M_n$ is 0. We also provide a detailed example of the extraction and recovery phases in Figure 7. In Figure 7, (a) presents the modified block $b{\prime }_i$ that follows the previous example in Figure 5, (b) shows the results of extracted $M_n$ and S in binary form and (c) is the resulting block $b_i$ after recovery. Firstly, calculate the frequency f and determine whether the value of f is greater than 2. Then, all $p_n^{\prime }$’s in the modified block $b{\prime }_i$ will be sorted in ascending order. The first and last values are $l_i$ and $h_i$, respectively. According to the first and last values in a sorted sequence corresponding positions in modified block $b{\prime }_i$, the positions of $r_1 \mathrm{and} r_2$ are 1 and 14, respectively. Next step, $M_n$ will be extracted from modified block $b{\prime }_i$ using Equation (8). Each $M_n$ will be converted into $a_i$ secret bits and added in the S. In the last step, recover each $p_n^{\prime }$ using Equation (9). Finally, we can get block $b_i$ and extract S from the modified block $b{\prime }_i$.

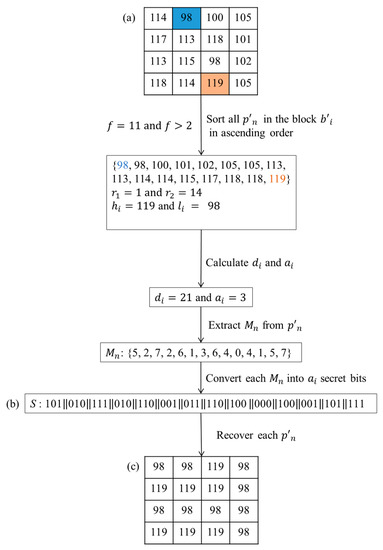
Figure 7. (a) The modified block $b{\prime }_i$ $\mathrm{sized} 4\times 4$, (b) Secret data S and (c) block $b_i \mathrm{sized} 4\times 4$.

4. The Proposed Scheme

The section provides some experimental results to show the hiding capacity (bits) and image quality (dB) of our proposed scheme. In Figure 8, all of the experiments were performed with six commonly used grayscale test images: Lena, F-16, Sailboat, Girl, Toys, and Barbara. All are of the same size, $512\times 512$. The size of each block $b_i$ is $4\times 4$. The embedded secret data are composed of a random bit-stream that was produced from a random number generator.

Figure 8. Test images (a) Lena; (b) F-16; (c) Sailboat; (d) Girl; (e) Toys; (f) Barbara.

In these experiments, the visual quality of the modified images was evaluated by using peak signal-to-noise ratio (PSNR) as defined in Equation (12).

$$PSNR=10\times {\log }_{10}\left(\frac{{255}^2}{MSE}\right),$$

(12)

The definition of mean square error (MSE) is shown in Equation (13).

$$MSE=\frac{1}{H\times W}{{\displaystyle \sum }}_{i=0}^{\frac{H}{k}\times \frac{W}{k}-1}{{\displaystyle \sum }}_{n=0}^{k\times k-1}{\left({p^{\prime }}_n^i-p_n^i\right)}^2,$$

(13)

where ${p^{\prime }}_n^i$ and $p_n^i$ are the stego pixels and original pixels in each modified block and original block, respectively.

To demonstrate the performance results for our proposed scheme, our method was compared with previous reversible data hiding methods in two aspects. In the first group, the proposed scheme was compared with other BTC-based schemes [21,22,23,24]. Figure 9a and Table 2 show the results of this comparison. Figure 9a shows, the good performance for embedding capacity that was achieved in our scheme. The proposed method can embed 56 bits in each $4\times 4$ pixel block while the difference between two quantization levels is larger than 32. However, Lin et al.’s scheme can embed 16 bits in each $4\times 4$ pixel block. And in the schemes of Chang et al.’s, Li et al.’s, and Sun et al.’s, each $4\times 4$ pixel block can only be embedded 1, 2 and 4 bits, respectively. In our scheme, the capacity for, “Lena”, “F-16”, “Sailboat”, “Girl”, “Toys” and “Barbara”, were 324,548 (bits); 267,386 (bits); 432,796 (bits); 388,780 (bits); 292,250 (bits) and 449,876 (bits), respectively.

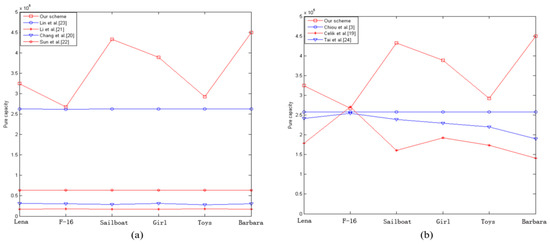
Figure 9. Comparative performance of pure hiding capacity for six test images between our method and other methods. (a) Comparisons with ours and other schemes based on BTC and (b) comparisons with ours and other schemes which are not based on BTC.

Table 2. Comparative performance of PSNR (dB) for six test images between our method and other methods base on BTC.

Scheme	Lena	F-16	Sailboat	Girl	Toys	Barbara	Average
Our scheme	32.59	32.22	30.16	33.30	32.12	28.82	31.54
Lin et al.’s [24]	33.05	31.64	30.32	33.36	30.99	28.63	31.33
Li et al.’s [22]	32.34	31.93	30.41	33.44	31.15	28.82	31.34
Chang et al.’s [21]	Cannot be constructed by the modified code stream
Sun et al.’s [23]	Cannot be constructed by the modified code stream

In our scheme, the image obtained a higher embedding capacity even with complex images such as “Barbara” and “Sailboat”, because our adaptive interpolation technique is related to the difference of two quantization levels. However, the capacity is relatively small in smooth images, such as “Lena”, “F-16′ and “Toys”. Table 2 shows a comparison of image quality. In Chang et al.’s and Sun et al.’s schemes, the cover image cannot be directly obtained from a stego compression code. Therefore, the two methods cannot be compared in terms of image quality of a modified image. From Table 2, the proposed scheme cannot achieve the best PSNR in every test image. In the “Lena”, Lin et al.’s scheme achieves the best results, and Li et al.’s scheme provides the best results in the “Sailboat”. But our method achieves a higher average. In brief, the first experiment shows that our scheme achieves the higher embedding capacity while maintaining relative good, modified image quality.

In the second group, we compared some reversible data methods that are not based on a BTC-compressed technique [4,20,25]. These three other techniques hide secret data in the spatial domain. As shown in Figure 9b and Table 3, our method obtains good performance in comparison with the other methods. In Chiou et al.’s scheme, secret data cannot be embedded into the blocks in the first row and first column. Tai et al.’s scheme and Celik et al.’s cannot embed secret data in some cases. In our method, although secret data cannot be embedded when the difference of two quantization levels is smaller than 4, our scheme still can obtain a better hiding capacity than other schemes when conditions were similar for PSNR. The experimental results show that, our proposed scheme was better than other reversible data hiding schemes.

Table 3. Comparative performance of PSNR (dB) for six test images between our method and other schemes.

Scheme	Lena	F-16	Sailboat	Girl	Toys	Barbara	Average
Our scheme	32.59	32.22	30.16	33.30	32.12	28.82	31.54
Chiou et al.’s [4]	31.05	30.23	28.43	31.11	28.73	25.53	29.18
Celik et al.’s [20]	32.54	31.33	30.41	32.76	31.15	29.82	31.34
Tai et al.’s [25]	31.61	29.84	27.25	31.43	34.84	28.42	30.57

5. Conclusions

This paper proposed an adaptive reversible image hiding method using AMBTC compression by considering the quantization level difference of each block. According to our adaptive embedding strategy, more bits are embedded into the image sub-block located in regions where the value of QLD is larger. However, in order to ensure the quality of the image, when the value of the QLD of a sub-block is greater than the threshold, this block will not embed information. Experimental results showed that the performance of the proposed scheme is better than the previous schemes in terms of payload and modified image quality.