Abstract
We present a quantitative analysis of the theoretical spin density map of two ferromagnetic perovskites, YTiO and SrRuO. We calculated the spin density using the standard density functional theory (DFT)+U method, where the Hubbard U correction is applied to the Ti and Ru ions, and with the pseudo-hybrid ACBN0 method, where the Hubbard U parameters are determined self-consistently. The ACBN0 calculations yielded a large value of the Hubbard U of the oxygen orbitals. We also used the screened hybrid HSE06 functional, which is widely used to describe the electronic structure of oxides. We used the Quantum Theory of Atoms in Molecules (QTAIM) theory and integrated the spin density in the atomic basins instead of projecting on atomic orbitals. This way, our results can be compared to experimental reports as well as to other DFT calculations.
1. Introduction
Density functional theory (DFT) [1,2] is the most used computational method for calculating the physical and chemical properties of materials. Its success is due to the possibility of obtaining reasonably accurate results at a convenient computational cost. In principle, DFT is an exact theory, but in practice, approximations to the exchange–correlation (XC) functional must be made. Therefore, the DFT’s accuracy and predictive power are strongly dependent on the choice of the XC functionals. Moreover, as it is a mean-field theory, the DFT is not self-interaction free [3], and no XC functional to date is able to exactly cancel the Hartree term. This is in contrast with the Hartree–Fock method, which is also a mean-field theory, but is one-electron self-interaction free [4].
The problem of the self-interaction is particularly severe for highly localized orbitals, like the d and f orbitals. The self-interaction leads to an excessive wavefunction delocalization and vanishing band gaps in many insulating systems. To solve these drawbacks, one should employ generalized DFT methods, such as DFT+U [5], hybrid functionals (i.e., mixing of the DFT and Hartree–Fock methods) [6], DMFT [7], or GW [8,9]. Nowadays, these methods are widely accepted, as they tremendously improve the description of the electronic properties (i.e., band structures, photoemission spectra) with respect to the plain DFT. Note that most of these methods are not, strictly speaking, fully ab initio, but depend on empirical parameters, like the on-site Hubbard terms U and J.
One relevant question is if and how these methods improve the description of other measurable quantities, such as the charge and spin density. For instance, it was observed that climbing Jacob’s ladder (LDA, GGA, mGGA, and higher rungs) does provide more accurate total energies, but this is not true for the charge density [10] when compared to experiments. There exist other papers in the literature comparing DFT charge density to the CCSD(T) one [11] and to quantitative electron diffraction data [12]. Clearly, one has to devise a method to perform a numerical comparison of charge/spin density [13]. Another relevant question is if it is possible to determine DFT parameters from experiments. For instance, the authors of Ref. [14] were able to determine the Hubbard U parameters of NiO from quantitative convergent-beam electron diffraction experiments. All these theoretical and experimental works mainly addressed the charge density, whereas critical discussions of if DFT can accurately reproduce the experimental spin density are rare.
In this work, we present a quantitative analysis of the theoretical spin density map of two ferromagnetic perovskites, YTiO and SrRuO, calculated using two DFT+U methods and one hybrid functional (HSE06) [15]. In the standard DFT+U method [16], the U correction is applied only to the Ti and Ru ions, while in the pseudo-hybrid ACBN0 method [17,18,19], the Hubbard U parameters of every ion are determined self-consistently. We used the Quantum Theory of Atoms in Molecules (QTAIM) [20] theory to integrate the spin density in the Bader atomic basins. The advantage of the QTAIM over projection (Mulliken, Löwdin) methods is that it does not depend on the set of atomic orbitals used to project the Bloch wavefunctions. Moreover, the QTAIM can be used to quantitatively analyze the experimental charge and spin densities on the same footing as the theoretical ones.
2. Computational Methods
We performed the total energy calculations of ferromagnetic YTiO and SrRuO at the experimental lattice and geometry reported in Refs. [21] and [22,23], respectively, using Quantum Espresso [24,25]. We used ONCV-optimized norm-conserving pseudopotentials [26], including semi-core orbitals and a plane wave expansion of 120 Ry to accurately integrate the charge and spin density. The QTAIM charge/spin populations were calculated with Critic2 [27] using the Yu–Trinkle algorithm [28]. The valence shell charge concentration (VSCC) points were located with Critic2 by searching the outermost minima of the laplacian of the charge density within a distance of 2 au from the individual Ti and Ru ions. Usually, the VSCCs are located in coincidence with the lone pairs in -bonded materials and with the lobes of the occupied d orbital in transition metal complexes [29].
We used the PBEsol [30] semilocal functional, which describes the structural properties of perovskites both at ambient and high pressure reasonably well. We applied the rotationally invariant Hubbard U correction on top of the PBEsol functional. We set up two different schemes of “+U” corrections: (1) We applied U = 0.5 eV to the d orbitals of the transition metal atoms; (2) we applied the U correction both to the metal d and oxygen p orbitals. For scheme (2), we self-consistently calculated the Hubbard U values using the ACBN0 method (using the standalone acbn0.py script in the PAOFLOW package [31,32]). Finally, we used the HSE06-screened hybrid functional using the ACE method [33] and a smaller k-point mesh to reduce the computational cost. We did not compute the band structure and the density of states with the HSE06 because they would require Wannier interpolation on a very fine k-point mesh.
3. Results
3.1. YTiO
YTiO is a ferromagnetic perovskite with a Curie temperature of 5 K, and it crystallizes in the GdFeO Pnma structure with large TiO octahedra tilting (19). The Ti-O-Ti angles are ∼144 on the plane and 140 along the b axis. The distance between the Ti and apical O along the b axis is the shortest (2.0167 Å), while the Ti-O distances in the plane are alternatively short and long (2.0178 Å and 2.0754 Å) [21]. Figure 1 shows the spin density isolines on the plane passing through the Ti ions. The oxygen atoms directly bound to the Ti ions are located 0.44 Å above and below the plane.
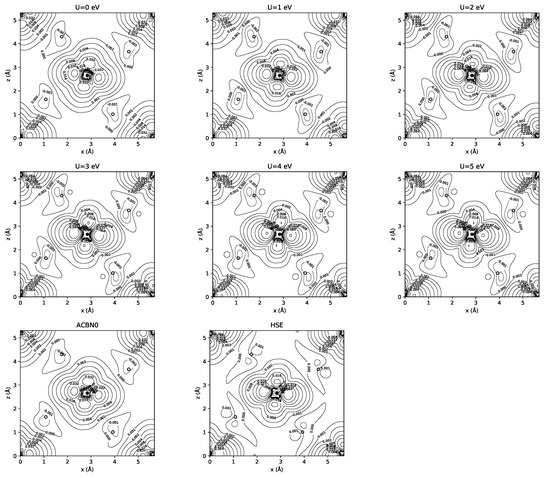
Figure 1.
Isodensity contour of the spin density of YTiO plotted on the plane. The Ti ion is in the center of the cell. The projections of the O2 ions are indicated by open circles (the O ions are 0.44 Å above and below the cut plane). The isovalues are with .
The atomic charges and spin densities integrated in the Bader basins of the charge density are reported in Table 1. The effect of the Hubbard U on the Ti ion is to concentrate both the charge and spin density on the metal ions. Interestingly, the ACBN0 method yielded U(Ti-3d) = 0.26 eV and a large value for oxygen, U(O-2p) = 8.31 eV.

Table 1.
Quantum Theory of Atoms in Molecules (QTAIM) charges and spin densities of YTiO. O1 is the apical oxygen, while O2 is the basal oxygen. Experimental polarized neutron diffraction (PND) results and PBE0+QTAIM results are from Ref. [21].
The calculated atomic charges are far from the formal valence charges (Y:+3, Ti:+3, O:−2). The sum of the partial charges, integrated on a real space mesh, differs by 10 electrons from the total number of electrons per unit formula. The total spin magnetization per unit formula is 1 k with 80–86% of it located on the Ti ion. This situation corresponds to a Ti ion in the configuration. Note that the spin density around the oxygen atoms shows a negative shell near the ion, surrounded by a region of positive spin density. The size of this negative spin region is large when the U is applied to the Ti ion, whereas it is reduced with ACBN0. The ACBN0 atomic charges and spins are close to those obtained with the hybrid HSE06 and PBE0 functionals. The PBE0 calculations accompanying the experimental paper were performed with the gaussian basis set code CRYSTAL [34], and the QTAIM analysis was performed with TOPOND [35]. Note that the small magnetic moment on the O1 (apical) ion is initially larger that those of the O2 ions at U = 0, but the situation changes for U > 3 eV. The larger magnetic moments on the basal O2 ions are also suggested by the experimental data, but this is not the case for ACBN0.
The electronic density of states (DOS) is shown in Figure 2. Upon increasing the Hubbard U on the Ti ion, the system undergoes a metal-to-insulator transition. The singly occupied orbital in the spin-up channel separates from the empty state manifold and moves to a lower energy below the Fermi level. The situation is different for ACBN0: The small value of U on the Ti ion preserves the metallic character, and the large U value on oxygen has the effect of shifting the occupied manifold down by ∼2 eV (which has a dominant oxygen character) and increasing its band width. Our results are in good agreement with those of Refs. [36,37], where it was found that a U(Ti) value of 3.7 eV yields a band gap of 2.20 eV. In the same paper, they also calculated a band gap of 2.07 eV with the HSE06 functional, and the manifold of occupied oxygen bands was found 6 eV below the bottom of the upper Hubbard band (UHB). Overall, the HSE DOS of Ref. [36] is more similar to the case of U = 5 eV, except that the the oxygen states are −5 eV below the left shoulder of the UHB. In ACBN0, the distance between the oxygen states and the UHB is ∼6 eV, which is similar to HSE. Unfortunately, ACBN0 is not able to split the lower Hubbard band (LHB ) from the UHB.
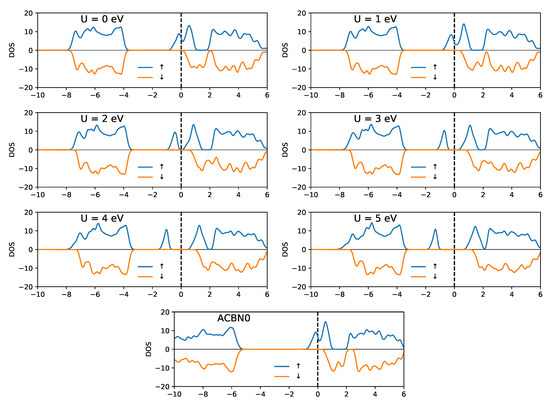
Figure 2.
Electronic density of states of YTiO calculated as function of U(Ti-3d) and with ACBN0 with respect to the Fermi level.
The spin density and the VSCCs are reported in Figure 3. The analysis of the laplacian of the charge density shows that the there are six VSCC points, which are located ∼0.37 Å from the Ti ion, corresponding to the outer shell of Ti. When U(Ti) is small (less than 2 eV), the VSCCs are arranged as a nearly regular octahedron. The VSCC octahedron is rotated such that two VSCCs are in the O1-Ti-O2 plane, and the remaining four VSCCs are located in the plane tilted by ∼40 from the Ti-O2-O2’ plane. For small values of U(Ti), the six VSCCs correspond to the six lobes of the spin density, showing that the spin density is given by a superposition of the orbitals. When the Hubbard U on Ti is larger than 2 eV and the system becomes insulating, the VSCC octahedron changes its shape and becomes highly distorted: Four VSCCs were found to correspond two the four spin density lobes, while the two remaining VSCCs were located close to the Ti-O1 bond. This is reflected by the values of the laplacian (curvature of the charge density): When U(Ti) is small, the laplacian at the VSCC ranges from −9.3 to −10.0 au, meaning that the charge density is concentrated nearly equally at the VSCC. When U(Ti) is larger that 2 eV, the laplacian is more negative (−12.5 au) at the four VSCCs corresponding to the spin density lobes, while it is less negative (−8.7 au) at the two remaining VSCCs. Therefore, in YTiO the curvature of the charge density distribution gives a direct indication of the shape of the spin density.
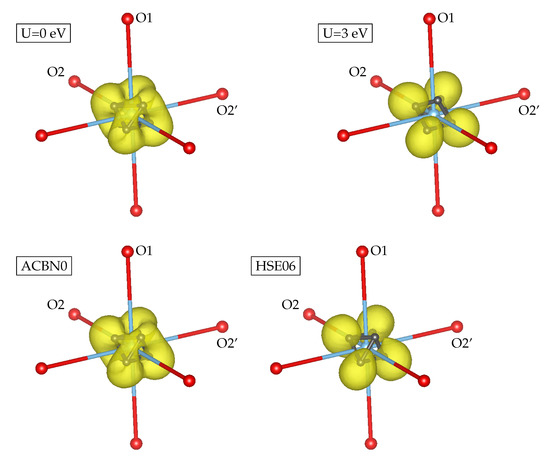
Figure 3.
Spin density and valence shell charge concentrations (VSCCs) of YTiO. The spin density isosurface is 0.3/au. O1 is the apical oxygen, and O2 and O2’ are the basal oxygens. Ti–O2’ is the largest Ti–O interatomic distance.
Unsurprisingly, the small U(Ti)=0.26 eV found by the ACBN0 method yields a spin density with six lobes, and the VSCCs form a nearly regular octahedron. However, the ACBN0 charge density around the Ti atom is more concentrated with respect to the U = 0 case: The laplacian at the six VSCCs ranges from −9.4 to −11.2 au, and this is due to the fact that the ACBN0 Bader charge on Ti is ∼10% larger than that computed with U = 0. In the HSE06 case, the spin density shows four large lobes and two small ones that become visible with an isosurface of 0.2 au. This situation is intermediate between the small and large U value cases. The laplacians at the VSCCs are −8.9 and −12.5 au, comparable to the case of U(Ti) > 2 eV.
3.2. SrRuO
SrRuO is a weakly interacting ferromagnetic metallic perovskite. SrRuO crystallizes in the Pnma structure, but differently from YTiO the octahedra in SrRuO are less tilted and less distorted. The Sr-O distances are 1.986 Å(Sr-O1 apical), 1.986 Å and 1.987 Å (Sr-O2 basal). The Sr-O-Sr angle is ∼161 [22].
Figure 4 shows the spin density isolines on the plane passing through the Ru ions. The plane containing the Sr and O atoms is almost parallel to the (010) plane. The atomic charges and spin densities integrated in the Bader basins of the charge density are reported in Table 2. Similarly to YTiO, the ACBN0 method yielded a relatively small value of U on the transition metal and a large value of U on the oxygen ions: U(Ru-4d) = 2.06 eV and U(O-2p) = 5.08 eV.
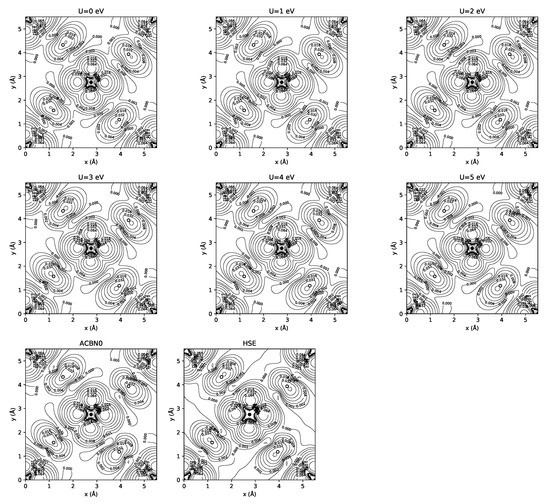
Figure 4.
Isodensity contour of the spin density of SrRuO plotted on the plane. The Ti ion is in the center of the cell. The projections of the O2 ions are indicated by open circles. The isovalues are with .

Table 2.
QTAIM charges and spin densities of YTiO. O1 is the apical oxygen, while O2 is the basal oxygen. Experimental results and the “other density functional theory (DFT)” are from Ref. [23]. Two experimental refinements are reported, including the orbital angular momentum (S + L) and without angular momentum (S). The “other DFT” magnetic moments are integrated inside atomic spheres of radii 1.25 Å (Ru) and 0.73 Å(O).
The calculated atomic charges are far from the formal valence charges (Sr:+2, Ru:+4, O:−2). The sum of the partial charges, integrated on a real space mesh, differs by 10 electrons from the total number of electrons per unit formula. The atomic charges of oxygen are smaller than those of YTiO. The ACBN0 and HSE06 functionals tend to concentrate both the charge and the spin on the Ru ion, making the system slightly more ionic in character. The total magnetization is close to 2 and is compatible with a Ru ion in the configuration. The atomic magnetic moments on the oxygen atoms are about 0.2 , one order of magnitude larger than those of YTiO. With respect to YTiO, the smaller Bader charge and the larger magnetic moment on oxygen can be explained by the larger overlap between the O-2p orbitals and the Ru-4d, which has a larger spatial extent than the Ti-3d orbital.
Differently from YTiO the spin density map, atomic charges, and spin populations are nearly insensitive to the value of U for the Ru ion. The spin density map shows only regions of positive spin density.
The electronic densities of states of SrRuO are shown in Figure 5. At U = 0, the system is a ferromagnetic metal, and upon increasing U(Ru), the system turns into a half-metal with a gap in the spin-up channel opening for U > 2 eV. Consequently, the total magnetic moment reaches the value of 2 in the half-metallic state. The system is also half-metal with the ACBN0 method (U(Ru) = 2.06 eV), but the bandwidth is larger than in the DFT+U calculations. The half-metallic character is consistent with previous reports [38], as well as with quasi-particle self-consistent GW (sc-QSGW) calculations [39]. The transition from the metal to the half-metal has important consequences for the structural parameters. In Figure 6, we report the equilibrium volume of SrRuO as a function of U(Ru-4d). For small values of U, the agreement with respect to experiments is rather good. However, as the system becomes half-metallic, the volume increases away from the experimental value. ACBN0 underestimates the equilibrium volume by 1.88%.
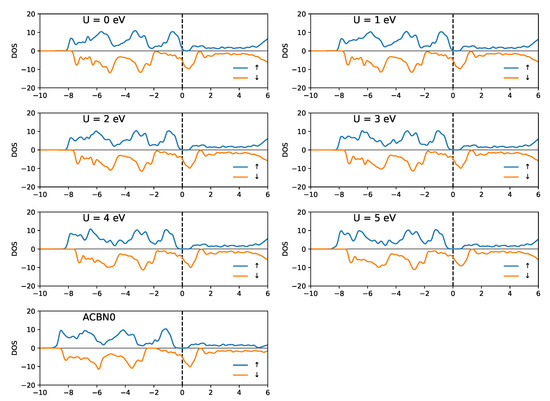
Figure 5.
Electronic density of states of SrRuO calculated as function of U(Ru-4d) and with ACBN0 with respect to the Fermi level.
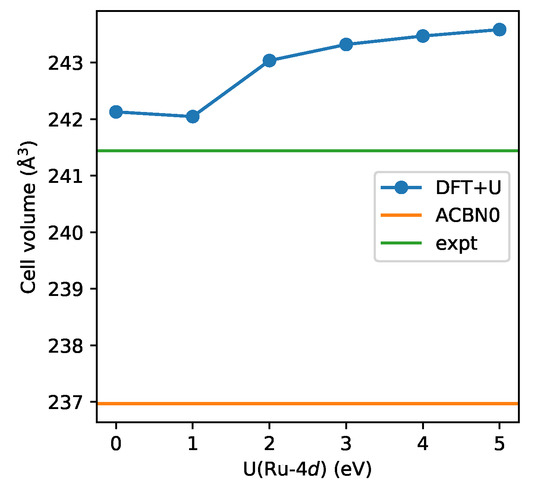
Figure 6.
Equilibrium volume of SrRuO calculated as a function of the U(Ru-4d) compared with ACBN0 and an experiment [22].
The spin density and the VSCC are reported in Figure 7. The analysis of the laplacian of the charge density shows that the there are eight VSCC points located ∼0.44 Å from the Ru ion. The VSCCs are arranged as a cube whose vertexes point in the directions of the center of the faces of the SrO octahedron. As already shown in Table 2, the spin density depends weakly on the U values and on the choice of the functional. The value of the laplacian at the VSCC goes from −8.18 au at U = 0 to −8.30 au at U = 5 eV, au for ACBN0, and au for HSE. Thus, the charge and spin concentrations around the Ru ion depend rather weakly on the DFT methods that we have used.
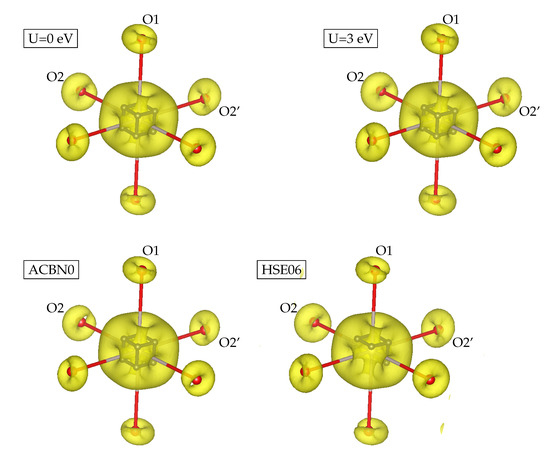
Figure 7.
Spin density and VSCC of SrRuO. The spin density isosurface is 0.3/au. O1 is the apical oxygen, and O2 and O2’ are the basal oxygens.
4. Discussion
The comparison of DFT results with experimental polarized neutron/X-ray diffraction [21,23] and magnetic Compton scattering [40] data has to be carried out with some caution. After removing the instrumental and thermal effects, diffraction experiments provide the structure factors that are related to the charge/spin density by a Fourier transform. The atomic and orbital contributions to the experimental charge/spin density are obtained from the multipolar model [41] or from the maximum entropy method [42]. However, it is possible to perform a detailed QTAIM analysis on the experimental charge and spin density after a multipolar refinement [43,44]. The other possibility is to calculate the theoretical structure factors directly from the DFT and perform multipolar refinement on them.
Therefore, in this paper, we can perform only a qualitative comparison between the calculated and experimental spin densities. As reported in Ref. [21], the experimental spin density of YTiO shows a four-lobe structure tilted by ∼45 degrees with respect to the Ti-O2-O2’ plane. This situation is well reproduced by hybrid functionals (HSE06 and PBE0) as well as by DFT+U with a Hubbard U value larger than 3 eV. Smaller U values and ACBN0 are not sufficient to open an insulating gap, and, as a result, the spin densities show a six-lobe structure with results from a superposition of the orbitals. Conversely, the calculated SrRuO spin density appears to be less sensitive to the DFT method and XC approximation. The spin density is always made of eight lobes centered on Ru and a non-negligible doughnut-shaped region center on O. Overall, its shape compares extremely well with the spin density maps that are reported in Ref. [23] without the color scale.
The electronic structure of these materials is better described by hybrid functionals [36] and by ACBN0 to the same extent. The large values of U on the O- orbitals found by ACBN0 have the effect of moving the occupied states (which mainly have an O character) to lower energy and increasing their bandwidth in agreement with photoemission experiments and many-body (i.e., GW) techniques. Large U values for oxygen are found with ACBN0 in a number of perovskites [45]. As discussed in Ref. [45], according to the cRPA calculations and spectroscopy results, the magnitude of U(2p) is expected to be of the same order of U(3d/4d). Based on our past experience with BaBiO [46], we noted that when the states at the Fermi level have a large O(2p) character, applying U on oxygen is more effective than applying it on the transition metal. The result is a slightly more ionic metal–oxygen bond, which allows charge disproportionation in BaBiO (i.e., Ba Bi Bi O). As a corollary, because ACBN0 acts both on the metal and on the oxygen ions, the Hubbard value of the transition metal is diminished. By changing the set of active orbitals (i.e., including O- and metal-s), we expect changes in the U values. Indeed, by removing oxygen from the active orbitals, the U value on the metal is expected to be large. We added this paragraph to the discussion. Therefore, the inclusion of s orbitals in elements and the empty orbital of Ti would constitute a big improvement to ACBN0 [45]. Unfortunately, the current implementation of DFT+U in Quantum Espresso is limited to one angular momentum per ion.
Finally, we stress that partitioning of the charge/spin density with methods that do not involve projection over atomic or local orbitals is a very meaningful way to compare different DFT methods among them and with experiments. In this work, we used QTAIM, but other space partitioning methods can be used—for instance, Voronoi or Hirshfeld partitioning [47]. Moreover, the first and second derivatives of the charge density provide a measurable indication of the extrema and of the concentration (localization) of the charge density. In the case of YTiO the VSCC and the value of the laplacian at the VSCC depend critically on the DFT method and could be used to gauge how well calculations compare to the experiments [13].
5. Conclusions
We presented a quantitative analysis of the theoretical spin density maps of two ferromagnetic perovskites, YTiO and SrRuO. We used different DFT methods: DFT+U, ACBN0, and hybrid functionals. We performed a QTAIM partitioning and integrated the spin density in the atomic basins. We also analyzed the VSCC in order to highlight the fine differences between the charge densities obtained with the different methods. We found that the charge density of YTiO depends strongly on the DFT method, whereas that of SrRuO is nearly independent. We found a non-negligible spin polarization on oxygen in SrRuO due to the overlap with the Ru- orbitals. The best agreement with the experimental spin densities was obtained with the HSE06 hybrid functional.
In perspective, this work could be extended to other DFT functionals (i.e., meta-GGAs) that have been shown to provide structural parameters in very good agreement with experiments [48,49,50], to extended-Hubbard methods (DFT+U+V [51,52,53]), and to self-consistent DMFT methods [54] in order to consider the effects of electron correlation. In addition to reproducing the features of the experimental charge/spin density, space partitioning techniques can be used to extract DFT parameters (i.e., U values, fraction of exact exchange) directly from experiments. Finally, the topological partitioning of the spin density is extremely sensitive to the electronic structure method and could be used to reveal the nature of magnetic interactions (direct exchange, super-exchange, double exchange) in solids [55]. We hope that, in the future, further experimental spin density maps of inorganic and molecular solids will be available.
Author Contributions
Both authors contributed equally to the realization and preparation of this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
F.M. was funded by the Center for Materials Crystallography (CMC) of Aarhus University.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank Carlo Gatti and Giovanna Bruno for the helpful discussions. Calculations were performed at the CINECA supercomputing center (ISCRA grants HP10C7BPGD, HP10C5WGQ7, and HP10CPXESJ.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Tsuneda, T.; Hirao, K. Self-interaction corrections in density functional theory. J. Chem. Phys. 2014, 140, 18A513. [Google Scholar] [CrossRef] [PubMed]
- Petukhov, A.G.; Mazin, I.I.; Chioncel, L.; Lichtenstein, A.I. Correlated metals and the LDA+U method. Phys. Rev. B 2003, 67, 153106. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13–125. [Google Scholar] [CrossRef]
- Hedin, L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 1965, 139, A796–A823. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Gunnarsson, O. The GW method. Rep. Prog. Phys. 1998, 61, 237–312. [Google Scholar] [CrossRef]
- Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density functional theory is straying from the path toward the exact functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef]
- Mezei, P.D.; Csonka, G.I.; Kállay, M. Electron Density Errors and Density-Driven Exchange-Correlation Energy Errors in Approximate Density Functional Calculations. J. Chem. Theory Comput. 2017, 13, 4753–4764. [Google Scholar] [CrossRef]
- Sang, X.; Kulovits, A.; Wang, G.; Wiezorek, J. Validation of density functionals for transition metals and intermetallics using data from quantitative electron diffraction. J. Chem. Phys. 2013, 138, 084504. [Google Scholar] [CrossRef] [PubMed]
- Choudhuri, I.; Truhlar, D.G. Calculating and Characterizing the Charge Distributions in Solids. J. Chem. Theory Comput. 2020, 16, 5884–5892. [Google Scholar] [CrossRef]
- Peng, D.; Nakashima, P.N.H. Measuring Density Functional Parameters from Electron Diffraction Patterns. arXiv 2020, arXiv:2010.09379. [Google Scholar]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Agapito, L.A.; Curtarolo, S.; Nardelli, M.B. Reformulation of DFT+U as a Pseudohybrid Hubbard Density Functional for Accelerated Materials Discovery. Phys. Rev. X 2015, 5. [Google Scholar] [CrossRef]
- Gopal, P.; Fornari, M.; Curtarolo, S.; Agapito, L.A.; Liyanage, L.S.I.; Nardelli, M.B. Improved predictions of the physical properties of Zn- and Cd-based wide band-gap semiconductors: A validation of the ACBN0 functional. Phys. Rev. B 2015, 91. [Google Scholar] [CrossRef]
- Gopal, P.; Gennaro, R.D.; dos Santos Gusmao, M.S.; Orabi, R.A.R.A.; Wang, H.; Curtarolo, S.; Fornari, M.; Nardelli, M.B. Improved electronic structure and magnetic exchange interactions in transition metal oxides. J. Phys. Condens. Matter 2017, 29, 444003. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Kibalin, I.A.; Yan, Z.; Voufack, A.B.; Gueddida, S.; Gillon, B.; Gukasov, A.; Porcher, F.; Bataille, A.M.; Morini, F.; Claiser, N.; et al. Spin density in YTiO3: I. Joint refinement of polarized neutron diffraction and magnetic x-ray diffraction data leading to insights into orbital ordering. Phys. Rev. B 2017, 96. [Google Scholar] [CrossRef]
- Masys, Š.; Jonauskas, V. On the crystalline structure of orthorhombic SrRuO3: A benchmark study of DFT functionals. Comput. Mater. Sci. 2016, 124, 78–86. [Google Scholar] [CrossRef][Green Version]
- Kunkemöller, S.; Jenni, K.; Gorkov, D.; Stunault, A.; Streltsov, S.; Braden, M. Magnetization density distribution in the metallic ferromagnet SrRuO3 determined by polarized neutron diffraction. Phys. Rev. B 2019, 100, 054413. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Schlipf, M.; Gygi, F. Optimization algorithm for the generation of ONCV pseudopotentials. Comput. Phys. Commun. 2015, 196, 36–44. [Google Scholar] [CrossRef]
- De-la Roza, A.O.; Johnson, E.R.; Luaña, V. Critic2: A program for real-space analysis of quantum chemical interactions in solids. Comput. Phys. Commun. 2014, 185, 1007–1018. [Google Scholar] [CrossRef]
- Yu, M.; Trinkle, D.R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef]
- Ruiz, E.; Cirera, J.; Alvarez, S. Spin density distribution in transition metal complexes. Coord. Chem. Rev. 2005, 249, 2649–2660. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Agapito, L.A.; Fornari, M.; Ceresoli, D.; Ferretti, A.; Curtarolo, S.; Nardelli, M.B. Accurate tight-binding Hamiltonians for two-dimensional and layered materials. Phys. Rev. B 2016, 93, 125137. [Google Scholar] [CrossRef]
- Nardelli, M.B.; Cerasoli, F.T.; Costa, M.; Curtarolo, S.; Gennaro, R.D.; Fornari, M.; Liyanage, L.; Supka, A.R.; Wang, H. PAOFLOW: A utility to construct and operate on ab initio Hamiltonians from the projections of electronic wavefunctions on atomic orbital bases, including characterization of topological materials. Comput. Mater. Sci. 2018, 143, 462–472. [Google Scholar] [CrossRef]
- Lin, L. Adaptively Compressed Exchange Operator. J. Chem. Theory Comput. 2016, 12, 2242–2249. [Google Scholar] [CrossRef] [PubMed]
- Dovesi, R.; Orlando, R.; Erba, A.; Zicovich-Wilson, C.M.; Civalleri, B.; Casassa, S.; Maschio, L.; Ferrabone, M.; Pierre, M.D.L.; D’Arco, P.; et al. CRYSTAL14: A program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. [Google Scholar] [CrossRef]
- Gatti, C.; Saunders, V.R.; Roetti, C. Crystal field effects on the topological properties of the electron density in molecular crystals: The case of urea. J. Chem. Phys. 1994, 101, 10686–10696. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Janotti, A.; Bjaalie, L.; de Walle, C.G.V. Interband and polaronic excitations in YTiO3 from first principles. Phys. Rev. B 2014, 90. [Google Scholar] [CrossRef]
- Varignon, J.; Bibes, M.; Zunger, A. Origin of band gaps in 3d perovskite oxides. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef]
- Jeng, H.T.; Lin, S.H.; Hsue, C.S. Orbital Ordering and Jahn-Teller Distortion in Perovskite Ruthenate SrRuO3. Phys. Rev. Lett. 2006, 97, 067002. [Google Scholar] [CrossRef]
- Ryee, S.; Jang, S.W.; Kino, H.; Kotani, T.; Han, M.J. Quasiparticle self-consistent GW calculation of Sr2RuO4 and SrRuO3. Phys. Rev. B 2016, 93, 075125. [Google Scholar] [CrossRef]
- Yan, Z.; Kibalin, I.A.; Claiser, N.; Gueddida, S.; Gillon, B.; Gukasov, A.; Voufack, A.B.; Morini, F.; Sakurai, Y.; Brancewicz, M.; et al. Spin density in YTiO3: II. Momentum-space representation of electron spin density supported by position-space results. Phys. Rev. B 2017, 96. [Google Scholar] [CrossRef]
- Hansen, N.K.; Coppens, P. Testing aspherical atom refinements on small-molecule data sets. Acta Crystallogr. Sect. A 1978, 34, 909–921. [Google Scholar] [CrossRef]
- Gilmore, C.J.; Shankland, K.; Bricogne, G. Applications of the Maximum Entropy Method to Powder Diffraction and Electron Crystallography. Proc. Math. Phys. Sci. 1993, 442, 97–111. [Google Scholar]
- Volkov, A.; Gatti, C.; Abramov, Y.; Coppens, P. Evaluation of net atomic charges and atomic and molecular electrostatic moments through topological analysis of the experimental charge density. Acta Crystallogr. Sect. A Found. Crystallogr. 2000, 56, 252–258. [Google Scholar] [CrossRef] [PubMed]
- Gatti, C.; Saleh, G.; Presti, L.L. Source Function applied to experimental densities reveals subtle electron-delocalization effects and appraises their transferability properties in crystals. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 180–193. [Google Scholar] [CrossRef]
- May, K.J.; Kolpak, A.M. Improved description of perovskite oxide crystal structure and electronic properties using self-consistent Hubbard U corrections from ACBN0. Phys. Rev. B 2020, 101. [Google Scholar] [CrossRef]
- Ceresoli, D.; Tosatti, E. Pressure-induced insulator-metal and structural transitions of BaBiO3 from first principles LDA+U. In Proceedings of the APS March Meeting Abstact L40.00008, New Orleans, LA, USA, 10–14 March 2008. [Google Scholar]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Yuk, S.F.; Pitike, K.C.; Nakhmanson, S.M.; Eisenbach, M.; Li, Y.W.; Cooper, V.R. Towards an accurate description of perovskite ferroelectrics: Exchange and correlation effects. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, J.; Perdew, J.P.; Wu, X. Comparative first-principles studies of prototypical ferroelectric materials by LDA, GGA, and SCAN meta-GGA. Phys. Rev. B 2017, 96. [Google Scholar] [CrossRef]
- Gautam, G.S.; Carter, E.A. Evaluating transition metal oxides within DFT-SCAN and SCAN+U frameworks for solar thermochemical applications. Phys. Rev. Mater. 2018, 2. [Google Scholar] [CrossRef]
- Jr, V.L.C.; Cococcioni, M. Extended DFT+U+V method with on-site and inter-site electronic interactions. J. Phys. Condens. Matter 2010, 22, 055602. [Google Scholar] [CrossRef]
- Lee, S.H.; Son, Y.W. Efficient First-Principles Approach with a Pseudohybrid Density Functional for Extended Hubbard Interactions. arXiv 2019, arXiv:1911.05967. [Google Scholar]
- Tancogne-Dejean, N.; Rubio, A. Parameter-free hybridlike functional based on an extended Hubbard model: DFT+U+V. Phys. Rev. B 2020, 102. [Google Scholar] [CrossRef]
- James, A.D.N.; Harris-Lee, E.I.; Hampel, A.; Aichhorn, M.; Dugdale, S.B. Wavefunctions, electronic localization and bonding properties for correlated materials beyond the Kohn-Sham formalism. arXiv 2020, arXiv:2010.04694. [Google Scholar]
- Bruno, G.; Macetti, G.; Presti, L.L.; Gatti, C. Spin Density Topology. Molecules 2020, 25, 3537. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
