Optimum Design of Flexural Strength and Stiffness for Reinforced Concrete Beams Using Machine Learning
Abstract
:1. Introduction
2. Response Surface Model
3. Dataset
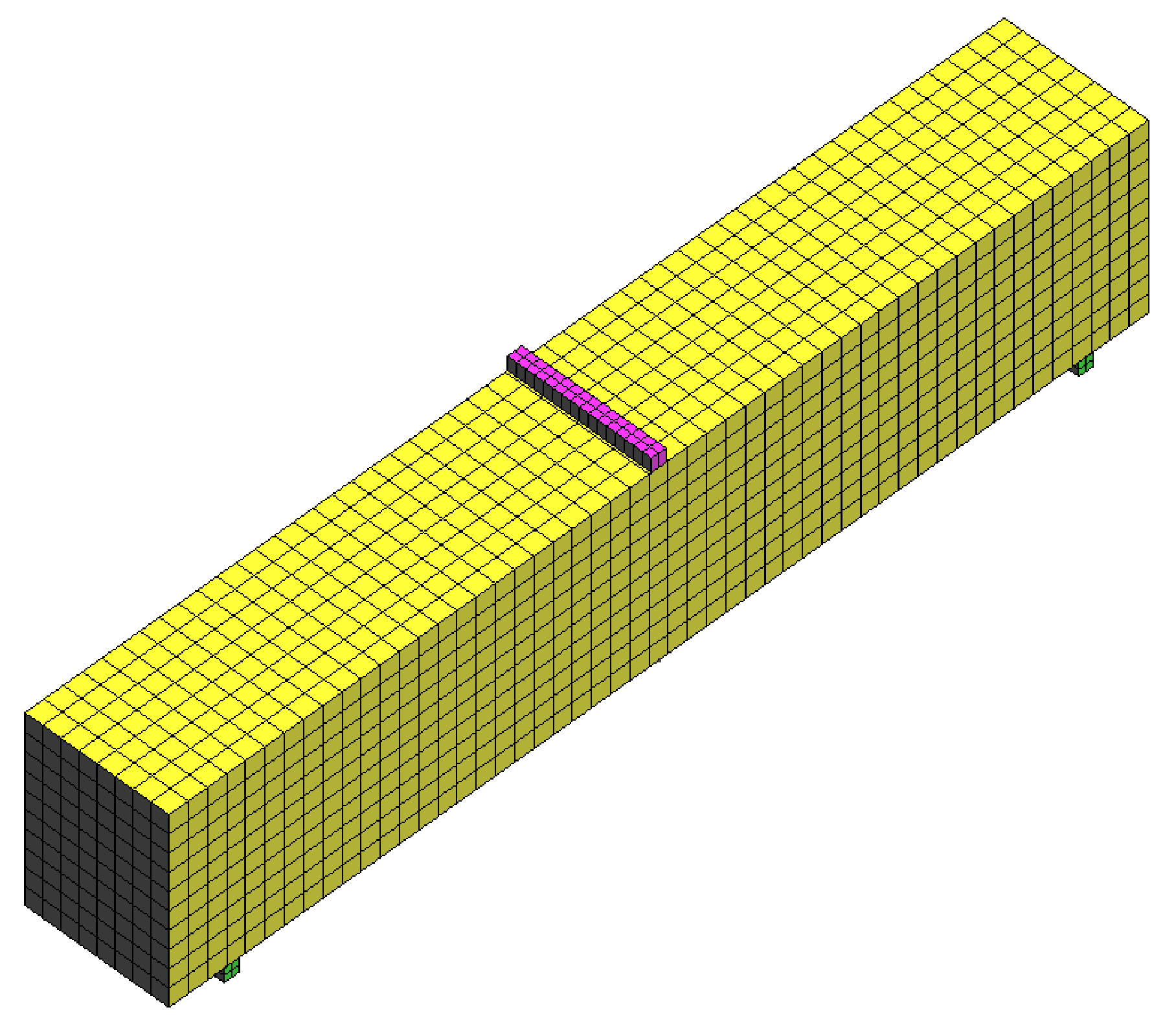
4. Finite Element Models
5. Surrogate Models
5.1. Flexural Stress
5.2. Maximum Deflection
5.3. Regression Analysis
5.3.1. Flexural Stress
5.3.2. Maximum Deflection
6. Optimization Results
6.1. Flexural Stress
6.2. Maximum Deflection
7. Conclusions
- The Box-Behnken design method manifested excellent strength in building the surrogate models to predict the responses of the structural system under loading and, as a result, a more efficient, safer, and lower-cost design.
- The numerical models generated in the ATENA program showed a good agreement with the experimental tests, where the results were very similar and very satisfactory. In addition, numerical models can be adopted to predict and optimize the design of the reinforced concrete beams for flexure and ductility.
- The optimization process produced minimum and maximum responses based on the factorial method of the predicted responses of the flexural strength and the stiffness from the surrogate models.
Author Contributions
Funding
Conflicts of Interest
References
- Rao, G.A.; Vijayanand, I.; Eligehausen, R. Studies on ductility and evaluation of minimum flexural reinforcement in RC beams. Mater. Struct. 2007, 41, 759–771. [Google Scholar] [CrossRef]
- Whitney, C.S. Design of Reinforced Concrete Members under Flexure or Combined Flexural and Direct Compression. J. Proc. 1937, 33, 483–498. [Google Scholar]
- Hognestad, E.; Hanson, N.W.; McHenry, D. Concrete stress distribution in ultimate strength design. ACI J. 1955, 52, 455–480. [Google Scholar]
- Mattock, A.; Kriz, L.; Hognestad, E. Rectangular concrete stress distribution in ultimate strength design. ACI J. 1961, 57, 875–928. [Google Scholar]
- Metwally, I.M. Can Different Design Codes Give the Accurate Prediction of Moment Capacities of High-Strength Concrete Members? In Proceedings of the International Conference on Sustainable Design and Construction (ICSDC), Kansas City, MO, USA, 23–25 March 2011; pp. 497–506. [Google Scholar]
- Pam, H.J.; Kwan, A.K.; Islam, M.S. Flexural Strength and Ductility of reinforced Normal and High-Strength Concrete Beams. Struct. Build. 2001, 146, 381–389. [Google Scholar] [CrossRef]
- Bernardo, L.F.A.; Lopes, S.M.R. Neutral Axis Depth versus Flexural Ductility in High-Strength Concrete Beams. J. Struct. Eng. 2004, 130, 452–459. [Google Scholar] [CrossRef]
- Sarkar, S.; Adwan, O.; Munday, J.G. High Strength Concrete: An Investigation of the flexural Behavior of High Strength RC Beams. Struct. Eng. 1997, 75, 115–121. [Google Scholar]
- Ashour, S.A. Effect of compressive strength and tensile reinforcement ratio on flexural behavior of high-strength concrete beams. Eng. Struct. 2000, 22, 413–423. [Google Scholar] [CrossRef]
- Neville, A.M. Properties of Concrete; Longman: London, UK, 1995; Volume 4. [Google Scholar]
- Hamdia, K.; Arafa, M.; Alqedra, M. Structural damage assessment criteria for reinforced concrete buildings by using a Fuzzy Analytic Hierarchy process. Undergr. Space 2018, 3, 243–249. [Google Scholar] [CrossRef]
- Bae, B.-I.; Choi, H.-K.; Choi, C.-S. Flexural Strength Evaluation of Reinforced Concrete Members with Ultra High Performance Concrete. Adv. Mater. Sci. Eng. 2016, 2016, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Namdar, A.; Darvishi, E.; Feng, X.; Zakaria, I.; Yahaya, F.M. Effect of flexural crack on plain concrete beam failure mechanism A numerical simulation. Frat. Integrità Strutt. 2016, 10, 168–181. [Google Scholar] [CrossRef] [Green Version]
- Nariman, A.N.; Mohammed, I.I.; Othman, K.; Dilshad, D.; Khidr, I. Analysis of stiffness and flexural strength of a reinforced concrete beam using an invented reinforcement system. Front. Struct. Civ. Eng. 2021, 15, 378–389. [Google Scholar] [CrossRef]
- Shishegaran, A.; Ghasemi, M.R.; Varaee, H. Performance of a novel bent-up bars system not interacting with concrete. Front. Struct. Civ. Eng. 2019, 13, 1301–1315. [Google Scholar] [CrossRef]
- Al-Kamal, M.K. Nominal flexural strength of high-strength concrete beams. Adv. Concr. Constr. 2019, 7, 1–9. [Google Scholar]
- Ghasemi, M.R.; Shishegaran, A. Role of slanted reinforcement on bending capacity SS beams. Vibroengineering Procedia 2017, 11, 195–199. [Google Scholar]
- Baran, E.; Arsava, T. Flexural Strength Design Criteria for Concrete Beams Reinforced with High-Strength Steel Strands. Adv. Struct. Eng. 2012, 15, 1781–1792. [Google Scholar] [CrossRef]
- Zhou, K.; Ho, J.; Su, R. Flexural Strength and Deformability Design of Reinforced Concrete Beams. Procedia Eng. 2011, 14, 1399–1407. [Google Scholar] [CrossRef] [Green Version]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: New York, NY, USA, 1995; pp. 134–174. [Google Scholar]
- Kwak, J.-S. Application of Taguchi and response surface methodologies for geometric error in surface grinding process. Int. J. Mach. Tools Manuf. 2005, 45, 327–334. [Google Scholar] [CrossRef]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 128–149. [Google Scholar]
- Amenaghawon, N.A.; Nwaru, K.I.; Aisien, F.A.; Ogbeide, S.E.; Okieimen, C.O. Application of Box-Behnken Design for the Optimization of Citric Acid Production from Corn Starch Using Aspergillus niger. Br. Biotechnol. J. 2013, 3, 236–245. [Google Scholar] [CrossRef]
- Pasma, S.A.; Daik, R.; Maskat, M.Y.; Hassan, O. Application of Box-Behnken Design in Optimization of Glucose Production from Oil Palm Empty Fruit Bunch Cellulose. Int. J. Polym. Sci. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Qiu, P.; Cui, M.; Kang, K.; Park, B.; Son, Y.; Khim, E.; Jang, M.; Khim, J. Application of Box-Behnken design with response surface methodology for modeling and optimizing ultrasonic oxidation of arsenite with H2O2. Open Chem. 2014, 12, 164–172. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Rabczuk, T. Key Parameters for Fracture Toughness of Particle/Polymer Nanocomposites; Sensitivity Analysis via XFEM Modeling Approach. In Proceedings of the 7th International Conference on Fracture Fatigue and Wear, Ghent University, Ghent, Belgium, 9–10 July 2019; pp. 41–51. [Google Scholar] [CrossRef]








| Parameter | Symbol | Minimum Value | Middle Value | Maximum Value |
|---|---|---|---|---|
| Compression Area of Steel (mm2) | 157.00 | 235.50 | 314.00 | |
| Tension Area of Steel (mm2) | 157.00 | 235.50 | 314.00 | |
| Shear Area of Steel (mm2) | 169.56 | 197.82 | 226.08 |
| Model | Area of Compression Steel Bars (mm2) | Area of Tension Steel Bars (mm2) | Area of Shear Steel Bars (mm2) |
|---|---|---|---|
| 1 | 157.00 | 157.00 | 197.82 |
| 2 | 157.00 | 314.00 | 197.82 |
| 3 | 314.00 | 157.00 | 197.82 |
| 4 | 314.00 | 314.00 | 197.82 |
| 5 | 157.00 | 235.50 | 169.56 |
| 6 | 157.00 | 235.50 | 226.08 |
| 7 | 314.00 | 235.50 | 169.56 |
| 8 | 314.00 | 235.50 | 226.08 |
| 9 | 235.50 | 157.00 | 169.56 |
| 10 | 235.50 | 157.00 | 226.08 |
| 11 | 235.50 | 314.00 | 169.56 |
| 12 | 235.50 | 314.00 | 226.08 |
| 13 | 235.50 | 235.50 | 197.82 |
| 14 | 235.50 | 235.50 | 197.82 |
| 15 | 235.50 | 235.50 | 197.82 |
| Cylinder Specimen | Maximum Compression Load (kN) | Cylinder Specimen | Maximum Tensile Load (kN) |
|---|---|---|---|
| C1 | 101.74 | T1 | 85.90 |
| C2 | 88.45 | T2 | 66.20 |
| C3 | 99.08 | T3 | 100.19 |
| Model | Maximum Flexure Load (kN) | Slope | Flexural Strain(mm/mm) | Young’s Modulus (N/mm2) | Maximum Deflection (mm) | Flexural Stress (MPa) |
|---|---|---|---|---|---|---|
| 1 | 77.240 | 0.7140 | 0.1639 | 104.860 | 4.430 | 17.190 |
| 2 | 94.680 | 0.8330 | 0.1722 | 122.340 | 5.68 | 21.070 |
| 3 | 79.320 | 0.7050 | 0.1704 | 103.540 | 5.62 | 17.650 |
| 4 | 97.040 | 0.7770 | 0.1892 | 114.120 | 6.24 | 21.590 |
| 5 | 79.260 | 0.7400 | 0.1623 | 108.680 | 5.35 | 17.640 |
| 6 | 97.900 | 0.8800 | 0.1685 | 129.240 | 5.56 | 21.780 |
| 7 | 91.900 | 0.8180 | 0.1702 | 120.140 | 5.61 | 20.450 |
| 8 | 93.560 | 0.7610 | 0.1862 | 111.770 | 6.10 | 20.820 |
| 9 | 78.750 | 0.9000 | 0.1326 | 132.180 | 4.37 | 17.520 |
| 10 | 75.240 | 0.4666 | 0.2442 | 68.530 | 8.06 | 16.740 |
| 11 | 97.380 | 0.4440 | 0.3323 | 65.210 | 10.96 | 21.670 |
| 12 | 107.700 | 0.6110 | 0.2670 | 89.740 | 8.81 | 23.960 |
| 13 | 93.930 | 0.6660 | 0.2137 | 97.810 | 7.05 | 20.900 |
| Model | Flexural Stress ATENA (MPa) | Flexural Stress Experiment (MPa) | Error % |
|---|---|---|---|
| 1 | 17.15611696 | 17.185900 | 0.17 |
| 2 | 21.09721253 | 21.066300 | 0.15 |
| 3 | 17.15664377 | 17.648700 | 2.79 |
| 4 | 21.59387950 | 21.591400 | 0.01 |
| 5 | 17.95554714 | 17.635350 | 1.82 |
| 6 | 21.44176454 | 21.782750 | 1.57 |
| 7 | 20.31767836 | 20.447750 | 0.64 |
| 8 | 20.70511776 | 20.817100 | 0.54 |
| 9 | 17.09409603 | 17.521875 | 2.44 |
| 10 | 16.33360424 | 16.740900 | 2.43 |
| 11 | 21.15750459 | 21.667050 | 2.35 |
| 12 | 24.50759912 | 23.963250 | 2.27 |
| 13 | 20.92028772 | 20.899425 | 0.10 |
| Model | Max. Deflection ATENA (mm) | Max. Deflection Experiment (mm) | Error % |
|---|---|---|---|
| 1 | 4.48 | 4.43 | 1.12 |
| 2 | 5.48 | 5.68 | 3.65 |
| 3 | 5.42 | 5.62 | 3.69 |
| 4 | 6.12 | 6.24 | 1.96 |
| 5 | 5.27 | 5.35 | 1.52 |
| 6 | 5.51 | 5.56 | 0.91 |
| 7 | 5.56 | 5.61 | 0.90 |
| 8 | 6.02 | 6.1 | 1.33 |
| 9 | 4.29 | 4.37 | 1.86 |
| 10 | 7.98 | 8.06 | 1.00 |
| 11 | 10.85 | 10.96 | 1.01 |
| 12 | 8.76 | 8.81 | 0.57 |
| 13 | 6.94 | 7.05 | 1.59 |
| Model | Constant | X1 | X2 | X3 | X1X1 | X2X2 | X3X3 |
|---|---|---|---|---|---|---|---|
| 1 | 1.00 | 157.00 | 157.00 | 197.82 | 24,649.00 | 24,649.00 | 39,132.75 |
| 2 | 1.00 | 157.00 | 314.00 | 197.82 | 24,649.00 | 98,596.00 | 39,132.75 |
| 3 | 1.00 | 314.00 | 157.00 | 197.82 | 98,596.00 | 24,649.00 | 39,132.75 |
| 4 | 1.00 | 314.00 | 314.00 | 197.82 | 98,596.00 | 98,596.00 | 39,132.75 |
| 5 | 1.00 | 157.00 | 235.50 | 169.56 | 24,649.00 | 55,460.25 | 28,750.59 |
| 6 | 1.00 | 157.00 | 235.50 | 226.08 | 24,649.00 | 55,460.25 | 51,112.17 |
| 7 | 1.00 | 314.00 | 235.50 | 169.56 | 98,596.00 | 55,460.25 | 28,750.59 |
| 8 | 1.00 | 314.00 | 235.50 | 226.08 | 98,596.00 | 55,460.25 | 51,112.17 |
| 9 | 1.00 | 235.50 | 157.00 | 169.56 | 55,460.25 | 24,649.00 | 28,750.59 |
| 10 | 1.00 | 235.50 | 157.00 | 226.08 | 55,460.25 | 24,649.00 | 51,112.17 |
| 11 | 1.00 | 235.50 | 314.00 | 169.56 | 55,460.25 | 98,596.00 | 28,750.59 |
| 12 | 1.00 | 235.50 | 314.00 | 226.08 | 55,460.25 | 98,596.00 | 51,112.17 |
| 13 | 1.00 | 235.50 | 235.50 | 197.82 | 55,460.25 | 55,460.25 | 39,132.75 |
| 14 | 1.00 | 235.50 | 235.50 | 197.82 | 55,460.25 | 55,460.25 | 39,132.75 |
| 15 | 1.00 | 235.50 | 235.50 | 197.82 | 55,460.25 | 55,460.25 | 39,132.75 |
| Model | X1X2 | X1X3 | X2X3 |
|---|---|---|---|
| 1 | 24,649.00 | 31,057.74 | 31,057.74 |
| 2 | 49,298.00 | 31,057.74 | 62,115.48 |
| 3 | 49,298.00 | 62,115.48 | 31,057.74 |
| 4 | 98,596.00 | 62,115.48 | 62,115.48 |
| 5 | 36,973.50 | 26,620.92 | 39,931.38 |
| 6 | 36,973.50 | 35,494.56 | 53,241.84 |
| 7 | 73,947.00 | 53,241.84 | 39,931.38 |
| 8 | 73,947.00 | 70,989.12 | 53,241.84 |
| 9 | 36,973.50 | 39,931.38 | 26,620.92 |
| 10 | 36,973.50 | 53,241.84 | 35,494.56 |
| 11 | 73,947.00 | 39,931.38 | 53,241.84 |
| 12 | 73,947.00 | 53,241.84 | 70,989.12 |
| 13 | 55,460.25 | 46,586.61 | 46,586.61 |
| 14 | 55,460.25 | 46,586.61 | 46,586.61 |
| 15 | 55,460.25 | 46,586.61 | 46,586.61 |
| Coefficient | Value (10−6) |
|---|---|
| −13.075 | |
| 138.61 × 10−3 | |
| 27.47 × 10−3 | |
| 77.41 × 10−3 | |
| −0.11 × 10−3 | |
| −0.14 × 10−3 | |
| −81.39 × 10−6 | |
| 2.43 × 10−6 | |
| −0.42 × 10−3 | |
| 0.35 × 10−3 |
| Coefficient | Value |
|---|---|
| −15.464 | |
| 154.89 × 10−3 | |
| 118.87 × 10−3 | |
| −130.48 × 10−3 | |
| −0.32 × 10−3 | |
| 67.95 × 10−6 | |
| 0.73 × 10−3 | |
| −25.56 × 10−6 | |
| 31.55 × 10−6 | |
| −0. 66 × 10−3 |
| Model | X1 (mm2) | X2 (mm2) | X3 (mm2) | |
|---|---|---|---|---|
| 1 | 157.00 | 157.00 | 169.56 | 15.645 |
| 2 | 157.00 | 157.00 | 197.82 | 16.638 |
| 3 | 157.00 | 157.00 | 226.08 | 17.500 |
| 4 | 157.00 | 235.50 | 169.56 | 18.124 |
| 5 | 157.00 | 314.00 | 169.56 | 18.878 |
| 6 | 235.50 | 157.00 | 169.56 | 17.589 |
| 7 | 314.00 | 157.00 | 169.56 | 18.207 |
| 8 | 314.00 | 235.50 | 169.56 | 20.716 |
| 9 | 314.00 | 235.50 | 197.82 | 20.591 |
| 10 | 314.00 | 235.50 | 226.08 | 20.336 |
| 11 | 235.50 | 314.00 | 169.56 | 20.851 |
| 12 | 235.50 | 314.00 | 197.82 | 22.436 |
| 13 | 235.50 | 314.00 | 226.08 | 23.891 |
| 14 | 235.50 | 235.50 | 169.56 | 20.083 |
| 15 | 235.50 | 235.50 | 197.82 | 20.900 |
| 16 | 235.50 | 235.50 | 226.08 | 21.588 |
| 17 | 314.00 | 314.00 | 169.56 | 21.500 |
| 18 | 314.00 | 314.00 | 197.82 | 22.143 |
| 19 | 314.00 | 314.00 | 226.08 | 22.655 |
| 20 | 235.50 | 157.00 | 197.82 | 17.639 |
| 21 | 314.00 | 157.00 | 197.82 | 17.315 |
| 22 | 157.00 | 314.00 | 197.82 | 21.405 |
| 23 | 157.00 | 314.00 | 226.08 | 23.803 |
| 24 | 235.50 | 157.00 | 226.08 | 17.559 |
| 25 | 314.00 | 157.00 | 226.08 | 16.293 |
| 26 | 157.00 | 235.50 | 197.82 | 19.883 |
| 27 | 157.00 | 235.50 | 226.08 | 21.514 |
| Model | X1 (mm2) | X2 (mm2) | X3 (mm2) | δmax (mm) |
|---|---|---|---|---|
| 1 | 157.00 | 157.00 | 169.56 | 2.776250 |
| 2 | 157.00 | 157.00 | 197.82 | 3.865000 |
| 3 | 157.00 | 157.00 | 226.08 | 6.116250 |
| 4 | 157.00 | 235.50 | 169.56 | 5.126250 |
| 5 | 157.00 | 314.00 | 169.56 | 8.313750 |
| 6 | 235.50 | 157.00 | 169.56 | 5.158750 |
| 7 | 314.00 | 157.00 | 169.56 | 3.588750 |
| 8 | 314.00 | 235.50 | 169.56 | 5.623750 |
| 9 | 314.00 | 235.50 | 197.82 | 5.392500 |
| 10 | 314.00 | 235.50 | 226.08 | 6.323750 |
| 11 | 235.50 | 314.00 | 169.56 | 10.381250 |
| 12 | 235.50 | 314.00 | 197.82 | 8.620000 |
| 13 | 235.50 | 314.00 | 226.08 | 8.021250 |
| 14 | 235.50 | 235.50 | 169.56 | 7.351250 |
| 15 | 235.50 | 235.50 | 197.82 | 7.050000 |
| 16 | 235.50 | 235.50 | 226.08 | 7.911250 |
| 17 | 314.00 | 314.00 | 169.56 | 8.496250 |
| 18 | 314.00 | 314.00 | 197.82 | 6.805000 |
| 19 | 314.00 | 314.00 | 226.08 | 6.276250 |
| 20 | 235.50 | 157.00 | 197.82 | 6.317500 |
| 21 | 314.00 | 157.00 | 197.82 | 4.817500 |
| 22 | 157.00 | 314.00 | 197.82 | 6.482500 |
| 23 | 157.00 | 314.00 | 226.08 | 5.813750 |
| 24 | 235.50 | 157.00 | 226.08 | 8.638750 |
| 25 | 314.00 | 157.00 | 226.08 | 7.208750 |
| 26 | 157.00 | 235.50 | 197.82 | 4.755000 |
| 27 | 157.00 | 235.50 | 226.08 | 5.546250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nariman, N.A.; Hamdia, K.; Ramadan, A.M.; Sadaghian, H. Optimum Design of Flexural Strength and Stiffness for Reinforced Concrete Beams Using Machine Learning. Appl. Sci. 2021, 11, 8762. https://doi.org/10.3390/app11188762
Nariman NA, Hamdia K, Ramadan AM, Sadaghian H. Optimum Design of Flexural Strength and Stiffness for Reinforced Concrete Beams Using Machine Learning. Applied Sciences. 2021; 11(18):8762. https://doi.org/10.3390/app11188762
Chicago/Turabian StyleNariman, Nazim Abdul, Khader Hamdia, Ayad Mohammad Ramadan, and Hamed Sadaghian. 2021. "Optimum Design of Flexural Strength and Stiffness for Reinforced Concrete Beams Using Machine Learning" Applied Sciences 11, no. 18: 8762. https://doi.org/10.3390/app11188762
APA StyleNariman, N. A., Hamdia, K., Ramadan, A. M., & Sadaghian, H. (2021). Optimum Design of Flexural Strength and Stiffness for Reinforced Concrete Beams Using Machine Learning. Applied Sciences, 11(18), 8762. https://doi.org/10.3390/app11188762







