Abstract
In this work, a mechanical vibrational analysis of an ultrasonic atomizer is carried out to control its atomization mass transfer rate. An ultrasonic atomizer is a device constructed with a piezoelectric ring coupled to a metallic circular thin plate with micro-apertures. The mechanism of mass transfer by atomization is a complex phenomenon to model because of the coupling effect between the fluid transfer and dynamic mechanics controlled by a piezoelectric vibrating ring element. Here, the effect of the micro-apertures shape of the meshed thin plate coupled to a piezoelectric ring during vibration, as well as the resonance frequency modes, are numerically studied using a finite element analysis and compared with theoretical and experimental results. Good correlations between the predicted and experimental results of the resonant frequencies and atomization rates were found.
1. Introduction
Piezoelectric materials (such as lead zirconate titanate (PZT) transducers) have found broad applications in areas such as elastic vibration sensing [1], force sensing in robotics [2], ultrasonic measurements of airflow in ducts [3], and ultrasonic cleaning in energy harvesting technologies, among others. Piezoelectric materials continue to be studied to achieve better performances with lower costs and low energy requirements [4]. Important uses of piezoelectric devices include an ultrasonic atomizer for medical inhalation therapy, combustion with liquid fluids, and printed circuits, among others, where the actuator converts a liquid to atomized particles [5].
In particular, an ultrasonic atomization device is composed of a piezoelectric ceramic and a metal cover plate. It uses the piezoelectric effect and converts electrical energy into mechanical energy at a high-frequency resonance, causing the breakup of the liquid structure [6,7,8].
More recently, ultrasonic atomizers are being considered as replacements for pneumatic pumps for soft robotics actuation through atomization and vaporization [9]. Soft robots have recently received attention due to its flexible adaptability and the low risk of damaging the work environment and the objects they handle. Many soft robots require small external compressors or pumps for driving the actuator. Actuator miniaturization could be achieved with the use of an ultrasonic atomizer. For example, Lee and Loh [10] proposed a soft inflatable one-DOF (degree of freedom) robot. It has a soft bellows structure that includes a lower chamber with an embedded ultrasonic atomizer of only 15 mm in diameter and a heater to evaporate the atomized liquid and to control the vertical displacement of the soft robot. In this system, the modes of vibration and resonance frequencies have a direct effect on the displacement and actuation speed. Thus, there is a need to develop a more comprehensive vibration analysis and mesh properties to have an optimum control of the soft robot compliance control.
Tuning of the frequency and vibration parameters is a main objective in the design and optimization of an ultrasonic transducer. There are conventional methods to calculate the modes in the free vibration of a plate, but they are limited to plates that have a continuous homogenous structure without changes in the cross-section. Additionally, there are methods to numerically approximate the modes of a vibration, for example, using the plane wave expansion method [11]; however, it can be computationally complex for inhomogeneous models. In addition, the coupling effect of piezoelectric energy with mechanical energy needs to be considered, making the theoretical analysis and its general solution difficult to obtain. With the increase in the computational capacity, numerical approximations of the piezoelectric phenomena can be studied using finite element (FE) methods.
A typical structure of an ultrasonic atomizer is described in Figure 1. A main component of the system is the mesh (i.e., light gray section), which is formed by a thin plate with a thickness of 50 μm and micro-perforations. The holes are distributed within a circular area with a diameter . The ring is the piezoelectric actuator (e.g., PZT) with a thickness of about 0.6 mm. A potential difference (voltage) is applied to the piezoelectric ring across the thickness using a signal generator. and are the inner and outer diameters of the piezoelectric ring, respectively, and is the diameter of the disperser or mesh.
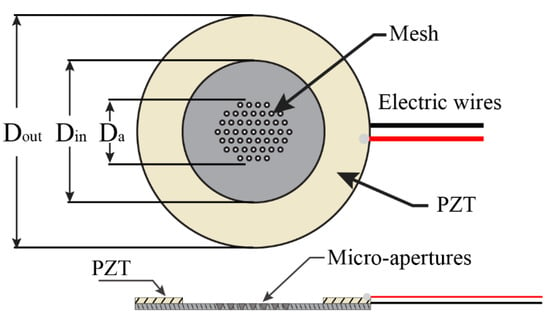
Figure 1.
Schematic diagram of a typical ultrasonic atomizer device indicating the location mesh and its micro-aperture distribution.
The objectives of this work are to first characterize the dynamic behavior of the complete piezoelectric ring and meshed thin plate using FE modeling. Second, the effect of the shape of the micro-apertures on the resonant frequency spectra of the vibrating thin plate is investigated. Last, the numerical simulation results of the atomization rate as a function of the frequency response and voltage are verified using experimental tests. The proposed parametric results could allow to predict and control the atomization rate that can be used to improve the performance of a soft actuation robot.
2. Ultrasonic Atomizer Fundamentals
An ultrasonic atomizer features a thin plate with micro-apertures (mesh) that is coupled to a vibrating PZT at the interface between two media. The first is the external medium, where the plate is in contact with the atmosphere, while the second is internal and is the chamber in which the liquid is contained. When the device is in operation, the mesh experiences small and periodic mechanical deformations. This periodic movement releases energy into the liquid in contact, which breaks the surface tension of the liquid and produces droplets that are ejected, thereby producing atomization. A pumping effect is achieved when the liquid ejects through the apertures to produce a homogeneous size of droplets and making the atomization process more controllable [12]. A mechanical model to explain atomization should consider the dynamic deformation of the structure (i.e., PZT ring and mesh) as a function of the applied voltage and frequency. Here, we first analyzed the piezoelectric mechanical phenomena before coupling them to a meshed thin plate.
2.1. Piezoelectricity Theory
Piezoelectric materials are a type of dielectric materials that can be polarized, and they respond in the presence of an electric field or mechanical stress. The piezoelectric effect is the generation of an electric charge due to an external force. Initially, the molecules of negative and positive charges are positioned so that the overall material is electrically neutral. However, when an external mechanical stress is applied, the internal structure can be deformed, thus causing displacement of the positive and negative centers of the molecule. As a result, small electrical dipoles are generated.
According to the linear theory of piezoelectricity [13], the linear constitutive relationship to identify the coupling between mechanical stress, mechanical strain, electric field, and electric displacement is given as:
where the superscript indicates that the values are measured at a constant strain, and the superscript means that they are measured at a constant electric field. In addition, is the stress tensor, is the electric displacement vector, is the strain tensor, is the electric field, is the elastic constant at a constant electric field, is the piezoelectric stress coefficients, and is the dielectric tensor at a constant mechanical strain. The conventional polarized ferroelectric ceramics used in ultrasonic transducers are governed by the constitutive expressions given in Equations (1) and (2) and by the equations of mechanical and electrical balance, respectively, such as:
To complete the description of the problem, the equations mentioned above are complemented by the appropriate boundary conditions. The behavior of the PZT controls the vibration modes of the thin plate, and these deformations give rise to the atomization process [14]. There are three different vibration modes in a piezoelectric hollow disc (ring) polarized in the thickness direction, which are thicknesses where the displacements of the upper and lower surfaces are in the opposite phase, radial where the inner and outer walls of the ring vibrate in the phase, and wall thickness direction where the inner and outer walls of the ring vibrate in the opposite phase. Since the outer radius is larger than the thickness in a thin ring, radial motion is induced due to Poisson’s ratio. Therefore, the first modes are radial modes governed by radial boundary conditions. In this vibration mode, the inner and outer surfaces of the ring vibrate in the phase, and this movement is transmitted to the thin plate [15,16].
2.2. Approximate Plate Theory
It has been demonstrated that the mechanical vibrating characteristics of the meshed circular thin plate in an ultrasonic atomizer controls the rate atomization [17]. There are two kind of vibrations that can be used to study the mechanical behavior of a homogeneous circular thin plate—namely, free and forced vibrations. In the case of the atomizer, the theoretical study is focused on a circular thin plate clamped on its edge. The analytical solution using the plate theory gives natural frequencies [18]:
where is the radius of a circular plate with thickness , is the density, is the Young’s modulus, is the Poisson’s ratio, and is a constant that depends on the number of nodal diameters (diameter lines that remain without displacement ) and the number of nodal circles (concentric circumferences without displacement ).
Figure 2 shows the behavior of the natural frequencies as a function of the thickness of the plate, as well as the elasticity modulus, respectively, for these modes. The frequency dependence on the thickness is linear, while a nonlinear behavior is observed as a function of the elastic modulus. It is expected that the addition of the micro-apertures to a homogeneous plate can have an inverse effect on the elastic modulus according to the rule of mixtures [19]. Using the volume fraction of the openings, the results show a decrease in the effective elastic modulus as a function of the size of the micro-openings affecting the dynamic response of the system. Therefore, a more complete dynamic and mechanical model of the atomizer should include the aperture shape and distribution of micro holes on the meshed thin plate.
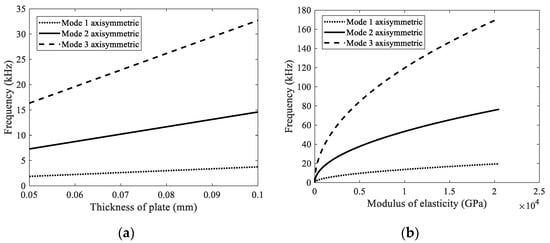
Figure 2.
Frequencies calculated as a function of (a) the plate thickness and (b) Young’s modulus for the first three axisymmetric modes.
However, including these variables makes the system too complex to be easily calculated through analytical methods. Thus, an FE model might provide a better approximation to understand the mechanical behavior of the atomizer and its effect on the atomization rate.
3. Finite Element Analysis
The dynamic performance of the piezoelectric atomizer and its vibration optimization were studied using a FE analysis. The device was considered as a multi-degree-of-freedom continuum system, which can be represented in a matrix notation as [6]:
where and represent the vector of displacement, velocity, and acceleration, respectively, for every node; [M] is the mass matrix; [C] is the damping matrix; [K] is the stiffness matrix; and is the external excitation force. Two types of analyses were performed—namely, free and forced vibrations. The modal (free) analysis is an eigenvalue problem assuming no external forces, . A forced harmonic analysis can also be carried out by applying a frequency sweep for different applied input voltages to the piezoelectric ring.
For the first example, a numerical modal analysis on a stainless-steel circular thin plate was carried out. The mechanical properties of the plate are given in Table 1. In these calculations, 16,746 elements (SOLID186 with 20 nodes that exhibit quadratic displacement in ANSYS) were used. The boundary conditions of the thin plate were clamped at the edge to the piezoelectric ring, as is shown in Figure 3. Thus, the displacements in the circumferential area were assumed to be zero ( at ). The simulation was carried out using an FE model implemented in ANSYS; the pseudocode for the analysis is given in Appendix A. Figure 4 shows the results for the lowest axisymmetric modes when the largest displacement is at the center of the plate. To check the validity of the calculations, Figure 5 shows the first nine resonant frequencies using the modal analysis of a single, clamped, circular, and homogeneous thin plate. These results are compared with the theoretical approximation given by Equation (5). The results shows that the FE analysis only deviated by ~0.12% on average from the theoretical predictions.

Table 1.
Mechanical and geometric parameters of the piezoceramic vibrating mesh atomizer reported in References [6,20].
Figure 3.
Clamped circular plate used for the FEM study.
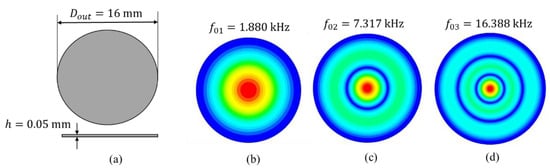
Figure 4.
(a) Geometry used for the FEM modal analysis. (b–d) Contour plots of the first three axisymmetric vibrational modes estimated for the homogeneous thin plate.
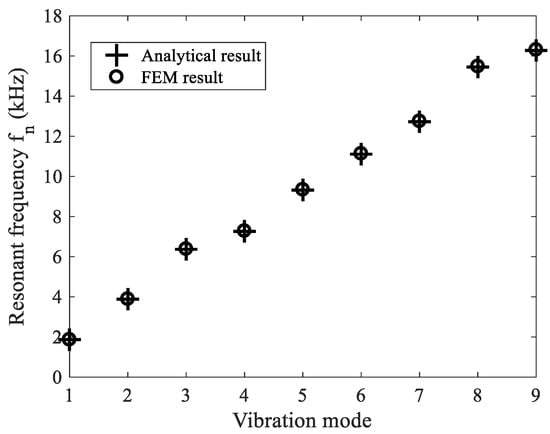
Figure 5.
Comparison between the analytical and FEM results of the resonant frequency of the vibration modes from a clamped circular plate.
The mechanical behavior of the thin plate is expected to be affected by the loading from the liquid that will be atomized. However, the theoretical and experimental results show that the shape of the vibration modes is not modified; that is, the presence of liquid loading only shifts the values of the resonant frequencies with the invariant shapes of the vibration modes [21].
In a preliminary numerical harmonic analysis (see the description of the pseudocode in Appendix A), a stainless-steel circular thin plate coupled to a piezoelectric ring was modeled. The mechanical, piezoelectric, and physical properties of the materials are given in Table 1 and Table 2. The thin plate was modeled as a deformable plate using fully integrated elements with 20 nodes. Due to the symmetry of the model, only a one-quarter model was needed, thus reducing the number of grids and the overall computational demand (see Figure 6) [22].

Table 2.
Piezoelectrical properties of the PZT ring [14].
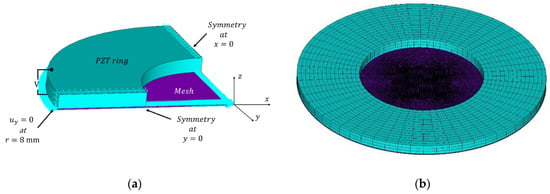
Figure 6.
FEM model showing (a) a sectional view of the atomizer and boundary conditions and (b) mesh of the system.
Next, micro-apertures with three different geometrical shapes: cylindrical, pyramidal, and conical were added to the model of the circular thin plate to form a meshed thin plate (thin-plated with micro-apertures), which was then coupled to the piezoelectric ring. The meshed plate contained 551 micro-apertures with the dimensions shown in Figure 7, where d and . These were distributed over the thin plate following a rectangular array.
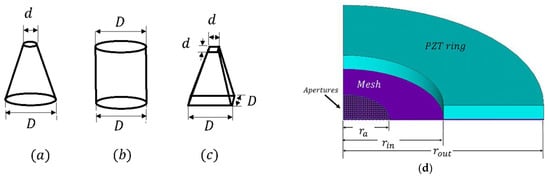
Figure 7.
Geometrical shapes of the micro-apertures of (a) conical, (b) cylindrical, and (c) pyramidal holes. (d) Section view of a solid model of the atomizer disc with micro-apertures on the meshed thin plate.
A forced harmonic analysis with a sinusoidal variation of the voltage was performed on this system as described in Figure 6. The resonant frequencies of the device and the maximum out-of-plane displacements of the mesh were recorded for the three micro-aperture shape geometries. Figure 8 shows a summary of results of the estimated out-of-plane displacement measured at the center of the thin plate against the voltage amplitude applied to the piezoelectric ring when the device was driven at the resonant frequency. The results indicate that the displacement increased linearly with the applied voltage for all three types of aperture shapes. The results show only a small change in the resonance frequency, which seems to be correlated to a loss of density due to the volume removed by micro-apertures in the thin plate, as predicted by the plate theory (Equation (5)). Thus, cylindrical openings with a constant diameter have the largest volume and, also, a resonance frequency, followed by the conical and pyramidal. However, in this work, our focus will be on the conical aperture because of the valveless pumping effect reported in the literature and its better atomization performance [23].
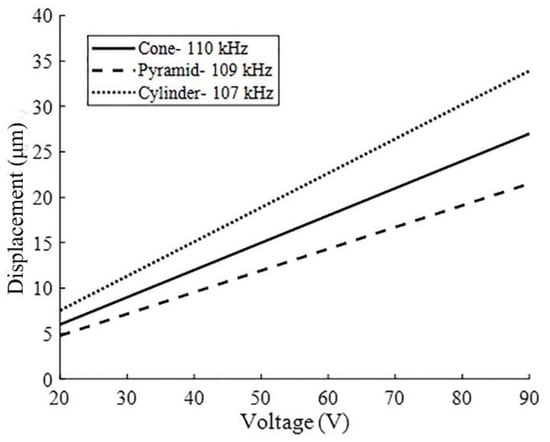
Figure 8.
Displacement against the voltage amplitude.
Table 3 shows the results of FEM analysis with a frequency sweep while applying 80 V to the PZT ring. A cross-section view of the vibration mode shape at the resonance frequency is also shown. These results were obtained using the model of the meshed thin plate with conical shape apertures. The results gave the first five vibration modes. The subscript “s” indicates that the mode was identified as axisymmetric. In all cases, the largest out-of-plane displacements were identified in the center of the meshed thin plate, with a maximum 110-kHz mode found, the value close to those reported for an ultrasonic atomizer, with similar materials reported in Reference [11].

Table 3.
A summary of the first five vibration modes, shapes, and amplitudes calculated with FEA.
Figure 9 provides details of the distribution of the displacement through the disk for the axisymmetric vibration mode obtained at a frequency of 110 kHz and using an applied voltage in the range of to . The location of the largest displacement was around the center of the thin plate where the micro-apertures were located. This value of displacement corresponded to the frequency tuning value, with the best performance of the atomizer found in our experimental results (discussed in the Experimental section). The modeling methodology for the atomizer dynamic performance was then used to study the control of the atomization rate by correlating it to the maximum displacements as a function of frequency and voltage amplitudes.
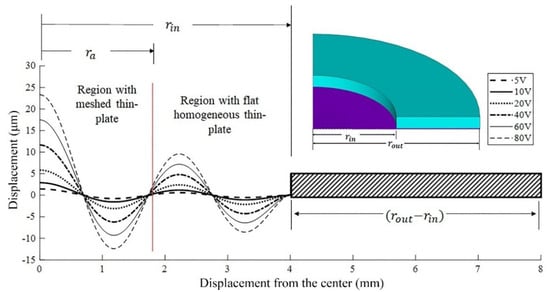
Figure 9.
Distribution of the displacements along the cross-section of the thin plate for the 110 kHz (axisymmetric mode) resonance frequency as a function of the voltage.
4. Model of Atomization Volume Flow
In mesh atomization, the atomizer releases energy into the liquid to break the surface tension and to allow the liquid droplets to escape from the surface. To control the droplet size distribution and to make the atomization process more controllable, micro-apertures are added to form a meshed thin plate driven by a piezoelectric ring. In Maehara et al. [14], the atomizer performance as a function of the number of micro-apertures was studied. A rough approximation of the deformation for the lowest symmetric modes can be found following the thin plate theory [24]. The coordinate system assumes that the neutral surface is in the plane, perpendicular to the -axis. The flow in the micro-tapered aperture is closely connected with the chamber volume change given by the deformation of the thin plate [25].
In Cai et al. [12], the atomization rate was studied, focusing on the effect of the volume change at the liquid chamber (container) due to the deformation of the thin plate during the vibrations at the lowest vibration mode. Additionally, the contribution by the small deformation of the micro-apertures of the mesh during the vibration to the mass flow was studied for that mode. This idea is illustrated in Figure 10, where the conical micro-aperture deforms by the global deformation of the thin plate. During the periodic vibration, any point on the non-neutral surface moves in two possible conditions. First, the point is bent in the upward direction and then is released back to equilibrium, followed by a compressed state to its lower limit and back to equilibrium. This mechanism acts as a micro-pump, promoting the generation of atomized drops [26].
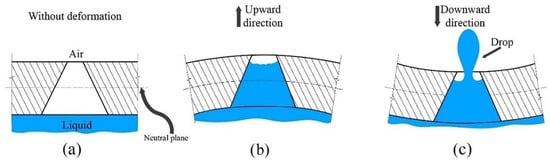
Figure 10.
Dynamic deformation of a micro-aperture with a conical shape, (a) prior to deformation, (b) with deformation in upward direction, and (c) downward direction.
Thus, the total flow could have two contributions—namely, one from the global volume change of the thin plate and another possible from the micro-aperture volume change (, which could then be expressed as:
where is the change in the volume in the micro-aperture during vibration that can be obtained by considering the deformation of the neutral surface and the estimation of a triple integral to calculate the change of volume of the micro-cone aperture. is the corresponding change in volume in the chamber created by the thin plate vibration, is the oscillation frequency of the plate, and is a pressure loss coefficient described below. The volume of the atomized liquid displaced by the mechanical oscillation of the plate for the lowest vibration mode is given by Reference [12]:
where is the radius of the plate, and is the thickness of the thin plate. However, since the vibrational modes studied in this work are of a higher order, there is a nonhomogeneous displacement distribution across the radius. In this case, numerical integration techniques were used to approximate the displaced volume, as will be described later. The effective pressure loss coefficient, , is expressed as:
where is the pressure loss coefficient related to the diffuser effect, and is related to the nozzle effect. To relate the volume changes to the mass flow, it is necessary to consider the resistance of the flow through the conical aperture. In a dynamic cycle, the cone aperture acts as nozzle or as diffuser, and the difference between the two flow resistances determines the flow rate. In Zhang et al. [23], the empirical curves of the cone angle against the diffuser and nozzle pressure loss coefficients on a macroscopic level are given. The pressure loss coefficient is a dimensionless number to characterize the pressure loss in a hydraulic system, which involves pressure loss by friction and by changes in the aperture geometry. In our case, the micro-apertures have a half angle of 35°, which, from the tables reported by Q. Yan et al. [27], give a loss factor of and when the cone acts as diffuser and as the nozzle, respectively. An equation for the net volume flow rate when the throat of the tapered aperture is exposed to the air and the flared side is in contact with the liquid was also reported by Q. Yan et al. [27]. The equation involves the change in volume of the apertures and the change in volume of the liquid chamber, where is the number of apertures, and is the vibration frequency of the PZT.
5. Experimental Setup
A commercial vibrating mesh atomizer was used for the experiments. The physical properties of the atomizer device are described in Table 4. The mesh atomizer consists of a piezoelectric ring and a thin metal plate meshed with conical holes. The atomizer was positioned so that the bottom layer of the mesh was in contact with the liquid stored in a small container. As the ring vibrated, small droplets were ejected into the air through the meshed thin plate.

Table 4.
Atomizer physical properties.
The experimental setup to measure the atomization rate is shown in Figure 11. The AC voltage was produced with a power amplifier (Electronics & Innovation, Ltd., model 500S06, Rochester, NY, USA), which was used to modulate the amplitude of the atomizer vibrations. To find the resonant frequency, a signal generator (Keysight, model 33210A, Santa Rosa, CA, USA) with a frequency sweep modulation in the range from 1 to 150 kHz was used. The atomizer was placed on the surface of water inside a plastic petri dish. This petri dish was placed above a scale (Mettler Toledo, model ME204E, Columbus, OH, USA) to measure the weight loss over time. The weight was measured every 5 s for 60 s to calculate the average of the atomization rate.
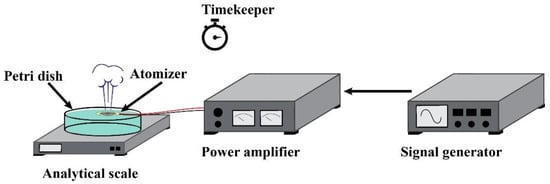
Figure 11.
Scheme of the atomization rate measurements.
6. Results and Discussion
Numerical FEM simulations of the atomizer were performed, and the vibration modes and the resonant frequencies were determined using a forced harmonic analysis (as described in Appendix A). In particular, a numerical frequency sweep of the system using the physical properties described in Table 4 was carried out, and the mesh atomizer surface displacements with conical apertures corresponding to different frequencies were estimated and plotted in Figure 12. The first five resonant frequencies were estimated, and after a further analysis, the vibrational modes with the largest out-of-plane displacements were located at two resonance frequencies of about 110 kHz () and 140 kHz ().
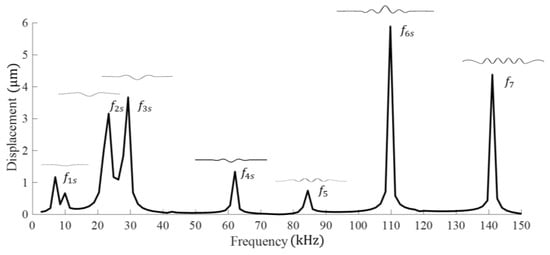
Figure 12.
Numerical results of the frequency sweep for 20 V obtained by FEM. A schematic of the frequency mode cross-section is shown above every detected frequency.
In Figure 13, the numerical simulation findings (line plots) at various voltage levels (20–80 V) are compared with the experimental results of the atomization rate obtained by a frequency sweep over the range from 100 kHz to 150 kHz. The small discrepancies were expected, as the PZT ring was bonded to the metal mesh using epoxy and the wires were soldered to the system. Overall, the peak atomization rates matched closely with the resonant frequencies from the numerical simulations, with the maxima occurring at frequencies around 110 kHz and 141 kHz. From these results, it is possible to observe that the resonance frequency is not altered with the voltage change; only the amplitude of the central displacement is affected.
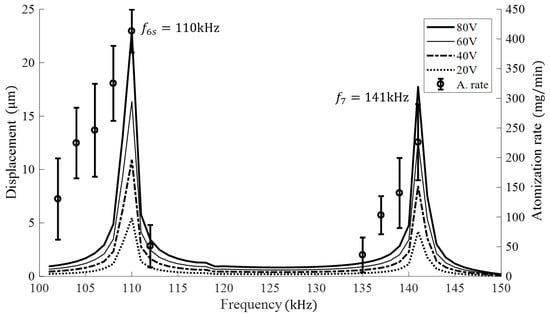
Figure 13.
Comparison between the frequency sweep FEM results for different voltages and the experimental results of the atomization rate.
The volume generated by the global deformation of the thin plate , as well as the additional contribution of the micro-aperture deformations , were also numerically estimated. The maximum deformation of the micro-aperture located near the center of the thin plate was measured directly from FEM at 110 kHz for the values of the voltage in the range [−80, 80] V, as shown in Figure 14. A symmetric cyclic behavior of the small () and large ( diameters was found; however, these changes were very small (about 0.025 with respect to their initial value at rest. Thus, its contribution to the total value change was not found to be significant.
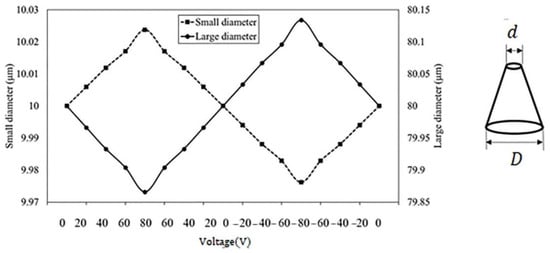
Figure 14.
FEM estimation of the maximum micro-aperture variations as a function of the cycling changes in the applied voltage.
Additionally, the global liquid volume displaced by the thin plate was calculated based on the FEM results (Figure 15). The distribution of the particle displacement at the surface of the thin plate as given by the FEM was calculated by using the shell method of integration [28]. An illustration of the integration method considering the limits (, ) is described in Figure 15. This method allows obtaining volumes generated by rotating an area between any two functions, and , where is the displacement curve and is a threshold.
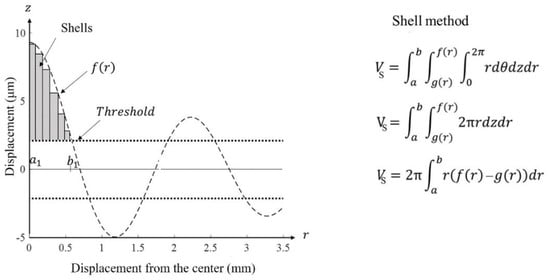
Figure 15.
Approximation of the volume caused by the out-of-plane displacement distribution. On the left, the shell method for integration of the solid of the revolution about the z-axis is described. The function is integrated along , with its value subtracted by the threshold function .
According to our experimental findings, atomization was not detected below 20 V. Therefore, the displacement amplitude (or volume variation) at that value was used as a threshold (). Thus, the effective volume used for the numerical results was given as . The changes in volume due to deformation of the apertures was neglected for the calculations of the atomization rate, since it was very small compared to the total volume change . On the other hand, the pressure loss coefficient is difficult to accurately assess its value, since the actual micro-apertures are manufactured by micro-abrasion electroforming and drilling techniques, which, in practice, give irregular conical shapes and edges [7]. Thus, in order to obtain an estimate of the approximate value of the loss coefficient , correlated to the experimental atomization rate () obtained at 80 V and 110 kHz, the following procedure was implemented. Figure 16 shows the linear relation (solid line) between the atomization rate and the pressure loss coefficient as given in Equation (7). By using this linear estimate, an approximate value of corresponding to the experimentally determined atomization rate () was estimated. The value was found to be smaller than the theoretical one ( for an ideal conical shape micro-aperture, but this can be a consequence of the actual conditions found in the micro-apertures of the experimental ultrasonic atomizer.
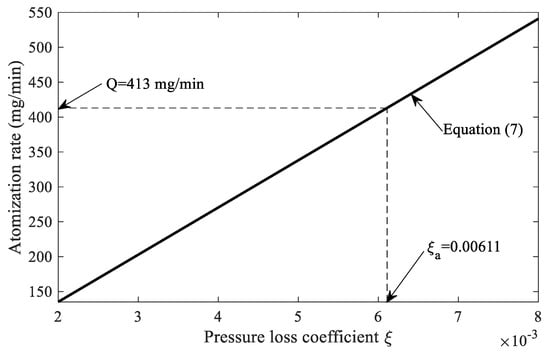
Figure 16.
Approximation of an effective pressure loss coefficient using the experimental results.
Using the found loss coefficient (, an approximation of the atomization rate as a function of the voltage can be obtained using Equation (7). The variations of the volume were calculated for every displacement distribution of the thin plate as given by the FEM at the resonance frequency of 110 kHz. For these calculations, the loss coefficient was kept constant.
Using these estimations, the results of the atomization rate measurements at the resonant frequency of 110 kHz were compared with the numerical calculations. As it was shown, at this frequency, the displacement amplitude distribution of the vibrational mode was rather complex, with a harmonic decreasing spatial distribution as a function of the thin plate radius. Thus, it is reasonable to assume that the total deformation between the compression and tension cycles was expected to contribute to the atomization rate. In Figure 17, the obtained results showed a good correlation between the experimental (scatter points) and numerical predictions (solid line) by FEM. The predicted atomization rate was nearly linear, with a minimum at 20 V, which was the preset threshold. A small rate was observed below 40 V, which we attributed to the set constant threshold, thus indicating that the shape of the mode was not affected by the voltage, only its amplitude.
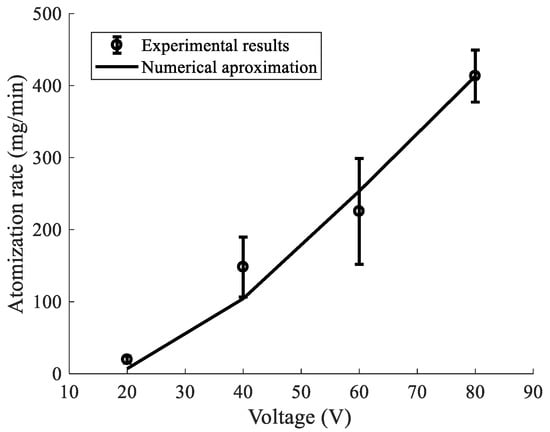
Figure 17.
Total atomization rate vs. voltage using , with the result used as a reference threshold in the calculation of the displaced volume.
The proposed approach assumes that the coefficient is constant for all voltage values and that the distribution of aperture openings during the dynamic cycles is homogenous over all the area, whilst, in reality, it depends on the vibrational mode behavior. Despite these considerations, it is interesting to notice that the predictions predicted well the experimental results. The predicted behaviors appeared to follow the experimental results with a roughly linear behavior, indicating a directly proportional relationship between the voltage and the out-of-plane displacements through the center of the thin plate, which controls the atomization rate and can be used to optimize it.
7. Conclusions
In this research, three main aspects were considered; first, a FEM dynamic modeling of an ultrasonic atomizer was developed; second, a study of a higher vibrational mode analysis as a function of the aperture shape of a meshed thin plate was investigated; and third, a numerical approximation of the atomization rate based on a combination of the experimental and numerical results was proposed. The finite element analysis provided a method to determine the vibration modes of the complete system (meshed thin plate coupled to a PZT) in response to an applied harmonic voltage, which is a complex problem to solve analytically. The behavior of the atomizer system for three types of apertures was analyzed. The results showed that the resonant frequency was only slightly affected by the shape of the aperture, with a larger response for the conical aperture when compared with a pyramidal shape. In all cases, the maximum out-of-plane displacement showed a linear behavior with the applied voltage. Numerical simulations of out-of-plane displacement distribution were used to obtain an approximation of the volume change generated by the dynamic oscillations at the resonant frequency. The experimental results also demonstrated that a minimum threshold voltage was required to achieve atomization. A prediction of the atomization rate was determined considering the effect of the mass transfer, vibration analysis, and geometry of the aperture. The results were compared with the experimental results, and a good correlation was found. This study indicated that FEM provides correct information of the mechanical behavior occurring during the ultrasonic atomizing process. The results could allow to optimize the atomization parameters by finding the optimum driving frequency and voltage for a specific design of the meshed thin-plate coupled to a PZT. The next step in our research could be to implement the results for soft actuation optimization of a soft robotic system.
Author Contributions
Conceptualization, E.G.-B., K.J.L., H.-J.L. and A.B.; methodology, E.G.-B.; validation, E.G.-B. and H.-J.L.; formal analysis, E.G.-B. and A.B.; writing—original draft preparation, E.G.-B., A.B. and K.J.L.; and writing—review and editing, E.G.-B., A.B. and K.J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by 2019 UC MEXUS-CONACYT, grant number CN-19-153 and partial support was also provided by the U.S. National Science Foundation under grant numbers CMMI-1762530 and CMMI-2032021 (principal investigator: Kenneth J. Loh).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated for this study are available on request by contacting the corresponding authors.
Acknowledgments
This project was supported by the 2019 UC MEXUS-CONACYT grant no. CN-19-153. Partial support was also provided by the U.S. National Science Foundation under grant numbers CMMI-1762530 and CMMI-2032021 (principal investigator: Kenneth J. Loh).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Pseudocode for the modal and harmonic analysis implemented in ANSYS to solve the single thin plate and the meshed thin plate coupled to the PZT ring system problems.

Table A1.
Stages of FEM implementation in ANSYS.
Table A1.
Stages of FEM implementation in ANSYS.
| Define the initial material and geometry parameters and element type (Solid-186). Attach the geometry (circular plate described before). Apply the mesh controls (discretize the domain). | |
A1: Modal analysis:
| A2: Harmonic analysis:
|
References
- Tinoco, H.A.; Cardona, C.I.; Peña, F.M.; Gómez, J.P.; Roldán-Restrepo, S.I.; Velasco-Mejía, M.A.; Barco, D.R. Evaluation of a Piezo-Actuated Sensor for Monitoring Elastic Variations of Its Support with Impedance-Based Measurements. Sensors 2019, 19, 184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, Y.; Zhou, Y.; Lin, Y.; Wang, L.; Xi, W. Development of a microforce sensor and its array platform for robotic cell microinjection force measurement. Sensors 2016, 6, 483. [Google Scholar] [CrossRef] [PubMed]
- Raine, A.B.; Aslam, N.; Underwood, C.P.; Danaher, S. Development of an ultrasonic airflow measurement device for ducted air. Sensors 2015, 15, 10705–10722. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.G.; Jung, W.S.; Kang, C.Y.; Yoon, S.J. Recent progress on PZT based piezoelectric energy harvesting technologies. Actuators 2016, 5, 5. [Google Scholar] [CrossRef]
- Lu, G.; Li, Y.; Wang, T.; Xiao, H.; Huo, L.; Song, G. A multi-delay-and-sum imaging algorithm for damage detection using piezoceramic transducers. J. Intell. Mater. Syst. Struct. 2017, 28, 1150–1159. [Google Scholar] [CrossRef]
- Li, F.; Li, G. Application of ANSYS APDL in the design of piezoelectric transducer. In Proceedings of the 5th International Conference on Advanced Engineering Materials and Technology, Guangzhou, China, 22–23 August 2015. [Google Scholar]
- Olszewseki, O.Z.; MacLoughlin, R.; Blake, A.; O’Neill, M.; Mathewson, A.; Jackson, N. A silicon-based MEMS vibrating mesh nebulizer for inhaled drug delivery. In Proceedings of the 30th Eurosensors Conference, Budapest, Hungary, 4–7 September 2016. [Google Scholar]
- Fan, B.; Song, G.; Hussain, F. Simulation of a piezoelectrically actuated valveless micropump. Smart Mater. Struct. 2005, 14, 400. [Google Scholar] [CrossRef]
- Lee, H.J.; Prachaseree, P.; Loh, K.J. Rapid Soft Material Actuation Through Droplet Evaporation. Soft Robot. 2020. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.-J.; Loh, K.J. Soft material actuation by atomization. Smart Mater. Struct. 2019, 28, 1–10. [Google Scholar] [CrossRef]
- Manzanares-Martínez, B.; Flores, J.; Gutiérrez, L.; Méndez-Sánchez, R.A.; Monsivais, G.; Morales, A.; Ramos-Mendieta, F. Flexural vibrations of a rectangular plate for the lower normal modes. J. Sound Vib. 2009, 329, 5105–5115. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, J.; Zhu, C.; Huang, J.; Jiang, F. Theoretical Calculations and Experimental Verification for the Pumping Effect Caused by the Dynamic Micro-tapered Angle. Chin. J. Mech. Eng. 2016, 29, 615–623. [Google Scholar] [CrossRef]
- ANSI; IEEE. IEEE Standard on Piezoelectricity; IEEE: New York, NY, USA, 1987; p. 176. [Google Scholar]
- Maehara, N.; Ueha, S.; Mori, E. Influence of the vibrating system of a multipinhole-plate ultrasonic nebulizer on its performance. Rev. Sci. Instrum. 1986, 57, 2870. [Google Scholar] [CrossRef]
- Piao, C.; Kim, D.J.; Kim, J.O. Radial-mode vibration characteristics of piezoelectric hollow-disc transducers. In Proceedings of the 21st International Congress on Sound and Vibration, Beijin, China, 13–17 July 2014. [Google Scholar]
- Andrade, M.A.B.; Alvarez, N.; Buiochi, F.; Adamowski, J.C.; Negreira, C. Analysis of 1–3 Piezocomposite and Homogeneous Piezoelectric Rings for Power Ultrasonic Transducers. J. Braz. Soc. Mech. Sci. Eng. 2009, 31, 312–318. [Google Scholar] [CrossRef] [Green Version]
- Lima-Rodríguez, A.; González-Herrera, A.; García-Manrique, J. Study of the Dynamic Behavior of Circular Membranes with Low Tension. Appl. Sci. 2019, 9, 4716. [Google Scholar] [CrossRef] [Green Version]
- Leissa, A.W. Vibration of Plates; National Aeronautics and Space Administration: Washington, DC, USA, 1969.
- Alger, M. Polymer Science Dictionary; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Dou, Y.; Luo, H.; Zhang, J. Elastic Properties of FeCr20Ni8Xn (X = Mo, Nb, Ta, Ti, V, W and Zr) Austenitic Stainless Steels: A First Principles Study. Metals 2019, 9, 145. [Google Scholar] [CrossRef] [Green Version]
- Kwak, M.K. Vibration of circular plates in contact with water. ASME J. Appl. Mech. 1991, 58, 480–484. [Google Scholar] [CrossRef]
- Thompson, M.K.; Thompson, J.M. ANSYS Mechanical APDL for Finite Element Analysis; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Akiyoshi, O. Flow direction of piezoelectric pump with nozzle/diffuser-elements. Chin. J. Mech. Eng. 2004, 107–109. [Google Scholar]
- Jr, W.W.; Timoshenko, S.P.; Young, D.H. Vibration Problems in Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Yan, Q.; Zhang, J.; Huang, J.; Wang, Y. The Effect of Vibration Characteristics on the Atomization Rate in a Micro-Tapered Aperture Atomizer. Sensors 2018, 18, 934. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olsson, A.; Stemme, G.; Stemme, E. Numerical and experimental studies of flat-walled diffuser elements for valve-less micropumps. Sens. Actuators 2000, 84, 165–175. [Google Scholar] [CrossRef]
- Yan, Q.; Wu, C.; Zhang, J. Effect of the Dynamic Cone Angle on the Atomization Performance of a Piezoceramic Vibrating Mesh Atomizer. Appl. Sci. 2019, 9, 1836. [Google Scholar] [CrossRef] [Green Version]
- Wrede, R.; Spiegel, M. Schaum’s Outline of Advanced Calculus; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).