Abstract
We investigate crustal seismic attenuation by the coda quality parameter () in the Gargano area (Southern Italy), using a recently released dataset composed of 191 small earthquakes (1.0 ≤ ML ≤ 2.8) recorded by the local OTRIONS and the Italian INGV seismic networks, over three years of seismic monitoring. Following the single back-scattering theoretical assumption, was computed using different frequencies (in the range of 2–16 Hz) and different lapse times (from 10 to 40 s). The trend of vs. frequency is the same as that observed in the adjacent Umbria-Marche region. at 1 Hz varies between 11 and 63, indicating that the area is characterized by active tectonics, despite the absence of high-magnitude earthquakes in recent decades. The 3D mapping procedure, based on sensitivity kernels, revealed that the Gargano Promontory is characterized by very low and homogeneous at low frequencies, and by high and heterogeneous at high frequencies. The lateral variations of at 12 Hz follow the trend of the Moho in this region and are in good agreement with other geophysical observations.
1. Introduction
Coda waves recorded from small local earthquakes are interpreted as body waves of backscattering from heterogeneities that are distributed randomly but uniformly in the Earth’s crust and upper mantle. Coda waves are predominantly composed of scattered S-waves and, in order to relate coda wave characteristics to seismic attenuation, a scattering model is necessary. In the early 1970s, Aki and Chouet [1] and Sato [2] developed a single-scattering model in the Born approximation, where the primary wave encounters a scatterer (inhomogeneity) only once, producing a secondary wave reaching the receiver with no other impact. This model parametrizes the seismic attenuation using a single parameter, , called Q-coda, which is easily calculated once the decay rate of the coda envelope is measured from data. Worldwide, , estimates generally report low values in regions with active tectonics, and high values in stable regions [3,4,5,6].
The physical interpretation of is a long-standing problem in seismology. Years after the development of the early single-scattering models, it was demonstrated by Zeng et al. [7] that the single-scattering model is a first-order approximation of the general solution to the energy transport equation (ET) ([8], which accounts for multiple scattering and is parametrized in terms of two parameters, intrinsic and scattering . New interpretations of coda wave envelopes, based on the Paasschens solution of the ET equation, then demonstrated that single-scattering models are unrealistic for most of the experiments carried out through the Earth (see, e.g., [9,10,11] for a review), while the other asymptotic approximations of the ET equation, the so-called diffusion model [12], are much more realistic in cases showing high geological heterogeneity, like volcanoes. Despite this evident limitation, , or, which is the same in practice, the coda envelope decay parameter, is still used, due to the easy application of the single-scattering model to experimental data.
In the single-scattering model, is a combination of scattering and intrinsic attenuation () [1]. It is interesting to note that the diffusion model predicts that asymptotically approaches the intrinsic attenuation at increasing times in the coda wave train (assuming a uniform half-space [12]). However, single-source-receiver couple estimates of and can only be obtained in strongly heterogeneous media, where the diffusion model is applicable. For all other cases, the separation is almost impossible and the only measurable (unbiased) parameter is [11].
Sato’s [2] derivation of the single-isotropic-scattering model, and the numerical computations of Frankel and Wennerberg [13], suggest that is an intrinsic attenuation parameter. Zeng’s [7] simulations imply that must be approximately from 5 to 15 times as to have a comparable effect on the coda decay rate.
To achieve a correct interpretation of the measured , the association of the attenuation within volumes crossed by the coda radiation with the structural, tectonic, or geodynamic maps must be performed. Starting from the early and approximative images [14], many attempts were made to spatially confine the attenuation anomalies measured through coda waves (as reviewed by del Pezzo et al. [11]), in order to reveal heterogeneous Earth structures and interpret them in terms of rock quality. Among the imaging methods, sensitivity kernels are essential to obtain an attenuation image from coda waves; the theoretical approach, in the framework of both radiative transfer theory and the diffusion model, focuses on the spatial changes of from distributed sources recorded at a seismic network [15,16]. In recent years, the sensitivity kernels of coda waves, in 2D and 3D, propagating in a medium with a realistic velocity model, were computed by numerical simulations following Yoshimoto [17]: assuming that the total seismic energy is subdivided in particles of unit energy that are randomly emitted from the source, the energy particle loses a fraction of its energy by anelastic absorption. When the energy particle encounters an elastic and isotropic scatter, it randomly changes its direction. After a number of collisions, it will arrive at the receiver at a given lapse time, measured from the origin time. Thus, the energy envelope is the sum of the energy particles arriving at the receiver from random directions at a given lapse time, sampling a portion of the Earth’s volume. Thus, it can be heuristically assumed that the more a volume element (in which the whole medium is divided) is crossed by energy particles, the more it weighs in the energy envelope of each seismogram. The space weighting function can be calculated in the whole propagation volume by counting the number of crosses and collisions of the energy particles in each volume element [11]. In the last few years, sensitivity kernels for scattering radiation have been used to image both volcanic structures [18,19,20] and tectonically active zones (e.g., [21,22]).
The first attempt to study the attenuation in the Gargano Promontory (Northern Apulia, Southern Italy) (hereafter GP) has been performed using a dataset of microearthquakes recorded by the OTRIONS Local Seismic Network (OT), managed by UniBa, in the period from April 2013 to July 2014 [23]. The obtained 2D image of revealed the presence of a well-resolved anomaly in the southwestern sector of the GP, at 5 Hz. The southwestern sector of the GP is characterized by the presence of fluid circulation in fractures at shallow crustal levels, as also revealed by 2D resistivity imaging [24] and by the heat flow map [25], which can cause both scattering and intrinsic attenuation effects on a local scale. The heterogeneity of the GP crust was recently highlighted by a local-scale seismotectonic study [26], thanks to a recently released dataset of microearthquakes recorded by both the National Seismic Network (IV), managed by the INGV, and the OT network in the period from August 2015 to August 2018 [27]. The authors [26] analyzed all possible focal mechanisms and found a great heterogeneity of solutions in the seismicity of the upper and intermediate crust; however, in the lower crust, the seismicity appears more concentrated in the NE sector, which is consistent with a thrust-faulting stress regime with maximum compressive axis () that is NW–SE oriented, and a shallow normal-faulting stress regime with a maximum horizontal compressive axis trending NW–SE [28].
The historical seismicity of northern Apulia reveals seismogenic structures that can generate destructive events. Among these, the 1627 earthquake (with an intensity X degree MCS and estimated magnitude of 6.7) and the 1646 earthquake (with an intensity IX–X degree MCS at Carpino and estimated magnitude of 6.2) [29]. Concerning the tectonic structures, many faults are recognized along the entire GP surface, the characteristics of which are poorly known. In Figure 1, we report the seismotectonic map of Italy ([30]) and the details on the GP sector, with the principal tectonic lineaments that could be responsible for the main historical earthquakes.
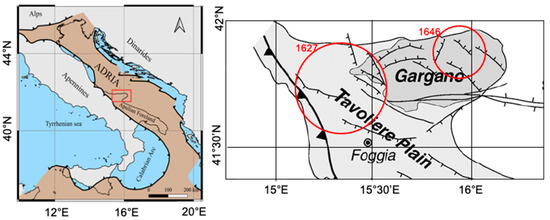
Figure 1.
Left: Seismotectonic map of Italy (modified after [30]); the red rectangle marks the study area. Right: detail showing the geological lineaments of the GP. The red circles represent the estimated focal volume of the two major historical earthquakes (modified after [29]).
Considering these recent results [26], related to the strong lateral and vertical crustal heterogeneity of the GP, in this paper we performed a new and more robust study of in order to address some still open questions: the first is the reason for the presence of lower crustal seismicity in the NE sector of the GP, with the absence of shallower seismicity; the second is the presence of very shallow seismicity in the SW sector of the GP, and its relationship with fluid circulation in the upper crust. This attenuation study benefits from the recently released dataset of GP microearthquakes [27,31] and from a 3D mapping approach based on sensitivity kernels [15]. The 3D tomography of was obtained by combining the new dataset with the previous one [23], used for the 2D mapping of . With respect to the previous estimate of in the GP [23], the used dataset is enlarged and consists of earthquakes with magnitudes ranging between 1 and 2.8, and the sampled area is extended to the NE, thanks to a change in the OT network geometry. All the details regarding the data and the network can be consulted in [27]. Moreover, 3D images of for the GP, using a projection method based on weighting functions derived from sensitivity kernels [15] have been performed for the first time in this area. The present tomography depicts the S-wave attenuation structure down to a 32-km depth, in three frequency bands centered at 3, 6 and 12 Hz, respectively. We will show how our present images provide evidence that the strongest attenuation contrasts are well correlated with the geotectonic setting of the GP.
2. Data and Methods
2.1. Dataset
The dataset consists of two hundred specifically located seismic events, extracted from the database of microearthquakes that has recently been released by [31] and described in [27]. We extracted data regarding the earthquakes recorded in the period from July 2015 to August 2018 to achieve better coverage of the GP crust, thanks to two OT stations that were added in the northern sector of the GP in June 2015. The OT network stations are equipped with short-period seismometers (Lennartz 3D-V seismometer (flat response above 1 Hz; 10 ms sampling rate)) [27]; the IV network stations are equipped with various types of seismic sensors, i.e., short period, broadband, and accelerometric instruments [32]. The selected dataset is composed of specifically located earthquakes ( s; horizontal and vertical location errors of less than 1 km, magnitude ) by using the 1D Gargano velocity model [33]. With respect to a previous study [23], we selected a dataset with a broader network geometry and a higher magnitude threshold, in order to validate the previous results obtained with very small earthquakes () in a narrower region. Details on data acquisition and management are described in [27]. We selected 191 events occurring in the period from 1 July 2015 to 30 August 2018, recorded to a maximum of 21 seismic stations. Foci depths range between 1 and 35 km, with shallower events located in the SW, and deeper events located NE of the promontory, as already observed in previous seismological studies of this area [26,29,34,35] (Figure 2).
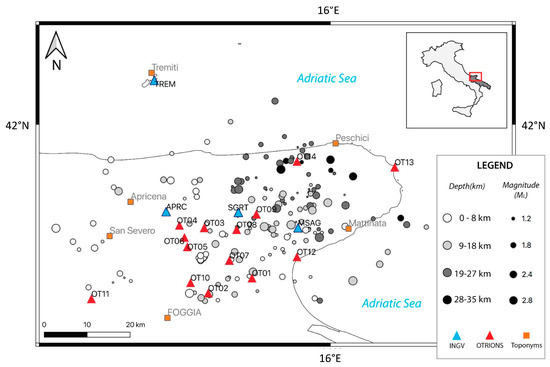
Figure 2.
An overview map of the seismic networks (red triangle of OT and blue triangles for IV) and the selected earthquakes (circle dimension is proportional to magnitude, circle color to depth, as indicated in the legend). The map was produced using the QGIS open-source software [36]. For OT and IV stations, please refer to [37] and [32], respectively.
2.2. Coda Attenuation Method
analysis as a function of frequency was performed by assuming the single isotropic scattering theory [1,38]. The theoretical decay rate of the coda energy envelope is given by [39]:
where is the source to receiver distance (km), is the reference distance (km), is a source term, is the central frequency (measured in Hz), , with the S-wave travel time, and is the time (measured in s) elapsed from the earthquake origin time, with . The observed energy envelope can be computed from a seismogram and its Hilbert’s transform :
The estimation for the investigated area was obtained by filtering the coda waves with a Butterworth two-poles filter in those frequency bands with a central frequency = 1, 2, 3, 4, 5, 6, 8, 10, 12, 14, and 16 Hz, with a bandwidth ranging inside the interval [, ]. Then, we least-squares fitted the envelope versus the time using Equation (1), with = 1 km. With this procedure, can be estimated as a function of frequency at the assigned lapse time window [10]. In fact, even though the coda envelope decay rate is theoretically independent of both the source-receiver distance and of magnitude, it depends on the time elapsed from the event origin time. In addition, Aki and Chouet [1] assumed that scattering is a weak process and is not strong enough to generate secondary waves, once they encounter other scatters (Born approximation). Scattered waves are produced once seismic waves encounter heterogeneities, faults, cracks, or irregular topography [40].
Generally, the quality factor increases with frequency through a power-law relationship between and due to Romanowicz and Mitchell [41]:
where is a reference value of the quality factor at = 1 Hz, and is the frequency dependence exponent, which is close to 1 and varies from one region to another region, on the basis of the heterogeneity of the medium [38]. Equation (3) indicates that the attenuation of seismic waves with the passage of time (i.e., the distance from the source) varies with frequency.
2.3. Coda Attenuation 3D Imaging
In order to obtain 3D coda attenuation images, we used the approach discussed by del Pezzo and Ibanez [11], based on the scattering kernels described by Pacheco and Snieder [15]. del Pezzo and Ibanez [11] computed the polynomial approximation of the analytically calculated sensitivity kernels, which noticeably reduces the calculation time costs. In particular, we used the sensitivity kernel as a weighting function, heuristically giving them a probabilistic meaning. The weighting functions (del Pezzo and Ibáñez, 2020) are here denoted as:
and represent the probability that, for the i-th source-receiver couple positioned, respectively, at {} and {}, the measured value of effectively corresponds to its true value at the space point with the coordinates . The subscript i spans from 1 to ( is the number of source-receiver couples in the data set); j spans from 1 to ( is the number of cells in which the space has been subdivided, here called “pixels”).
We indicated with the measure of for the i-th source-receiver pair, and with the measure of for the j-th pixel. In this heuristic scheme, represents the un-normalized probability that the i-th measure, , is associated with the j-th pixel. Averaging over the events and weighting for the kernel, at the single position j, the method yields:
The measure set thus produces for any pixel, j, a set of point values of multiplied by their probability, . We consider their weighted average as the characteristic value of at the specific point. In other words, we simply back-project the measure by attributing the measure to a space point of given coordinates, as weighted for the weighting functions.
By applying the ordinary error propagation equation to Equation (5) and by assuming the standard deviation of , we obtain the standard deviation of the j-th pixel:
We used Equation (6) to estimate the error on in any j-th pixel. Since represents the uncertainty of in the j-th pixel, and the diffusive waves are not related to seismic rays, we do not need to evaluate the ray crossing inside each j-th pixel. In fact, the weighting functions used are peaked at source and receiver. Consequently, the sole distribution of sources and receivers gives a sufficient idea of the areas where the coda radiation has the maximum probability of passing through. On the other hand, the coda tomography concept goes beyond the ray tracing assumption, taking into account the energy space distribution more than the wave front of the direct (ballistic) radiation, depicted by the ray trace space distribution. [20].
3. Results
3.1. Qc Estimates
The collected seismograms were visually checked to prevent erroneous estimates. The visual inspection of the envelopes was carried out on recordings filtered with a Butterworth two-pole filter with a central frequency = 8 Hz (bandwidth ranging between 5.7 Hz and 11.3 Hz). We removed all the recordings that present abrupt variations in the amplitude of the envelope, i.e., bumps of energy due to concomitant seismic events or other environmental or artificial sources. We also removed the recordings with sudden changes in the envelope slope in the portion of the seismogram immediately following the S-wave arrival [42]. The suitable recordings were processed with the addition of two time-markers (Figure 3):
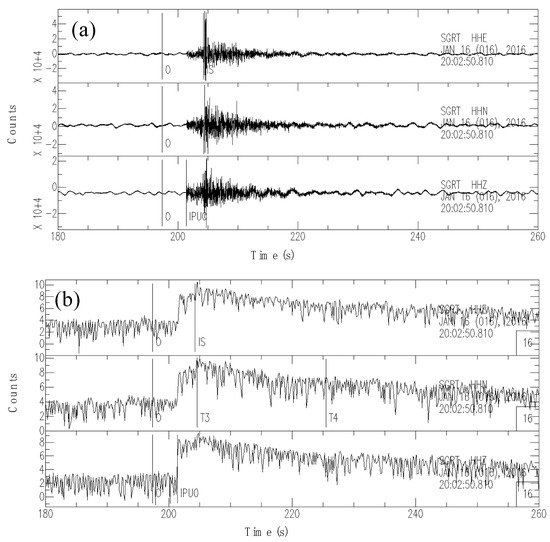
Figure 3.
(a) Original three-component record (count/s) at station SGRT (IV network) with origin O, P-wave and S-wave arrival markers. (b) Energy envelope (count/s) filtered around = 6 Hz, with and markers (see the text for explanation).
- An initial marker, named , placed after the S-wave arrival, when the envelope shows a decreasing trend;
- A terminal marker, named , placed before a bump, or an abrupt change of the slope, or when the oscillations cannot be distinguished from the seismic noise.
The selected envelopes were linearly fitted inside the time interval [] in a logarithmic diagram for different = 10, 15, 20, 25, 30, 35, 40 s and = 2, 3, 4, 5, 6, 7, 8, 10, 12, 14, 16 Hz, reaching a maximum of 70 measures of for each seismogram component. We accepted only the components for which the condition was satisfied. was computed from the slope of the linear regression in Equation (1): . Any coda amplitude decay with a positive was rejected. In Figure 4, the number of estimates was plotted. It can be inferred that, for = 20, 25, and 30 s, the maximum number of estimates is reached at all frequencies, while for = 10 s the minimum number of estimates is available; all series show stability in the number of estimates starting at = 3 Hz, indicating that for Hz, the results are less robust.
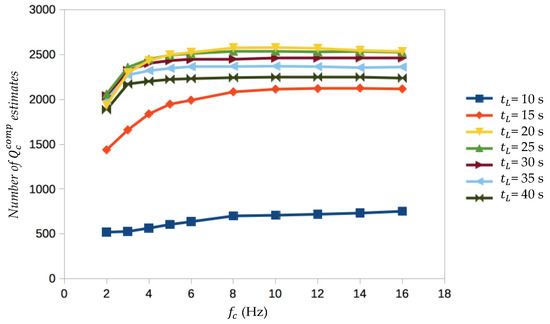
Figure 4.
Number of estimates, versus the central frequencies , for each lapse time .
All the analyzed envelopes, cut in the time window between the markers and , are available in for the reproducibility of our results.
3.2. Qc Averaged
To improve the quality of the dataset, we removed all those estimates with off-scaled values to avoid the invalidation of the average . The removed outliers represent 5% of the initial dataset. The error on each was computed from the error on the slope of the linear regression: . was then computed from a weighted average, by using the inverse square of as weights. The results are plotted in Figure 5, and it can be observed that regularly increases at a fixed for an increasing and at the same for increasing , indicating a satisfying regularization of the data. The observed correlations between vs. and are in total agreement with previous studies conducted in the same area [23] or in other tectonic areas as, for instance, in the central Apennines [39].
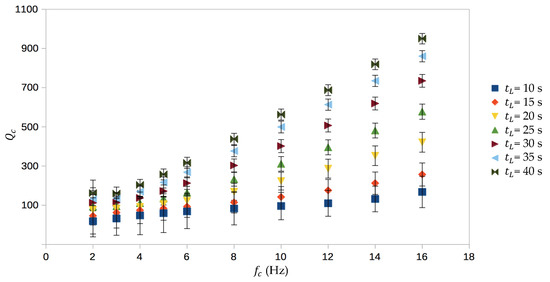
Figure 5.
Average versus at all the . The error bars quantify the average percentage errors on .
Taking the logarithm of Equation (3), we get:
Through the linear regression of versus , we obtained from the intercept and from the slope. We performed this analysis for all single-trace seismograms to obtain average and values for the different lapse times . The results are reported in Table 1, together with a comparison with other studies in the same area or in other worldwide areas. The increasing trend of vs. in Table 1 reflects the size of the Earth’s volume, sampled by seismic waves. By adopting the simplifications of Aki and Chouet [1], it is possible to define an order of magnitude of the investigation depth. Estimating a mean value of = 3.86 km/s for the Gargano crust [33], we computed the radii of the spherical volumes (and therefore the maximum depths investigated) for all the considered lapse time windows (Table 1).

Table 1.
For each lapse time , and estimates, with their errors and the radius of investigation in the Earth lithosphere, are reported.
The average for each station, named , is plotted vs. in Figure 6a–g. These plots exhibit the pattern of variation of the quality factor with central frequencies at different lapse times . The station trend versus is irregular for = 10 s, for which the least number of estimates is available; for > 20 s, more regular trends are observed.
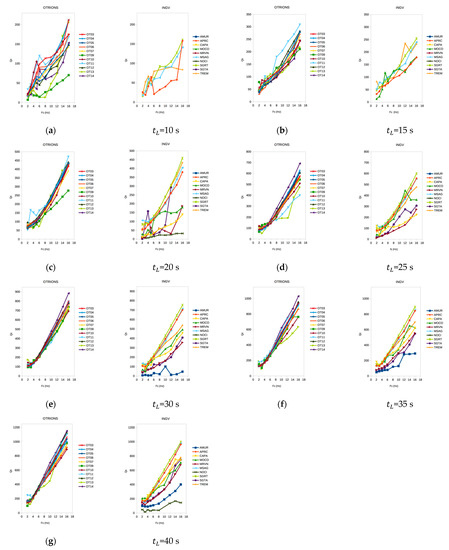
Figure 6.
estimates for each central frequency , for all the recording OT and IV stations. The values are distributed more irregularly for the 10 s lapse time. (a–g) show the station vs. for increasing lapse times.
In Figure 7, we plotted the estimates with respect to other regions of Italy (Figure 7a) and other regions worldwide (Figure 7b). The same comparison is given in Table 2 for and .
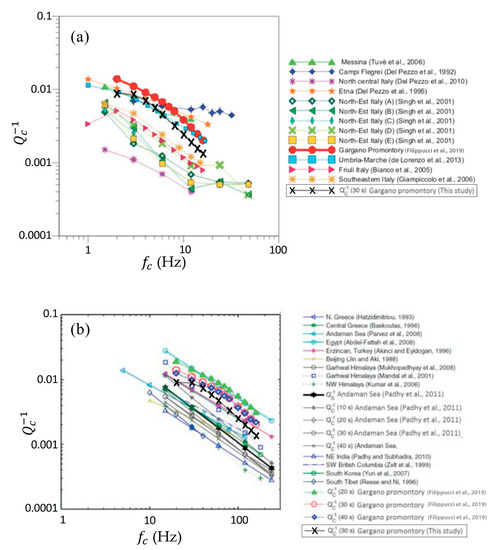
Figure 7.
Comparison between the estimates for each central frequency obtained in this work ( = 30 s) and the literature. (a) Literature referring to studies from other areas of Italy (modified from Filippucci et al., 2019 [23]). Letters from A to E refer to the subdivisions of Northeastern Italy by Singh et al. [43]. (b) Literature referring to other areas worldwide.

Table 2.
Comparison of of other regions with active tectonics in Italy and worldwide, for approximately the same .
3.3. 3D Mapping
For the 3D mapping of , we followed the procedure described by [20] for the tomography of Mount Etna. We considered for our imaging the results gathered at = 30 s. Three non-overlapping frequency bands, centered on were selected: = 3 Hz ranging within [2.1, 4.2] Hz; = 6 Hz ranging inside [4.2, 8.5] Hz; = 12 Hz, ranging within [8.5, 17.0] Hz.
To make our images more reliable, we added to our results as hitherto described, as well as adding the results previously published by [23]. We then built a merged database of estimates and errors, (respectively, and in Equations (5) and (6)). In this way, we collected a total number of source-receiver three-component estimates as follows: = 651 for each recording station, that is, 1953 values and errors. The Earth medium was subdivided in cubic pixels having side of 5 km. images at each depth are representative of a layer of 5-km thickness. For the section maps, we used an 8-km depth step. Thus, we plotted images at 0, 8, 16, 24, 32 km, each depth being representative of a 5-km j-th pixel. In Figure 8a–c, we plotted the images for = 3 Hz, = 6 Hz and = 12 Hz, respectively. tomographic images show very low errors since is more than one order of magnitude less then in the whole area at all the considered frequencies. Therefore, our results can be considered robust and significant.
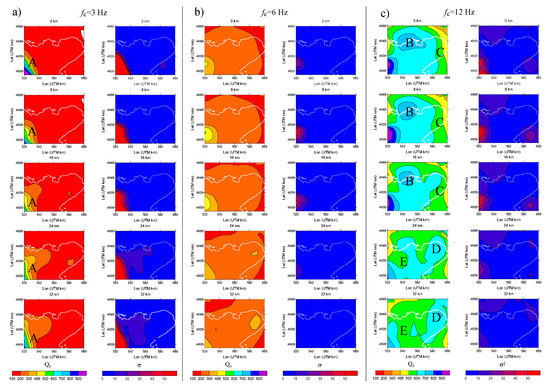
Figure 8.
Section maps of and at various depths for = 30 s: (a) = 3 Hz; (b) = 6 Hz; (c) = 12 Hz. The coastline is in white. Labels A, B, C, D and E refer to the anomalies commented in the discussion section.
4. Discussion
The quality factor has been estimated in order to assess the effect of tectonic and seismic activity in the hazardous region of the GP.
Before drawing conclusions about the GP tectonics, the meaning of what physically measures should be re-addressed. Within the frame of the single-scattering theory, is considered representative of the total attenuation. The total attenuation of seismic waves is the sum of intrinsic and scattering attenuation: the first term accounts for the conversion of seismic energy into heat through anelastic absorption; the second term accounts for seismic energy redistribution through refraction, reflection and diffraction at random discontinuities distributed inside a homogeneous medium. The severe trade-off between the estimates of the intrinsic and the scattering is due to the mathematical formulation of the model itself [1] and it is impossible to deduce from the estimates which quality factor ( or ) prevails. Many studies indicate that, in a fairly homogeneous crust, would prevail over in the value ([39,61,62] among others). This could be true on a regional scale; where an average Earth crust is sampled, heterogeneities appear as smoothed and the distribution can be considered representative of the anelastic absorption. If is analyzed with respect to frequency, it appears that at frequencies < 6 Hz, scattering is dominant, whereas, at frequencies > 6 Hz, intrinsic attenuation is dominant [9,63]. Monte Carlo simulations based on the law of energy conservation showed that for short lapse times, the single-scattering model is applicable, while for long lapse times, the diffusion model is more appropriate [64]. In particular, at long lapse times, when coda waves are in the diffusive regime, asymptotically approaches the intrinsic in a uniform half-space model [12].
By using different methods, the separation of and from has been estimated both in Italy and worldwide, in many tectonic contexts: the Adaman Sea [65]; the Alborz region (Iran) [66]; the Almeria Basin, Southwestern Iberian Peninsula (for > 3 Hz) [47]; Spain and Turkey [67]; the Tokai region (Japan) [1]; Northeastern Italy [61]; the Messina Strait (Southern Italy) [45]. The results of all these studies suggest that the attenuation of coda waves is dominated by intrinsic attenuation. The same result was achieved for the Southern Apennines (Italy) [62], in a regional-scale study that included the GP.
In this work, with respect to a previous analysis [23], we used an improved dataset of microearthquakes that was one order of magnitude greater, recorded by both the OT and IV network stations, extending the seismic coverage of the area. The differences between the results of this study and those obtained in the previous one [23] are due to the different magnitude ranges considered. In fact, by increasing the event magnitude, the signal-to-noise ratio also increased, giving rise to more reliable results. Moreover, since the network geometry used for this study was larger than the previous one, the values were averaged at different distances. Several observations from different regions worldwide [40] indicate an increase of the value of when increasing the lapse time window , due to the greater penetration of waves in the deeper Earth, where the seismic attenuation is less pronounced. Therefore, seven windows were taken, from 10 to 40 s, with a 5-s time step, to estimate the attenuation at different lapse times, i.e., at different depths. The penetration depth ranges between 19 and 77 km (Table 1). The frequency-dependence of in Equation (4) is interpreted as a tectonic parameter. Regions of high tectonic activity are characterized by low when compared to stable regions.
Many measurements of and , in different tectonic and geological settings, have indicated a trend of higher (roughly 100 to 1000) and lower (about 0.3 to 0.7) for stable continental regions, while a lower (from 40 to 200) and a higher (from 0.7 to 1.1) are found in tectonically active areas (e.g., [68,69,70]). In Table 2, we reported the results of the and measurements in several regions of active tectonics worldwide, for comparable values of . In this study, varied between 26 and 66 (Table 1), indicating that the upper lithosphere is seismically active. The frequency dependence exponent, , varies between 0.79 and 1 (Table 1); the lower value of occurs for = 15 s, corresponding to a penetration depth of 30 km, in the lower crust, suggesting that the higher degree of heterogeneities corresponds to the depth where the seismicity of the GP is concentrated. , computed for each station, shows a low-quality factor and great variability at low , while at high , estimates appear to be regular and higher (Figure 6). This result may indicate, as observed worldwide, that the upper crust is more heterogeneous than the lower crust, with the presence of high-frequency scattering. Stations of the OT network have very similar values and regular trends of at all the lapse time windows (Figure 6). Regarding the IV stations, estimates are always higher for stations that are inside the GP (SGRT, MSAG, APRC) than those outside the GP (AMUR, CAPA, MOCO, MRVN, SGTA, TREM) at all , reflecting the heterogeneous characteristics of the crust in this area (Figure 6). It is worth noting that for the GP follows a trend very similar to that of the Central and Southern Apennines, Italy [39,62]. The Italian Apennines are the site of both historical and recent destructive earthquakes [71], so the similarity in with that of the GP may have evident and important implications regarding the seismic hazard. In fact, although for several decades, the GP has been affected by earthquakes of small or very small magnitude, it has historically been the site of very destructive earthquakes (Figure 1). Differences among estimated in this study and that estimated in other areas in Italy and worldwide (Figure 7a,b) can be ascribed to the different geological–structural settings derived from distinct geodynamic and paleogeographic domains.
Considering that is representative of the intrinsic attenuation and that this similarity increases at high frequencies, as already discussed, we can interpret the tomographic images in Figure 8. All images are coupled with the standard deviation , which indicates the high quality and robustness of the results. Seismic attenuation is homogeneous and high at all depths, at both low and medium frequencies (Figure 8a,b). A high anomaly (marked with A in Figure 8a) is present in the southwestern GP sector at all depths but, since it corresponds to an increased it is poorly resolved.
Some heterogeneities can be observed at high frequencies (Figure 8c). In the shallowest map sections (at 0 km, 8 km and 16 km) shows a well-localized high anomaly (labeled B in Figure 8c) and a north-eastward decreasing trend (toward label C in Figure 8c). The high anomaly (zone labeled B, in Figure 8c) is observed at depth down to about 16 km in the northernmost part of the GP. This anomaly is remarkable, since it corresponds with the area studied by Loddo et al. [72], where the author found the presence of a high-density and high-susceptibility body that was 10 km wide, at 4–7 km depth. The presence of this body agrees very well with the inferred low seismic attenuation in that portion of the crust. Loddo et al. [72] explained the presence of the deduced high-density/susceptibility body with the presence of an intrusive body within the sedimentary sequence, as outlined by the presence of minor outcrops of mafic intrusive rocks along the GP coastline. The observed northeastward-decreasing trend (toward the zone labeled C in Figure 8c) correlates well with the evidence of an anomalous absence of seismic activity in this sector at a depth of up to 20 km. In this frame, in the Northeastern sector of the GP, the low in the upper/intermediate crust could be representative of ductile behavior, a speculation that deserves further investigation. We did not find any correlation with major surface fault lineaments of the area, as depicted in Figure 1.
In Figure 8c, at greater depths (24 km and 32 km), down to about 35 km, a high anomaly (labeled D, in Figure 8c) appears in the easternmost sector of the GP. In this area, seismicity is deeper, as can be also observed in Figure 2. With respect to the previous 2D mapping of [23], the easternmost part of the GP is covered by a seismic network, and it is now included in our results. It is very interesting that, in Figure 8c, in the two deepest map sections (24 km and 32 km), shows a decreasing trend (toward label E in Figure 8c) toward the southwest: in this sector, at a depth greater than 18 km, seismicity is not present [26], the Adriatic Moho is shallower [73] and the crustal rheology has a ductile behavior [34]. All these independent observations agree well with the result of a lower (zone labeled E, in Figure 8c). At the same depth, the easternmost sector of the GP is seismogenic [26] and in a fragile regime [34,73], and this agrees with the observed higher (zone labeled D, in Figure 8c).
As discussed in a previous study [23], with increasing , shows the effect of the intrinsic and scattering attenuation of back-scattered body waves coming from deeper portions of the lithosphere [1]. At a higher frequency, in Figure 8c, it can be observed that, with increasing depth, tends to decrease. This behavior can be ascribed to the effect of the intrinsic attenuation that increases with the sampled Earth volume. In confirmation of this behavior, as we plotted in Figure 9, the trend with the source-to-receiver distance of , with = 12 Hz and = 30 s, the linear decreasing trend of () that confirms this hypothesis can be clearly observed.
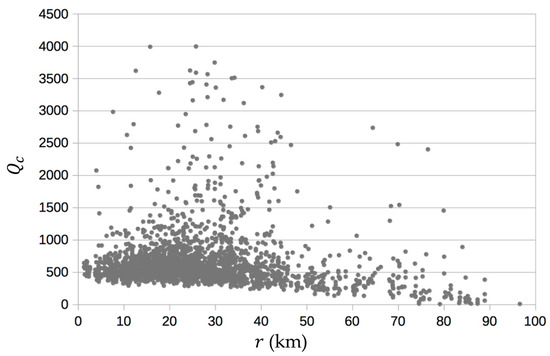
Figure 9.
trend versus the source-to-receiver distance (km) for = 12 Hz and = 30 s.
In summary, from the tomography at 12 Hz (Figure 8c), it can be observed that in the upper/intermediate crust, decreases toward the northeast (trend toward the C zone); in the lower crust, increases toward the northeast (trend from the zone with label D to the zone labeled E). Therefore, the intermediate crust would act as a separation interface between these two trends of in opposite directions. The attenuation maps confirm the high heterogeneity of the GP crust, as already evinced from the analysis of seismicity and the stress field [26,34].
5. Conclusions
Thanks to the improvement of the OT network, with the addition of two new stations in the northeastern sector of the GP, an enhanced dataset of microearthquakes was recently collected and released [27]. In this study, with this new dataset, the total of S-waves was studied for the GP area. values indicate that the Gargano area is tectonically active when compared with other regions as, for instance, the Central and Southern Apennines (Italy); the comparative results of indicate that the GP crust is strongly heterogeneous at a penetration depth of about 30 km in the lower crust, and this result agrees with the observed seismicity, which concentrates at that depth, indicating a high degree of fracturing of the GP’s lower crust.
In this work, using attenuation kernels, we present the first 3D maps of the Gargano (Southern Italy) area for different depths and frequencies. The geophysical knowledge of the area greatly benefits from this 3D approach, providing a marked improvement with respect to the averaged estimates alone. The imaging was performed at different frequencies and depths. Results at low and medium frequency indicate a fairly homogeneous at all depths, whereas, at high frequency, results indicate:
- (1)
- The presence of a high body in the northern sector of the GP at a depth of up to 16 km, which would support the hypothesis of a high density/susceptibility body, as deduced by Loddo et al. [72] in the same sector and at the same depth (zone labeled B (Figure 8c));
- (2)
- The presence of a low area, down to a depth of 16 km, suggesting a ductile regime in the upper/intermediate crust in the northeastern sector of the GP (zone labeled C (Figure 8c));
- (3)
- The presence of a low area in the southwestern sector of the GP at depth down to 32 km that would support the presence of a ductile behavior in the lower crust [34], responsible for the absence of seismicity at that depths (zone labeled E (Figure 8c));
- (4)
According to these interpretations, the GP area reveals many interesting features that are promising for further investigation.
Author Contributions
Conceptualization, M.F., E.D.P., S.d.L., G.P. and A.T.; data curation, S.L.; formal analysis, M.F., S.L., E.D.P. and S.d.L.; funding acquisition, E.D.P. and A.T.; methodology, M.F., E.D.P. and S.d.L.; project administration, A.T.; resources, E.D.P. and A.T.; software, S.L. and E.D.P.; supervision, M.F., E.D.P., S.d.L., G.P. and A.T.; validation, M.F., E.D.P. and S.d.L.; visualization, M.F.; writing—original draft, M.F., E.D.P. and S.d.L.; writing—review and editing, M.F., S.L., E.D.P., S.d.L., G.P. and A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by Project PRIN n. 201743P29 FLUIDS (Detection and tracking of crustal fluid by multi-parametric methodologies and technologies). E.D.P. was partially funded by the Spanish Mineco Project FEMALE, PID2019-106260GB-I00.
Data Availability Statement
Envelope data used in this study are described in the data paper Filippucci et al. 2021 (submitted to Data MDPI). Data are available online on Mendeley repository: http://dx.doi.org/10.17632/w9hsj2whzm.1.
Acknowledgments
The computational work has been executed on the IT resources of the ReCaS-Bari data center, which have been made available by two projects financed by the MIUR (Italian Ministry for Education, University and Re-search) in the “PON Ricerca e Competitività 2007–2013” Program: ReCaS (Azione I-Interventi di rafforzamento strutturale, PONa3_00052, Avviso 254/Ric) and PRISMA (Asse II-Sostegno all’innovazione, PON04a2_A). We thank an anonymous reviewer for the suggestion about the plot of .
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aki, K.; Chouet, B. Origin of Coda Waves: Source, Attenuation, and Scattering Effects. J. Geophys. Res. 1975, 80, 3322–3342. [Google Scholar] [CrossRef]
- Sato, H. Energy Propagation Including Scattering Effects Sengle Isotropic Scattering Approximation. J. Phys. Earth 1977, 25, 27–41. [Google Scholar] [CrossRef]
- Ibáñez, J.M.; Pezzo, E.D.; Miguel, F.D.; Herraiz, M.; Alguacil, G.; Morales, J. Depth-Dependent Seismic Attenuation in the Granada Zone (Southern Spain). Bull. Seismol. Soc. Am. 1990, 80, 1232–1244. [Google Scholar]
- Jin, A.; Aki, K. High-Resolution Maps of Coda Q in Japan and Their Interpretation by the Brittle-Ductile Interaction Hypothesis. Earth Planets Space 2005, 57, 403–409. [Google Scholar] [CrossRef][Green Version]
- Carcolé, E.; Sato, H. Spatial Distribution of Scattering Loss and Intrinsic Absorption of Short-Period S Waves in the Lithosphere of Japan on the Basis of the Multiple Lapse Time Window Analysis of Hi-Net Data. Geophys. J. Int. 2010, 180, 268–290. [Google Scholar] [CrossRef]
- Wang, W.; Shearer, P.M. An Improved Method to Determine Coda-Q, Earthquake Magnitude, and Site Amplification: Theory and Application to Southern California. J. Geophys. Res. Solid Earth 2019, 124, 578–598. [Google Scholar] [CrossRef]
- Zeng, Y.; Su, F.; Aki, K. Scattering Wave Energy Propagation in a Random Isotropic Scattering Medium: 1. Theory. J. Geophys. Res. Solid Earth 1991, 96, 607–619. [Google Scholar] [CrossRef]
- Paasschens, J.C.J. Solution of the Time-Dependent Boltzmann Equation. Phys. Rev. E 1997, 56, 1135–1141. [Google Scholar] [CrossRef]
- Mayeda, K.; Koyanagi, S.; Hoshiba, M.; Aki, K.; Zeng, Y. A Comparative Study of Scattering, Intrinsic, and Coda Q−1 for Hawaii, Long Valley, and Central California between 1.5 and 15.0 Hz. J. Geophys. Res. Solid Earth 1992, 97, 6643–6659. [Google Scholar] [CrossRef]
- Sato, H.; Fehler, M.C.; Maeda, T. Envelope Synthesis Based on the Radiative Transfer Theory. In Seismic Wave Propagation and Scattering in the Heterogeneous Earth, 2nd ed.; Sato, H., Fehler, M.C., Maeda, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 245–318. ISBN 978-3-642-23029-5. [Google Scholar]
- Del Pezzo, E.; Ibáñez, J.M. Seismic Coda-Waves Imaging Based on Sensitivity Kernels Calculated Using an Heuristic Approach. Geosciences 2020, 10, 304. [Google Scholar] [CrossRef]
- Shapiro, N.M. The Energy Partitioning and the Diffusive Character of the Seismic Coda. Bull. Seismol. Soc. Am. 2000, 90, 655–665. [Google Scholar] [CrossRef]
- Frankel, A.; Wennerberg, L. Energy-Flux Model of Seismic Coda: Separation of Scattering and Intrinsic Attenuation. Bull. Seismol. Soc. Am. 1987, 77, 1223–1251. [Google Scholar] [CrossRef]
- Singh, S.; Herrmann, R.B. Regionalization of Crustal Coda Q in the Continental United States. J. Geophys. Res. Solid Earth 1983, 88, 527–538. [Google Scholar] [CrossRef]
- Pacheco, C.; Snieder, R. Time-Lapse Traveltime Change of Singly Scattered Acoustic Waves. Geophys. J. Int. 2006, 165, 485–500. [Google Scholar] [CrossRef]
- Mayor, J.; Margerin, L.; Calvet, M. Sensitivity of Coda Waves to Spatial Variations of Absorption and Scattering: Radiative Transfer Theory and 2-D Examples. Geophys. J. Int. 2014, 197, 1117–1137. [Google Scholar] [CrossRef]
- Yoshimoto, K. Monte Carlo Simulation of Seismogram Envelopes in Scattering Media. J. Geophys. Res. Solid Earth 2000, 105, 6153–6161. [Google Scholar] [CrossRef]
- De Siena, L.; Del Pezzo, E.; Thomas, C.; Curtis, A.; Margerin, L. Seismic Energy Envelopes in Volcanic Media: In Need of Boundary Conditions. Geophys. J. Int. 2013, 195, 1102–1119. [Google Scholar] [CrossRef]
- Del Pezzo, E.; De La Torre, A.; Bianco, F.; Ibanez, J.; Gabrielli, S.; De Siena, L. Numerically Calculated 3D Space-Weighting Functions to Image Crustal Volcanic Structures Using Diffuse Coda Waves. Geosciences 2018, 8, 175. [Google Scholar] [CrossRef]
- Giampiccolo, E.; Del Pezzo, E.; Tuvé, T.; Grazia, G.D.; Ibáñez, J.M. 3-D Q-Coda Attenuation Structure at Mt. Etna (Italy). Geophys. J. Int. 2021, 227, 544–558. [Google Scholar] [CrossRef]
- Mayor, J.; Calvet, M.; Margerin, L.; Vanderhaeghe, O.; Traversa, P. Crustal Structure of the Alps as Seen by Attenuation Tomography. Earth Planet. Sci. Lett. 2016, 439, 71–80. [Google Scholar] [CrossRef]
- Sketsiou, P.; Napolitano, F.; Zenonos, A.; De Siena, L. New Insights into Seismic Absorption Imaging. Phys. Earth Planet. Inter. 2020, 298, 106337. [Google Scholar] [CrossRef]
- Filippucci, M.; Del Pezzo, E.; de Lorenzo, S.; Tallarico, A. 2D Kernel-Based Imaging of Coda-Q Space Variations in the Gargano Promontory (Southern Italy). Phys. Earth Planet. Inter. 2019, 297, 106313. [Google Scholar] [CrossRef]
- Tripaldi, S. Electrical signatures of a permeable zone in carbonates hosting local geothermal manifestations: Insights for the deep fluid flow in the Gargano area (south-eastern Italy). Boll. Di Geofis. Teori. Ed. Appl. 2020, 61, 219–232. [Google Scholar] [CrossRef]
- Della Vedova, B.D.; Bellani, S.; Pellis, G.; Squarci, P. Deep temperatures and surface heat flow distribution. In Anatomy of an Orogen: The Apennines and Adjacent Mediterranean Basins; Vai, G.B., Martini, I.P., Eds.; Springer: Dordrecht, The Netherlands, 2001; pp. 65–76. ISBN 978-94-015-9829-3. [Google Scholar]
- Miccolis, S.; Filippucci, M.; de Lorenzo, S.; Frepoli, A.; Pierri, P.; Tallarico, A. Seismogenic Structure Orientation and Stress Field of the Gargano Promontory (Southern Italy) From Microseismicity Analysis. Front. Earth Sci. 2021, 9, 179. [Google Scholar] [CrossRef]
- Filippucci, M.; Miccolis, S.; Castagnozzi, A.; Cecere, G.; de Lorenzo, S.; Donvito, G.; Falco, L.; Michele, M.; Nicotri, S.; Romeo, A.; et al. Seismicity of the Gargano Promontory (Southern Italy) after 7 Years of Local Seismic Network Operation: Data Release of Waveforms from 2013 to 2018. Data Brief 2021, 35, 106783. [Google Scholar] [CrossRef]
- Filippucci, M.; Pierri, P.; de Lorenzo, S.; Tallarico, A. The Stress Field in the Northern Apulia (Southern Italy), as Deduced from Microearthquake Focal Mechanisms: New Insight from Local Seismic Monitoring. In International Conference on Computational Science and Its Applications; Springer: Cham, Switzerland, 2020; Volume 12255 LNCS, pp. 914–927. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Pierri, P.; Frepoli, A.; Calcagnile, G.; Venisti, N.; Cimini, G.B. A Critical Revision of the Seismicity of Northern Apulia (Adriatic Microplate—Southern Italy) and Implicationsfor the Identification of Seismogenic Structures. Tectonophysics 2007, 436, 9–35. [Google Scholar] [CrossRef]
- Mantovani, E.; Babbucci, D.; Viti, M.; Albarello, D.; Mugnaioli, E.; Cenni, N.; Casula, G. Post-late miocene kinematics of the adria microplate: Inferences from geological, geophysical and geodetic data. In The Adria Microplate: GPS Geodesy, Tectonics and Hazards; Pinter, N., Gyula, G., Weber, J., Stein, S., Medak, D., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 51–69. [Google Scholar]
- Filippucci, M.; Miccolis, S.; Castagnozzi, A.; Cecere, G.; de Lorenzo, S.; Donvito, G.; Falco, L.; Michele, M.; Nicotri, S.; Romeo, A.; et al. Gargano Promontory (Italy) Microseismicity (2013-2018): Waveform Data and Earthquake Catalogue. Mendeley Data 2021, 3. [Google Scholar] [CrossRef]
- INGV. Seismological Data Centre Rete Sismica Nazionale (RSN). 2006, Approx. 20 GByte/day of New Waveform Data, Approx. 366 Active Seismic Stations, the Archive Totals to More Than 500 Distinct Seismic Stations. Available online: http://cnt.rm.ingv.it/instruments/network/IV (accessed on 28 May 2021).
- De Lorenzo, S.; Michele, M.; Emolo, A.; Tallarico, A. A 1D P-Wave Velocity Model of the Gargano Promontory (South-Eastern Italy). J. Seism. 2017, 21, 909–919. [Google Scholar] [CrossRef]
- Filippucci, M.; Tallarico, A.; Dragoni, M.; de Lorenzo, S. Relationship Between Depth of Seismicity and Heat Flow: The Case of the Gargano Area (Italy). Pure Appl. Geophys. 2019, 176, 2383–2394. [Google Scholar] [CrossRef]
- Milano, G.; Di Giovambattista, R.; Ventura, G. Seismic Constraints on the Present-Day Kinematics of the Gargano Foreland, Italy, at the Transition Zone between the Southern and Northern Apennine Belts. Geophys. Res. Lett. 2005, 32, L24308. [Google Scholar] [CrossRef]
- QGIS. Available online: https://www.qgis.org/it/site/index.html (accessed on 28 May 2021).
- University of Bari “Aldo Moro” OTRIONS, Seismic Networks of Gargano Area (Italy). 2013. Available online: https://www.fdsn.org/networks/detail/OT/ (accessed on 28 May 2021).
- Aki, K. Analysis of the Seismic Coda of Local Earthquakes as Scattered Waves. J. Geophys. Res. 1969, 74, 615–631. [Google Scholar] [CrossRef]
- De Lorenzo, S.; Del Pezzo, E.; Bianco, F. Qc, Qβ, Qi and Qs Attenuation Parameters in the Umbria–Marche (Italy) Region. Phys. Earth Planet. Inter. 2013, 218, 19–30. [Google Scholar] [CrossRef]
- Kumar, N.; Parvez, I.A.; Virk, H.S. Estimation of Coda Wave Attenuation for NW Himalayan Region Using Local Earthquakes. Phys. Earth Planet. Inter. 2005, 151, 243–258. [Google Scholar] [CrossRef]
- Romanowicz, B.; Mitchell, B.J. Q of the Earth: Global, Regional, and Laboratory Studies; Birkhäuser: Basel, Switzerland, 2012; ISBN 978-3-0348-8711-3. [Google Scholar]
- Eva, C.; Cattaneo, M.; Augliera, P.; Pasta, M. Regional Coda Q Variations in the Western Alps (Northern Italy). Phys. Earth Planet. Inter. 1991, 67, 76–86. [Google Scholar] [CrossRef]
- Singh, D.D.; Govoni, A.; Bragato, P.L. Coda QcAttenuation and Source Parameter Analysis in Friuli (NE Italy) and Its Vicinity. Pure Appl. Geophys. 2001, 158, 1737–1761. [Google Scholar] [CrossRef]
- Giampiccolo, E.; Tuvè, T. Regionalization and Dependence of Coda Q on Frequency and Lapse Time in the Seismically Active Peloritani Region (Northeastern Sicily, Italy). J. Seism. 2018, 22, 1059–1074. [Google Scholar] [CrossRef]
- Tuvè, T.; Bianco, F.; Ibáñez, J.; Patanè, D.; Del Pezzo, E.; Bottari, A. Attenuation Study in the Straits of Messina Area (Southern Italy). Tectonophysics 2006, 421, 173–185. [Google Scholar] [CrossRef]
- Giampiccolo, E.; Tusa, G.; Langer, H.; Gresta, S. Attenuation in Southeastern Sicily (Italy) by Applying Different Coda Methods. J. Seismol. 2002, 6, 487–501. [Google Scholar] [CrossRef]
- Pujades, L.G.; Ugalde, A.; Canas, J.A.; Navarro, M.; Badal, F.J.; Corchete, V. Intrinsic and Scattering Attenuation from Observed Seismic Codas in the Almeria Basin (Southeastern Iberian Peninsula). Geophys. J. Int. 1997, 129, 281–291. [Google Scholar] [CrossRef]
- Dasović, I.; Herak, M.; Herak, D. Coda-Q and Its Lapse Time Dependence Analysis in the Interaction Zone of the Dinarides, the Alps and the Pannonian Basin. Phys. Chem. Earth Parts A/B/C 2013, 63, 47–54. [Google Scholar] [CrossRef]
- Boulanouar, A.; Moudnib, L.E.; Padhy, S.; Harnafi, M.; Villaseñor, A.; Gallart, J.; Pazos, A.; Rahmouni, A.; Boukalouch, M.; Sebbani, J. Estimation of Coda Wave Attenuation in Northern Morocco. Pure Appl. Geophys. 2018, 175, 883–897. [Google Scholar] [CrossRef]
- Shengelia, I.; Jorjiashvili, N.; Godoladze, T.; Javakhishvili, Z.; Tumanova, N. Intrinsic and Scattering Attenuations in the Crust of the Racha Region, Georgia. J. Earthq. Tsunami 2019, 14, 2050006. [Google Scholar] [CrossRef]
- Gupta, A.K.; Sutar, A.K.; Chopra, S.; Kumar, S.; Rastogi, B.K. Attenuation Characteristics of Coda Waves in Mainland Gujarat (India). Tectonophysics 2012, 530–531, 264–271. [Google Scholar] [CrossRef]
- Kandel, T.P.; Yamada, M.; Pokhrel, P. Determination of High-Frequency Attenuation Characteristic of Coda Waves in the Central Region of Nepal Himalaya. J. Nepal Geol. Soc. 2020, 60, 75–86. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Tyagi, C. Lapse Time and Frequency-Dependent Attenuation Characteristics of Coda Waves in the Northwestern Himalayas. J. Seism. 2007, 11, 149–158. [Google Scholar] [CrossRef]
- Thirunavukarasu, A.; Kumar, A.; Mitra, S. Lateral Variation of Seismic Attenuation in Sikkim Himalaya. Geophys. J. Int. 2017, 208, 257–268. [Google Scholar] [CrossRef]
- Chung, J.-K.; Chen, Y.-L.; Shin, T.-C. Spatial Distribution of Coda Q Estimated from Local Earthquakes in Taiwan Area. Earth Planet Space 2009, 61, 1077–1088. [Google Scholar] [CrossRef][Green Version]
- Kosuga, M. Dependence of Coda Q on Frequency and Lapse Time in the Western Nagano Region, Central Japan. J. Phys. Earth 1992, 40, 421–445. [Google Scholar] [CrossRef]
- Parvez, I.A.; Sutar, A.K.; Mridula, M.; Mishra, S.K.; Rai, S.S. Coda Q Estimates in the Andaman Islands Using Local Earthquakes. Pure Appl. Geophys. 2008, 165, 1861–1878. [Google Scholar] [CrossRef]
- Vieira Barros, L.; Assumpção, M.; Quintero, R.; Ferreira, V.M. Coda Wave Attenuation in the Parecis Basin, Amazon Craton, Brazil: Sensitivity to Basement Depth. J. Seism. 2011, 15, 391–409. [Google Scholar] [CrossRef]
- Biescas, B.; Rivera, Z.; Zapata, J.A. Seismic Attenuation of Coda Waves in the Eastern Region of Cuba. Tectonophysics 2007, 429, 99–109. [Google Scholar] [CrossRef]
- Dobrynina, A.A.; Albaric, J.; Deschamps, A.; Perrot, J.; Ferdinand, R.W.; Déverchère, J.; San’kov, V.A.; Chechel’nitskii, V.V. Seismic Wave Attenuation in the Lithosphere of the North Tanzanian Divergence Zone (East African Rift System). Russ. Geol. Geophys. 2017, 13, 253–265. [Google Scholar] [CrossRef]
- Bianco, F.; Pezzo, E.D.; Malagnini, L.; Luccio, F.D.; Akinci, A. Separation of Depth-Dependent Intrinsic and Scattering Seismic Attenuation in the Northeastern Sector of the Italian Peninsula. Geophys. J. Int. 2005, 161, 130–142. [Google Scholar] [CrossRef]
- Bianco, F.; Del Pezzo, E.; Castellano, M.; Ibanez, J.; Di Luccio, F. Separation of Intrinsic and Scattering Seismic Attenuation in the Southern Apennine Zone, Italy. Geophys. J. Int. 2002, 150, 10–22. [Google Scholar] [CrossRef]
- Del Pezzo, E.; Giampiccolo, E.; Tuvé, T.; Di Grazia, G.; Gresta, S.; Ibàñez, J.M. Study of the Regional Pattern of Intrinsic and Scattering Seismic Attenuation in Eastern Sicily (Italy) from Local Earthquakes. Geophys. J. Int. 2019, 218, 1456–1468. [Google Scholar] [CrossRef]
- Hoshiba, M. Simulation of Multiple-Scattered Coda Wave Excitation Based on the Energy Conservation Law. Phys. Earth Planet. Inter. 1991, 67, 123–136. [Google Scholar] [CrossRef]
- Padhy, S.; Subhadra, N.; Kayal, J.R. Frequency-Dependent Attenuation of Body and Coda Waves in the Andaman Sea Basin. Bull. Seismol. Soc. Am. 2011, 101, 109–125. [Google Scholar] [CrossRef]
- Farrokhi, M.; Hamzehloo, H.; Rahimi, H.; Allameh Zadeh, M. Separation of Intrinsic and Scattering Attenuation in the Crust of Central and Eastern Alborz Region, Iran. Phys. Earth Planet. Inter. 2016, 253, 88–96. [Google Scholar] [CrossRef]
- Akinci, A.; Del Pezzo, E.; Ibáñez, J.M. Separation of Scattering and Intrinsic Attenuation in Southern Spain and Western Anatolia (Turkey). Geophys. J. Int. 1995, 121, 337–353. [Google Scholar] [CrossRef]
- Jin, A.; Aki, K. Spatial and Temporal Correlation between Coda Q−1 and Seismicity and Its Physical Mechanism. J. Geophys. Res. Solid Earth 1989, 94, 14041–14059. [Google Scholar] [CrossRef]
- Sharma, B.; Teotia, S.S.; Kumar, D. Attenuation of P, S, and Coda Waves in Koyna Region, India. J. Seism. 2007, 11, 327–344. [Google Scholar] [CrossRef]
- Morozov, I.B. Geometrical Attenuation, Frequency Dependence of Q, and the Absorption Band Problem. Geophys. J. Int. 2008, 175, 239–252. [Google Scholar] [CrossRef]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P. The Italian Earthquake Catalogue CPTI15. Bull. Earthq. Eng. 2020, 18, 2953–2984. [Google Scholar] [CrossRef]
- Loddo, M.; Quarto, R.; Schiavone, D. Integrated Geophysical Survey for the Geological Structural and Hydrogeothermal Study of the North-Western Gargano Promontory (Southern Italy). Ann. Geophys. 1996, 39. [Google Scholar] [CrossRef]
- Catalano, R.; Di Stefano, P.; Nigro, F.; Vitale, F.P. The Sicily mainland thrust belt: Evolution during the Neogene. Boll. Geofis. Teor. Appl. 1994, 36, 127–138. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).