Flow Control Techniques for Enhancing the Bio-Recognition Performance of Microfluidic-Integrated Biosensors

Featured Application

Microfluidic-integrated biosensor design for point-of-care applications.

Abstract

Biosensors are favored devices for the fast and cost-effective detection of biological species without the need for laboratories. Microfluidic integration with biosensors has advanced their capabilities in selectivity, sensitivity, controllability, and conducting multiple binding assays simultaneously. Despite all the improvements, their design and fabrication are still challenging and time-consuming. The current study aims to enhance microfluidic-integrated biosensors’ performance. Three different functional designs are presented with both active (with the help of electroosmotic flow) and passive (geometry optimization) methods. For validation and further studies, these solutions are applied to an experimental setup for DNA hybridization. The numerical results for the original case have been validated with the experimental data from previous literature. Convection, diffusion, migration, and hybridization of DNA strands during the hybridization process have been simulated with finite element method (FEM) in 3D. Based on the results, increasing the velocity on top of the functionalized surface, by reducing the thickness of the microchamber in that area, would increase the speed of surface coverage by up to 62%. An active flow control with the help of electric field would increase this speed by 32%. In addition, other essential parameters in the fabrication of the microchamber, such as changes in pressure and bulk concentration, have been studied. The suggested designs are simple, applicable and cost-effective, and would not add extra challenges to the fabrication process. Overall, the effect of the geometry of the microchamber on the time and effectiveness of biosensors is inevitable. More studies on the geometry optimization of the microchamber and position of the electrodes using machine learning methods would be beneficial in future works.

1. Introduction

A biosensor is a device that uses an immobilized agent (enzymes, antibiotics, organelles, or whole cells) to detect the biological targets. The biological targets are nearly always transported by a carrier fluid, in vitro and in vivo. Especially for point-of-care applications and human body samples, bio-MEMS and microsystems must deal with body fluids [1,2]. Hence, microfluidics is a crucial element in the design and fabrication of biosensors. Since 1990, with the advent of microfluidics, the development of microfluidic-integrated biosensors has been intensive due to their potential in early diagnosis, on-site and routine analysis, and high selectivity [3]. Microfluidics also improve sensitivity by providing a more stable sensing environment, integrating multiple functions, and enhancing efficiency, accuracy, and controllability while reducing the sensing region [4,5,6]. The attention towards microfluidic-integrated biosensors is enhanced extra by its capability of detecting a low concentration of biomarkers [7,8]. It also has application in various fields such as real-time health monitoring, point-of-care (POC) disease diagnosis, significant data statistics in health management, food safety, and environmental monitoring [9,10,11].

Although there has been a significant improvement in current biosensors, the design and fabrication are still challenging and time-consuming. These challenges are bolder in bio-receptors and assay matrix design, achieving specific binding and detecting low concentration target molecules within a low-volume sample [12,13,14,15,16]. Scientists have been using various active and passive methods to improve biosensors’ sensing and fabrication to resolve these challenges. In passive methods, sensing is enhanced with new materials and geometry optimization, while in active methods, moving parts and external forces such as electric or pressure field are applied. Some solution in this matter include utilizing conducting polymers for high-performance biosensors due to their chemical versatility and charge transport [17,18], use of metamaterials in resonators for better and durable biosensors [19,20], microelectrode array approach for high sensitivity and live detection [21,22], and microfluidic approach for DNA analysis [23,24,25]. In the current study, to enhance the performance of microfluidic-integrated biosensors, three different types of functional designs, with both active (E cases) and passive (H cases) methods, are presented. It is shown that these designs would improve the efficiency (in sensing and time of detection) by 6–62%, while they would not have a considerable effect on the fabrication and costs. Additional advantages of these designs are simplicity and application to different channels. Finally, for validation and further studies, these methods are applied on an experimental setup of DNA hybridization. Figure 1 illustrates the bio-recognition process for DNA hybridization.

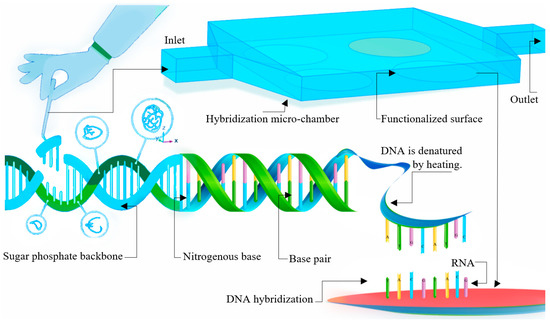
Figure 1. Bio-recognition process for DNA hybridization in a microchamber equipped with four functionalized surfaces for recognizing a specific sequence, dissociation of the double helix structure of the DNA, and hybridization with the functionalized surface.

In a specific condition of pH or temperature, the double helix can start denaturing. Then, the single DNA strands can be used in the bio-recognition process. First, a known DNA sequence is fabricated and copied; then, they are used to functionalize the surface to recognize the complementary sequence of specific DNA strands [26,27]. The buffer fluid carrying the targeted DNA strands would pass through the functionalized surfaces in the microchamber. As a result, the targeted DNA strands would bond with their complementary DNA strands on the surface. This is a reversible equilibrium reaction, which is called hybridization [28]. Then, the methodology for numerical simulation of DNA hybridization in microchamber, governing equations, and boundary conditions are presented. In this numerical method [2,29], the microchamber’s convection, diffusion, hybridization, and DNA-strand migration are modelled. The numerical results for the original setup have been validated with experimental data from the previous literature [28]. In the final part, through numerical results, the performance of different cases has been studied. The ‘best’ design choices have been introduced based on the efficiency, ease of fabrication, cost, and applicability of different cases.

2. Model Setup

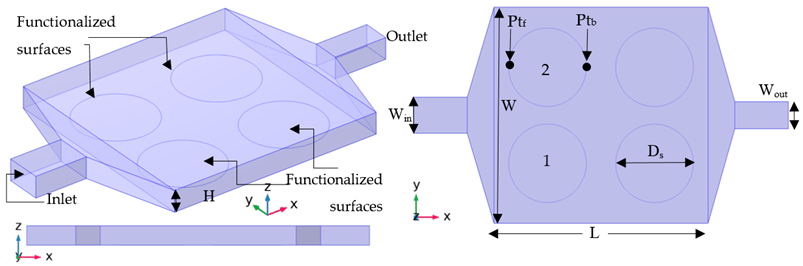
DNA hybridization is another sensing application of a functionalized surface in the microchannel. An experimental device for the bio-recognition of DNA is used as the base case study (Case A-01). The experimental setup corresponds to the model in Table 1 and Table 2—this microchamber comprising four reactive surfaces. The buffer fluid carries DNA strands with 15 $\mathrm{bp}$(basis pairs) and goes through the microchamber, and passes the functionalized surfaces. The flow is on for the first 50 $\min$ ($t_1)$ and then it is stopped for the next 100 $\min$ ($t_0)$. Dimension of the microchamber, the buffer fluid conditions, and the hybridization properties are presented in Table 1.

Table 1. The experimental properties for hybridization of short DNA strands.

Sign	Name	Value
$\mathrm{bp}$	Number of essential pairs DNA strands	15
$D$	Diffusion coefficient ($\mathrm{m}/\mathrm{s}$)	7.5 × 10−10
$c_0$	Inlet Concentration of targets or analytes ($\mathrm{mol}/{\mathrm{m}}^3$)	4.6 × 10−6
$k_{on}$	Adsorption coefficient at the wall (${\mathrm{m}}^3/\left(\mathrm{s}·\mathrm{mol}\right)$)	125
$k_{off}$	Desorption coefficient at the wall or elution ($1/\mathrm{s}$)	10−5
$b_m$	Initial concentration in available hybridization sites ($\mathrm{mol}/{\mathrm{m}}^2$)	9.064 × 10−8
$V_{av}$	Average flow velocity ($\mathrm{m}/\mathrm{s}$)	10−3
${\sigma }_w$	The conductivity of the ionic solution ($\mathrm{S}/\mathrm{m}$)	1.1845 × 10−1
${\epsilon }_r$	The relative permittivity of the fluid	80.2
ζ	Zeta potential ($\mathrm{V}$)	−0.1
$V_0$	The maximum value of AC potential ($\mathrm{V}$)	0.1
ω	Angular frequency of AC potential ($\mathrm{Hz}$)	50.265
$P_2$	Pressure in the second outlet for case S-05 ($\mathrm{pa}$)	−2
$H$	Height of the microchamber ($\mathrm{m}$)	10−3
$H_s$	Height of the volume above the biosensor for case H-03 ($\mathrm{m}$)	2.5 × 10−4
$L$	Length of the microchamber ($\mathrm{m}$)	10−2
$W$	Width of the micro ($\mathrm{m}$)	10−2
$W_{in}$	Width of the inlet ($\mathrm{m}$)	1.25 × 10−3
$W_{out}$	Width of the outlet ($\mathrm{m}$)	10−3

Table 2. The geometry of the microchamber for four types of setups; original experimental setup (Case A), thin chamber (series H), suction (series S), and electroosmotic flow (series E).

Case A-01
Case Series H
Case Series S
Case Series E

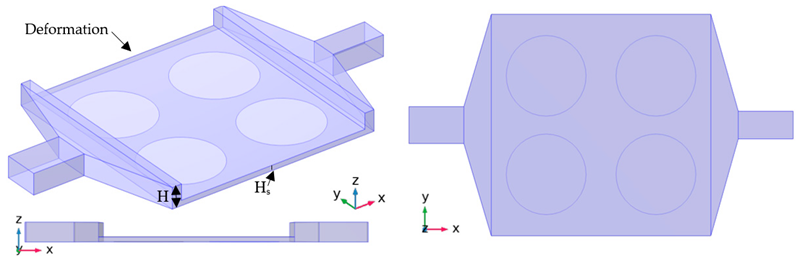
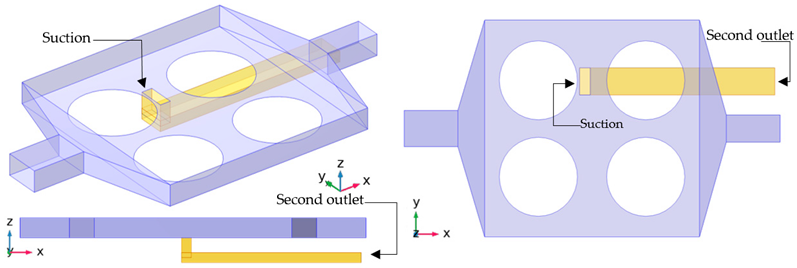
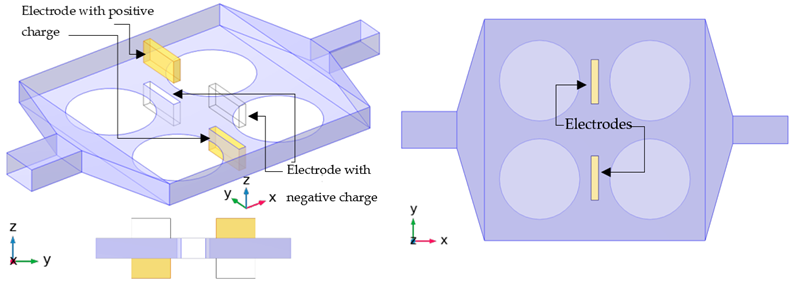
The primary purpose of this biochip is the analysis and recognition of DNA strands. Therefore, the detection process should be fast, reliable, and sensitive. In addition, the design must be suitable for simultaneous and parallel recognition. With this aim, three other types of designs are applied to the original case (A-01). Details of these cases are presented in Table 2 and Table 3. In the first design, the flow volume on top of the functionalized surfaces is reduced to improve the sensing performance and reducing the detection time by applying a deformation in the geometry (cases H-02 and H-03). In the second design, a second outlet is added to the setup to improve one of the functionalized surfaces (cases S-04 and S-05). In the last design, the efficiency is enhanced with the help of electroosmotic flow (cases E-06 and E-07).

Table 3. Difference of the setups; original experimental setup (case A-01), thin chamber (series H-02), the thin chamber with half-height (case H-03), second outlet with zero pressure (case S-04), suction (case S-05), electroosmotic flow (cases E-06 and E-07).

Name	Hs	Po2	V	Description
Case A-01	$H$	$N/A$	$0$	The original experimental setup.
Case H-02	$H_s$	$N/A$	$0$	Deformation is added at the top of the channel of case A-01.
Case H-03	$H_s/2$	$N/A$	$0$	The height of the deformation in case H-02 is halved.
Case S-04	$H$	$0$	$0$	A second outlet is added close to case A-01.
Case S-05	$H$	$P_2$	$0$	A suction is added to the case S-04.
Case E-06	$H$	$N/A$	$V_0$	The Electroosmotic effect is applied to case A-01.
Case E-07	$H$	$N/A$	$2\times V_0$	The potential in Case E-06 is doubled for this case.

3. Methods

DNA strands are immersed and carried by buffer fluid in the microchamber. Flow behavior, biochemical reaction kinetics, and the presence of DNA in the vicinity of the reagents are important design factors. Hence, in the numerical simulation, coupling these critical parameters is essential. For this matter, the current approach consists of three steps: (1) modelling the microfluidic flow as a carrier fluid, (2) modelling the behavior of DNA strands in the microchamber, and (3) modelling the electroosmotic flow. These three models have been coupled and solved with the 3D finite element method (FEM) in the commercial code, COMSOL, for all 7 cases in Table 3. However, the third approach is only applicable for cases E-01 and E-02.

Since the concentration of DNA strands is lower than 10% of the concentration of the buffer fluid, the targeted species could be assumed to be diluted. Due to the dilution, the whole sample fluid’s properties would be considered as the solvent (water). The flow is highly ordered laminar in this microchamber as the Reynolds number is less than 10.

For the first step, the Navier–Stokes Equations (Equations (1)–(4)) describe the flow in the microchamber [2].

$$\frac{\partial \rho }{\partial t}+\rho \left[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\right]=0$$

(1)

$$\rho \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}=-\frac{\partial p}{\partial x}+\mu \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)$$

(2)

$$\rho \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}=-\frac{\partial p}{\partial y}+\mu \left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial z^2}\right)$$

(3)

$$\rho \frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}=-\frac{\partial p}{\partial z}+\mu \left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)$$

(4)

where $u$ and $v$ ($\mathrm{m}/\mathrm{s}$) are the velocity in the $x$ and $y$ direction, respectively, while $\rho$ ($\mathrm{kg}/{\mathrm{m}}^3$) is the density, and $\mu$ $(\mathrm{kg}/\left(\mathrm{m}·\mathrm{s}\right))$ is the molecular viscosity. The fluid is considered as continuum and incompressible because of its negligible changes in density.

In the second step, the focus is on the adsorption reactions for DNA hybridization. The adsorption and desorption reactions at the functionalized surfaces are described by reaction in Equation (5) [28].

$$A { }_{\underset{ k_{off }}{\leftarrow }}^{\stackrel{ k{ }_{on }}{\to }} A_s$$

(5)

where $k_{on}$ denotes the adsorption coefficient at the wall (${\mathrm{m}}^3/\left(\mathrm{s}·\mathrm{mol}\right)$), $k_{off}$ refers to the desorption coefficient at the wall or elution ($1/\mathrm{s}$), $A$ represents the DNA strands in the buffer fluid and $A_s$ refers to the ones adsorbed on the functionalized surfaces. Electrokinetic flow or ionic migration only occur in case series $E$ (the third step). Overall, for steps two and three, the general mass balance equation for convection, diffusion, and migration is solved (Equation (6)) [30].

$$\frac{\partial c}{\partial t}=\nabla ·\left(-D\nabla c+z{u}_{m}Fc\nabla V-cU\right)+S$$

(6)

where $c$ ($\mathrm{mol}/{\mathrm{m}}^3$) denotes the bulk concentration of DNA strands, $D$ (${\mathrm{m}}^2/\mathrm{s}$) is the diffusion coefficient of it, $z$ is the charge number of ionic species, $U$ ($\mathrm{m}/\mathrm{s}$) is the velocity field, $F$ ($\mathrm{A}.\mathrm{s}/\mathrm{mol}$) is Faraday’s constant, $V$ ($\mathrm{V}$) refers to the electric potential, $u_m$ ($\mathrm{mol}.\mathrm{s}/\mathrm{kg}$) denotes the ionic mobility, and $S$ is the reaction rate expression for the chemical species or any other source or sink terms. The velocity can be computed with the Navier-stokes equations (Equations (1)–(4)). Based on the Langmuir model [28], the source term in the equation is generated with the rate of adsorption and desorption of DNA strands (Equations (7)–(9)).

$$r_{ads}=k_{on}c\left(b_m-b\right)$$

(7)

$$r_{des}=k_{off}b$$

(8)

$$S=r_{ads}-r_{des}$$

(9)

in which $b_m$ ($\mathrm{mol}/{\mathrm{m}}^2$) is the total surface concentration of active sites, $b$ ($\mathrm{mol}/{\mathrm{m}}^2$) is the surface concentration of $A$, $r_{ads}$ ($\mathrm{mol}/({\mathrm{m}}^2·\mathrm{s})$) refers to the adsorption rate and $r_{des}$ ($\mathrm{mol}/({\mathrm{m}}^2·\mathrm{s})$) refers to the desorption rate of the targeted species.

The Helmholtz–Smoluchowski [31] relation is used for relating the tangent component of the applied electric field with the electroosmotic velocity (Equation (10)).

$$u=\frac{{\epsilon }_w{\zeta }_0}{RT}{\nabla }_{T}V$$

(10)

where ${\epsilon }_w$ ($\mathrm{F}/\mathrm{m}$) is the fluid’s electric permittivity, ${\zeta }_0$ ($\mathrm{V}$) is the zeta potential at the channel wall, $R$ ($\mathrm{J}/\left(\mathrm{mol}·\mathrm{K}\right)$) refers to the molar gas constant, and $T$ ($\mathrm{K}$) is the temperature. The reactions are modelled based on the mass action law. The current balance can be expressed with Ohm’s law (Equation (11)) by assuming no concentration gradients in the ions.

$$\nabla ·\left(\sigma \nabla V\right)=0$$

(11)

in which $\sigma$ ($\mathrm{S}/\mathrm{m}$) is the conductivity.

4. Boundary Conditions

The diluted solutions enter from the inlet with a constant velocity ($u_0)$ and concentration ($c_0)$. Fluid goes through the microchamber with the no-slip condition for its velocity. At the same time, the concentration of bio-species in the solution would have the homogeneous Neumann condition on the walls and Neumann condition on the functionalized surfaces. The boundary conditions are the same for all cases and are summarized in Table 4, although in the S series, an extra outlet is added close to the functionalized surface 3 to study its efficiency. In E, electrokinetic force field is added with four electrodes placed on two sides of the microchamber, as shown in Table 2.

Table 4. Boundary conditions for four setups: original experimental setup (Case A), thin chamber (series H), suction (series S), and electroosmotic flow (series E).

Boundary	Concentration, Velocity, and Electric Potential
Inlet	$c=c_0$, $u=u_0$
Outlet	$n.\left(-D\nabla c+cu\right)=n.cu$
Walls	$\frac{\partial c}{\partial n}=0$, no-slip
Functionalized surfaces	$\frac{\partial c}{\partial n}=-\frac{1}{D}\frac{\partial b}{\partial t}$, no-slip
Insulated (E setup)	$n.\left(-D\nabla \mathrm{b}\right)=0$, $-\sigma \nabla V·n=0$
Electrodes (E setup)	$V_0$

5. Results and Discussion

The geometries in Table 1 are used for conducting the present numerical simulations. First, a mesh independence study has been carried out to ensure adequate resolution. Based on the results, 443,000 tetrahedral elements would provide reliable and comparably fast results for this dimension. Subsequently, the validity of the numerical model is tested by modelling the experimental setup (case A-01) [28]. In this setup, a constant carrier fluid flow, which carries different sequences and lengths of DNA strands, starts at the time $t_0$. After 50 $\min$ ($t_1$), the flow stops for the next 100 $\min$ (until $t_2$). The details of the experimental setup, the flow conditions, and the kinetics of oligonucleotide are presented in Table 2 and Table 3.

Figure 2 shows the surface coverage ($\theta$) over time for both numerical study and the experimental results [28]. The numerical model is validated based on the results since it shows a good agreement with the experimental data.

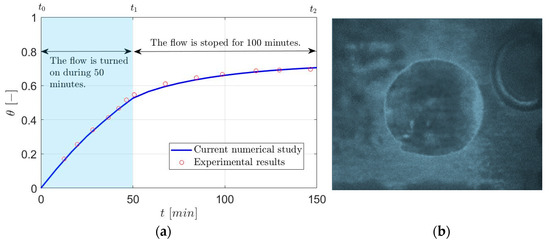
Figure 2. The time-dependent solution from the beginning of the test ($t_0$) to 50 $\min$ ($t_1$), and 150 $\min$ ($t_2$) [28].

For a better comparison, the surface coverage ($\theta )$, the fraction of active sites occupied by adsorbed DNA strands (Equation (12)) are used for presenting the results.

$$\theta =\frac{b}{b_m}$$

(12)

Figure 3 shows the bulk concentration of DNA strands as the flow goes through the microchamber. As time passes, the bulk concentration around the functionalized surfaces reduces since the targeted DNA strands are binding with their specific ligand on the surface. This can be more evident in the surface coverage and surface concentration results in Figure 4, as it shows an increase in the surface coverage over time. After the validation, the numerical simulation is carried out for various cases of the three other setups: thin chamber (H series), suction (S series), and electroosmotic flow (E series). For each set, only the optimized values are presented in this paper. For instance, for the H series, the height ${\mathrm{H}}_{\mathrm{s}}$ varied from $\mathrm{H}/1.2$ to $\mathrm{H}/20$, but only case H-02 (${\mathrm{H}}_{\mathrm{s}}=\mathrm{H}/2$) and H-03 (${\mathrm{H}}_{\mathrm{s}}=\mathrm{H}/4$) are presented here since they have shown the best performance while not causing extra fabrication challenges. Figure 5a presents a comparison between cases H-02, H-03 and the original case for the first 50 min of the test. In the ${\mathrm{t}}_1$ (50 $\min$) case, H-02 has 24% more surface coverage than the original case (Figure 6). The surface coverage increases even further, by 9%, as the height of the channel on the functionalized surfaces halved in case H-03. However, this would put excessive pressure on the structure, which is evident from Figure 7, where the maximum pressure through the microchamber for all cases is shown.

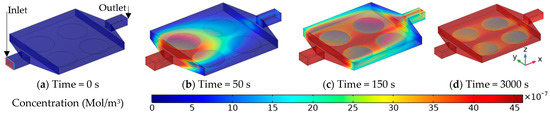
Figure 3. Concentration contour for the original case (A-01) at the start of the time (a), after 50 s (b), after 150 s (c), and at the end of 50 min (d).

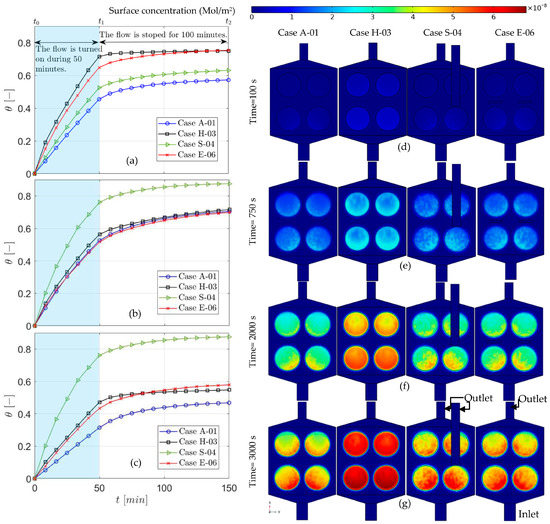
Figure 4. The time-dependent solution for surface coverage of the original experimental setup (Case A) in comparison to cases H-03, S-04, and E06 for the whole surface (a), $P{t}_f$ (b) and $P{t}_b$ (c). A slide of surface concentration contour on the functionalized surfaces for cases A-01, H-03, S-04, and E06, after 100 $s$ (d), 750 $s$ (e), 2000 $s$ (f) and 3000 $s$ (g).

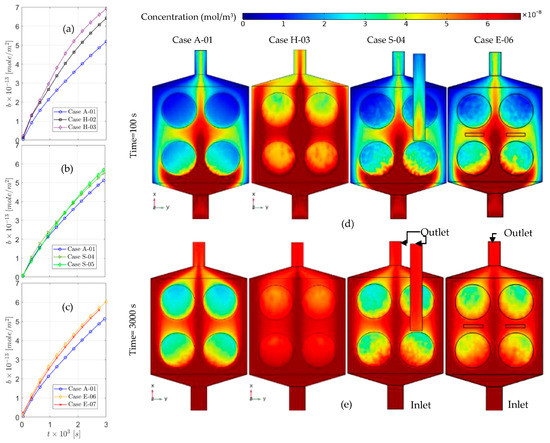
Figure 5. The time-dependent solution for surface concentration in the first 50 $\min$ for the original experimental setup (Case A) in comparison to the: thin chamber (a), suction (b), and electroosmotic flow (c). A slide of bulk concentration on the functionalized surfaces for cases A-01, H-03, S-04, and E06, after 100 $s$ (d) and 3000 $s$ (e).

Figure 6. The coverage speed and maximum coverage after 50 $\min$ and 150 $\min$ through the microchamber for the original experimental setup (case A-01), thin chamber (series H-02), the thin chamber with half-height (case H-03), second outlet with zero pressure (case S-04), suction (case S-05), and electroosmotic flow (cases E-06 and E-07). All values are calculated based on the original case.

Figure 7. The maximum pressure through the microchamber for the original experimental setup (case A-01), thin chamber (series H-02), the thin chamber with half-height (case H-03), second outlet with zero pressure (case S-04), suction (case S-05), electroosmotic flow (cases E-06 and E-07).

For the S series, the pressure at the end of the second outlet is varied from 0 to −2 $pa$. For the sake of brevity, only cases S-04 and S-05 are presented in this paper. In Figure 5b, by the end of 50 $\min ,$ cases S-04 and S-05 show 6% and 10% enhancement in the surface coverage, respectively. It is worth noting that the fabrication of the first case would be simple and would not add any extra cost, while in the second case, the device must be equipped with a suction.

In the E series, the electroosmotic flow starts with the applied electric field. Diffusion would be sufficient for the rapidly diffusive species. However, other methods could enhance the bio-recognition process for nucleic acids and proteins with high molecular weight. For the first type of species (lightweight), diffusion would occur in a matter of seconds over the microchamber, although for the second type, the required time for equilibration would be from minutes to hours. Hence, active approaches, such as electroosmotic flow, would be beneficial for DNA hybridization. After 5 min, case E-06 has 16% more surface coverage (Figure 5 and Figure 6), while in comparison to E-06, increasing the electric potential in E-07 negatively affects the speed of surface coverage. This might be caused by the position of the electrodes, which is where optimization methods can play a role in improving the outcome. This effect is evident in the results presented in Figure 4. Full surface coverage of one of the functionalized surfaces (number 2 in Table 2), the surface coverage of its front ($P{t}_f$) and its back ($P{t}_b$) are demonstrated in Figure 4a–c, respectively. The effect of electroosmotic flow is almost negligible in $P{t}_f$, as it has more distance from the electrodes. Benefit of the electroosmotic flow is more evident in the second part of the test, while the flow has stopped (Figure 4a) since, in other cases, the surface coverage remains almost the same in the second stage.

It is also worth mentioning that in order to obtain an optimum design for the biosensors considered here, a full set of parametric studies need to be carried out, similar to those commonly used in conjunction with Computational fluid dynamics (CFD). In recent years, CFD has successfully been applied to numerous biomedical-related projects involving design, validation and proof-of-concept; some examples from the present authors include [32,33,34,35,36,37]. Making use of more advanced design optimization techniques is one of the main future works, which the authors are pursuing at the moment.

6. Conclusions

With the aim of enhancing the bio-recognition process in a microchamber, three flow control techniques have been applied to an experimental. The evolution of DNA strands transported by convection, diffusion, and migration due to electric field, as well as the hybridization process on the functionalized surfaces are modelled numerically. The 3D-coupled finite element method (FEM) is used to carry out the numerical simulations, validated against the experimental results from the literature. Among the three setups tested, reducing the volume of the flow on top of the functionalized surfaces returns the largest improvement in the performance of the DNA hybridization. In this case, the speed of surface coverage is increased by 62% compared to the original case, in spite of adding an excessive pressure (1.41 $\mathrm{pa}$) on the structure, which would consequently reduce the durability and stability of the microchamber. This pressure is then reduced by up to 75% by increasing the height of the chamber to $2.5\times {10}^{-4} \mathrm{m}$. Following this design, electroosmotic flow shows a promising effect on the hybridization process. It can enhance the surface coverage by 32% simultaneously, while implementing a suction in the microchamber could increase it by a maximum of 10%. Overall, the present results show that increasing the flow velocity close to the surface of the biosensor to be the best choice for improving the efficiency while keeping the device stable, reliable, and cheap. These designs were optimized for the original setup, although this approach is applicable and practical for other microfluidic-integrated biosensing devices too, particularly with the help of machine learning methods and introducing vital parameters.