An Enhanced Deep Convolutional Neural Network for Classifying Indian Classical Dance Forms

Abstract

Indian classical dance (ICD) classification is an interesting subject because of its complex body posture. It provides a stage to experiment with various computer vision and deep learning concepts. With a change in learning styles, automated teaching solutions have become inevitable in every field, from traditional to online platforms. Additionally, ICD forms an essential part of a rich cultural and intangible heritage, which at all costs must be modernized and preserved. In this paper, we have attempted an exhaustive classification of dance forms into eight categories. For classification, we have proposed a deep convolutional neural network (DCNN) model using ResNet50, which outperforms various state-of-the-art approaches. Additionally, to our surprise, the proposed model also surpassed a few recently published works in terms of performance evaluation. The input to the proposed network is initially pre-processed using image thresholding and sampling. Next, a truncated DCNN based on ResNet50 is applied to the pre-processed samples. The proposed model gives an accuracy score of 0.911.

1. Introduction

Indian classical dance (ICD) is an umbrella term used to refer to dance forms whose theory can be traced back to Sanskrit text—Natya Shastra. Classical dance forms form a major part of Indian culture. These forms combine complex body postures produced by rotating, bending, and twisting fingers, hands, and body. Some of the dance forms and their postures are highly in sync with different geometrical concepts. “Dancers often create basic geometric shapes—like the line, square, rectangle or triangle—with their bodies to tell their stories” [1]. The costume is almost as important as the dance itself in identifying dance styles, and the diversity of these costumes can be utilized to distinguish Indian classical dance genres.Additionally, the aesthetics of the costume end up playing a huge role in the final look of the dance. As dance is a powerful art form in expressing different gestures and emotions, the communication made in Indian classical dance is expressive gestures (Mudras or Hastas) and pantomime set to music. The gestures and facial expressions convey the ras (sentiment, emotional taste) and bhava (mood) of the underlying story. The eight forms identified by Sangeet Natak academy are as follows:

• Bharatanatyam;
• Kathak;
• Kuchipudi;
• Odissi;
• Kathakali;
• Sattriya;
• Manipuri;
• Mohiniyattam.

Though there is an ample amount of content related to ICD available online and more keeps pouring in day by day, the data are highly scattered. It is important to organize the data digitally and efficiently store it to be accessible by everyone. The objective behind the paper is to develop a framework that can classify images into the above eight major classical dance forms. Extending unconventional yet convenient ways to learn traditional dance would help preserve the dance form. With an increasing shift in learning modes, from conventional ways to online platforms, the significance of automated teaching solutions is inevitable. Self-learning enables the student to set their own learning pace, and there is the added flexibility of setting a schedule that fits you.

Small intricacies in the posture for a specific dance form with very minutiae detailing in the hand gestures (mudras) make this problem of Indian classical dance form recognition even more challenging. Not only this, but the background disturbances in the input frames also pose a hindrance to the feature extraction and classification process. This paper proposes using image thresholding for pre-processing the input images and deep convolutional neural networks (DCNN) to classify 8 Indian classical dance forms. The proposed model follows a generic approach to predict the class of dance form on a small dataset where the neural network with Resnet50 architecture outperforms other baseline models.

2. Literature Survey

The diversity in Indian classical dance forms comes from the diversity in Indian traditions and culture. Moreover, these dance forms are often symbolized for expressing human emotions. Thus, to preserve the Indian culture of fine arts, dance form recognition becomes an important problem statement and the subtle differences found in these dance forms make this task even more challenging. The authors in [1] explore the use of classical Indian dance to teach geometry and other mathematical concepts. The given methodology of categorical content analysis suggests a framework for Asian Indian students to learn mathematical shapes through Bharatanatyam. The study also acknowledges the benefits of classical dance in learning basic geometric patterns. Extensive research work has been published by authors in [2], wherein they established chronological relation between kathak footwork and geometry. Many such publications indicate the high correlation between ICD and mathematics, especially geometry. In the paper [3], researchers propose a novel framework to classify Indian classical dance forms from videos. The representations are extracted through deep convolutional neural network (DCNN) [4] and optical flow. Moreover, these representations are trained on a multi-class linear support vector machine (SVM [5]. Nrityantar, a pose oblivious Indian classical dance sequence classification system [6], shows the working of deep descriptors with handcrafted pose signature on the ICD dataset. The authors in [7] present a novel classification solution by giving a new action descriptor. The proposed descriptor not only classifies ICD but also classifies common human actions. The research article by authors in [8] focuses on feature extraction and then uses AdaBoost multi-class classifier [9] on multi-feature fusion. The authors in [10] give another pioneer contribution specific to recognizing classical dance forms and mudras using an imagery dataset of hand mudras from different classical dance forms. The support vector machine (SVM) classifier is given histogram of oriented (HOG) features as input for classification. Additionally, the use of transfer learning with different CNN architectures is optimal for solving various classification problem statements. The application compares different architectures, namely AlexNet, GoogLeNet, ResNet-18, VGG-16, and VGG-19 for transfer learning with pre-trained CNNs applied to breast cancer detection on infrared images given by authors in [11], cancer detection from a small dataset. An objective quality metric to evaluate the perceived visual quality of 3D meshes is proposed. The method relies on a pre-trained convolutional neural network, i.e., VGG, to extract features from the distorted mesh. Image classification also involves class prediction based on object detection. It needs object localization for which various models have been proposed and implemented [12,13,14]. Object detection includes instance segmentation as well [15]. The state-of-the-art approaches for object detection have been implemented for various use cases which include both image and video dataset [16].

This paper provides an in-detail description of feature extraction techniques on a dataset with pre-processed dance form images using different CNN architectures, followed by the results and evaluation section, which compares the performance of these architectures with the proposed approach. Another paper [17] proposes a deep learning three-step-pipeline for Indian dance style classification. The first step is to extract essential joint locations of the dancer from each video frame, which helps identify the region’s location. For the last step, high-level recurrent neural networks are used. The whole pipeline provides a way to use multiple representations from a single video. [18] used histogram of oriented optical flow (HOOF) features with sparse representations. Firstly, they represent each frame of a dance video by a pose descriptor based on a histogram of oriented optical flow (HOOF) hierarchically. The pose basis is learned using an online dictionary learning technique. Each video is represented sparsely as a dance descriptor by pooling pose descriptors of all the frames. Dance videos are classified using a support vector machine (SVM) with an intersection kernel. They achieve an accuracy of 86.67%. [18] also proposes to use CNN to classify ICD images achieving a 93.33% recognition rate compared to other classifier models reported on the same dataset. The authors used convolutional windows of sizes 16 × 16, 9 × 9, 5 × 5, and 5 × 5 from layers 1 to 4, respectively. Video processing pipelines are used in the previous works [17,18]; however, our proposed solution uses a pre-processing image pipeline. Table 1 presents a short survey of key contributions made in this field.

Table 1. A survey capturing major contributions in the related field.

Paper Reference	Algorithm Used for Feature Extraction	Classification Technique
[3]	DCNN and Optical Flow for feature extraction	multi-class linear support vector machine(SVM)
[6]	3-tier framework combining Inception V3 features, 3D CNN features and novel pose signatures	LSTM layer + 2 fully connectedlayers with BN + softmax layer
[8]	FeatureExtraction: Zernike moments, Hu moments, shape signature, LBP features, and Haar features.	AdaBoost multi feature fusion classification
[10]	Histogram of oriented (HOG) features of hand mudras	SVM classifier
[17]	Pipeline—joints identification, patches centered around regions important with respect to movement, and this forms a hierarchical dance pose descriptor.	High level RNN
[18]	Histogram of oriented optical flow (HOOF) features with representations	SVM with intersection kernel

Therefore, three kinds of pooling strategies, including pooling, max pooling, stochastic pooling, and stochastic pooling, are used and found suitable for our application.

3. Proposed Methodology

For the classification of input images into eight different dance form categories, namely—Bharatanatyam, Kathak, Kuchipudi, Odissi, Kathakali, Sattriya, Manipuri, and Mohiniyattam, the proposed approach as given in Figure 1, works by creating a uniformly distributed dataset across all eight classes which then goes through a series of pre-processing steps including resizing, thresholding, and scaling. These processed frames fed to our deep convolutional neural network based on Resnet50 architecture classify the images into the above described eight categories.

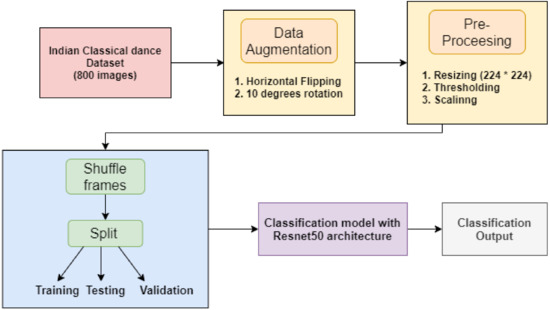
Figure 1. Proposed methodology.

3.1. Dataset Creation

In the proposed study, the dataset acquired has a total of 800 images which are collected from publicly available sources [10], and by capturing frames from YouTube videos as shown in Figure 2. It is ensured that data are equally distributed among the eight classes. Though the dataset is small, but the variation in the number of dancers in the image and different backgrounds makes the dataset challenging for classification tasks.

Figure 2. Sample images from the dataset.

3.2. Data Augmentation

Image augmentation is a process of manipulating input images to create different versions of similar content to expose the model to a wider array of training examples. In visual recognition models, over-fitting can be prevented by artificially increasing the training data using data augmentation techniques involving cropping, padding, rotating, and flipping the input images. In the proposed approach, the input images are horizontally flipped, following which a rotation of 10° is performed. Without data augmentation, over-fitting occurs, so it becomes difficult for the model to generalize to new examples that were not in the training set.

3.3. Data Pre-Processing

The accuracy of an image classification model is highly dependent on the data the neural network it is trained with. Image recognition algorithms rely on the dataset’s quality, and image pre-processing allows us to focus on the features we want the neural network to learn by removing all the noise and disturbance in the input image. Indian classical dance forms have a steep range of color intensities due to vibrant costumes and stage drama; hence thresholding and scaling images into range −1 to 1 sample-wise proves beneficial in learning. Algorithm 1 (https://github.com/VibhutiBansal-11, accessed on 4 September 2020) lists out the entire implementation workflow of the proposed approach.

Algorithm 1: Workflow of the approach.

The algorithm takes the images as input 1: for each image in Dataset: 2: function Preprocess (image, x_dim = 224, y_dim, threshold = 127, scale) 3: Return ProcessedImage 4: end function 5: Append(image) to array(X) 6: end for 7: read labels csv in array(Y) 8: categorical_labels = encode(Y) 9: Shuffle (X, categorical_labels) 10: X_train, Y_train, X_test, Y_test = train_test_split(X, categorical_labels) 11: function Create model 12: Initialize base_model = ResNet50 13: for layers in resnet.layer[:−14]: 14: Layers.trainable = false 15: end for 16: Add_layers (GlobalAveragePooling2D (), Dropout (0.5), Dense (256), Dropout (0.5), SoftmaxLayer) 17: Return model 18: Model.Compile (loss = Categorical_crossentropy, optimizer = Adam, metric = Accuracy) 19: function Create_Callbacks (monitor, patience, cooldown, min_lr) 20: return callbacks 21: function Train_Model (train_data, num_epochs = 15, val_frequency, callbacks) 22: return model

Step 1: This involves resizing all the images to 224 × 224 using Interarea interpolation, as shown in Figure 3c.

Figure 3. (a) Original image, (b) RGB to BGR, (c) resized image, (d) threshold image (e) sampled image.

Step 2: The simplest thresholding methods, as mentioned in [19], replace every pixel in the image with user-defined values, which can then be used to create binary black and white images or reduce the range of intensity in the image pixels. Thresholding is the simplest method of segmenting images in which we use truncate thresholding on images. The value of the threshold used is 127, all values above the threshold (127) are set to 127, and all values less than or equal to 127 are unchanged, as depicted in Figure 3a–d.

$$dest \left(x, y\right)=\left\{thresh , if src \left(x, y\right)>threshsrc \left(x, y\right) , otherwise\right\}$$

(1)

In Equation (1), src(x, y) gives the intensity values of the source image. In contrast, thresh shows the maximum intensity value for the pixels, and intensity values for the destination image are given by dest(x, y). The graph for the intensity of image pixels can be seen in Figure 4.

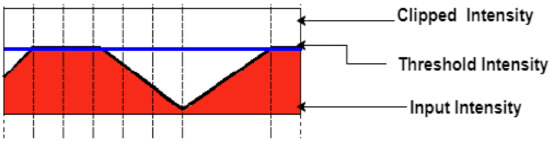
Figure 4. Truncate image thresholding graph.

Step 3: After thresholding, a sample-wise scaling of pixels to a range of −1 to 1 is performed as shown in Figure 3e.

Step 4: Later, the dataset is shuffled to ensure that each data point creates a distinct, independent change on the model without being biased by the same points and thus preventing the model from overfitting on the input data. The shuffled images are divided into training (70%), testing (15%), and validation (15%) splits.

Following the above stated four steps that are resizing, thresholding, scaling, and shuffling, the dataset is now ready for training the image classification model as inferred from Figure 5.

Figure 5. Sample images from dataset after pre-processing.

We designed our DCNN on top of ResNet50 architecture [20]. The pre-trained model, initially trained for 1000 categories, is used for feature extraction using Transfer Learning. The head of the pre-trained ResNet50 model is removed and replaced with our own set of layers. The last 14 layers of ResNet50 were un-frozen and made trainable. The following sections describe the architecture of the proposed deep convolution neural network (DCNN) [21].

3.4. Model Architecture

3.4.1. Identity Block

The identity block is the standard block used in ResNet50 and corresponds to the case where the output activation has the same dimension as the input activation. It is simply when the activation of a layer is fast-forwarded to a deeper layer in the neural network. The activation from a previous layer is added to the activation of a deeper layer in the network, as shown in Figure 6.

Figure 6. Model architecture containing Covolutional and identity block and placed after. (a) Complete Architecture; (b) ConvBlock used in Figure 6a; (c) IdentityBlock used in Figure 6a.

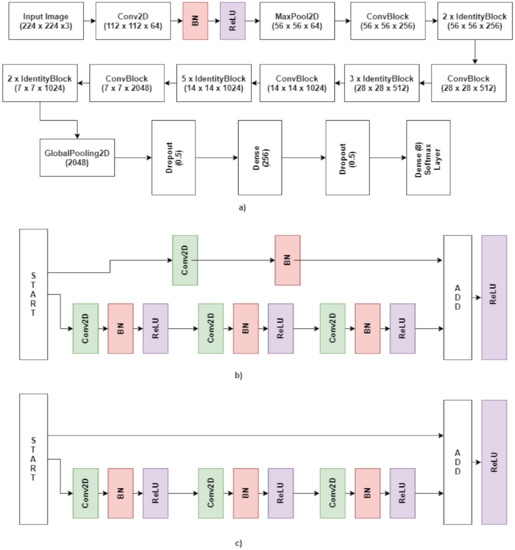
ConvBlock is similar to Identity Block as both pave the way for residual learning for the network, the only difference being that ConvBlock is used when the input and output dimensions donot match. Figure 7 shows the global average 2D pooling layer.

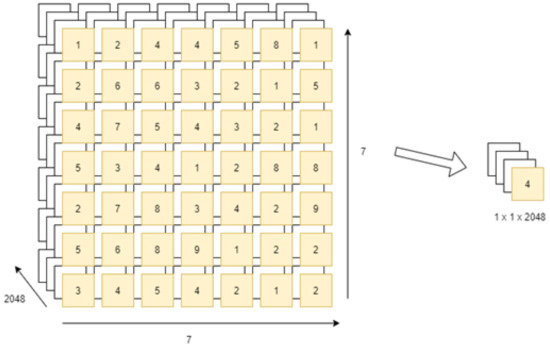
Figure 7. Global average 2D pooling layer.

3.4.2. Convolutional Block (ConvBlock)

For any given convolution operation, assuming a square input, the dimension of the output volume can be obtained through Equation (2), where n is the input dimension, p is gives zero-padding, f the filter dimension, and s is the stride.

$$\left(n+2\times p-f\right)÷s+1$$

(2)

3.4.3. Global Average Pooling Layer

The 2D Global average pooling block takes a tensor of size given by Equation (3), where w is the input width, h is the input height, and n gives the input dimension. It calculates the mean of all values present in one feature map [(input width) × (input height)] for each input channel.

$$size=\left(w\times h\times n\right)$$

(3)

3.4.4. Dropout Layer

A dropout is an approach to regularization in neural networks which helps reduce interdependent learning amongst the neurons and is often used to prevent overfitting and improve generalization while training. Every neuron has a probability p of being “dropped” in a training step. The hyperparameter p is called the dropout rate. The dropout layer is applied twice in the proposed approach, taking the dropout rate (p) to be 0.5.

3.4.5. SoftMax Layer

It is a dense layer with eight neurons corresponding to 8 mutually exclusive classes and uses the SoftMax activation function for producing estimated class probabilities using an Equation (4).

$$\sigma (x_i)=e^{x_i}/{{\displaystyle \sum }}_{k=1}^n\hspace{1em}{e}^{x_{ k}}\mathrm{for}\mathrm{i}=1,2\dots \mathrm{n}$$

(4)

where $\sigma$($x_i$) gives the probability of the class, and n is the number of classes. In the proposed approach, n is taken to be 8.

3.4.6. Approach

The categorical cross-entropy loss function is given in the Equation (5) with Adam Optimizer [22] is used in the proposed approach. The weights are calculated using an optimizer with a learning rate of 3$e^{-4}$ using an Equation (6).

$$Loss=-{\displaystyle \sum }_{i=1}^n\hspace{1em}{y}_{i }log{\widehat{ y}}_i$$

(5)

$${\theta }_{ n,t }={\theta }_{ n-1,t}-\frac{\alpha }{\sqrt{ ϵ+ {{\displaystyle \sum }}_{T=1}^t\hspace{1em}(\mathit{\nabla }J{\left({\theta }_{n-1, T})\right)}^2}}*\mathit{\nabla }J\left({\theta }_{n-1, T}\right)$$

(6)

where ${\widehat{y}}_i$ is the ith scalar value in the model output, n is the number of classes and $y_{i }$ is the corresponding target (true) value and ${\theta }_{ n,t }$ is the weight at $n^{th }$ iteration and time step t, $\alpha$ is learning rate, $ϵ$ is a smoothing term to avoid division by zero, $*\mathit{\nabla }J\left({\theta }_{n-1, T}\right)$ is the gradient of cost function w.r.t weights, and ${{\displaystyle \sum }}_{T=1}^t\hspace{1em}(\mathit{\nabla }J{\left({\theta }_{n-1, T})\right)}^2$ is the summation of the square of all gradients squared varying from time step T = 1 to time step T = t. As inferred from Figure 8a, the validation loss for the proposed approach is reduced to 0.29 after 12 epochs.

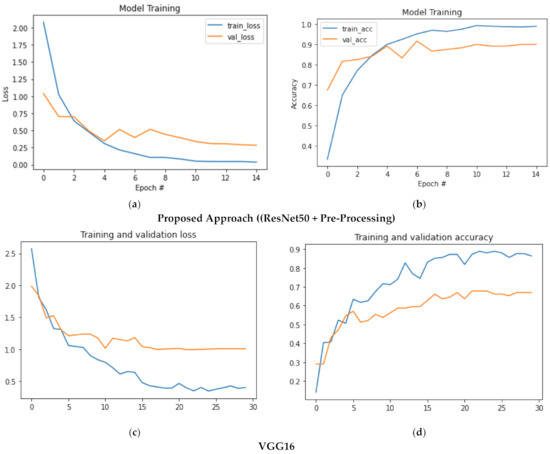
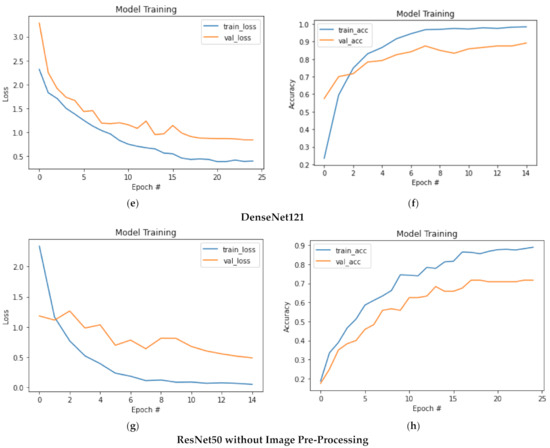
Figure 8. (a–h). Plots for learning curves for the different convolutional neural networks used.

4. Results

Classifying emotions on a large dataset is a multi-class classification problem. In this paper, each sample in the prepared dataset has been categorized into eight different classes. Standard metrics-precision, recall, F1-score, and accuracy score have been computed for each class for evaluation.

Different deep convolutional neural networks (DCNN), namely, ResNet50, VGG16, and DenseNet121 application on a challenging dataset, provided considerable results. However, the fine-tuned ResNet50 with pre-processed images as input results, given in the best accuracy of 0.91 and an f1-score of 0.85, outperformed all the other baseline models. A balanced dataset of 800 classical dance form images is used for training and fine-tuning the ResNet50 DCNN (the model used in our proposed approach). Before training, the image dataset is pre-processed by applying various image manipulation techniques, including resizing, thresholding, and scaling, making it easier for the neural network to fit the dataset accurately.

Following this, the ResNet50 model is trained and fine-tuned by unfreezing a few of the last layers resulting in the best evaluation scores. This section compares the evaluation metrics for different deep convolutional neural networks used in this work.

Evaluation and Analysis

Table 2 shows the results of the other two baseline models without any pre-processing. Without any pre-processing, these models (VGG and DenseNet) perform poorly as they are unable to learn the features of the dance posture, which are required for a particular form recognition. This occurs because these models pick up non-essential elements from the image’s backdrop, where the pre-processing stage can help by capturing the essential ones only.

Table 2. Classification report for baseline comparisons.

VGG16					DenseNet121
	Precision	Recall	F1-Score	Support		Precision	Recall	F1-Score	Support
Bharatanatyam	0.67	0.75	0.71	16	Bharatanatyam	0.57	0.50	0.53	16
Kathak	0.67	0.67	0.67	9	Kathak	0.80	0.73	0.76	11
Kathakali	0.81	1	0.9	13	Kathakali	0.82	1.00	0.90	18
Kuchipudi	0.78	0.39	0.52	18	Kuchipudi	0.67	0.71	0.69	14
Manipuri	0.67	0.8	0.73	15	Manipuri	0.93	0.87	0.90	15
Mohiniyattam	0.72	0.75	0.73	24	Mohiniyattam	0.65	0.87	0/90	15
Odissi	0.5	0.62	0.55	13	Odissi	0.86	0.80	0.83	15
Sattriya	0.44	0.33	0.38	12	Sattriya	0.91	0.62	0.74	16
Accuracy			0.67	120	Accuracy			0.77	120
Macro average	0.66	0.66	0.65	120	Macro average	0.78	0.76	0.76	120
Weighted average	0.67	0.67	0.65	120	Weighted average	0.78	0.77	0.76	120
ResNet50 (without Pre-Processing)					Proposed Approach (ResNet50 + Pre-Processing)
	Precision	Recall	F1-Score	Support		Precision	Recall	F1-Score	support
Bharatanatyam	0.83	0.88	0.86	17	Bharatanatyam	0.8	0.8	0.8	10
Kathak	0.87	0.87	0.87	15	Kathak	0.82	0.9	0.86	10
Kathakali	0.9	1	0.95	18	Kathakali	1	1	1	16
Kuchipudi	0.83	0.5	0.62	10	Kuchipudi	0.85	0.89	0.87	19
Manipuri	1	0.87	0.93	15	Manipuri	1	0.94	0.97	17
Mohiniyattam	0.92	0.92	0.92	13	Mohiniyattam	0.88	1	0.94	15
Odissi	0.67	0.93	0.78	15	Odissi	0.93	0.93	0.93	15
Sattriya	1	0.82	0.9	17	Sattriya	0.93	0.78	0.85	18
Accuracy			0.87	120	Accuracy			0.91	120
Macro average	0.88	0.85	0.85	120	Macro average	0.9	0.91	0.9	120
Weighted average	0.88	0.87	0.87	120	Weighted average	0.93	0.91	0.91	120

Table 2 shows the classification report for the deep learning models trained on the Indian classical dance form dataset. The deep learning models used for the comparison include VGG16, Densenet121, ResNet50 (without pre-processing), and ResNet50 with the pre-processing step. All of the classification metric values have improved as a result of the picture thresholding pre-processing.

In addition, results in Table 2 also show that the proposed ResNet50 approach with the pre-processing step outperforms the other deep learning models fine-tuned on the classical dance dataset.

Learning curves play a vital role in the analysis and in improving the performance of deep learning models. Furthermore, by observing the trends in the learning curve, one can determine the type of fit attained by the model. Apart from Table 2, loss versus epoch plots and accuracy versus epoch plots are given in Figure 8, also provide an evident comparison of training and validation learning curves for the other evaluated models. It can be inferred from Figure 8a,b that the proposed ResNet50 approach outperforms other neural networks by achieving an accuracy of 0.91 and a loss of 0.30. Additionally, as the dataset used to train the model is balanced; thus the model is prevented from over-fitting to a specific class. In addition, the plots of VGG16 and DenseNet121 are given in Figure 8c–f show poor performance where these models fail to learn many features from the input dataset and, thus, achieve a low validation accuracy of 0.67 and 0.77, respectively. Figure 8g–h again validates our proposed approach where a ResNet50 model underperforms compared to a pre-processed one.

The confusion matrix is an evaluation metric used to measure the performance of a machine learning classification problem. As inferred from the matrix given in the Figure 9, the number of true positives can be defined as the number of correctly predicted classes (dark blue squares in the given confusion matrix corresponds to the correctly predicted classes). For example, in a specific class, for instance, kathak, the total number of true negatives can be defined as the total number of non-kathak poses or frames predicted to be non-kathak. Additionally, using the same confusion matrix, we can calculate the total false positives as the sum of falsely predicted kathak images. The below-given sub-sections use the confusion matrix (Figure 9) to calculate individual precision and recall scores for the eight dance classes.

Figure 9. Confusion matrix for the proposed approach.

High precision values for the Kathakali and Manipuri class across all the different models prove to be much easier to learn due to a definite pattern in the costumes and poses. High precision scores show models more accurate in predicting Kathakali and Manipuri classes than the remaining six classes and are calculated using Equation (7). Varied results are obtained for different dance classes; for instance, precision for Sattriya class is 0.44 for the VGG16 model but 0.93 for the proposed approach. A similar pattern can be observed for the Odissi dance class, where the precision score for the VGG16 model is 0.5 but 0.93 for the ResNet50 proposed approach. A similar pattern can be observed for the recall values obtained for each class and calculated using Equation (8). For multi-class classification:

$$\mathrm{Precision}={{\displaystyle \sum }}_{i=1}^n\hspace{1em}t{p}_i/{{\displaystyle \sum }}_{i=1}^n\hspace{1em}(t{p}_i+f{p}_i)$$

(7)

$$\mathrm{Recall}={{\displaystyle \sum }}_{i=1}^n\hspace{1em}t{p}_i/{{\displaystyle \sum }}_{i=1}^n\hspace{1em}(t{p}_{i }+f{n}_i)$$

(8)

F1 score = 2 * precision * recall/precision + recall

(9)

where $tp$ is the number of true positives, $fp$ is the number of false positives, $fn$ is the number of false negatives, and n is the number of classes.

Though a clear distinction of the efficiencies and performance of the models cannot be stated concerning one another as the datasets used across different literature is varied. However, a comparison can still be reported based on several evaluation factors like accuracy, f1-score, recall, precision for each class, as this would further allow room for analysis and conclusions. Table 3 revisits the existing classification models as we can see that none of the pre-existing papers include all eight categories identified by Natya-Shashtra.Authors in [6] incorporate pose, flow, and spatio-temporal dependencies in the pose signature to capture the adjacency relationship between anchor joints in the skeletal pattern of the dancer. CS_ISI [7] proposes a descriptor to classify ICD forms. ICD classification, whereas [3] proposes a technique that relies on a combination of 3 sub-frameworks that utilize representations from pre-trained convolutional neural networks—and optical flows.

Table 3. Existing literature and proposed methodology.

	Nrityantar [3]	CS_ISI [7]	ICD_IITR [3]	Proposed Approach
Precision	0.75	-	75.42	0.93
Recall	0.72	-	70.96	0.91
F1-score	0.71	-	73.12	0.9
Accuracy	72.35	86.67	75.83	91.1
Number of classes	6	3	7	8
Learning rate	1e-4	-	-	3.00E-04
Optimiser	Adam	-	-	Adam
Loss	Categorical Entropy	-	-	Categorical Entropy
Decay	0.000001	-	-	0.000001
Batch size	32	-	-	32
Maximum Epoch	100	-	-	15

5. Conclusions

Indian classical dance form recognition is an interesting subject due to complex body postures and subtle hand mudras. It gives a playground to experiment with different CNN architectures for classification purposes. Although significant contributions have been made in the existing literature for recognition and classification of different Indian classical dance forms, the possibility of improving on these works with more dance forms is an interesting field of research. This paper proposes a model to recognize and classify the eight major classical dance forms identified by Natya Shastra as Bharatanatyam, Kathak, Kuchipudi, Odissi, and Kathakali Sattriya, Manipuri, and Mohiniyattam. We propose to use deep convolutional neural networks (DCNN), using ResNet50 as the base model by fine-tuning the last 14 layers. For this purpose, a dataset consisting of 800 images of different dance forms has been created and augmented. Following this, several pre-processing steps, including image thresholding and sampling, have aided the feature extraction process. The model is based on a small but diverse dataset, achieving an accuracy score of 0.911 and an F1-score of 0.90. The results also compare the other (two) DCNN’s performance and the proposed approach. Another evidence-based comparison of ResNet50 with and without pre-processing shows that the former outperforms the latter. We further intend to increase the dataset size and explore the problem statement with a viewpoint of auto-generation dance poses and mudras.