Explainable Internet Traffic Classification

Abstract

The problem analyzed in this paper deals with the classification of Internet traffic. During the last years, this problem has experienced a new hype, as classification of Internet traffic has become essential to perform advanced network management. As a result, many different methods based on classical Machine Learning and Deep Learning have been proposed. Despite the success achieved by these techniques, existing methods are lacking because they provide a classification output that does not help practitioners with any information regarding the criteria that have been taken to the given classification or what information in the input data makes them arrive at their decisions. To overcome these limitations, in this paper we focus on an “explainable” method for traffic classification able to provide the practitioners with information about the classification output. More specifically, our proposed solution is based on a multi-objective evolutionary fuzzy classifier (MOEFC), which offers a good trade-off between accuracy and explainability of the generated classification models. The experimental results, obtained over two well-known publicly available data sets, namely, UniBS and UPC, demonstrate the effectiveness of our method.

1. Introduction

Network traffic classification represents one of the main challenges in network management nowadays. Indeed, Internet Service Providers (ISPs) devote most of their efforts to Internet traffic classification and management. Historically, the Internet traffic classification task was performed primarily for security reasons, as it permits the detection and identification of intrusions and malicious behavior. However, over recent years, the identification of Internet traffic type and workload has become necessary not only for security purposes, but also to perform traffic engineering and to make decisions on policing, traffic shaping, billing, dynamic Quality of Service, and so on. Most of the management techniques are built on top of classification results: as an example, consider billing and accounting, which are only possible if the traffic is first correctly classified. Moreover, attack detection techniques are usually built on top of a traffic classifier. Nonetheless, despite many years of research on the topic, an ultimate solution able to provide “good enough” performance is still under study.

In the literature, several approaches have been proposed to classify IP traffic flows according to the application that generated the traffic. Historically, the most commonly used method is to associate the observed traffic (using flow level data or a packet sniffer) with an application, on the basis of TCP or UDP port numbers [1]. However, port-based classification is inadequate [2], as mapping between ports and applications is not always well defined. As a consequence, in the last decade, research efforts have moved towards classification tools based on Machine Learning (ML) and Artificial Intelligence (AI) algorithms, which rely on statistical features [3].

Among these, Support Vector Machine (SVM) [4] and deep learning techniques [5] have emerged as powerful tools for traffic classification and other network application, such as intrusion detection [6] and other cyber security application [7,8]. Indeed, these techniques, and especially SVM, represent an almost de facto standard in the field. Such methods are able to provide very high accuracy values, often just observing a few traffic statistics computed over the first packets of each flow.

Nonetheless, all of the methods based on machine learning algorithms present a common drawback, as the generated models are seen as black boxes characterized by a low “explainability” level. Indeed, the classification result does not provide the practitioners with any information regarding the criteria that have taken to the given classification, or what information in the input data makes them arrive at their decisions. This is usually justified by the fact that the main goal traditionally pursued is to make the model matching reality (i.e., accurate models), without actually caring for explainable models.

Nowadays, several new requirements have emerged related to fairness or unbiasedness, privacy, reliability, robustness, causality, and/or trust posing the need of deploying systems that must provide explanations for the taken decisions, where necessary [9]. Therefore, traffic classifiers, as well as other traffic analysis systems, must be optimized not only for accuracy but also for the other criteria previously listed.

In such a context, a lot of research efforts are nowadays focusing on “explainable” methods (e.g., explainable artificial intelligence), where explainability “encompasses ML/AI systems for opening black box models, for improving the understanding of what the models have learned and/or for explaining individual predictions” [9]. In this specific area, a recent work in [10] clearly indicates that exploiting the synergy between Fuzzy Rule-Based Systems (FRBSs) and Evolutionary Algorithms is one of the most straightforward ways of combining accuracy and interpretability/explainability in machine learning-based tools.

For such a reason, in this work, which significantly extends the preliminary results presented in [11], we propose a traffic classification approach based on multi-objective evolutionary fuzzy classifiers (MOEFCs) [12,13]. Specifically, MOEFCs deal with the application of Multi-Objective Evolutionary Algorithms (MOEAs) [14] for generating a collection of Fuzzy Rule-Based Classifiers (FRBCs) characterized by different trade-offs between their accuracy and their explainability level [15]. We recall that FRBCs adopt (i) a rule base composed of linguistic IF-THEN rules and (ii) a database which contains the description of the linguistic terms adopted for the fuzzy discretization of each input variable. A specific inference mechanism is adopted for taking a decision whenever a new input is presented to the system.

In this contribution, we exploit the PAES-RCS algorithm, in which the accuracy is calculated in terms of percentage of correctly classified flows of internet traffic. As regards the explainability level, it is calculated in terms of total rule length (TRL), namely, the total number of conditions taken into consideration in the whole rule base. Low values of TRL are associated with rule bases which contain a reduced number of simple rules (i.e., rules in which a low number of conditions are adopted in their antecedent). Note that PAES-RCS has been successfully exploited in a number of recent contributions on real-world applications [15,16].

To evaluate and validate the proposed approach, we have used two publicly available data sets, namely, UniBS and UPC, showing that our system can achieve nearly optimal performance, while simultaneously guaranteeing the explainability of the classification results. We also compared the results achieved by MOEFCs with the ones achieved by two classical ML-based classification algorithms, namely, SVM and Decision Trees. SVM algorithms have been chosen as they represent the de facto standard among machine learning algorithms commonly adopted for solving the internet traffic classification problem. However, SVM models are characterized by a very low explainability level. Regarding decision trees, as from the trees it is possible to extract a set of decision rules, they represent a category of interpretable models among classical machine learning classifiers. However, their rules are not linguistic and the final models are often described by a large number of parameters, namely, the number of nodes and leaves. Thus, also the explainability level of decision trees is often compromised. As a counterpart, the proposed approach, based on MOEFCs, generates models characterized by good trade-offs between their accuracy and their explainability.

The remainder of the paper is organized as follows. In Section 2, we discuss some notable related works, while in Section 3.1 we describe the used data sets. Then, in Section 3.2 we introduce the experimented explainable traffic classification approach. The achieved results are shown in Section 4. Finally, Section 5 concludes the paper with some final remarks and future work.

2. Related Work

Research on traffic classification has been quite prolific in the years and, as a consequence, many works have been written on the topic. Therefore, the aim of this section is not to provide the reader with a comprehensive review of the related works (for which we refer the reader to the surveys on the topic), but just to point out some works significant for our specific proposal.

Machine Learning techniques have been first applied to network traffic classification in 1994 [17] and since then many different methods have been proposed, as detailed in some recent surveys [3,18].

Among the many proposals, particular interest has been raised by classifiers based on Support Vector Machine (SVM). One of the first significant work on the application of SVM to traffic classification is [19], where the authors apply one of the approaches to solving multi-class problems with SVMs and describe a simple optimization algorithm that allows the classifier to perform correctly with as little training as a few hundred samples. Since then, many other works have proposed SVM-based methods [4,20,21,22,23] and, as a result, SVM is nowadays considered as a de facto standard in the field. Nonetheless, as already discussed, all of these works propose methods based on black-box models that do not provide any information about the classification criteria.

As far as Fuzzy Rule-Based Classifiers (FRBCs) are concerned, given their ability to deal with vague and noisy data and to explain how the classification task is performed, they have been widely exploited in several contexts, such as medical diagnosis applications [24], industrial applications [25], and Internet of Things [26]. In the years, several techniques to generate and optimize the structure of FRBCs have been proposed, often without taking into consideration how this maximization affects the FRBC explainability, but only in the last decade, researchers have also focused their attention on the explainability aspects of FRBCs [27]. As accuracy and explainability are conflicting objectives, the generation of the FRBS structure has been modeled as a multi-objective optimization problem. Multi-objective evolutionary algorithms (MOEAs) have been successfully employed to tackle this optimization problem and the term multi-objective evolutionary fuzzy systems (MOEFSs) has been coined [12,28] to identify FRBSs generated by MOEAs. Since then, many papers have proposed the use of MOEFSs in classification problems [16,29,30,31,32,33].

In the specific context of traffic classification, there are some works [34,35] that propose the use of fuzzy models. The work in [34] discusses the application of hybrid models in which fuzzy theory elements are included into a neural network architecture. As regards the contribution discussed in [35], the authors propose an approach which combines a decision trees and fuzzy membership functions for dealing with noisy and vague data. Note that both works include in their experimental analysis a comparison with the traffic classification methods based on SVM. Nonetheless, to the best of our knowledge, our work is the first to propose and evaluate in a systematic way, the application of MOEFCs to generate explainable models for network traffic classification.

3. Materials and Methods

In this section, we first describe the data sets used to evaluate and validate our study, and then we detail the proposed Traffic Classification System.

3.1. Data Sets

We have used two distinct well-known and publicly available data sets: UniBS and UPC.

3.1.1. UniBS Data Set

The UniBS data set [36] is made of traffic collected in the University of Brescia campus network during three consecutive days (from 30 September 2009 to 1 October 2009), anonymized with the Crypto-PAn tool [37]. The dataset has been employed recently in the contributions discussed in [38,39].

The data set is coupled with a log file, containing for each flow, the information

 

<timestamp> : <IP src> : <IP dst> :

<transport port src> : <transport port dst> :

<DPI verdict(s)> : <application name> :

<transport protocol>

 

In this work, we have considered the classes corresponding to the following applications: Mail, Skype, Firefox, Safari, BitTorrent, and Amule. Table 1 reports the number of instances per class, considering flows made of at least three, five, and ten packets.

Table 1. UniBS data set: number of instances per each class.

Class	>3 pkts	>5 pkts	>10 pkts
Mail	4628	4627	4621
Skype	2516	2484	2412
Firefox	906	906	901
Safari	13,204	13,300	13,178
BitTorrent	2414	2411	1761
Amule	5311	5296	5202

3.1.2. UPC Data-Set

The UPC data set [40] is made from a subset (about 5.23 GB) of the full-payload traffic traces used in [41] and collected in the Universitat Politecnica de Catalunia during 66 days (from 25 February 2013 to 1 May 2013). Furthermore, these data have been recently used in the experiments on internet traffic classification carried out in [42,43].

As for the UniBS data-set, a log file accompanying the data set contains, for each flow, the information:

 

flow_id#start_time#end_time#local_ip

#remote_ip#local_port#remote_port

#transport_protocol#operating_system

#process_name#urls#referers#

content_types#

 

where process_name corresponds to the application that generated the flow.

Table 2 reports the number of instances per class, considering flows made of at least three, five, and ten packets.

Table 2. UPC data set: number of instances per each class.

Class	>3 pkts	>5 pkts	>10 pkts
SSHD	7863	7769	7739
XRDP	3196	3031	2926
DNSMasq	2993	1731	631
Chrome	4549	4540	3635
Firefox	1926	1924	1147
Amule	4594	2362	1282

3.2. The Proposed Traffic Classification System

In the following, we detail the proposed approach for generating explainable traffic classification models. The diagram depicted in Figure 1 represents the schema of the proposed internet traffic classification system. The data (both the Training Internet Flow ($T\_IF$) and the Real-Time Internet Flow ($RT\_IF$)) are preprocessed through a Feature Extraction strategy (discussed in Section 3.2.2), which generates a representation of the data by means of the chosen features. Note that while $T\_IF$ is composed of historical data collected for training the classification model, the $RT\_IF$, in a real-world application, is continuously extracted from a network. The representation of the training data ($T\_IF$ representation) is used by the PAES-RCS algorithm to build a collection of FRBCs, namely, a collection of XAI classification models. Each model is characterized by a specific trade-off between accuracy and explainability, therefore the final user can select the one that best satisfies her/his requirements. This model (Selected XAI Model in the figure) is then applied on the representation of the Real-Time Internet Flow ($RT\_IF$ representation) to classify it. In the following, we first focus on the description of adopted multi-objective evolutionary learning scheme for generating FRBCs. Then, we describe two different feature extraction strategies, that we have experimented as preprocessing stage of the overall traffic classification task.

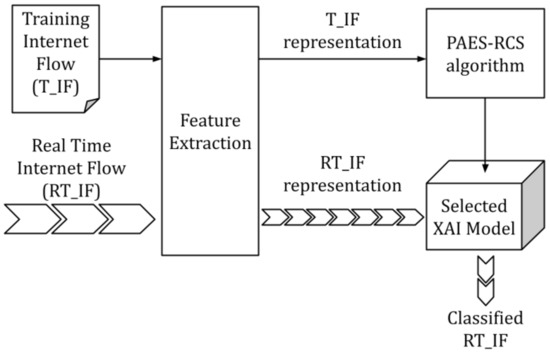
Figure 1. Block diagram of the proposed Traffic Classification System.

3.2.1. PAES-RCS Method

Evolutionary fuzzy systems, which consist of evolutionary algorithms applied to the design of fuzzy systems, are one of the greatest advances within the area of computational intelligence.

Among these, multi-objective evolutionary fuzzy classifiers (MOEFCs) are characterized by a good trade-off between accuracy and explainability level [12,16]. Therefore, these models have been widely used for approaching classification problems. Indeed, MOEFCs deal with the design of fuzzy rule based classifiers (FRBCs) by means of multi-objective evolutionary algorithms: during the evolutionary design process, both the accuracy and the explainability level of the models are concurrently optimized. At the end of the design process, a set of classification models, characterized by different trade-offs between accuracy and interpretability (Pareto front approximation), are available for the final user that will select the most suitable solution for its problem domain. The final models are usually characterized by compact fuzzy rules, namely, linguistic IF-THEN rules, which can describe the classification process in an explainable way.

An FBRC basically includes a rule base (RB), a database (DB) containing the definition of the fuzzy sets used in the RB, and an inference engine. RB and DB comprise the knowledge base of the rule-based system.

Let $X=\{X_1,\dots ,X_F\}$ be the set of input variables and $X_{F+1}$ be the output variable of the classifier. Let $U_f$, with $f=1,...,F$, being the universe of the $f^{th}$ input variable $X_f$. Let $P_f=\{A_{f,1},\dots ,A_{f,j},\dots ,A_{f,T_f}\}$ be a partition of variable $X_f$ consisting of $T_f$ fuzzy sets. The output variable $X_{F+1}$ is a categorical variable assuming values in the set $\Gamma$ of K possible classes $\Gamma =\{C_1,\dots ,C_K\}$. Let $\{({\mathbf{x}}_1,x_{F+1,1}),\dots ,({\mathbf{x}}_N,x_{F+1,N})\}$ be a training set composed of N input–output pairs, with ${\mathbf{x}}_t=[x_{t,1}\dots ,x_{t,F}]\in {\Re }^F$, $t=1,\dots ,N$ and $x_{F+1,t}\in \Gamma$.

With the aim of determining the class of a given input vector, we adopt an RB composed of M rules expressed as

$$\begin{array}{c}\hfill R_m:\mathbf{IF}{X}_1\mathbf{is}{A}_{1,j_{m,1}}\mathbf{AND}\dots \mathbf{AND}{X}_F\mathbf{is}{A}_{F,j_{m,F}}\\ \hfill \mathbf{THEN}{X}_{F+1}\mathbf{is}{C}_{j_m}withR{W}_m\end{array}$$

(1)

where $C_{j_m}$ is the class label associated with the $m^{th}$ rule, and $R{W}_m$ is the rule weight, i.e., a certainty degree of the classification in the class $C_{j_m}$ for a pattern belonging to the subspace delimited by the antecedent of rule $R_m$.

Usually, a purposely defined fuzzy set $A_{f,0}$ ($f=1,\dots ,F$) is considered for all the F input variables. This fuzzy set, which represents the “do not care” condition, is defined by a membership function equal to 1 on the overall universe. The term $A_{f,0}$ allows generating rules that contain only a subset of the input variables.

A specific reasoning method employs the information it receives from the RB to determine the class label for a given input pattern. We adopt the maximum matching as reasoning method (see [16] for details).

Concerning the DB, we adopted triangular fuzzy sets: each fuzzy set $A_{f,j}$ is identified by the tuples $(a_{f,j},b_{f,j},c_{f,j})$, where $a_{f,j}$ and $c_{f,j}$ correspond to the left and right extremes of the support, and $b_{f,j}$ to the core. In particular, in the experiments, we use strong fuzzy partitions, where $a_{f,1}=b_{f,1},b_{f,T_f}=c_{f,Tf}$ and, for $j=2,...,T_f-1$, $b_{f,j}=c_{f,j-1}$ and $b_{f,j}=a_{f,j+1}$. In Figure 2, we show an example of a strong fuzzy partition composed by three triangular fuzzy sets.

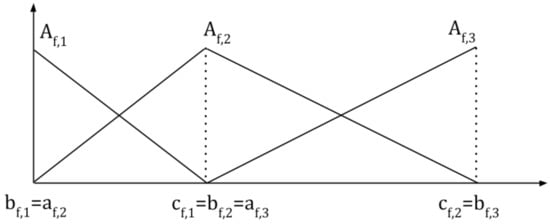
Figure 2. An example of a strong fuzzy partition.

In order to concurrently design the RB and tune the parameters of the fuzzy sets, we adopt the PAES-RCS algorithm introduced in [44]. The multi-objective evolutionary learning scheme is based on the (2 + 2)M-PAES, which is an MOEA successfully employed in the context of MOEFSs during the last years. We concurrently optimize two objectives: the first objective considers the interpretability of the RB, calculated as the total rule length (TRL), that is, the number of propositions used in the antecedents of the rules contained in the RB; the second objective takes into account the accuracy, assessed in terms of classification rate.

In the learning scheme, we first generated an initial RB and then selected, during the evolutionary process, the most relevant rules and their conditions. Moreover, we concurrently tune the parameters of the fuzzy sets by using a mapping strategy based on a piecewise linear transformation [44]. Once we had defined an initial strong fuzzy partition for each input variable, we extracted the initial set of candidate fuzzy rules from a decision tree: in particular, in this work, we use a recent algorithm, discussed in [45], for generating multi-way fuzzy decision trees. One rule is then created for each path from the root to a leaf node.

In PAES-RCS, each solution is codified by a chromosome C composed of two parts $(C_R,C_T)$, which define, respectively, the RB and the positions of the representatives of the fuzzy sets, namely, the cores, in the transformed space.

Let $J_{DT}$ and $M_{DT}$ be the initial set of candidate rules generated by the decision tree and the number of rules of this RB, respectively. In order to generate compact and interpretable RBs, we allow that the RB of a solution contains at most $M_{max}$ rules. The $C_R$ part, which codifies the RB, is a vector of $M_{max}$ pairs ${\mathbf{p}}_m=\left(k_m,{\mathbf{v}}_m\right)$, where $k_m\in \left[0,M_{DT}\right]$ identifies the selected rule of $J_{DT}$ and ${\mathbf{v}}_m=\left[v_{m,1},\dots ,v_{m,F}\right]$ is a binary vector which indicates, for each variable $X_f$, if the condition is present or not. In particular, if $k_m=0$ the $m^{th}$ rule is not included in the RB. Thus, we can generate RBs with a lower number of rules than $M_{max}$. Further if $v_{m,f}=0$ the $f^{th}$ condition of the $m^{th}$ rule can be replaced by a “don’t care” condition.

$C_T$ is a vector containing F vectors of $T_{max}-2$ real numbers: the $f^{th}$ vector $\left[b_{f,2},\dots ,b_{f,T_{max}-1}\right]$ determines the positions of the fuzzy set representatives in the specific variable $X_f$.

In order to generate the offspring populations, we exploit both crossover and mutation. We apply separately the one-point crossover to $C_R$ and the BLX-$\alpha$-crossover, with $\alpha$ = 0.5, to $C_T$. As regards the mutation, we apply two distinct operators for $C_R$ and an operator for $C_T$. More details regarding the mating operators and the steps of PAES-RCS can be found in [16,44].

3.2.2. Feature Extraction

The feature extraction phase has been designed and implemented so as to process real-time traffic captured by means of the pcap libraries. First of all, the traffic is reconstructed to identify the flows, defined by the 5-uple: source and destination IP addresses, source and destination ports, and protocol (note that, in this work, we consider bidirectional flows). Then, each 5-uple is transformed in a vector of features to be used as input of the FRBC, which is in charge of estimating the type of traffic.

In this work, we have experimented two distinct typologies of traffic features:

• Statistical features: the flow is described by a set of statistical values (namely 21), reported in Table 3.
  Table 3. Statistical features.

  Description of the Feature	U/M	Features
  		Forward	Reverse
  Flow duration	$ms$	Δ
  Number of transferred packets	-	f_N	r_N
  Transferred volume	B	f_V	r_V
  Minimum packet size	B	f_Sm	r_Sm
  Maximum packet size	B	f_SM	r_SM
  Average packet size	B	f_Sµ	r_Sµ
  Standard deviation of packet size	B	f_Sσ	r_Sσ
  Minimum inter-packet time	$ms$	f_Tm	r_Tm
  Maximum inter-packet time	$ms$	f_TM	r_TM
  Average inter-packet time	$ms$	f_Tµ	r_Tµ
  Standard deviation of inter-packet time	$ms$	f_Tσ	r_Tσ

  It is important to highlight that in this work, such features have only been computed for flows made of five or more packets.
• Composite features: the flow is described by an array $\mathbf{x}\in {\mathbb{R}}^{3H-1}$, where H is the number of analyzed flow packets, of higher granularity (i.e., packet level) features [34]:

  $$\mathbf{x}=(d_1,l_1,d_2,l_2,t_2,\dots d_H,l_H,t_H)$$

  (2)

  where

  -

  $d_i\in [0,1]$ with $i=1,2,\dots H$ is the direction of the $i^{th}$ packet

  -

  $l_i$ with $i=1,2,\dots H$ is the dimension in Byte of the $i^{th}$ packet, normalized with respect to $l_{MAX}$

  -

  $t_i$ with $i=1,2,\dots H$ is the time in seconds between packet i and packet $i-1$

  Clearly, such features depend on the parameter H and can only be computed for those flows made of at least H packets. In the experimental results, we will consider $H\in [3,5,10]$.

4. Experimental Results

In this section, we present the results of the experimental tests, carried out to validate and evaluate our proposal. The performance have been measured in terms of the following metrics (defined per class):

• True Positive Rate

  $$TPR=\frac{TP}{TP+FN}$$
• False Positive Rate

  $$FPR=\frac{FP}{FP+TN}$$
• Accuracy

  $$ACC=\frac{TP+TN}{TP+TN+FP+FN}$$

In the previous formulas, $TP$, $TN$, $FP$, and $FN$, respectively, represent the number of true positives, of true negatives, of false positives, and of false negatives. Moreover, for some significant cases (for sake of brevity not for all the cases), the confusion matrix is also reported.

Note that in all the tests, we have adopted a k-fold cross-validation approach, with $k=5$.

In the following, to allow a proper comparison of our system against state-of-the-art classifiers, we present, at first, the performance achieved by SVM and C4.5 decision tree, used as benchmarks, and then the results obtained by our system.

4.1. SVM Classifier

As far as the SVM classifier is concerned, we have used the implementation available in WEKA Toolkit (https://www.cs.waikato.ac.nz/ml/weka/ accessed on 20 May 2021) based on the Sequential Minimal Optimization training algorithm [46]. The parameters of the algorithm have been set as

• $ϵ={10}^{-12}$
• $tolerance={10}^{-13}$

In Table 4, we show the achieved accuracy on both datasets and for each feature extraction method. Moreover, Table 5 and Table 6 show the results in terms of $TPR$ and $FPR$ for each class of the UniBS and UPC data sets, respectively.

Table 4. Accuracy achieved by the support vector machine (SVM) classifier.

Data-Set	Features	Accuracy
UniBS	Statistical	0.759
	Composite ($H=3$)	0.662
	Composite ($H=5$)	0.717
	Composite ($H=10$)	0.874
UPC	Statistical	0.71
	Composite ($H=3$)	0.538
	Composite ($H=5$)	0.776
	Composite ($H=10$)	0.896

Table 5. SVM: TPR and FPR over UniBS data set.

Feature	Class	TPR	FPR
Statistical	Mail	0.75	0.06
	Skype	0.55	0.006
	Firefox	0.38	0.001
	Safari	0.81	0.12
	BitTorrent	0.95	0.003
	Amule	0.71	0.13
Composite ($H=3$)	Mail	0	0
	Skype	0.59	0.01
	Firefox	0	0.001
	Safari	0.86	0.31
	BitTorrent	0.89	0.001
	Amule	0.77	0.18
Composite ($H=5$)	Mail	0.19	0.002
	Skype	0.57	0.007
	Firefox	0.9	0.01
	Safari	0.86	0.3
	BitTorrent	0.96	0.002
	Amule	0.726	0.12
Composite ($H=10$)	Mail	0.9	0.004
	Skype	0.56	0.005
	Firefox	0.96	0.001
	Safari	0.89	0.005
	BitTorrent	0.95	0.002
	Amule	0.95	0.06

Table 6. SVM: TPR and FPR over UPC data set.

Feature	Class	TPR	FPR
Statistical	SSHD	0.93	0.297
	XRDP	0.64	0.66
	DNSMasq	0.95	0
	Chrome	0.54	0.05
	Firefox	0	0
	Amule	0.79	0.004
Composite ($H=3$)	SSHD	1	0.63
	XRDP	0	0
	DNSMasq	0.78	0.004
	Chrome	0	0
	Firefox	0	0
	Amule	0.72	0.028
Composite ($H=5$)	SSHD	0.99	0.11
	XRDP	0.95	0.1
	DNSMasq	0.89	0
	Chrome	0.74	0.007
	Firefox	0	0
	Amule	0.46	0.001
Composite ($H=10$)	SSHD	0.97	0.01
	XRDP	0.97	0.01
	DNSMasq	0.99	0
	Chrome	0.98	0.008
	Firefox	0.001	0
	Amule	0.76	0.01

Regarding the accuracy, the best performance is achieved, for both datasets, adopting composite features and $H=10$ ($ACC=0.874$ over the UPC data set and $ACC=0.896$ over the UniBS data set). In both cases, adopting statistical features, the SVM classifier achieves better performances rather than adopting composite features with $H=3$, and even with $H=5$ in the case of UniBS data set.

Finally, for a deeper analysis, Table 7 reports the confusion matrix for the UniBS case with composite features and $H=10$ (note that for sake of brevity we do not show the confusion matrix for all the cases, as they would not add any significant insight). Note that, for the considered case, the worst results are obtained for Skype, which is often classified as Amule. Such a result can be justified by the fact that the two applications have a similar architecture.

Table 7. SVM: confusion matrix (UniBS, composite—$H=10$).

	Mail	Skype	Firefox	Safari	BitTorrent	Amule
Mail	4174	0	0	411	0	36
Skype	31	1351	0	110	40	880
Firefox	0	6	865	5	0	25
Safari	964	0	0	11,778	1	435
BitTorrent	0	68	2	0	1685	6
Amule	82	55	34	314	7	4710

4.2. C4.5 Decision Tree

The C4.5 decision tree has been taken into consideration because of the partly explainability of the results. Indeed, depending on the dimension of the tree and on the number of leaves, the classification results can be accompanied by an analysis of the criteria that take to a given decision. In this work, we have used the J48 classifier available in WEKA toolkit. As regards the parameters of the decision tree, we used the default parameters suggested in WEKA. In particular, the pruning of the decision tree is activated with a confidence parameter value of 0.25. In addition, the minimum number of instances per leaf is set equal to 2.

Similarly to the UniBS case, Table 8 shows the achieved overall performance, while Table 9 and Table 10 report the results in terms of $TPR$ and $FPR$ for each class of the UniBS and UPC data sets, respectively.

Table 8. Performance achieved by the C4.5 classifier.

Data-Set	Features	Accuracy
UniBS	Statistical	0.969
	Composite ($H=3$)	0.82
	Composite ($H=5$)	0.86
	Composite ($H=10$)	0.961
UPC	Statistical	0.981
	Composite ($H=3$)	0.867
	Composite ($H=5$)	0.964
	Composite ($H=10$)	0.966

Table 9. C4.5: Performance over UniBS data set.

Feature	Class	TPR	FPR
Statistical	Mail	0.96	0.005
	Skype	0.92	0.008
	Firefox	0.98	0.001
	Safari	0.97	0.02
	BitTorrent	0.97	0.001
	Amule	0.96	0.006
Composite ($H=3$)	Mail	0.78	0.07
	Skype	0.59	0.008
	Firefox	0.98	0.002
	Safari	0.83	0.11
	BitTorrent	0.96	0.001
	Amule	0.83	0.058
Composite ($H=5$)	Mail	0.85	0.05
	Skype	0.7	0.01
	Firefox	0.98	0.01
	Safari	0.86	0.07
	BitTorrent	0.97	0.001
	Amule	0.84	0.04
Composite ($H=10$)	Mail	0.95	0.005
	Skype	0.9	0.01
	Firefox	0.98	0
	Safari	0.97	0.02
	BitTorrent	0.953	0
	Amule	0.95	0.01

Table 10. C4.5: Performance over UPC data set.

Feature	Class	TPR	FPR
Statistical	SSHD	0.99	0.001
	XRDP	0.99	0.001
	DNSMasq	0.99	0.001
	Chrome	0.97	0.001
	Firefox	0.9	0.007
	Amule	0.98	0.001
Composite ($H=3$)	SSHD	0.95	0.002
	XRDP	0.74	0.002
	DNSMasq	0.99	0.001
	Chrome	0.86	0.007
	Firefox	0.349	0.002
	Amule	0.94	0.003
Composite ($H=5$)	SSHD	0.99	0.002
	XRDP	0.99	0.02
	DNSMasq	0.99	0.01
	Chrome	0.94	0.02
	Firefox	0.79	0.01
	Amule	0.98	0.001
Composite ($H=10$)	SSHD	0.99	0.001
	XRDP	0.99	0.001
	DNSMasq	0.98	0.001
	Chrome	0.94	0.02
	Firefox	0.72	0.01
	Amule	0.97	0.002

Note that in this case, the best accuracy is obtained in both cases with the statistical features ($ACC=0.981$ over the UPC data set and $ACC=0.969$ over the UniBS data set). Furthermore, differently from the SVM case, we can notice that the C4.5 does not present any critical result in terms of almost always unrecognized classes.

For allowing a deeper analysis of the achieved results, in Table 11 we report the confusion matrix for the UPC data set and statistical features. Note that the C4.5 offers almost optimal results over all the classes in this case. Indeed, the only misclassifications occur with the most similar classes, that is when considering Chrome and Firefox.

Table 11. C45: confusion matrix (UPC, statistical).

	SSHD	XRDP	DNSMasq	Chrome	Firefox	Amule
SSHD	7756	5	1	2	1	4
XRDP	6	3017	0	4	2	2
DNSMasq	2	1	1726	0	0	2
Chrome	1	0	5	4404	129	1
Firefox	0	0	2	183	1735	4
Amule	10	10	6	14	3	2319

4.3. PAES-RCS

As for the previous cases, and also for the proposed method, we have run a 5-fold cross-validation, and for each fold we have run three trials (each with a different seed of the random number generator). The algorithm has been run with the parameters indicated in Table 12, and for each fold and each trial we have generated an approximation of the optimal Pareto front. In the following, we report the average results of three representative solutions ordered according to decreasing accuracy. Specifically, as discussed in [44], we sorted the FRBCs in each Pareto front approximation in ascending order of accuracy. Then, we extracted the First (the most accurate and the less explainable), the Median, and the Last solution (the less accurate and the most explainable).

Table 12. Values of the parameters for PAES-RCS used in the experiments.

Parameter	Description	Value
$A_S$	PAES archive dimension	64
$T_f$	Number of fuzzy sets per variable $X_f$	7
$M_{min}$	Minimum number of rules in $C_{RB}$	5
$M_{max}$	Maximum number of rules in $C_{RB}$	100
$E_{max}$	Total number of fitness evaluations	50,000
$P_{C_R}$	Probability of applying crossover operator to $C_R$	0.1
$P_{C_T}$	Probability of applying crossover operator to $C_T$	0.5
$P_{MR{B}_1}$	Probability of applying first mutation operator to $C_R$	0.1
$P_{MR{B}_2}$	Probability of applying second mutation operator to $C_R$	0.7
$P_{M_T}$	Probability of applying mutation operator to $C_T$	0.2

Similarly to what done so far, in Table 13 and Table 14 we present the overall performance over the UniBS and the UPC data-set, respectively, in terms of accuracy, number of rules $Rules$, and total rule length $TRL$. From the tables we can see that out system is able to achieve nearly optimal results, with an accuracy close to $0.9$ in both the cases.

Table 13. Performance achieved by the proposed classifier over the UniBS data set.

Feature	Solution	Acc	Rules	TRL
Statistical	First	0.875	17.86	95.8
	Median	0.86	10.83	32.9
	Last	0.595	7.6	8.47
Composite ($H=3$)	First	0.704	35.3	98.13
	Median	0.691	26.63	79.23
	Last	0.64	25.0	76.93
omposite ($H=5$)	First	0.72	21.4	41.86
	Median	0.704	10.8	13.8
	Last	0.652	8.4	8.4
Composite ($H=10$)	First	0.802	15.6	40.53
	Median	0.734	10.03	18.67
	Last	0.629	8.07	8.2

Table 14. Performance achieved by the proposed classifier over the UPC data set.

Feature	Solution	$\mathit{Acc}$	$\mathit{Rules}$	$\mathit{TRL}$
Statistical	First	0.861	15.93	59.06
	Median	0.843	11.17	24.9
	Last	0.61	8.73	9.06
Composite ($H=3$)	First	0.662	14.86	22.2
	Median	0.647	10.9	13.57
	Last	0.612	7.07	7.07
Composite ($H=5$)	First	0.816	17.53	36.46
	Median	0.79	12.37	18.63
	Last	0.6	8.67	8.67
Composite ($H=10$)	First	0.886	16.73	50.87
	Median	0.877	11.27	20.4
	Last	0.645	8.87	9.0

Then, in Table 15 and Table 16, we present the results in terms of $TPR$ and $FPR$ for each class on the UniBS and UPC data sets, respectively. Note that, apart with composite feature and $H=3$, there is not any class that is mostly unrecognized (as for the SVM classifier). Moreover, it is also interesting to see that, differently from the C4.5 classifier, the proposed method is able to correctly classify Chrome, while it presents some issues in the classification of Firefox.

Table 15. Proposed method: Performance over UniBS data set.

		First		Median		Last
Feature	Class	TPR	FPR	TPR	FPR	TPR	FPR
Statistical	Mail	0.814	0.006	0.801	0.006	0.152	0.027
	Skype	0.636	0.006	0.619	0.007	0.503	0.009
	Firefox	0.696	0.002	0.653	0.002	0.375	0.004
	Safari	0.955	0.005	0.941	0.006	0.810	0.018
	BitTorrent	0.955	0.001	0.949	0.001	0.653	0.006
	Amule	0.836	0.006	0.819	0.007	0.499	0.019
Composite ($H=3$)	Mail	0.000	0.032	0.000	0.032	0.000	0.032
	Skype	0.588	0.007	0.592	0.007	0.592	0.007
	Firefox	0.892	0.001	0.736	0.002	0.637	0.002
	Safari	0.876	0.013	0.865	0.014	0.944	0.006
	BitTorrent	0.968	0.001	0.968	0.001	0.807	0.003
	Amule	0.791	0.008	0.771	0.009	0.312	0.025
Composite ($H=5$)	Mail	0.088	0.029	0.029	0.031	0.000	0.032
	Skype	0.583	0.007	0.583	0.007	0.583	0.007
	Firefox	0.902	0.001	0.822	0.001	0.492	0.003
	Safari	0.896	0.011	0.877	0.013	0.901	0.010
	BitTorrent	0.969	0.001	0.969	0.001	0.839	0.003
	Amule	0.758	0.009	0.776	0.009	0.564	0.016
Composite ($H=10$)	Mail	0.547	0.015	0.502	0.017	0.048	0.031
	Skype	0.572	0.007	0.572	0.007	0.572	0.007
	Firefox	0.892	0.001	0.768	0.001	0.398	0.004
	Safari	0.917	0.009	0.892	0.011	0.891	0.012
	BitTorrent	0.957	0.001	0.956	0.001	0.750	0.003
	Amule	0.788	0.008	0.779	0.009	0.506	0.019

Table 16. Proposed method: Performance over UPC data set.

		First		Median		Last
Feature	Class	TPR	FPR	TPR	FPR	TPR	FPR
Statistical	SSHD	0.948	0.004	0.941	0.005	0.813	0.014
	XRDP	0.883	0.003	0.885	0.003	0.531	0.014
	DNSMasq	0.969	0.001	0.961	0.001	0.694	0.005
	Chrome	0.933	0.003	0.894	0.005	0.510	0.021
	Firefox	0.201	0.015	0.203	0.014	0.156	0.015
	Amule	0.871	0.003	0.835	0.004	0.567	0.010
Composite ($H=3$)	SSHD	0.950	0.004	0.952	0.003	0.945	0.004
	XRDP	0.592	0.011	0.582	0.011	0.524	0.012
	DNSMasq	0.853	0.004	0.845	0.004	0.752	0.006
	Chrome	0.101	0.033	0.089	0.033	0.015	0.036
	Firefox	0.000	0.015	0.000	0.015	0.002	0.015
	Amule	0.917	0.003	0.903	0.004	0.854	0.006
Composite ($H=5$)	SSHD	0.972	0.002	0.973	0.002	0.896	0.008
	XRDP	0.636	0.011	0.646	0.010	0.432	0.016
	DNSMasq	0.930	0.001	0.906	0.002	0.371	0.010
	Chrome	0.943	0.003	0.877	0.005	0.534	0.020
	Firefox	0.033	0.017	0.000	0.018	0.022	0.018
	Amule	0.848	0.003	0.835	0.004	0.600	0.009
Composite ($H=10$)	SSHD	0.972	0.003	0.972	0.003	0.871	0.012
	XRDP	0.887	0.004	0.881	0.004	0.495	0.017
	DNSMasq	0.970	0.000	0.949	0.000	0.556	0.003
	Chrome	0.954	0.002	0.947	0.002	0.562	0.019
	Firefox	0.113	0.012	0.091	0.012	0.086	0.012
	Amule	0.809	0.003	0.773	0.003	0.389	0.009

For a deeper analysis, Table 17 and Table 18 report the confusion matrix for the UniBS and UPC case with statistical features, respectively. As expected, these results highlight that, in the UPC case, the most critical case is represented by Firefox, which is often classified as Chrome.

Table 17. Proposed method: confusion matrix (UniBS, statistical).

	Mail	Skype	Firefox	Safari	BitTorrent	Amule
Mail	823	0	0	99	0	9
Skype	0	326	0	111	4	73
Firefox	0	0	173	2	2	2
Safari	26	4	0	2538	0	64
BitTorrent	0	15	2	2	451	12
Amule	6	34	19	112	0	896

Table 18. Proposed method: confusion matrix (UPC, statistical).

	SSHD	XRDP	DNSMasq	Chrome	Firefox	Amule
SSHD	1449	91	0	8	0	0
XRDP	3	581	0	40	0	1
DNSMasq	0	0	342	1	0	8
Chrome	24	2	0	887	3	0
Firefox	11	0	01	256	106	0
Amule	15	8	1	39	0	395

4.4. Comparison among the Different Classification Models

To easily compare the achieved results, Table 19 reports the best results, in terms of accuracy, per each classifier on the two considered data sets, both for the training set and the test set, respectively.

Table 19. Performance comparison: Accuracy (for the PAES-RCS algorithm the First solution has been considered).

		Training			Test
Data-Set	Feature	SVM	C4.5	PAES-RCS	SVM	C4.5	PAES-RCS
UniBS	Statistical	0.864	0.972	0.893	0.759	0.969	0.875
	Composite ($H=3$)	0.741	0.842	0.752	0.662	0.828	0.704
	Composite ($H=5$)	0.85	0.871	0.804	0.717	0.86	0.72
	Composite ($H=10$)	0.964	0.974	0.839	0.874	0.961	0.802
UPC	Statistical	0.854	0.99	0.883	0.71	0.981	0.861
	Composite ($H=3$)	0.635	0.887	0.721	0.538	0.867	0.662
	Composite ($H=5$)	0.884	0.983	0.892	0.776	0.964	0.816
	Composite ($H=10$)	0.977	0.973	0.904	0.896	0.966	0.886

Starting by comparing the performance of our method with those of SVM on the test set, it is easy to see that our method achieves more or less the same accuracy than SVM, with a maximum accuracy of 0.875 (against 0.874) on the UniBS data set, and 0.886 (against 0.896) over the UPC data set. On the contrary, considering again the test set, our method is outperformed, in terms of accuracy, by C4.5 over both the data sets.

Similar results are obtained on the training set. Nevertheless, in this case, note that the overfitting is very high for the SVM algorithm. Furthermore, the decision tree and the proposed PAES-RCS algorithms suffer from this problem, but in this case the phenomenon is less evident.

Nonetheless, as already discussed, our method is characterized by a high level of explainability. To quantify such an aspect, in Table 20 we report the complexity of our method (in terms of number of rules and TRL) and of the C4.5 algorithm (in terms of number of leaves and tree dimension). Note that we do not take into consideration SVM in this analysis, as it is well known that SVM must be considered as a “black box”.

Table 20. Performance comparison: Complexity (for the PAES-RCS algorithm the First solution has been considered).

		C4.5		PAES-RCS
Data-Set	Feature	Tree Dimension	Leaves	TRL	Rules
UniBS	Statistical	449	228	95.8	17.86
	Composite ($H=3$)	194	118	98.13	35.3
	Composite ($H=5$)	889	435	41.86	21.4
	Composite ($H=10$)	712	383	40.53	15.6
UPC	Statistical	3321	147	59.06	15.93
	Composite ($H=3$)	247	134	22.2	14.86
	Composite ($H=5$)	364	176	36.46	17.53
	Composite ($H=10$)	447	223	50.87	16.73

As it can be observed from the table, the higher accuracy of C4.5 is paid with a much higher complexity, which directly results in a lower explainability. Note that as far as complexity is concerned, that for our proposed method we have considered the “First” case, which has a much higher complexity, but an only slightly better accuracy, with respect to the “Median” case. Therefore, out method results even more convenient, considering the “Median” case.

To further clarify the level of explainability of the proposed method, we finally analyze some examples of classification rules (created for the UniBS data-set). In Figure 3, we show a generic strong fuzzy partition that has been used for each variable in the experiment. The fuzzy partition consists of seven fuzzy sets, labeled with linguistic values ranging from Very Low (VL) to Very High (VH).

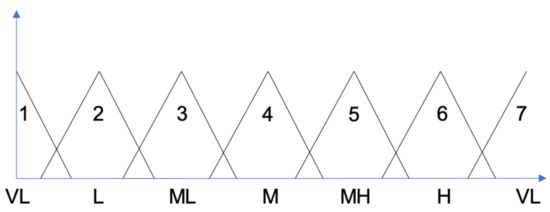
Figure 3. The fuzzy partition adopted in the experiments.

Given such fuzzy sets, the following are a few examples of classification rules:

• R1: IF f_S_µ is VL THEN Y is Skype
• R2: IF f_N is L THEN Y is Amule
• R3: IF r_S_M is H AND r_T_M is M THEN Y is Mail
• R4: IF f_N is H AND f_V is VH AND r_V is H AND r_S_m is L AND f_S_M is F ML AND r_S_M is H AND r_S_µ is H AND f_S_σ is VH AND r_S_σ is VH AND f_T_M is H THEN Y is Mail

It is clear, that such rules, being linguistic rules, can be easily read and understood by an operator.

For the sake of completeness, we highlight that both UniBS and UPC are data sets that exhibit some level of imbalance. Therefore, we have applied a set of re-balancing techniques, but the obtained results did not show appreciable improvements. This is probably due to the fact that the level of unbalancing is not very high. Indeed, as can be seen from the tables and the confusion matrices discussed above, we have verified that poor results on specific classes are not due to the imbalance level but rather to the adopted feature extraction procedure and/or to classification model selected. Due to space reasons and to their scarce relevance, we have not reported all the results achieved adopting a re-balancing step of the training set.

5. Conclusions and Future Work

The development of “explainable” classification methods is attracting a lot of research efforts in several fields, such as network monitoring. This is highly justified by the newly emerged requirements in terms of fairness or unbiasedness, privacy, reliability, robustness, causality, and/or trust, which make the standard methods inadequate. For this reason, in this paper, we have proposed a traffic classification tool based on multi-objective evolutionary fuzzy classifiers.

Our proposal has been validated and evaluated over two well-known publicly available traffic data-sets (namely, UniBS and UPC) and has demonstrated optimal performance both in term of accuracy end explainability. Indeed, the achieved results show that our method is able to outperform the de facto standard method (i.e., SVM) both in terms of accuracy and explainability. Moreover, the proposed method is also able to offer a better accuracy–explainability trade-off than C4.5 classifier, in which a very high accuracy is paid in terms of very low level of explainability.

The main limitation of the proposed approach, based on XAI models for internet traffic classification, regards the fact that it may suffer from the “concept drift issue”. Indeed, if a new set of internet applications appears in the monitored network, the system will not be able to identify it. This is due to the fact that the traffic flows associated with the new applications have never been seen by the XAI models during the training stage. This means that the models should be retrained or an incremental learning algorithm should be adopted for updating in real time the parameters of the models (i.e., the rules). This issue, not trivial at all, represents a hot research topic that will be considered in future works.