Energy Capacity of Waffle-Flat-Plate Structures with Hysteretic Dampers Subjected to Bidirectional Seismic Loadings
Abstract
Featured Application
Abstract
1. Introduction
2. Test, Numerical Model, and Validation of Reinforced Concrete (RC) Waffle-Flat-Plate (WFP) Structure
2.1. Shake-Table Tests
2.2. Numerical Model of the WFP Structure
2.3. Experimental Validation of the Numerical Model
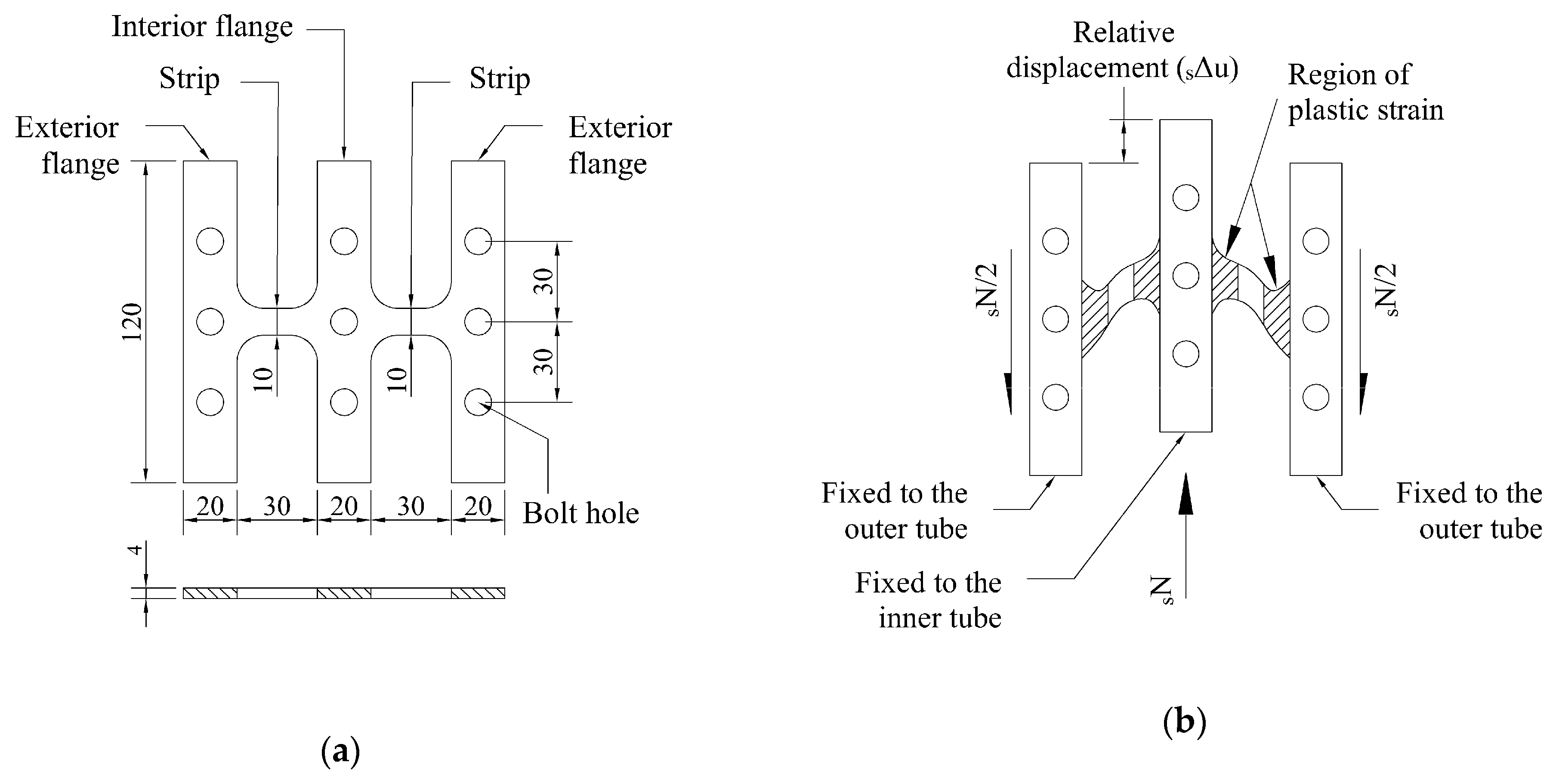
3. Test and Numerical Model of Dampers
4. Numerical Analyses of a WFP Structure Upgraded with Slit-Plate Dampers (SPDs)
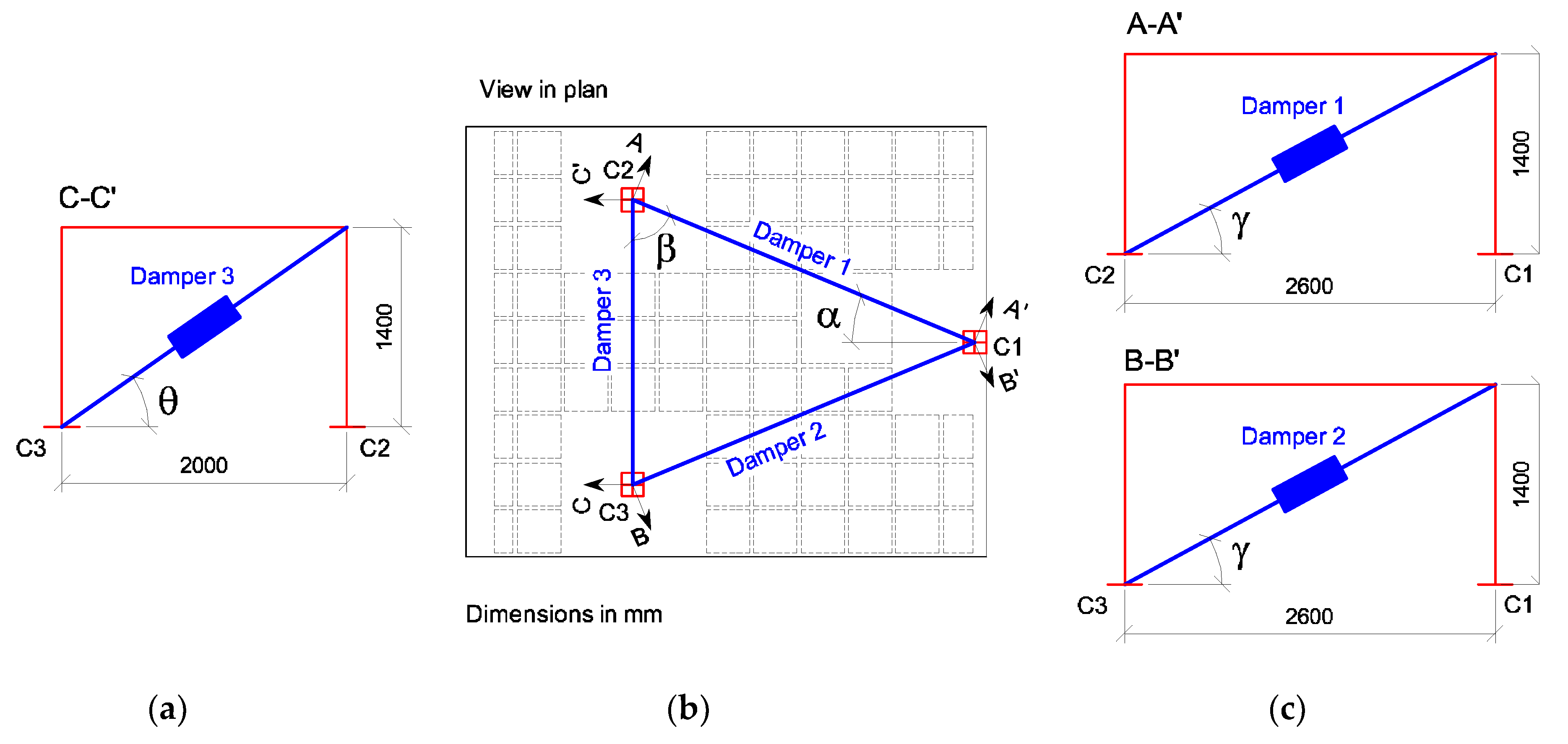
4.1. Design of the Hysteretic Dampers
4.2. Numerical Model of WFP System with Dampers
4.3. Numerical Analyses
5. Results: Seismic Capacity of a WFP Structure Upgraded with Hysteretic Dampers
5.1. Input Energy and Dissipated Energy
5.2. Differences for the Seismic Capacity Under Unidirectional and Bidirectional Loadings
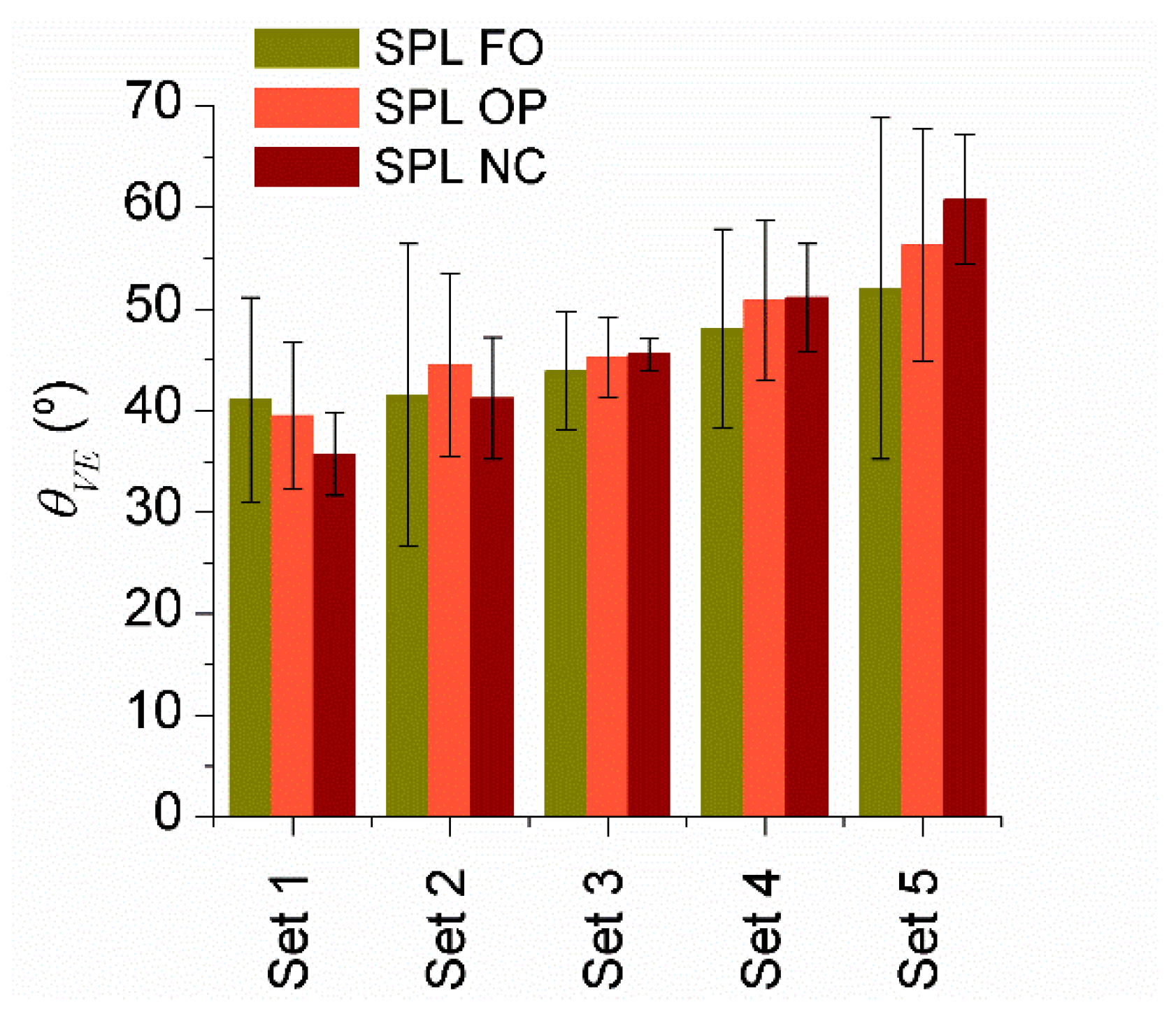
5.3. Ductility Level for Seismic Performance Levels (SPL) Near Collapse (NC)
5.4. Energy Dissipated by Plastic Deformations for SPL NC
5.5. Equivalent Number of Cycles for SPL NC
6. Conclusions
- The total input energy or the total hysteretic energy—expressed in the form of equivalent velocities VE or VD—required to attain SPLs FO, OP, and NC remains basically constant, irrespective of the ground motion considered when the two horizontal components of the ground motion are simultaneously applied.
- The VE that the structure can endure until SPL NC was, on average, about three times the value obtained SPL OP, and eight times the value for OP and FO. Meanwhile, the VD when the structure reaches SPL NC was, on average, about three times that obtained for SPL OP.
- Past studies on conventional structures pointed out that torsion effects tend to redistribute the damage in the structure, which in terms of energy means to balance the energy input by the X and Y components of the ground motion. This was not found for the structure under study, most probably due to the fact that the dampers controlled the torsional movements.
- The capacity of the structure under bidirectional loadings is in most cases slightly higher than under unidirectional loadings. Nevertheless, for some ground motions the response is opposite.
- The values of VE and VD estimated from the energies obtained independently for the X and Y components of the ground motion (unidirectional analysis) are always larger than the actual value obtained applying the two components simultaneously (bidirectional analysis). The values are 18% larger for SPL OP and 27% larger for SPL NC.
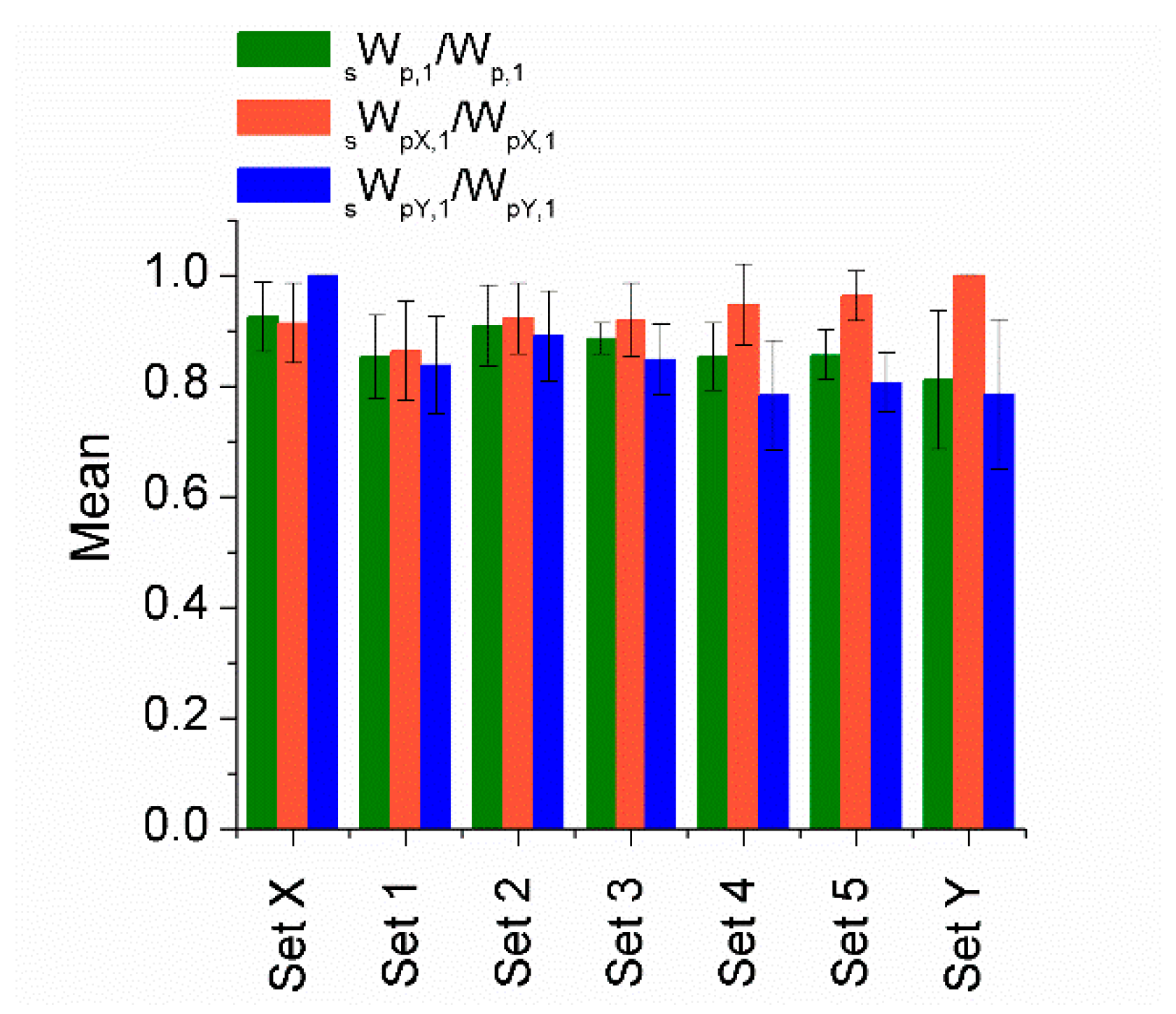
- The relationship VD/VE obtained for SPL OP (0.70 with COV = 0.09) was very similar to that predicted with Akiyama’s Equation (2) (0.74). Nevertheless, for SPL NC, the value obtained (0.80) was markedly higher than that provided by Akiyama’s equation (0.61).
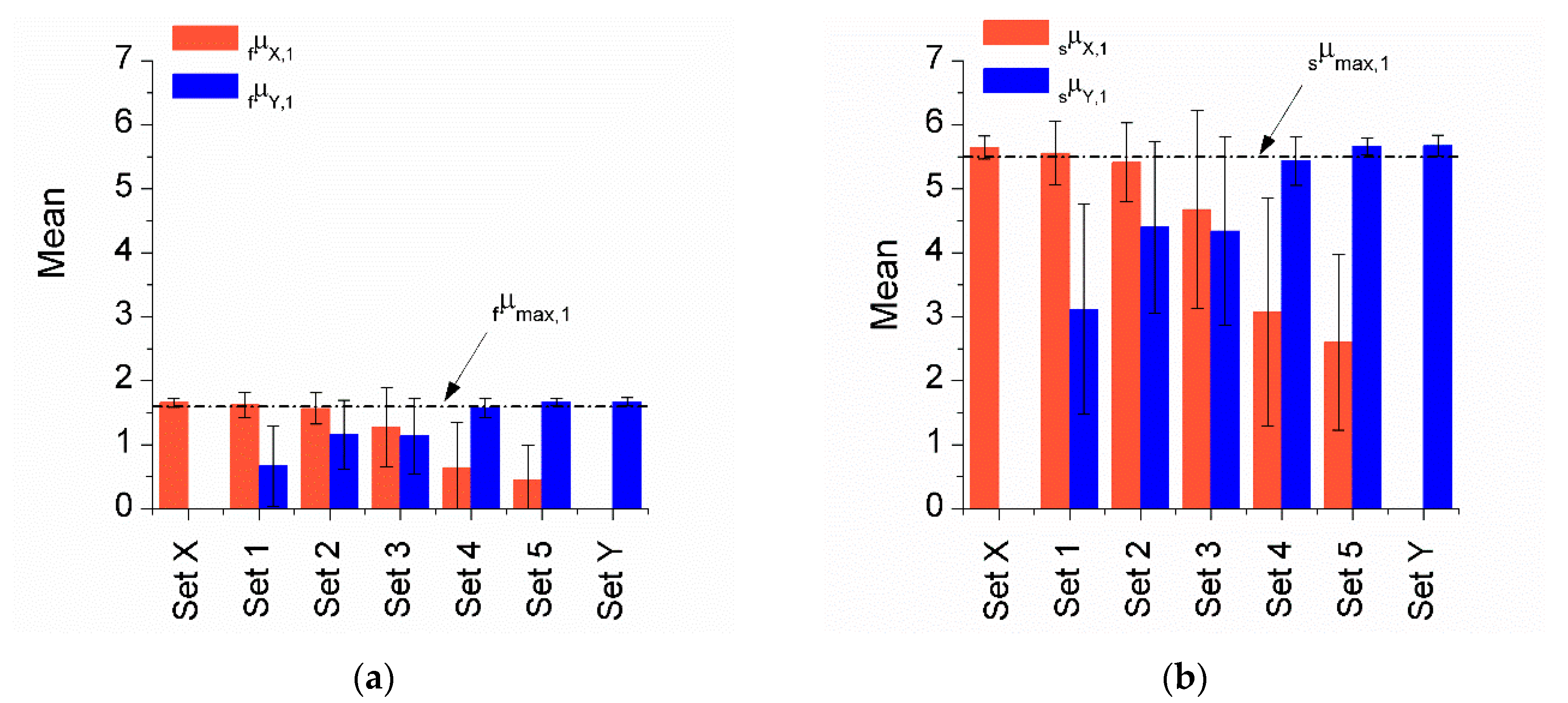
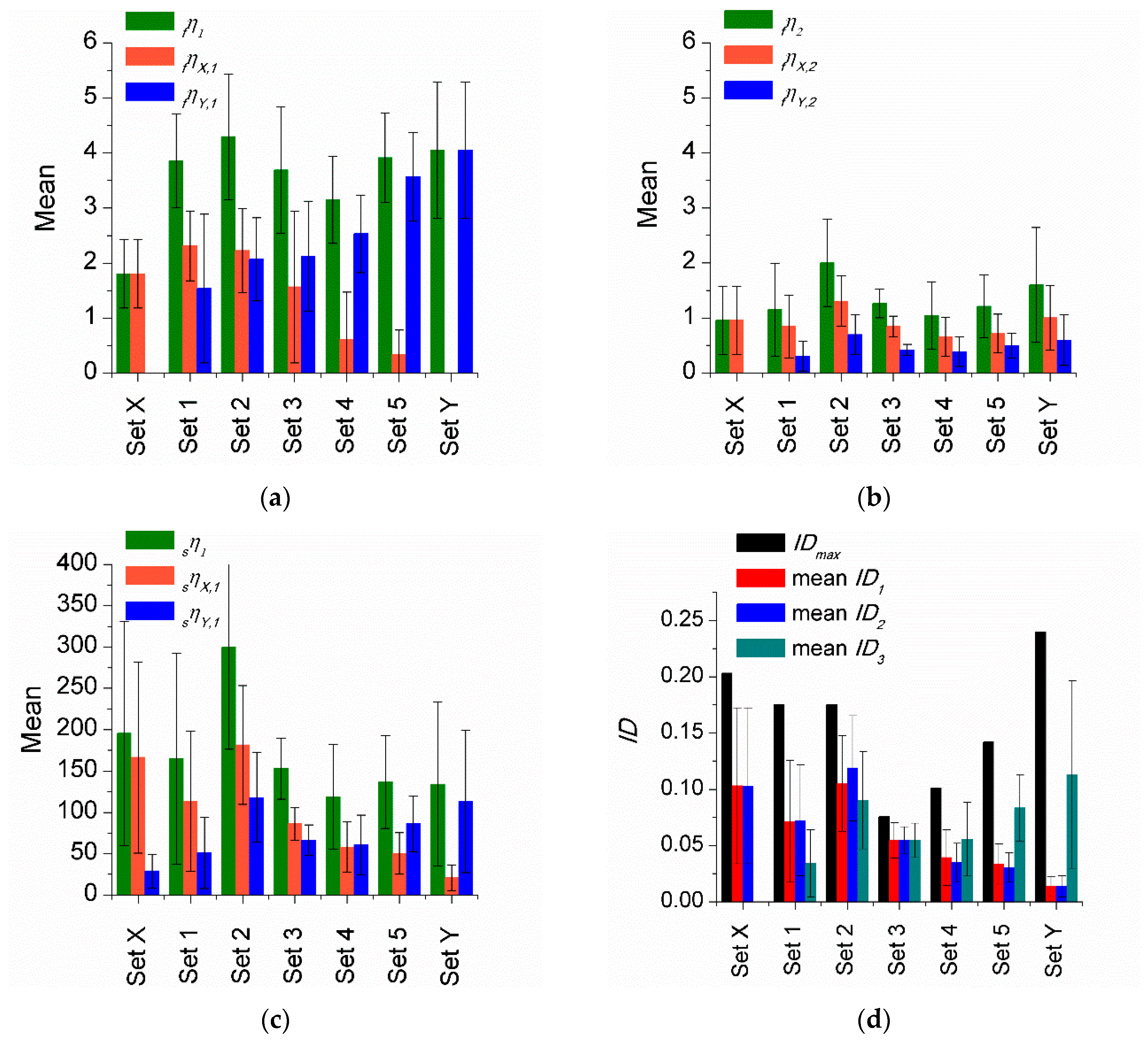
- The maximum ductility level, estimated through the maximum apparent plastic deformation, was 1.6 in the WFP system and 5.5 in SPDs.
- Most of the energy (80%) input and dissipated by the structure was absorbed by the dampers.
- The equivalent number of cycles obtained for the flexible and stiff parts would rely on the characteristics of the main structure and the layout of dampers in X and Y directions. The average and minimum values obtained are fneq,1 = 2 and fneq,min1 = 1.20, respectively, for the flexible part; sneq,1 ranged between 15 and 24, with a minimum value of sneq,min1 = 6.36. The values found here are in accordance with those proposed by Akiyama [15].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Earthquake Name | Year | Sta. Name (Record Seq. No.) | Mw | SF70 | PGAX (g) | PGAY (g) | VEX (cm/s) | VEY (cm/s) | θ (°) |
|---|---|---|---|---|---|---|---|---|---|
| Manjil (Irán) | 1990 | Qazvin (1636) | 7.37 | 1.05 | 0.18 | 0.13 | 57.94 | 32.84 | 29.54 |
| Cape Mendocino (USA) | 1992 | Eur.Myrtle&West (826) | 7.01 | 1.07 | 0.15 | 0.18 | 57.15 | 32.41 | 29.56 |
| San Fernando (USA) | 1971 | Hollywood Stor FF (68) | 6.61 | 1.12 | 0.21 | 0.17 | 52.63 | 33.57 | 32.53 |
| Sierra Madre (USA) | 1991 | LA-City Terrace (1643) | 5.61 | 1.70 | 0.11 | 0.09 | 35.24 | 21.37 | 31.23 |
| Chi-Chi (Taiwan) | 1999 | TAP051 (1435) | 7.62 | 1.74 | 0.11 | 0.06 | 35.08 | 19.89 | 29.55 |
| Imperial Valley (USA) | 1979 | Niland Fire Sta. (186) | 6.53 | 1.77 | 0.11 | 0.07 | 33.29 | 21.19 | 32.48 |
| Landers (USA) | 1992 | Anaheim-WB Rd (833) | 7.28 | 2.69 | 0.05 | 0.04 | 22.08 | 13.76 | 31.94 |
| Earthquake Name | Year | Sta. Name (Record Seq. No.) | Mw | SF70 | PGAX (g) | PGAY (g) | VEX (cm/s) | VEY (cm/s) | θ (°) |
|---|---|---|---|---|---|---|---|---|---|
| Chi-Chi (Taiwan) | 1999 | TCU050 (1490) | 7.62 | 1.00 | 0.15 | 0.13 | 53.39 | 45.78 | 40.62 |
| Northridge (USA) | 1994 | Elizabeth Lake (971) | 6.69 | 0.98 | 0.15 | 0.11 | 57.76 | 41.97 | 36.00 |
| Hector Mine (USA) | 1999 | Amboy (1762) | 7.13 | 0.95 | 0.18 | 0.15 | 59.38 | 43.37 | 36.15 |
| Duzce (Turkey) | 1999 | Mudumu (1619) | 7.14 | 1.06 | 0.12 | 0.06 | 53.85 | 38.40 | 35.50 |
| Morgan Hill (USA) | 1984 | Gilroy Array 7 (460) | 6.19 | 0.89 | 0.19 | 0.11 | 60.11 | 50.94 | 40.28 |
| Imperial Valley (USA) | 1979 | EL Centro 12 (175) | 6.53 | 1.18 | 0.14 | 0.12 | 46.25 | 37.23 | 38.83 |
| Loma Prieta (USA) | 1989 | Intern. Airport (799) | 6.93 | 0.59 | 0.24 | 0.33 | 91.34 | 77.28 | 40.24 |
| Earthquake Name | Year | Sta. Name (Record Seq. No.) | Mw | SF70 | PGAX (g) | PGAY (g) | VEX (cm/s) | VEY (cm/s) | θ (°) |
|---|---|---|---|---|---|---|---|---|---|
| Chi-Chi (Taiwan) | 1999 | TCU107 (1534) | 7.62 | 1.01 | 0.12 | 0.16 | 45.00 | 53.05 | 49.69 |
| Kobe (Japan) | 1995 | Sakai (1115) | 6.90 | 0.99 | 0.16 | 0.12 | 50.13 | 50.13 | 45.00 |
| Northridge (USA) | 1994 | Brentwood-VAHosp. (986) | 6.69 | 1.03 | 0.19 | 0.16 | 43.79 | 51.58 | 49.67 |
| Landers (USA) | 1992 | Desert Hot Springs (850) | 7.28 | 0.94 | 0.17 | 0.15 | 51.91 | 53.78 | 46.02 |
| Hector Mine (USA) | 1999 | Baker Fire Sta. (1766) | 7.13 | 1.25 | 0.13 | 0.09 | 36.32 | 42.60 | 49.55 |
| Coalinga (USA) | 1983 | Parkfield VinC2W (362) | 6.36 | 1.59 | 0.07 | 0.08 | 27.53 | 34.44 | 51.37 |
| Whittier Narrows (USA) | 1987 | Panorama City-Roscoe (673) | 5.99 | 1.65 | 0.10 | 0.11 | 29.51 | 30.61 | 46.04 |
| Earthquake Name | Year | Sta. Name (Record Seq. No.) | Mw | SF70 | PGAX (g) | PGAY (g) | VEX (cm/s) | VEY (cm/s) | θ (°) |
|---|---|---|---|---|---|---|---|---|---|
| Superstition Hills (USA) | 1987 | Wild Life Liq. Ar (729) | 6.54 | 0.84 | 0.18 | 0.21 | 43.34 | 71.56 | 58.80 |
| Irpinia (Italy) | 1980 | Calitri (289) | 6.90 | 0.82 | 0.13 | 0.18 | 44.95 | 72.46 | 58.18 |
| Kocaeli (Turkey) | 1999 | Goynuk (1162) | 7.51 | 1.26 | 0.13 | 0.12 | 34.03 | 44.19 | 52.40 |
| Hector Mine (USA) | 1999 | San Bernardino – Mont.M (1829) | 7.13 | 1.28 | 0.09 | 0.13 | 29.25 | 46.39 | 57.77 |
| Coalinga (USA) | 1983 | Parkfield – Gold Hill 3W (352) | 6.36 | 1.55 | 0.14 | 0.12 | 24.03 | 38.40 | 57.96 |
| Landers (USA) | 1992 | San Bernardino – E&Hosp. (888) | 7.28 | 1.48 | 0.08 | 0.09 | 27.36 | 38.49 | 54.59 |
| Friuli (Italy) | 1976 | Tolmezzo (125) | 6.50 | 0.56 | 0.35 | 0.31 | 64.73 | 107.60 | 58.97 |
| Earthquake Name | Year | Sta. Name (Record Seq. No.) | Mw | SF70 | PGAX (g) | PGAY (g) | VEX (cm/s) | VEY (cm/s) | θ (°) |
|---|---|---|---|---|---|---|---|---|---|
| Hector Mine (USA) | 1999 | Joshua Tree (1794) | 7.13 | 0.79 | 0.15 | 0.19 | 36.78 | 80.52 | 65.45 |
| Chi-Chi (Taiwan) | 1999 | ILA066 (1349) | 7.62 | 1.28 | 0.08 | 0.10 | 19.92 | 51.12 | 68.71 |
| Chalfant Valley (USA) | 1986 | Bishop – LADWP (549) | 6.19 | 0.75 | 0.25 | 0.17 | 33.97 | 86.80 | 68.62 |
| Landers (USA) | 1992 | Featherly Park –Maint (854) | 7.28 | 1.68 | 0.05 | 0.05 | 18.72 | 37.18 | 63.28 |
| Northridge (USA) | 1994 | Seal Beach – Off Bldg. (1079) | 6.69 | 1.84 | 0.06 | 0.08 | 17.16 | 33.99 | 63.21 |
| Chi-Chi (Taiwan) | 1999 | ILA036 (1328) | 7.62 | 2.54 | 0.06 | 0.07 | 9.82 | 25.75 | 69.12 |
| Loma Prieta (USA) | 1989 | Gilroy Array 1 (765) | 6.93 | 0.36 | 0.41 | 0.47 | 79.93 | 179.16 | 65.96 |
References
- Ministerio Fomento. Norma de Construcción Sismorresistente. Parte General y Edificación (NCSE-02); Centro Publicaciones. Secretaria General Técnica; Ministerio Fomento: Madrid, España, 2003.
- European Committee for Standardization. European Standard EN 1998-1:2004 Eurocode 8: Design of Structures for Earthquake Resistance; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318M-14) and Commentary (ACI 318RM-14); American Concrete Institute: Farmington Hills, MI, USA, 2014; ISBN 978-0-87031-964-8. [Google Scholar]
- Fardis, M. Seismic Design, Assessment and Retrofitting of Concrete Buildings: Based on EN-Eurocode 8; Springer: Heidelberg, Germany, 2009; Volume 8, ISBN 9781402098413. [Google Scholar]
- Rodriguez, M.; Meli, R. Seismic Load Tests on two-story Waffle-Flat Plate Structures. J. Struct. Eng. 1995, 121, 1287–1293. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Donaire-Avila, J.; Oliver-Saiz, E. Shaking table tests of a reinforced concrete waffle-flat plate structure designed following modern codes: Seismic performance and damage evaluation. Earthq. Eng. Struct. Dyn. 2016, 45, 315–336. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Galé-Lamuela, D.; Donaire-Avila, J. Energy capacity and seismic performance of RC waffle-flat plate structures under two components of far-field ground motions: Shake table tests. Earthq. Eng. Struct. Dyn. 2019, 48, 949–969. [Google Scholar] [CrossRef]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; Mcnamara, R.J. Energy Dissipation Systems for Seismic Applications: Current Practice and Recent Developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Oviedo, A.; Midorikawa, M.; Asari, T. Earthquake response of ten-story story-drift-controlled reinforced concrete frames with hysteretic dampers. Eng. Struct. 2010, 32, 1735–1746. [Google Scholar] [CrossRef]
- Kasai, K.; Nakai, M.; Nakamura, Y.; Asai, H.; Suzuki, Y.; Ishii, M. Building Passive Control in Japan. J. Disaster Res. 2009, 4, 261–269. [Google Scholar] [CrossRef]
- Providakis, C.P. Effect of LRB isolators and supplemental viscous dampers on seismic isolated buildings under near-fault excitations. Eng. Struct. 2008, 30, 1187–1198. [Google Scholar] [CrossRef]
- Tributsch, A.; Adam, C. Evaluation and analytical approximation of Tuned Mass Damper performance in an earthquake environment. Smart Struct. Syst. 2012, 10, 155–179. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A. Partial mass isolation system for seismic vibration control of buildings. Struct. Control Health Monit. 2018, 25, 1–16. [Google Scholar] [CrossRef]
- Connor, J.J. Introduction to Structural Motion Control; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Akiyama, H. Earthquake Resistant Limit-State Design for Buildings (English Version); University of Tokyo Press: Tokyo, Japan, 1985. [Google Scholar]
- Benavent-Climent, A. An energy-based method for seismic retrofit of existing frames using hysteretic dampers. Soil Dyn. Earthq. Eng. 2011, 31, 1385–1396. [Google Scholar] [CrossRef]
- Donaire-Ávila, J.; Benavent-Climent, A. Optimum strength distribution for structures with metallic dampers subjected to seismic loading. Metals (Basel) 2020, 10, 127. [Google Scholar] [CrossRef]
- Building Research Institute. The Building Standard Law of Japan; The Building Center of Japan: Tokyo, Japan, 2009. [Google Scholar]
- Benavent-Climent, A.; Donaire-Avila, J.; Oliver-Sáiz, E. Seismic performance and damage evaluation of a waffle-flat plate structure with hysteretic dampers through shake-table tests. Earthq. Eng. Struct. Dyn. 2018, 47, 1250–1269. [Google Scholar] [CrossRef]
- Donaire-Ávila, J. Proyecto Sismorresistente de Estructuras con Forjado Reticular y Disipadores Histeréticos Basado en el Balance de Energia. Ph.D. Thesis, University of Granada, Granada, Spain, 2013. [Google Scholar]
- Feng, M.Q.; Chai, W. Design of a mega-sub-controlled building system under stochastic wind loads. Probabilistic Eng. Mech. 1997, 12, 149–162. [Google Scholar] [CrossRef][Green Version]
- Anajafi, H.; Medina, R.A. Comparison of the seismic performance of a partial mass isolation technique with conventional TMD and base-isolation systems under broad-band and narrow-band excitations. Eng. Struct. 2018, 158, 110–123. [Google Scholar] [CrossRef]
- Fardis, M.N. From force- to displacement-based seismic design of concrete structures and beyond. In Proceedings of the 16 European Coinference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018; pp. 1–20. [Google Scholar]
- Mckenna, F.T. Object-Oriented Finite Element Programming: Frameworks for Analysis, Algorithms and Parallel Computing. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1997. [Google Scholar]
- Mohd, Y.M. Nonlinear Analysis of Prestressed Concrete Structures under Monotonic and Cyclic Loads. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1994. [Google Scholar]
- Maekawa, K.; Pimanmas, A.; Okamura, H. Non Linear Mechanics of Reinforced Concrete; Spon Press: New York, NY, USA, 2003. [Google Scholar]
- Rodrigues, H.; Furtado, A.; Arêde, A. Behavior of Rectangular Reinforced-Concrete Columns under Biaxial Cyclic Loading and Variable Axial Loads. J. Struct. Eng. (United States) 2016, 142, 1–8. [Google Scholar] [CrossRef]
- Rodrigues, H.; Varum, H.; Arêde, A.; Costa, A.G. Behaviour of reinforced concrete column under biaxial cyclic loading—State of the art. Int. J. Adv. Struct. Eng. 2013, 5, 1–12. [Google Scholar] [CrossRef]
- Valipour, H.R.; Foster, S.J. Nonlinear reinforced concrete frame element with torsion. Eng. Struct. 2010, 32, 988–1002. [Google Scholar] [CrossRef]
- Charney, F.A. Unintended Consequences of Modeling Damping in Structures. J. Struct. Eng. 2008, 134, 581–592. [Google Scholar] [CrossRef]
- Jehel, P.; Léger, P.; Ibrahimbegovic, A. Initial versus tangent stiffness-based Rayleigh damping in inelastic time history seismic analyses. Earthq. Eng. Struct. Dyn. 2014, 43, 467–484. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A.; Santini-Bell, E. Effects of the improper modeling of viscous damping on the first-mode and higher-mode dominated responses of base-isolated buildings. Earthq. Eng. Struct. Dyn. 2020, 49, 51–73. [Google Scholar] [CrossRef]
- Chopra, A.K.; Mckenna, F. Modeling viscous damping in nonlinear response history analysis of buildings for earthquake excitation. Earthq. Eng. Struct. Dyn. 2016, 45, 193–211. [Google Scholar] [CrossRef]
- Abarkane, C.; Galé-Lamuela, D.; Benavent-Climent, A.; Suárez, E.; Gallego, A. Ultrasonic pulse-echo signal analysis for damage evaluation of metallic slit-plate hysteretic dampers. Metals (Basel) 2017, 7, 526. [Google Scholar] [CrossRef]
- ASCE/SEI 41-13. Seismic Evaluation and Retrofit of Existing Buildings; American Society of Civil Engineers: Reston, VA, USA, 2014; ISBN 9780784412855. [Google Scholar]
- Lucchini, A.; Franchin, P.; Mollaioli, F. Uniform hazard floor acceleration spectra for linear structures. Earthq. Eng. Struct. Dyn. 2017, 46, 1121–1140. [Google Scholar] [CrossRef]
- Marušić, D.; Fajfar, P. On the inelastic seismic response of asymmetric buildings under bi-axial excitation. Earthq. Eng. Struct. Dyn. 2005, 34, 943–963. [Google Scholar] [CrossRef]
- De Stefano, M.; Faella, G. An evaluation of the inelastic response of systems under biaxial seismic excitations. Eng. Struct. 1996, 18, 724–731. [Google Scholar] [CrossRef]
- Rodrigues, H.; Arêde, A.; Varum, H.; Costa, A. Damage evolution in reinforced concrete columns subjected to biaxial loading. Bull. Earthq. Eng. 2013, 11, 1517–1540. [Google Scholar] [CrossRef]
- Benavent-Climent, A. An energy-based damage model for seismic response of steel structures. Earthq. Eng. Struct. Dyn. 2007, 36, 1049–1064. [Google Scholar] [CrossRef]
- Abarkane, C.; Ríos-García, G.; Gale-Lamuela, D.; Rescalvo, F.; Gallego, A.; Benavent-Climent, A. Metallic slit-plate dampers: Damage evaluation with metal magnetic memory technique and application to structures with rocking columns. Metals (Basel) 2019, 9, 953. [Google Scholar] [CrossRef]
- Abarkane, C.; Galé-Lamuela, D.; Benavent-Climent, A.; Rescalvo, F.J.; Gallego, A. Diagnosis of hysteretic dampers used for seismic protection of structures by means ultrasonic measurements. Meas. J. Int. Meas. Confed. 2019, 137, 344–354. [Google Scholar] [CrossRef]
- Manfredi, G.; Polese, M.; Cosenza, E. Cumulative demand of the earthquake ground motions in the near source. Earthq. Eng. Struct. Dyn. 2003, 32, 1853–1865. [Google Scholar] [CrossRef]
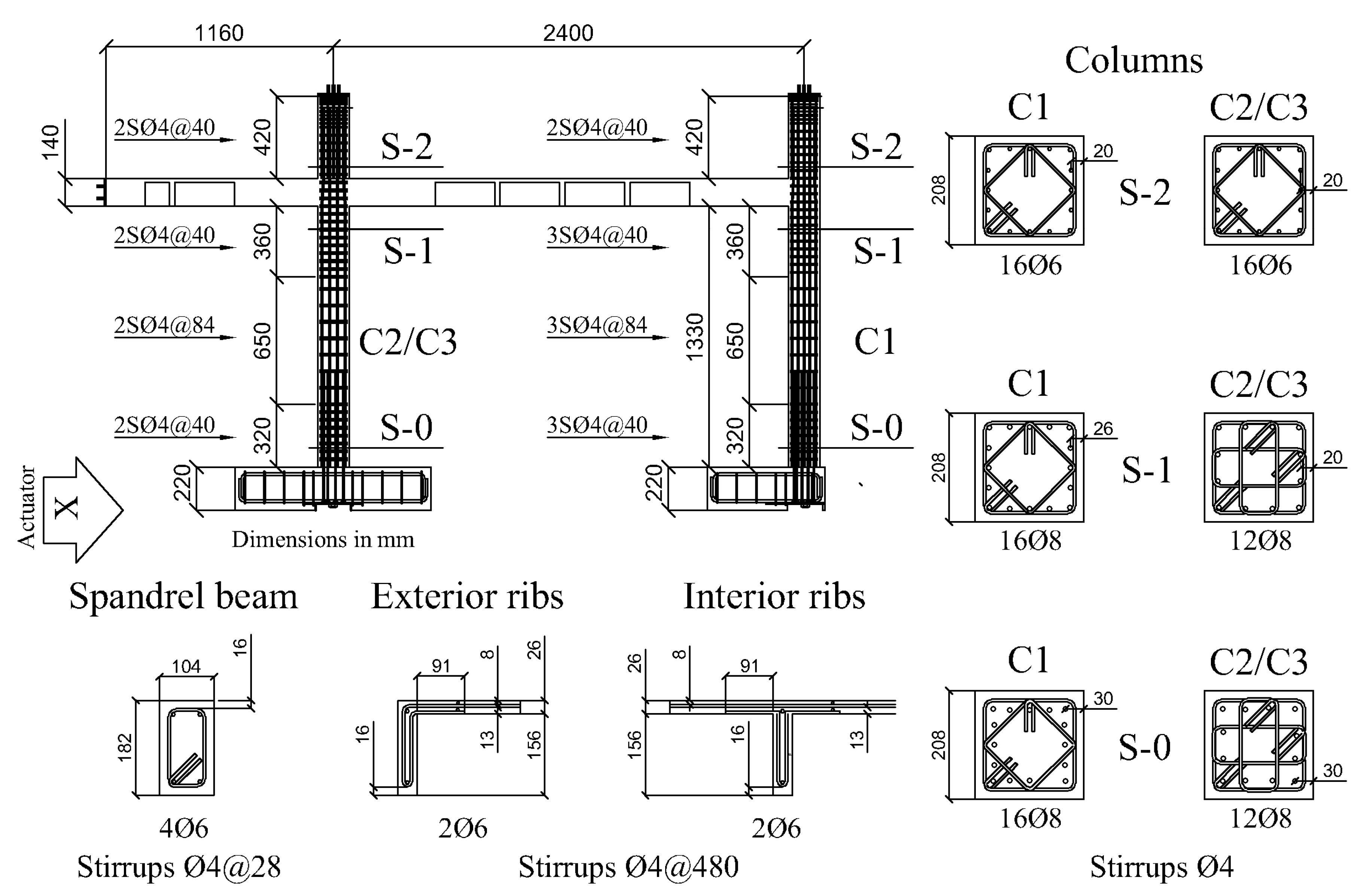
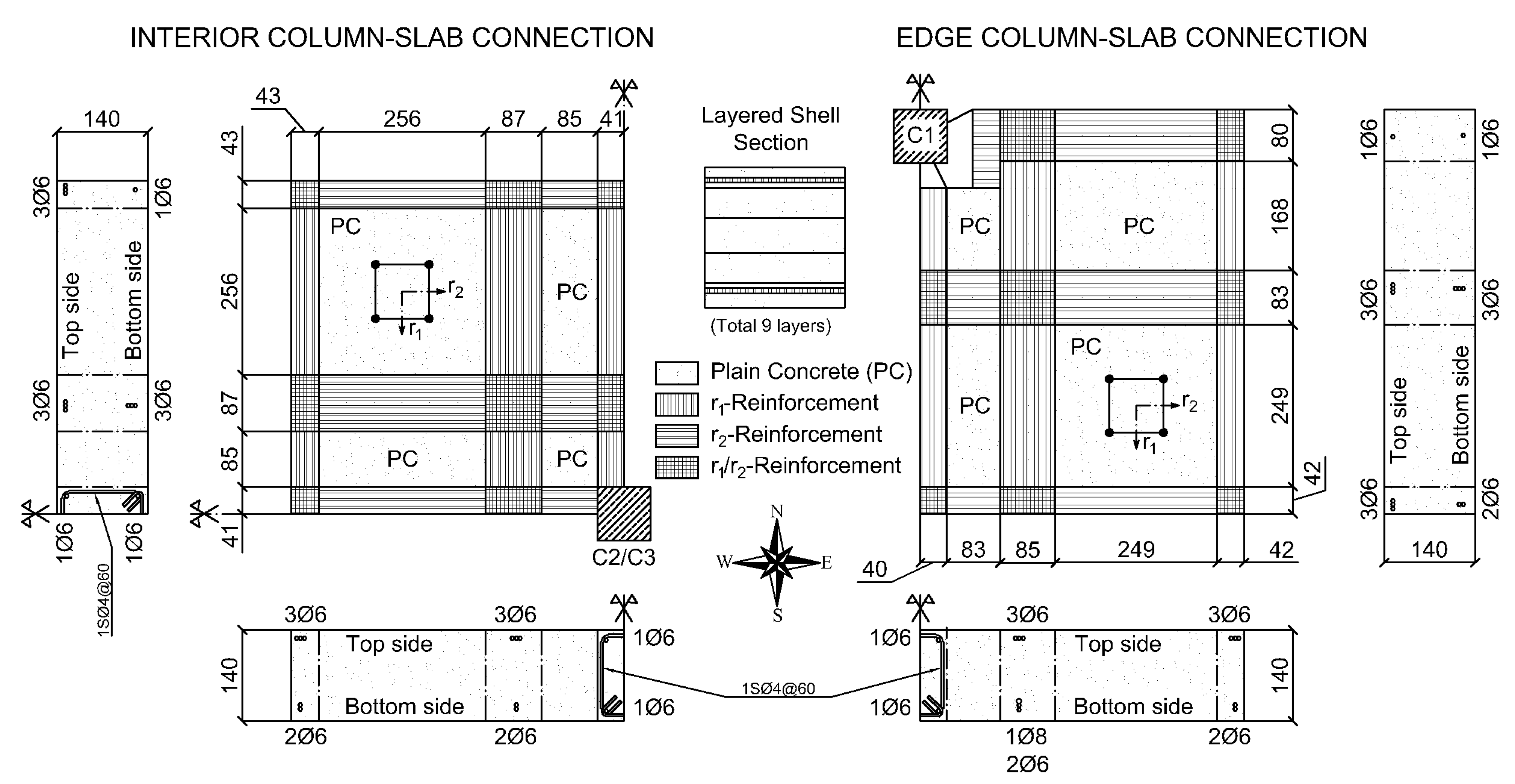
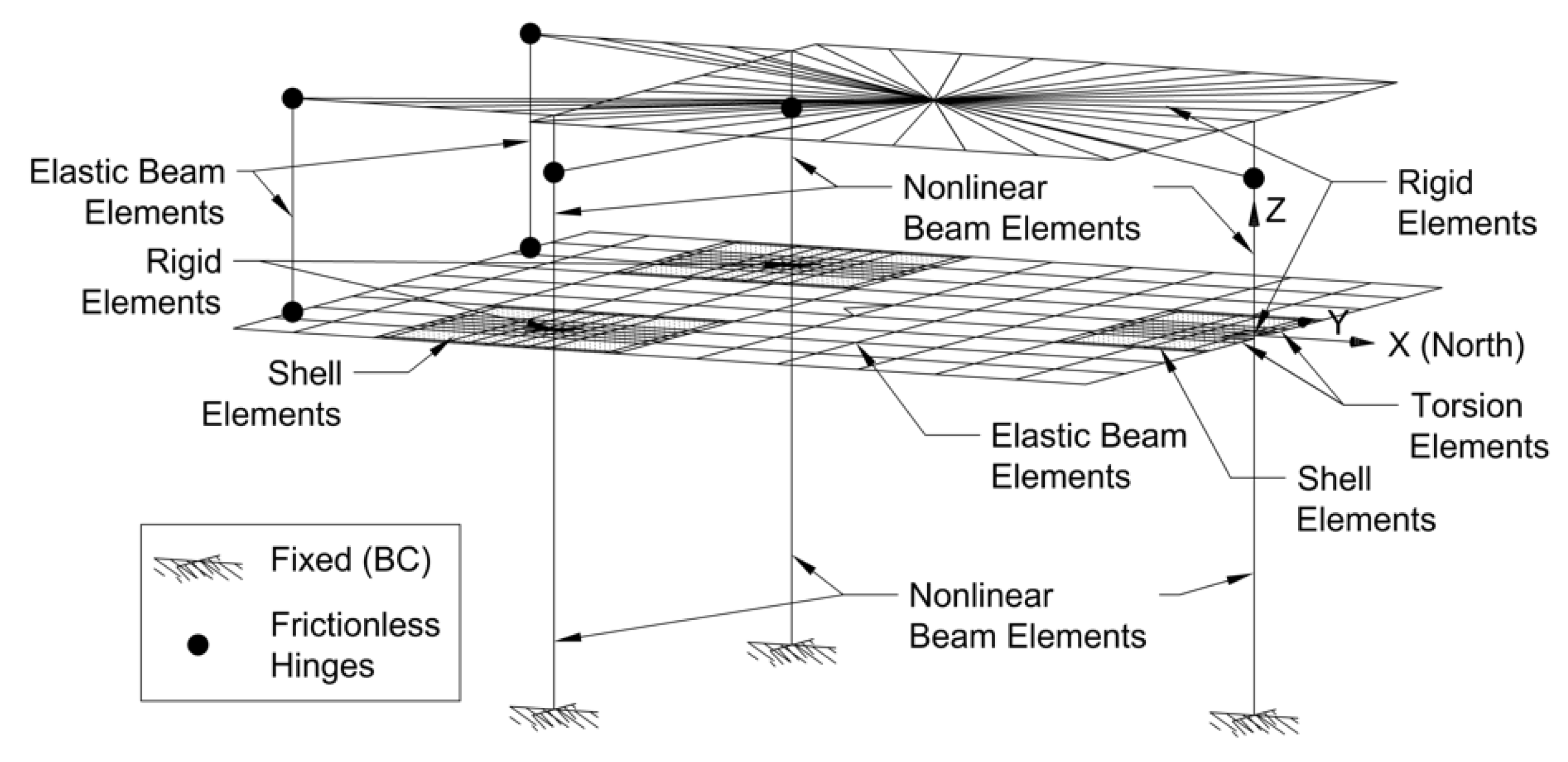
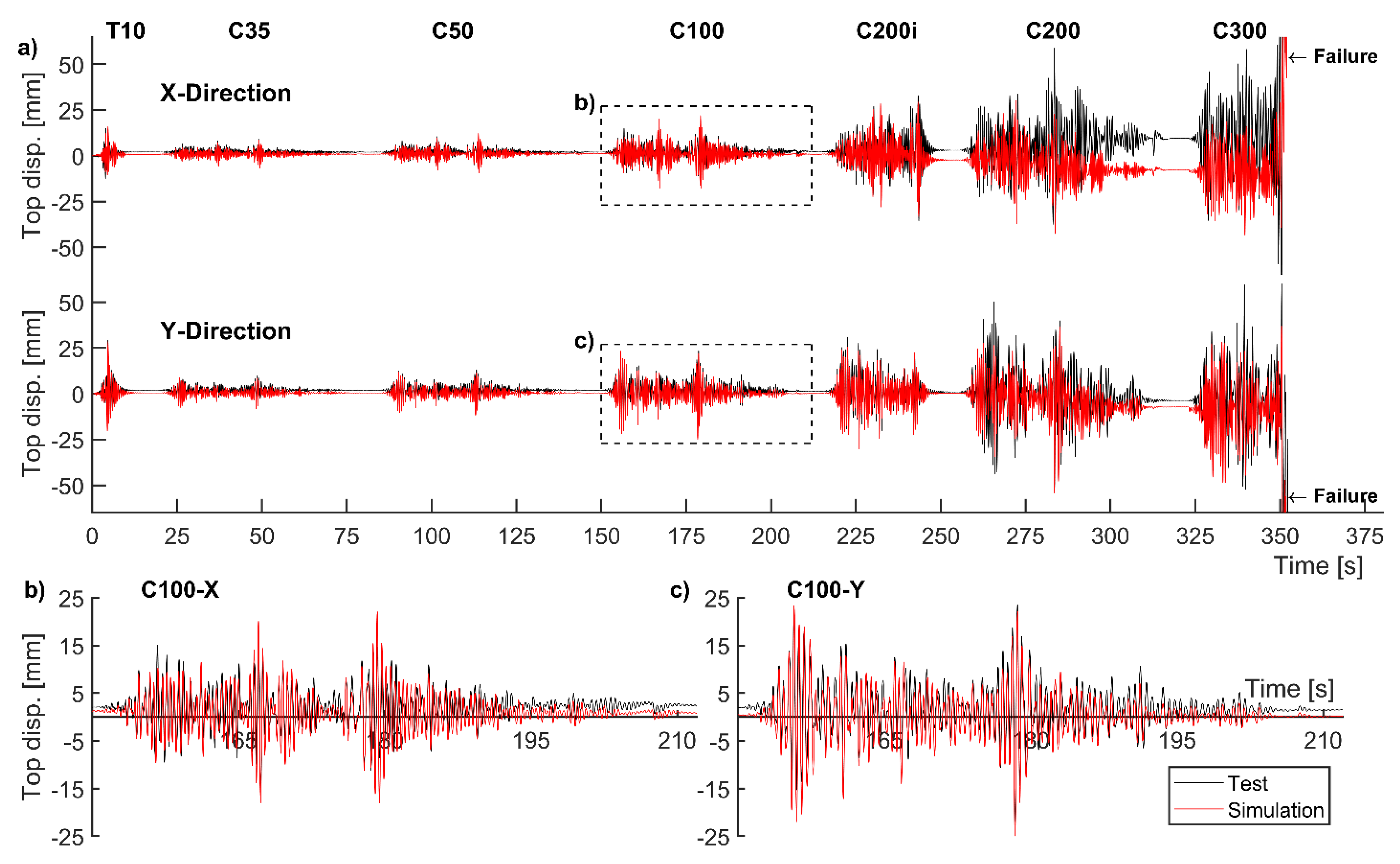





| Uniaxial Material | sNy [kN] | sk [kN/mm] | b | R0 | cR1 | cR2 | a1 | a2 | a3 | a4 | sigInit |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Steel02 | 16 | 100 | 0.005 | 22.0 | 0.925 | 0.15 | 0.13 | 1.0 | 0.13 | 1.0 | 0.0 |
| Set | mean VE,FO (cm/s) | COV VE,FO | mean VE,OP (cm/s) | COV VE,OP | mean VE,NC (cm/s) | COV VE,NC | mean | COV | mean | COV |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 30.36 | 0.25 | 98.58 | 0.33 | 294.89 | 0.28 | 3.28 | 0.21 | 10.15 | 0.31 |
| 1 | 32.15 | 0.15 | 104.14 | 0.17 | 289.98 | 0.30 | 3.29 | 0.18 | 9.19 | 0.31 |
| 2 | 32.94 | 0.29 | 127.21 | 0.29 | 391.20 | 0.24 | 4.00 | 0.29 | 12.23 | 0.23 |
| 3 | 38.64 | 0.20 | 136.04 | 0.16 | 301.72 | 0.12 | 3.64 | 0.24 | 8.04 | 0.19 |
| 4 | 40.87 | 0.35 | 113.43 | 0.40 | 255.92 | 0.24 | 2.92 | 0.32 | 6.69 | 0.26 |
| 5 | 40.85 | 0.36 | 92.30 | 0.26 | 278.61 | 0.16 | 2.44 | 0.24 | 7.55 | 0.30 |
| Y | 36.77 | 0.25 | 105.36 | 0.27 | 293.24 | 0.31 | 2.93 | 0.25 | 8.02 | 0.19 |
| All records | 36.31 | 0.31 | 111.81 | 0.31 | 301.39 | 0.28 | 3.22 | 0.30 | 8.82 | 0.33 |
| Set | mean VD,OP (cm/s) | COV VD,OP | mean | COV | mean VD,NC (cm/s) | COV VD,NC | mean | COV | mean | COV |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 70.04 | 0.27 | 0.72 | 0.09 | 241.06 | 0.27 | 0.82 | 0.02 | 3.53 | 0.26 |
| 1 | 73.08 | 0.11 | 0.71 | 0.11 | 235.98 | 0.31 | 0.81 | 0.03 | 3.22 | 0.28 |
| 2 | 89.77 | 0.33 | 0.70 | 0.06 | 320.27 | 0.25 | 0.82 | 0.02 | 3.77 | 0.29 |
| 3 | 94.53 | 0.13 | 0.70 | 0.07 | 240.51 | 0.13 | 0.80 | 0.03 | 2.57 | 0.16 |
| 4 | 78.98 | 0.37 | 0.70 | 0.07 | 202.71 | 0.21 | 0.80 | 0.04 | 2.80 | 0.33 |
| 5 | 61.92 | 0.19 | 0.68 | 0.09 | 220.27 | 0.15 | 0.79 | 0.03 | 3.60 | 0.10 |
| Y | 67.36 | 0.18 | 0.66 | 0.11 | 223.43 | 0.31 | 0.76 | 0.04 | 3.27 | 0.18 |
| All records | 77.22 | 0.29 | 0.70 | 0.09 | 241.35 | 0.29 | 0.80 | 0.04 | 3.24 | 0.28 |
| Rec. Name No. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SMADRE 1643 | 0.86 | 0.80 | 1.18 | 0.85 | 0.56 | 1.02 | 0.88 | 0.80 | 1.19 | 0.85 | 0.54 | 1.01 |
| CHICHI 1490 | 0.63 | 0.92 | 1.12 | 0.78 | 0.65 | 1.02 | 0.63 | 1.00 | 1.19 | 0.80 | 0.62 | 1.01 |
| KOBE 1115 | 0.78 | 1.06 | 1.31 | 0.71 | 1.46 | 1.62 | 0.81 | 1.07 | 1.34 | 0.72 | 1.49 | 1.66 |
| LANDERS 888 | 0.81 | 0.68 | 1.06 | 1.17 | 1.00 | 1.54 | 0.79 | 0.67 | 1.04 | 1.23 | 1.03 | 1.61 |
| CHALFANT 549 | 0.86 | 0.79 | 1.17 | 0.81 | 0.78 | 1.13 | 0.88 | 0.84 | 1.22 | 0.82 | 0.79 | 1.13 |
| mean | 0.79 | 0.85 | 1.17 | 0.86 | 0.89 | 1.26 | 0.80 | 0.70 | 1.19 | 0.88 | 0.78 | 1.28 |
| COV | 0.10 | 0.14 | 0.07 | 0.17 | 0.33 | 0.19 | 0.10 | 0.17 | 0.07 | 0.19 | 0.36 | 0.21 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Donaire-Ávila, J.; Galé-Lamuela, D. Energy Capacity of Waffle-Flat-Plate Structures with Hysteretic Dampers Subjected to Bidirectional Seismic Loadings. Appl. Sci. 2020, 10, 3133. https://doi.org/10.3390/app10093133
Donaire-Ávila J, Galé-Lamuela D. Energy Capacity of Waffle-Flat-Plate Structures with Hysteretic Dampers Subjected to Bidirectional Seismic Loadings. Applied Sciences. 2020; 10(9):3133. https://doi.org/10.3390/app10093133
Chicago/Turabian StyleDonaire-Ávila, Jesús, and David Galé-Lamuela. 2020. "Energy Capacity of Waffle-Flat-Plate Structures with Hysteretic Dampers Subjected to Bidirectional Seismic Loadings" Applied Sciences 10, no. 9: 3133. https://doi.org/10.3390/app10093133
APA StyleDonaire-Ávila, J., & Galé-Lamuela, D. (2020). Energy Capacity of Waffle-Flat-Plate Structures with Hysteretic Dampers Subjected to Bidirectional Seismic Loadings. Applied Sciences, 10(9), 3133. https://doi.org/10.3390/app10093133





