Flexural Behavior of a 30-Meter Full-Scale Simply Supported Prestressed Concrete Box Girder

Abstract

Compared with scaled-model testing, full-scale destructive testing is more reliable since the test has no size effect and can truly record the mechanical performance of the structure. However, due to the high cost, only very few full-scale destructive tests have been conducted on the flexural behavior of prestressed concrete (PC) box girders with girders removed from decommissioned bridges. Moreover, related destructive testing on the flexural behavior of a new precast box girder has been rarely reported. To investigate the flexural behavior and optimize the design, destructive testing of a 30-meter full-scale simply supported prestressed box girder was conducted at the construction site. It is illustrated that the failure mode of the tested girder was fracture of the prestressing tendon, and the corresponding maximum compressive strain in the top flange was only 1456$\mu \epsilon$, which is far less than the ultimate compressive strain (3300$\mu \epsilon$). Therefore, the concrete in the top flange was not fully utilized. A nonlinear analysis procedure was performed using the finite strip method (FSM). The validity of the analysis was demonstrated by comparing the analytical results with those of the full-scale test in the field and a scaled model test in a laboratory. Using the developed numerical method, parametric analyses of the ratio of reinforcement were carried out. The prestressing tendon of the tested girder was increased from four strands to six strands in each duct. After the optimization of the prestressed reinforcement, the girder was ductile and the bearing capacity could be increased by 44.3%.

1. Introduction

Many civil infrastructures are operated under adverse service conditions [1], such as corrosion [2,3,4], vibration [5,6], overload [7,8], and impact [9], which may cause structural damages at different levels, including loosened connections [10], cracks [11,12], reduced bending stiffness [13,14], and decreased or even lost load carrying capacity [15,16]. Structural damages have received much attention in recent years from different directions [17,18]. On one hand, structural health monitoring (SHM) [19,20,21] and damage detection technologies [22,23] have been developed to report structural health status and damage situations by using various integrated sensors [24,25,26] and advanced algorithms with the goal of issuing early warnings in the presence of structural damage. On the other hand, destructive tests are conducted on various structures to better understand the structural behavior under failure [27,28]. However, civil infrastructures often involve large-sized structural components, making destructive tests of such large components difficult. A good example is the prestressed concrete (PC) box girder, which has the advantage of long span capacity at relatively low cost. A large number of studies have been conducted on the mechanical behavior and failure mode of PC box girders using small-scale models [29,30]. It is known that full-scale experiments, without the influence of size effects, are more intuitive and reliable. However, due to them consuming a lot of human, financial, and material resources, only very few studies have been carried out with full-scale model tests on the flexural behavior of PC box girders from decommissioned bridges around the world.

McClure, R.M. and West, H.H. conducted a full-scale experiment on a segmental PC box girder bridge with a length of 36.88 meters (m) [31]. They found that the structure was 15% more stiff than theoretical predictions suggested. The failure mode was that a wide crack occurred at a segmental joint and the strand was broken in the tensile zone, while the concrete was crushed in the compression area. Shenoy and Frantz carried out a destruction experiment on two PC box girders removed from a 27-year-old bridge with a span length of 16.5 m [32]. It was illustrated that the PC girders were ductile and behaved as predicted. The load–deflection curve performance was as anticipated, while the flexural strength was more than that required. Miller, R. and Parekh K. carried out a destructive experiment on a deteriorated PC girder with a length of 21.32 m [33,34]. The tested PC girder failed suddenly just after the yielding of the prestressing strand. The cracking moment could be predicted using the American Association of State Highway and Transportation Officials (AASHTO) Standard, while the specification was not suitable for the ultimate moment. Labia, Y. et al. tested two PC box girders with a length of 21.34 m [35]. Due to a low amount of prestress, both PC girders experienced an unexpected brittle failure. Chung, W. and Kang, D tested the static and dynamic behavior of a 20 m PC box girder subjected to four-point bending load until failure with an fibre Bragg grating (FBG) sensing system [36]. It was observed that at the failure stage, the bending moment of the girder was lost abruptly after the prestressing tendon yielded. Huffman, J.M. conducted destructive testing of a three-span PC box girder bridge to determine the mechanical behavior of the bridge under varying magnitudes of damage [37]. The bridge behaved well as a system, and the shear keys and transverse tie rods were able to transfer load to adjacent beams. Su, J.Z. et al. tested a 30 m span prestressed ultra-high-performance concrete (UHPC) box girder until failure with four-point bending [38]. Based on the test and parametric analyses, a verified strain–stress diagram for cross-sectional analysis and a simplified calculation formula for the prestressed UHPC box girder were proposed. These studies reviewed above were conducted to research the flexural behavior, such as material properties, failure mode, and ultimate capacity, of PC box girders from decommissioned bridges [39,40,41]. However, investigation of the flexural behavior of a new precast box girder at a construction site has been rarely reported [42,43]. Therefore, the flexural behavior of a 30 m full-scale simply supported PC box girder is studied in the present work.

The nonlinear behavior in the ultimate limit state of a destructive full-scale model provides a valuable reference for the designing of new bridges [44]. At present, commercial finite element software [45,46] and some professional procedures [47] are used to conduct analysis of concrete structures. However, it is still difficult to calculate the descending section of the load–deflection curve. To achieve this goal, a nonlinear numerical model is developed using the finite strip method (FSM) in this paper. FSM was originally introduced by Cheung [48,49] and has been proven to be efficient and widely used in the analysis of structural members [50,51,52]. This article presents some tentative work to apply FSM to full-scale PC box girders. Based on FSM, the load–deflection curve of the structure can be obtained based on the bending–curvature relationship, so that the bearing capacity of the section can be checked directly. Parametric analyses are conducted with the proposed numerical model, and the design is optimized.

The rest of this paper is organized as follows. Section 2 introduces the engineering background and materials. Section 3 describes and discusses the flexural behavior of the 30 m full-scale simply supported PC box girder. Section 4 illustrates the nonlinear numerical model and presents parametric analyses of the ratio of reinforcement. Finally, Section 5 concludes the article and gives some recommendations for future work.

2. Engineering Background and Materials

2.1. Details of the Engineering Background

The 30 m box girder was randomly selected from the prefabrication plant and was prepared for the North Approach Bridge of the Jingyue Yangtze River Bridge, located in Hubei province, China. The North Approach Bridge has four links which each consist of four continuous spans of 30 m precast PC box girders. The elevation and cross section of the mid-span of the bridge are shown in Figure 1a,b, respectively.

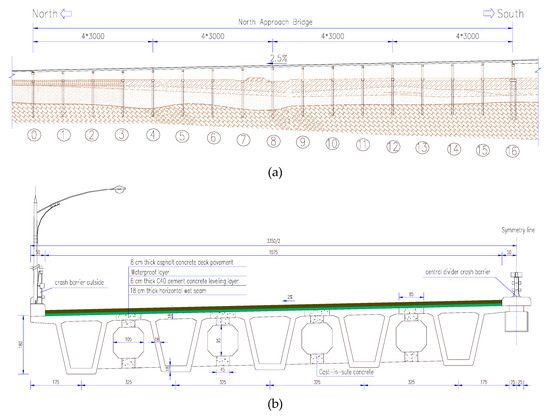
Figure 1. Detail of the North Approach Bridge (Unit: cm): (a) Elevation view; (b) Cross-sectional view of the mid-span.

The assembly method was applied to the North Approach Bridge. The 30 m box girders were prefabricated at the plant and assembled using a bridge erecting machine. Firstly, the girders were simply supported with temporary supports on the pier; then, the longitudinal wet joints were poured, and the prestressing tendons in the negative moment zone were stretched; finally, the continuous girder structure was formed after the temporary supports were replaced.

2.2. Details of the Tested Girder

The elevation and cross section of the tested box girder are illustrated in Figure 2. The prefabricated girder was 29.4 m in length, 1.8 m in height, and 2.4 m in width, with a cross slope of 2%. The thickness of the top flange was 0.18 m, and the thicknesses of the bottom flange in the support and mid-span cross section were 0.28 m and 0.18 m, respectively. The thicknesses of web in the support and mid-span cross section were 0.25 m and 0.18 m, respectively.

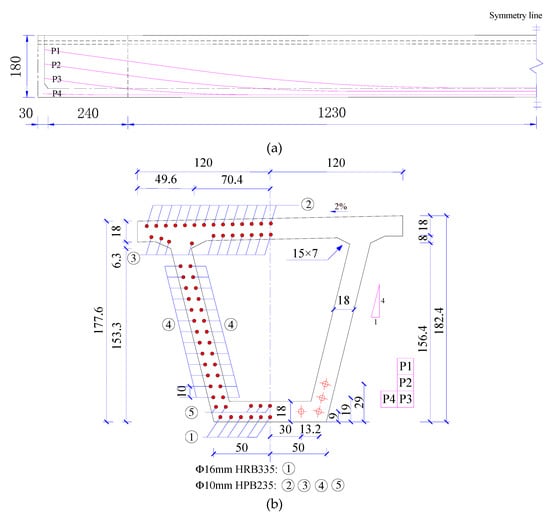
Figure 2. Detail of the 30 m box girder (Unit: cm): (a) Elevation view; (b) Cross-sectional view of the mid-span.

2.3. Material Properties

A 30 m box girder is a bonded, post-tensioned PC structure. The materials applied in the prefabricated girder include C50 concrete, Ø10 mm HPB235 (hot rolled plain bar, yield tensile strength = 235 MPa) and Ø16 mm HRB335 (hot rolled ribbed bar, yield tensile strength = 335 MPa) reinforcement, and seven-wire prestressing strands (nominal diameter is 15.24 mm). There are 32 high-strength, low-relaxation prestressing tendons, divided into eight bunches with four strands each. The standard tensile strength and controlled prestressing stress are 1860 MPa and 1395 MPa, respectively. The mix proportions of C50 concrete are shown in Table 1. The mechanical behavior of the concrete and steel material was measured and is illustrated in Table 2 and Table 3, respectively.

Table 1. The mix proportions of C50 concrete (Unit: kg/m³).

Cement	Fly Ash	Coarse Aggregate	Fine Aggregate	Water	Polycarboxylate Superplasticizers
380	87	1078	705	152	5.60

Table 2. Material properties of concrete.

Age of Concrete (d)	Cubic Compressive Strength (MPa)	Prism Compressive Strength (MPa)	Modulus of Elasticity (MPa)
28	64.2	48.1	4.22 × 104
96	74.3	55.0	4.45 × 104

Table 3. Material properties of reinforcement.

Type	Diameter (mm)	Yield Tensile Strength (MPa)	Ultimate Tensile Strength (MPa)	Modulus of Elasticity (MPa)
Prestressing tendon	Ø15.24	1740.8	1944.6	1.96 × 105
HPB235	Ø10	286	472.3	2.1 × 105
HRB335	Ø16	413	515.6	1.9 × 105

3. Full-Scale Destructive Experiment

3.1. Loading Instrumentation and Procedure

After 90 days of curing, the box girder was transported to the precast concrete pedestals and simply supported at both ends. Then, the reaction frame was built and connected to the pile foundation of the bridge. All the preparations were completed within 5 days; then the full-scale testing was conducted. The concrete samples were tested on the same day.

As illustrated in Figure 3, the load was applied at the mid-span section of the girder using a jack. A steel distributive girder divided the concentrated load into two equal halves, which were respectively applied on the top flange located above the web-top flange junction. The load was measured by load cells.

Figure 3. The loading device: (a) Photo of the loading device; (b) Cross-sectional view (Unit: mm).

3.2. Loading Procedure

We note that the tested PC box girder was just simply supported at both ends, while the North Approach Bridge has four links which consist of four continuous spans of box girders each. In this test, the bending moments in the continuous PC girder were calculated and were equivalent to the moments at the mid-span of the tested girder. Therefore, the corresponding applied load was obtained. Based on this principle, the applied loads corresponding to the design serviceability limit state (long term), serviceability limit state (short term), and design ultimate bending capacity were 133 kN, 186 kN, and 380 kN, respectively.

A concentrated load was applied repeatedly by the loading device. As shown in Table 4, the load was applied in multiple steps until the tested girder failed. After each load step was completed, the loading process was stopped for 10 minutes to record the load, strain, displacement, and cracking of the girder.

Table 4. Loading procedure.

Load Case	Applied Load	Detail
1	0→100 kN→0	Loading to the self-weight of the girder and then unloading to eliminate the initial deformation and verify working condition of the instruments.
2	0→133 kN→186→380→0	Loading to the design serviceability limit state and design ultimate state of bearing capacity, then unloading.
3	0→780 kN→0	Loading until the first crack occurs, then unloading.
4	0→1100 kN→0	Loading until about 60% of ultimate bending capacity, then unloading.
5	0→1300 kN→0	Loading until about 70% of ultimate bending capacity, then unloading.
6	0→1500 kN→0	Loading until about 80% of ultimate bending capacity, then unloading.
7	0→1600 kN→0	Loading until about 85% of ultimate bending capacity, then unloading.
8	0→1700 kN→0	Loading until about 90% of ultimate bending capacity, then unloading.
9	0→1800 kN→1872 kN→0	Loading until the structure is about to fail, then unloading.

3.3. Arrangement of Test Instrumentation

The load, strain of the concrete, displacement, and cracking of the girder were observed after every load step. Two JMZX type load cells were used to measure the load to keep the structure under uniform stress. As illustrated in Figure 4a, resistance strain gauges T1 through T5 for concrete were arranged on the top flange to measure the strain of the compression zone, located at 1/4, 1/2, and 3/4 of the span along the length. Resistance strain gauges W1 through W14 were arranged on the web to measure the strain along the depth of the mid-span section of the girder. DH3816 static strain test system was used for strain data acquisition. As shown in Figure 4b, five JMDL type displacement sensors D1 through D5 were installed at the support point and the quarter points of the girder to observe the deflection. JMCD type crack width meter was used for measuring the crack widths of girder.

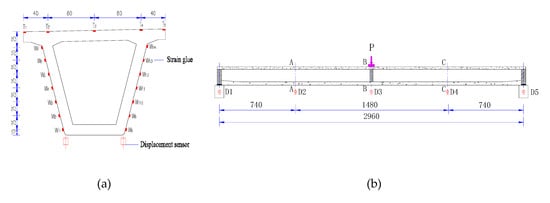
Figure 4. Arrangement of test instrumentation (Unit: cm): (a) Strain gauges; (b) Displacement sensors.

3.4. Test Results

3.4.1. Load–Deflection Curve

The load–deflection curve of the mid-span section is shown in Figure 5. It can be seen from the figure that the envelope line of the load–deflection curve can be approximated as five lines, representing five stages. These are the elastic stage (OA), concrete crack developing stage (AB), reinforced steel tendon yielding stage (BC), prestressing tendon inelastic stage (CD), and failure stage (DE).

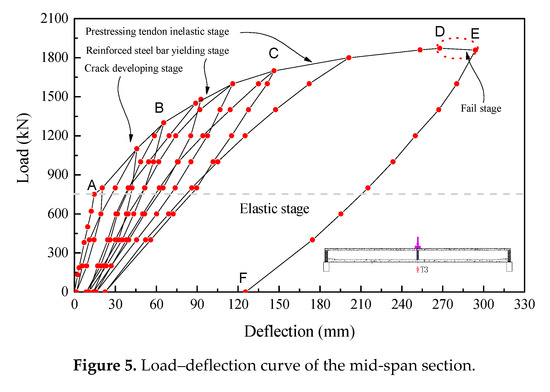
Figure 5. Load–deflection curve of the mid-span section.

It is observed that at the failure stage, the load began to decrease from 1872 kN (Point D) to 1858 kN (Point E), while the deflection increased rapidly from 267.85 mm to 294.05 mm. It could be inferred that the box girder structure would fail. Therefore, the test was terminated due to safety considerations. The maximum deflection at the middle span was 294.05 mm, which is 1/102 of the total length of the span. The residual deformation of the middle span was only 22.6 mm before the yielding of the prestressing tendon, while the value increased abruptly to 125.40 mm after the prestressing tendon yielded and broke.

3.4.2. Strain

Figure 6a shows the measured strain along the depth at the mid-span cross section. It is clear that the average strain distributed along the depth of the girder agreed well with the plane section assumption. Moreover, with the load increase after cracking, the neutral axis moved toward the top of the girder.

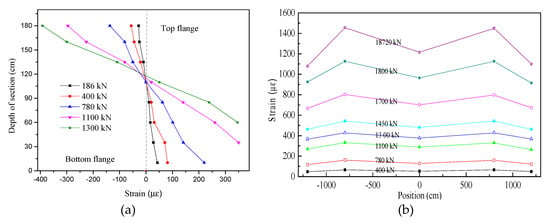
Figure 6. The strain of the box girder at the mid-span: (a) The strain distribution along the depth of the girder; (b) The strain distribution in the top flange.

The strain distribution in the top flange of the box girder at the mid-span is shown in Figure 6b. It can be seen that the strain was nonuniform due to the shear lag effect [53,54]. The web–flange junction was the maximum point, decreasing towards the midpoint and the cantilever flanges. When the load was 1872 kN, the corresponding maximum compressive strain was only 1456$\mu \epsilon$, which is far less than the ultimate compressive strain (3300$\mu \epsilon$) [55].

3.4.3. Cracks

The crack distribution on the web and the maximum crack widths are shown in Figure 7 and Table 5, respectively. It can be seen that when the load was 750 kN, the first crack appeared in the web, 9.2 cm in length and 47.0 cm away from the mid-span. As the applied load increased, the original crack continued to develop in the length and width directions; on the other hand, new cracks occurred at the mid-span. From 750 kN to 1100 kN, the crack was almost completely closed after unloading at each stage. As the load increased to 1600 kN, the maximum width of the unclosed crack was 0.04 mm. When the applied load was more than 1700 kN, the width of the original crack and unclosed crack increased rapidly. At the end of the test, the maximum crack was 176.2 cm in length and 6 mm in width, for which the unclosed width was 0.40 mm. All cracks were distributed within 16 m of the mid-span, and the average crack spacing was about 150 mm.

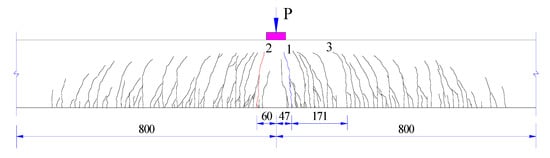
Figure 7. Crack distribution of the box girder (Unit: cm).

Table 5. The maximum crack widths.

Load/kN	750	1100	1200	0	1300	0	1450	0	1600	0	1700	0	1800	0	1872	0
Crack width/mm	0.01	0.20	0.38	0	0.44	0.01	0.6	0.02	1.0	0.04	1.2	0.1	3.0	0.18	6.0	0.40

3.5. Discussion

3.5.1. Failure Mode

The measured cracking load was 750 kN, which is 1.98 times the applied load corresponding to the designed ultimate state of bearing capacity. Moreover, the measured maximum load was 1872 kN, which is 2.50 times the cracking load. It can be seen that the tested girder has a sufficient safety margin.

The failure mode of the tested girder was fracture of the prestressing tendon. It was observed that at the failure stage in the load–deflection curve, the load began to decrease, while the deflection increased rapidly. It could be inferred that the box girder structure would fail. When the applied load was 1872 kN, the measured maximum compressive strain of concrete in the compression zone was only 1456$\mu \epsilon$, which is far less than the ultimate compressive strain (3300$\mu \epsilon$). Therefore, the design may be further optimized for the concrete in the top flange that was not fully utilized.

3.5.2. Ductility

The large deformation that occurred before failure does not mean that the structure possesses good ductility [56]. While the ductility of a structure depends only on its inelastic deformation or energy dissipation capability, in consideration of the elastic and inelastic energy, Naaman and Jeong [57] defined the ductility index as

$$\mu =\frac{1}{2}\left(\frac{E_{\mathrm{tol}}}{E_{\mathrm{el}}}+1\right)$$

(1)

where $\mu$ denotes the ductility index, $E_{\mathrm{tol}}$ is the total energy, $E_{\mathrm{tol}}=E_{\mathrm{el}}+E_{\mathrm{pl}}$, and $E_{\mathrm{el}}$ and $E_{\mathrm{pl}}$ are the elastic energy and the plastic energy, respectively. As illustrated in Figure 8, $E_{\mathrm{el}}$ and $E_{\mathrm{pl}}$ can be calculated from the area of the corresponding part in the load–deflection curve. Based on Equation (1), the ductility index of the tested girder was 1.99. Therefore, the tested girder possessed good ductility.

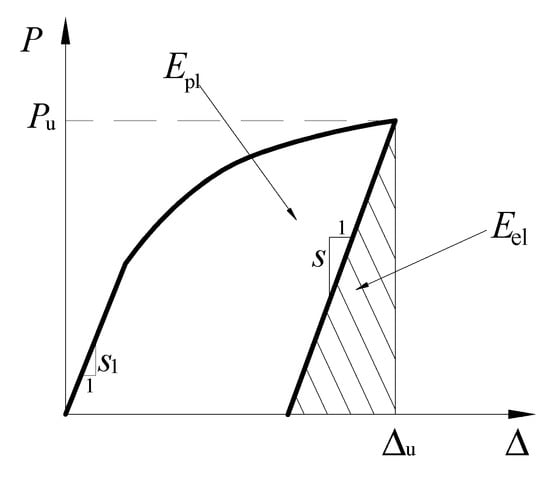
Figure 8. Load–deflection curve.

4. A Nonlinear Numerical Model for the Tested Box Girder

4.1. Assumptions

Full-scale testing of a large structural member involves high cost; therefore, it is necessary to establish a reasonable numerical model on the basis of test results. A nonlinear numerical model was developed using the FSM. The basic assumptions are as follows:

(1)

The plane section assumption is applied, and normal strains along the depth are distributed linearly.

(2)

The reinforcement and concrete are well bonded without relative sliding.

(3)

The shear deformation is negligible.

(4)

The failure characteristics of the girder are the crushing of concrete in the compression zone or fracture of the prestressing tendon.

(5)

The section of concrete is divided into finite strips in which the strain is assumed to be uniformly distributed.

4.2. Method of Analysis

The load application was simulated by changing of the curvature, that is, increasing curvature for loading and reducing curvature for unloading. A flow chart of the analysis procedure is shown in Figure 9, and the detailed steps are as follows:

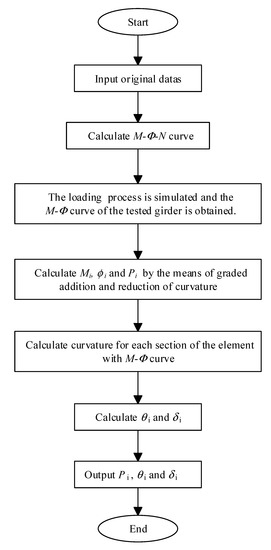
Figure 9. A flow chart of the analysis procedure of the suggested model.

(1)

The beam is divided into n-many elements with the same length along the length direction, and each element is divided into finite strips in the height direction.

(2)

The moment–curvature–axial force ($M-\Phi -N$) relationship is solved, by which the initial strain of each section under prestress is obtained.

(3)

The loading and unloading process of the prestressed concrete beam is simulated, and the bending moment–curvature ($M-\Phi$) curve of the tested girder is obtained by the method of adding or reducing curvature, respectively.

(4)

Based on the moment–curvature ($M-\Phi$) curve, by means of changing the curvature, $M_i$, ${\Phi }_i$, and $P_i$ are obtained. $M_i$, ${\Phi }_i$, and $P_i$ are the moment, curvature, and applied load at the ith load step, respectively.

(5)

Then, the bending moment of each element under applied load $P_i$ can be calculated. Therefore, the curvature for each section of the element can be obtained from the $M-\Phi$ curve.

(6)

${\theta }_i$ and ${\delta }_i$ can be obtained, where ${\theta }_i$ and ${\delta }_i$ are the rotation angle and deflection of each section under the ith applied load $P_i$, respectively.

(7)

Repeat Steps (4)–(6) to complete the whole analysis process for the flexural behavior of the tested girder.

4.3. Material Stress–Strain (σ–ε) Relationship

(1) Concrete Stress–Strain Relationship

The compression and tension constitutive model developed in references [55,58] was adopted herein. The compression constitutive model is as follows:

$$\{\begin{array}{cc}\frac{{\sigma }_c}{f_c}=2x-x^2& x=\frac{{\epsilon }_c}{{\epsilon }_{cp}}\le 1\\ \frac{{\sigma }_c}{f_c}=1& x=\frac{{\epsilon }_c}{{\epsilon }_{cp}}>1\end{array}$$

(2)

where ${\sigma }_c$ and ${\epsilon }_c$ are, respectively, the concrete compressive stress and strain, ${\epsilon }_{cp}$ is the compressive strain when the stress is $f_c$ (${\epsilon }_{cp}$ = 2000$\mu \epsilon$), and ${\epsilon }_{cu}$ is the ultimate compressive strain of concrete (${\epsilon }_{cu}$ = 3300$\mu \epsilon$).

The constitutive model of the uniaxial tension stress–strain is given as [55,58]

$$\{\begin{array}{cc}\frac{{\sigma }_t}{f_t}=1.2x-0.2x^6& x=\frac{{\epsilon }_t}{{\epsilon }_{tp}}\le 1\\ \frac{{\sigma }_t}{f_t}=\frac{x}{0.312f_t^2{(x-1)}^{1.7}+x}& x=\frac{{\epsilon }_t}{{\epsilon }_{tp}}>1\end{array}$$

(3)

$$\{\begin{array}{c}{\epsilon }_{tp}=f_t/E_c\\ {\epsilon }_{tu}=2{\epsilon }_{tp}\end{array}$$

(4)

where ${\sigma }_t$ and ${\epsilon }_t$ are, respectively, the concrete tensile stress and strain, and $f_t$ and $E_c$ are the tensile strength and elastic modulus of concrete, respectively.

(2) Reinforcement Stress–Strain Relationship

The following elastic hardening model was adopted for the tension and compression stress–strain relationship of the reinforcement [59,60]:

$$\{\begin{array}{cc}{\sigma }_s=E_s\epsilon & \epsilon \le {\epsilon }_y\\ {\sigma }_s=f_y+E_{s2}(\epsilon -{\epsilon }_y)& \epsilon >{\epsilon }_y\end{array}$$

(5)

where ${\sigma }_s$ and $\epsilon$ are the stress and strain of the reinforcement, and $f_y$ and ${\epsilon }_y$ are the yield stress and strain of the reinforcement, respectively. $E_S$ and $E_{S2}$ ($E_{S2}=0.01E_S$) are the elastic modulus of the reinforcement before and after yielding, respectively.

The tension stress–strain relationship of the prestressed reinforcement is shown as [59,60]

$${\epsilon }_p=\frac{{\sigma }_p}{E_p}+0.002{\left(\frac{{\sigma }_p}{f_{0.2}}\right)}^{13.5}$$

(6)

where ${\epsilon }_p$ and ${\sigma }_p$ are, respectively, the strain and stress of the prestressed reinforcement, $E_p$ is the elastic modulus of the prestressed reinforcement, and $f_{0.2}$ is the nominal yield stress of the prestressed reinforcement.

(3) Unloading Stress–Strain Relationship

The initial stiffness of the material is $E_0$, as shown in Equation (7).

$$E_0={\frac{d\sigma }{d\epsilon }|}_{\epsilon =0}$$

(7)

When the strain increases to its maximum value, the unloading elastic modulus is $E_1$, and $E_1=0.6E_0$ [59,60]. In other cases, the elastic modulus is calculated by linear interpolation with $E_0$ and $E_1$.

4.4. Verification of the Nonlinear Numerical Model

The load–deflection curve was computed using the nonlinear numerical model. In Figure 10, the calculated load–deflection curve is compared with the measured one. It can be seen that the calculated result agreed well with the measured values. Moreover, the ductility index obtained by the calculated load–deflection curve was 1.83, which was in good agreement with the measured one as well.

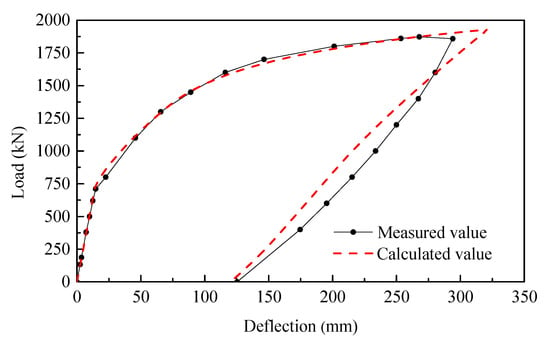
Figure 10. Load–deflection curves for the tested girder.

To further verify the effectiveness of the program, the load–deflection curve of another concrete composite beam was checked. Related experimental overviews and test results were reported by Deng et al. [61]. A 1/3 scaled PC I-beam with a length of 9.98 m was constructed to act compositely with a 1100 × 80 mm concrete slab. Three grouted seven-wire prestressing strands (nominal diameter of 15.24 mm) were used for post-tensioning of the beam. Five-point loads were applied using actuators, and the displacement was measured by transducers. As illustrated in Figure 11, the calculated value obtained by the proposed nonlinear numerical model was in good agreement with the measured one.

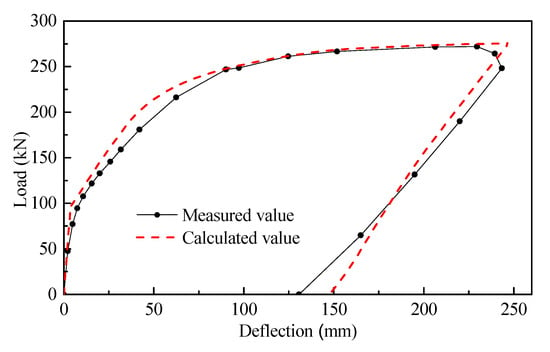
Figure 11. Load–deflection curves for a composite girder.

4.5. Discussion

It is known from experiments that the box girder failure is via fracture of the prestressing tendon. The corresponding maximum compressive strain of concrete in the compression zone is only 1456$\mu \epsilon$, which is far less than the ultimate compressive strain (3300$\mu \epsilon$). Therefore, it is necessary to optimize the reinforcement design and improve the bearing capacity of the structure. For this purpose, the design of the reinforcement and prestressing tendon is discussed in the following.

4.5.1. Reinforcement in the Compression Zone of the Top Flange

The tested box girder is equivalent to an I-beam, for which the reinforcement ratio in the compression zone of the top flange is defined as follows:

$${\rho }_y^{\prime }=A_y^{\prime }/(b_w{h}_0)$$

(8)

where $A_y^{\prime }$ and ${\rho }_y^{\prime }$ are the reinforcement area and reinforcement ratio in the compression zone, and $b_w$ and $h_0$ represent the thickness of the web and effective height of the section, respectively.

The reinforcement ratio in the compression zone of the tested box girder is 0.655%. Girders with reinforcement ratios of 0.355%, 0.655%, 1.230%, 1.830%, and 2.830% are discussed. The load–deflection curve of the mid-span for each reinforcement ratio is shown in Figure 12.

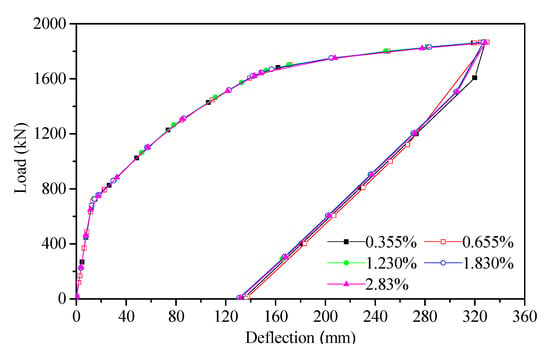
Figure 12. Load–deflection curves for different ratios of reinforcement in the compression zone.

As can be seen from the figure, the load–deflection curves of the different reinforcement ratios almost overlap each other. This is because the tested girder failed due to fracture of the prestressing tendon. Therefore, the reinforcement ratio in the compression zone has no obvious influence on the failure mode of the tested girder and can be ignored.

4.5.2. Reinforcement in the Tension Zone of the Bottom Flange

We define the degree of prestress (PPR) as

$$PPR=\frac{A_p{f}_p}{A_p{f}_p+A_s{f}_y}$$

(9)

where $A_p$ and $f_p$ are the area and ultimate strength of the prestressing tendon, and $A_s$ and $f_y$ are the area and yield strength of the reinforcement in the tensile zone of bottom flange.

The PPR of the tested girder is 0.878. Girders with different PPRs of 0.795, 0.820, 0.846, 0.878, 0.921, and 0.972 are discussed. The load–deflection curve at the mid-span and ductility index for each PPR are shown in Figure 13 and Figure 14.

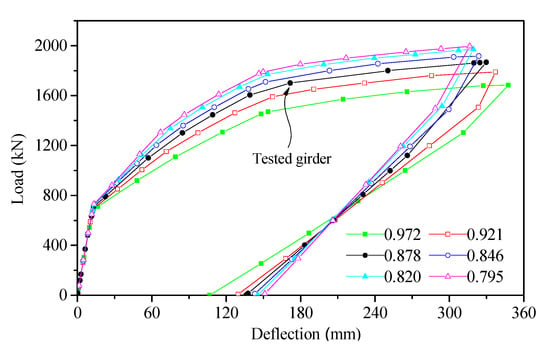
Figure 13. Load–deflection curves for different degrees of prestress (PPRs).

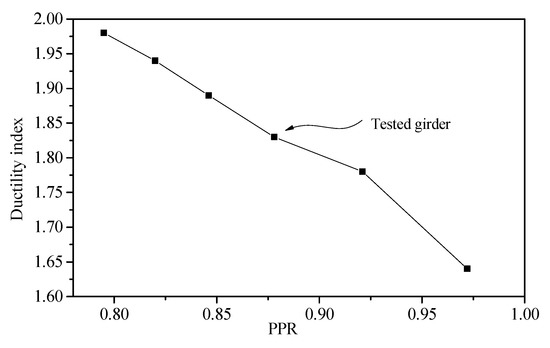
Figure 14. Ductility index values for different PPRs.

It can be seen from Figure 13 and Figure 14 that as the PPR increases, the bearing capacity decreases, the maximum deformation at the mid-span increases, and the residual deformation and ductility index decrease. For instance, as the PPR increases from 0.795 to 0.972, the ultimate load decreases from 1995.5 kN to 1684.0 kN, the maximum deformation at the mid-span increases from 317.0 mm to 348.2 mm, the residual deformation decreases from 150.7 mm to 107.1 mm, and the ductility index of the component decreases from 1.98 to 1.64. Therefore, the reinforcement in the tensile zone has a small effect on the bearing capacity and deformation, but has a large effect on the ductility index of the tested girder. This is because when the PPR increases, the reinforcement area in the tension zone of the bottom flange decreases.

4.5.3. Prestressing Tendons

The equilibrium destructive state of PC structures is that, when the prestressing tendon breaks, the concrete in the compression zone is crushed and damaged. In this failure mode, the ratio of prestressing tendons is called the equilibrium reinforcement ratio (${\rho }_b$), which is defined as [55]

$${\rho }_b=\frac{\alpha f_c}{f_u}\left[\beta \left[\frac{{\epsilon }_{cu}}{{\epsilon }_{cu}+{\epsilon }_p}\right]+\left[\frac{b}{b_w}-1\right]\frac{t}{h_0}\right]-\frac{f_y}{f_u}{\rho }_y$$

(10)

where $\alpha$ and $\beta$ are the coefficients of the equivalent rectangular stress diagram, and $t$ is the flange thickness. The tested box girder is equivalent to an I-beam, and $b_w$ and $h_0$ represent the thickness of the web and effective height of the section, respectively. ${\rho }_y$ is the ratio of reinforcement in the tensile zone of the bottom flange.

The ratio of prestressing tendons (${\rho }_p$) is defined as

$${\rho }_p=A_p/(b_w{h}_0).$$

(11)

For the tested girder, the ratio of prestressing tendons is 0.934%, and the equilibrium reinforcement ratio is 1.446%. Girders with different ratios of prestressing tendon of 0.934%, 1.168%, 1.401%, 1.446%, 1.635%, and 1.868% are discussed. The load–deflection curve at the mid-span and the ductility index for each parameter are shown in Figure 15 and Figure 16, respectively.

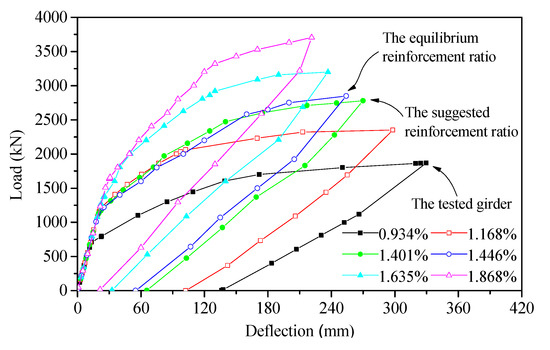
Figure 15. Load–deflection curves for different reinforcement ratios.

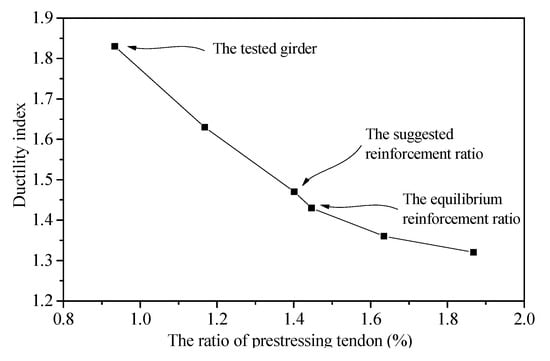
Figure 16. Ductility index values for different reinforcement ratios.

It can be seen from Figure 15 and Figure 16 that the ratio of prestressing tendons has an obvious influence on all of the control indices. The bearing capacity of the girder was observed to increase with increasing ratio of prestressing tendons, while the maximum deformation at the mid-span, the residual deformation, and ductility index decrease. For instance, as the ratio of prestressing tendons increases from 0.934% to 1.868%, the ultimate load increases from 1876.8 kN to 3706.2 kN, the maximum deformation at the mid-span decreases from 329.8 mm to 221.3 mm, the residual deformation decreases from 138.2 mm to 21.8 mm, and the ductility index of the component decreases from 1.83 to 1.32. With comprehensive consideration of the influence of various parameters, such as the bearing capacity, deformation, and ductility index of the structure, it is suggested that the ratio of prestressing tendons be increased to 1.401%. That is, the prestressing tendons should be increased from four strands to six strands in each duct of the tested girder. After the optimization of prestressing reinforcement, the ultimate load increases from 1876.8 kN to 2708.1 kN, the maximum deformation at the mid-span decreases from 329.8 mm to 269.2 mm, the residual deformation decreases from 136.2 mm to 65.4 mm, and the ductility index of the component decreases from 1.83 to 1.47.

5. Conclusions

This paper reports destructive experiments on a 30-meter-long simply supported prestressed concrete box girder. A nonlinear numerical model was developed using the finite strip method (FSM) on the basis of the experiment. Parametric analyses were conducted, and the design was optimized. The following conclusions may be drawn:

(1)

The failure mode of the tested girder was fracture of the prestressing tendon. The maximum compressive strain of concrete in the compression zone was only 1456$\mu \epsilon$, which is far less than the ultimate compressive strain (3300$\mu \epsilon$). Therefore, the concrete in the top flange was not fully utilized.

(2)

The maximum deflection was 1/102 of the span, and the ductility index of the tested girder was 1.99. Therefore, the tested girder possessed good ductility.

(3)

The measured cracking load was 750 kN, which is 1.98 times the applied load corresponding to the designed ultimate state of bearing capacity. Moreover, the measured maximum load was 1872 kN, which is 2.50 times the cracking load. It can be seen that the tested girder had a sufficient safety margin.

(4)

A nonlinear analysis procedure was performed using the FSM. The analysis procedure was demonstrated to be effective by comparing the analytical results with those of the tested girder and a laboratory-scale model.

(5)

The ratio of reinforcement in the compression zone has no obvious influence on the failure mode of the tested girder and can be ignored. The reinforcement in the tensile zone has a small effect on the bearing capacity and deformation of the tested girder, but has a large effect on the ductility index.

(6)

The ratio of prestressing tendons has an obvious influence on the bearing capacity, deformation, and ductility index. Considering the influence on the bearing capacity and ductility index of the structure, it is suggested that the ratio of prestressing tendons be increased to 1.041%. The prestressing tendons should thus be increased from four strands to six strands in each duct of the tested girder. After optimization of the prestressed reinforcement, the girder is ductile and the bearing capacity can be increased by 44.3%.