1. Introduction
One of the main goals and challenges for telecoms and backbone optical networks operators is to provide high network throughput (amount of served traffic) in a cost-effective way. In recent years, we have been observing an evolution of optical networks from fixed-grid
wavelength division multiplexing (WDM) networks to flex-grid spectrally flexible
elastic optical networks (EONs) which allow for adaptive use of different modulation formats and multi-carrier (super-channel) transmission. Another possible step towards providing higher network throughput is using a
space division multiplexing (SDM) paradigm—a relatively new optical network idea that extends the capacity and capabilities of optical networks. In particular, SDM enables parallel transmissions of a number of co-propagating spatial modes in appropriately designed optical fibers.
Spectrally–spatially flexible optical networks (SS-FONs), which join the main features of SDM and EONs, provide numerous advantages such as substantial growth of transmission capacity, cost savings due to the use of integrated devices, and extended flexibility in resource management due to the introduction of the spatial domain (spatial modes) [
1,
2,
3].
Another concept that has the capability to allow increasing network throughput are
translucent networks. The key motivation behind translucent networks is to mitigate the limited transmission reach in optical networks by using signal regeneration to re-amplify, reshape, and retime the optical signals. Translucent optical networks are planned to account for limited transmission reach and deal with this issue by regenerating signals in selected nodes. Such networks enable a compromise between network design cost and service provisioning performance including network capacity. However, the regenerator placement becomes one of the main problems to be addressed when planning and operating the translucent networks [
4].
The idea of translucent networks emerged in the context of WDM optical networks, and the key design challenge in such networks is to select regeneration nodes that allow for regeneration of WDM lightpaths. The arrival of EONs triggered a new research effort in the context of translucent networks because of the introduction of flexible frequency grids and the possibility to apply different modulation formats of different spectral efficiency and transmission reaches. In particular, in the case when the transmission distance of a particular lightpath exceeds the transmission reach of the applied modulation format, it is required to regenerate the signal. It should be mentioned that modulation formats offer a trade-off between the spectral efficiency and transmission reach, i.e., more spectrally efficient modulation formats provide shorter transmission reaches, but, at the same time, they require less spectrum resources [
5].
In this work, for regeneration, we used an approach based on the application of transponders (TRXs) operating in back-to-back (B2B) configurations, i.e., with interconnections at the client side [
6,
7,
8,
9,
10]. The main benefit of B2B regeneration is the fact that dedicated regenerators are not required. The optical network can be equipped only with tunable transponders that are utilized for two purposes: transmitting/receiving of the signal at the source/destination nodes (add/drop) and regeneration of the signal at some intermediate nodes. Therefore, semi-transparent (translucent) lightpath connections are established in optical networks with B2B regeneration. Moreover, according to Reference [
10], the advent of elastic optical transponders allows to change the output signal modulation format during the regeneration process. This can be achieved by means of patch-cords or electronic cross-connects providing traffic interchange among several transponders. In consequence, the lightpath may consist of several transparent segments, where each segment uses a different modulation format. This leads to potentially lower consumption of spectrum and transponders resources and thus allows to allocate more traffic in the network and increase the network capacity.
According to our previous results presented in References [
8,
11], full flexibility in the B2B regeneration, which means the possibility of regeneration with modulation conversion in each node traversed by a lightpath, can significantly increase the amount of served traffic in the network and thus provide higher network throughput without the need to upgrade the network by adding new fibers. Nevertheless, using the B2B regeneration complicates the network operation and optimization, since the basic optimization problem in SS-FONs (i.e., routing, spatial mode, and spectrum allocation (RSSA)) must be extended to account for allocation of transponders to lightpaths as well as for the fact that various nodes can be selected for regeneration.
Another important aspect that may also have a large impact on the network throughput in the context of translucent networks with B2B regeneration is transponder placement (i.e., predeployment) which is a new—when compared to classic regenerators placement—optimization problem that appears here. As mentioned above, the key aspect of the B2B regeneration is the fact that transponders are used for two goals: transmitting/receiving (add/drop) of the signal at the source/destination nodes and regeneration of the signal at some intermediate nodes. In consequence, the placement of transponders must address these two potential usage scenarios of transponders, as the lack of free transponders can be the reason of request blocking when there are not enough devices to transmit, receive or regenerate optical signals. The previous works focused on regenerator placement have accounted only for the optical signal regeneration scenario, while the transponders used to transmit/receive the signal have been assumed to be unlimited in the network, and thus the transponder placement has not been addressed. Moreover, legacy regenerators receive a signal at a given data rate and, after regeneration, retransmit it with the same modulation format.
To the best of our knowledge, the only paper that concerns the transponder placement problem in SS-FONs with B2B regeneration is our work [
12] that presents some initial research in this topic. In this paper, as the main novelty and contribution, we present a new algorithm for transponder predeployment in SS-FONs with B2B regeneration. The reported results obtained by means of extensive simulation experiments, run on two representative network topologies with realistic assumptions, clearly show that our method outperforms other reference methods. Moreover, according to the recent trends in optical networking, in this paper we consider a data analytics approach assuming that the proposed algorithm is traffic and routing aware. We assume that based on historical data on network traffic or traffic prediction methods, we know the key characteristics of the traffic, which can be next used as an input to dynamic routing simulations. By these means, we can observe the network performance and collect various data that then are applied to improve network performance. To verify this approach, we ran experiments for five various traffic profiles, while the overwhelming majority of previous papers focusing on optimization of dynamic optical networks have assumed only one traffic profile based on uniform distribution of communicating nodes. In consequence, we provide a study showing how the network traffic characteristics influence performance of the algorithms and the general performance of the SS-FON.
The rest of the paper is organized in the following way. In
Section 2, we discuss related works. In
Section 3, we describe the considered network and lightpath regeneration scenarios. In
Section 4, we develop a transponder predeployment algorithm. In
Section 5, we evaluate the algorithm performance with reference to other methods and analyze various network scenarios. Finally,
Section 6 concludes the whole work.
2. Related Works
The basic optimization problem related to the design of translucent optical networks is regenerator placement (RPL). The RPL problem consists of selecting regeneration nodes in the network and deciding on the number of regenerators that should be installed in each of these nodes. This problem is addressed under the consideration of the transmission reach in optical networks. An optical signal can only travel a maximum distance before its quality deteriorates to the point that it must be regenerated using an installed regenerator. As the regenerator cost is high, the objective is to deploy in the network as few regenerators as possible while ensuring all nodes can communicate with each other [
4,
13].
In Reference [
14], four regenerator placement algorithms were proposed: two of them were topology based (i.e., information on the network topology is utilized in the algorithms), and two methods were traffic prediction based (i.e., certain information about foreseen network traffic is available). The problem of network planning with routing and wavelength assignment (RWA) and RPL for a set of static traffic demands was studied in translucent WDM networks in Reference [
15]. Moreover, various RWA methods were verified together with the RPL methods in order to find the best combination of RPL and RWA methods guaranteeing the lowest blocking probability. The authors of Reference [
13] showed that the RLP is NP-Complete and developed three heuristics for the RLP based on various graph theory approaches. In Reference [
16], analytical results showing the complexity of the RPL problem were presented. Four cases were considered with an upper bound on the number of regenerators installed at each node and where information on routing and/or information on the requests were given. The authors of Reference [
17] proposed two new strategies for sparse regenerator placement in translucent optical networks, named most-used regenerator placement (MU-RP) and most-simultaneous-used regenerator placement (MSU-RP). Both proposed methods are based on preliminary simulations of the network to obtain statistics on regenerator usage, which are next applied for regenerator placement. The reported results showed that the MSU-RP algorithm outperformed all previous approaches. In Reference [
18], four strategies for regenerator predeployment in WDM network were presented, starting with a basic uniform distribution of regenerators followed by three topology-based methods that can be enriched with information on network traffic.
However, it should be underlined that all of the abovementioned papers were focused on fixed-grid WDM networks. Now, we briefly discuss previous research on regenerator placement in EONs. In Reference [
19] in which the spectrum allocation and regenerator placement problem was considered, a heuristic method was proposed for a static optimization scenario. The reported results showed that use of regenerators considerably decreases the utilization of spectrum resources in a translucent EON. The authors of Reference [
20] addressed jointly power management and regenerator placement in mixed line rate (MLR) optical networks, and they formulated an integer linear program for the regenerator placement problem. The authors of Reference [
7] proposed a dynamic algorithm for energy-efficient routing and spectrum assignment in EONs with regenerator placement. The algorithm is based on a virtual graph, and the cost is computed according to the energy consumption of the corresponding links and intermediates routers. In Reference [
21], four algorithms of regenerator placement for cloud-ready EONs were described. Two of the proposed methods utilize additional knowledge of data center location and these methods provide better performance results than simpler approaches. The author of Reference [
22] described an approach for regenerator placement, routing, modulation level selection, and spectrum allocation in translucent EONs. For regenerator placement, an iterative method was proposed, where at each iteration a new regenerator site is added to a set of preset regenerator sites obtained in previous iterations, and the model is solved repeatedly for the remaining candidate locations. In Reference [
23], a new regenerator allocation algorithm CIRA (circuit invigorating regenerators assignment) was proposed. The CIRA method accounts for quality of transmission (QoT) requirements. In more detail, the algorithm chooses the regenerators to be allocated in the network to reduce the effect of the physical layer and to minimize the QoT blocking. This is achieved by selecting more resistant signal modulation formats, when it is available. In the end, it leads to better overall performance (lower blocking ratio). Four different placement algorithms, namely, MSU, MU, NDF (node degree first), and DA (distance adaptive) were analyzed in the simulations, and the MSU provided the best results. The authors of Reference [
24] developed and evaluated an auxiliary-graph-based approach for regenerator assignment in translucent elastic optical networks. The proposed method allows to analyze each possible transparent segment in the considered route. A special cost function was defined for each edge of the auxiliary graph representing a single segment that allows to apply a standard routing algorithm to find a path in the considered auxiliary graph. Several edge cost functions were examined. For regeneration placement, the NDF method was applied. Finally, in Reference [
25], the problem of regenerator assignment in dynamic translucent optical networks was examined. It was assumed that each lightpath could be divided into several transparent segments, connected by 3R regenerators capable of accomplishing modulation format and spectrum conversion. It was assumed that the regenerators were placed uniformly in the network, i.e., each node had the same number of regenerators.
All the above discussed works are focused on various aspects related to the classic regenerator placement problem. However, we should stress that in this paper—due to the use of the B2B regeneration—instead of the elementary regenerator placement problem, a more broad problem of transponder placement (predeployment) is considered, where the transponders are used flexibly either for signal transmission/reception (add/drop) or signal regeneration purposes. As discussed below in the paper, a proper placement of transponders can significantly increase the amount of network traffic served in the network without any additional capital expenditures, since only the existing resources available in the network are utilized. Therefore, in our opinion, the problem addressed in this paper is of significant importance for network operators. The considered problem is relatively new, and the only paper that addresses the problem of transponders placement in optical networks with B2B regeneration is our work [
12], where we presented preliminary research in this area. In particular, in Reference [
12], we proposed several simple heuristic algorithms and compared their performance using a US topology. In this work, we continued our research on this problem, namely, we propose a more advanced algorithm based on a data analytics approach and report the results of extensive simulations performed on two representative topologies with deep and insightful discussion of the obtained results.
Moreover, we want to mention that we have been working for the last few years on different types of RSA (routing and spectrum allocations) and RSSA problems in EONs and SS-FONs with B2B regeneration (e.g., [
8,
11]). However, all our previous papers that concerned B2B regeneration—except Reference [
12]—do not address the problem of transponder placement.
3. Network Model
To model the SS-FON, we used a graph
G = (
V,
E), where
V is a set of optical nodes, and
E is a set of fiber links. Let set
K include spatial modes available in each link
e ∊
E. In each spatial mode
k ∊
K, the available optical frequency spectrum is divided into frequency slices denoted as
S = {
s1,
s2, …,
s|S|}. We assume that each slice is of 12.5 GHz width. The transmission of optical signals is provided by means of spectral super-channels (SChs). A SCh can contain a number of optical carriers (OCs), each using
∆OC frequency slices, where an OC is transmitted/received by one transponder. As proposed in [
26] and [
27], we assume that
∆OC = 3 slices, what is equivalent to 37.5 GHz. A set of modulation formats
M = {
m1, …,
m|M|} is defined. Each modulation format
m ∊
M is characterized by a certain transmission reach and spectral efficiency. Moreover, modulation format
m ∊
M can support bit rate
g(
m) on a single optical carrier.
In this paper, we considered a dynamic routing scenario assuming that a node-to-node dynamic traffic request
d with a certain bit rate volume
h(
d) is to be served in the network using a provisioned lightpath connection. For each request
d, set
P(
d) contains candidate routing paths generated using the
k-shortest path algorithm. Each path
p ∊
P(
d) connects the request source node and destination nodes and traverses intermediate nodes included in set
V(
p) ⊆
V. Each of intermediate nodes included in
V(
p) can be selected as a regeneration point. As mentioned above, for regeneration we apply transponders operating in B2B configurations (i.e., with interconnections at the client side) [
6,
7].
Figure 1 illustrates the general idea of the B2B regeneration. For more information on the SS-FON with B2B regeneration network model refer to Reference [
11].
In our previous papers, we examined three B2B regeneration scenarios: minimal regeneration, regeneration without modulation conversion, and flexible regeneration allowing for modulation conversion. Since, according to the results presented in References [
11,
25,
28], the flexible approach provides the best results in terms of blocking probability, in this paper we focused only on this scenario. In the flexible B2B regeneration, a full flexibility of the B2B regeneration was assumed [
29]. In more detail, an extra regeneration of SChs with modulation conversion can be applied in any intermediate node of the routing path. The motivation behind full flexibility is to use more efficient modulation formats for shorter transparent path segments with the possibility to apply different modulation formats on different segments, i.e., modulation conversion and spectrum conversion is allowed in regeneration nodes. Nevertheless, the flexible regeneration, apart from switching the regenerated data units, may require to (dis)aggregate them in order to match the capacity of transponders operating with different modulation formats. It should be stressed that the presented model can be easily adapted to other assumptions that described above, e.g., different values of
∆OC.
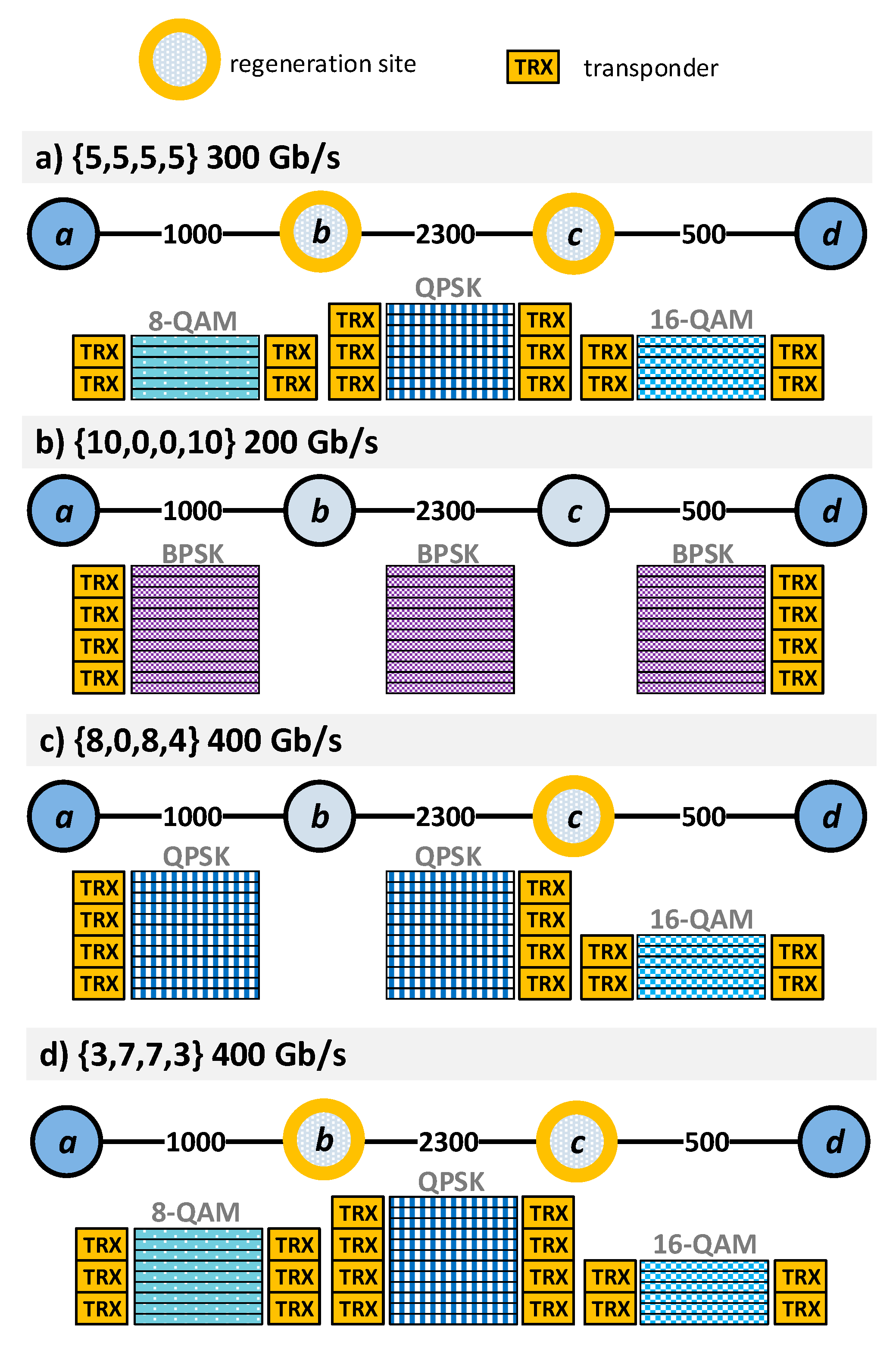
To illustrate the considered B2B regeneration approach and the effect of transponder placement, we consider a simple example shown in
Figure 2. We assume four modulation formats, namely, BPSK, QPSK, 8-QAM, and 16-QAM, with the bit rates transmitted by OCs and the transmission reaches of considered modulation formats based on data presented in [
26] and [
27] and shown in
Table 1. A request (lightpath) is allocated on a routing path (
a,
b,
c,
d) of an overall length 3800 km consisting of three links: (
a,
b) 1000 km, (
b,
c) 2300 km, and (
c,
d) 500 km. Moreover, every link (i.e., (
a,
b), (
b,
c), (
c,
d)) has 12 free adjacent slices available that can be used to allocate the request. Twenty transponders are available in the network to be located in nodes
a,
b,
c, and
d using various predeployment policies. We consider the following four scenarios of transponder location:
{5, 5, 5, 5}, i.e., every node has 5 transponders, and the lightpath uses transponders in the following way <2, 5, 5, 2> (
Figure 2a);
{10, 0, 0, 10}, i.e., 10 transponders are placed in nodes
a and
d, and the lightpath uses transponders in the following way <4, 0, 0, 4> (
Figure 2b);
{8, 0, 8, 4}, i.e., 8 transponders are placed in nodes
a and
c, 4 transponders are placed in node
d, and the lightpath uses transponders in the following way <4, 0, 6, 2> (
Figure 2c);
{3, 7, 7, 3}, i.e., 3 transponders are placed in nodes
a and
d, 7 transponders are placed in nodes
b and
c, and the lightpath uses transponders in the following way <3, 7, 7, 2> (
Figure 2d).
Note that the numbers in curly brackets { } represent the number of transponders located in each network node that can be used for establishing the considered lightpath. However, some of these transponders can remain non-allocated, and numbers in angle brackets < > and
Figure 2 show only the transponders that are used to establish the considered lightpath, i.e., other spare transponders are not presented in the figure.
For each of transponder placement scenarios, the request can be established using different regeneration options (configurations), where each option divides the transmission path into a number of transparent path segments. For each segment, we select the best allowable modulation format. The objective is to provision the request with the highest possible bit rate (throughput) accounting for limited resources of spectrum (12 adjacent slices) and transponders (20 devices located in various scenarios). We assume the flexible B2B regeneration approach. We can easily observe that the placement of transponders has a significant impact on the allowable bit rate of the considered request, since the following bit rates are achieved for the considered four scenarios: (a) 300 Gb/s, (b) 200 Gb/s, (c) 400 Gb/s, (d) 400 Gb/s. From the above example, we can notice that in spectrally flexible optical networks, such as EONs and SS-FONs with B2B regeneration, the placement of transponders is a key issue, since by proper predeployment of transponders one can allow to establish lightpaths with higher bit rate and thus serve more traffic without the need to deploy extra fibers.
4. Algorithms
In this section, we describe several algorithms developed for predeployment of transponders in SS-FONs with B2B regeneration. First, we present reference methods, mostly based on simple greedy algorithms. Next, we propose a new method scaled average used regenerators (SAUR) based on a data analytics approach. Let us assume that we are given T transponders to be located in network nodes in order to allow provisioning of the requests (lightpaths) with the possibility to use the B2B regeneration in some intermediate nodes of the routing path. Moreover, let t(v) denote the number of transponders predeployed in node v ∊ V.
The basic approach proposed in our previous paper [
12] assumes that the transponders are located in the network nodes proportionally to a selected metric. The following versions of this approach are considered in this paper.
Uniform location (UNI) assumes that each node is assigned with the same number of transponders [
18]:
Nodal degree (ND) assumes that transponders are located proportionally to the degree of network node [
18]:
where
nd(
v) denotes the node degree of node
v.
Routing only (RO) assumes that transponders are located proportionally to the number of times a particular node is included in the shortest path considering all node pairs [
18]:
where
nsp(
v) denotes the number of times node
v is included in the shortest path between a node pair considering all node pairs.
Configurations only (CONF) works similarly to RO; however, here, all the possible configurations (regeneration options) for the shortest path for each node pair are analyzed, and transponders are located proportionally to the number of times a particular node is included in the configuration considering all node pairs [
12]:
where
ncsp(
v) denotes the number of times node
v is included in a configuration based on the shortest path between a node pair considering all node pairs [
12].
Combined (COMB) assumes that transponders are located according to a metric that includes three elements: nodal degree (weight 40%, proportionally), number of transponders in the end nodes in the best configuration according to a metric showing usage of network resources (weight 40%, proportionally), and average distance to other nodes (weight 20%, inversely proportionally) [
12]:
where
tND(
v) = ⎿
T ·
nd(
v)/ ∑
w∊V nd(
w)⏌ denotes the number of transponders assigned to node
v according to nodal degree,
tENC(
v) = ⎿
T ·
enc(
v)/ ∑
w∊V enc(
w)⏌ denotes the number of transponders assigned to node
v according to number of transponders in the end nodes in the best configuration, and
tAD(
v) = ⎿(
T ·(1/
ad(
v))/∑
w∊V (1/
ad(
w))⏌ denotes the number of transponders assigned to node
v according to number of transponders in the end nodes in the best configuration.
It should be noted that the above presented algorithms do not account for additional knowledge that can be obtained by a data analytics approach which provides information on the network traffic profile observed in the near past or predicted for the future. Now, we present two traffic-based methods. In both proposed methods, for solving the dynamic RSSA problem we use the adaptive routing with back-to-back regeneration (ARBR) algorithm proposed in our previous paper [
11]. Note that the results from Reference [
11] clearly confirm that the ARBR method provides much better results in terms of bandwidth blocking probability when compared to other methods in the context of SS-FONs with B2B regeneration.
The key element of the ARBR algorithm is that it accounts for two types of important resources in optical networks, namely, spectrum and transponders. In a nutshell, the ARBR is a highly adaptive routing algorithm that utilizes the key benefits of B2B regeneration. In the preprocessing phase of ARBR, using
k shortest paths, a set of configurations defined by routing paths and location of regeneration points are computed for each node pair. For each transparent segment of a particular configuration, the most spectrally efficient modulation format is selected that supports transmission reach larger than the length of the considered segment. For each new request that occurs in the network, the ARBR algorithm executes the following procedure. Given the set of pre-computed configurations, a special adaptive metric is calculated for each configuration. This metric contains two elements: (i) static usage of spectrum (i.e., the number of slices essential to provision the considered configuration for a particular request) and transponders (i.e., the number of transponders essential to provision the considered configuration for a particular request); and (ii) dynamic usage of the spectrum and transponders resources (i.e., cost of the configuration that represents the current utilization of spectrum and transponders resources). Both elements (i.e., static and dynamic) are weighted with parameter
α. Next, the configurations are processed in increasing order of the obtained configuration’s metric. The ARBR tries to provision the request on the currently analyzed configuration, namely, using the first-fit approach, the algorithm searches for a sufficient range of spectrum checking various spatial modes. If the analyzed configuration is feasible, the request is provisioned in the network using this configuration. Otherwise, if none of the configurations is feasible, the request is rejected. To summarize, ARBR is able to analyze different configurations of routing paths and regeneration points to select the best option that balances between two key resources in the network, namely, spectrum resources (slices) and transponders. Moreover, the ARBR algorithm can adapt to the dynamically changing conditions in the network by selecting routing paths and regeneration points according to the current utilization of spectrum and transponders resources. For more details on ARBR, the reader is referred to Reference [
11].
The first traffic-based transponder placement algorithm is MSU proposed in Reference [
17] and adapted to our problem. In particular, MSU distributes
T transponders over the network based on the maximum instantaneous number of transponders used in each node during the simulation of the dynamic routing simulation with the use of the ARBR method. During the simulations, it was assumed that nodes were equipped with an unlimited number of transponders and the traffic is generated following a known (predicted) traffic pattern.
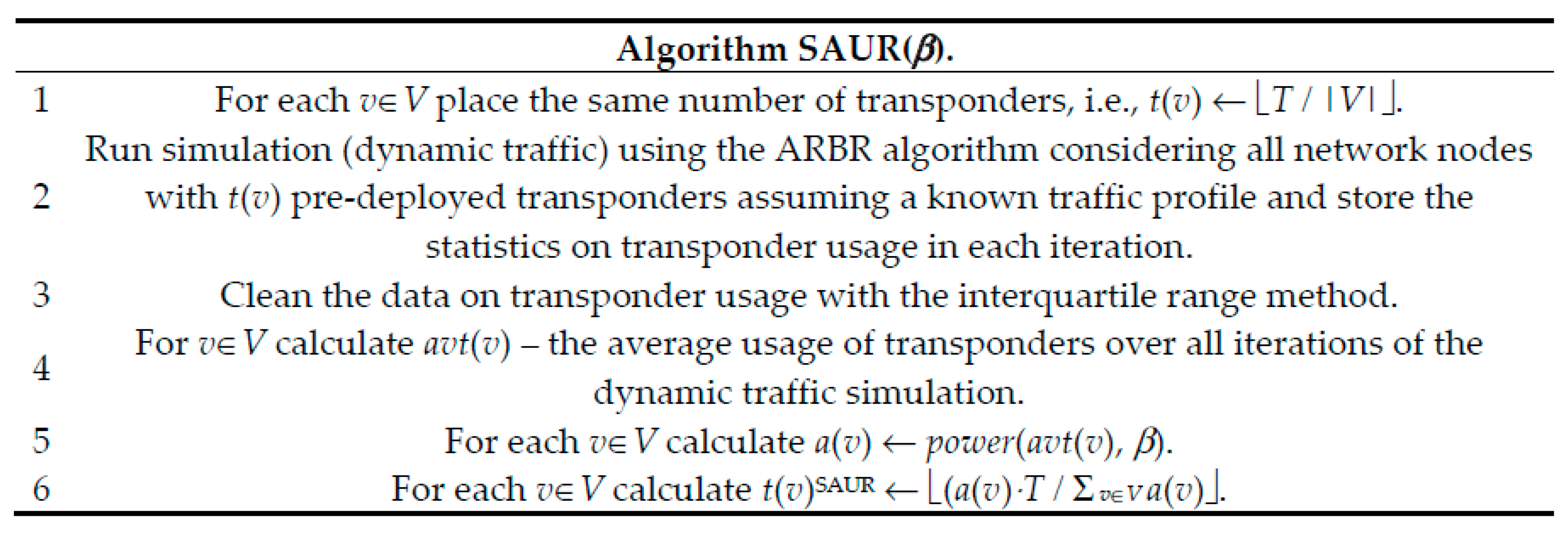
Finally, we present a novel SAUR algorithm. In
Figure 3, we report the general workflow of this method, while
Figure 4 shows the pseudocode. The idea of SAUR is to utilize knowledge on network traffic and allocation method in order to predeploy the transponders in such a way that the network performance in terms of bandwidth blocking probability is improved, or in other words, more traffic can be accepted in the network.
The key idea of SAUR is quite simple. First, each network node is assigned with the same number of transponders (Step 1), i.e.,
t(
v) = ⎿
T/|V|⏌, which according to Reference [
12] provides good results. Next, we run the ARBR dynamic routing algorithm described above to simulate the network operation assuming a randomly generated lightpath requests following a known (predicted) traffic pattern (Step 2). During simulation, various statistics on transponder usage in network nodes are collected. Since the traffic in the network is stochastic, therefore, to improve the quality of the obtained statistics of transponder usage, we perform data cleaning using the interquartile range method to remove outliers for each of analyzed nodes (Step 3). The interquartile range method is a measure of variability, based on dividing a rank-ordered data set into four equal parts (quartiles). The values that divide each part are denoted by Q1, Q2, and Q3. Interquartile range (IQR) is equal (Q3 – Q1), i.e., the difference between third and first quartiles. Outliers are defined as observations that fall below (Q1 − 1.5 IQR) or above (Q3 + 1.5 IQR). Next, for each node parameter,
avt(
v) is obtained (Step 4). In more detail,
avt(
v) denotes the average usage of transponders estimated over all time iterations. In particular, the time scale is divided into time slots (iterations) in which new requests arrive to the network and some other requests are finished according to the assumed average arrival rates and lifetimes. After each iteration, various statistics on the network usage are calculated, including usage of transponders at network nodes. To account for different traffic characteristics, in SAUR we use
scaled allocation, i.e., transponders are allocated proportionally to the average usage scaled by using the power function with exponent
β. To this end, in Step 5, parameter
a(
v) is calculated using the following formula:
Finally, in Step 6, the number of transponders assigned to each node is computed using
a(
v):
As mentioned above, MSU and SAUR are both traffic-based approaches that use data obtained by simulation of the routing algorithm for a selected network profile. However, when compared to MSU, SAUR provides the following key differences. First, SAUR addresses the fact that in our network model, B2B regeneration is allowed, i.e., we predeploy transponders that are used not only for regeneration of the signal at some intermediate nodes (as in MSU) but also for transmitting/receiving (add/drop) of the signal at the source/destination. Second, in our previous research on performance of SS-FONs with B2B regeneration, we noticed that, according to the number of available transponders in the network (parameter
T), the performance of the network changes (for instance, see the results in References [
11,
12]). Therefore, we assume that every node has a limit of available transponders in the dynamic routing simulations, and thus there is the possibility of a lack of transponders at some network nodes which will affect the performance of the dynamic routing algorithm. In contrast, the MSU method assumes that during the simulations there are no limits on the number of regenerators available in the network nodes. Third, SAUR allocates transponders according to their average usage observed during the whole simulation, while MSU focuses on the maximum usage. This difference between both methods is motivated by the fact that, in our opinion, the average utilization observed over a longer period of time is more important than short-term dependencies that can occur due to the stochastic nature of the network traffic and dominate the final allocation of transponders. Finally, the proposed SAUR method can be tuned, i.e., transponders are allocated proportionally to the average usage scaled by using the power function with exponent
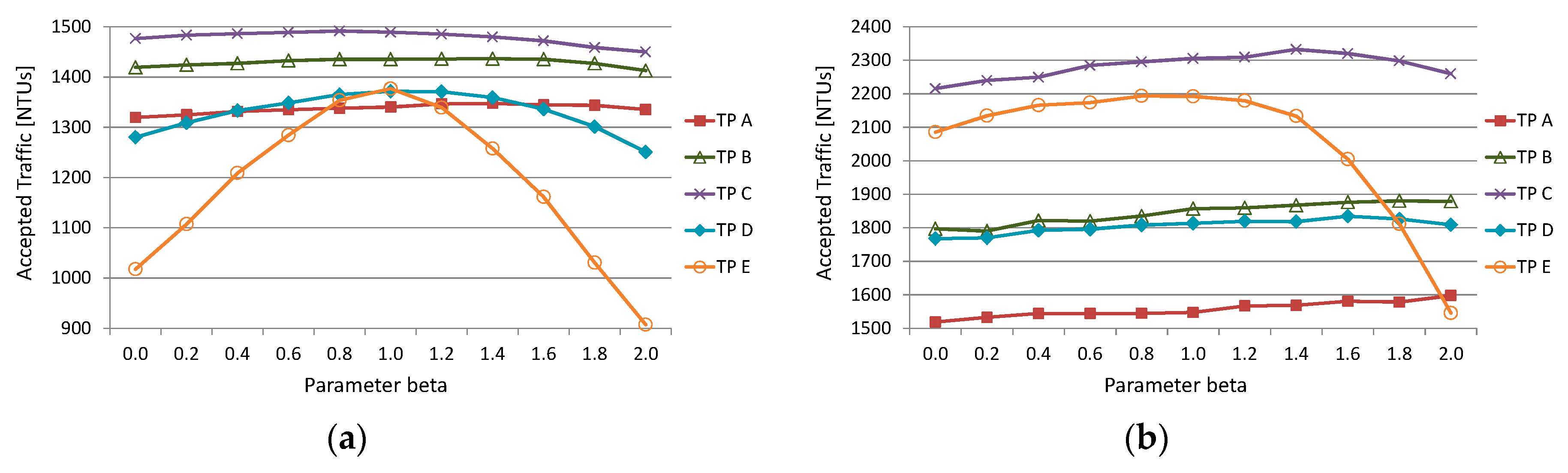
β. In this way, we can adjust the performance of SAUR to account for different traffic profiles that can occur in the network.
It should be stressed that the two traffic-based methods described above (i.e., MSU and SAUR) strongly rely on the data analytics approach. Firstly, these methods depend on the knowledge on the network traffic obtained by analysis of historical data or traffic prediction methods. With this information, both methods can tune their performance to different traffic profiles which results in different decisions in terms of the transponder placement. Without the detailed knowledge on the traffic profile, usually a uniform traffic profile is assumed, which results in a particular placement of transponders which may not be the best for traffic profiles different than uniform. Secondly, both methods during their run (i.e., simulation of network routing over a period of time) collect data on transponder usage for each node in subsequent iterations of the considered time period which allows to find some statistics such as maximum usage (MSU) or average usage (SAUR). Next, these statistics are directly applied to make the final decision on transponder placement.
In terms of time complexity of the above described algorithms, the time complexity of the UNI and ND methods is simply O(|V|), where |V| denotes the number of nodes. In the case of RO, CONF, and COMB, the time complexity is dominated by the shortest path calculation and can be estimated as O(|V|3) assuming the Floyd–Warshall algorithm. Finally, the time complexity of the two last methods, MSU and SAUR, depend on the execution time of the ARBR algorithm and the size of network traffic to be simulated. However, the final placement of transponders has simple complexity of O(|V|). Thus, the overall complexity of MSU and SAUR can be formulated as O(|V| + time(ARBR)), where time(ARBR) denotes the execution time required to simulate the analyzed traffic with the use of the ARBR method.
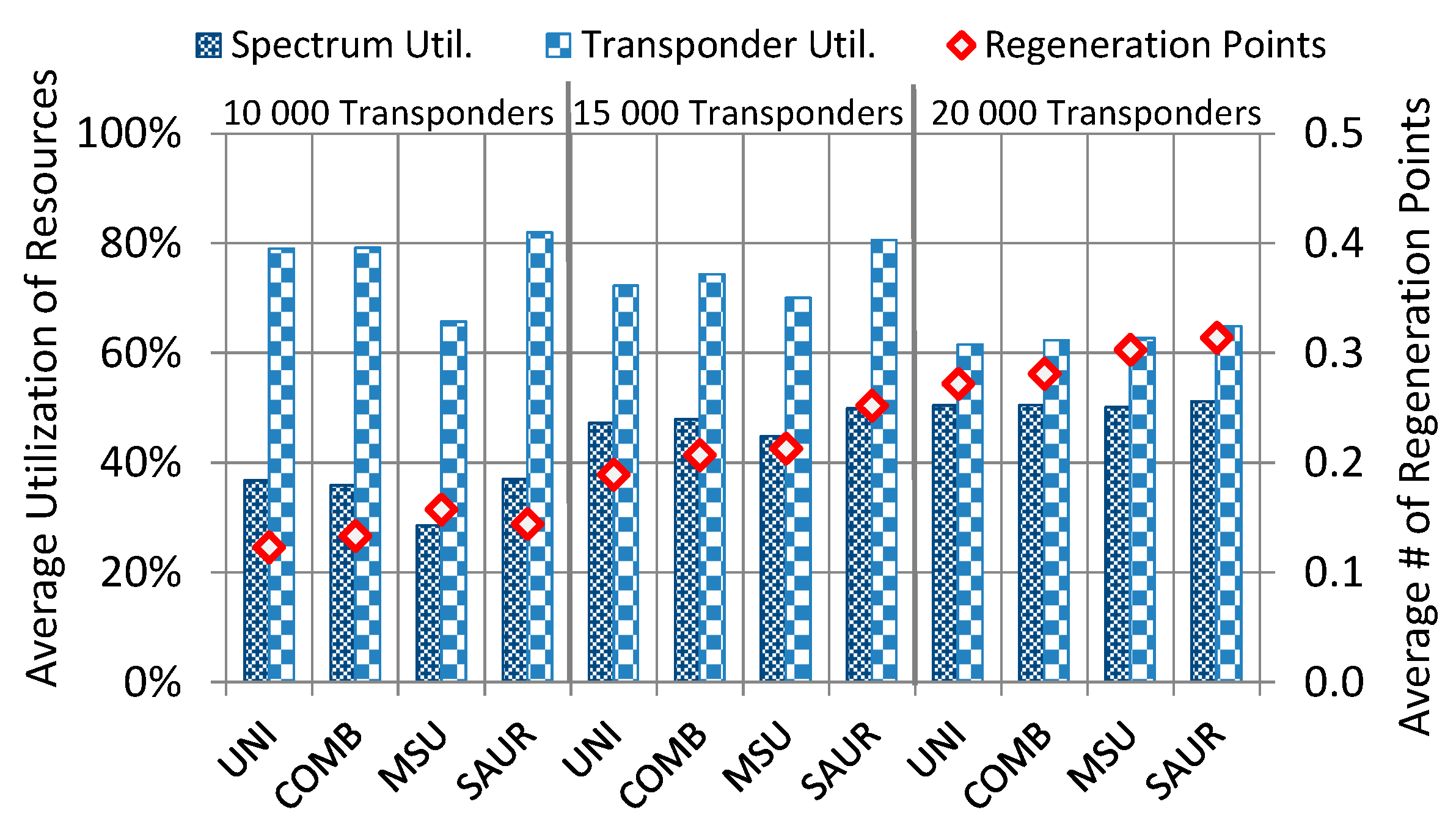
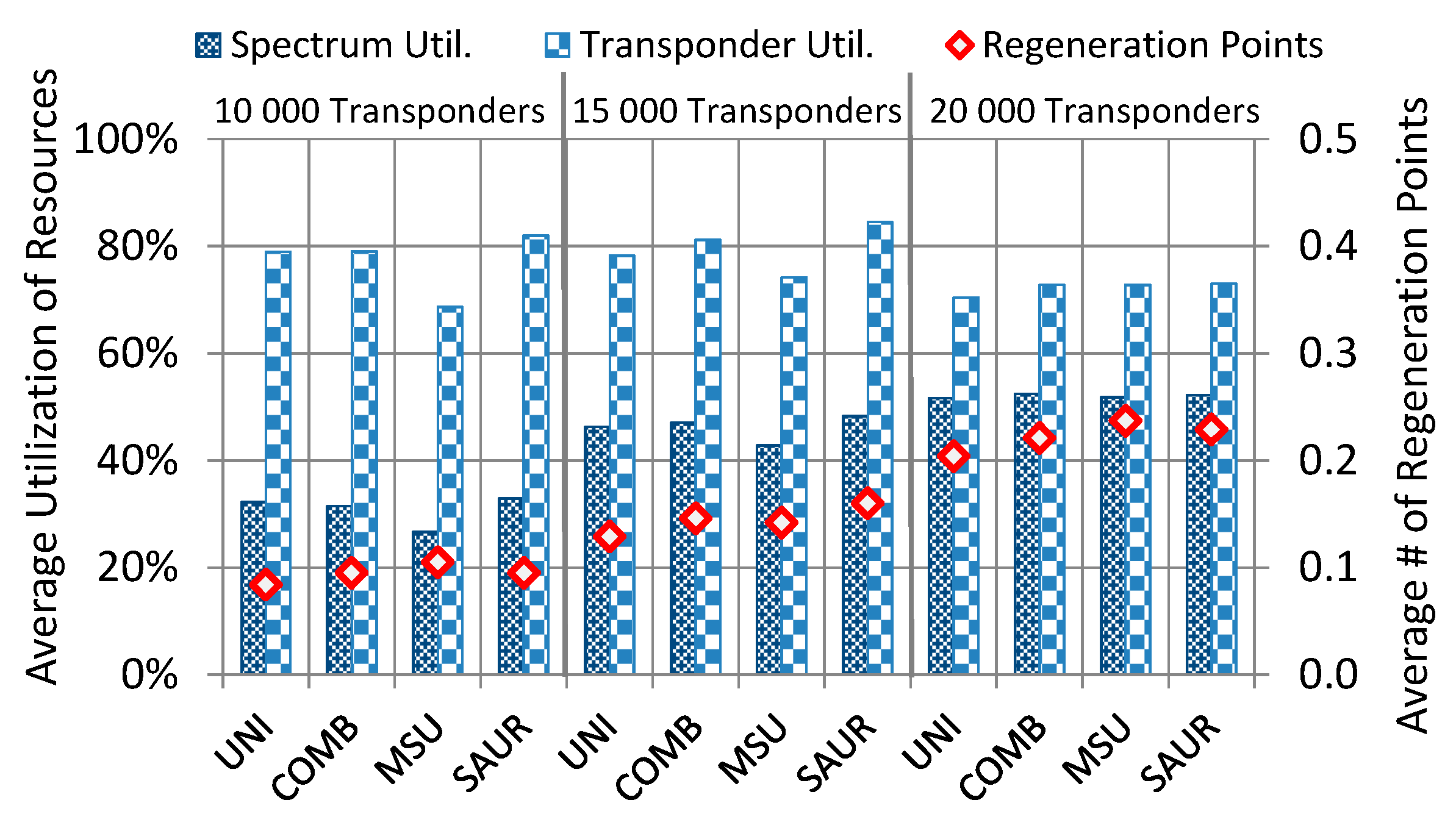
6. Conclusions
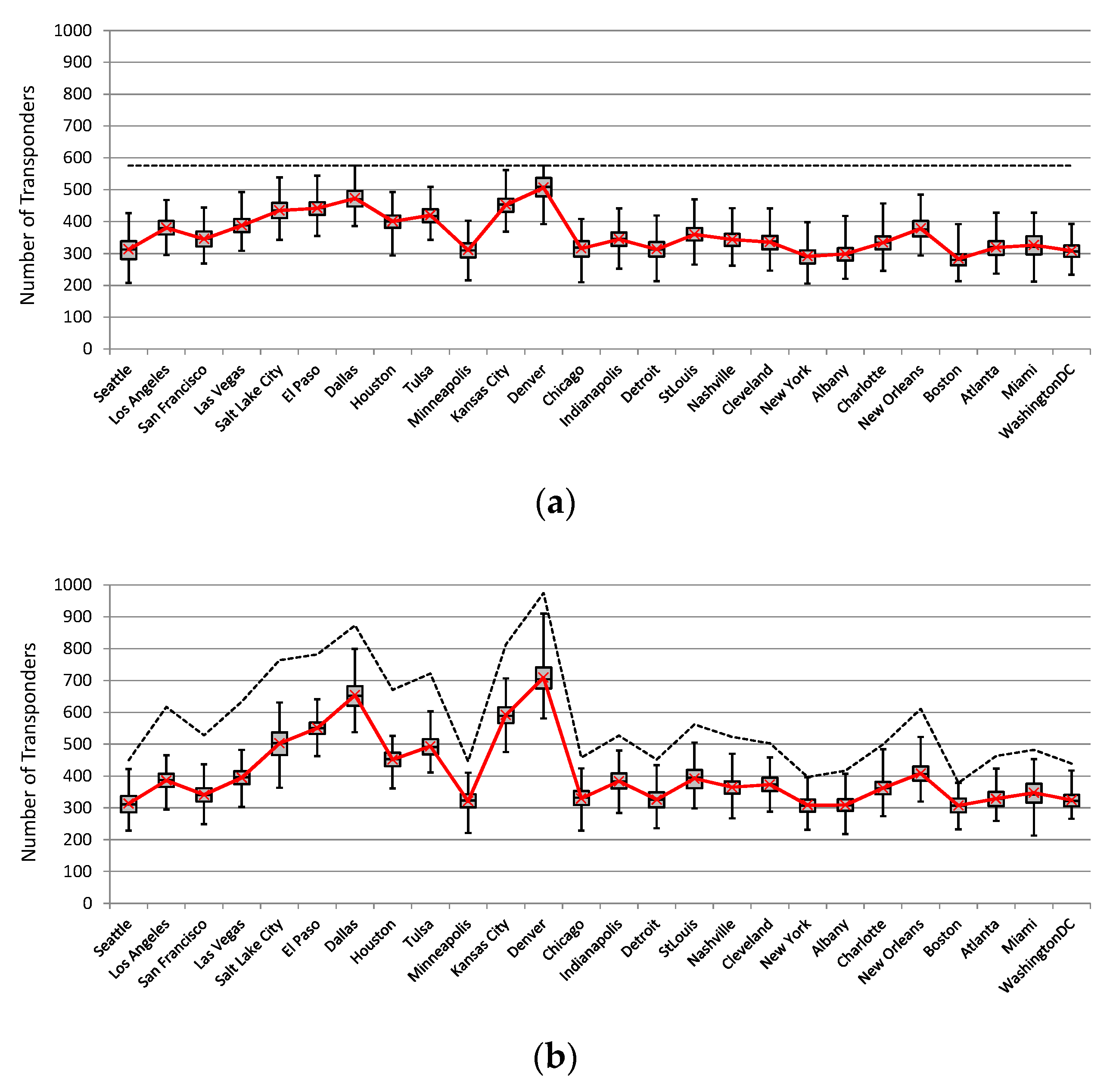
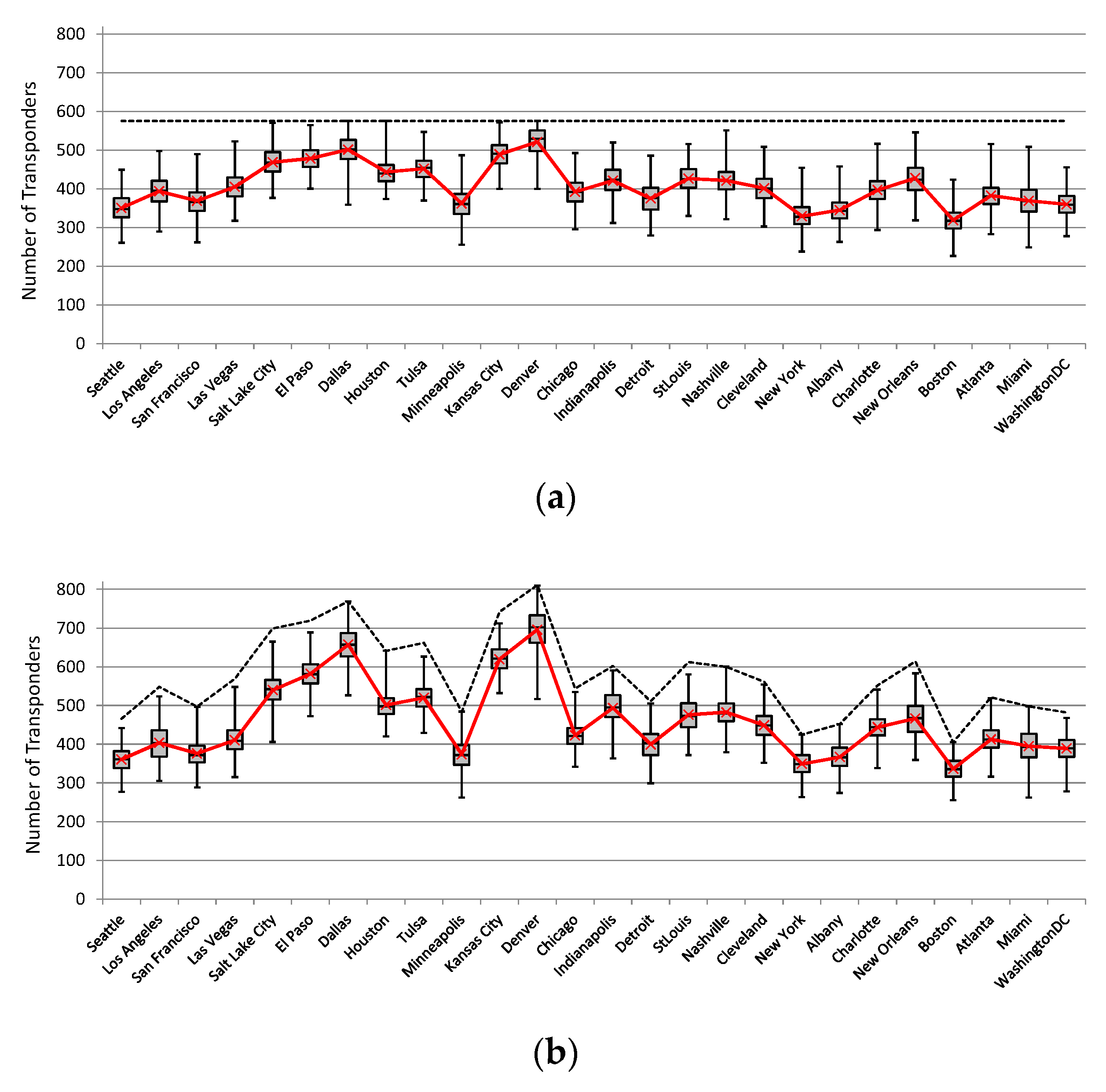
We have addressed the optimization problem of transponder predeployment in dynamic spectrally and spatially flexible optical networks in which the transponder resources are used both for transmitting/receiving (add/drop) spectral super-channels at source/destination nodes and for flexible super-channel regeneration in intermediate nodes which is achieved by means of the B2B regeneration approach. This problem consists in deciding on the number of transponders located in each network node, where the total number of transponders to be deployed in the network is limited. The problem was addressed under the consideration of multiple modulation formats, where each modulation format had specific spectral efficiency and transmission reach, and it was applied in accordance to the length of transparent segments that form translucent (regenerated) lightpaths. We showed that the decision on where the transponders are located has a significant impact on network performance, in particular, on the amount of accepted traffic. We proposed a heuristic method called scaled average used regenerators (SAUR) which makes use of a data analytics approach and decides on the transponder placement by exploiting information about network traffic characteristics and evaluated network performance. To assess the algorithm performance, we performed extensive simulation experiments on two representative network topologies and using several traffic profiles.
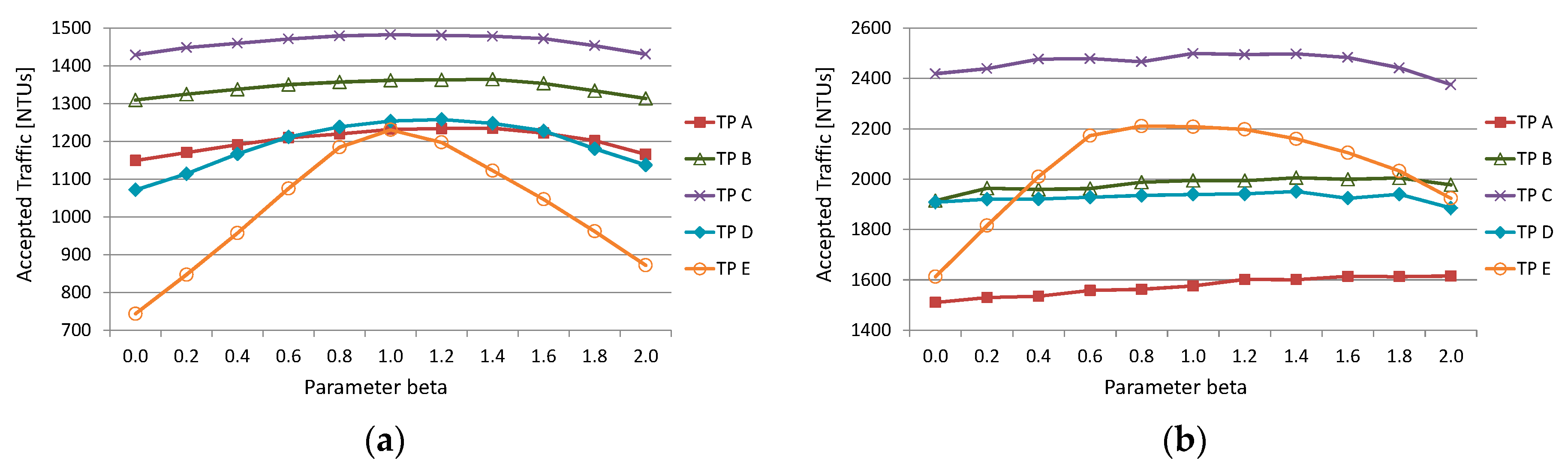
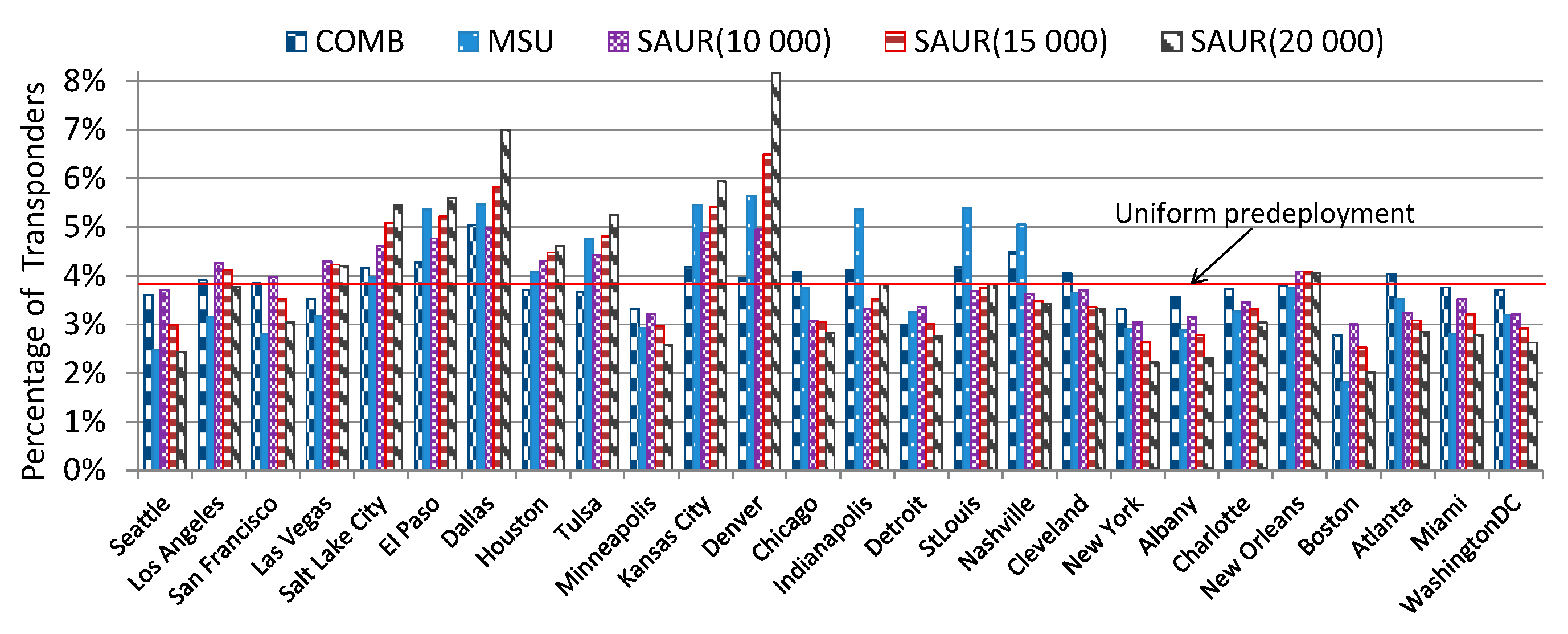
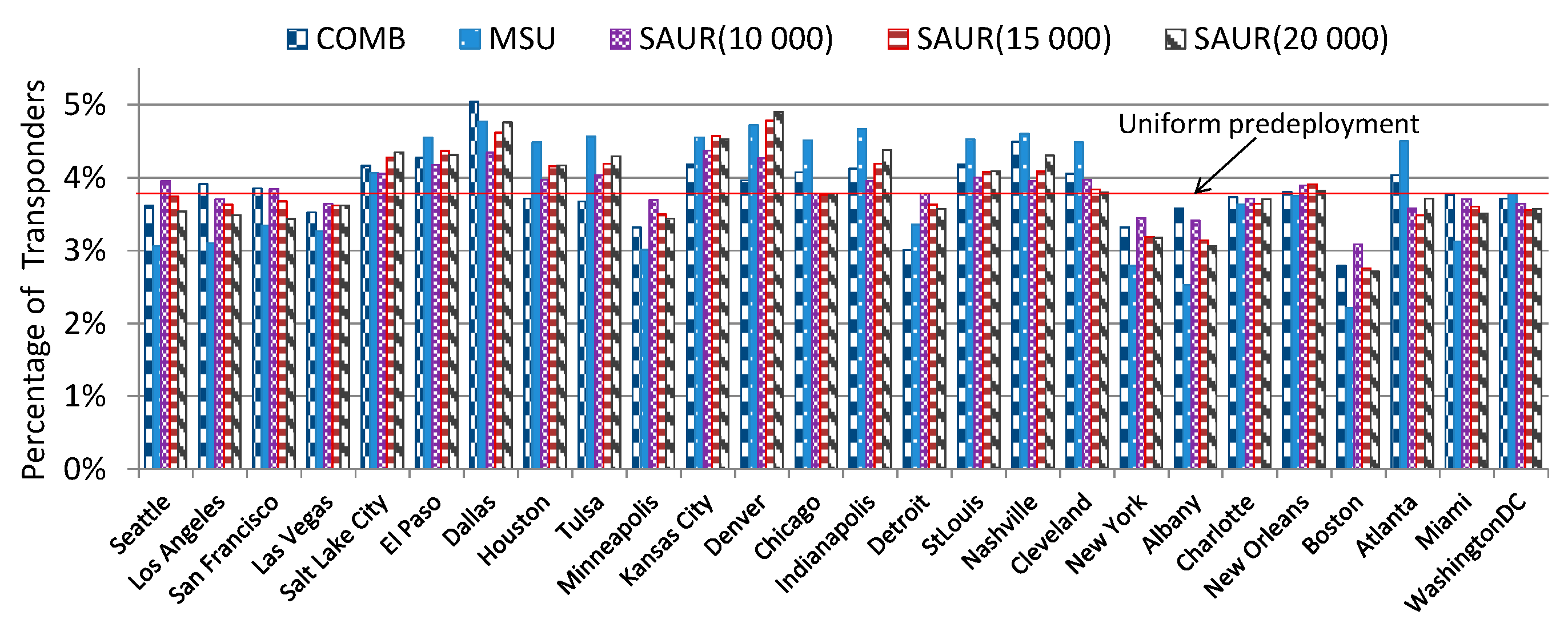
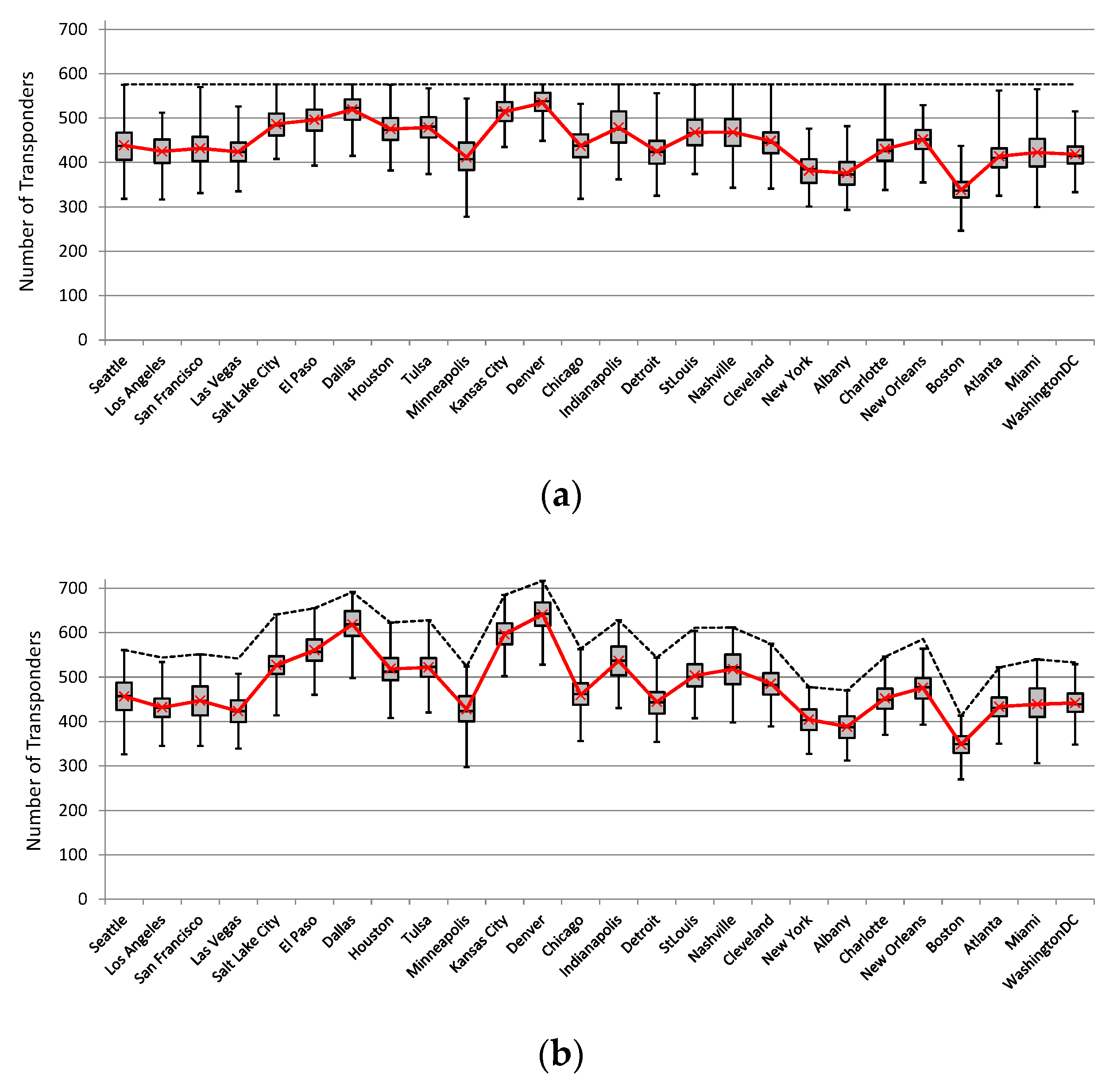
The main conclusions from this study are the following. Firstly, the SAUR algorithm provided much better performance results (in terms of accepted traffic) in all the evaluated network and traffic scenarios than the reference methods that were implemented and evaluated in this study. It is important to notice that an optimized placement of transponders in an SS-FON, which was achieved with SAUR, allows to increase the network throughput using only the existing resources, i.e., the network operator does not have to invest in new transponder devices or fibers to increase the served traffic and, in consequence, to increase the income.
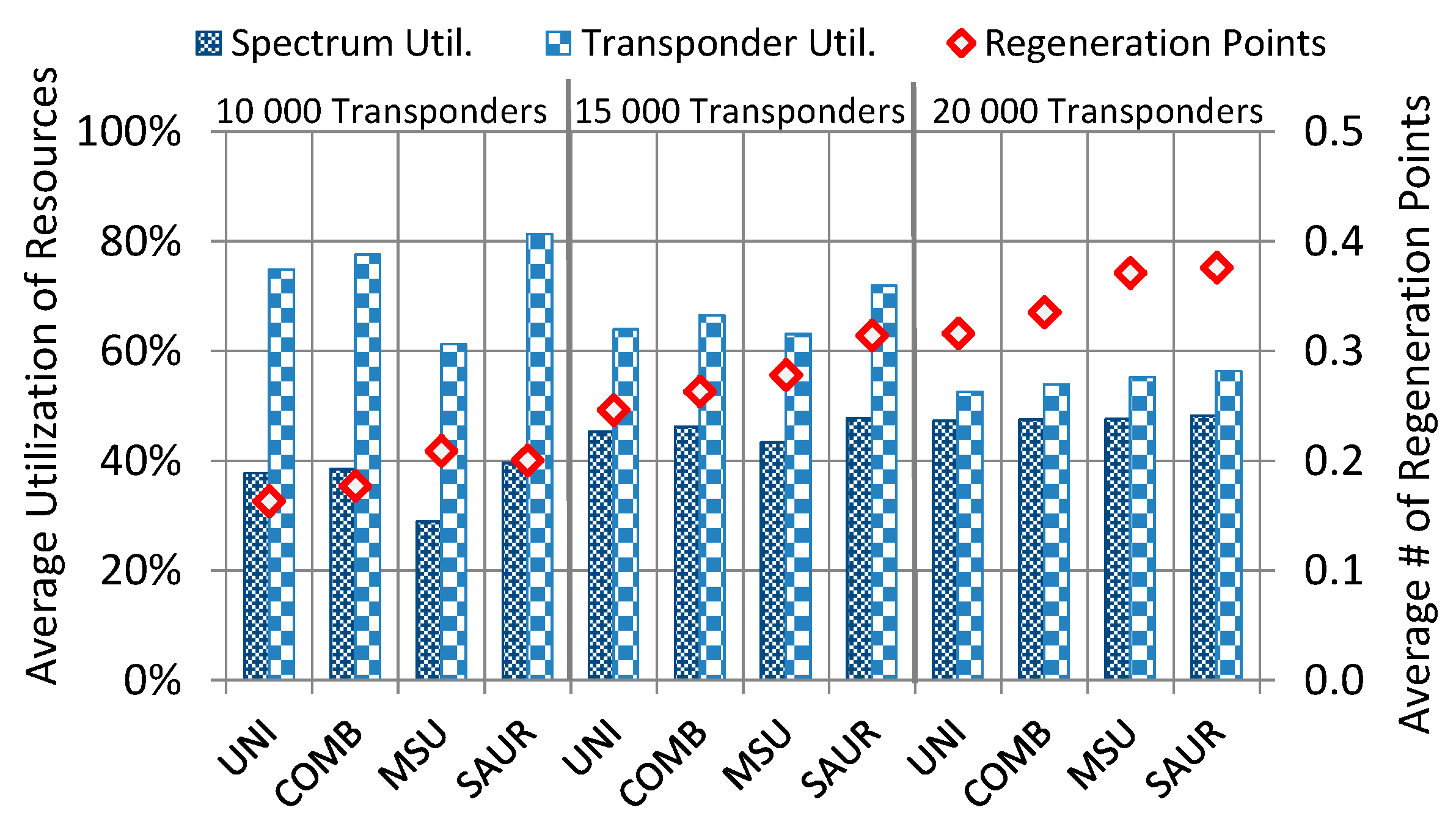
The next conclusion is that the performance gaps between SAUR and the reference methods were larger for the US26 network than for the Euro28 network. It was due to the larger average distance between node pairs in US26 for which optimal placement of transponders is more beneficial since more spectrally efficient modulation formats than BPSK can be used and, therefore, savings in the spectrum usage can be achieved. Moreover, the SAUR method provided the best (highest) utilization of transmission resources (spectrum and transponders). In other words, the placement of transponders yielded by SAUR allowed to utilize the network resources to the highest extent which in consequence allowed to allocate more traffic than the other methods.
Furthermore, the proposed SAUR method can be used to estimate the number of transponders required in the network to serve a given amount of traffic. In particular, by running the SAUR method assuming different transponders’ budgets (number of available transponders), we can obtain the estimated amount of traffic that can be provisioned in the network within a particular transponder budget. Next, by a simple comparison of the obtained values against the predicted network traffic, we can acquire the required number of transponders. This approach is valid for different traffic profiles. In consequence, a better placement of transponders provided by SAUR opens an opportunity to reduce the number of transponders required to serve a particular amount traffic in the network compared to other placement methods. This can also lead to a reduction in the energy consumption of the network.
In future work we will investigate the offline version of the optimization problem related to predeployment of transponders solved together with routing, space, and spectrum allocation in SS-FONs. Additionally, we plan to extend the study on the SS-FON scenarios in which multi-core fiber (MCF) links are used and the inter-core crosstalk effect that affects transmission quality is taken into account. Moreover, an interesting direction for future research is taking into account more accurate transmission reach models that would also include the type of equipment (e.g., optical amplifiers, reconfigurable optical add-drop multiplexers (ROADMs)) when considering the actual reach of the lightpaths with different modulation formats and with the use of the Gaussian noise (GN) model for accurate OSNR (optical-signal-to-noise Ratio) estimation in nonlinear fiber propagation.