Featured Application
The systematic and generic method proposed in this study for the kinematic design and dynamic modelling for a class of complex hybrid robots is useful and applicable for the development of new hybrid robot products. Based on the proposed method, the mechanism of a new hybrid robot can be synthesized and analysed effectively; the dynamicmodel and control law of a complex robot can be formulated and simulated in a simplified and effective manner.
Abstract
Recently, more and more hybrid robots have been designed to meet the increasing demand for a wide spectrum of applications. However, development of a general and systematic method for kinematic design and dynamic analysis for hybrid robots is rare. Most publications deal with the kinematic and dynamic issues for individual hybrid robots rather than any generalization. Hence, in this paper, we present a novel method for kinematic and dynamic modelling for a class of hybrid robots. First, a generic scheme for the kinematic design of a general hybrid robot mechanism is proposed. In this manner, the kinematic equation and the constraint equations for the robot class are derived in a generalized case. Second, in order to simplify the dynamic modelling and analysis of the complex hybrid robots, a Lemma about the analytical relationship among the generalized velocities of a hybrid robot system is proven in a generalized case as well. Last, examples of the kinematic and dynamic modelling of a newly designed hybrid robot are presented to demonstrate and validate the proposed method.
1. Introduction
Generally, the robotic mechanisms can be categorized into three main groups: the open-loop mechanism, the closed-loop mechanism and the hybrid mechanism. A robot of the first group is usually designed with an end-effector connected to a fixed base by means of a single serial kinematic chain. Meanwhile, each robot of the second group is a mechanism which is usually composed of a moving end-effector connected to a fixed base by at least two kinematic chains, such as the parallel robots. A hybrid manipulator is a mechanism which is usually composed of some open-loop kinematic chains combined with some closed-loop linkages [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34].
The main advantages of the serial robots are the large workspace, the high dexterity of the end-effector and the large non-singular range of the joint variables. However, the robots of this group suffer from several drawbacks, such as relatively low stiffness and accuracy, low nominal load/weight ratio and heavy structure [21]. Therefore, in the last decades, several types of robots having closed-loop kinematic chains have been investigated in order to obtain better kinematic performances. The main advantages of these robots are low weight, compact structure, better accuracy and stiffness. Nevertheless, this robot group also have some disadvantages, such as a small workspace, a complex mechanical design and a complex procedure for dynamic modelling and control. For these reasons, in recent years, great attention has been paid to the development of hybrid robots which have combined advantages of the serial robots and the closed-loop architectures. More and more hybrid robots are designed and developed to meet the increasing demand for a wide spectrum of hybrid robotic applications [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30].
In practice, the hybrid robots have been designed in a large variety of kinematic configurations and structures, and they can be classified into three main classes as follows:
The first class (Class I) includes all the hybrid robots whose structure has several parallel modules connected in series [1,2,3,4,5,6,7,8,9,10] (Figure 1a).
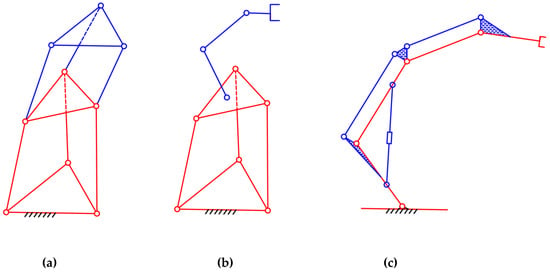
Figure 1.
Three main classes of the hybrid robots: (a) Class I; (b) Class II and (c) Class III
Class II consists of the hybrid robots which have a basic parallel module combined with a serial manipulator [11,12,13,14,15,16,17,18,19,20,21,22,23,24] (Figure 1b).
Class III is a family of the hybrid robots which are composed of some local closed-loop chains appended to a main serial mechanism [25,26,27,28,29,30,31,32,33] (Figure 1c).
It is clearly seen that the main architecture of a hybrid robot Class I or II is a parallel mechanism. Other parallel modules or serial links are connected to such the main structure to complete a hybrid serial-parallel robot.
Different from the robots Class I and II, each hybrid robot Class III is usually designed with a serial module as the main structure of a robot. To provide with desirable mechanical advantages for a hybrid robot, some local closed-loop mechanisms are added to the main serial module. For example, when designing manipulators which suffer a heavy payload and operate in a large workspace, parallelograms were added and hydraulic cylinders were used for driving some revolute joints of the manipulators [26,28,29,30,31]. The addition of parallelograms to the main arm is to increase the rigidity of the robot, and also to restrict the orientation of the end- effector as desired. The use of the hydraulic cylinders is to increase the structural stiffness and to avoid the counterweights for the robot structure. The parallelograms and cylinders and other links of the serial arm naturally compose local closed loops of the entire robot mechanism. Other examples of using local closed-loop linkages to optimize the design and control for a robot can be found in [26,27,28,29,30,31,32,33,34].
In recent decades, a huge number of hybrid robot prototypes and products have been designed and developed [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. The dynamic modelling and control for some of these complex robots have been addressed as well. However, to develop a generic method for formulating the dynamic model of a generalized hybrid robot mechanism is challenging.
In the literature, there have been efforts that focused on the kinematic modelling of the hybrid robots Class I [1,2,3,4,5]. The kinematic modelling and analysis of two serially connected parallel mechanisms were investigated in [1]. In [2], the kinematic redundancy issue of a serial-parallel manipulator was addressed. The Screw theory and the Jacobian approach were applied for the kinematic modelling of a serial-parallel robot [3,4]. In particular, the dynamics and the structural stiffness models of some specific hybrid robots Class I were formulated and analysed [6,7,8,9].
There have also been attempts working on the modelling and analysis of the hybrid robots Class II [11,12,13,14,15,16,17,18,19,20,21]. A real-time implementation of path planning, trajectory generation, and servo control for a hybrid manipulation was presented in [11]. The kinematic modelling, the kinematic design, the workspace modelling and other aspects related to the kinematics of the hybrid robots Class II were studied [12,13,14,15,16,17]. The dynamic modelling and analysis of the robots Class II were also investigated [18,19]. In addition, the structural synthesis and the stiffness of the hybrid robots of this class were studied [20,21,22].
Apart from the aforementioned works, there have been investigations that emphasized on design and development of the hybrid robots Class III [25,26,27,28,29,30,31,32,33]. A valuable comparison of the conventional serial robot architectures and the hybrid robots Class III was presented in [34]. In the research [25], some theoretical issues related to the kinematic modelling of multi closed-loop mechanisms were addressed. In addition, some closed-form solutions to the kinematics problem of individual hybrid robots Class III were presented in [26,27,28]. These solutions played an important role in validating the design of the robots. The workspace and mobility analysis were also investigated in [28,29]. Other aspects related to the design analysis of heavy-duty robots were presented in [30,31]. The control issues were studied in [32,33]. It is noticeable that the dynamic modelling of a hybrid manipulator Class III (forestry robot) was investigated in [33]. However, the effects of the local closed-loops on the dynamic responses of this robotic system were overlooked.
Most of the efforts working on the hybrid robots Class III mainly focused on the design and control of some individual robots for the kinematical aspects. Though the dynamic modelling of the robots was addressed in a few researches, e.g., [33], however, the mass and inertia of the local closed-loop linkages that have significant effects on the robot motion were neglected; the geometrical and kinematical constraints due to the presence of the local closed-loop linkages were usually ignored. Moreover, little attention has been paid to the development of a general method for the kinematic and dynamic modelling of this robot class. Therefore, in this paper, a new method for designing the kinematic chain and formulating the dynamic model of the hybrid robots is developed. First, a generic scheme for the kinematic design of a generalized hybrid robot mechanism is proposed. In this scheme, the generalized hybrid mechanism is synthesized with m local closed-loop linkages appended to a general n-link serial manipulator. Each locally closed linkage is regarded as a four bars mechanism which is made up of two successive links of the main serial arm, and other two added links. Second, the kinematic equation for the generalized hybrid mechanism and constraint equations for the closed loops are derived in a generalized case. Third, a Lemma about the relationship among the generalized velocities of the hybrid robots is proven, which is useful for transforming the dynamic equation and constraint equations into a minimal and compact form. Last, the kinematic and dynamic modelling of a real robot prototype are presented to demonstrate and validate the proposed method. It is shown clearly that, since the kinematic and dynamic modelling of a hybrid robot take into account the constraint equations and the dynamic effects of all the local closed loops, the kinematics and dynamics models of a hybrid robot are formulated in a better and more accurate manner. Therefore, the method proposed in this study is advantageous and plays a crucial role in the development of hybrid robot products.
2. Kinematics of a Generalized Mechanism for The Hybrid Robots Class III
Let us consider a manipulator which is designed with n serial links and m local closed-loop mechanisms , () as shown in Figure 2. The serial chain of n links is the main mechanism of the robot arm, and the closed-loop mechanisms are designed as sub-mechanisms appended to the main one. The degree of freedom number (DOFs) of the designed robot equals the DOFs of the main mechanism, . The presence of the local closed-loop mechanisms does not change the DOFs of the robot.
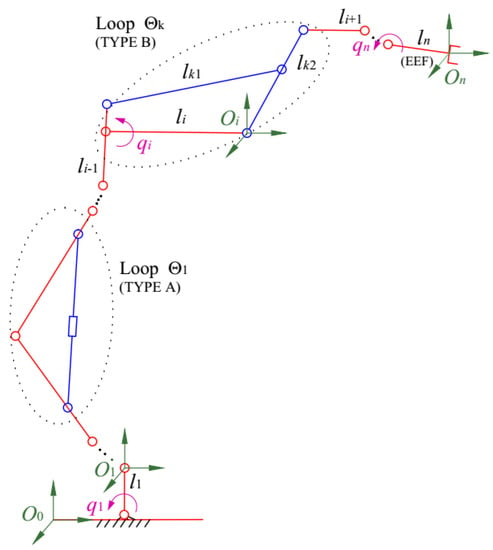
Figure 2.
A generalized configuration of the hybrid robots Class III.
Each local closed mechanism is designed with two successive links and of the main arm and other two appended links and . See Figure 2 and Figure 3. In other words, each local closed-loop mechanism is designed as a four bar linkage which is composed of the links , , and . In a local closed chain linkage, the link is a local base link, and the remained links , and move relative to the base link .
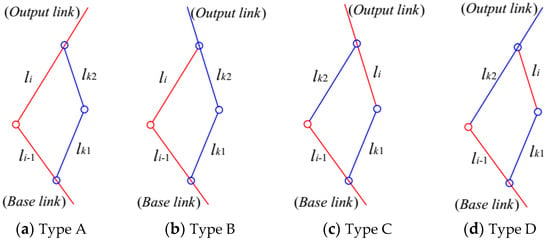
Figure 3.
Four types of the local closed-loops.
As shown in Figure 3, there exists four types of the local closed-loops, Type A, B, C and D, which can be designed by combining a couple of successive links and of the main arm and other two links and added to the robot architecture.
In a local closed-loop Type A (Figure 3a), the two links and are added to the main arm, and the output link is a link . Meanwhile in Type B (Figure 3b), the two links and are inserted in between the links and , but the output link is the link . When a loop Type B is added to the main kinematic chain, the link is inserted in between and .
When the two links and are not connected together, there exists two more combinations of the links , , and as shown in Figure 3c,d. In a loop Type C, the output link is , meanwhile in Type D, the output link is .
For all four types of the local linkages, the base link is , and the formation of all the closed-loop mechanisms does not change the DOFs of the robot.
Let us consider the main kinematic chain of the hybrid robot. In Figure 2, is the reference frame, and to are the local coordinate systems which are attached to all the links of the main arm. Let us denote as the vector of joint variables on the main arm, correspondingly.
As usual, the geometric and kinematic parameters of a link are denoted as , , and . By using the Denavit–Hartenberg notation, the transformation matrix for the end-effector (EEF) can be calculated as follows:
where is the transformation matrix for a link .
In other words, can be expressed as follows:
where is the rotation matrix, and is the translation vector for the EEF. Equation (2) describes the kinematic relationship of the robot. If we denote as the posture of the EEF in , where is the position and the orientation of the EEF, the kinematic equation can be written as follows:
Let us consider all the local-closed loops Type A, B, C or D, which can be added to the main kinematic chain, as shown in Figure 3. The presence of a closed chain Type A does not change Equation (1). However, Equation (1) must be recalculated if a closed loop Type B, C or D is designed for the robot.
For a local linkage Type B, since a link is inserted in between and , the transformation matrix in Equation (1) must be recalculated as follows:
For a local linkage Type C and D, the matrix is replaced by the following matrix:
In particular, for a linkage Type D, not only is re-calculated with Equation (5), but also the matrix must be re-calculated as follows:
Note that the variables and in Equations (4)–(6) can be determined with respect to via the two constraint equations of a corresponding closed-loops , which will be presented later in the next section.
Constraint equations
Different from the formulation of the kinematics model for a serial robot, the formulation of the hybrid kinematics models of the hybrid robots Class III must take into account the constraints due to the presence of the local closed-loops.
As discussed before, each linkage includes two sub-kinematic chains that move relative to the base link. For example, as shown in Figure 4a, the first sub-chain of a linkage Type A is the link , and the second sub-chain includes the two link and . Obviously, the two sub-chains of a linkage are closed at an intersection point M (see Figure 4).
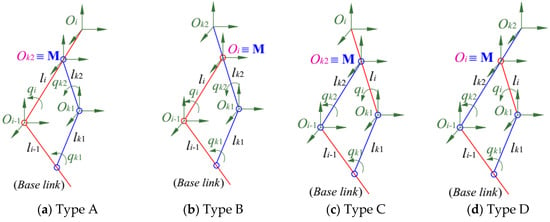
Figure 4.
The closed kinematic chain of the local linkages.
In order to derive the constraint equation for a loop , the position of the point M are determined along the two sub-chains.
On one hand, the point M, represented in the coordinate of the link , can be determined via the position and orientation of the link that can be calculated relative to the base link . On the other hand, the point M, expressed in , can be calculated through the position and orientation of the link . Consequently, the constraint equation for a loop Type A and B can be yielded as follows:
For a loop Type C and D the constraint equation can be written as follows:
Note that, for a closed-loop Type A or Type C, the point M coincides the point , thus . In addition, for a closed-loop Type B or Type D, .
In essence, Equations (7) and (8) can be rewritten as three constraint equations corresponding to three axes of the coordinate system . However, among such the three constraint equations, there exist only two independent ones, since all the closed-loops under consideration are planar four bar linkages. As a consequence, corresponding to a loop , the two independent constraint equations can be written as follows:
For every local linkage, only one joint variable among , and is independent. The kinematic relationships among , and are determined via the two constraint equations, Equation (9), for each closed-loop . Therefore, in the case that, instead of , the variable or is selected as the independent joint variable of , the variable in the transformation matrix in Equation (1) must be changed by the variable or , respectively, where the functions and can be determined with respect to the kinematic relationships among , and .
3. Dynamic Modelling of the Hybrid Robots Class III
is the vector of independent generalized coordinates which are selected among joint variables of the main arm, and joint variables of closed-loops. In other words, is the vector of all active joint variables.
is the vector of dependent generalized coordinates.
is the vector of all generalized coordinates of the robot system.
is the vector of constraint equations.
is the vector of applied torques/forces.
By using the Lagrangian formulation, the equations of motion including constraint equations for the robot can be written as follows:
Note that the size of the global matrices and is . The global mass matrix must be formulated with respect to all the links of the robot including links of the serial chain and links added to local closed-loops.
The global mass matrix is calculated as follows:
where and are the mass and inertia of a link . The translational and rotational Jacobian matrices are calculated as and , where is the centre of mass, and is the angular velocity of a link , respectively.
The Coriolis and centrifugal matrix is calculated by using Cristoffel notation.
The matrix is calculated as follows:
where the total potential energy of the entire system is calculated as
The Jacobian matrix is derived with respect to constraint equations as , and is the vector of Lagrangian Multipliers.
It is clear that the system of DAE equations seen in Equation (11) consists of differential equations of second order and constraint equations . Moreover, Equation (10) has not only independent variables , but also dependent variables and unknown Lagrangian Multipliers . Therefore, if using this complex system of DAEs to analyse the dynamics behaviour and to design a control law for the robot, the time complexity of the formulation and computation will be increased dramatically. For this reason, it is necessary to transform Equation (10) into a more compact form in which the Lagrangian Multipliers should be cancelled, and the number of the differential equations is minimized.
By using the following Lemma, differential equations of second order, Equation (10), can be transformed into only differential equations of second order which are expressed in terms of only independent generalized coordinates, not including Lagrangian Multipliers .
Lemma.
Consider a generalized hybrid robot mechanism Class III which has independent joint variables and dependent joint variables . The relationship between and is expressed as , in which the matrix is explicitly calculated as , where is an identity matrix of appropriate dimension, and , where is the constraint equation.
As a consequence of this Lemma, the following important relationships, Equations (14) and (15), can be proved easily.
In Equation (14), the Jacobian matrix can be expressed as follows:
Note that Equations (14) and (15) play a very important role in transforming the complex system Equation (10) into a minimal form. With respect to Equations (14) and (15), multiplying with both sides of Equation (10) yields
where
,,, and .
Different from the complex ADEs system in Equation (10), which has differential equations with the presence of dependent variables , and unknown Lagrangian Multipliers , the minimal form of the dynamic equation, Equation (17), consists of only differential equations which are expressed for independent generalized coordinates only. Moreover, the matrix form of Equation (17) is similar to the form of any dynamic equation that is usually written for a conventional industrial robot. Hence, by using Equation (17), the dynamic analysis and control law computation for any complex hybrid robot Class III can be implemented in an effective and simplified manner.
Proof of the Lemma.
Taking a time derivative of the constraint equation yields
Substituting Equation (16) into Equation (18) obtains
Rewriting the relationship in the following form:
Note that is an identity matrix and is an unknown matrix which needs to be proved.
With respect to Equation (20), the vector can be expressed as follows:
Multiplying with both sides of Equation (21) yields
Substituting Equation (22) into Equation (19) yields
Hence
Finally, substituting Equation (24) into Equation (20) yields
Equation (25) completes the proof. □
4. Example: Kinematic and Dynamic Modelling of a Real Robot
In this section, the kinematic and dynamic modelling of a newly designed hybrid robot Class III are presented. The robot was designed and implemented with the purpose of handling material for a hot forging press shop floor. The 3D design of the robot and the robot prototype are shown in Figure 5a,b, respectively. The functional tests of the robot prototype and the numerical simulation of the kinematic and dynamic responses shows clearly the effectiveness and advantages of the method proposed in this study.

Figure 5.
The forging robot: (a) The 3D design, and (b): The robot prototype.
The kinematic diagram of the robot is presented in Figure 6, which is designed with 4 serial links , and 4 local closed loops ( Figure 7). The reference frame is located on the ground. The coordinate systems , , and are located on the serial links.
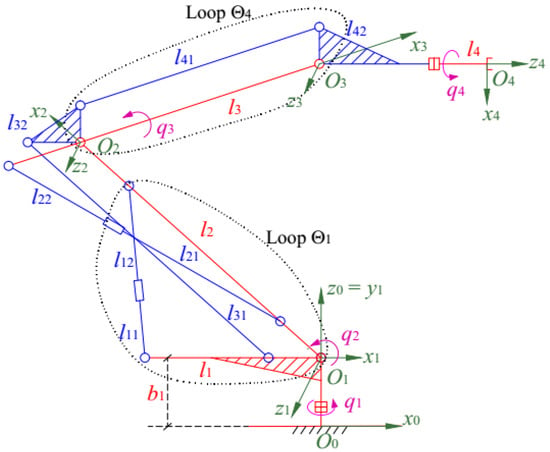
Figure 6.
The kinematic chain of the forging robot.
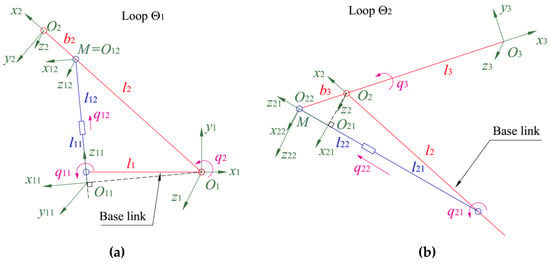
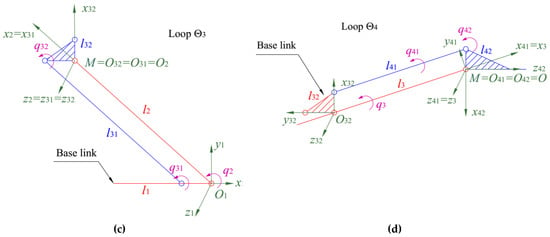
Figure 7.
The local closed-loop linkages of the forging robot: (a) Loop ,(b) Loop , (c) Loop , and (d) Loop .
The joint variables of the main serial chain are (Figure 6).
Each local closed loop presented in Figure 7 is a four-bar linkage which is made up of two serial links (in red colour) and other two additional links (in green colour). Note that and are the loops of Type A; and are the loops of Type B.
The loop includes the link , , and . The joint variables of the loop are , and . The loop consists of , , and . The joint variables of the loop are , and . The loop consists of , , and . The joint variables of the loop are , and . The loop consists of , , and . The joint variables of the loop are , and . Table 1 presents the Denavit–Hartenberg notations of the four loops. Table 2 presents the dynamics parameters of the robot.

Table 1.
The D-H notations of the four local closed loops.

Table 2.
Dynamic parameters of the robot.
The length of the links are given as follows: ; ; ; ; ; ; ; ; ; ; ; .
Note that , , , , , , , , , , and are 12 generalized coordinates of the robot, in which
is the vector of 4 independent generalized coordinates,
is the vector of 8 dependent generalized coordinates and
is the vector of all 12 generalized coordinates of the robot.
Constraint equations
By using the formulation Equation (7), the constraint equations can be derived for 4 closed loops as follows:
Kinematics of the robot
By using the formulation Equation (1), the transformation matrix for the end-effector is calculated as follows:
Since and are the loops of Type B, by applying Equation (4), the matrices and are recalculated as follows:
Finally, the position of the end-effector is yielded as follows:
Note that
Note that all the joint variables and the position of the end-effector in Equations (34)–(39) must be functions of time . However, to simplify the representation of such the complex equations, the term is truncated.
In order to verify the formulation of the kinematics model, the following numerical experiments were carried out:
1. Calculate the trajectory of the end effector , with the input data is given as , and . Figure 8 shows the curves of .
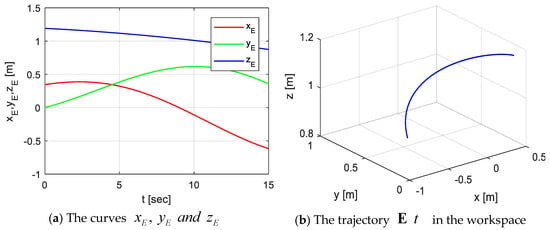
Figure 8.
The trajectory of the end-effector.
2. Take the data obtained in Step 1 as the input for the inverse kinematic analysis, and calculate the displacement of the joints , and . The results are shown in Figure 9.
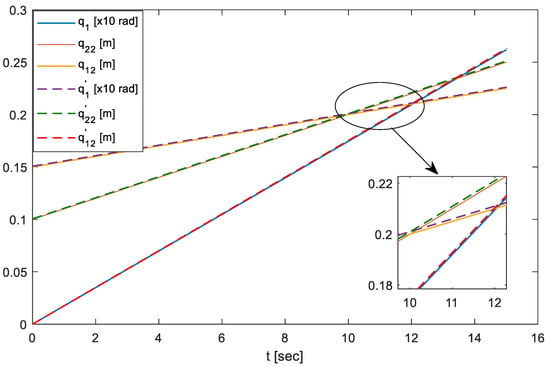
Figure 9.
The displacement of the active joints.
It is clearly shown in Figure 9 that the curves , and obtained in Step 2 match exactly the given data , and , respectively. This demonstrates and validates the proposed kinematic modelling method.
Dynamic Modelling and Analysis of the Robot
The dynamic equation of this robot can be derived directly by using the formulation Equation (17). In order to formulate ,, and , the matrices , , and must be computed.
In this manner, can be calculated with Equation (11), where the masses are given in Table 2, and the inertias can be calculated based on the geometrical dimension of the links given in Table 2 as well. In Equation (11), the Jacobian matrices are calculated as and , where the centre of mass and the angular velocity are calculated and presented in the Appendix A. Based on all the components of , the matrix is then calculated by using Cristoffel notation.
The component is calculated with Equation (13), where the total potential energy of the robot, , is calculated and presented in the Appendix A also.
The matrix is calculated with Equation (25), where the Jacobian matrices and are presented in the Appendix A, respectively.
Finally, all the terms of Equation (17) can be formulated properly that can be used for the dynamic analysis and the control law computation. In the following example, we demonstrate an inverse dynamic solution that was calculated with respect to a input data given as follows: , , and . The responses of are shown in Figure 10.
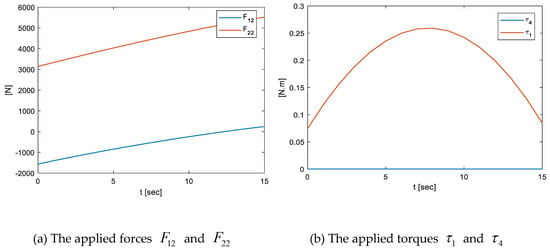
Figure 10.
The forces/torques applied on the active joints.
It has shown that instead of the complex governing equations seen in Equation (10), the minimal form of the dynamic Equation (17) can be used directly for computation of the control (the inverse dynamic analysis) for the robot. In addition, analysing the dynamic model of a hybrid robot does not need to take into account the unknown Lagrangian Multipliers .
5. Conclusions
A new method for the kinematic and dynamic modelling for a class of hybrid robots was introduced in this study. The proposed method can be applied for the kinematic design of a robot mechanism composed of m local closed-loop linkages appended to a general n-link serial manipulator. In this manner, the kinematic equation for a generalized hybrid robot mechanism and the constraint equations due to the closed-loop linkages of a robot are derived effectively. Since a Lemma about the analytical relationship among the generalized velocities of a hybrid robot system was proven in a generalized case, the dynamic equation and constraint equations can be transformed into a minimal and compact form, so that the dynamics model of any hybrid robot can be formulated and analysed in an effective and simplified manner. Finally, to demonstrate and validate the proposed method, examples about the kinematic and dynamic modelling of a real robot are presented. It was shown clearly that, since the kinematic synthesis and the dynamic modelling of a hybrid robot take into account the constraint equations and the dynamic effects of all the local closed loops, the kinematics and dynamics model of a hybrid robot is formulated in a better and more accurate manner. In addition, since the method presented in this study was proposed and validated in a generalized case, it can be applied effectively for the kinematic and dynamic modelling of any individual hybrid robot Class III. In particular, when designing a new hybrid robot, the designers can follow all the steps of the kinematic design procedure presented in this paper to archive easily an optimal mechanism for the robot. The control law of the designing robot is then designed and simulated in an effective and useful manner by using the dynamic modelling procedure presented in this study as well. Therefore, the method proposed in this study is advantageous and plays an important role in the development of the hybrid robot products. All the experimental procedures for development of next versions of the robot prototype will be the future work of this study. The simulation of the kinematic and dynamic modelling of the hybrid robots having closed loops Type C and D will be the future study of the authors.
Author Contributions
Conceptualization, A.M.C. and C.D.N.; methodology, A.M.C. and C.D.N.; software, M.H.V.; validation M.H.V., A.M.C. and X.B.D.; formal analysis A.M.C., C.H.L. and M.H.V.; investigation, A.M.C., C.H.L. and T.A.N.; writing—original draft preparation, A.M.C.; writing—review and editing, C.H.L. and T.A.N.; project administration, A.M.C.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Vingroup Innovation Foundation (VINIF), project code VINIF.2019.DA08. This research received no external funding.
Conflicts of Interest
The authors declare that there is no conflict of interest.
Appendix A
The centre of mass calculated for all the links of the robot
The angular velocities of the robot links
The potential energy of the robot
The Jacobian matrices and
References
- Tanev, T.K. Kinematics of a hybrid (parallel–serial) robot manipulator. Mech. Mach. Theory 2000, 35, 1183–1196. [Google Scholar] [CrossRef]
- Cha, S.H.; Lasky, T.A.; Velinsky, S.A. Kinematic redundancy resolution for serial-parallel manipulators via local optimization including joint constraints. Mech. Based Des. Struct. Mach. 2006, 34, 213–239. [Google Scholar] [CrossRef]
- Gallardo-Alvarado, J. Kinematics of a hybrid manipulator by means of screw theory. Multibody Syst. Dyn. 2005, 14, 345–366. [Google Scholar] [CrossRef]
- Hu, B. Formulation of unified Jacobian for serial-parallel manipulators. Robot. Comput. Integr. Manuf. 2014, 30, 460–467. [Google Scholar] [CrossRef]
- Gallardo-Alvarado, J. Mobility analysis and kinematics of the semi-general 2 (3-RPS) series-parallel manipulator. Robot. Comput. Integr. Manuf. 2013, 29, 463–472. [Google Scholar] [CrossRef]
- Hu, B.; Yu, J. Unified solving inverse dynamics of 6-DOF serial–parallel manipulators. Appl. Math. Model. 2015, 39, 4715–4732. [Google Scholar] [CrossRef]
- Ibrahim, O.; Khalil, W. Inverse and direct dynamic models of hybrid robots. Mech. Mach. Theory 2010, 45, 627–640. [Google Scholar] [CrossRef]
- Lu, Y.; Dai, Z. Dynamics model of redundant hybrid manipulators connected in series by three or more different parallel manipulators with linear active legs. Mech. Mach. Theory 2016, 103, 222–235. [Google Scholar] [CrossRef]
- Lu, Y.; Dai, Z.; Ye, N. Stiffness analysis of parallel manipulators with linear limbs by considering inertial wrench of moving links and constrained wrench. Robot. Comput. Integr. Manuf. 2017, 46, 58–67. [Google Scholar] [CrossRef]
- Yuan, H.; You, X.; Zhang, Y.; Zhang, W.; Xu, W. A Novel Calibration Algorithm for Cable-Driven Parallel Robots with Application to Rehabilitation. Appl. Sci. Theory 2019, 9, 2182. [Google Scholar] [CrossRef]
- Cheng, H.H. Real-time manipulation of a hybrid serial-and-parallel-driven redundant industrial manipulator. J. Dyn. Syst. Meas. Control 1994, 116, 687–701. [Google Scholar] [CrossRef]
- Harib, K.H.; Ullah, A.S.; Moustafa, K.A.F. Optimal design for improved hybrid kinematic machine tools structures. Procedia CIRP 2013, 12, 109–114. [Google Scholar] [CrossRef]
- Kanaan, D.; Wenger, P.; Chablat, D. Kinematic analysis of a serial–parallel machine tool: The VERNE machine. Mech. Mach. Theory 2009, 44, 487–498. [Google Scholar] [CrossRef]
- Xu, P.; Cheung, C.F.; Li, B.; Ho, L.T.; Zhang, J.F. Kinematics analysis of a hybrid manipulator for computer controlled ultra-precision freeform polishing. Robot. Comput. Integr. Manuf. 2017, 44, 44–56. [Google Scholar] [CrossRef]
- Zeng, Q.; Ehmann, K.F. Design of parallel hybrid-loop manipulators with kinematotropic property and deployability. Mech. Mach. Theory 2009, 71, 1–26. [Google Scholar] [CrossRef]
- Pisla, D.; Szilaghyi, A.; Vaida, C.; Plitea, N. Kinematics and workspace modeling of a new hybrid robot used in minimally invasive surgery. Robot. Comput. Integr. Manuf. 2013, 29, 463–474. [Google Scholar] [CrossRef]
- Tönshoff, H.K.; Grendel, H.; Kaak, R. Structure and characteristics of the hybrid manipulator Georg V. In Parallel Kinematic Machines; Springer: London, UK, 1999; pp. 365–376. [Google Scholar]
- Guo, W.; Li, R.; Cao, C.; Gao, Y. Kinematics, dynamics, and control system of a new 5-degree-of-freedom hybrid robot manipulator. Adv. Mech. Eng. 2016, 8, 1687814016680309. [Google Scholar] [CrossRef]
- Nasseri, M.A.; Eder, M.; Eberts, D.; Nair, S.; Maier, M.; Zapp, D.; Knoll, A. Kinematics and dynamics analysis of a hybrid parallel-serial micromanipulator designed for biomedical applications. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 293–299. [Google Scholar]
- Zeng, Q.; Fang, Y. Structural synthesis and analysis of serial–parallel hybrid mechanisms with spatial multi-loop kinematic chains. Mech. Mach. Theory Manuf. 2012, 4, 198–215. [Google Scholar] [CrossRef]
- Zeng, Q.; Fang, Y.; Ehmann, K.F. Design of a novel 4-DOF kinematotropic hybrid parallel manipulator. J. Mech. Des. 2011, 133, 121006. [Google Scholar] [CrossRef]
- Carbone, G.; Ceccarelli, M. A stiffness analysis for a hybrid parallel-serial manipulator. Robotica 2004, 22, 567–576. [Google Scholar] [CrossRef]
- Doan, Q.V.; Le, T.D.; Vo, A.T. Synchronization full-order terminal sliding mode control for an uncertain 3-DOF planar parallel robotic manipulator. Appl. Sci. Theory 2019, 9, 1756. [Google Scholar] [CrossRef]
- Acevedo, M.; Orvañanos-Guerrero, M.T.; Velázquez, R.; Arakelian, V. An Alternative Method for Shaking Force Balancing of the 3RRR PPM through Acceleration Control of the Center of Mass. Appl. Sci. 2020, 10, 1351. [Google Scholar] [CrossRef]
- Kecskemethy, A.; Krupp, T.; Hiller, M. Symbolic processing of multiloop mechanism dynamics using closed-form kinematics solutions. Multibody Syst. Dyn. 1997, 1, 23–45. [Google Scholar] [CrossRef]
- My, C.A.; Le, C.H.; Packianather, M.; Bohez, E. Novel robot arm design and implementation for hot forging press automation. Int. J. Prod. Res. 2018, 57, 4579–4593. [Google Scholar] [CrossRef]
- Yan, C.; Gao, F.; Zhang, Y. Kinematic Modeling of a Serial–Parallel Forging Manipulator with Application to Heavy-Duty Manipulations. Mech. Based Des. Struct. Mach. 2010, 38, 105–129. [Google Scholar] [CrossRef]
- Li, F.; Zhu, X.; Cao, J.; Yao, B. Kinematics Modeling and Workspace Analysis of a 5-DOF Hydraulic Manipulator. In Proceedings of the 5th International Conference on Control., Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 713–718. [Google Scholar]
- Bajpai, A.; Roth, B. Workspace and mobility of a closed-loop manipulator. Int. J. Robot. Res. 1986, 5, 131–142. [Google Scholar] [CrossRef]
- Chung, G.J.; Kim, D.H.; Park, C.H. Analysis and Design of Heavy Duty Handling Robot. In Proceedings of the IEEE Conference on Robotics, Automation and Mechatronics, San Francisco, CA, USA, 7–10 April 1986; pp. 774–778. [Google Scholar]
- Yang, C.; Wang, Y.; Yao, F. Driving performance of underwater long-arm hydraulic manipulator system for small autonomous underwater vehicle and its positioning accuracy. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417747104. [Google Scholar] [CrossRef]
- Kikuchi, H.; Niinomi, T.; Sato, M.; Matsumoto, Y.; Tokoro, Y. Heavy parts assembly by coordinative control of robot and balancing manipulator. IFAC Proc. Vol. 1984, 17, 2349–2354. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Mu, B.; Frenette, R. On modeling, identification, and control of a heavy-duty electrohydraulic harvester manipulator. IEEE/ASME Trans. Mechatron. 2003, 8, 178–187. [Google Scholar] [CrossRef]
- Klimchik, A.; Pashkevich, A. Serial vs. quasi-serial manipulators: Comparison analysis of elasto-static behaviors. Mech. Mach. Theory 2017, 107, 46–70. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).