Abstract
The velocity pulse contained in near-fault ground motions have a tremendous impact on dam safety. Previous studies have mainly focused on the response of dams under near-fault seismic records without considering the obliquely incident seismic waves. In this study, the structure–soil interaction (SSI) is taken into consideration, and the nonlinear behavior of a conventional concrete roller-compacted concrete (CC-RCC) gravity dam under near-fault pulse records and non-pulse records is investigated with consideration of the obliquely incident P waves. On the basis of the dam site conditions, three groups of near-fault pulse records are chosen, and three corresponding non-pulse records are fitted by their acceleration response spectra. Combining with the viscous-spring artificial boundary, the wave input method is proposed to transform the near-fault seismic records into the equivalent nodal forces at the boundary of the foundation. The concrete damaged plasticity model is used for the nonlinear analysis. The results show that the pulse ground motions are more destructive than the non-pulse motions. The nonlinear behavior of the dam varies with the incidence angle of P waves and generally reaches a maximum at 60° and 75°, the worst damage occurs at the interface between different materials of the dam, and the spatial variation of its damage is very obvious under near-fault seismic records with various incidence angles. Therefore, the effect of the angle of obliquely incident seismic waves and near-fault pulse effect should be considered comprehensively in the seismic analysis of dams.
1. Introduction
The meizoseismal area in southwest China is rich in water energy resources [1], and therefore the problem of selecting sites for high dams and large reservoirs is “difficult to avoid”. Moreover, some of the high dams that have been built, are under construction, or in the planning stage are located near the seismic fault zone [1], which is subject to complicated rules of near-fault ground motions. Near-fault earthquakes occur within 20 km of the fault and include displacement and velocity pulses, as well as permanent ground displacement [2,3,4], additionally, their characteristics are remarkably different from those of far-fault earthquakes. Several major earthquakes in the last twenty years, such as Northridge (1994), Kobe (1995), Chi-Chi (1999), and Iran (2003), and especially the Wenchuan earthquake in China (2008) and the earthquake in Haiti (2010) have confirmed the remarkable impact of velocity pulses contained in near-fault seismic records on building damage [5,6,7,8,9]. At present, based on the time-history method and the theory of the response spectrum, the latest “Code for seismic design of hydraulic structures of hydropower project” (2015) of China does not distinguish between the near-fault seismic records and far-fault seismic records. In addition, most of the current studies on near-fault ground motions were based on the uniform seismic excitation method and assumption that the wave was propagating along a vertical direction [10], because the vertical direction is the weakest and critical direction in dam structures. However, this assumption did not fully consider the elasticity of foundation and the structure–soil interaction. It is now generally accepted that the traditional uniform seismic motion input method would overestimate the response of the dam [11]. Moreover, many studies have confirmed that quite different responses in infrastructures can occur under the non-uniform motion caused by oblique incidence [12,13,14]. According to the current research status, it is necessary to further analyze the behavior of a dam under near-fault earthquakes. The influence of the incidence angle of the seismic waves on various dam bodies should also be taken seriously. RCC (roller-compacted concrete) has been widely used in engineering due to its structural and construction advantages [15,16], and the joint construction of RCC with other materials has become the future development trend [17,18]. However, material properties and deformation characteristics of CC (conventional concrete) and RCC are significantly different from each other, and high deformation gradients tend to occur at the interface under seismic excitation. In addition, currently, the dynamic behavior of combined dam structures subjected to obliquely incident seismic waves is rarely considered. Therefore, it is of great significance to study the dynamic response of the combined dam structures under the oblique incidence of near-fault ground motions.
Some scholars have done related work on the dynamic characteristics of dams to near-fault ground motions. Bayraktar et al. [19,20,21] focused on the dynamic response of different types of dams under near-fault ground motions and far-fault ground motions, and they indicated the dynamic analysis of structures under different near-fault earthquakes should be evaluated. Akkose and Seismik [22] took into account the rock interactions of a dam-water-sediment-foundation system and analyzed elastoplastic behavior of the dam under near-fault and far-fault seismic records. They concluded the near-fault earthquakes were more destructive than the far-fault earthquakes. Wang et al. [5,23] studied the plastic damage response of the dam-reservoir-foundation system of the Koyna dam under near-fault and far-fault earthquakes and pointed out the important effect of near-fault earthquakes on dam damage. Altunisik et al. [24] focused their research on the long-period velocity pulse contained in near-fault seismic records and found that, although the near-fault and far-fault records have the same PGA (peak ground acceleration), the larger stresses and displacements of the dam were attained under near-fault records. Moreover, according to the characteristics of near-fault earthquakes, many scholars have conducted correlation analysis. Yazdani and Alembagheri [25] proposed a seismic demand model of dams to estimate the vulnerability of the gravity dam subjected to the near-fault earthquakes. Yazdani et al. [26] compared the dynamic characteristics of a gravity dam under forward-directivity (FD) and normal near-fault seismic records, and the impacts of FD records on the seismic demand analysis of structures were discussed. Pang et al. [27] established a new reliability assessment method for the dam, and the random dynamic response of rockfill dam slopes under near-fault earthquakes was evaluated.
When studying the seismic dynamic characteristics of a dam, it was usually assumed that seismic wave propagated along a vertical direction, which was reasonable for far-field earthquakes, but the wave usually had the obliquely incident angle in near-field earthquakes. Many studies have shown that there are significant differences between near-field and far-field earthquakes [28,29,30]. In recent years, the dynamic response of dams under oblique incidence of near-field seismic waves has been widely concerned. Xu et al. [31] proposed an input method of oblique seismic waves for three-dimensional calculation and found the seismic oblique incidence may cause a significant increase in the amplitude amplification factors of displacement, velocity, and acceleration of the arch dam. Yuan et al. [32] took radiation damping of foundation and design seismic component into account and found obliquely incident SV waves and P waves had a greater influence on the area near the interface of dam and foundation than that of vertically incident seismic waves. Chen and Zhang [33] discussed the nonlinear behavior of a gravity dam under obliquely incident SV waves and P waves and pointed out the vertically incident seismic angle was not suitable for near-field earthquakes. Li et al. [34] analyzed the nonlinear behavior of a concrete gravity dam under obliquely incident SV waves and P waves. They found that the damage distribution of the dam was significantly different with the various incident angle.
The main significance of this research lies in the improvement of the original research ideas. Most studies on the dynamic response of dam under near-fault ground motions were based on the uniform seismic excitation method with the assumption of the wave propagating along a vertical direction. This study investigates the nonlinear dynamic behavior of the CC-RCC gravity dam under near-fault pulse and non-pulse seismic records, and also considers the effect of the seismic incident angles. Taking a CC-RCC gravity dam in southwest China as an example, a three-dimensional nonlinear numerical model of the gravity dam-foundation system is built. From the Pacific Earthquake Engineering Research Center website (PEER) [35], three as-recorded near-fault earthquake records with pulse effect are chosen on the basis of the target response spectrum which is determined by the site conditions. In addition, three corresponding non-pulse ground motions are fitted by the above pulse ground motions’ response spectra. Considering the P wave incidence of an earthquake, the above six seismic records are input through the equivalent load force calculation method which is based on the viscous-spring artificial boundaries. Adopting the concrete damage plasticity(CDP) model [5], the influence of pulse effect and multi-angle seismic incidence on the gravity dam are considered. In this research, we present the time-history curves of dam crest horizontal relative displacements and the maximum of relative displacements and we also analyze the damage distribution of the dam and the tensile damage of the interface structures. This paper provides a reference for future study on the nonlinear response of combined dam structures under oblique incident near-fault seismic records.
2. Characteristics and Selection of Near-Fault Ground Motions
2.1. Characteristics of Near-Fault Ground Motions
Currently, the area within 20 km from the fault rupture surface is regarded as a near-fault field in this study. Because of the directivity effects, fling step effects, and hanging wall/footwall effects contained in the near-fault earthquakes, near-fault seismic records and far-fault records have significantly different characteristics [36,37].
When the rupture is exactly on the fault toward the site, and the ruptured velocity is close to the S wave velocity, the directivity effects occur. Researchers classify the directivity effects as forward directivity effect, neutral directivity effect, and reverse directivity effect. Among them, the forward directivity effect is due to the accumulation of energy in front of the propagating rupture, which tends to aggravate the damage of the infrastructures, therefore, the directivity effect usually refers to the forward directivity effect. The seismic records with the directivity effect can be seen as a bidirectional velocity pulse at the beginning with obvious characteristics of long-period and short duration [36], as shown in Figure 1.
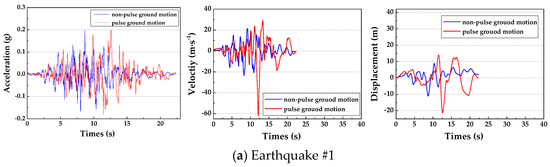
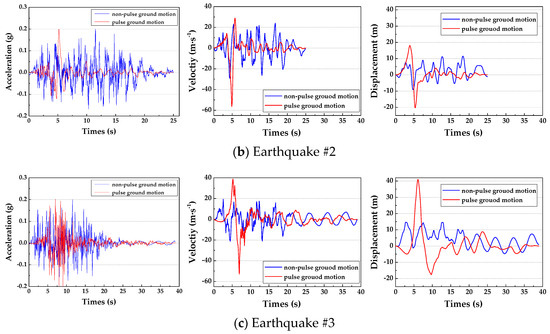
Figure 1.
The time-history curves of acceleration, velocity, and displacement of seismic records.
The relative movement of two plates of fault produces the static deformation field, and there is a permanent ground displacement [38] in the time history curves of displacement near the fault, which is called the fling step effect. This permanent ground displacement causes a single pulse of velocity, which is generally parallel to the fault. The hanging wall/footwall effect refers to the phenomenon that the site located in the hanging wall is closer to the fault than the site located at the same distance from the footwall, and therefore the ground motion amplitude of the hanging wall is larger.
This paper mainly studies the pulse ground motions caused by the directivity effect which aggravates the structural damage.
2.2. Selection of Near-Fault Pulse and Non-Pulse Ground Motions
A comparison with the non-pulse ground motions show that the pulse ground motions have the greater long-duration velocity and displacement pulse and peak ground acceleration (PGA). The ratio of PGV (peak ground velocity)/PGA is relatively large in the pulse ground motions, and 0.2 is generally used as the index to divide the pulse ground motions and non-pulse motions.
The pulse seismic records considered in this study were selected in accordance with the site response spectrum based on actual engineering. Taking into consideration a gravity dam that is in southwest China as the research object, the region of seismic intensity for design is VIII degrees, the designed seismic acceleration is 0.2 g, the site category is II class, and the design seismic grouping is the first group. The design response spectrum was generated according to the above seismic requirements and bedrock conditions of the region. The three near-fault pulse records with the best fitting accuracy were obtained by taking the above design response spectrum as the initial screening condition and taking into account the earthquake magnitude (above magnitude six), the distance to fault (within 20 km), and the condition of pulse type (PGV/PGA > 0.2). All earthquake records were obtained from the database of PEER [35], they are at Parachute Test Site station in the Superstition Hills earthquake, Newhall-W Pico Canyon Rd station in Northridge earthquake, and Parachute Test Site station in El-Centro earthquake.
The corresponding non-pulse ground motions were synthesized according to the acceleration response spectra of the pulse records by SeismoArtif software, and the fitting situation is shown in Figure 2. The red curves show the pulse ground motions, and blue curves show the non-pulse motions.
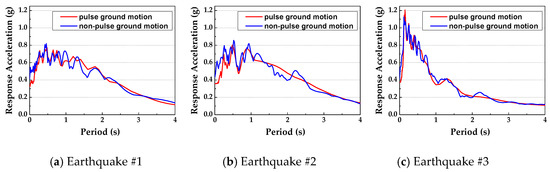
Figure 2.
Acceleration response spectra for selected near-fault seismic motions.
In addition, the peak accelerations of six seismic records were uniformly adjusted to 0.2 g in order to avoid being affected by earthquake amplitude, and Table 1 shows the properties of selected seismic records. Figure 1 shows the time-history curves of acceleration, velocity, and displacement of seismic records. A comparison with the non-pulse seismic motions show that the pulse seismic motions have an obvious long period pulse at the beginning stage and have the larger PGV and PGD (peak ground displacement).

Table 1.
Properties of the near-fault pulse and non-pulse seismic records.
3. The Input Method of the Obliquely Incident P Wave
3.1. The Viscous-Spring Artificial Boundary
In recent years, the structure–soil interaction (SSI) has gained extensive attention, and it can only be solved by numerical methods due to its complex nature [12]. However, only part of the near-domain foundation is usually taken in modeling because of the limitation of calculation amount. When the scattering waves propagate from the selected near-field region into the infinite medium, global or local artificial boundaries are established to absorb the energy of them, which can simulate the radiation damping of the continuum. Recently, many artificial boundary conditions have been proposed [39,40,41], among them, the viscous-spring artificial boundary has attracted more attention [42,43,44] due to its good stability and high accuracy, which takes into account the elastic resilience of the medium and overcomes the low-frequency instability of the viscous boundary. As shown in Figure 3, the essence of the viscous-spring artificial boundary is a parallel spring-dashpot system with continuous distribution applied on the boundary node, the coefficient of the spring and the coefficient of damping can be expressed as follows [13]:
where KT and KN represent tangent spring coefficient and normal spring coefficient, G is the shear modulus of the foundation, λ is the lame constant, r is the distance from the scattering wave source to the boundary, Al represents the area of all the elements containing the node l. CT and CN are tangential damping coefficient and normal damping coefficient, ρ is the medium density, cs is the S wave velocity, and cp is the P wave velocity. A is the coefficient of 0.8, and B is the coefficient of 1.1.
Figure 3.
The input of obliquely incident P waves and the model of the viscous-spring artificial boundary.
3.2. P Waves Input Method
The complex wave field under seismic excitation can be decomposed into the incident wave, reflected wave, and scattered wave, which the first two is called free wave field. The artificial boundary can absorb scattered wave energy to make sure that the input is the free wave field. Liu et al. [45] proposed a wave input method applicable to the viscous-spring artificial boundary and converted seismic motions into equivalent loads. Then, they applied the loads on the nodes of the boundary, the equivalent nodal loads can be expressed as:
where is the equivalent nodal load, and , , are the acceleration, velocity, and displacement of input motions, M is the mass of the soil-structures finite element model, K and C are the spring and damping coefficients of the spring-dashpot system in Section 3.1.
On the basis of Equation (3), this method has been extended to obliquely incident P waves. According to the research results of previous scholars [12,13,46,47], the principles of the wave input method are integrated and redefined according to the previous formulas. The obliquely incident P waves shear and squeeze when passing through the boundary, and therefore they not only generate reflected P waves but also reflected SV waves, assuming that incident P waves propagate obliquely from the bottom left corner, i.e. point P (x0, y0, z0) of the model, as shown in Figure 3.
The angle between the incident P waves and the y-axis positive direction is θ1, the angle between the plane determined by the incident waves and the reflected waves and the xoy plane is α (in order to control a single variable, assuming α is 0° in this research), and the angle between the reflected SV waves and the y-axis positive direction is θ2. Then, the time-histories of displacement of any point in three directions under the action of free wave field can be expressed as:
where , , represent the displacement time-history function caused by incident P waves, reflected P waves, and reflected SV waves, respectively. A1, A2, and B2 correspond to the amplitude of the potential function of them. Assuming the medium is homogeneous, isotropic, and elastic, and considering the wave theory and stress state of element, the equivalent nodal load in the three directions of the left boundary can be obtained based on Equation (3):
where , , represent the velocity time histories of any point in three directions, which can be derived by the displacement formulas. The expressions of each normal stress and shearing stress are shown in Equation (10).
where μ represents the Poisson’s ratio of the foundation.
The equivalent nodal load calculation method on the boundaries of the right, the bottom, the front, and the back are similar to that on the left boundary, and only the directivity of the stress should be paid attention to in the calculation.
3.3. Numerical Verification on the Input Method
The element software ABAQUS can implement the input method of seismic waves by modifying the INP file. The dynamic behavior of three-dimensional uniform elastic half-space under obliquely incident P waves was discussed to verify the accuracy rate of the input method in this research. The density of the semi-infinite space medium is 2630 kg /m3, the elastic modulus is 32.5 GPa, and Poisson’s ratio is 0.22. A cube finite region of 2000 m × 2000 m × 2000 m was cut out, and the cube was discretized into the solid elements with the side length of 50 m, which meet the requirements of finite element accuracy, and Figure 4 shows the model of the cube. At the side face and bottom face of the cube, the artificial boundary was used. Figure 5 shows the input P wave displacement time-history curve, and the total time is 5.0 s with an interval of 0.005 s.
Figure 4.
Finite element model of the cube.
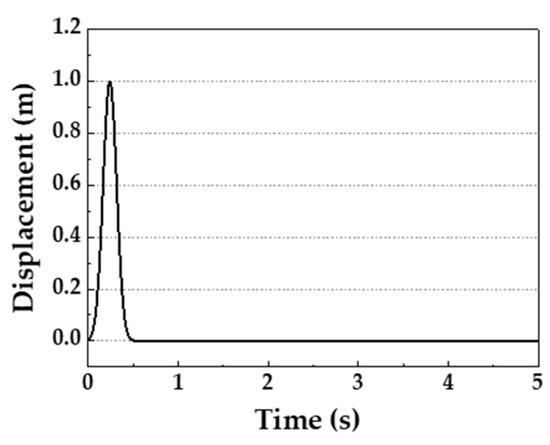
Figure 5.
The input P wave displacement time-history curve.
Figure 6 shows the vertical displacement time history of point O (1000,1000,2000) when the incident angles of the P wave are 30° and 45°, respectively. The exact theoretical solution based on wave theory is also given in the figure. As shown in Figure 6, the numerical solution almost coincides with the theoretical solution [31], which shows that the input method has the simulation precision.
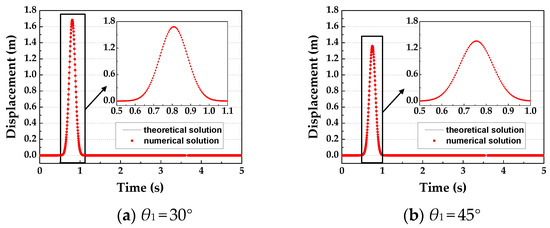
Figure 6.
Time history of vertical displacement at point O.
4. CC-RCC Gravity Dam-Foundation Numerical Model
4.1. 3D Dam-Foundation Finite Element Model
In this research, the dam is a CC-RCC gravity dam built on the lower Jinsha River between Shuifu city and Yibin city in Southwest China. The dam is 162 m high, its crest length is 909.26 m, and the normal depth of the reservoir is 177 m. The dam site is located at the exit of the canyon and the geological conditions of the foundation are complex, in which the main structural surfaces are flexural core fracture zones, compression zones, soft interlayers, small faults, and joints. Therefore, the region is prone to near-fault earthquakes, and the incident angle of seismic waves is difficult to determine. The biggest earthquake intensity of this dam site was VI degrees since records began, and this region also experienced many earthquakes of V degrees.
Taking a typical flood discharge dam section as an example, the three-dimensional gravity dam-foundation system finite element model and the partition diagram of dam body material are shown in Figure 7. This discharge dam section is 144 m in height and 196 m in width, and the foundation extends almost twice of the dam height in upstream, downstream, and downward. C3D8R units in ABAQUS were used to divide the whole model into 27,630 elements and 12,693 nodes. For the static step, the node displacements on the truncated model boundary were set to 0 in the normal direction; for the dynamic step, the spring/dashpot elements were used to simulate viscous-spring artificial boundary.
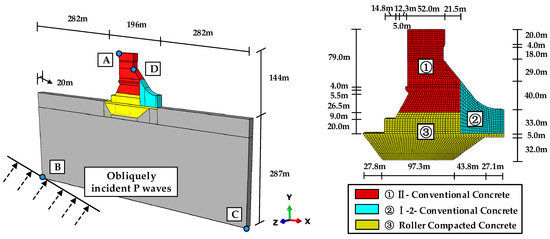
Figure 7.
Three-dimensional (3D) gravity dam-foundation system finite element model and the partition diagram of dam body material.
4.2. Material Parameters and Loading
To reflect the vibration characteristics of the dam more reasonably, the concrete damaged plasticity damage model (CDP) was adopted for three kinds of materials of the dam. Considering that the concrete has strong compressive strength, only the tensile damage of the dam was analyzed. Taking the II-conventional concrete as an example, the strain-stress curve and tensile damage-strain curve of it are shown in Figure 8. The linear elastic model was selected as the model for the foundation. The static properties of materials were confirmed by the mechanical test of materials that are used in actual engineering. The dynamic elastic modulus of concrete and foundation rocks increased by 30% over the static elastic modulus, and the Poisson’s ratio and density of the materials remained the same [48,49]. The dynamic material parameters of the dam-foundation system are listed in Table 2. Moreover, the modified Rayleigh damping was adopted in the seismic researches [50,51].
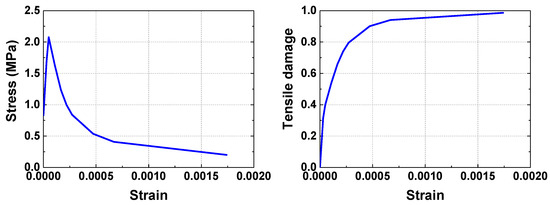
Figure 8.
The CDP model parameters of the II-conventional concrete.

Table 2.
Dynamics material parameters for the dam-foundation system.
The calculated water level is the normal reservoir level of the dam. The dam was first statically analyzed under its self-weight and hydrostatic pressure, and the system was then dynamically loaded under the selected near-fault pulse and non-pulse seismic records. The dynamic load adopted obliquely incident P wave. Assuming the wave obliquely propagates from the bottom left foundation corner, with incidence angles of 0°(vertical), 15°, 30°, 45°, 60°, 75°, and 90°, respectively. There are 42 (3 × 2 × 7: 3 earthquakes, pulse and non-pulse ground motions, 7 angles) different conditions in total.
5. Results and Discussion
In this research, the nonlinear dynamic behavior of the dam body under three groups of pulse and non-pulse seismic records with consideration of the seismic incident angle was investigated. The time-history curves of dam crest horizontal relative displacements and the maximum relative displacements with various incident angles are presented. Damage distribution of the dam and the tensile damage of the interface structures are also analyzed and compared with each other.
5.1. Horizontal Relative Displacements of the Dam Crest
Because the dam monolith is unsymmetric and the foundation is elastic, it is necessary to evaluate the relative displacements separately in opposite directions. The horizontal relative displacements of the dam crest (point A) to the bottom left corner (point B) and the bottom right corner (point C) of the foundation are analyzed, respectively, and Figure 9 and Figure 10 show the time-histories of them. Here, limited to space, only the displacements of the dam crest under an incident angle of 75° are shown. The red curves show the pulse seismic records, and blue curves show the non-pulse records.
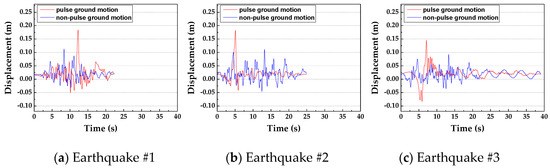
Figure 9.
The horizontal displacement of point A with respect to point B (under the input angle of 75°).
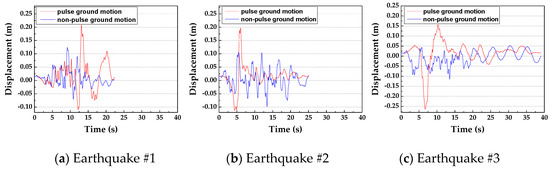
Figure 10.
The horizontal displacement of point A with respect to point C (under the input angle of 75°).
The horizontal relative displacements of the dam crest vary with the input seismic waves displacement time histories. Although the selected near-fault pulse seismic records and non-pulse records have the same PGA, the pulse records are more destructive to the dam than the non-pulse records. When the input angle is 75°, the maximum relative displacements of point A with respect to point B under three pulse ground motions are 0.184 m, 0.183 m, 0.146 m, respectively. The maximum relative displacements of point A with respect to point B under three non-pulse ground motions are 0.113 m, 0.110 m, 0.093 m, respectively. The average maximum relative displacement of point A and point B under pulse seismic motions is 1.62 times as compared with that under non-pulse seismic motions, and the average maximum relative displacement of point A and point C under pulse seismic motions is 1.71 times as compared with that under non-pulse seismic motions.
It is worth noting that the horizontal relative displacements between the dam crest and the different parts on the foundation are different. It can be seen that the previous analysis method which assumes the foundation to be rigid cannot truly reflect the vibration performance of the dam body.
The maximum absolute values of the displacement time-history curve under various input angles are extracted and compared with each other, as shown in Figure 11 and Figure 12. The dynamic response of the dam under pulse seismic motions is remarkably higher than that under non-pulse seismic motions in all cases, especially when the incidence angle is large.
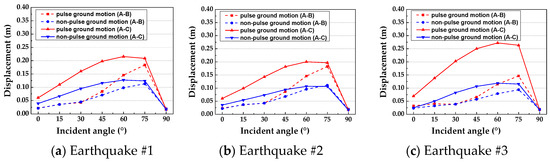
Figure 11.
The maximum absolute value of the relative horizontal displacements (under different input angles).
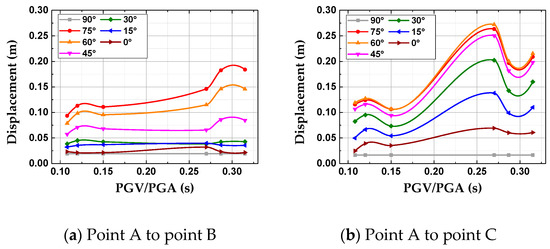
Figure 12.
The maximum absolute value of the relative horizontal displacements (under different PGV/PGA ratio).
Figure 11 shows that with an increase of the P wave incident angle, the relative displacements first increase and then decrease. The maximum relative displacement between point A and point B under the three near-fault pulse seismic records reaches the maximum value with the input angle of 75°, and they are 7.48, 6.84, 3.54 times that with the angle of 0°, respectively. The maximum relative displacement between point A and point B under the three non-pulse earthquake records also reaches the maximum value with the input angle of 75°, and they are 4.31, 4.14, 3.02 times higher than that at the angle of 0°, respectively. The maximum relative displacement between point A and point C under the three near-fault pulse earthquake records reaches the maximum value with the input angle of 60°, and they are 2.44, 2.27, 2.81 times higher than that at the angle of 0°, respectively. The maximum relative displacement between point A and point C under the three non-pulse earthquake records also reaches the maximum value with the input angle of 60°, and they are 2.24, 2.02, 3.82 times higher than that at the angle of 0°, respectively. That indicates the traditional assumption of the wave propagating along a vertical direction cannot reasonably reflect the real situation.
Figure 12 shows the maximum absolute value of the relative horizontal displacements of point A with respect to points B and C, respectively. The relative horizontal displacement increases with the ratio of PGV/PGA. (Although the PGV/PGA ratio of Earthquake #3 is not the largest, it has the longest duration, so the damage of the dam is serious [52] and the curves have a slight drop at the end in Figure 12.) which indicates that the velocity pulse has a prominent impact on the dynamic displacement of the dam.
5.2. Damage Distribution of Dam
The damage profiles of the dam under three groups of near-fault pulse seismic motions and non-pulse seismic motions, with consideration of the incident angle of seismic waves, are shown in Figure 13. When the P wave incident angles are 0° and 90°, the dynamic response of the dam is very small, which is not shown in this paper. The tensile damage factors of the dam body (shown in the software according to the calculated stress of the finite element) are represented in the top left corner of the figures.
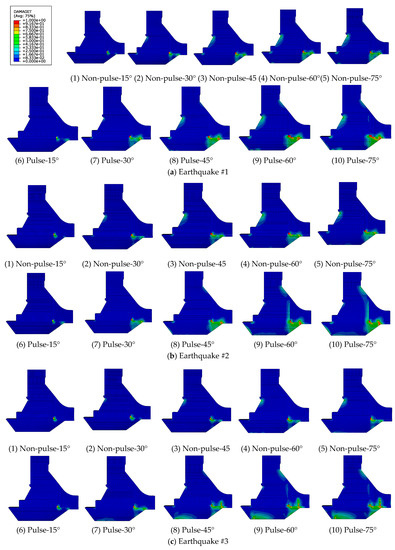
Figure 13.
The seismic plastic-damage response of the gravity dam under pulse and non-pulse ground motions.
As shown in Figure 13, the damage is concentrated in the part at the junction of three different materials of the dam body, as well as the longitudinal seam and the inflection points of the dam. With an increase of the incident angle of the P wave, the damage of the dam tends to increase first, and then decrease. The worst damage of the dam occurs when the incident angles of the P wave are 60° and 75°, which is also synchronous with the law of displacement of the dam crest. In addition, near-fault pulse seismic motions are more destructive to the dam than non-pulse seismic motions when the input angle of the P wave is the same. It is noteworthy that in some cases, the dam damage subjected to non-pulse seismic motions with a small angle of P waves is more severe than that subjected to pulse seismic motions with a large angle of P waves, which shows that seismic incidence angle is also a significant factor besides pulse effect.
5.3. Damage Analysis of Interface Structures
As can be seen from Figure 13, the worst damage of the dam body occurs at the interface between II-CC and RCC, and the inflection point of the dam. Under the action of complex dynamic load, the interface of different materials is a weak link, and the spatial variation of its damage is very obvious, as shown in Figure 14. The solid curves represent the pulse ground motions, and dash curves represent non-pulse ground motions. The damage here is the damage of the dam at the end of the near-fault earthquakes.
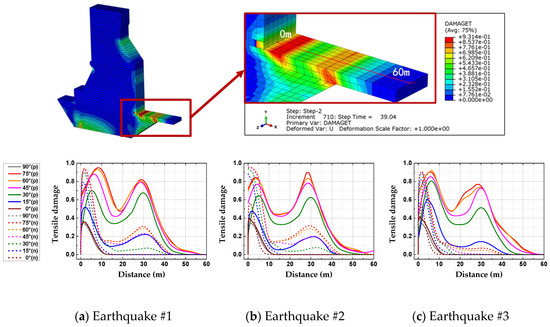
Figure 14.
The spatial variation of dam body tensile damage.
Under the pulse ground motions, the greatest damage occurs in the part (4 to 7 m range) close to the junction of the three materials of the dam, and the maximum is about 0.9. The second peak point of damage curves appears right above an inflection point which is at the lower-right part of the dam, about 30 m from the junction point. Under the non-pulse records, the maximum damage occurs at the interface endpoint, in which the maximum is about 0.9. Although the second peak also appears right above an inflection point which is at the lower-right part of the dam, it is less than 0.3 and obviously smaller than that under pulse records. The differences between the damages caused by the two types of seismic motions are not only the numerical magnitude but also the spatial distribution. In addition, it can be found from the figures that the difference between the damage of the dam under pulse seismic motion records and that under non-pulse seismic motion records goes up with the incidence angle. It can also be inferred that with an increase of earthquake magnitude, the impact of pulse ground motions to the dam increases.
Figure 15 shows the tensile damage on inflection point D under the input angle of 45°, 60°, 75°, respectively. The red curves show the pulse ground motions, and the blue curves show the non-pulse motions. When the P wave incident angle increases, the damage of the inflection point is more and more serious. In addition, the maximum of tensile damage under pulse ground motions with the incident angles of 45°, 60°, and 75° are 2.96, 2.22, and 2.26 times higher than that under non-pulse ground motions with the incident angles of 45°, 60°, and 75°, respectively.
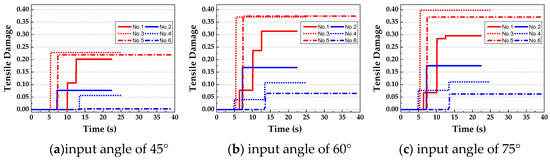
Figure 15.
Tensile damage on inflection point D of the dam.
5.4. Summary of Results
On the basis of the dynamic behavior of a dam under near-fault ground motions, it can be seen that the near-fault pulse ground motions are more destructive than the non-pulse ground motions. When the incidence angle is 75°, the average maximum relative displacement of dam crest point with respect to bottom left (bottom right) corner under pulse records is 1.62 (1.71) times higher than that under non-pulse records. The response of the dam increase with the ratio of PGV/PGA.
With an increase of the P wave incident angle, the displacement of the dam crest and the damage of the dam first increase, and then decrease; when the incident angle of P wave is 60° or 75°, the dynamic response of the dam reaches the maximum. The maximum relative displacement of dam crest point with respect to bottom left (right) corner under the three near-fault non-pulse ground motion records reaches the maximum value at 75° (60°), and they are 4.31, 4.14, 3.02 (2.24, 2.02, 3.82) times higher than that with the vertical incidence of seismic waves, respectively.
In addition, the damage of the gravity dam under non-pulse records with a small incident angle of the P wave is more severe than that under pulse records with a large incident angle of the P wave. For example, in three earthquakes, the damage of the dam under non-pulse ground motions with the incident angle of 75° is more serious than that under pulse ground motions with the incident angle of 0°.
Moreover, the worst damage of the combined dam structure occurs at the interface structures, and the spatial variation of the damage on the interface of different materials varies with different types of near-fault earthquakes and seismic incident angles. The maximum damage occurs at different part of the interface under different earthquakes.
6. Conclusions
In this research, the nonlinear dynamic response of a CC-RCC combined dam structure under near-fault pulse seismic records and non-pulse records with consideration of the incidence angle of seismic P waves is investigated. The selected seismic records have the same PGA of 0.2 g. Different from the uniform excitation input method, this study takes the dam-foundation system into account. Combining with the viscous-spring artificial boundary, the wave input method is used. The relative horizontal displacements between the dam crest and foundation, and damage of the gravity dam under P wave incidence angles of 0° (vertical), 15°, 30°, 45°, 60°, 75°, and 90° are analyzed. Conclusions are as follows.
(1) When the seismic incident angle is the same, the destruction of the dam to the near-fault pulse ground motions is significantly larger than that to the non-pulse motions. In addition, the relative horizontal displacement of the dam crest increases with the ratio of PGV/PGA in the entire trend.
(2) When the seismic incident angle increases, the nonlinear behavior of the dam increases first, and then decreases, and generally reaches the maximum when the incidence angle is 60° and 75°.
(3) In some cases, the damage of the gravity dam subjected to non-pulse records with considering the small incident angle of the P wave is more severe than that subjected to pulse records with considering the large incident angle of the P wave.
(4) The worst damage of the dam body occurs at the interface between II-CC and RCC, and the inflection point of the dam. The interface of different materials is a weak link, and the spatial variation of its damage is very different subjected to obliquely incident seismic records.
The response of combined dam structure under near-fault ground motions is complicated. Due to the limitation of space, this paper only discusses the oblique incidence of the P wave. In practical engineering, SV wave and SH wave should be considered comprehensively.
Author Contributions
J.Z. did the finite element simulation and wrote the paper; M.Z. provided the idea and edited the manuscript; M.L. gave professional seismic guidance of hydraulic structures; Q.M. gave professional guidance on finite element simulation; B.S. collected the engineering data in this paper; L.S. gave professional seismic guidance of hydraulic structures. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (grant no. 51879185), the Tianjin Natural Science Foundation for Distinguished Young Scientists of China (grant no. 17JCJQJC44000) and the Fund of National Dam Safety Research Center (grant no. CX2019B02).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, J.G. Practical Manual for Hydroelectric Power; China Electric Power Press: Beijing, China, 2014. [Google Scholar]
- Yang, D.; Wang, W. Nonlocal period parameters of frequency content characterization for near-fault ground motions. Earthq. Eng. Struct. Dyn. 2012, 41, 1793–1811. [Google Scholar] [CrossRef]
- Shahbazi, S.; Karami, A.; Hu, J.W.; Mansouri, I. Seismic response of steel moment frames (SMFs) considering simultaneous excitations of vertical and horizontal components, including fling-step ground motions. Appl. Sci. 2019, 9, 2079. [Google Scholar] [CrossRef]
- Xia, C.; Liu, C. Identification and representation of multi-pulse near-fault strong ground motion using adaptive wavelet transform. Appl. Sci. 2019, 9, 259. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, G. Effects of near-fault and far-fault ground motions on nonlinear dynamic response and seismic damage of concrete gravity dams. Soil Dyn. Earthq. Eng. 2013, 53, 217–229. [Google Scholar] [CrossRef]
- Wang, W.L.; Wang, T.T.; Su, J.J.; Lin, C.H.; Seng, C.R.; Huang, T.H. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi. Earthq. Tunn. Undergr. Sp. Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Yashiro, K.; Kojima, Y.; Shimizu, M. Historical earthquake damage to tunnels in Japan and case studies of railway tunnels in the 2004 Niigataken-Chuetsu earthquake. Q. Rep. RTRI 2007, 48, 136–141. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Gao, B.; Jiang, Y.J.; Yuan, S. Investigation and assessment on mountain tunnels and geotechnical damage after the Wenchuan earthquake. Sci. China Ser. E Technol. Sci. 2009, 52, 546–558. [Google Scholar] [CrossRef]
- Assimaki, D.; Jeong, S. Ground-Motion observations at Hotel Montana during the M 7.0 2010 Haiti earthquake: Topography or soil amplification? Bull. Seismol. Soc. Am. 2013, 103, 2577–2590. [Google Scholar] [CrossRef]
- Zhang, Z.; Bilotta, E.; Yuan, Y.; Yu, H.; Zhao, H. Experimental assessment of the effect of vertical earthquake motion on underground metro station. Appl. Sci. 2019, 9, 5182. [Google Scholar] [CrossRef]
- Xu, B.; Zhou, Y.; Zhou, C.; Zou, D. Dynamic responses of concrete-faced rockfill dam due to different seismic motion input methods. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718804687. [Google Scholar] [CrossRef]
- Wang, D.G.; Shi, P.X.; Zhao, C.G. Two-Dimensional in-plane seismic response of long-span bridges under oblique P-wave incidence. Bull. Earthq. Eng. 2019, 17, 1–27. [Google Scholar] [CrossRef]
- Huang, J.Q.; Du, X.L.; Jin, L.; Zhao, M. Impact of incident angles of P waves on the dynamic responses of long lined tunnels. Earthq. Eng. Struct. Dyn. 2016, 45, 2435–2454. [Google Scholar] [CrossRef]
- Huang, J.; Zhao, M.; Du, X. Non-Linear seismic responses of tunnels within normal fault ground under obliquely incident P waves. Tunn. Undergr. Sp. Technol. 2017, 61, 26–39. [Google Scholar] [CrossRef]
- Mridha, S.; Maity, D. Experimental investigation on nonlinear dynamic response of concrete gravity dam-reservoir system. Eng. Struct. 2014, 80, 289–297. [Google Scholar] [CrossRef]
- Gharibdoust, A.; Aldemir, A.; Binici, B. Seismic behaviour of roller compacted concrete dams under different base treatments. Struct. Infrastruct. Eng. 2019, 1–12. [Google Scholar] [CrossRef]
- Li, M.C.; Zhang, M.X.; Hu, Y.; Zhang, J.R. Mechanical properties investigation of high-fluidity impermeable and anti-cracking concrete in high roller-compacted concrete dams. Constr. Build. Mater. 2017, 156, 861–870. [Google Scholar] [CrossRef]
- Zhang, M.X.; Li, M.C.; Shen, Y.; Ren, Q.B.; Zhang, J.R. Multiple mechanical properties prediction of hydraulic concrete in the form of combined damming by experimental data mining. Constr. Build. Mater. 2019, 207, 661–671. [Google Scholar] [CrossRef]
- Bayraktar, A.; Altunısık, A.C.; Sevim, B.; Kartal, M.E.; Turker, T. Near-Fault ground motion effects on the nonlinear response of dam-reservoir-foundation systems. Struct. Eng. Mech. 2008, 28, 411–442. [Google Scholar] [CrossRef]
- Bayraktar, A.; Altunisik, A.C.; Sevim, B.; Kartal, M.E.; Türker, T.; Bilici, Y. Comparison of near-and far-fault ground motion effect on the nonlinear response of dam-reservoir-foundation systems. Nonlinear Dyn. 2009, 58, 655–673. [Google Scholar] [CrossRef]
- Bayraktar, A.; Turker, T.; Akkose, M.; Ates, S. The effect of reservoir length on seismic performance of gravity dams to near-and far-fault ground motions. Nat. Hazards 2010, 52, 257–275. [Google Scholar] [CrossRef]
- Akkose, M.; Simsek, E. Non-Linear seismic response of concrete gravity dams to near-fault ground motions including dam-water-sediment-foundation interaction. Appl. Math. Model. 2010, 34, 3685–3700. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, S.; Wang, C.; Yu, M. Seismic performance evaluation of dam-reservoir foundation systems to near-fault ground motions. Nat. Hazards 2014, 72, 651–674. [Google Scholar] [CrossRef]
- Altunisik, A.C.; Sesli, H.; Hüsem, M.; Akköse, M. Performance evaluation of gravity dams subjected to near- and far-fault ground motion using Euler approaches. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 297–325. [Google Scholar] [CrossRef]
- Yazdani, Y.; Alembagheri, M. Seismic vulnerability of gravity dams in near-fault areas. Soil Dyn. Earthq. Eng. 2017, 102, 15–24. [Google Scholar] [CrossRef]
- Yazdani, Y.; Alembagheri, M. Nonlinear seismic response of a gravity dam under near-fault ground motions and equivalent pulses. Soil Dyn. Earthq. Eng. 2017, 92, 621–632. [Google Scholar]
- Pang, R.; Xu, B.; Kong, X.; Zhou, Y.; Zou, D. Seismic performance evaluation of high CFRD slopes subjected to near-fault ground motions based on generalized probability density evolution method. Eng. Geol. 2018, 246, 391–401. [Google Scholar] [CrossRef]
- Khan, B.L.; Azeem, M.; Usman, M.; Farooq, S.H.; Hanif, A.; Fawad, M. Effect of near and far Field Earthquakes on performance of various base isolation systems. Procedia Struct. Integr. 2019, 18, 108–118. [Google Scholar] [CrossRef]
- Gorai, S.; Maity, D. Seismic response of concrete gravity dams under near field and far field ground motions. Eng. Struct. 2019, 196, 109292. [Google Scholar] [CrossRef]
- Schauer, M.; Rodriguez, G.R. A coupled FEM-SBFEM approach for soil-structure-interaction analysis using non-matching meshes at the near-field far-field interface. Soil Dyn. Earthq. Eng. 2019, 121, 466–479. [Google Scholar] [CrossRef]
- Xu, H.; Du, X.; Zhao, M.; Wang, J. Effect of oblique incidence of seismic waves on seismic responses of high arch dam. J. Hydroelectr. Eng. 2011, 30, 159–165. (In Chinese) [Google Scholar]
- Yuan, J.W.; Du, C.; Liu, Z. Time-Domain seismic response for gravity dam to obliquely incident and seismic waves. J. Vib. Shock 2011, 30, 120–126. [Google Scholar]
- Chen, L.; Zhang, L. A seismic wave oblique incidence method and the application in gravity DAM seismic research. J. Earthq. Tsunami 2014, 8, 1450011. [Google Scholar] [CrossRef]
- Li, M.C.; Zhang, J.W.; Zhang, M.X.; Min, Q.L.; Shi, B.W. Plastic damage response analysis of concrete gravity dam due to obliquely incident seismic waves. J. Hydraul. Eng. 2019, 50, 1326–1338, 1349. (In Chinese) [Google Scholar]
- Pacific Earthquake Engineering Research Center (PEER). PEER Strong Motion Database. Available online: http://ngawest2.berkeley.edu/search.html (accessed on 28 January 2020).
- Somerville, P.G.; Smith, N.F.; Graves, R.W.; Abrahamson, N.A. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity. Seismol. Res. Lett. 1997, 68, 199–222. [Google Scholar] [CrossRef]
- Wang, G.Q.; Zhou, X.Y.; Zhang, P.Z.; Igel, H. Characteristics of amplitude and duration for near fault strong ground motion from the 1999 Chi-Chi, Taiwan, earthquake. Soil Dyn. Earthq. Eng. 2002, 22, 73–96. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Xiang, C.L.; Chen, Y.L.; Cheng, Q.G.; Xiao, L.; Yu, P.C.; Chang, Z.W. Permanent displacement models of earthquake-induced landslides considering near-fault pulse-like ground motions. J. Mt. Sci. 2019, 16, 1244–1257. [Google Scholar] [CrossRef]
- Kausel, E. Local transmitting boundaries. ASCE J. Eng. Mech. 1988, 114, 1011–1027. [Google Scholar] [CrossRef]
- Wolf, J.P.; Song, C. Finite Element Modelling of Unbounded Media; John Wiley & Sons: Chichester, UK, 1996. [Google Scholar]
- Tsynkov, S.V. Numerical solution of problems on unbounded domains. A review. Appl. Numer. Math. 1998, 27, 465–532. [Google Scholar] [CrossRef]
- Deeks, A.J.; Randolph, M.F. Axisymmetric time-domain transmitting boundaries. ASCE J. Eng. Mech. 1994, 120, 25–42. [Google Scholar] [CrossRef]
- Liu, J.B.; Du, Y.X.; Du, X.L.; Wang, Z.Y.; Wu, J. 3D viscous-spring artificial boundary in time domain. Earthq. Eng. Eng. Vib. 2006, 5, 93–102. [Google Scholar] [CrossRef]
- Du, X.L.; Zhao, M. A local time-domain transmitting boundary for simulating cylindrical elastic wave propagation in infinite media. Soil Dyn. Earthq. Eng. 2010, 30, 937–946. [Google Scholar] [CrossRef]
- Liu, J.B.; Tan, H.; Bao, X.; Wang, D.Y.; Li, S.T. Seismic wave input method for three-dimensional soil-structure dynamic interaction analysis based on the substructure of artificial boundaries. Earthq. Eng. Eng. Vib. 2019, 18, 747–758. [Google Scholar] [CrossRef]
- Zarzalejos, J.M.; Aznárez, J.J.; Padrón, L.A.; Maeso, O. Influences of type of wave and angle of incidence on seismic bending moments in pile foundations. Earthq. Eng. Struct. Dyn. 2014, 43, 41–59. [Google Scholar] [CrossRef]
- Zhou, C.G. Research on the Mechanism of Seismic Wave Input about High Rockfill Dam. Master’s Thesis, Dalian University of Technology, Dalian, China, 2009. [Google Scholar]
- Wang, G.H.; Wang, Y.X.; Lu, W.B.; Yu, M.; Wang, C. Deterministic 3D seismic damage analysis of Guandi concrete gravity dam: A case study. Eng. Struct. 2017, 148, 263–276. [Google Scholar] [CrossRef]
- Wang, R.K.; Chen, L.; Zhang, C. Seismic design of Xiluodu ultra-high arch dam. Water Sci. Eng. 2018, 11, 288–301. [Google Scholar] [CrossRef]
- Hall, J.F. Problems encountered from the use (or misuse) of Rayleigh damping. Earthq. Eng. Struct. Dyn. 2006, 35, 525–545. [Google Scholar] [CrossRef]
- Alembagheri, M.; Ghaemian, M. Damage assessment of a concrete arch dam through nonlinear incremental dynamic analysis. Soil Dyn. Earthq. Eng. 2013, 44, 127–137. [Google Scholar] [CrossRef]
- Zhang, S.R.; Wang, G.H.; Pang, B.H.; Du, C.B. The effects of strong motion duration on the dynamic response and accumulated damage of concrete gravity dam. Soil Dyn. Earthq. Eng. 2013, 45, 112–124. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).