On the Cattaneo–Christov Heat Flux Model and OHAM Analysis for Three Different Types of Nanofluids
Abstract
1. Introduction
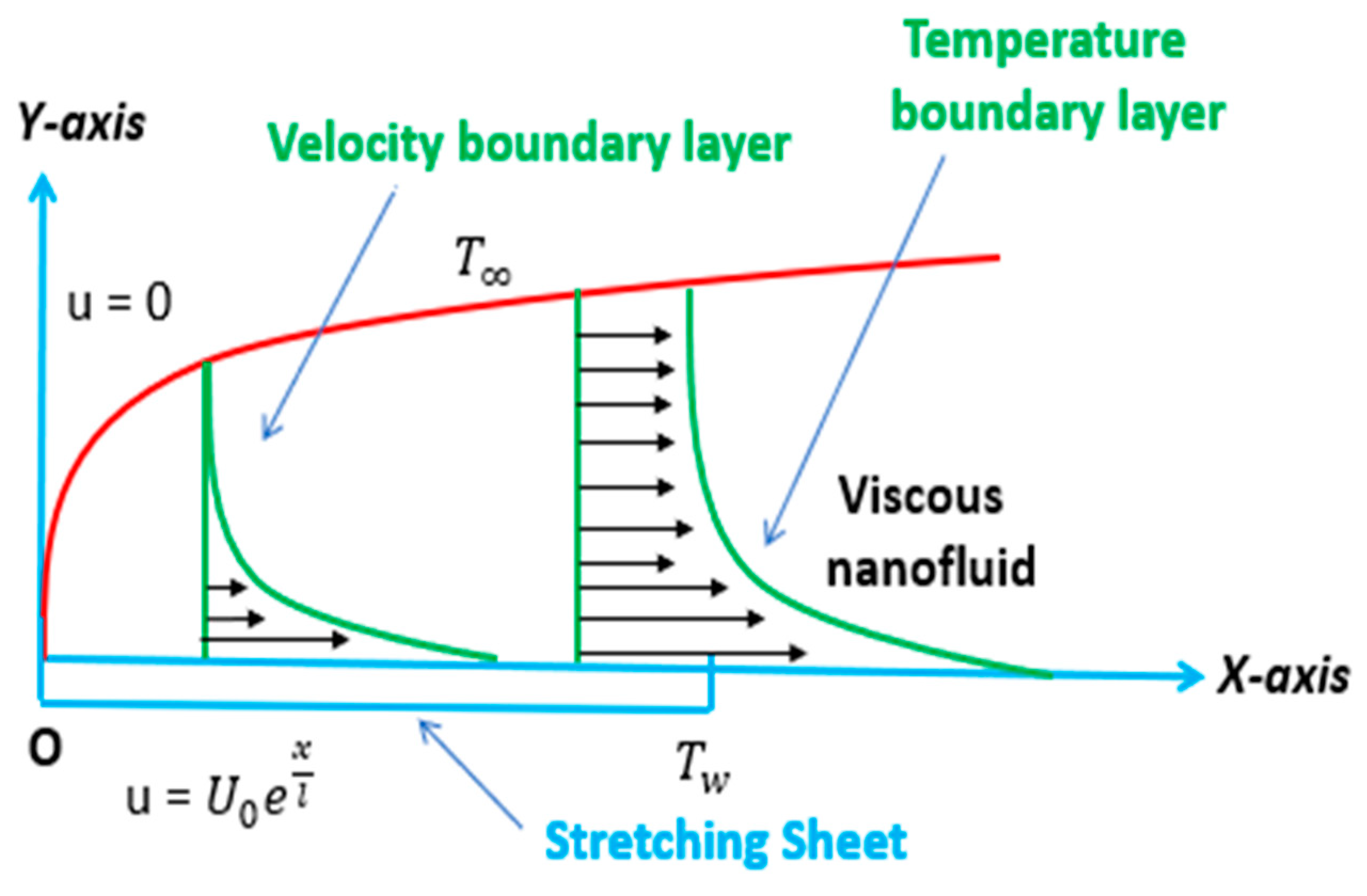
2. Problem Formulation
3. Variables of Engineering Interest
4. Optimal Homotopy Analysis Method (OHAM)
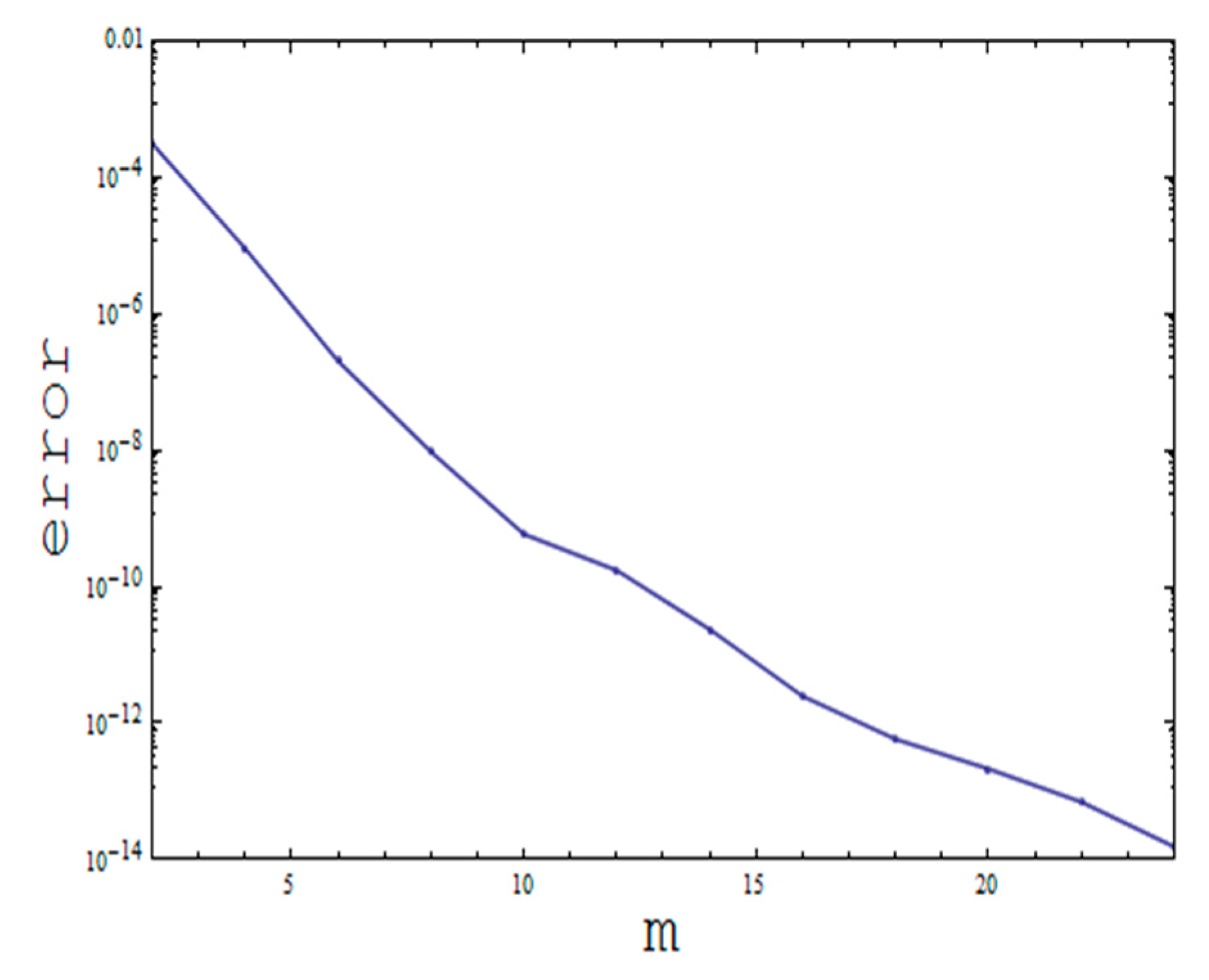
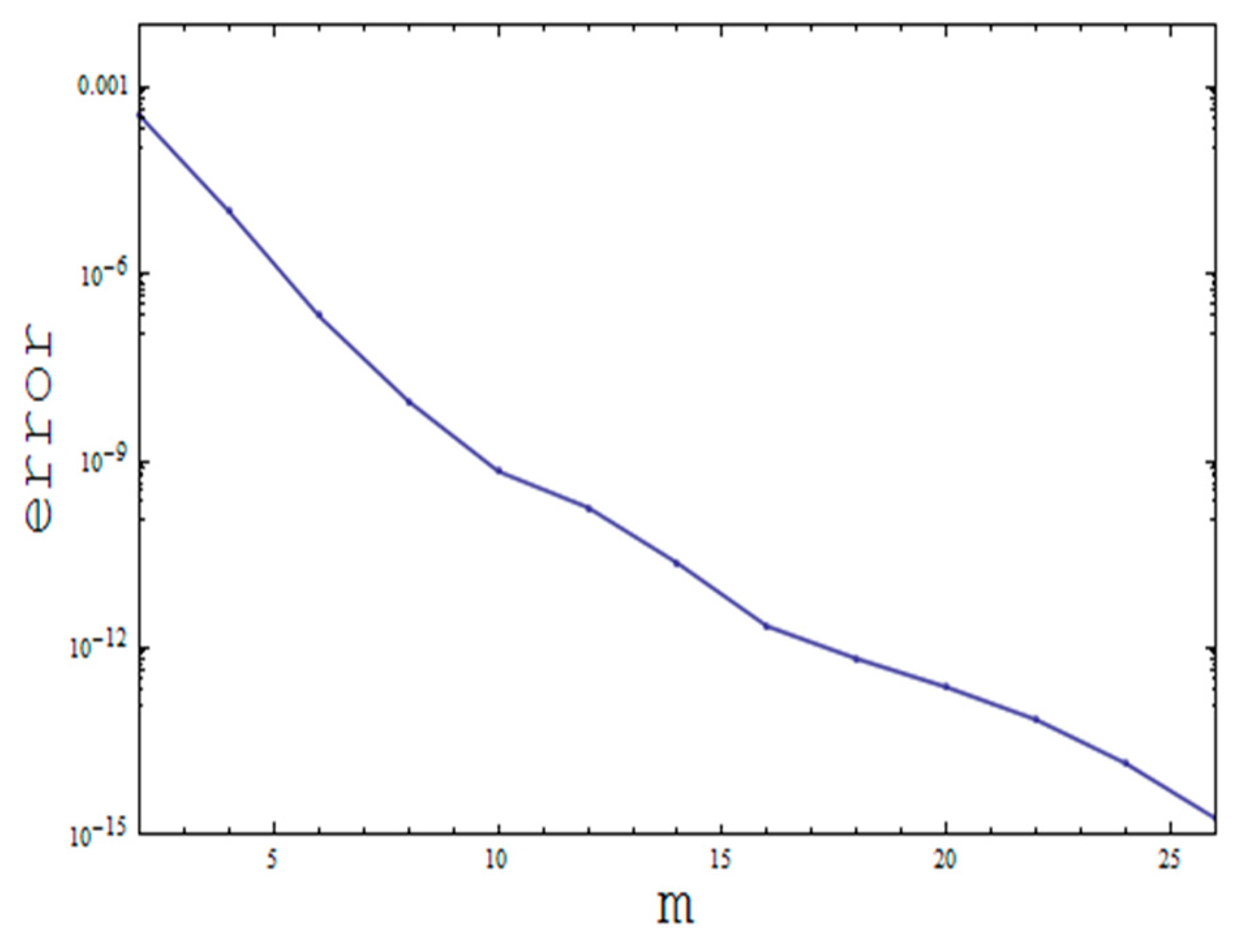
Convergence Analysis
5. Results and Discussion
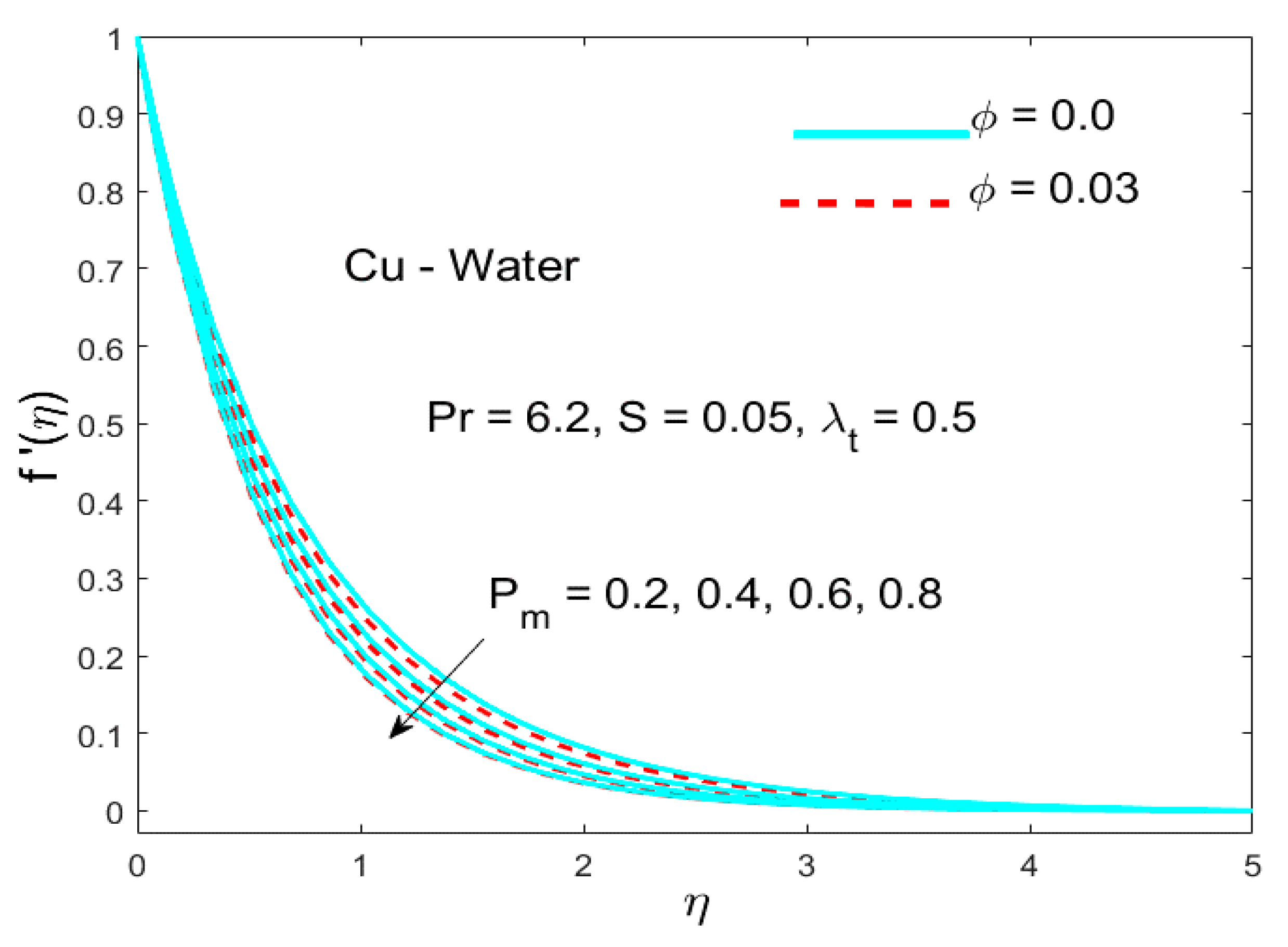
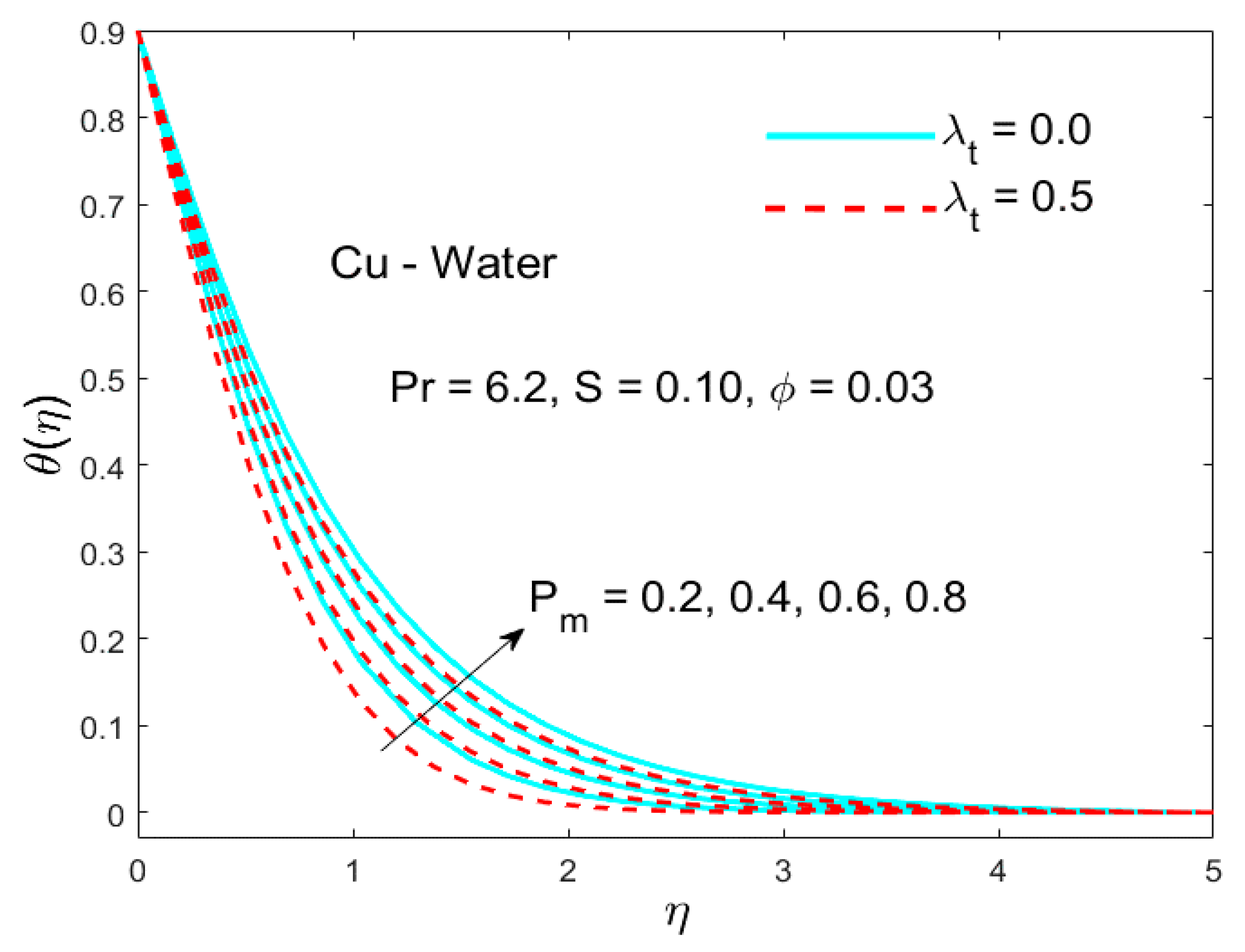
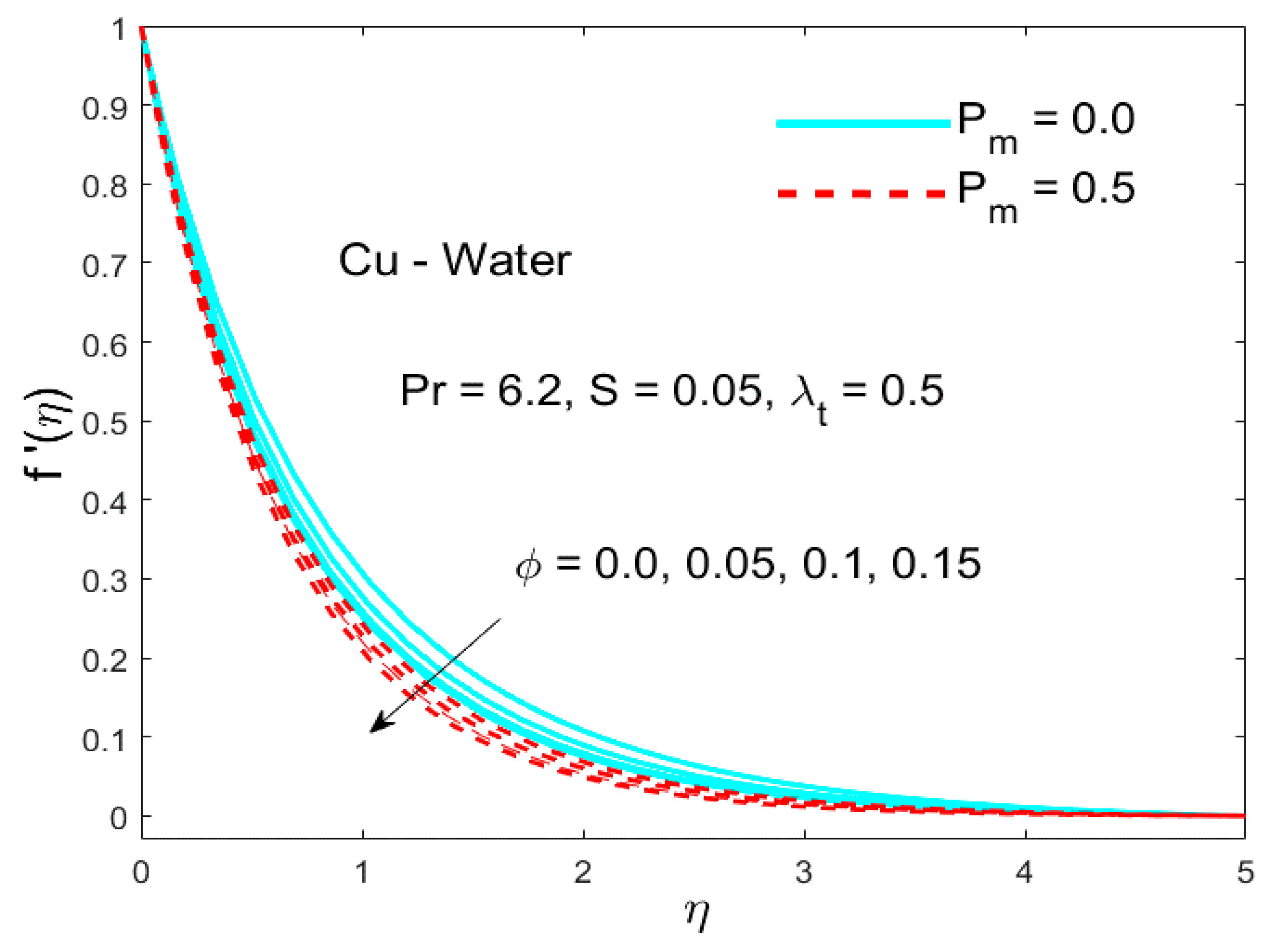
5.1. The Impact of the Parameter (Called Porosity Parameter)
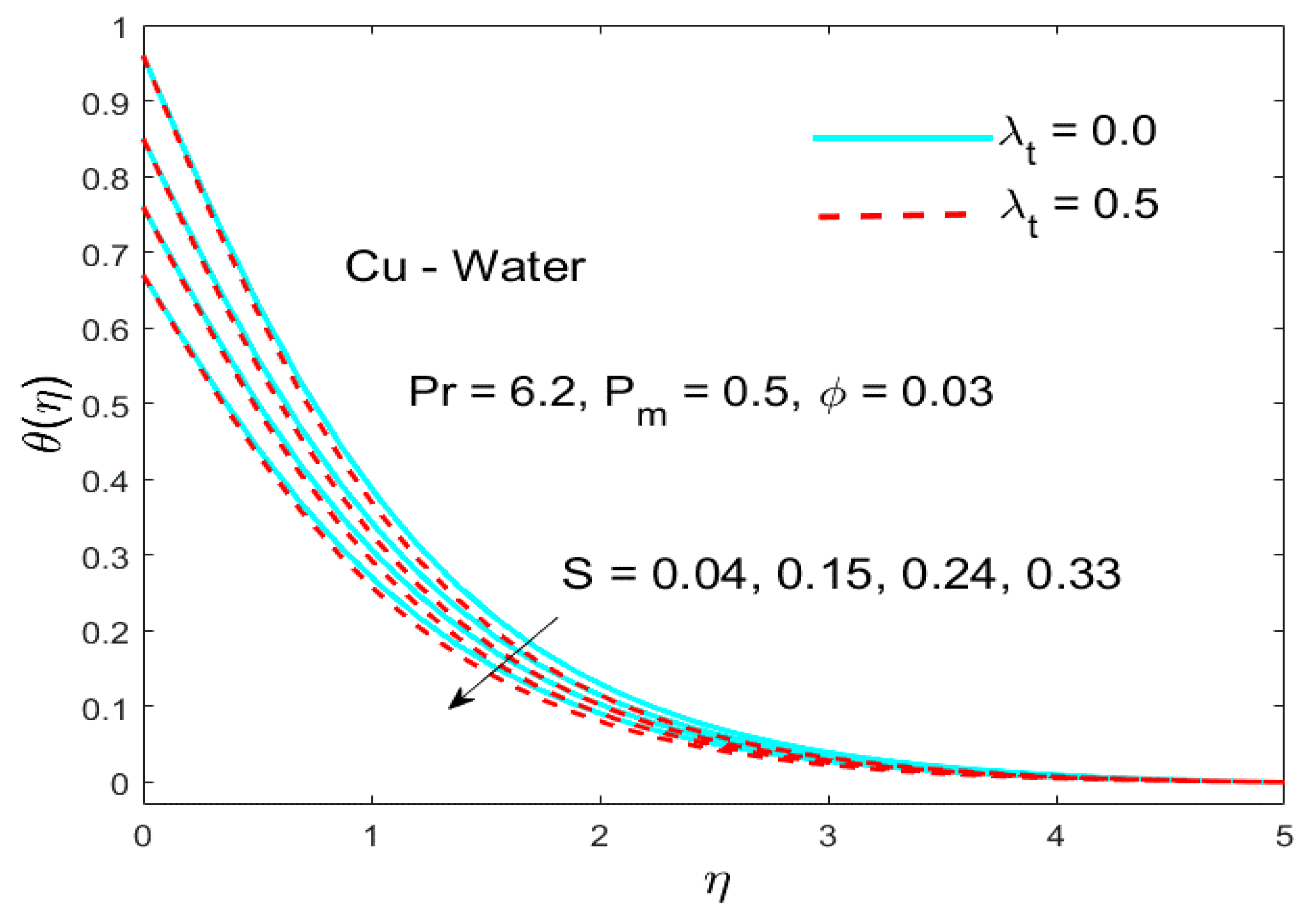
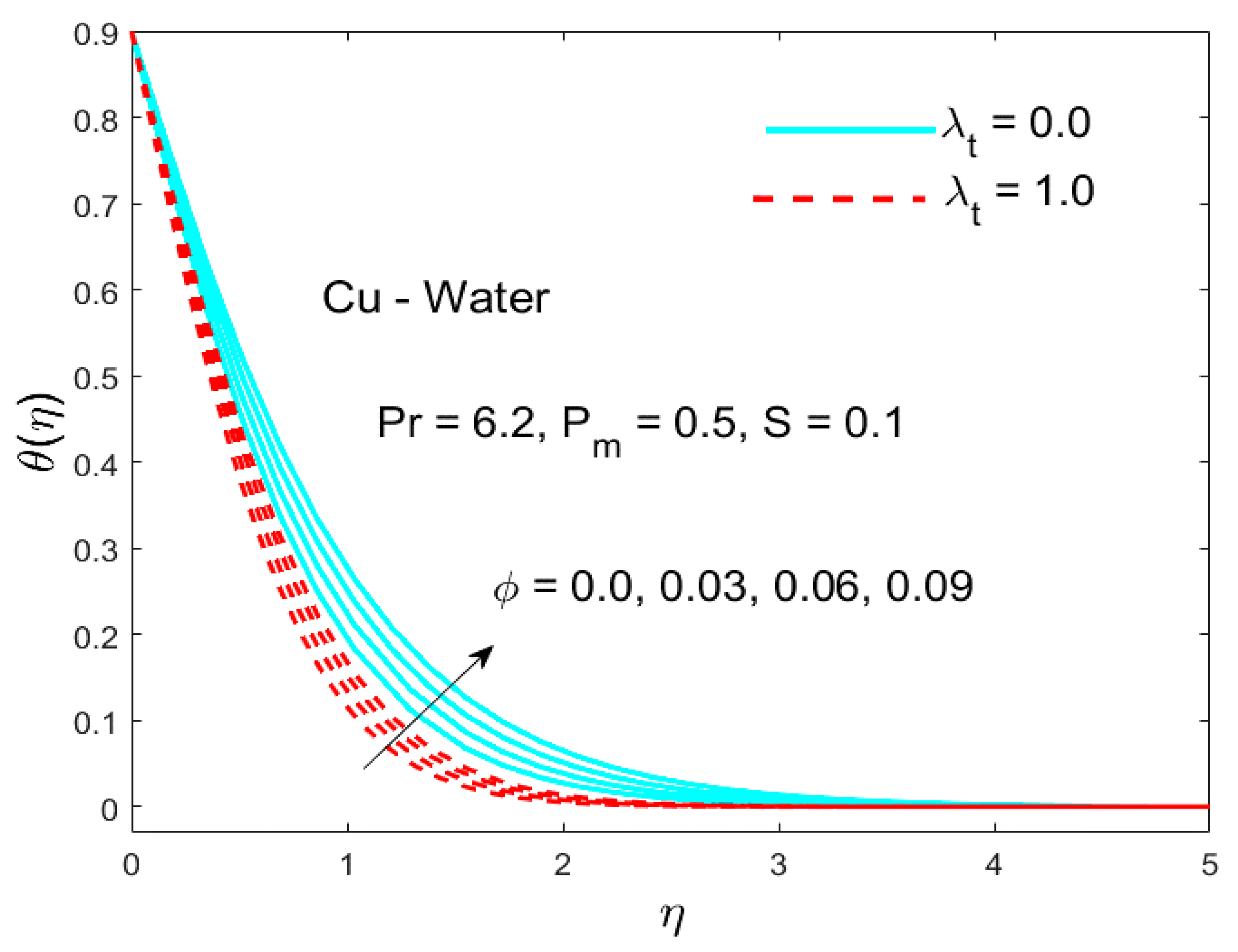
5.2. The Impact of the Parameter (Thermal Stratification)
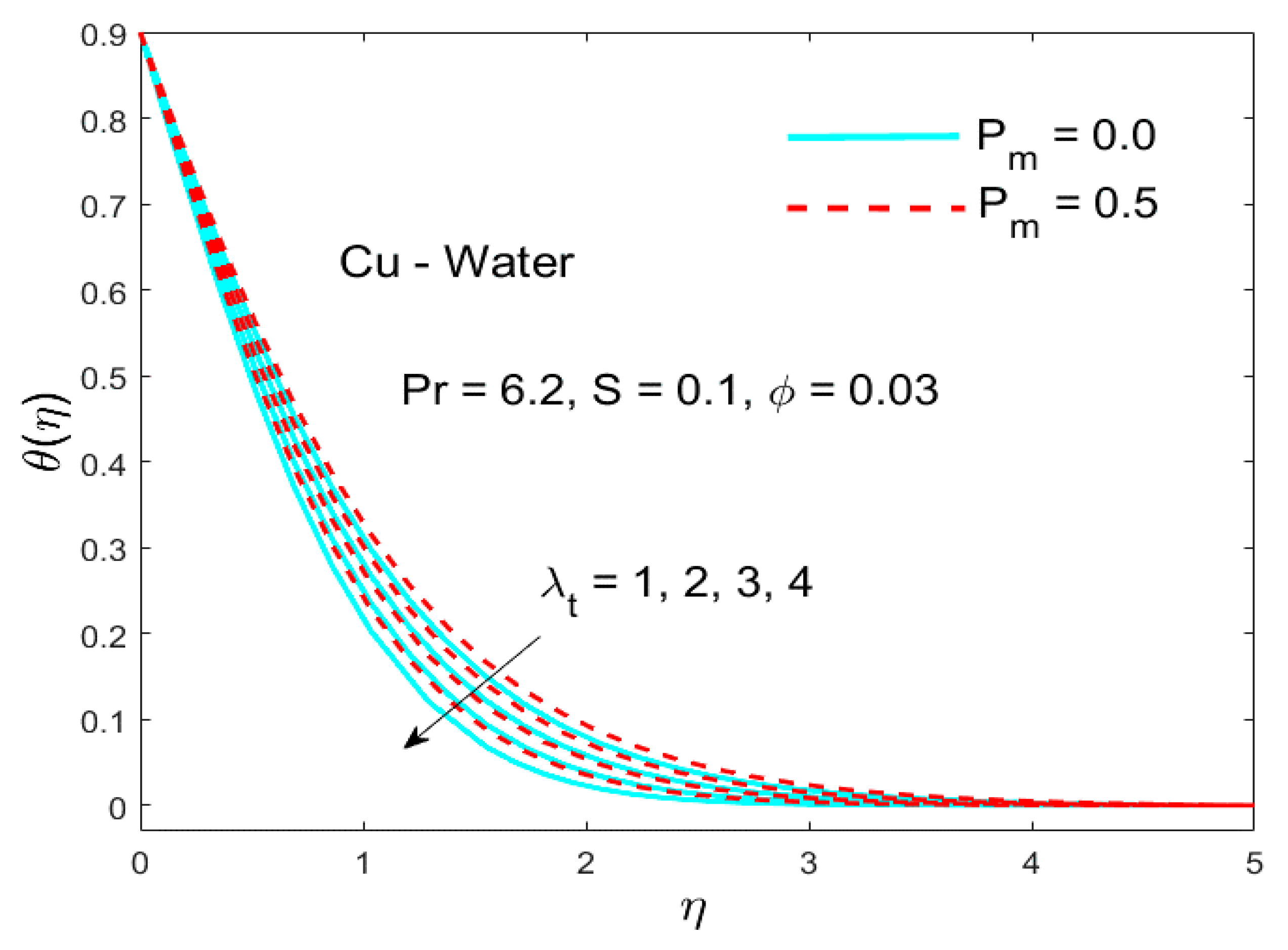
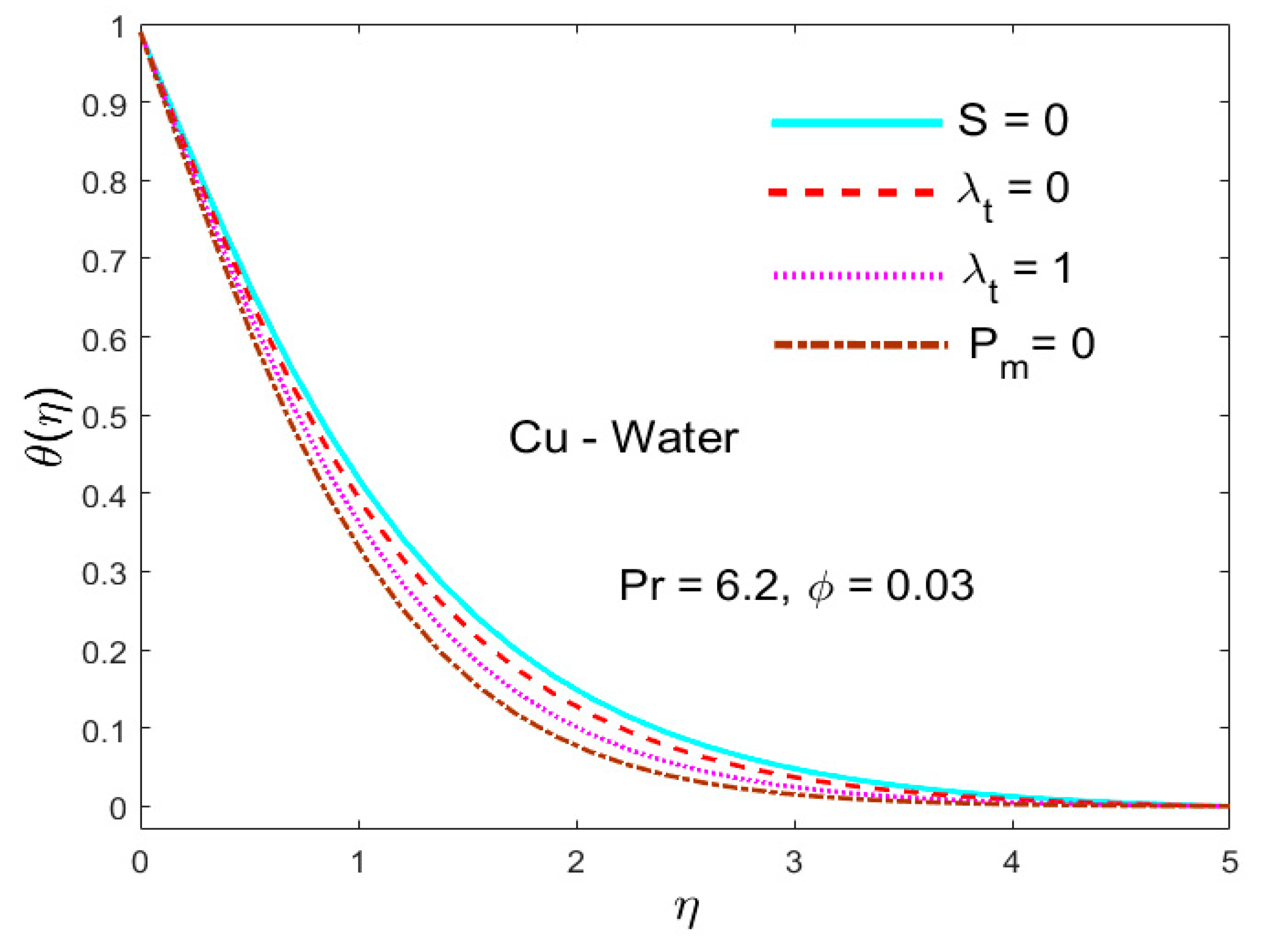
5.3. The Influence of the Parameter Called (Thermal Relaxation)
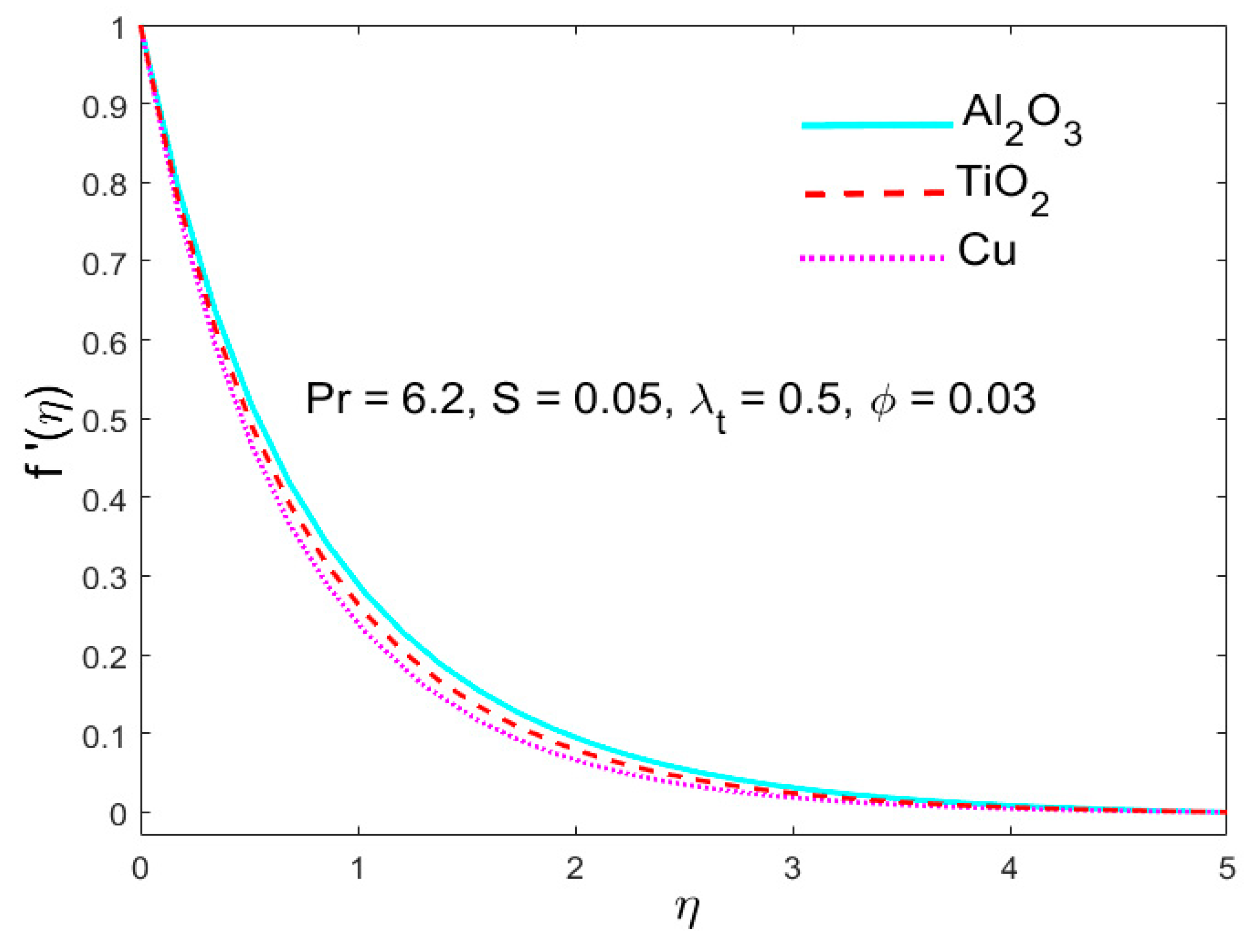
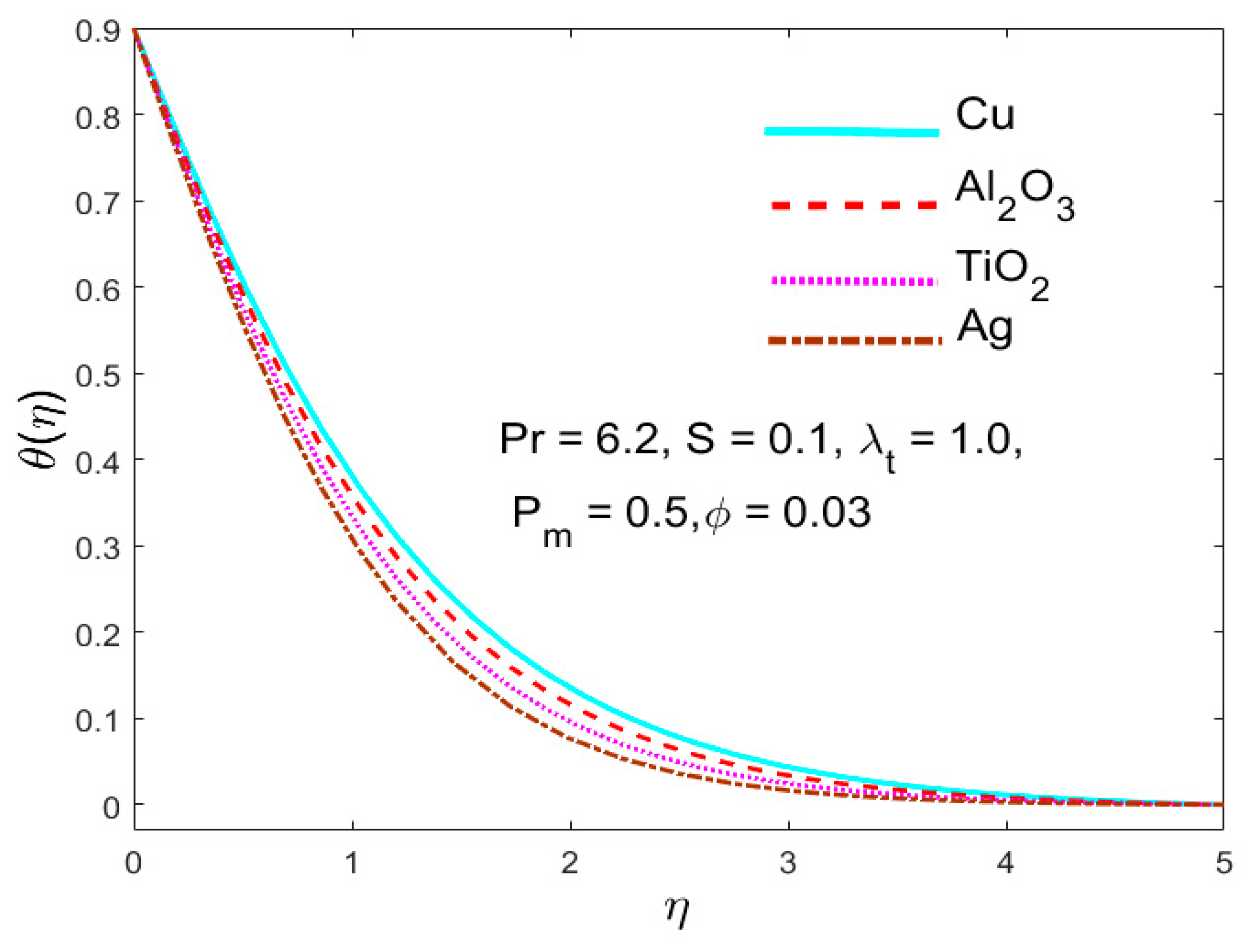
5.4. The Stimulus of the Parameter (Nanoparticle Volume Fraction)
6. Concluding Remarks
- ➢
- The enhancement in the porosity parameter shows a decreasing trend in the velocity profile.
- ➢
- Both the temperature field and its associated layer thickness were condensed for bigger values of the thermal stratification parameter .
- ➢
- A larger thermal relaxation parameter reduced the temperature field and corresponding boundary layer thickness.
- ➢
- The effect of the thermal relaxation parameter was qualitatively identical in both the Cattaneo–Christov model of heat flux and Fourier models.
- ➢
- For nanofluids with copper nanoparticles, the velocity components show a decreasing behavior as the volume fraction of nanoparticle rose along with the saddle and nodal points.
- ➢
- For Cu-nanoparticles expansion in liquid, the resistance to the motion of the liquid (along x- and y-axes) was found to be higher as compared to titanium dioxide (TiO2) and alumina (Al2O3).
- ➢
- The temperature also improved for the Cu-water nanofluid with the increment in the volume fraction of the nanoparticles.
Author Contributions
Funding
Conflicts of Interest
References
- Baptiste, J.; Fourier, J. Theorie Analytique de La Chaleur; F. Didot: Paris, France, 1822. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 200, 523–541. [Google Scholar]
- Tibullo, V.; Zampoli, V. A uniqueness result for the Cattaneo–Christov heat conduction model applied to incompressible fluids. Mech. Res. Commun. 2011, 38, 77–79. [Google Scholar] [CrossRef]
- Han, S.; Zheng, L.; Li, C.; Zhang, X. Coupled flow and heat transfer in viscoelastic fluid with Cattaneo–Christov heat flux model. Appl. Math. Lett. 2014, 38, 87–93. [Google Scholar] [CrossRef]
- Straughan, B. Thermal convection with the Cattaneo–Christov model. Int. J. Heat Mass Transf. 2010, 53, 95–98. [Google Scholar] [CrossRef]
- Haddad, S.A.M. Thermal instability in Brinkman porous media with Cattaneo–Christov heat flux. Int. J. Heat Mass Transf. 2014, 68, 659–668. [Google Scholar] [CrossRef]
- Carragher, P.; Crane, L.J. Heat transfer on a continuous stretching sheet. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Mech. 1982, 62, 564–565. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577. [Google Scholar] [CrossRef]
- Mustafa, M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper convected Maxwell fluid. AIP Adv. 2015, 5, 047109. [Google Scholar] [CrossRef]
- Khan, M.; Khan, W.A. Three-dimensional flow and heat transfer to burgers fluid using Cattaneo-Christov heat flux model. J. Mol. Liq. 2016, 221, 651–657. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Lee, C. MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci. Iran. 2012, 19, 1550–1553. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S.; Khan, Z.H. MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alex. Eng. J. 2013, 52, 577–582. [Google Scholar] [CrossRef]
- Muhammad, N.; Nadeem, S.; Haq, R.U. Heat transport phenomenon in the ferromagnetic fluid over a stretching sheet with thermal stratification. Results Phys. 2017, 7, 854–861. [Google Scholar] [CrossRef]
- Partha, M.K.; Murthy, P.V.S.N.; Rajasekhar, G.P. Effect of viscous dissipation on the mixed convection heat transfer from an exponentially stretching surface. Heat Mass Transf. 2005, 41, 360–366. [Google Scholar] [CrossRef]
- Nadeem, S.; Ahmad, S.; Muhammad, N.; Mustafa, M.T. Chemically reactive species in the flow of a Maxwell fluid. Results Phys. 2017, 7, 2607–2613. [Google Scholar] [CrossRef]
- Pop, I.; Ingham, D.B. Convective Heat Transfer: Mathematical and Computational Modelling of Viscous Fluids and Porous Media; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Vafai, K. (Ed.) Porous Media: Applications in Biological Systems and Biotechnology; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Alizadeh-Pahlavan, A.; Aliakbar, V.; Vakili-Farahani, F.; Sadeghy, K. MHD flows of UCM fluids above porous stretching sheets using two-auxiliary-parameter homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 473–488. [Google Scholar] [CrossRef]
- Raftari, B.; Yildirim, A. The application of homotopy perturbation method for MHD flows of UCM fluids above porous stretching sheets. Comput. Math. Appl. 2010, 59, 3328–3337. [Google Scholar] [CrossRef]
- Lesnic, D.; Ingham, D.B.; Pop, I.; Storr, C. Free convection boundary-layer flow above a nearly horizontal surface in a porous medium with Newtonian heating. Heat Mass Transf. 2004, 40, 665–672. [Google Scholar] [CrossRef]
- Lesnic, D.; Ingham, D.B.; Pop, I. Free convection boundary-layer flow along a vertical surface in a porous medium with Newtonian heating. Int. J. Heat Mass Transf. 1999, 42, 2621–2627. [Google Scholar] [CrossRef]
- Aliakbar, V.; Alizadeh-Pahlavan, A.; Sadeghy, K. The influence of thermal radiation on MHD flow of Maxwellian fluids above stretching sheets. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 779–794. [Google Scholar] [CrossRef]
- Nadeem, S.; Ahmad, S.; Muhammad, N. Cattaneo-Christov flux in the flow of a viscoelastic fluid in the presence of Newtonian heating. J. Mol. Liq. 2017, 237, 180–184. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995; No. ANL/MSD/CP-84938; CONF-951135-29. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Nadeem, S.; Ahmad, S.; Muhammad, N. Computational study of Falkner-Skan problem for a static and moving wedge. Sens. Actuators B Chem. 2018, 263, 69–76. [Google Scholar] [CrossRef]
- Khan, U.; Ahmad, S.; Ramzan, M.; Suleman, M.; Lu, D.; Inam, S. Numerical Simulation of Darcy–Forchheimer 3D Unsteady Nanofluid Flow Comprising Carbon Nanotubes with Cattaneo–Christov Heat Flux and Velocity and Thermal Slip Conditions. Processes 2019, 7, 687. [Google Scholar]
- Khan, U.; Zaib, A.; Khan, I.; Nisar, K.S. Activation energy on MHD flow of titanium alloy (Ti6Al4V) nanoparticle along with a cross flow and streamwise direction with binary chemical reaction and non-linear radiation: Dual Solutions. J. Mater. Res. Technol. 2019. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Tlili, I.; Tian, Z.; Bakouri, M.; Safaei, M.R.; Goodarzi, M. Thermal evaluation of graphene nanoplatelets nanofluid in a fast-responding HP with the potential use in solar systems in smart cities. Appl. Sci. 2019, 9, 2101. [Google Scholar] [CrossRef]
- Suleman, M.; Ramzan, M.; Ahmad, S.; Lu, D.; Muhammad, T.; Chung, J.D. A Numerical Simulation of Silver–Water Nanofluid Flow with Impacts of Newtonian Heating and Homogeneous–Heterogeneous Reactions Past a Nonlinear Stretched Cylinder. Symmetry 2019, 11, 295. [Google Scholar] [CrossRef]
- Nnamdi, A.H.; Briggs, T.M.D.; Togunde, O.O.; Obanya, H.E. Antagonistic Effects of Sublethal Concentrations of Certain Mixtures of Metal Oxide Nanoparticles and the Bulk (Al2O3, CuO, and SiO2) on Gill Histology in Clarias gariepinus. J. Nanotechnol. 2019, 2019, 7686597. [Google Scholar] [CrossRef]
- Liu, X.; Tang, J.; Song, B.; Zhen, M.; Wang, L.; Giesy, J.P. Giesy. Exposure to Al2O3 nanoparticles facilitates conjugative transfer of antibiotic resistance genes from Escherichia coli to Streptomyces. Nanotoxicology 2019, 13, 1422–1436. [Google Scholar] [CrossRef]
- Goodarzi, H.; Akbari, O.A.; Sarafraz, M.M.; Karchegani, M.M.; Safaei, M.R.; Shabani, S.; Ahmadi, G. Numerical simulation of natural convection heat transfer of nanofluid with Cu, MWCNT, and Al2O3 nanoparticles in a cavity with different aspect ratios. J. Therm. Sci. Eng. Appl. 2019, 11, 061020. [Google Scholar] [CrossRef]
- Liao, S. Beyond Perturbation: Introduction to the Homotopy Analysis Method; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liao, S. An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2003–2016. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Ibraheem, R.O.; Mahanthesh, B.; Babatunde, H.A. A meta-analysis on the effects of haphazard motion of tiny/nano-sized particles on the dynamics and other physical properties of some fluids. Chin. J. Phys. 2019, 60, 676–687. [Google Scholar] [CrossRef]
- Wakif, A.; Animasaun, I.L.; Satya Narayana, P.V.; Sarojamma, G. Meta-analysis on thermo-migration of tiny/nano-sized particles in the motion of various fluids. Chin. J. Phys. 2019. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Sehaqui, R. Numerical Analysis of the Onset of Longitudinal Convective Rolls in a Porous Medium Saturated by an Electrically Conducting Nanofluid in the Presence of an External Magnetic Field. Results Phys. 2017, 7, 2134–2152. [Google Scholar] [CrossRef]
- Amanulla, C.H.; Wakif, A.; Boulahia, Z.; Suryanarayana Reddy, M.; Nagendra, N. Numerical investigations on magnetic field modeling for Carreau non-Newtonian fluid flow past an isothermal sphere. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 462. [Google Scholar] [CrossRef]
- Makinde, O.D.; Omojola, M.T.; Mahanthesh, B.; Alao, F.I.; Adegbie, K.S.; Animasaun, I.L.; Wakif, A.; Sivaraj, R.; Tshehla, M.S. Significance of Buoyancy, Velocity Index and Thickness of an Upper Horizontal Surface of a Paraboloid of Revolution: The Case of Non-Newtonian Carreau Fluid. Defect. Diffus. Forum 2018, 387, 550–561. [Google Scholar] [CrossRef]
- Zaib, A.; Khan, U.; Khan, I.; HSeikh, A.; MSherif, E.S. Entropy Generation and Dual Solutions in Mixed Convection Stagnation Point Flow of Micropolar Ti6Al4V Nanoparticle along a Riga Surface. Processes 2020, 8, 14. [Google Scholar] [CrossRef]
- Amanulla, C.H.; Saleem, S.; Wakif, A.; AlQarni, M.M. MHD Prandtl fluid flow past an isothermal permeable sphere with slip effects. Case Stud. Therm. Eng. 2019, 14, 100447. [Google Scholar] [CrossRef]
- Qasim, M.; Ali, Z.; Wakif, A.; Boulahia, Z. Numerical Simulation of MHD Peristaltic Flow with Variable Electrical Conductivity and Joule Dissipation Using Generalized Differential Quadrature Method. Commun. Theor. Phys. 2019, 71, 509–518. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Mishra, S.R.; Rashidi, M.M.; Sehaqui, R. Influence of a uniform transverse magnetic field on the thermo-hydrodynamic stability in water-based nanofluids with metallic nanoparticles using the generalized Buongiorno’s mathematical model. Eur. Phys. J. Plus 2018, 133, 181. [Google Scholar] [CrossRef]
- Zaib, A.; Khan, U.; Shah, Z.; Kumam, P.; Thounthong, P. Optimization of entropy generation in flow of micropolar mixed convective magnetite (Fe3O4) ferroparticle over a vertical plate. Alex. Eng. J. 2019, 58, 1461–1470. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Amine, A.; Animasaun, I.L.; Afridi, M.I.; Qasim, M.; Sehaqui, R. Magneto-Convection of Alumina—Water Nanofluid Within Thin Horizontal Layers Using the Revised Generalized Buongiorno’s Model. Front. Heat Mass Transf. 2019, 12. [Google Scholar] [CrossRef]
- Wakif, A.; Qasim, M.; Afridi, M.I.; Saleem, S.; Al-Qarni, M.M. Numerical Examination of the Entropic Energy Harvesting in a Magnetohydrodynamic Dissipative Flow of Stokes’ Second Problem: Utilization of the Gear-Generalized Differential Quadrature Method. J. Non Equilib. Thermodyn. 2019, 44, 385–403. [Google Scholar] [CrossRef]
| Cu | Al2O3 | TiO2 | |||
|---|---|---|---|---|---|
| 0.01 | 0.1 | 0.3 | 1.3228 | 1.4760 | 1.5230 |
| 0.03 | 1.6384 | 1.7334 | 1.8384 | ||
| 0.05 | 1.8550 | 2.0755 | 2.2550 | ||
| 0.05 | 0.2 | 0.3 | 1.3230 | 1.3759 | 1.4229 |
| 0.4 | 1.5307 | 1.5898 | 1.6306 | ||
| 0.6 | 1.7151 | 1.7785 | 1.8150 | ||
| 0.05 | 0.6 | 0.1 | 1.3312 | 1.4211 | 1.5311 |
| 0.2 | 1.3312 | 1.4212 | 1.5312 | ||
| 0.4 | 1.3312 | 1.4212 | 1.5312 | ||
| Physical Properties | H2O | Cu | Al2O3 | TiO2 |
|---|---|---|---|---|
| 4179 | 385 | 765 | 686.2 | |
| 997 | 8933 | 3970 | 4250 | |
| 0.613 | 400 | 40 | 8.9538 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, U.; Ahmad, S.; Hayyat, A.; Khan, I.; Nisar, K.S.; Baleanu, D. On the Cattaneo–Christov Heat Flux Model and OHAM Analysis for Three Different Types of Nanofluids. Appl. Sci. 2020, 10, 886. https://doi.org/10.3390/app10030886
Khan U, Ahmad S, Hayyat A, Khan I, Nisar KS, Baleanu D. On the Cattaneo–Christov Heat Flux Model and OHAM Analysis for Three Different Types of Nanofluids. Applied Sciences. 2020; 10(3):886. https://doi.org/10.3390/app10030886
Chicago/Turabian StyleKhan, Umair, Shafiq Ahmad, Arsalan Hayyat, Ilyas Khan, Kottakkaran Sooppy Nisar, and Dumitru Baleanu. 2020. "On the Cattaneo–Christov Heat Flux Model and OHAM Analysis for Three Different Types of Nanofluids" Applied Sciences 10, no. 3: 886. https://doi.org/10.3390/app10030886
APA StyleKhan, U., Ahmad, S., Hayyat, A., Khan, I., Nisar, K. S., & Baleanu, D. (2020). On the Cattaneo–Christov Heat Flux Model and OHAM Analysis for Three Different Types of Nanofluids. Applied Sciences, 10(3), 886. https://doi.org/10.3390/app10030886







