Abstract
The paper reports the forecasting model for multiple time-domain photovoltaic power plants, developed in response to the necessity of bad weather days’ accurate and robust power generation forecasting. We provide a brief description of the piloted short-term forecasting system and place under close scrutiny the main sources of photovoltaic power plants’ generation forecasting errors. The effectiveness of the empirical approach versus unsupervised learning was investigated in application to source data filtration in order to improve the power generation forecasting accuracy for unstable weather conditions. The k-nearest neighbors’ methodology was justified to be optimal for initial data filtration, based on the clusterization results, associated with peculiar weather and seasonal conditions. The photovoltaic power plants’ forecasting accuracy improvement was further investigated for a one hour-ahead time-domain. It was proved that operational forecasting could be implemented based on the results of short-term day-ahead forecast mismatches predictions, which form the basis for multiple time-domain integrated forecasting tools. After a comparison of multiple time series forecasting approaches, operational forecasting was realized based on the second-order autoregression function and applied to short-term forecasting errors with the resulting accuracy of 87%. In the concluding part of the article the authors from the points of view of computational efficiency and scalability proposed the hardware system composition.
1. Introduction
Statistics show that photovoltaic power plants (PVPP) demonstrate the highest dynamics of installed capacity growth among renewable-based power plants worldwide [1]. However, given the climatic and geographical characteristics of Russian Federation territory, for the Unified Power System of Russia, as a whole, there is no considerable impact of stochastic renewable generation on the power system operation modes, but for the regional interconnected power systems (IPS) of the South and the Urals, a relatively high share of the installed capacity of PVPP is already observed. An increase of such power plants’ share in the total power generation fleet leads to an even greater increase in their influence on the power balance [2], frequency [3,4], electric energy quality [5,6], static and dynamic stability [7,8,9], voltage levels [10,11] and electrical energy losses [12,13]. The first response to the PVPP installed capacity growth should be the development of forecasting systems, allowing reliable planning of power system operation modes.
In general terms power system planning is understood as an action schedule aimed at ensuring the balance of power consumption and generation, reliability and efficiency of the entire technological chain: power generation, transmission, distribution and consumption [14,15]. Short-term planning is typically carried out for the day-ahead perspective by the dispatch control centers. Operational planning is also carried out by dispatch centers, but within the operational day in order to sustain power balance and power supply reliability online.
When analyzing the renewable energy sources’ (RES) influence on the power system operation mode, it is necessary to take into account the stochastic nature of weather conditions, especially for the PVPPs and wind power plants, power generation of which largely depends on meteorological factors [16,17]. This kind of uncertainty can be taken into account in their forecasting models both from the point of view of the probability theory [18] and the possibility theory [19]. When using the possibility theory, both qualitative and quantitative methods can be applied [20].
The PVPP generation forecasting is one of the most effective and least capital-intensive measures that allow the integration of stochastic generation sources into the power system and reduce the negative impact on the power system’s operation mode. In this regard, the issue of day-ahead PVPP forecasting becomes a task with increasing priority in many countries [21].
Methods for PVPP generation forecasting can be divided into four main classes [22]: statistical, physical, intelligent and hybrid. Statistical models use statistical analysis to describe the relations between weather conditions and time series of solar irradiance or power generation of PVPPs, using retrospective data, as, for example, in [23,24,25,26]. Numerical weather forecast and satellite images, as suggested in the studies [27,28,29,30], form the basis for compiling PVPP generation forecasts for physical models. Intelligent models use artificial intelligence and machine learning methods to obtain forecasts of solar irradiance or PVPP power generation, mainly based on neural networks, as presented in [31,32,33,34]. Hybrid models for PVPP generation forecasting typically combine either physical or statistical or intelligent models. Examples of such models are presented in [35,36,37,38].
The authors of the article have previously developed their own step-by-step approach of PVPP generation short-term forecasting (STF), which is presented in detail in [39,40] and schematically given in Figure 1.

Figure 1.
Flowchart of the photovoltaic power plants (PVPP) generation short-term forecasting algorithm.
The major advantage of the proposed approach is characterized by its flexibility in terms of accounting for the external factors, including the operational state of the power generation equipment, switchgear composition, operation modes of the adjacent power system, etc. due to the effective combination of solar irradiance forecasting algorithms with imitation model of the PVPP under consideration. Moreover, step-by-step calculation of PVPP generation provides extensive opportunities for the interpretation of forecasting results, unlike “black box” models, establishing correlation links between inputs (for instance, weather data) and output (PVPP generation). The PVPP short-term forecasting system was implemented in the industrial software package and piloted at the real PVPP allocated in one of the southern regions of the Russian Federation.
In general, in the course of piloting, the PVPP forecasting system demonstrated a satisfactory accuracy level for sunny and cloudy days [39,41]. However, the performance of the model significantly decreased during partly cloudy days and days with precipitation, which put the study on the model accuracy and robustness at the top of the priority list.
The present study focuses on the measures to be introduced to improve the PVPP forecasting system performance in terms of accuracy and robustness. The authors scrutinize the weather data analysis and highlight the actions to be taken in terms of source dataset processing to improve PVPP forecasting accuracy. It should be noted that since the source data processing is aimed at eliminating the noise (outliers, produced by extreme weather conditions), the proposed actions are applicable regardless of the initially applied forecasting methodology.
The second part of the study demonstrates the multiple time-domain hybrid approach, establishing the link between short-term PVPP generation forecast for the day-ahead perspective and operational forecast for intra-hour/intra-day planning of PVPP energy output. The latter one is implemented based on the supplementary function, characterizing the short-term forecast mismatch, giving the opportunity to evaluate the PVPP output for one hour-ahead time horizon, which resulted in integrated PVPP short-term and operational forecasting model.
The remainder of the article is organized as follows. In Section 2, the PVPP forecasting errors are analyzed and major error sources are highlighted. Section 3 presents the results of the studies on source data filtration to improve the forecasting accuracy and the model performance for unstable weather conditions. Section 4 introduces the concept of PVPP short-term forecast operational correction and implements PVPP operational forecast based on the short-term forecasting errors analysis. Section 6 describes the hardware required for the presented forecasting system implementation, focusing on computational performance and scalability. Finally, the Conclusion Section provides brief study outcomes.
2. The Main Sources of the PVPP Generation Forecasting Errors
Given the step-by-step procedure, introduced in the PVPP generation short-term forecasting algorithm, the total forecasting error of the PVPP generation is the sum of the errors of individual mathematical models, used at each step consequently. Moreover, there are special cases when the error of one of the models compensates for the error of the other one, but there are also scenarios when the errors of the models overlap each other, causing a significant increase in the total error.
As a rule, at the PVPP, there are measurements of the solar irradiance and the corresponding electrical energy generation at the alternating current side of the group of the inverters. Unfortunately, it is not possible to separately estimate the forecasting error that is introduced at each stage. However, these measurements allow for isolating the error components of the model, associated with tilted irradiance identification and PV panels and inverters outputs calculation (from 3 to 6 stages) and to estimate the total error of the forecasting methodology (from 1 to 6 stages). The calculation procedure uses data on the actual measurements of the solar irradiance acquired from the horizontally installed pyranometers. Figure 2 illustrates the forecasting error of the entire methodology on an hourly basis while using the actual metering data on solar irradiance. It is notable that the forecasted values of the PVPP generation are mainly conditioned by the forecasted values of the cloudiness, which were not observed at the given site. This also brings up an issue of the PVPP forecasting error estimation, including identification of the errors introduced by the data sources.
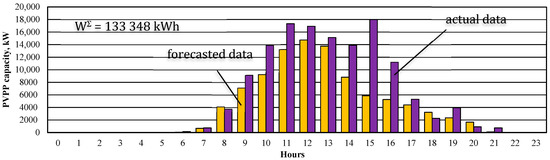
Figure 2.
Actual versus Forecasted values of PVPP generation for day-ahead time horizon (stages 1–6).
Table 1 shows the calculation results for two PVPP forecasting scenarios and presents an estimate of the mean absolute percentage error (MAPE) without taking into account the error of stages 1–2 for the first scenario and taking into account the error of all stages for the second scenario.

Table 1.
Errors for the daily forecast.
The calculation results presented in Table 1 demonstrate that the main share of the PVPP forecasting error is introduced at the stage of calculating the global horizontal solar irradiance.
The value of the global horizontal solar irradiance, as well as the transparency index of the atmosphere, is largely determined by the cloudiness. The proportion of solar energy passing through the cloud layer is not constant. It depends on a several factors [40]:
- the numerical estimation of cloudiness (the proportion of the sky covered by clouds);
- type of clouds (cirrus, cumulus, stratus, etc.);
- cloud heights from the base to the top;
- the microstructure of clouds (e.g., water content per unit volume);
- distribution of clouds relative to the solar disk position, etc.;
In the majority of studies and for practical applications, given the limited amount of available meteorological data from local data providers, to assess the effect of cloudiness on the value of solar irradiance and the transparency index, as a rule, only one of the listed parameters is used—the cloudiness (in proportions or percentages)—since for this parameter it is the easiest to determine (to observe) and the easiest to forecast [41].
As a result, a situation arises when the parameter for which the forecast is made has an ambiguous effect on the forecasted value. Examples of such situations are described by the authors in [42,43]. As a result, at this stage of calculating the PVPP generation forecast, a significant forecasting error is introduced.
3. Data Filtering for Short-Term Forecasting of Photovoltaic Power Plants Generation
3.1. Case Study of the PVPP Generation Short-Term Forecast
The study object was a real PVPP located in the Astrakhan region of Russia, with an installed capacity of 15 MW. In total, 6076 observations are being examined for the period from 26 September 2017 to 05 February 2019. To verify the forecasting models, data for various characteristic periods were considered:
- spring weather period: 26 February 2018–11 March 2018, 14 days, 164 observations;
- summer weather period: 21 May 2018–1 June 2018, 12 days, 199 observations;
- autumn weather period: 11 September 2018–20 September 2018, 10 days, 130 observations;
- winter weather period: 28 January 2019–03 February 2019, 7 days, 81 observations.
The division into periods given in the upper list is intended to characterize the weather conditions corresponding to a particular season, not the calendar seasons. Therefore, those periods were chosen that corresponded to certain season from the point of view of weather conditions. In total, there are 574 observations in the studied data for a period of 43 days. Each observation includes the following information:
- measured directly on site:
- ○
- actual PVPP generation, kWh;
- ○
- actual global horizontal irradiance, W/m2;
- ○
- actual ambient temperature, °C;
- ○
- actual wind speed, m/s;
- formed by the meteorological service:
- ○
- actual and forecasted cloudiness, p.u.;
- ○
- forecasted air temperature, °C;
- ○
- forecasted wind speed, m/s;
- ○
- actual and forecasted air humidity, p.u.
In addition, the calculations used passport and operational data of the PV panels and inverters.
3.2. Data Filtration Methods Application
One of the possible ways to improve the accuracy of calculating the transparency index can be the data sample filtering, which is used to calculate the coefficients of the regression model [40].
In order to study the possibility and evaluate the effectiveness of methods for improving the PVPP generation STF accuracy, a reference case study without data filtration is described in detail (Table 2, Figure 3).

Table 2.
Analysis of PVPP generation forecasting accuracy.
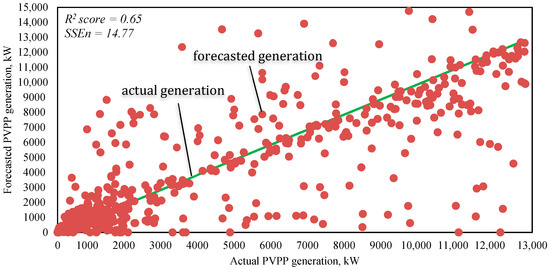
Figure 3.
The scatter diagram of the PVPP generation forecasted values.
Table 2 represents the numerical assessment of the forecasting quality without introducing data filtration approaches. The following denominations are used: WΣ is the total PVPP energy production for the period under consideration, (kWh); EΣ is the total absolute error for the period under consideration, (kWh); Eavg is the mean absolute error for the period under consideration, (kWh); σE is the absolute error standard deviation, (kWh); R2 score is the determination coefficient, (p.u.); SSEn is normalized sum of errors.
Due to the fact that when calculating SSE (sum of square error), very large values are obtained (for example, for the Figure 3 scenario the SSE would be equal to 3,322,661,719.61 kW2), the SSEn indicator is applied. It is calculated as the sum of squared errors normalized with respect to the square of the installed capacity of the photovoltaic power plant, SSEn = SSE/(Pinst)2, measured in p.u.
In Figure 3 there is a diagram showing the scatter of the forecasted values of PVPP generation relative to the actual values.
The determination coefficient characterizes a significant value of the PVPP generation forecasted values relative to the actual values. The reason for this is the cloudiness influence ambiguity on the value forecasted by the regression function—the transparency index.
Figure 4 shows an example of the transparency index dependence on cloudiness for the solar altitude angles, characterizing the morning and evening conditions (), as an example, and shows a significant uncertainty of the cloudiness influence on the transparency index . For the same cloudiness value, the scatter in the transparency index values can reach 0.9 p.u.
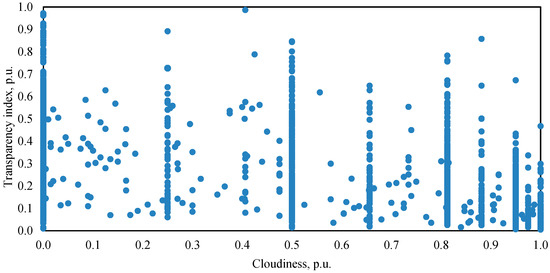
Figure 4.
Transparency index versus cloudiness for morning/evening altitude angles.
3.3. Empirical Data Filtration
In determining outliers when analyzing the transparency index dependence on the cloudiness amount, an empirical formula can be used:
where —the transparency index, (p.u.); —the cloudiness, (p.u.).
This expression is determined on the assumptions that come from the experience of PVPP solar forecasting system application at the real power generation facility: under absolutely cloudless weather conditions the transparency index value cannot exceed 0.9 p.u., and under the most cloudy weather the transparency index value cannot exceed 0.5 p.u.
All observations above the straight line , are treated as outliers and are considered unreliable. Figure 5 shows the transparency index dependencies on cloudiness, filtered in accordance with the expression (1), for the above-described ranges of the solar altitude angle, characterizing the morning and evening conditions ().
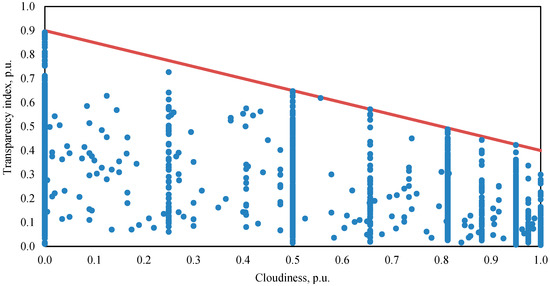
Figure 5.
Transparency index versus cloudiness for morning/evening altitude angles with empirical filtration.
From Figure 5 it appears an uncertainty decrease in the cloudiness influence on the transparency index due to the introduced filtering of the observations. The results of PVPP generation forecasting accuracy assessment using empirical filtering are shown in Figure 6.
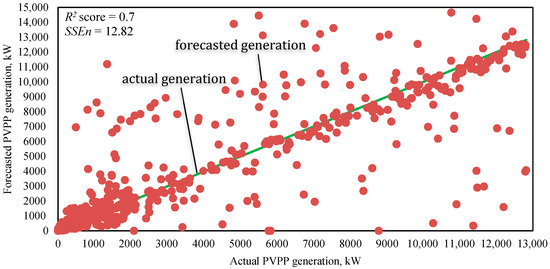
Figure 6.
The scatter diagram of the PVPP generation forecasted values with empirical filtering.
The comparison of Figure 3 and Figure 6 allows one to evaluate the efficiency of using simple filtration. The total error value for all the specific periods under consideration using an empirical filter is lower than for the calculations without using the filter, which is confirmed by the scatter on the diagrams. The determination coefficient has also increased.
The advantages of the empirical filtering method are the usability and the fewer required computing resources. Disadvantages of the filtering method are as follows: the difficulty to accurately identify outliers of the transparency index , the excessive observations filtering (in addition to outliers, reliable observations can be discarded) and the lack of empirical expressions versatility.
3.4. The K-Means Filtration Method
In order to more accurately identify outliers, the authors of the study used the k-means method. The k-means method is implemented in accordance with the following algorithm [42], as shown in Figure 7 for 200 randomly generated observations and 6 cluster centers for two-dimensional space (the number of features describing each observation is 2). The step-by-step procedure of the methodology is given in Figure 8. A silhouette measure is used to assess the quality of data clustering.
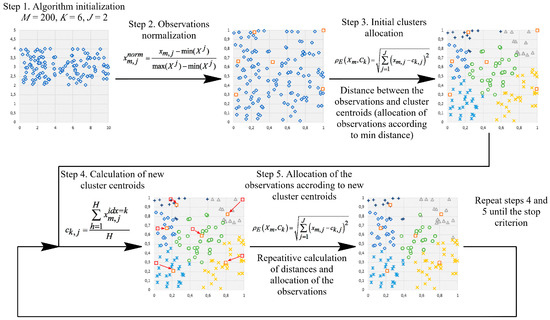
Figure 7.
K-means based data clustering.
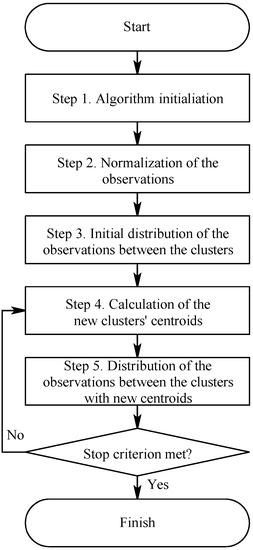
Figure 8.
Flow-chart of the algorithm.
The silhouette measure characterizes the distance of the observation from the nearest cluster to which it does not belong. The silhouette measure is determined in accordance with the expression:
where —the silhouette measure for the observation; —the distance from the observation to the nearest cluster center, to which this observation belongs; —the distance from the observation to the nearest cluster center to which this observation does not belong.
By the silhouette measure value, the division quality is determined: poor division quality is characterized by the measure values from −1 to 0.2; middle division quality—from 0.2 to 0.5; good division quality—from 0.5 to 1.
To identify the transparency index anomalous behavior and to solve the problem of more accurate outliers identification, a three-dimensional feature space was used in the study, based on the k-means clustering method. 6076 observations were analyzed for the period from 26/09/17 to 05/02/19. Cloudiness , solar altitude angle sine and solar inclination angle were used as features describing the observations.
Solar altitude angle is determined according to the expression below:
where —the latitude, (deg); —the solar inclination angle, (deg); —the solar hourly angle, (deg).
To calculate the solar inclination angle, the following expression is used:
where n is the day number.
To select the number of clusters and determine the initial approximations of the cluster centers, a combination of various characteristic values of each feature was used. The list of characteristic values and the corresponding descriptions are presented in Table 3.

Table 3.
Description and features values for clusters initial approximations.
According to Table 3, various combinations of cloudiness values, solar altitude angle sine and solar inclination angle are formed to determine the initial approximations of the cluster centers.
The number of possible combinations is 43. Since in the range of the solar altitude angle sine close to 0.7 (midday), there are no points with coordinates along the axis in the range of 0.1–0.33 (winter-off-season closer to winter), combinations with such values are not included in the final set of cluster centers’ initial approximations.
A total set of 56 different combinations is formed. Figure 9a,b illustrate the location of 6076 observations (blue markers) and 56 initial approximations of cluster centers (black markers) in a three-dimensional feature space − − . The clustering observations results using the k-means method are presented in Figure 9c,d, as well as in Table 4. The value of the final silhouette measure obtained from the clustering results by the k-means method, averaged between all observations, is 0.52, which confirms the good quality of the observations division into clusters. The calculation time was 1 h 56 min.
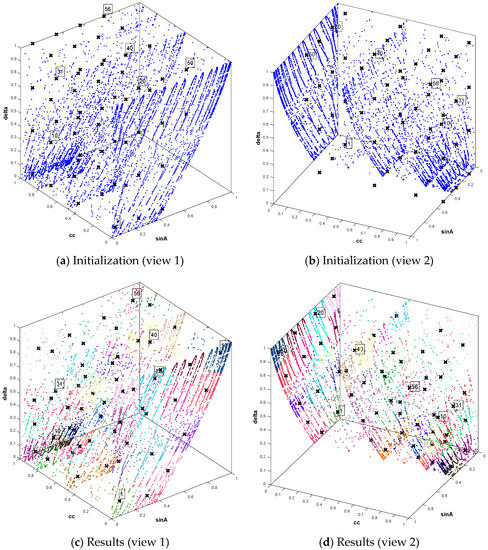
Figure 9.
Geometric interpretation of data initialization and clustering results using the k-means method.

Table 4.
Results of calculating the parameters for forecast accuracy estimating for various combinations.
The k-means clustering makes it possible to divide observations into clusters that are similar in terms of cloudiness, time of day and season. Observations combined in this way should have similar transparency index values .
A number of parameters are used for the numerical evaluation of transparency index observations obtained within the clusters: arithmetic mean value, median, mode, mean-square deviation. Observations that differ significantly from the rest in the cluster are recognized as outliers and are considered unreliable. The following expression is used for determining the cluster outliers:
where —the transparency index, (p.u.); —the transparency index standard deviation, (p.u.); —the number of transparency index standard deviations; —arithmetic mean, median or mode of the transparency index for a given cluster (p.u.).
Table 4 shows the results of calculating the parameters for forecasting accuracy estimation for various combinations of and .
The analysis of the Table 4 shows that the observations filtering using the transparency index median of each cluster has the greatest efficiency in determining outliers within the clusters; the number of the transparency index mean-square deviations for the confidence range is 1.5. The results of calculating the parameters for estimating the PVPP generation forecasting accuracy using the k-means method for filtering data are presented in Table 5.

Table 5.
Results of calculating the parameters for estimating the PVPP generation forecasting accuracy using the k-means method for data filtering.
Advantages of filtering the initial data using the k-means method: more accurate transparency index outliers identification compared to an empirical model, since the analysis takes into account the season and day time; the versatility of the proposed method for power plants various geographic locations; less chance of over-filtering observations compared to the empiric approach.
Disadvantages of filtering the initial data using the k-means method: high costs of computing resources, the calculation time for the considered example reached almost two h; more complex algorithm compared to the empirical model.
3.5. Filtration Models Comparative Analysis
Table 6 shows the comparison of the parameters for assessing the PVPP generation forecast accuracy for three scenarios: without filtering the source data, using an empirical filter, introducing the k-means approach.

Table 6.
Comparison of the short-term forecasting (STF) results for various filtration models.
The error assessment criteria analysis shows that the observations filtering using the k-means method has the best performance. The total error value is reduced by almost 2 times compared with the calculation without filtering and more than 1.5 times compared with the calculation using an empirical filter.
4. Photovoltaic Power Plants Generation Short-Term Forecast Operational Correction
4.1. General Approach to the PVPP Generation Operational Forecasting Models
When addressing the problem of PVPP short-term forecasting accuracy improvement, it should be outlined that there are several fundamentally different degrees of latitude. Typically, at first, the investigators justify the particular types and parameters of the forecasting approach. The next step is often addressing the data analytics issues, including Feature Engineering, applying practical knowledge to the dataset processing, data gaps elimination, outlier filtration, etc. The last, but not the least, direction to minimize the PVPP generation forecasting error is an adjustment of time resolution of the model. Indeed, it is naturally evident, that very-short term forecasts of PVPP generation demonstrate more accurate results for intra-hour or intra-day periods than multiple day-ahead forecasting models, based on numerical weather predictions. However, typically, the investigators address the behavior of their approaches for static time-domain models, which is justified in the majority of cases by the necessity to introduce another mathematical basis for different time-domains or other structures of the mathematical core of the proposed models, other features with different time resolutions, etc. The static time-domain operational forecasts of PVPP generation for an hour ahead perspective often turns out to be problematic, since the hourly interval is founded to be too large for the models with smaller time resolution (1-min, 5-min, 15-min, etc.) as far as one hour-ahead calculations in such circumstances are to be treated as 60, 12, 4 periods ahead forecasts, respectively. For this reason, the correlation between the PVPP generation at two adjacent hourly intervals is often poorly traced. Furthermore, vice versa, using single hour resolution models for hour-ahead perspective does meet the requirements of the power system operational control since the intra-hour deviations of PVPP generation are not taken into account.
In the present study, the authors have attempted to establish the bridge between the STF day-ahead forecasting system, implemented on multiple regression with k-means initial dataset filtration, with the operational hour-ahead PVPP generation forecast. The latter one is implemented on the basis of the supplementary STF error forecasting function, giving the opportunity to evaluate the STF error for the hour-ahead time horizon. The knowledge on what would be the mismatch of the STF for the hour-ahead perspective gives the opportunity to implement an operational (very-short term) forecast on the basis of the initially developed and optimized STF approach by providing STF forecasting error correction. The proposed approach is justified by another fact that PVPP generation STF error, if it occurs, exists for several time intervals straight, that is, several hours. This circumstance initiates using retrospective STF error data to make operational forecasts, since the STF errors time series turns out to be more predictable than of the PVPP operational forecast one because of the data noise, appearing in smaller time-domain models.
The object of study for operational forecasting is the same PVPP, as was investigated for the STF. Within this study, different methodologies of calculating the forecast for 1 h ahead are considered. In order to implement the operational forecast, based on the retrospective data of the STF errors, an STF error forecast is calculated for an hour ahead horizon. Based on the calculation results, the STF is corrected for the STF forecasted error, which will be essentially the operational forecast.
Thus, when compiling the operational forecast in all the models, the STF error appears as the forecasted value when determining the one-hour-ahead PVPP generation:
where —PVPP generation STF error, (kW∙h); —PVPP generation actual value, (kW∙h); —PVPP generation STF, (kW∙h).
The calculation algorithm used for operational PVPP generation forecasting consists of the following items, presented in Figure 10, where —PVPP generation operational forecast, (kW∙h); —PVPP generation STF, (kW∙h); —operational forecast of PVPP generation STF error, (kW∙h).
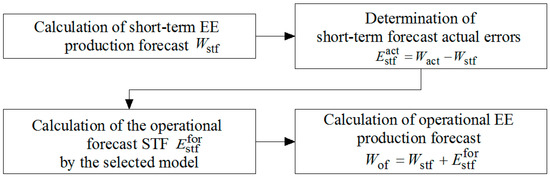
Figure 10.
Block diagram of operational forecast algorithm.
The proposed algorithm makes it possible to promptly (1 h ahead) correct STF stationary errors (that is, those that occur for several hours straight). In this case, the cumulative error of the methodology for calculating the STF will be corrected: the error associated with the assessment of the cloudiness influence on the share of solar energy losses when passing through the cloud layer; errors in cloudiness forecasts, as well as errors of other mathematical models.
4.2. PVPP Generation Operational Forecasting Models Description
To implement the operational forecasting on the basis of retrospective data on STF errors, the possibility of using a number of statistical mathematical models is considered [43].
4.2.1. Persistence Model (Represents the So-Called “Naive” Approach)
According to this approach, it is assumed that the forecasted value at the next time step is equal to the actual value at the current step. Thus:
where —time interval, (hour); —STF error operational forecast for 1 h ahead, (kW∙h); —actual value of the STF error, (kW∙h).
This model makes it possible to obtain fairly accurate transparency index operational forecasts in those cases when a stationary STF error occurs, which persists for several time intervals straight, constant in magnitude and sign. At the same time, in the case of a rapid change in the STF error value or sign, the operational forecast will be less accurate than the STF.
4.2.2. Moving Average Model (Is an Advanced Inertial Model)
This is a well-known time series smoothing technique that eliminates random fluctuations in the time series. The moving average model (MA (M)) can be represented in accordance with the following expression:
where —the number of observations in the period used to calculate the mean, (dimensionless value); —the offset relative to the current time interval, (hour); —STF error actual value for the time interval , (p.u.), the number of observations in the period—, used to calculate the average value, denotes the model order.
When using the MA (M) model, the initial values of the time series are replaced by the arithmetic mean within the selected time period. When forecasting for the next interval, the period is shifted by one observation, and the calculation of the mean is repeated. The periods use the same time frames for determining the average. The wider the frame used for smoothing, the smoother the trend is.
4.2.3. Autoregressive Model
Time series model (AR (p)), where the time series values are linearly dependent on the previous values of the same series. It is assumed that STF errors time series can be represented as an autoregressive function, since this random process proceeds approximately uniformly in time, while random fluctuations occur around some mean value close to zero. Moreover, neither the average amplitude nor the nature of these fluctuations show significant changes over time. The autoregressive process is defined as follows:
where —the constant (free) term, (dimensionless quantity); —the model order, that is the number of previous time intervals used for the calculation, (dimensionless value); —the autoregressive coefficient for time interval, (dimensionless quantity).
To estimate the autoregression coefficients, as well as for other regression models, the least squares method can be used. The autoregression coefficients are calculated using the Gauss transformation:
where —the autoregression coefficients vector; —the independent variables matrix, composed of actual values ; —the dependent variables vector, composed of actual values .
4.2.4. Autoregressive Moving Average Model
The ARMA(p,T) model is a generalization of MA и AR processes. The STF errors time series treatment, which was smoothed using the moving average model, shows that it is stationary, as the original time series. Thus, it is also possible to use an autoregressive model for the moving averages time series. The autoregressive process for a moving average is defined as follows:
where —the model order, that is, the number of the moving average previous values used for the calculation, (dimensionless value); —the autoregressive coefficient for the moving average value, (p.u.); —the shift relative to the time interval corresponding to the moving average current value, (hour); —the shift relative to the current time interval, (hour); —the number of observations in the period used to calculate the average, (dimensionless value); —the STF error actual value for the time interval within the period , (kW∙h), where the number of observations in the period , used to calculate the average denotes the order of the MA model, and the number of moving averages , used for the calculation denotes the order of the AR model.
4.2.5. Autoregressive Model with Exogenous Inputs
ARX(p,q) model represents an autoregressive process that also takes into account the values that do not belong to the considered time series. As previously noted, a simple autoregressive AR model uses the previous time series values as features, without using any other features. At the same time, when making the forecast, one may take into account other features that affect the transparency index, that is, the cloudiness . The autoregressive process using cloudiness as an exogenous feature is defined as follows:
where —the order of the autoregressive inputs, that is the number of STF error previous values used for the calculation, (dimensionless value); —the autoregression coefficient for of STF error value, (dimensionless value); —the exogenous inputs order, that is, the number of cloudiness values used for the calculation, (dimensionless value); —the autoregression coefficient for of cloudiness, (dimensionless value); the actual cloudiness value for the time interval , (p.u.); the number of the STF error previous values p, used for the calculation denotes the AR model order, and the number of cloud values q, used for the calculation denotes the X model order.
5. Comparison of Operational and Short-Term Forecasting Models
Table 7 shows the parameters comparison for assessing the PVPP generation forecast accuracy for various operational forecast models. As far as the models under consideration have different number of predictors, the adjusted R2 metrics is introduced as a model quality criterion. As in the previous case (short-term forecast), adjusted R2 also demonstrates how well the model fits the data, but the total score is adjusted according to the number of terms in the model:
where —R-square measure; n—number of samples in the set; k—number of variables in the model.

Table 7.
Parameters comparison for PVPP operational forecast accuracy assessment.
The error assessment analysis shows that the second-order autoregressive model AR(2) has the best indicators among the operational forecast models. The parameters characterizing the results of PVPP generation operational forecast accuracy assessment using the second-order autoregressive model AR(2) are presented in Table 8.

Table 8.
The parameters calculating results for assessing the PVPP generation operational forecast accuracy.
Figure 11 demonstrates the comparison of the PVPP generation actual values, the PVPP generation STF using the initial data filtration by the k-means method and the operational forecast using the second-order autoregressive model AR(2).
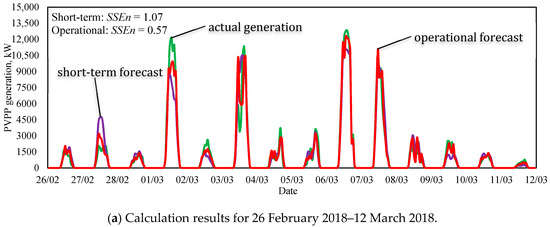
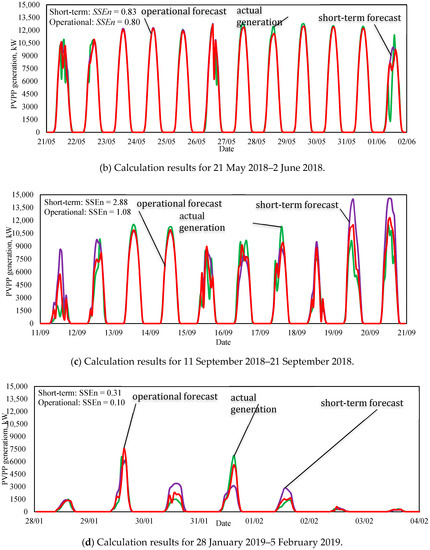
Figure 11.
The comparison of short-term and operational PVPP forecasts with actual values.
As one can see from Figure 11a–d, the operational forecast makes it possible to refine the short-term forecast, the curve of operational forecast absolute errors has a flat character compared to the short-term forecast, the absolute forecasting error values are closer to zero. Table 9 demonstrates the comparison of the short-term and operational PVPP generation forecasting accuracy.

Table 9.
The parameters comparison for assessing the short-term and operational PVPP generation forecast accuracy.
When dealing with stochastic phenomena, providing a 100% accurate forecast is problematic. In most cases, we can only talk about the probability of the forecasted to meet the confidence range. To assess the reliability of the proposed short-term and operational forecasting models, the confidence probabilities corresponding to the intervals of ±1 MW and ±2 MW were also calculated. The values of these probabilities are presented in Table 10.

Table 10.
The reliability parameters comparison of PVPP generation operational and short-term forecast.
As can be seen from Table 10, for STF 78.9% of forecasts are characterized by an error not exceeding 1 MW (6.7% of the plant’s installed capacity), 92.2% of forecasts are characterized by an error not exceeding 2 MW (13.3% of the plant’s installed capacity). At the same time, for operational forecast, 88.5% of the forecasts are characterized by an error not exceeding 1 MW, and 97.5% of forecasts are characterized by an error not exceeding 2 MW.
The results of the parameter comparison for assessing the PVPP generation short-term and operational forecasts show that the error characteristics are finally improved by almost 1.5 times. At the same time, the operational forecast makes it possible to obtain more reliable estimates of the PVPP generation forecasted values: the number of operational forecasts belonging to the confidence interval of ±1 MW is almost 10% more, and the number of forecasts belonging to the confidence interval of ±2 MW is observed 5% more frequently. Thus, we can conclude about the effectiveness of the proposed methodology for operational forecasting based on retrospective data on short-term forecasting errors.
6. Forecasting System Hard-Ware Implementation for Autonomous Photovoltaic Power Plants
The discussed above forecasting algorithms were implemented using a distributed computing system that included a low-cost x86 embedded computer and an FPGA (Figure 12).

Figure 12.
Hardware architecture used for forecasting algorithms implementation.
In general, the architecture of the implemented computing system repeats the one proposed in [44]. FPGA in this architecture is used as a custom accelerator, which is built on a basis of one of more specialized computational cores (SCCs) and Ethernet POWERLINK communication core [45]. Each SCC, which includes a combination of a matrix coprocessor [46] and a general-purpose processor and performs computations requested by managing device, built on the basis of an x86 embedded computer running Linux operating system. This architecture is inspired by the ones used in space robotics [47], which makes it suitable and attractive for adaptation to other application areas where the robust and maintenance-free operation of equipment is required in long terms; for example, for autonomous PVPPs.
The developed x86 software algorithms and FPGA firmware were first verified using the Vmodel toolbox [48] simulation tool, and then uploaded into Intel NUC8IN computer and a Digillent Nexys 4 DDR kit FPGA (Figure 12). The estimation evaluated during model verification was the same as the ones provided by the real hardware. The worst-case difference between evaluated forecasts and reference ones presented in Table 7 was 0.04883%. This error is caused by the use of fixed-point calculations on FPGA accelerators. Meanwhile, as it can be seen from Table 7, it is significantly less than the error of the forecasting methods themselves.
This experiment demonstrates that the discussed forecasting methods can be implemented using embedded equipment and integrated into autonomous photovoltaic power plants. Moreover, the proposed implementation approach is scalable and, as it was shown in [44], even a significantly larger amount of data can be processed without the use of high-performance servers just by increasing the number of distributed FPGA-based accelerators.
7. Conclusions
The present study addresses the development of short-term and operational forecasting methods of photovoltaic power plants, which arose in response to the energy sector transition, characterized by the growing share of stochastic power generation. As it was stated in the introduction, reliable forecasting systems are the most effective and least capital-intensive measures that allow for the integration of stochastic generation sources into the power systems.
Based on the results of the previously carried out investigations, a short-term day-ahead PVPP generation forecasting system was developed by an effective combination of astronomical and statistical approaches. The step-by-step forecasting procedure, comprising the global horizontal irradiance identification, tilted surface irradiance assessment and, finally, calculation of the PV power plant output was implemented, providing rich opportunities for forecasting results’ interpretation and overall model flexibility, allowing us to take into account the operational state of the power generation equipment, switchgear composition, operation modes of the adjacent power system and other external factors.
In the course of the short-term forecasting system industrial piloting, it was determined that the greatest error (more than 70% of the total value of mean absolute percentage error) in the PVPP generation forecast calculation is introduced at the stage of determining the transparency index according to the regression model due to the ambiguity of cloudiness impact on the forecasted value of the transparency index. Given that from the point of view of PVPP power output, there is a fundamental difference of various meteorological conditions and events, which may be characterized by similar weather forecasting parameters, acquired from the open-source weather data provider, it was decided to focus the attention on the dataset filtration. The idea was to eliminate the dataset outliers and to use separate training sets for various weather conditions and/or seasons to enhance the “sensibility” of the model to the weather type.
The results of studying the possibility of filtering the initial data to improve the PVPP generation short-term forecast accuracy allow us to conclude that the application of the k-means methodology is the most effective. The PVPP generation forecast error is reduced by almost 2 times compared with the calculation without filtering and more than 1.5 times compared with the calculation using an empirical filter. The mean absolute percentage error for PVPP day-ahead forecasting with k-means data filtration was calculated to be 18.66%. Thus, it can therefore be concluded that the use of the k-means method for filtering the initial data allows for reducing the PVPP generation forecast error introduced at the stage of forecasting the transparency index to obtain a more accurate forecasting result.
Subsequent improvement of PVPP forecasting accuracy was achieved by adjusting the time-domain of the model by adding the intra-day forecasting procedure, realized in the form of forecasting error prediction. It was assumed that the knowledge of present-day forecasted PVPP generation and the mismatch of the forecasted values compared to the actual data, acquired from irradiance and electrical meters, will give us the opportunity to develop a powerful multi-time-domain forecasting tool. Unlike the other existing approaches, the authors have attempted to establish the bridge between the day-ahead PVPP forecast and the operational hour-ahead PVPP generation forecast by introducing an error forecasting procedure. We provided the comparison of the persistence model, moving average, autoregression, autoregressive moving average and autoregression with exogenous features for short-term forecast error prediction. It was found that the second-order autoregression model AR(2) for short-term forecasting error prediction outperformed all of the methods under consideration.
The developed approach of operational forecasting makes it possible to reduce the total error by almost 1.5 times in comparison with the short-term forecast. The mean average percentage error was calculated to be about 13%. At the same time, the operational forecast makes it possible to obtain more robust estimates of the PVPP generation predicted values: the percentage of operational forecasts meeting the confidence interval of ±1 MW (for 15 MW PVPP) is more than 88%, and the percentage of the forecasts meeting the confidence interval of ±2 MW is more than 97%. Thus, this confirms the effectiveness of the proposed methodology for an operational forecast based on retrospective data on short-term forecasting errors.
The proposed forecasting software was installed on a low-cost distributed computing system, characterized by robust and maintenance-free operation, which is of great importance for power generation facilities operated in the autonomous mode and/or providing system service at the wholesale energy market. Moreover, in the course of PVPP operation, the retrospective dataset is being permanently updated with the newly introduced measurements and calculation results. The proposed hardware system has outstanding scaling properties, so there is no need to introduce high-performance computing facilities even for the Big Data sets.
Author Contributions
Conceptualization, S.A.E. and D.A.S.; data curation, S.A.E., A.I.K., D.A.S. and A.M.R.; formal analysis, V.V.D. and A.M.R.; funding acquisition, A.I.K.; investigation, S.A.E., D.A.S. and D.N.B.; methodology, S.A.E., A.I.K. and D.A.S.; project administration, A.I.K.; resources, S.A.E., V.V.D. and D.N.B.; software, S.A.E., A.I.K., V.V.D. and A.M.R.; Supervision, S.A.E. and A.I.K.; validation, D.A.S., V.V.D., A.M.R. and D.N.B.; visualization, D.A.S.; writing—original draft, S.A.E., A.I.K. and D.A.S.; writing—review and editing, D.N.B. All authors have read and agreed to the published version of the manuscript.
Funding
No funding was received for this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- REN21. Renewables 2017 Global Status Report; REN21: Paris, France, 2017; ISBN 978-3-9818107-6-9. [Google Scholar]
- Stiphout, A.; Brijs, T.; Belmans, R.; Deconinck, G. Quantifying the importance of power system operation constraints in power system planning models: A case study for electricity storage. J. Energy Storage 2017, 13, 344–358. [Google Scholar] [CrossRef]
- Habib, A.; Sou, C.; Hafeez, M.H.; Arshad, A. Evaluation of the effect of high penetration of renewable energy sources (RES) on system frequency regulation using stochastic risk assessment technique (an approach based on improved cumulant). Renew. Energy 2018, 127, 204–212. [Google Scholar] [CrossRef]
- Tielens, P.; Van Hertem, D. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Farhoodnea, M.; Mohamed, A.; Shareef, H.; Zayandehroodi, H. Power quality impact of renewable energy-based generators and electric vehicles on distribution systems. Procedia Technol. 2013, 11, 11–17. [Google Scholar] [CrossRef]
- Triviño-Cabrera, A.; Longo, M.; Foiadelli, F. Impact of renewable energy sources in the power quality of the Italian electric grid. In Proceedings of the 11th IEEE International Conference on Compatibility, Power Electronics and Power Engineering, Cadiz, Spain, 4–6 April 2017; pp. 576–581. [Google Scholar]
- Balaban, G.; Lazaroiu, G.C.; Dumbrava, V.; Sima, C.A. Analysing Renewable Energy Source Impacts on Power System National Network Code. Inventions 2017, 2, 23. [Google Scholar] [CrossRef]
- Lee Hau Aik, D.; Andersson, G. Impact of Renewable Energy Sources on Steady-state Stability of Weak AC/DC Systems. CSEE J. Power Energy Syst. 2017, 3, 319–430. [Google Scholar] [CrossRef]
- Ameur, A.; Loudiyi, K.; Aggour, M. Steady State and Dynamic Analysis of Renewable Energy Integration into the Grid using PSS/E Software. Energy Procedia 2017, 141, 119–125. [Google Scholar] [CrossRef]
- Tonkoski, R.; Turcotte, D.; El-Fouly, T.H.M. Impact of High PV Penetration on Voltage Profiles in Residential Neighborhoods. IEEE Trans. Sustain. Energy 2012, 3, 518–527. [Google Scholar] [CrossRef]
- Petinrin, J.O.; Shaaban, M. Impact of renewable generation on voltage control in distribution systems. Renew. Sustain. Energy Rev. 2016, 65, 770–783. [Google Scholar] [CrossRef]
- Begovic, M.; Pregelj, A.; Rohatgi, A.; Novosel, D. Impact of renewable distributed generation on power systems. In Proceedings of the 34th Annual Hawaii International Conference on System Science, Maui, HI, USA, 3–6 January 2001; pp. 654–663. [Google Scholar]
- Essallah, S.; Bouallegue, A.; Khedher, A. Optimal Sizing and Placement of DG Units in Radial Distribution System. Int. J. Renew. Energy Res. 2018, 8, 166–167. [Google Scholar]
- Lajda, P. Short-Term Operation Planning in Electric Power Systems. J. Oper. Res. Soc. 1981, 32, 675–682. [Google Scholar] [CrossRef]
- Navarro, R. Short and medium term operation planning in electric power systems. IEEE/PES Power Syst. Conf. Expo. 2009, 1, 1–8. [Google Scholar]
- Talari, S.; Shafie-khah, M.; Osório, G.J.; Aghaei, J.; Catalão, J.P. Stochastic modelling of renewable energy sources from operators’ point of-view: A survey. Renew. Sustain. Energy Rev. 2018, 81, 1953–1965. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, N.; Su, W. A Literature Review of Stochastic Programming and Unit Commitment. J. Power Energy Eng. 2015, 3, 206–214. [Google Scholar] [CrossRef]
- Aien, M.; Rashidinejad, M.; Firuz-Abad, M.F. Probabilistic power flow of correlated hybrid wind-PV power systems. IET Renew. Power Gener. 2014, 8, 649–658. [Google Scholar] [CrossRef]
- Zachary, S.; Dent, C.J. Probability theory of capacity value of additional generation. J. Risk Reliab. 2012, 226, 33–43. [Google Scholar] [CrossRef]
- Ioannou, A.; Angus, A.; Brennan, F. Risk-based methods for sustainable energy system planning: A review. Renew. Sustain. Energy Rev. 2017, 74, 602–615. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Akpeji, K.O.; Akinola, O.O. Prioritized Rule Based Load Management Technique for Residential Building Powered by PV/Battery System. Eng. Sci. Technol. Int. J. 2017, 20, 859–873. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- Prema, V.; Rao, K.U. Development of statistical time series models for solar power prediction. Renew. Energy 2015, 83, 100–109. [Google Scholar] [CrossRef]
- Kaplanis, S.; Kaplani, E. A model to predict expected mean and stochastic hourly global solar radiation I(h;nj) values. Renew. Energy 2007, 32, 1414–1425. [Google Scholar] [CrossRef]
- Ferrari, S.; Lazzaroni, M.; Piuri, V.; Cristaldi, L.; Faifer, M. Statistical models approach for solar radiation prediction. IEEE Int. Instrum. Meas. Technol. Conf. 2013, 1, 1734–1739. [Google Scholar]
- Li, Y.; He, Y.; Su, Y.; Shu, L. Forecasting the daily power output of a grid-connected photovoltaic system based on multivariate adaptive regression splines. Appl. Energy 2016, 180, 392–401. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Moore, K.; Kmiecik, M.; Chain, C.; George, R.; Vignola, F. A new operational model for satellite-derived irradiances: Description and validation. Sol. Energy 2002, 73, 307–317. [Google Scholar] [CrossRef]
- Mathiesen, P.; Collier, C.; Kleissl, J. A high-resolution, cloud-assimilating numerical weather prediction model for solar irradiance forecasting. Sol. Energy 2013, 92, 47–61. [Google Scholar] [CrossRef]
- Gohari, M.I.; Urquhart, B.; Yang, H.; Kurtz, B.; Nguyen, D.; Chow, C.W.; Ghonima, M.; Kleissl, J. Comparison of solar power output forecasting performance of the total sky imager and the University of California, San Diego Sky Imager. Energy Procedia 2014, 49, 2340–2350. [Google Scholar] [CrossRef]
- Larson, D.P.; Nonnenmacher, L.; Coimbra, C.F.M. Day-ahead forecasting of solar power output from photovoltaic plants in the American Southwest. Renew. Energy 2016, 91, 11–20. [Google Scholar] [CrossRef]
- Chaouachi, A.; Kamel, R.M.; Ichikawa, R.; Hayashi, H.; Nagasaka, K. Neural Network Ensemble-based Solar Power Generation Short-Term Forecasting. Int. J. Inf. Math. Sci. 2009, 5, 332–337. [Google Scholar] [CrossRef]
- Monteiro, C.; Santos, T.; Fernandez-Jimenez, L.A.; Ramirez-Rosado, I.J.; Terreros-Olarte, M.S. Short-term power forecasting model for photovoltaic plants based on historical similarity. Energies 2013, 6, 2624–2643. [Google Scholar] [CrossRef]
- Zeng, J.; Qiao, W. Short-term solar power prediction using a support vector machine. Renew. Energy 2013, 52, 118–127. [Google Scholar] [CrossRef]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M. Numerical weather prediction (NWP) and hybrid ARMA/ANN model to predict global radiation. Energy 2012, 39, 341–355. [Google Scholar] [CrossRef]
- Zheng, F.; Zhong, S. Time series forecasting using a hybrid RBF neural network and AR model based on binomial smoothing. Int. J. Math. Comput. Sci. 2011, 75, 1471–1475. [Google Scholar]
- Khan, I.; Zhu, H.; Yao, J.; Khan, D.; Iqbal, T. Hybrid Power Forecasting Model for Photovoltaic Plants Based on Neural Network with Air Quality Index. Int. J. Photoenergy 2017, 1. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, H.; Wu, Y.; Dong, Y. Forecasting solar radiation using an optimized hybrid model by Cuckoo Search algorithm. Energy 2015, 81, 627–644. [Google Scholar] [CrossRef]
- Snegirev, D.A.; Eroshenko, S.A.; Valiev, R.T.; Khalyasmaa, A.I. Algorithmic Realization of Short-term Solar Power Plant Output Forecasting. In Proceedings of the II International Conference on Control in Technical Systems (CTS’2017), Saint Petersburg, Russia, 25–27 October 2017; pp. 49–52. [Google Scholar]
- Snegirev, D.A.; Valiev, R.T.; Eroshenko, S.A.; Khalyasmaa, A.I. Functional assessment system of solar power plant energy production. In Proceedings of the International Conference on Energy and Environment (CIEM), Bucharest, Romania, 19–20 October 2017; pp. 349–353. [Google Scholar]
- Matuszko, D. Influence of the extent and genera of cloud cover on solar radiation intensity. Int. J. Climatol. 2012, 32, 2403–2414. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.; Netanyahu, N.; Piatko, C.; Silverman, R.; Wu, A. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 24, 881–892. [Google Scholar] [CrossRef]
- Boland, J. Time series and statistical modelling of solar radiation. In Recent Advances in Solar Radiation Modelling; Springer: Berlin/Heidelberg, Germany, 2008; pp. 283–312. [Google Scholar]
- Romanov, A.M.; Romanov, M.P.; Manko, S.V.; Volkova, M.A.; Chiu, W.-Y.; Ma, H.-P.; Chiu, K.-Y. Modular Reconfigurable Robot Distributed Computing System for Tracking Multiple Objects. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Romanov, A.M. A novel architecture for Field-Programmable Gate Array-based Ethernet Powerlink controlled nodes. Tr. MAI 2019, 106, 15–30. [Google Scholar]
- Romanov, A.M.; Slaschov, B.V. FPGA-based Kalman filtering for motor control. In Network Security and Communication Engineering; CRC Press: Boca Raton, FL, USA, 2015; pp. 569–572. [Google Scholar] [CrossRef]
- Romanov, A.M. A review on control systems hardware and software for robots of various scale and purpose. Part 3. Extreme robotics. Russ. Technol. J. 2020, 8, 14–32. (In Russian) [Google Scholar] [CrossRef]
- Romanov, A.; Bogdan, S. Open source tools for model-based FPGA design. In Proceedings of the 2015 International Siberian Conference on Control and Communications (SIBCON), Omsk, Russia, 21–23 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).