Next Article in Journal
Feasibility Study of SQp and SQs Attributes Application for Facies Classification
Next Article in Special Issue
Assessing Flood Hazard at River Basin Scale with an Index-Based Approach: The Case of Mouriki, Greece
Previous Article in Journal / Special Issue
The Integrated System of Hydrological Forecasting in the Ussuri River Basin Based on the ECOMAG Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 8
Issue 1
10.3390/geosciences8010006
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Flood Hazard Management in Public Mountain Recreation Areas vs. Ungauged Fluvial Basins. Case Study of the Caldera de Taburiente National Park, Canary Islands (Spain)

by
Julio Garrote
1,*,
Andrés Díez-Herrero
2,
José M. Bodoque
3,
María A. Perucha
2,
Pablo L. Mayer
4 and
Mar Génova
5
1
Department of Geodynamics, Complutense University of Madrid, E-28040 Madrid, Spain
2
Geological Survey of Spain (IGME), Ríos Rosas 23, E-28003 Madrid, Spain
3
Mining and Geological Engineering Department, University of Castilla-La Mancha, E-45071 Toledo, Spain
4
Physical Geography and Environment Group, Institute of Oceanography and Global Change (IOCAG), University of Las Palmas de Gran Canaria, E-35003 Las Palmas de Gran Canaria, Spain
5
Forest Engineering Technic School, Technic University of Madrid, E-28040 Madrid, Spain
*
Author to whom correspondence should be addressed.
Geosciences 2018, 8(1), 6; https://doi.org/10.3390/geosciences8010006
Submission received: 13 November 2017 / Revised: 20 December 2017 / Accepted: 22 December 2017 / Published: 31 December 2017
(This article belongs to the Special Issue Integrated Risk Analysis and Management of Floods)
Browse Figures
Versions Notes

Abstract

:
Las Angustias River is an ungauged stream in the Caldera de Taburiente National Park (Spain), where frequent intense flash-flood events occur. The aim of this research is to analyze the flood hazard at the Playa de Taburiente. Based on the limited information available (short time-series of daily precipitation), a statistical frequency analysis of 24 h rainfall was completed and the precipitation results were transformed into surface runoff. To determine if the model underestimates the flows that are generated in the basin, the dendro-geomorphological information available was used to calibrate results. The results of the HMS model were significantly lower. At this point, both the rainfall data and the rainfall-runoff model were re-analyzed to maximize the rainfall intensity values and the runoff generated (increasing the CN value for the basin). For the 1997 flood event, a 1250 m3·s−1 flood minimizes the RMSE for the disturbed tree sample; this flow value also clearly exceeds any peak flow derived from the rainfall-runoff analysis. It is only when rainfall intensity and surface runoff are maximized that the peak flows obtained approximate those associated with dendro-geomorphological data. The results highlight the difficulties of flood hazard management in ungauged torrential basins in mountain recreational areas (such as National Parks). Thus, in the absence of flow records, when considering the maximum rainfall intensity scenario may be a useful and effective tool for flood risk management.

1. Introduction

Flash floods are common in mountain basins, as a result of their high slopes and quasi-circular morphology, the resulting strong connectivity, and high order streams [1,2,3]. The precipitation in these basins also has an important orographic component, and as a result, is very variable in spatio-temporal terms [4,5]. This means that mountain basins are highly prone to extreme precipitation events, in both total volume and intensity. The resulting floods have a rapid hydrological response, characteristically defining peaky hydrographs (i.e., short lag time), and reach their peak flows within a few hours, thus allowing for little or no advance warning to predict flood damage [6,7]. These basins usually have high landscape value and recreational use and with the characteristic hydrological response of mountain basins this poses a considerable risk to life [8], as evidenced in Spain in the 1996 Biescas disaster [9,10].
Flash-floods in the Caldera de Taburiente National Park have caused the death of several hikers in an area where over 65,000 visitors use the hiking trails each year. Four people died in 2001 when they were swept away while walking along the bottom of the ravine. Many people have been stranded in the park as a result of rising river levels during floods, leading to rescue operations and the temporary closure of the trails. In October 2011, more than forty visitors were stranded in the camping area, and had to be rescued by helicopter. Finally, flash-floods have important financial implications for the national park infrastructure, causing damage to trails, bridges, and aqueducts, and for reforestation projects using endemic species which are currently underway. Since 2009, the managers of the national park have spent considerable resources (over 700,000 euros just in 2010) on planting endemic willow species (Salix canariensis) in the alluvial river bed. During the first flood event after planting, most of the established endemic trees were carried out to the Atlantic Ocean. Flood risk analysis and planning is therefore essential for national park managers, civil protection, and other authorities, including water resources managers.
Flood risk analysis and management is clearly conditioned by data availability. Flow quantile estimates can be obtained directly by statistical flood frequency analysis (FFA) of maximum discharge provided that the time series are statistically significant. When flow data is unrepresentative but there is enough precipitation data, the alternative is to run, calibrate, and validate hydrologic rainfall-runoff models, which provide output data to determine the flood-prone area and the hazard parameters using hydraulic models. However, there is often insufficient data in mountain basins, either because the data simply does not exist, or because the accuracy is poor in terms of spatio-temporal statistical significance. As a result, indirect flood characterization methods are increasingly being used as an alternative [11]. In this context, different paleostage indicators (PSI) and high-water marks (HWM) have been used to characterize past floods, forming the basis of paleohydrology and post-event flood analysis [12,13]. Indirect data sources can be grouped as: (i) geological/geomorphological; (ii) historical; and, (iii) botanical.
There are very few studies available of peak flow assessment in ungauged basins located within National Parks. The studies carried out in the 1980s by the U.S. Geological Survey (USGS) in collaboration with the National Park Service could be mentioned here, including Glacier, Olympic, and Yellowstone National Parks [14,15,16]. In general terms, these studies were carried out in national parks in areas that are much larger than the one in the Caldera de Taburiente National Park. In the USGS research, the methodological approach for peak flow estimation is based on the use of regional multiple regression equations, obtained from flood behavior in gauged basins. This type of approach is not applicable to the study of peak flows in Caldera de Taburiente N.P. due to the absence of both gauged basins in the area, and of regional multiple regression equations.
Calibrating hydrological and hydraulic models of ungauged basins requires further assessments, and remains an ongoing task for hydrological sciences [17,18,19,20]. In this context, estimating model parameters is usually achieved by transference, regionalization, or using local physical characteristics.
For the above reasons, this paper offers an analysis of peak flows that are associated with different return periods and a 1997 flood event, from the only available basin information: a short record from a few rainfall gauging stations, and dendro-geomorphological data. Based on the available data, a classic statistical frequency analysis of 24 h rainfall data is proposed, followed by reprocessing available rainfall information to generate high intensity precipitation events. Implementing all of these rainfall events in a hydrological model obtains high variability in peak flow values in the study area. The availability of dendro-geomorphological data in the area enables us to establish which of the previously generated rainfall events show a stronger relationship with peak flows derived from dendro-geomorphological evidence. This allows for us to propose the best methodological approach for flood hazard assessment in ungauged basins within a National Park, where flood risk management needs differ from other natural areas.

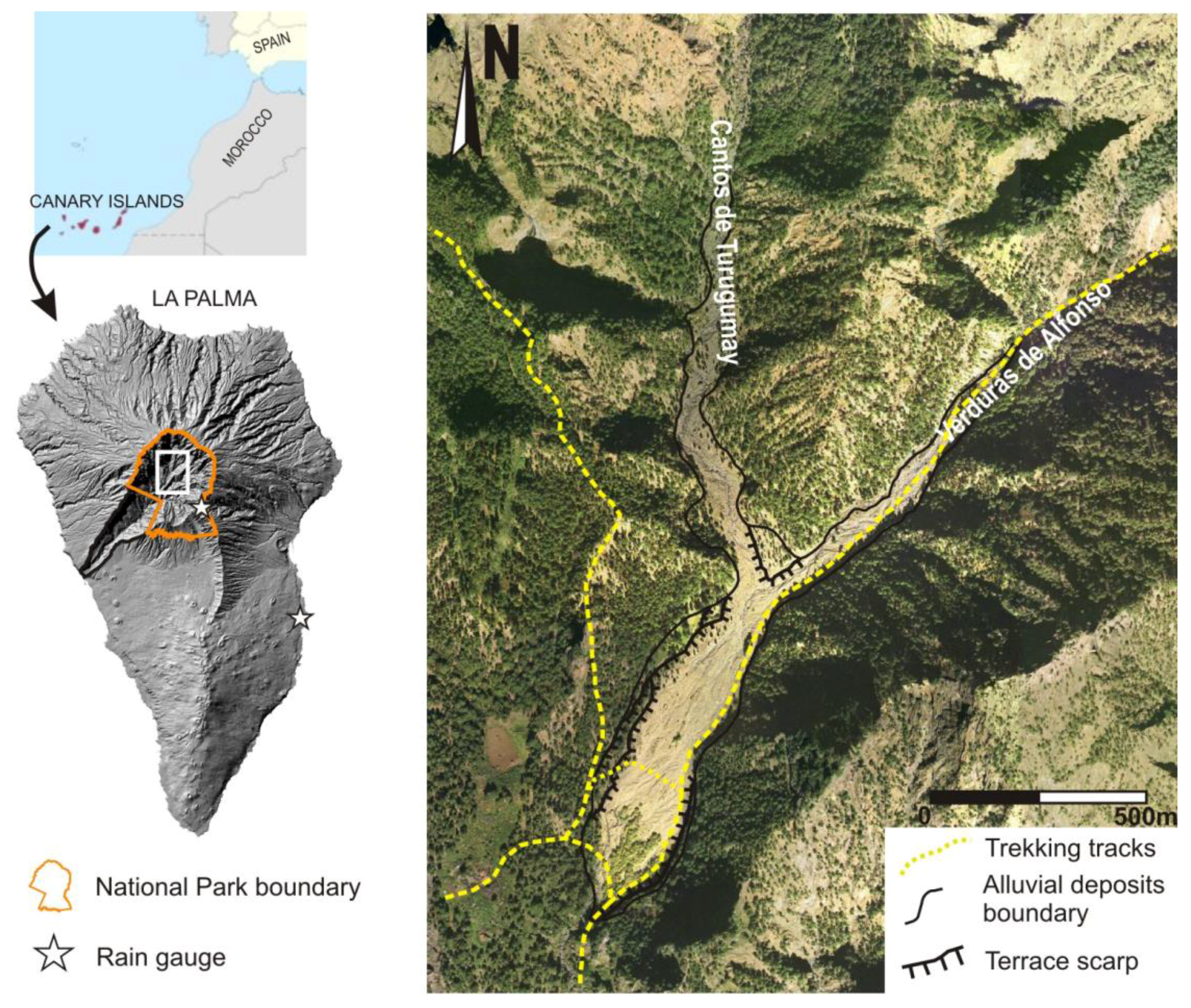
2. Case Study Area

The Caldera de Taburiente National Park is on the island of La Palma, the north-westernmost island of the Canary Islands archipelago, Spain (Figure 1). Declared a national park in 1954, this area of 47 km2 is centrally situated in the northern part of the island (28°40′–28°46′ N, 14°08′–14°13′ W (Greenwich Meridian)). The altitude ranges from 2426 m above sea level (a.s.l.) in the Roque de Los Muchachos to 430 m a.s.l. in the Barranco de Las Angustias just on the edge of the park.
The main part of the park is formed by the headwaters of the Barranco de Las Angustias, a semi-circular basin 8 km in diameter and 2000 m from top to bottom, resembling a great volcanic crater or caldera, although its morphology is in fact the result of the superposition of several volcanic edifices, erosive phases, and large landslides [21]. This research focuses on the central area of the park, known as ‘Playa de Taburiente’, which is a Y-shaped 2 km long stream reach, formed by two gorges, the ‘Verduras de Alfonso’ and ‘Cantos de Turugumay’ ephemeral rivers, and the Taburiente River, the result of their confluence (Figure 1).

2.1. Geology

The Canary Islands were formed by volcanic activity around 20 Ma ago with an approximately westward age progression, with La Palma and El Hierro the two most recent islands of the archipelago. The volcanic history of La Palma originated around 4 Ma ago when a seamount formed on the Jurassic oceanic crust and was subsequently elevated to an altitude of up to 1500 m a.s.l., where it now forms the Basal Complex [22]. Subaerial activity started around 2.0 Ma [23], when a multi-stage shield volcano was formed. This central edifice experienced at least one major collapse, resulting in a landslide and subsequent rebuilding of the edifice [23,24]. Subaerial volcanic reactivation, with explosive volcanism predominating during its initial stages producing abundant volcanoclastic and phreatomagmatic materials at the base of the subaerial edifice, continued until at least 0.41 Ma. Landslides on the Taburiente and Cumbre Nueva around 0.7 Ma resulted in the formation of the Caldera de Taburiente by incision and retrogressive erosion [23].

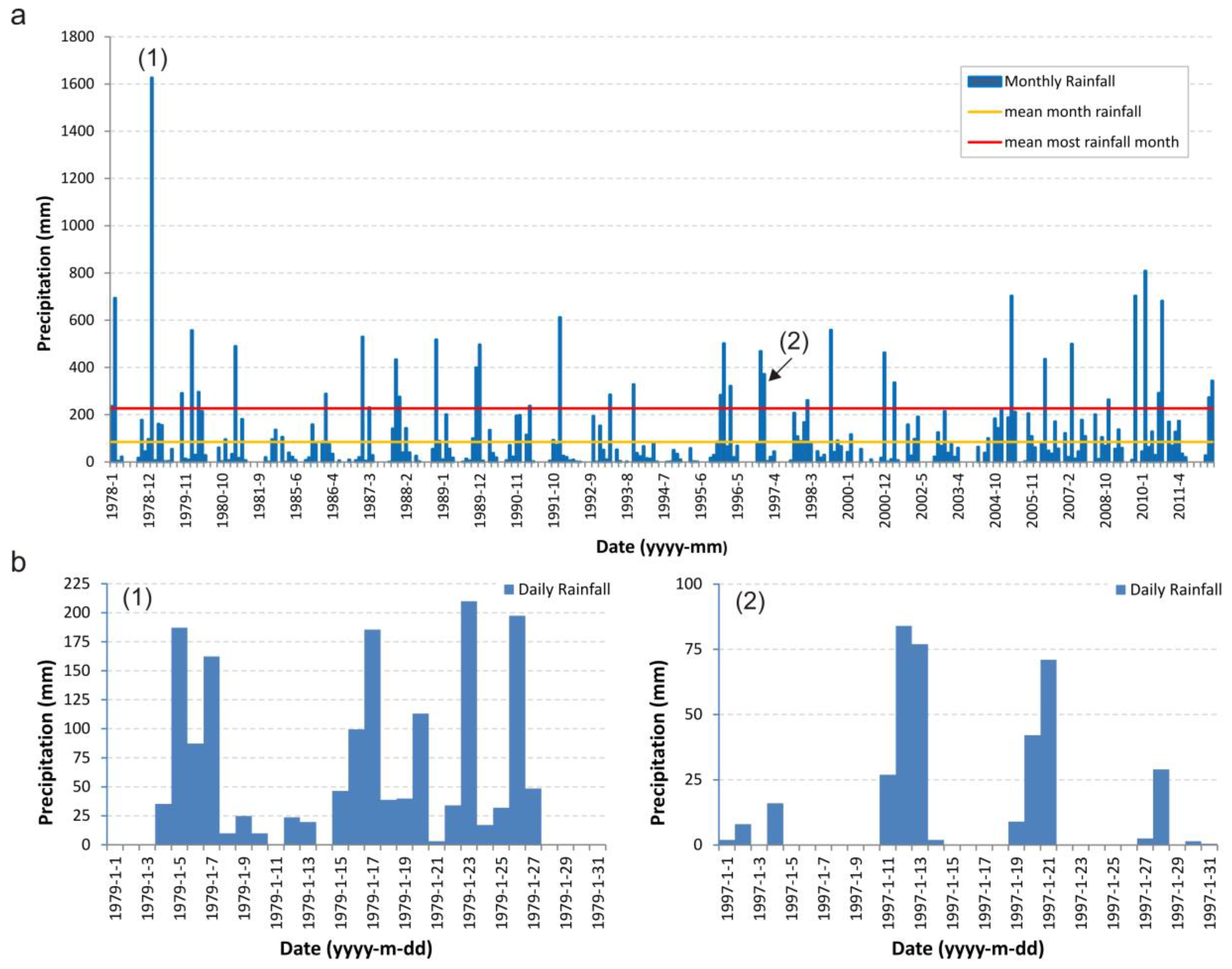
2.2. Precipitation

The three main characteristics of the rainfall in the Caldera de Taburiente are: (i) inter-annual irregularity; (ii) seasonality; and, (iii) torrentiality. These characteristics are also evident on the E and SE slopes of other islands in the Canary archipelago [25,26]. The mean annual rainfall is 1018.6 mm, but this is irregularly distributed (i), so that the coefficient of variance is 51.7% and the standard deviation 526.8. The marked seasonality (ii) is evident as over half of all precipitation falls during the winter, but in the summer months, when the islands are affected by the Azores anticyclone, less than 1% of the annual rainfall is recorded. Finally, the torrential rainfall (iii) is one of the most significant traits as in some months several times the average monthly rainfall has been recorded; e.g., more than seven times in January 1979; or six times in February 2010. The torrential nature of the precipitation is also evidenced by the 200 mm of rainfall in a single day recorded on 44 occasions in just 34 years (Figure 2); this amount of rain therefore represents a significant percentage of the monthly and annual totals (average 40% and 25%, respectively).

2.3. Vegetation and Land Use

Pinus canariensis forest is the most characteristic vegetation of the Caldera de Taburiente where it forms extensive forests and nowadays is one of the best preserved forests of this species in the Canary Islands. On the riverbed, there are occasional groves of willows (Salix canariensis) and some stands of the less demanding laurisilva species in the most protected shaded areas; while at higher altitudes, the plant cover is formed by different shrub species [27]. Although the Caldera de Taburiente is very sparsely populated due to its rugged topography, the research results of Garzón-Machado et al. [28] indicate that the Canary pine forest has been severely impoverished by herbivore activity, probably resulting from the introduction of goats by the Auaritas, the original inhabitants of La Palma. Other land uses include forest harvesting, hunting, and a few relatively recent rainfed crops of low economic value which share the land with grazing.

3. Material and Methods

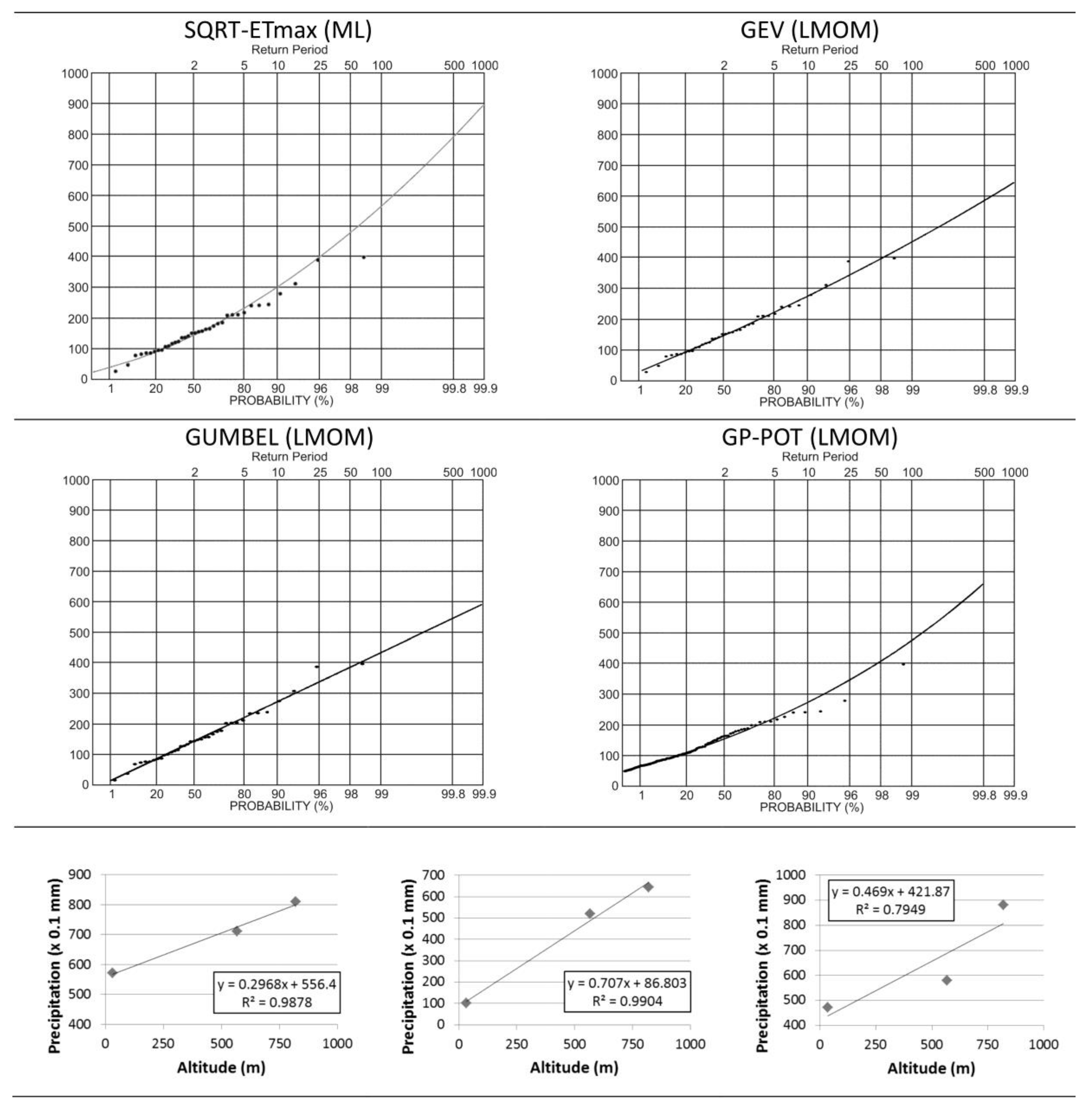
3.1. Precipitation Analysis

Data was used from two stations: a pluviometer (C106U, daily data) installed inside the Caldera de Taburiente N.P., and a continuous record pluviograph (C139E, hourly data) installed in La Palma airport, thirty km from the basin (Figure 1). Other measuring stations are installed in the Caldera, including another rain gauge situated at a lower altitude than the area of interest with a short, poor quality record series; there are also other gauges (monthly total data) that are installed at higher altitudes, but their monthly values were not considered useful for the aims of this case study.
Using data obtained from the rain gauge installed in the Caldera, a frequency distribution analysis was carried out to estimate the precipitation quantiles that are associated with different return periods. These quantile estimates were obtained from annual maximum series (SQRT-ETMAX, an extreme value distribution proposed by Etoh et al. [29], which has been widey used in Spain for annual maximum rainfall data statistical analysis; Gumbel and GEV functions) [30], and from exceedance series (Generalized Pareto—POT). The use of exceedance series to estimate or assign frequencies to extreme events is supported by many previous studies [31,32,33], enabling a better fit of the high range of the frequency function [34,35], and has been applied to both flow and precipitation estimates. These exceedance series were derived from precipitation events with a duration of 24 h, defined by an absence of precipitation recorded in the 24 h before and after this rainfall event. The precipitation threshold value (the process was carried out by the graphic method) was 25 mm rainfall. This value produced an exceedance series of 357 values above the threshold, which is significantly higher than the length of the annual maximum series (37 years).
Based on the results of the goodness-of-fit test performed (Kolmogorov-Smirnov test and Mean Square Error test), the Generalized Pareto frequency function was chosen, with parameters of fit estimated by the L-Moments method, applied to the exceedance series over the threshold. Kolmogorov-Smirnov test shows very similar values for all of the distribution functions: while MSE test shows that GP-POT distribution has the lowest error value (Table 1).
Daily rainfall distribution in the form of hourly time series has been obtained with the IDF curves currently used in Spain for the study area [36]. The precipitation time distribution throughout the event is important, as this will have a clear influence on parameters, such as initial abstractions and runoff generation, and therefore on the flows generated. These data were used to generate synthetic hyetographs using the alternating blocks method [37], for the three day duration of the event.
The attempts to maximize rainfall intensity from the available rainfall data focused on two aspects. On the one hand, we considered the influence of the rainfall event duration by using different values. Rainfall events of 72, 24, and 1 h were considered; these values are related to the duration of the maximum volume rainfall volume event in 1997 (selected for the availability of dendro-geomorphological information), duration of the event considered in the maximum rainfall frequency analysis, and duration of a local convective rainfall event. On the other hand, we considered the possible effect of orography on the total basin rainfall volume. This effect was considered because of the high basin relief, with the resulting difference in altitude between the location of rainfall gauging stations and the upper basin where the study area is located. The orographic effect was estimated using linear regression from the available rainfall data.

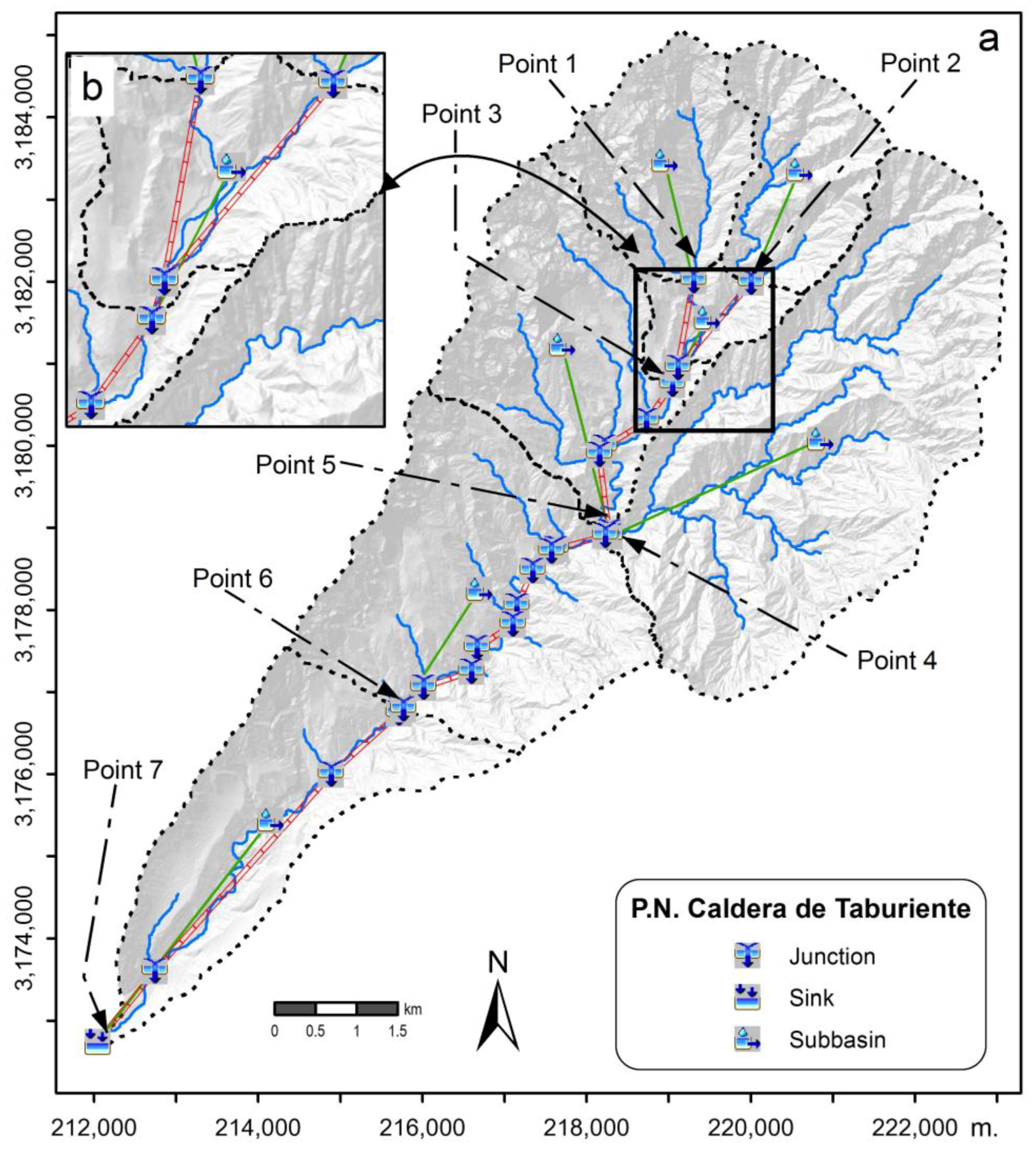
3.2. Rainfall-Runoff Modeling

The basin model (Figure 3) was derived from a 5 m Digital Elevation Model (DEM). Disaggregation was based on both the spatial distribution of the physiographic factors that determine a homogenous hydrologic response (i.e., lithology, soils, cover type, hydrologic conditions, and slope) and those control sections where dendro-geomorphological data was available. The use of simulation methods for the various processes involved was based on the information available for the basin. The use of the SCS-CN loss method, which is well-developed and widely accepted in the US and other countries [38,39,40], was based on the availability of high resolution orthophotos for the area and also on the possibility of conducting fieldwork to test and adjust the values that were previously obtained by photointerpretation. The use of other methods of estimating initial losses or abstractions (e.g., Green-Ampt) was discarded due to the lack of more detailed soil composition and texture data.
The absence of rainfall and flow data associated with the same event reduces the availability of transformation methods in the HEC-HMS environment to only two options, so the runoff hydrograph was obtained using the Clark unit hydrograph [41], with estimated concentration time (tc) and storage coefficients. Time of concentration was derived using the Témez formula, which depends on the length of the main channel for each sub-basin and its slope [42]. The storage coefficient was calculated assuming that it represents 0.6 tc. The Muskingum-Cunge method was implemented for the flood wave routing [43], due to the absence of observed flow data. The Muskingum-Cunge parameters were calculated based on the flow and channel characteristics. This method involved the use of a finite difference scheme for solving the Muskingum equation, where the parameters in the Muskingum equation were determined based on the grid spacing for the finite difference scheme and the channel geometry characteristics. The channel geometry and roughness were accurately defined using LIDAR (0.5 points per m2) and orthophoto data combined with GIS tools.
Although we considered the associated uncertainties an essential point, the absence of flow data to calibrate and validate the hydrological output model flows makes it impossible to estimate this in each hydrological calculation, and its overall effect as the methodology unfolds. However, the sensitivity of the HEC-HMS model to SCS-CN value variations was considered (CN increase in 10% and 25%) in fluvial sub-basins upstream of the “Playa de Taburiente”.

3.3. Flood Discharge Estimation Using Manning’s Equation

In paleoflood reconstruction, event dating and frequency estimation are essential, and also a description of the magnitude of discharges, volumes, and water circulation times [44]. Estimates of peak discharges of past flood events in ungauged streams, such as the Taburiente river basin, are usually obtained using different types of paleostage indicators (PSI), hydraulic formulae, and models. PSIs can be high-water marks (HWM) from slack water deposits, floating wood jams or dendro-evidence, such as tree stem scars. Hydraulic methods range from very simple formulae (Manning, Chèzy, Froude, Darcy-Weisbach...) to very complex mathematical-numerical models (simultaneous simulations from one-dimensional to three-dimensional and from monophasic to biphasic).
For the reconstruction of peak discharges in the Taburiente streams the height of scar dendro-evidence and Manning’s equation were used. These were chosen in preference to more complex methods, such as two-dimensional (2D) or three-dimensional (3D) numerical models since: (i) there are several sources of uncertainty, such as the mobile riverbed, that only allow estimation of the order of magnitude of peak flows; (ii) the flow regime during floods is mainly one-dimensional and generally uniform; and, (iii) the geometric data does not allow for the adjustment of very complex numerical models, taking into account turbidity, eddy structures, etc. Sometimes it is more reasonable to use simpler methods than more complex techniques without the necessary data sources.
Manning’s equation, or, more accurately, the Strickler-Manning equation, is widely used (see Díez-Herrero et al. [45], and many other authors), to relate flow velocity to channel morphometry parameters with a roughness coefficient listed for different bed materials:
v = R 2 / 3 · S 1 / 2 n
where: v is average streamflow velocity; R is hydraulic radius (A/P); S is energy grade line slope (coincident with the bed); and, n is roughness coefficient.
The channel morphometry parameters come from a digital elevation model with 1 × 1 m spatial resolution, from LiDAR images. The transverse cross-sections were placed where trees with dendro-evidence have been dated and assigned to a specific event; and, obtained using ArcGIS 10.3 tools (ESRI Geosystems, Redlands, CA, USA). The roughness values for the riverbed and margins were assigned using ortophoto reclassification and fieldwork, using visual guide classes [46]. Finally, the computations were performed using special macro tools implemented in a Microsoft Excel spreadsheet.

3.4. 2D Hydraulic Modeling

The hydraulic modelling was carried out with numerical simulation using a finite differences model (St Venant 2D equations), using the Iber hydraulic simulation free software [47], with the following characteristics:
- Peak flows associated with precipitation recorded during 11–13 January 1997 event, obtained from the hydro-meteorological model.
- Peak flow range (300–2500 m3·s−1), to minimize errors (RMSE) when compared with the vegetation disturbance data (tree scars), by comparing the water sheet depths with the height of the disturbances. The aim here was to define the liquid flows needed to minimize this error.
The topographical information relating to the channel geometry of the Caldera de Taburiente examined in this case study was included in a 1 m resolution DEM covering the whole area where disturbed trees were found and the reaches immediately upstream in the Cantos de Turugumay and Verduras de Alfonso ravines. The altimetric accuracy of the data in this DEM is shown by the RMSE data, with an estimated value of z ≤ 0.5 m.
To set the boundary conditions, two independent inflow points were identified, corresponding to the Cantos de Turugumay and Verduras de Alfonso ravines; and, a single outflow point was identified in the channel of the Taburiente, approx. 500 m from the area of the disturbed trees. A dry scenario was also considered as an initial condition for the model since the function of the river is ephemeral, with an estimated basin concentration time of 4.5 h to its outlet into the sea. Finally, the roughness of the terrain (expressed by the Manning n coefficient) was derived from the photointerpretation of the satellite orthoimages with 0.5 m spatial resolution, and field work. These delimited a series of zones with homogeneous relief roughness, grain size, and appearance, and vegetation density, which were then classified following the relevant tables and graphic guides [46].
Once the hydraulic model was developed, the most important results obtained from model simulation include data related to depth, absolute elevation level, and velocity field variables. But, just as with the results of the rainfall-runoff model, the absence of flow gauge stations in the basin did not allow for the calibration of the model, and, therefore, the validation of results.

3.5. Dendrogeomorphological Data Sources

Dendro-geomorphological evidences consisted of 266 samples collected from 60 disturbed trees of P. canariensis (i.e., those presenting scars, exposed roots, resprouting or apical bud loss, and dead trees) following Díez-Herrero et al. [48]. In some cases, trees showed several wounds corresponding to different events, but more often only one impact signal per tree was observed. Other nearby trees with no visible injuries were also sampled, as scars may have already closed if they are old or not very wide. Furthermore, 16 undisturbed trees were sampled to provide a reference chronology.
63 wounds were dated, in some cases, more than one for each tree, with very different percentages in the two cohorts and in total. Especially relevant were the injuries occurring in 1962 and in 1997, both presenting a large number of replications (48% and 22%, respectively, of the total number of trees).Wounds dated to 1993 and 2003 are represented in 23% and 20% of the younger trees. Over the last decade injuries have been dated to 2001, 2003, 2007, and 2009, which together account for 18%. Other anomalies in the samples were also found with evidence of injuries but were not reliably dated [49].

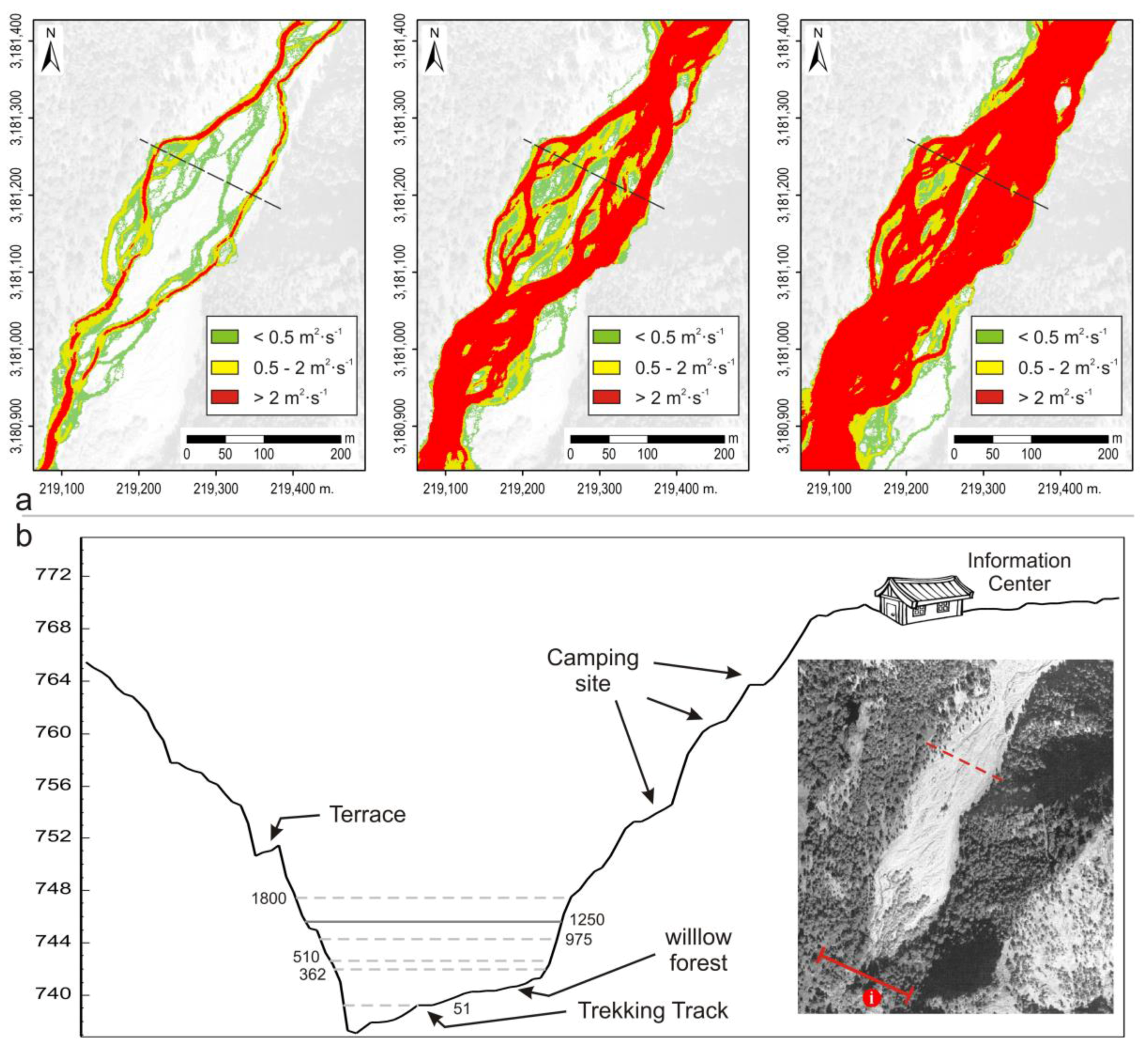
4. Results

4.1. Maximum Precipitation Results

The results obtained, from precipitation frequency analysis shown in Figure 4 and Table 1, show how the GEV distribution function systematically underestimates the values of the precipitation quantiles when compared with SQRT-ETMAX and GP-POT distribution functions. On the other hand, the SQRT-ETMAX function applied to the maximum series yields results higher than those obtained by the GP function applied to the exceedance series. From goodness-of-fit analysis (Table 1), we concluded that the best overall results could be assigned to General Pareto-POT distribution function.
In the analysis of rainfall data associated with the 1997 flash flood event, the first attempt considered the greatest rainfall volume for that year (11–13 January 1997), which recorded 191 mm rainfall in 72 h. However, the 1997 rainfall record at meteorological station C106U shows that the rainfall event for 19–20 January reached a value of 156 mm, and therefore greater rainfall intensity (Figure 2). In addition, this second event suggests the possibility that this volume of precipitation, although recorded in two days, was associated with heavy rains occurring in a time interval of only one hour, divided between these two days. This would be the most favorable situation for generating a high magnitude flash flood.
On the other hand, the influence of a rainfall—elevation gradient in the basin has also been considered, and for this, rainfall that was recorded at three meteorological stations located on the island of La Palma has been observed: Station C139E (La Palma airport), located at 33 m a.s.l.; C106U (Caldera de Taburiente) at 820 m a.s.l.; and, ESICA3800000238750A at 568 m a.s.l. These stations share records for years 2005 to 2013. Within this time period, four high rainfall events were selected, and a linear regression was fitted to the daily rainfall data (Figure 4). The degree of fit (R2) for linear regression varies between 0.74 and 0.99. For the best adjustment obtained (R2 = 0.99), a linear rainfall—elevation gradient of +0.071 mm m−1 was estimated, with +0.079 mm m−1 being the mean value for the four events.
Applying the best-fit rainfall—elevation, it was estimated that a hypothetical rainfall event lasting 1 h (between 19–20 January 1997) could reach mean values of 236 mm (“Verduras de Alfonso” gorge—W1580), 234 mm (“Cantos de Turugumay” gorge—W1530), and 184 mm (“Playa de Taburiente” sub-basin—W1570). All of these represent a significant increase in the possible rainfall intensities that were associated with triggering the flash flood analyzed here. Finally, a situation was envisaged in which the return period rainfalls considered were also produced in a time interval of 1 h, or even less, in view of other historical events. Table 2 shows hourly rainfall intensity for all rainfall event models considered.

4.2. Flood Discharges

When considering the three precipitation distribution scenarios over the 72 and 24 h duration of the event mentioned above allows for a study of the basin behavior in each case, especially of aspects that are related to the ground infiltration capacity in each scenario, and therefore to the surface runoff that produces variations in the flow rates generated. These flow rates (Figure 5) show how the three scenarios that are considered represent situations, which may be more or less favorable to flash flood generation. In all cases, the right skewed hyetograph produces the highest peak flows, as usual.
The different hyetograph models used obtain high variability in their associated peak flows (Table 3), ranging from tens to hundreds of cubic meters. These differences are linked in the first instance to the different precipitation return periods considered. In view of the results obtained, the variability linked to peak flow values cannot be related only to differences in rainfall return periods (which may explain approximately 50% of the observed variability), highlighting the influence of the other variables that are considered on the results. These variables would therefore be responsible for the remaining variability.
The results also highlight the importance of rainfall intensity (ranging from 72 h to 1 h), which by itself can increase 2–3 times the peak flow rate generated for both the 1997 flash flood event and the considered return periods, a much higher increase than the one associated with the variation in the CN value, which may be linked to a 35%–50% variation (when considering a 25% increase in the CN values). Shortening the duration from 24 h to 1 h in the hyetograph associated with the different return periods considered obtains an increase in peak flow values close to 50%. In addition, the effect of the CN parameter is conditioned by the rainfall intensity value, showing a positive correlation.
Directly related to rainfall intensity, the rainfall—elevation gradient derived from the precipitation record analysis at three stations on La Palma increased the values of the generated peak flows by up to 50%. When considering all these factors (Table 3), may mean a four to five-fold increase in the 1997 flash flood peak flow.
On the other hand, using the available dendro-geomorphological data for the study area [49], the peak flow rate that is associated with each case was then estimated using the Manning´s formula. The results obtained for the data set for the 1997 flood event show high variability, which is reduced if only six cases are used, shown grouped (Table 4 and Figure 6). Independently of whether all the data are used or only the data for the grouped cases, the mean data value (~1800 m3 s−1) is double the maximum peak flow value obtained by processing the rainfall data and implementing it in a hydrological model. The first results obtained from a preliminary 2D hydraulic model for the study area obtain a peak flow value approaching 1250 m3 s−1, minimizing the RMSE coefficient when comparing flow depth and the height of the dendro-geomorphological evidence. This would be an intermediate value between the maximum value obtained in the hydrological model (HEC-HMS), and the average peak flow value obtained using Manning’s formula.

4.3. Comparing Results

The first and most important point to highlight when comparing the results obtained using hydrological-hydraulic models is the significant difference between the flows obtained from the rainfall-runoff transformation process of the statistical approximation (~50 m3 s−1, for the 11–13 January, rainfall recorded data), and those that were obtained taking the dendro-geomorphological data into account (~1250–1800 m3 s−1). This latter flow value clearly exceeds the return periods considered (maximum 500 years, Table 3) in the rainfall-runoff hydrological model developed for the study area, and the hydrological models where rainfall intensity, CN, and rainfall—altitude gradient are considered. The main outcome of the results shown in Table 3 is variability, which obviously does not facilitate decision making. Depending on the data used and how they are processed, the results show a high standard deviation.
In addition, these flow differences mean a distinct behavioral change in this gorge. As shown in Figure 7, it functions either as a braided channel with emerged bars (~50 m3 s−1) or as a single channel occupying the whole river bed (~1250 m3 s−1). The difference in channel behavior is less evident (Figure 7) if we compare the flows that minimize RMSE value versus dendro-geomorphological data height (~1250 m3 s−1), and those that are associated with the 500-years return period (510 m3 s−1, from 500-years return period rainfall according to the GP-POT distribution function). In these cases, a single channel occupying the whole river bed is the main river configuration. Figure 8 shows the clear differences in flow-depth data in this channel for each peak flow considered.
Therefore, the peak flow results obtained using different types of information show significant differences when considering dendro-geomorphological evidence versus rainfall data (processed to maximize precipitation intensity); and, these differences become extreme if peak flows obtained using dendro-geomorphological evidence are compared with those obtained from a classic statistical maximum frequency analysis of 24 h rainfall events.

4.4. Uncertain Sources

Hydrological models, such as HEC-HMS, are inherently uncertain, due both to the random nature of floods and to the uncertainty component of epistemic origin (due to limited data and knowledge; [50]). In this context, model calibration and validation enable an understanding and mitigation of the model uncertainty, by iterative variation of parameter values within a predefined range. However, this proved impossible in this case due to the lack of observed flow data. The above limitation is mitigated to some extent by an in-depth knowledge of the basin physiography and hydrological response. Flash floods in mountain basins may trigger the mobilization of varying amounts of solid load (i.e., sediment and woody debris), modifying the channel dynamics and morphology [51]. In this respect, the HEC-HMS version here obtains hydrographs that only represent clear water flow as output data. This means that discharges calculated in this way may be underestimated, and therefore cannot be used to assess risks [52], since estimated hazard parameters (i.e., depth and velocity) obtain values lower than they should be.
Ruiz-Villanueva et al. [51] present the differences in the precipitation curve recorded in a small mountain basin from the effect of altitude and slope orientation, concluding that these factors play an essential role in the basin precipitation distribution, and that the curves generated (positive with altitude) have a direct influence, which explains total precipitation values and gauged flow rates in the basin.
On the other hand, applying frequency distribution functions to extrapolate the maximum precipitation values associated with extreme quantiles (with very low occurrence probability) always generates a degree of uncertainty in the results obtained. This uncertainty (epistemic uncertainty; [53]) is the result of the insufficient length of the data series used as the basis of these predictions; so that the insufficiently representative data series, loss of high magnitude records, measurement errors, undetected anomalous values, etc., may lead to significant variations in the values that are associated with the lowest frequency quantiles. Using threshold exceedance series, thus incrementing the length of the data series and enabling better fit of the high range of the frequency function [34,35], was the method chosen in an attempt to limit the uncertainties linked to these statistical analyses.

5. Discussion

One of possible reasons for the general non-coincidence between the event dates documented or in the systematic record of intense precipitations, and those deduced from the dendrochronological analysis of samples is the non-linear nature of the rainfall-runoff process and its effect on riparian vegetation.
Thus, the most intense precipitation events in the meteorological station do not necessarily produce the highest flood flow rates. The spatial-temporal variability between precipitation and flow rates is influenced by the local or general character of the maximum precipitation intensities, so that the hydrological response may or may not be limited to one sector of the basin; and, by the ground moisture content previous to the most intense precipitation event, conditioned by the preceding precipitation (previous three days, month, or even hydrological year), which strictly controls the runoff threshold, and therefore the runoff coefficient. Thus, the possible combination of the factors mentioned above could justify the considerable discrepancy found in the model results.
For this reason, peak flow assessment in ungauged basins has been approached from different points of view. The most widely used method is probably regionalization [54,55,56], where statistical methods are used to transfer the hydrological characteristics of gauged basins located in the same area as the ungauged basin in question. The use of images and data collected by different satellite sensors has also been considered [57,58], and has mainly proved effective for large rivers (even taking into account the limitations presented by the use of satellite images [59]). Other authors, such as Ballesteros-Cánovas et al. [60,61,62], show that dendro-geomorphological information is useful for estimating these peak flows. The method proposed by Diakakis [63], uses the fluvial morphometry for peak flow assessment in ungauged basins. Another interesting approach use Bayesian statistic (Monte Carlo analysis) for hydrological modeling [20], allowing for an uncertainty estimation of peak flow results, which improve information for manage makers.
Based on the available information for the study area, this analysis follows the Ballesteros-Cánovas proposal, using dendro-geomorphological data for peak flow assessment in ungauged basins. However, here, this dendro-geomorphological data is used first to calibrate the results obtained from the hydrological models, which are based on statistical processing of available rainfall information. Our aim was to see if this processing of rainfall data could be considered as a new way to estimate peak flows in ungauged basins, where all of the approaches mentioned above do not offer optimum results or are not applicable. We must consider that these approaches to peak flow assessment in ungauged basins require various indispensable information sources: gauged basins with similar hydrological characteristics; sufficiently high-quality satellite images, where the vegetation does not limit interpretation; and, dendro-geomorphological data associated with the flood event occurrence; or a compilation of locations damaged by flood events.
Another approach to using rainfall data in ungauged basin analysis is atmospheric event modeling [64], although the results are not conclusive. This method obtains the space-time rainfall distribution, which is an advantage for hydrological modeling, but offers low spatial resolution for small basin analysis, and may underestimate rainfall volume, which are disadvantages of this approach.
Early warning systems (EWS) may also be considered in flood hazard mitigation in ungauged basins. An alert is activated when a rainfall event exceeds a pre-defined threshold. However, EWS present weaknesses in this study area: absence of automatic rainfall gauging stations in the upper part of the basin, and a very limited basin lag time (about 1 h).
It is important to remember here that the study area is located in the exceptional environment of a National Park with an important influx of visitors. Earlier studies by the USGS [14,15,16] opted for regionalization methods that are based on regional equations obtained by multiple regressions of data from gauged basins. These papers, dating back to the 1980s and 1990s, are prior to the expansion and generalization of the use of paleostage indicators. The analysis presented in this paper could therefore be considered as reactivating and updating studies of peak flows in ungauged basins located in exceptional environments that are used by the general public, such as National Parks.

Flooded Areas in Caldera de Taburiente N.P. Past Flood Events

Combining the use of rainfall data and dendro-geomorphological evidence with detailed hydrological and hydraulic models enabled us to describe the hydrodynamics of the 1997 flash flood event analyzed here. This is of vital importance in flood hazard assessment and for generating the relevant maps to determine the zones that are affected, or unaffected, by flash floods (Figure 7). For example, taking into account the particular characteristics of the study area (a National Park used by a large number of hikers), delimiting risk areas where visitors may suffer loss of stability due to flow [65,66], will be very important for the park managers (even more in an area with 65,000 visitors each year and previous human dies, isolated visitors on the campsite, and trekking paths damages by flood events). The results of the hydraulic models (Figure 9a) show considerable differences in terms of high risk areas. Thus, in the 50 m3 s−1 peak flow model, the high-risk areas in the “Playa de Taburiente” are marginal, limited to the most highly developed channels within a braided channel pattern. In the 510 m3 s−1 peak flow model, the high-risk areas are much more extensive, with all of the channels and lower topographic development bars included in the high-risk zone. Finally, in the 1250 m3 s−1 peak flow model, the high-risk zones represent about 85% of the total area, defining a main central channel with important secondary channels on each side.
It has been shown that when meteorological information alone is used, even when it is processed to maximize both precipitation intensity and volume in a theoretical storm event, the peak flows obtained are still far lower than when dendro-geomorphological data is included in the analysis. This is the case for both the hydrodynamic aspects (peak flow, water depth, flow velocity) and the related flood risk. Thus, improved spatial probability of the areas affected when flash floods occur in the zone can be obtained by including dendro-geomorphological data in the analysis, taking into account the inherent uncertainties in the limited data available to compare and contrast the results.
Nevertheless, processing rainfall data to maximize both the intensity and precipitation volume brings the associated peak flow values closer to those that are obtained using dendro-geomorphological information. This is especially true if the results that are offered by this technique are compared with those associated with classic rainfall frequency analysis of maximum precipitation in 24 h. Perhaps the uncertainty associated with this approach to peak flow assessment in ungauged basins does not allow for the correct link between frequency and event. However, using the highest intensity rainfall event calculated for the area can provide the approximate area of the flood-prone areas, thus determining the flood hazard zone. The availability of this simple information (flood hazard zones) can be very useful in management and decision-making in natural environments, such as National Parks (Figure 9b).
The discussion above highlights the dilemma of whether or not these studies of this type are feasible and the results reliable. Even taking this into account, another and perhaps more important question must be asked: When systematic meteorological-hydrological data is not available or very limited, should the study of river dynamics and the associated risks in basins be ruled out? We believe that the results of this study show that the answer here is no, it should not be ruled out. Even with all of the uncertainties raised, the combined use of all available sources of flood event data enables an approximation of the fluvial dynamics and associated flood risks to be obtained. More importantly, if the answer to this question is yes, then it should be ruled out, as this research is not feasible, then most river basins worldwide would not be studied, due to the very limited statistically consistent hydrological data available.

6. Conclusions

The combined and successive use of systematic meteorological and dendro-geomorphological data sources with hydrological analysis, rainfall-runoff models, and hydraulic models has enabled improved flow magnitude assessment for the 1997 flash-flood event in the Playa de Taburiente.
The main findings and contributions of this paper are:
-
Work undertaken in areas with very scarce availability of systematic information, and disparity in time-space data resolution. Thus, the proposed methodology can be applied to other areas with similar characteristics, a high proportion of drainage basins in mountain areas worldwide (especially outside Europe and the US).
-
Different techniques and methods (hydrological, hydraulic, dendro-geomorphological ...) have been combined to make best use of the scarce data available.
-
Most attention has been paid to the rainfall data, processed first in a classic statistical frequency analysis of 24 h rainfall data. This rainfall data was subsequently re-processed (duration, altitudinal gradient, hyetograph bias) to generate maximum intensity and volume events.
-
Is has been noted the results differences derived from a classical rainfall-runoff process modelling (limited by ungauged fluvial basin site place), and those obtained through the incorporation into the analysis of re-worked rainfall data (looking for maximum rainfall intensity events).
-
The incorporation of indirect flood dendro-evidence (FDEs) has been included in peak flow assessment, and to calibrate the results obtained previously from statistical analysis of the rainfall data.
-
The peak flow results obtained from the rainfall data processed to maximize intensity are lower than those obtained using FDE, but enable an approximate definition of the flooded area, and therefore the flood hazard area.
-
These results show the high variability in estimated discharge and water-stage values in study areas where data is scarce, and how this variability, when transferred to risk assessment, can generate important errors and uncertainties.
This paper is a new example of the feasibility of using dendro-geomorphological data as PSI, and of its evident potential usefulness in peak flow assessment in both ungauged and gauged basins. In addition, the study proposes an alternative method to assess peak flows and flood hazard zones in areas where the information available is limited to scarce and inconveniently located rainfall data. Looking for the most favorable events (in terms of rainfall intensity and volume) for flash-flood generation, has allowed for us to estimate peak flows and obtain flood hazard distribution. This information, in areas with very scarce data availability, can be useful for decision-making and management in the context of public natural environments such as National Parks.

Acknowledgments

This study was funded by the MARCoNI research project (Integración de Metodologías Avanzadas para la mejora de la ResilienCia en zonas urbaNas ante avenidas e Inundaciones; CGL2013-42728-R; www.marconiresearch.com) and MAS Dendro-Avenidas research project (CGL2010-19274; www.dendro-avenidas.es), Spanish Ministry of Economy and Competitiveness; and by the IDEA-GesPPNN project (OAPN 163/2010; www.idea-gesppnn.es) funded by the Spanish Ministry of Agriculture, Food and Environment (National Parks Research Program). The authors wish to acknowledge the collaboration of other members of the research teams of three projects; the Director (Angel Palomares), technicians and rangers of the Caldera de Taburiente National Park; and the Geographic Institute of Spain (IGN and CNIG; Juan Carlos Ojeda and Juan Sagües) for the transfer of information and LIDAR images. We would like to thank two anonymous reviewers for their helpful suggestions, comments and corrections that significantly improved the paper.

Author Contributions

All authors have a significative contribution to final version of the paper. J.G., A.D.-H. and J.M.B conceived and designed the experiments. M.A.P., P.M. and M.G. contributed materials and description of geology, rainfall, and dendro-geomorphological data. J.G. analyzed the data. All authors wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Nakamura, F.; Swanson, F.J.; Wondzell, S.M. Disturbance regimes of stream and riparian systems—A disturbance-cascade perspective. Hydrol. Process. 2000, 14, 2849–2860. [Google Scholar] [CrossRef]
  2. Viviroli, D.; Weingartner, R.; Messerli, B. Assessing the hydrological significance of the world’s mountains. Mt. Res. Dev. 2003, 23, 32–40. [Google Scholar] [CrossRef]
  3. Rickenmann, D.; Koschni, A. Sediment loads due to fluvial transport and debris flows during the 2005 flood events in Switzerland. Hydrol. Process. 2010, 24, 993–1007. [Google Scholar] [CrossRef]
  4. Roe, G.H. Orographic precipitation. Annu. Rev. Earth Planet. Sci. 2005, 33, 645–671. [Google Scholar] [CrossRef]
  5. Rotunno, R.; Houze, R.A. Lessons on orographic precipitation from the mesoscale alpine programme. Q. J. R. Meteorol. Soc. 2007, 133, 811–830. [Google Scholar] [CrossRef]
  6. Borga, M.; Boscolo, P.; Zanon, F.; Sangati, M. Hydrometeorological analysis of the 29 August 2003 flash flood in the Eastern Italian Alps. J. Hydrometeorol. 2007, 8, 1049–1067. [Google Scholar] [CrossRef]
  7. Borga, M.; Gaume, E.; Creutin, J.D.; Marchi, L. Surveying flash floods: Gauging the ungauged extremes. Hydrol. Process. 2008, 22, 3883–3885. [Google Scholar] [CrossRef]
  8. Seger, M. Landscapes and Living Spaces in the Alps—Between Value Generation and Value Appreciation. Mitt. Osterr. Geogr. G. 2009, 151, 406–407. [Google Scholar]
  9. White, S.; Garcia-Ruiz, J.M.; Marti, C.; Valero, B.; Errea, M.P.; Gomez-Villar, A. The 1996 Biescas Campsite Disaster in the central Spanish Pyrenees, and its temporal and spatial context. Hydrol. Process. 1997, 11, 1797–1812. [Google Scholar] [CrossRef]
  10. Benito, G.; Grodek, T.; Enzel, Y. The geomorphic and hydrologic impacts of the catastrophic failure of flood-control-dams during the 1996-Biescas flood (central Pyrenees, Spain). Z. Geomorphol. 1998, 42, 417–437. [Google Scholar]
  11. Gaume, E.; Borga, M. Post-flood field investigations in upland catchments after major flash floods: Proposal of a methodology and illustrations. J. Flood Risk Manag. 2008, 1, 175–189. [Google Scholar] [CrossRef]
  12. Benito, G.; Thorndycraft, V.R. Palaeoflood hydrology and its role in applied hydrological sciences. J. Hydrol. 2005, 313, 3–15. [Google Scholar] [CrossRef]
  13. Gaume, E. On the asymptotic behavior of flood peak distributions. Hydrol. Earth Syst. Sci. 2006, 10, 233–243. [Google Scholar] [CrossRef]
  14. Omang, R.J.; Parrett, C.; Hull, J.A. Flood Estimates for Ungaged Streams in Glacier and Yellowstone National Parks, Montana; Water-Resources Investigations Report 83-4147; U.S. Geological Survey: Helena, MT, USA, 1983.
  15. Kresch, D.L. Flood Hazard Assessment of the Hoh River at Olympic National Park Ranger Station, Washington; Water-Resources Investigations Report 86-4198; U.S. Geological Survey: Tacoma, WA, USA, 1987.
  16. Smillie, G.M.; Ellerbroek, D. Flood Hazard Evaluation for Divide and Wild Creeks Glazier National Park; Technical Report NPS/NR WRD/NRTR-91/02; Bibliogov: Fort Collins, CO, USA, 1991. [Google Scholar]
  17. Sivapalan, M. Prediction in ungauged basins: A grand challenge for theoretical hydrology. Hydrol. Process. 2003, 17, 3163–3170. [Google Scholar] [CrossRef]
  18. Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
  19. Efstratiadis, A.; Koussis, A.D.; Koutsoyiannis, D.; Mamassis, N. Flood design recipes vs. reality: Can predictions for ungauged basins be trusted? Nat. Hazards Earth Syst. 2014, 14, 1417–1428. [Google Scholar] [CrossRef]
  20. Biondi, D.; De Luca, D.L. Process-based design flood estimation in ungauged basins by conditioning model parameters on regional hydrological signatures. Nat. Hazards 2015, 79, 1015–1038. [Google Scholar] [CrossRef]
  21. Colmenero, J.R.; De la Nuez, J.; Casillas, R.; Castillo, C. Epiclastic deposits associated with large-scale landslides and the formation of erosive calderas in oceanic islands: The example of the La Palma Island (Canary Archipelago). Geomorphology 2012, 177, 108–127. [Google Scholar] [CrossRef]
  22. Staudigel, H.; Féraud, G.; Giannerini, G. The history of intrusive activity on the island of La Palma (Canary Islands). J. Volcanol. Geotherm. Res. 1986, 27, 299–322. [Google Scholar] [CrossRef]
  23. Ancochea, E.; Hernán, F.; Cendrero, A.; Cantagrel, J.M.; Fuster, J.M.; Ibarrola, E.; Coello, J. Constructive and destructive episodes in the building of a young oceanic island, La Palma, Canary Islands, and genesis of the Caldera de Taburiente. J. Volcanol. Geoth. Res. 1994, 60, 243–262. [Google Scholar] [CrossRef]
  24. Carracedo, J.C.; Day, S.J.; Guillou, H.; Pérez Torrado, F.J. Giant Quaternary landslides in the evolution of La Palma and El Hierro, Canary Islands. J. Volcanol. Geotherm. Res. 1999, 94, 169–190. [Google Scholar] [CrossRef]
  25. Marzol, M.V.; Yanes, A.; Romero, C.; Brito de Azevedo, S.; Parada, A.; Martins, A. Los riesgos de las lluvias torrenciales en las islas de la Macaronesia (Azores, Madeira, Canarias y Cabo Verde). In Clima, Sociedad y Medio Ambiente; Cuadrats, J.M., Saz, M.A., Vicente, S.M., Lanjeri, S., De Luis, M., Gonzalez-Hidalgo, J.C., Eds.; Spanish Association of Climatology: Zaragoza, Spain, 2006; pp. 443–452. [Google Scholar]
  26. Dorta, P. Catálogo de riesgos climáticos en Canarias: Amenazas y vulnerabilidad. Geographicalia 2007, 51, 133–160. [Google Scholar]
  27. Arco, M.J.; Wildpret, W.; Pérez de Paz, P.L.; Rodríguez, O.; Acebes, J.R.; García, A.; Martín, V.E.; Reyes, A.; Salas, M.; Díaz, M.A.; et al. Mapa de la Vegetación de Canarias; GRAFCAN: Santa Cruz de Tenerife, Spain, 2006. [Google Scholar]
  28. Garzón-Machado, V.; González-Mancebo, J.M.; Palomares-Martínez, A.; Acevedo-Rodríguez, A.; Fernández-Palacios, J.M.; Del Arco, M.J.; Pérez de Paz, P.L. Strong negative effect of alien herbivores on endemic legumes of the Canary pine forest. Biol. Conserv. 2010, 143, 2685–2694. [Google Scholar] [CrossRef]
  29. Etoh, T.; Murota, A.; Nakanishi, M. SQRT-Exponential Type Distribution of Maximum. In Hydrologic Frequency Modelling, Proceedings of the International Symposium on Flood Frequency and Risk Analyses, Baton Rouge, LA, USA, 14–17 May 1986; Shing, V.P., Ed.; Reidel Publishing Co.: Boston, MA, USA, 1987; pp. 253–264. [Google Scholar]
  30. Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
  31. Wang, Q.J. The POT model described by the generalized Pareto distribution with Poisson arrival rate. J. Hydrol. 1991, 129, 263–280. [Google Scholar] [CrossRef]
  32. Wilks, D.S. Comparison of three-parameter probability distributions for representing annual extreme and partial duration precipitation series. Water Resour. Res. 1993, 29, 3543–3549. [Google Scholar] [CrossRef]
  33. Coles, S.; Pericchi, L.R.; Sisson, S. A fully probabilistic approach to extreme rainfall modelling. J. Hydrol. 2003, 273, 35–50. [Google Scholar] [CrossRef]
  34. Cunnane, C. A particular comparison of annual maxima and partial duration series methods of flood frequency prediction. J. Hydrol. 1973, 18, 257–271. [Google Scholar] [CrossRef]
  35. Madsen, H.; Pearson, C.P.; Rosbjerg, D. Comparison of annual maximum series and partial duration methods for modelling extreme hydrologic events. 1. At-site modelling. Water Resour. Res. 1997, 33, 759–769. [Google Scholar] [CrossRef]
  36. Salas, L.; Fernandez, J.A. “In-site” regionalization to estimate an intensity-duration-frequency law: A solution to scarce spatial data in Spain. Hydrol. Process. 2007, 21, 3507–3513. [Google Scholar] [CrossRef]
  37. Chow, V.T.; Maidment, D.R.; Mays, L.W. Hidrología Aplicada; Mc Graw Hill: Bogota, Colombia, 1994. [Google Scholar]
  38. U.S. Department of Agriculture; Natural Resources Conservation Service. National Engineering Handbook Hydrology Chapters; Chapters 4–10. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detailfull/national/water/manage/hydrology/?cid=stelprdb1043063 (accessed on 1 October 2017).
  39. Boughton, W.C. A review of the USDA SCS Curve Number method. Aust. J. Soil Res. 1989, 27, 511–523. [Google Scholar] [CrossRef]
  40. Ponce, V.M.; Hawkins, R.H. Runoff Curve Number: Has it reached maturity? J. Hydrol. Eng. 1996, 1, 11–19. [Google Scholar] [CrossRef]
  41. Adib, A.; Salarijazi, M.; Shooshtari, M.M.; Akhondali, A.M. Comparison between characteristics of geomorphoclimatic instantaneous unit hydrograph be produced by GcIUH based Clark model and Clark IUH model. J. Mar. Sci. Technol. 2011, 19, 201–209. [Google Scholar]
  42. Rico, M.; Benito, G.; Barnolas, A. Combined palaeoflood and rainfall-runoff assessment of mountain floods (Spanish Pyrenees). J. Hydrol. 2001, 245, 59–72. [Google Scholar] [CrossRef]
  43. Ponce, V.M.; Yevjevich, V. Muskingum-Cunge method with variable parameters. J. Hydraul. Eng. Div. Am. Soc. Civ. Eng. 1978, 104, 1663–1667. [Google Scholar] [CrossRef]
  44. Benito, G.; Díez-Herrero, A. Palaeoflood Hydrology: Reconstructing Rare Events and Extreme Flood Discharges. In Hydro-Meteorological Hazards, Risks, and Disasters; Paron, P., Di Baldassarre, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 65–104. [Google Scholar]
  45. Díez-Herrero, A.; Lain-Huerta, L.; Llorente-Isidro, M. A Handbook on Flood Hazard Mapping Methodologies; Geological Survey of Spain (IGME): Madrid, Spain, 2009. [Google Scholar]
  46. Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; United States Geological Survey (USGS): Denver, FL, USA, 1989.
  47. Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 2014, 30, 1–10. [Google Scholar] [CrossRef]
  48. Díez-Herrero, A.; Ballesteros, J.A.; Ruiz-Villanueva, V.; Bodoque, J.M. A review of dendrogeomorphological research applied to flood risk analysis in Spain. Geomorphology 2013, 196, 211–220. [Google Scholar] [CrossRef]
  49. Génova, M.; Ballesteros, J.A.; Mayer, P.; Rubiales, J.M.; Saz, M.A.; Díez-Herrero, A. Multidisciplinary study of flash floods in the Caldera de Taburiente National Park (Canary Islands, Spain). Catena 2015, 131, 22–34. [Google Scholar] [CrossRef]
  50. Ballesteros-Cánovas, J.A.; Sanchez-Silva, M.; Bodoque, J.M.; Díez-Herrero, A. An Integrated Approach to Flood Risk Management: A Case Study of Navaluenga (Central Spain). Water Resour. Manag. 2013, 27, 3051–3069. [Google Scholar] [CrossRef]
  51. Ruiz-Villanueva, V.; Bodoque, J.M.; Díez-Herrero, A.; Eguibar, M.A.; Pardo-Igúzquiza, E. Reconstruction of a flash flood with large wood transport and its influence on hazard patterns in an ungauged mountain basin. Hydrol. Process. 2013, 27, 3424–3437. [Google Scholar] [CrossRef]
  52. Bodoque, J.M.; Eguibar, M.A.; Díez-Herrero, A.; Gutiérrez-Perez, I.; Ruiz-Villanueva, V. Can the discharge of a hyperconcentrated flow be estimated from paleoflood evidence? Water Resour. Res. 2011, 47, W12535. [Google Scholar] [CrossRef]
  53. Merz, B.; Thieken, A.H. Separating natural and epistemic uncertainty in flood frequency analysis. J. Hydrol. 2005, 309, 114–132. [Google Scholar] [CrossRef]
  54. Vandewiele, G.L.; Atlabachew, E. Monthly water balance of ungauged catchments obtained by geographical regionalization. J. Hydrol. 1995, 170, 277–291. [Google Scholar] [CrossRef]
  55. Bárdossy, A. Calibration of hydrological model parameters for ungauged catchments. Hydrol. Earth Syst. Sci. 2007, 11, 703–710. [Google Scholar] [CrossRef]
  56. Rafiei Emam, A.; Kappas, M.; Hoang Khanh Nguyen, L.; Renchin, T. Hydrological Modeling in an Ungauged Basin of Central Vietnam Using SWAT Model. Hydrol. Earth Syst. Sci. 2016, 2016, 1–33. [Google Scholar] [CrossRef]
  57. Smith, L.C. Satellite remote sensing of river inundation area, stage, and discharge: A review. Hydrol. Process. 1997, 11, 1427–1439. [Google Scholar] [CrossRef]
  58. Khan, S.I.; Hong, Y.; Wang, J.; Yilmaz, K.K.; Gourley, J.J.; Adler, R.F.; Brakenridge, G.R.; Policelli, F.; Habib, S.; Irwin, D. Satellite Remote Sensing and Hydrologic Modeling for Flood Inundation Mapping in Lake Victoria Basin: Implications for Hydrologic Prediction in Ungauged Basins. IEEE Trans. Geosci. Remote Sens. 2011, 49, 85–95. [Google Scholar] [CrossRef]
  59. Knebl, M.R.; Yang, Z.-L.; Hutchison, K.; Maidment, D.R. Regional scale flood modeling using NEXRAD rainfall, GIS, and HEC-HMS/RAS: A case study for the San Antonio River Basin Summer 2002 storm event. J. Environ. Manag. 2005, 75, 325–336. [Google Scholar] [CrossRef] [PubMed]
  60. Ballesteros-Cánovas, J.A.; Eguibar, M.; Bodoque, J.M.; Díez-Herrero, A.; Stoffel, M.; Gutierrez-Perez, I. Estimating flash flood discharge in an ungauged mountain catchment with 2D hydraulic models and dendrogeomorphic paleostage indicators. Hydrol. Process. 2011, 25, 970–979. [Google Scholar] [CrossRef]
  61. Ballesteros, J.A.; Bodoque, J.M.; Díez-Herrero, A.; Sanchez-Silva, M.; Stoffel, M. Calibration of floodplain roughness and estimation of flood discharge based on tree-ring evidence and hydraulic modelling. J. Hydrol. 2011, 403, 103–115. [Google Scholar] [CrossRef]
  62. Ballesteros-Cánovas, J.A.; Stoffel, M.; St George, S.; Hirschboeck, K. A review of flood records from tree rings. Prog. Phys. Geogr. 2015, 39, 1–23. [Google Scholar] [CrossRef]
  63. Diakakis, M. A method for flood hazard mapping based on basin morphometry: Application in two catchments in Greece. Nat. Hazards 2011, 56, 803–814. [Google Scholar] [CrossRef]
  64. Karymbalis, E.; Katsafados, P.; Chalkias, C.; Gaki-Papanastassiou, K. An integrated study for the evaluation of natural and anthropogenic causes of flooding in small catchments based on geomorphological and meteorological data and modeling techniques: The case of the Xerias torrent (Corinth, Greece). Z. Geomorphol. 2012, 56, 45–67. [Google Scholar] [CrossRef]
  65. Abt, S.R.; Wittler, R.J.; Taylor, A.; Love, D.J. Human stability in a high hazard flood zone. JAWRA J. Am. Water Resour. Assoc. 1989, 25, 881–890. [Google Scholar] [CrossRef]
  66. Merz, B.; Thieken, A.H.; Gocht, M. Flood risk mapping at the local scale: Concepts and challenges. In Flood Risk Management in Europe; Begum, S., Stive, M.J.F., Hall, J.W., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 231–251. [Google Scholar]
Geosciences 08 00006 g001 550
Figure 1. Map showing location of the “Playa de Taburiente” area, within the Caldera de Taburiente National Park, with main features of interest.
Figure 1. Map showing location of the “Playa de Taburiente” area, within the Caldera de Taburiente National Park, with main features of interest.
Geosciences 08 00006 g001
Geosciences 08 00006 g002 550
Figure 2. Precipitation record (a) for station C106U, downstream of the study area; and precipitation record for two selected months (b).
Figure 2. Precipitation record (a) for station C106U, downstream of the study area; and precipitation record for two selected months (b).
Geosciences 08 00006 g002
Geosciences 08 00006 g003 550
Figure 3. Rainfall-runoff model (HEC-HMS) developed for Taburiente river basin, with (a) main features: sub-basins, drainage network, junctions, propagation reach, etc.; (b) detailed view of the model in the “Playa de Taburiente” area.
Figure 3. Rainfall-runoff model (HEC-HMS) developed for Taburiente river basin, with (a) main features: sub-basins, drainage network, junctions, propagation reach, etc.; (b) detailed view of the model in the “Playa de Taburiente” area.
Geosciences 08 00006 g003
Geosciences 08 00006 g004 550
Figure 4. Results of rainfall frequency analysis in the study area and original data plotting positions. SQRT-ETmax, Gumbel and GEV functions were applied to annual maximum data series, while the Generated Pareto (GP) function has been applied to exceedances over threshold data series (POT technique). The linear regression fit for rainfall vs. altitude analysis from rainfall data available is shown at the bottom of the table.
Figure 4. Results of rainfall frequency analysis in the study area and original data plotting positions. SQRT-ETmax, Gumbel and GEV functions were applied to annual maximum data series, while the Generated Pareto (GP) function has been applied to exceedances over threshold data series (POT technique). The linear regression fit for rainfall vs. altitude analysis from rainfall data available is shown at the bottom of the table.
Geosciences 08 00006 g004
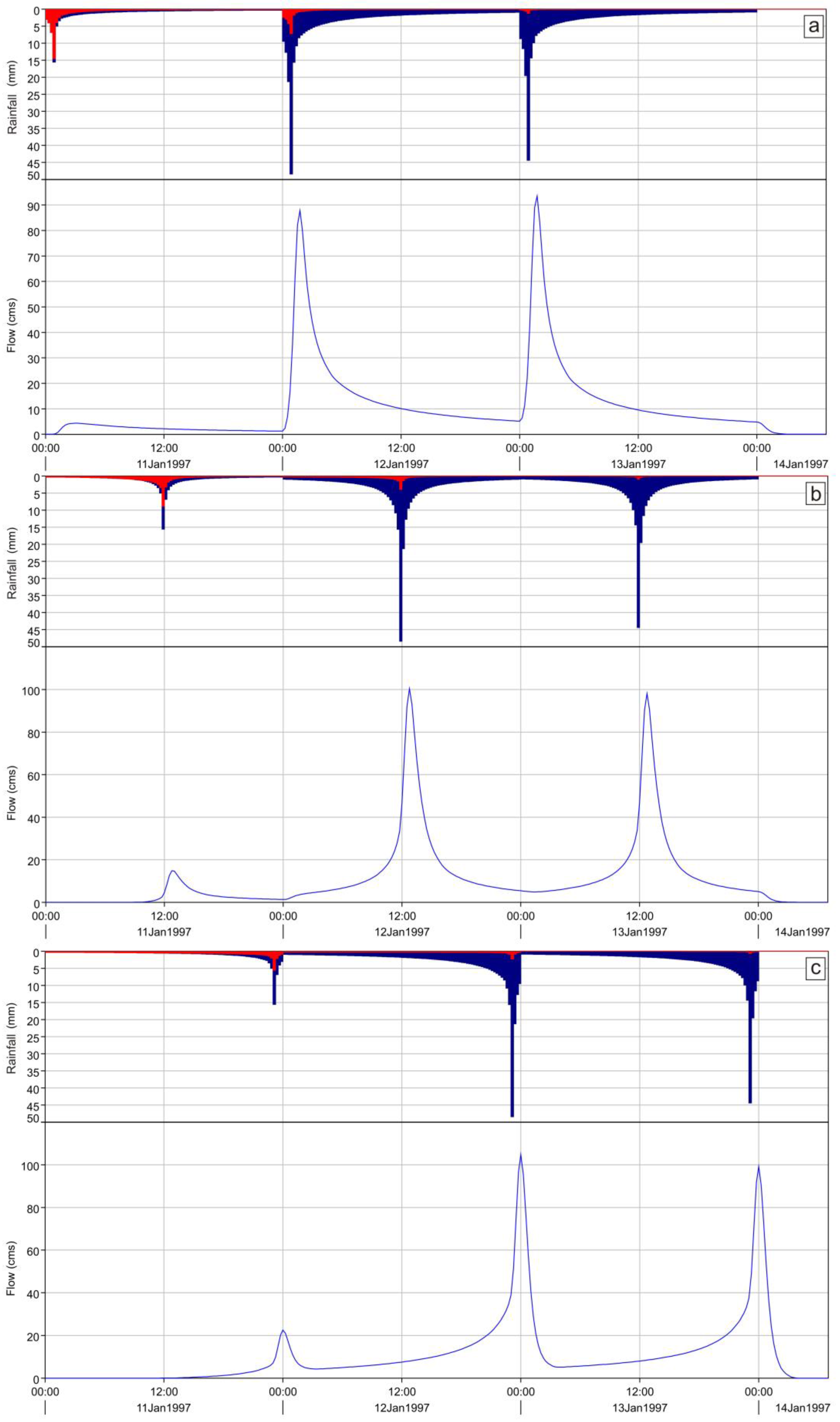
Geosciences 08 00006 g005 550
Figure 5. Rainfall—runoff graph for the three simulated rain scenarios: left skewed (a); symmetric (b) and right skewed (c). The different hydrological response of the basin in runoff generation is shown.
Figure 5. Rainfall—runoff graph for the three simulated rain scenarios: left skewed (a); symmetric (b) and right skewed (c). The different hydrological response of the basin in runoff generation is shown.
Geosciences 08 00006 g005
Geosciences 08 00006 g006 550
Figure 6. Location of dendro-geomorphological evidence for 1997 flood event.
Figure 6. Location of dendro-geomorphological evidence for 1997 flood event.
Geosciences 08 00006 g006
Geosciences 08 00006 g007 550
Figure 7. Flood prone areas for 51 m3 s−1, 510 m3 s−1, and 1250 m3 s−1 peak flow from two-dimensional (2D) hydraulic modeling (a). Solid red line shows location of channel cross-section. Channel cross-section shows flow depths for different peak flows using Manning´s formula (b).
Figure 7. Flood prone areas for 51 m3 s−1, 510 m3 s−1, and 1250 m3 s−1 peak flow from two-dimensional (2D) hydraulic modeling (a). Solid red line shows location of channel cross-section. Channel cross-section shows flow depths for different peak flows using Manning´s formula (b).
Geosciences 08 00006 g007
Geosciences 08 00006 g008 550
Figure 8. Flow depth differences between 1250 m3 s−1 and 510 m3 s−1 2D hydraulic models (a). Solid black line shows location of channel cross-section on the right (b).
Figure 8. Flow depth differences between 1250 m3 s−1 and 510 m3 s−1 2D hydraulic models (a). Solid black line shows location of channel cross-section on the right (b).
Geosciences 08 00006 g008
Geosciences 08 00006 g009 550
Figure 9. (a) Flood risk maps showing where people may suffer loss of stability due to flow (left: 50 m3 s−1; center: 510 m3 s−1; right: 1250 m3 s−1); and, (b) Flow—flood stage graph near the Caldera de Taburiente National Park Information Center. Solid red line shows location of the cross section associated with flood stage values, and Caldera de Taburiente National Park Information Center. Dashed red line shows channel cross section used in Figure 7 and Figure 8.
Figure 9. (a) Flood risk maps showing where people may suffer loss of stability due to flow (left: 50 m3 s−1; center: 510 m3 s−1; right: 1250 m3 s−1); and, (b) Flow—flood stage graph near the Caldera de Taburiente National Park Information Center. Solid red line shows location of the cross section associated with flood stage values, and Caldera de Taburiente National Park Information Center. Dashed red line shows channel cross section used in Figure 7 and Figure 8.
Geosciences 08 00006 g009
Table
Table 1. Rainfall quantiles obtained by fitting different frequency distribution functions. Parameter estimation methods for frequency distribution functions: L-moments (LMOM); and, Maximum Likelihood (ML).
Table 1. Rainfall quantiles obtained by fitting different frequency distribution functions. Parameter estimation methods for frequency distribution functions: L-moments (LMOM); and, Maximum Likelihood (ML).
24 h Rainfall Events
T (year)p (T)SQRT ML 1GEV LMOM 1GEV ML 1Gumbel LMOM 1Gumbel ML 1GP-POT LMOM 2Mean Value
20.5145147150150150156150
50.8234224224226224224226
100.9304277273277272275280
250.96402346337341334349352
500.98482400384388380411408
1000.99569455432435425480466
2000.995662512480482470551526
5000.998793590544544530660610
K-S Test0.08110.05410.05410.08110.05410.0336
Mean Error0.08080.04940.04900.04350.04900.0191
R20.98930.99500.99510.99430.99490.9944
1 Annual maximum series (SQRT-ETmax; GEV; and Gumbel); 2 Exceedances over the threshold series (GP).
Table
Table 2. Maximum hourly rainfall intensity used in hydrological modeling (HEC-HMS).
Table 2. Maximum hourly rainfall intensity used in hydrological modeling (HEC-HMS).
Rainfall Event ModelsMaximum Hourly Rainfall Intensity (mm h−1)
11–13 January 1997. C106U station rainfall. 72 h (27 + 87 + 77 mm) hyetograph (Right Skewed)14
C106U T2 rainfall (GP-POT). 24 h hyetograph21
C106U T5 rainfall (GP-POT). 24 h hyetograph30
C106U T10 rainfall (GP-POT). 24 h hyetograph36
C106U T25 rainfall (GP-POT). 24 h hyetograph46
C106U T50 rainfall (GP-POT). 24 h hyetograph54
C106U T100 rainfall (GP-POT). 24 h hyetograph63
C106U T200 rainfall (GP-POT). 24 h hyetograph73
C106U T500 rainfall (GP-POT). 24 h hyetograph87
19–20 January 1997. C106U station rainfall. 1 h hyetograph.176
C106U T2 rainfall (mean value). 1 h hyetograph150
C106U T5 rainfall (mean value). 1 h hyetograph226
C106U T10 rainfall (mean value). 1 h hyetograph280
C106U T25 rainfall (mean value). 1 h hyetograph352
C106U T50 rainfall (mean value). 1 h hyetograph408
C106U T100 rainfall (mean value). 1 h hyetograph466
C106U T200 rainfall (mean value). 1 h hyetograph526
C106U T500 rainfall (mean value). 1 h hyetograph610
19–20 January 1997. C106U station rainfall. Rainfall—Elevation gradient (0.071 mm m−1). 1 h hyetograph.236
Table
Table 3. Rainfall-runoff model (HEC-HMS) peak flows (m3 s−1) at Taburiente fluvial basin location points.
Table 3. Rainfall-runoff model (HEC-HMS) peak flows (m3 s−1) at Taburiente fluvial basin location points.
Rainfall-Runoff Event Models“Verduras de Alfonso” Ravine“Cantos de Turugumay” Ravine“Playa de Taburiente” Outflow Point
11–13 January 1997. C106U station rainfall. 72 h (27 + 87 + 77 mm) hyetograph (Right Skewed)192551
11–13 January 1997. C106U station rainfall. 72 h (27 + 87 + 77 mm) hyetograph (RS). CN + 10%202754
11–13 January 1997. C106U station rainfall. 72 h (27 + 87 + 77 mm) hyetograph (RS). CN + 25%233060
C106U T2 rainfall (GP-POT). 24 h hyetograph354795
C106U T5 rainfall (GP-POT). 24 h hyetograph5774152
C106U T10 rainfall (GP-POT). 24 h hyetograph7394194
C106U T25 rainfall (GP-POT). 24 h hyetograph95123255
C106U T50 rainfall (GP-POT). 24 h hyetograph114147306
C106U T100 rainfall (GP-POT). 24 h hyetograph136174362
C106U T200 rainfall (GP-POT). 24 h hyetograph157202420
C106U T500 rainfall (GP-POT). 24 h hyetograph190244509
19–20 January 1997. C106U station rainfall. 1 h (176 mm) hyetograph.6594180
19–20 January 1997. C106U station rainfall. 1 h (176 mm) hyetograph. CN + 10%78111216
19–20 January 1997. C106U station rainfall. 1 h (176 mm) hyetograph. CN + 25%98135268
C106U T2 rainfall (mean value). 1 h hyetograph4973137
C106U T5 rainfall (mean value). 1 h hyetograph95134264
C106U T10 rainfall (mean value). 1 h hyetograph130179358
C106U T25 rainfall (mean value). 1 h hyetograph178242489
C106U T50 rainfall (mean value). 1 h hyetograph216290592
C106U T100 rainfall (mean value). 1 h hyetograph256342702
C106U T200 rainfall (mean value). 1 h hyetograph297395815
C106U T500 rainfall (mean value). 1 h hyetograph357470975
19–20 January 1997. C106U station rainfall. Rainfall—Elevation gradient (0.071 mm/m). 1 h (236 mm) hyetograph.100143265
19–20 January 1997. C106U station rainfall. Rainfall—Elevation gradient (0.071 mm/m). 1 h (236 mm) hyetograph. CN + 10%116162306
19–20 January 1997. C106U station rainfall. Rainfall—Elevation gradient (0.071 mm/m). 1 h (236 mm) hyetograph. CN + 25%138187362
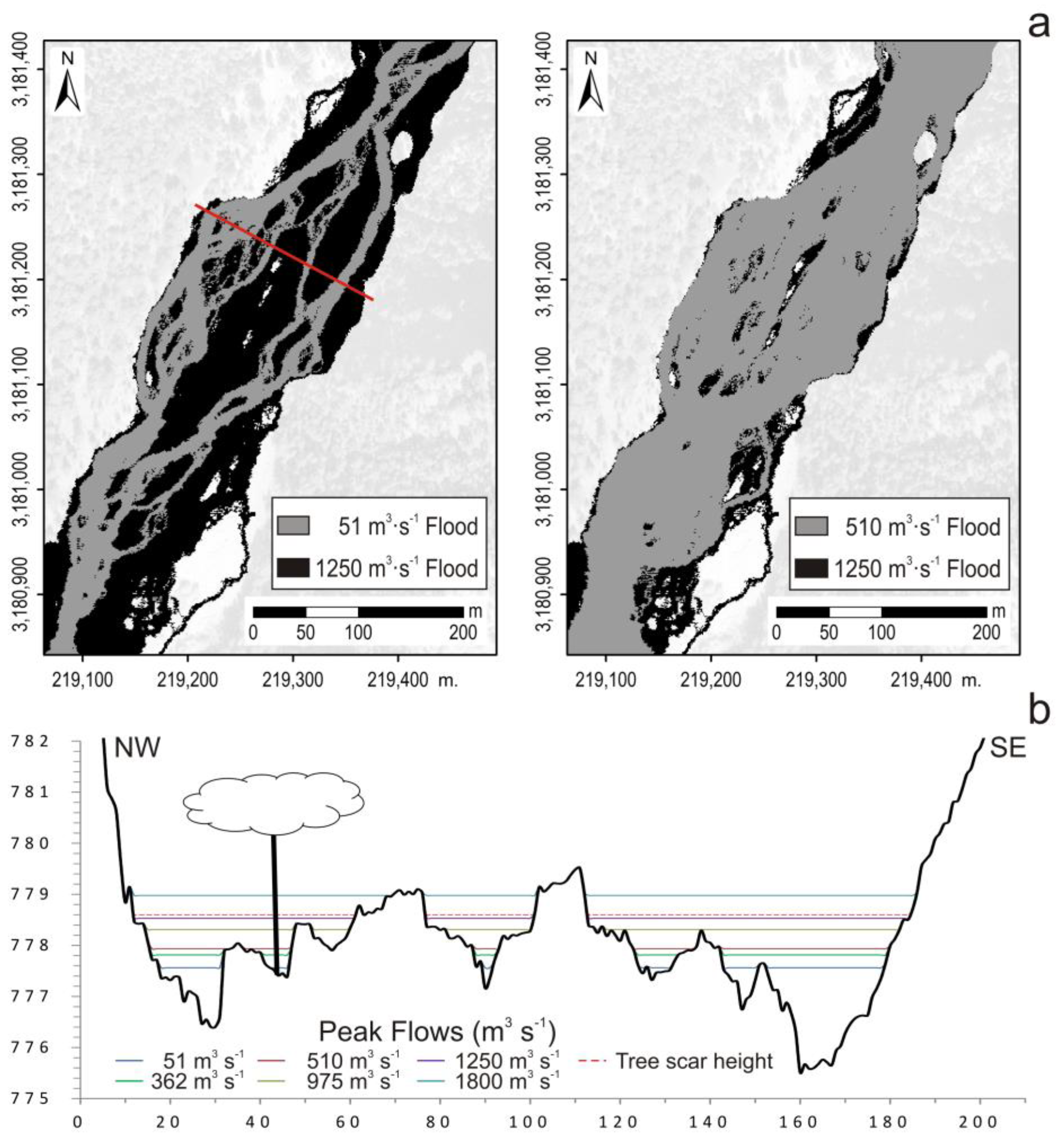
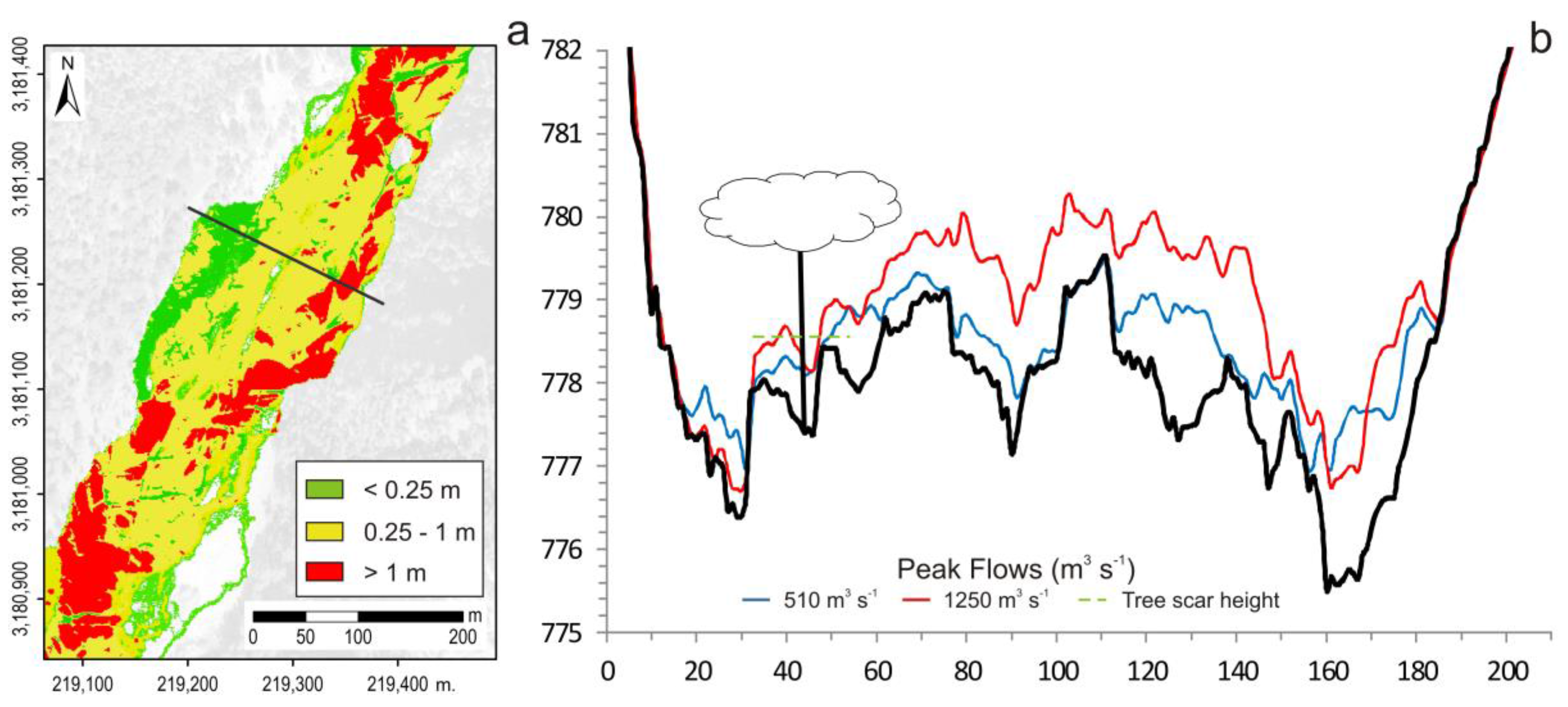
Peak flows that minimize RMSE for dendro-geomorphological evidences.--~1250
Table
Table 4. Peak flow values (Manning’s formula) linked to 1997 flood event dendro-geomorphological evidence.
Table 4. Peak flow values (Manning’s formula) linked to 1997 flood event dendro-geomorphological evidence.
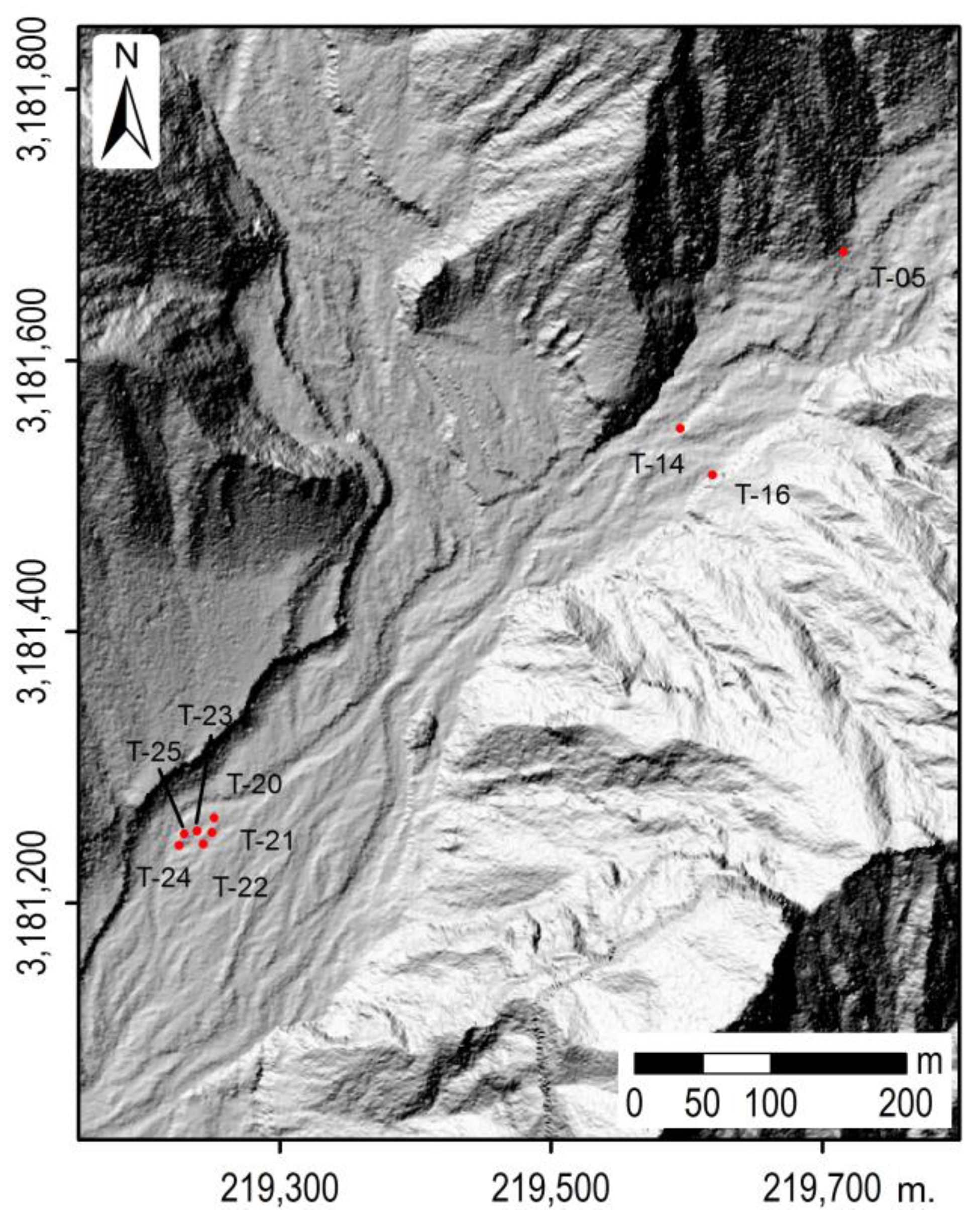
Tree SamplePeak Flow (m3 s−1)Mean Peak Flow (m3 s−1)
T-052416-1798 (629)
T-14780-
T-162162-
T-2025741804 (569)
T-212210
T-22928
T-231765
T-241504
T-251845

Share and Cite

MDPI and ACS Style

Garrote, J.; Díez-Herrero, A.; Bodoque, J.M.; Perucha, M.A.; Mayer, P.L.; Génova, M. Flood Hazard Management in Public Mountain Recreation Areas vs. Ungauged Fluvial Basins. Case Study of the Caldera de Taburiente National Park, Canary Islands (Spain). Geosciences 2018, 8, 6. https://doi.org/10.3390/geosciences8010006

AMA Style

Garrote J, Díez-Herrero A, Bodoque JM, Perucha MA, Mayer PL, Génova M. Flood Hazard Management in Public Mountain Recreation Areas vs. Ungauged Fluvial Basins. Case Study of the Caldera de Taburiente National Park, Canary Islands (Spain). Geosciences. 2018; 8(1):6. https://doi.org/10.3390/geosciences8010006

Chicago/Turabian Style

Garrote, Julio, Andrés Díez-Herrero, José M. Bodoque, María A. Perucha, Pablo L. Mayer, and Mar Génova. 2018. "Flood Hazard Management in Public Mountain Recreation Areas vs. Ungauged Fluvial Basins. Case Study of the Caldera de Taburiente National Park, Canary Islands (Spain)" Geosciences 8, no. 1: 6. https://doi.org/10.3390/geosciences8010006

APA Style

Garrote, J., Díez-Herrero, A., Bodoque, J. M., Perucha, M. A., Mayer, P. L., & Génova, M. (2018). Flood Hazard Management in Public Mountain Recreation Areas vs. Ungauged Fluvial Basins. Case Study of the Caldera de Taburiente National Park, Canary Islands (Spain). Geosciences, 8(1), 6. https://doi.org/10.3390/geosciences8010006

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop