Abstract
Micromanipulation is a hot topic due to its enabling role in various research fields. In order to perform a high precision operation at a small scale, compliant mechanisms have been proposed and applied for decades. In microscale manipulation, micro-/nano-positioning is the most fundamental operation because a precision positioning is the premise of subsequent operations. This paper is concentrated on reviewing the state-of-the-art research on complaint micro-/nano-positioning stage design in recent years. It involves the major processes and components for designing a compliant positioning stage, e.g., actuator selection, stroke amplifier design, connecting scheme of the multi-DOF stage and structure optimization. The review provides a reference to design a compliant micro-/nano-positioning stage for pertinent applications.
1. Introduction
With the advance and development of science and technology, research of the microscale has became a hot trend in recent decades. Since the interaction with the microscale object is a major step in research, micromanipulation technology becomes an essential tool. It has been widely used in various fields including micro-electromechanical systems (MEMS), micro-assembly, biology, etc. [1,2,3,4,5].
Specific operations of micromanipulation include positioning, griping, puncturing, injecting, etc. Among different operations, micro-/nano-positioning is considered as the most basic one [6], because most of the other operations are the extended application of positioning. For example, gripping is implemented by the relative positioning of two gripper tips; puncturing is the positioning of the needle, etc. The precision of the used positioning method directly affects the accuracy of the corresponding operation, especially at a small scale at the micro-/nano-meter level. Therefore, precision positioning plays a key role in the micromanipulation domain.
The majority of conventional positioning stages transmit force and motion by using rigid mechanisms, e.g., joints and linkages, lead screw driving and rack gear driving. Due to the existence of unavoidable friction and backlash between the interconnected rigid components, the positioning accuracy is greatly degraded. Although it is unapparent in large-scale (like centimeter- or meter-level) applications, the inaccuracy caused is significant at the small scale (micro- and nano-meter level).
Unlike rigid mechanisms, compliant mechanisms transmit force and motion by using the deformation of the structure within the elastic range of the material [7,8]. In this way, no friction and backlash will be incurred during the operation. Therefore, to fulfill the demand of high accuracy, compliant mechanisms are more suitable to use in micro-/nano-positioning technology [9].
As the main part of compliant mechanisms, the flexure hinge affects the overall performance in terms of three aspects: kinematic accuracy, dexterity and distribution of stress. In practical applications, different priorities can be adopted to determine the shape of the flexure hinge, which includes rectangular, circular, elliptical, parabolic, hyperbolic, etc. [8]. For example, in general, the rectangular type has high dexterity and low concentrated stress, but its kinematic accuracy is low; the right-circle type has good kinematic accuracy, but it has lower dexterity and higher concentrated stress. Besides, the fabrication should be also considered, e.g., the right angle of the rectangular type is usually fabricated as the corner-filleted type in practice, and the performance may be changed. In addition, machining imperfections also lead to a different kinematic performance [10].
With many years of research, there are many designs for compliant micro-/nano-positioning stages. In the literature, the research works of compliant mechanisms in micro-/nano-scale manipulation have been well developed and concluded [11,12,13,14,15,16,17]. In this paper, by surveying the related research in recent years and summarizing the methods, processes and components used in the designs, a design flow is proposed by considering the main design factors. It provides a reference for future work.
The following sections of the paper are organized as follows. Section 2 gives a brief introduction of the most-used actuators, including their working principles, advantages and disadvantages. Section 3 presents two kinds of stroke amplifiers and their improved derivative types. Section 4 classifies three popular kinematic connecting schemes for constructing a multi-degree-of-freedom (multi-DOF) positioning stage. Section 5 introduces the application of the dimension, shape and topology optimizations in the design process. Section 6 discusses the current problem of compliant micro-/nano-positioning stages. At last, Section 7 concludes the paper with the proposal of a design flow as a reference.
2. Actuators
This section briefly introduces four kinds of actuators, which are popularly adopted in micro-/nano-positioning stage design [11,18]. The classification is based on their working principles, i.e., electromagnetic, electrostatic, electrothermal and piezoelectric effects. The introduced actuators can cover the stroke requirement ranging from the sub-nanometer to centimeter scale. Therefore, they are widely used with compliant mechanisms in the field of micro-/nano-positioning. Furthermore, a detailed survey about the performance and selection of actuators can be found in [19].
2.1. Electromagnetic Actuator
Based on the interaction between the magnetic field from the permanent magnet and energized coil, the electromagnetic actuator (EMA) can convert electrical energy into mechanical energy without friction [20]; Figure 1a shows a typical EMA, i.e., voice coil motor (VCM).
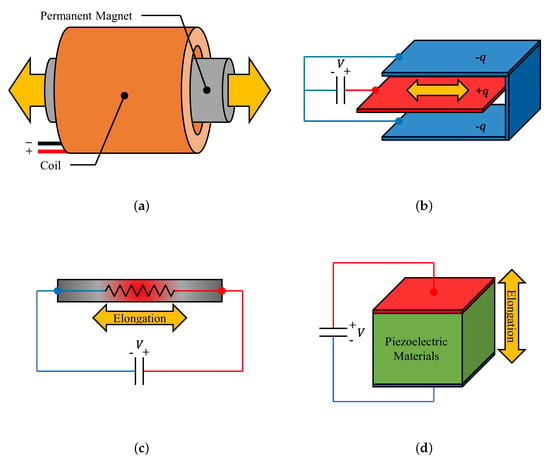
Figure 1.
Working principles of: (a) electromagnetic actuator (EMA); (b) electrostatic actuator (ESA); (c) electrothermal actuator (ETA); and (d) piezoelectric actuator (PEA).
Depending on various sizes and designs, EMAs can provide effective strokes ranging from the micrometer to centimeter scale [21,22]. Since the positioning accuracy only relates to the feedback and control system, the EMA can easily achieve nanometer-level resolution with a suitable configuration. Meanwhile, the inertia of the moving part (either coil or magnet) needs attention in the design of control systems. Moreover, unlike the relationship between displacement and force of the other three types of actuators, the force output of EMA is adjustable under a fixed displacement output by changing the applied current [23]. This property can be used in the control system, which emphasizes robustness [24].
In general, due to its bulky size and difficulty in fabrication, EMA is considered if a relative large stroke (in the millimeter or centimeter scale) is required [25,26].
2.2. Electrostatic Actuator
The electrostatic actuator (ESA) is a kind of microactuator driven by electrostatic force. As a capacitor with one of its electrodes fixed, when a voltage is applied, its free electrode will move to change its capacitance to counteract the voltage change [27]. Figure 1b shows a simplified comb-drive actuator.
The output direction of ESA depends on how its free electrode is constrained by the guiding mechanisms, e.g., normal or parallel to the capacitor’s plate surface. Besides, the ESA can also provide in-plane rotary output by curving the plate, which is widely applied in microgrippers [28,29,30,31]. In previous research, ESAs were generally integrated into the mechanical part to form a monolithic structure and then fabricated by chip manufacturing processes, e.g., silicon on insulator (SOI), low pressure chemical vapor deposition (LPCVD) [32,33,34,35], etc. Therefore, ESA is mostly used to drive a planar structure.
The advantages of ESA include high power efficiency, high dynamic performance, and a hysteresis-free input-output relationship [36,37,38]. However, its generated force is relative low, which lies at the nanonewton to millinewton level [11]. On the other hand, most ESAs are integrated into a monolithic structure. Therefore, the relatively high driving voltage may affect the applicability in operating the target, e.g., cell gripping in the field of bio-technology [39].
2.3. Electrothermal Actuator
The electrothermal actuator (ETA) is a kind of actuator based on the material’s thermal expansion. As the conductor has resistance, according to Ohm’s law, when the current passes through the conductor, it will generate joule heat. Then, the joule heat will cause thermal expansion of the conductor. Figure 1c shows the working principle of ETA. In addition, ETA involves three main types, i.e., hot/cold arm, chevron-shaped (V-beam) and bi-morph [11].
Both ESA and ETA are usually fabricated by chip manufacturing process with a monolithic structure. As compared to ESA, ETA can generate a larger force with a more compact structure and relative lower driving voltage requirement, and it also provides high accuracy output with good repeatability [40]. However, ETA’s working principle governs that it has some problems like low frequency, high power consumption and nonlinear movement [41,42]. Nevertheless, the high operating temperature may have a great impact on the ambient environment and operated target [43,44,45].
2.4. Piezoelectric Actuator
The piezoelectric actuator (PEA) is a kind of actuator based on the reverse piezoelectric effect of ionic crystals [46], i.e., by applying an external electrical field, the piezoelectric material will elongate to adjust its internal electrical field to resist the change. Figure 1d shows the reverse piezoelectric effect of a single layer of piezoelectric material (in d33 mode). The forms of PEA can be stack-based and film-based. At present, stack-based PEA is mostly used for actuation, because it is stacked by multiple layers of piezoelectric material, which provides a reasonably large output force and stroke. In addition, the ease of use makes PEA the most widely-used actuator in micro-/nano-positioning.
The greatest advantage of PEA is the large generated force up to the kilonewton level. Besides, the high response speed and sub-nanometer-scale resolution are also beneficial to implement precision manipulation [47,48]. However, PEA’s capacity will be changed during the operation, which causes a severe hysteresis to its input voltage-output displacement relationship. To achieve a higher precision control, the modeling of PEA’s hysteresis is important for designing controllers [49,50,51,52,53]. In addition, since the tensile strength of PEA is much lower than its compressive strength, preloaded PEA is a solution to avoid damage. A suitable preload is recommended to ensure that PEA retains a good dynamic performance. Therefore, a preload adjustable design needs to be integrated into the stage.
3. Stroke Amplifiers
The maximum stroke of an actuator is fixed and limited, especially for PEA, the stroke of which is only 0.1% to 0.2% of the length of the piezoelectric material [54,55]. Once a larger stroke is desired, the available solutions include reselecting the actuator with a larger stroke, using more actuators in series or using a stroke amplifier. In practice, by either reselecting the actuator or using more actuators, the cost is much more than that of using an amplifier, because the amplification mechanisms are able to be integrated in the original mechanical design. Therefore, using a stroke amplifier to amplify the small stroke is an efficient choice to obtain a large stroke. The most widely-used amplification mechanisms can be classified into bridge type and lever type [56].
In this section, these two kinds of amplifiers and their improved derivative types are reviewed.
3.1. Lever-Type Amplifier
The compliant lever amplifier is based on the simple lever principle. With a certain input force, the magnitude and direction of output force are able to be adjusted by adjusting the length of the effort arm, load arm and the position of the fulcrum. Besides, the input and output strokes also depend on the stiffness of the amplifier and the connected external mechanisms. With a small deflection, the input and output motion can be approximated as a linear relation. Although the size of the lever-type amplifier is relatively large, its large lateral stiffness is still a non-negligible benefit for some applications. Figure 2 shows the fundamental mechanism of a lever amplifier.
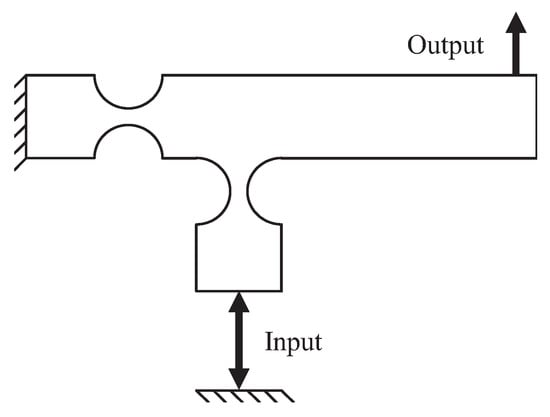
Figure 2.
Schematic diagram of a lever amplifier.
Owing to the simple mechanism and principle, many researchers have adopted the lever amplifier to obtain a desired stroke. For instance, Gan et al. [57] used a lever amplifier to amplify the stroke of PEA. More researchers, such as Bhagat et al. [58], Li et al. [59], Dao et al. [60], Qu et al. [61] and Ren et al. [62], used a similar lever amplifier. In addition, the guiding mechanism is added to the output end of the lever to enhance the directionality of the output motion. Gao et al. [63] designed a differential lever amplifier (see Figure 3), which has a high lateral stiffness. With the same space, it is able to obtain a larger amplification ratio as compared to the conventional design.
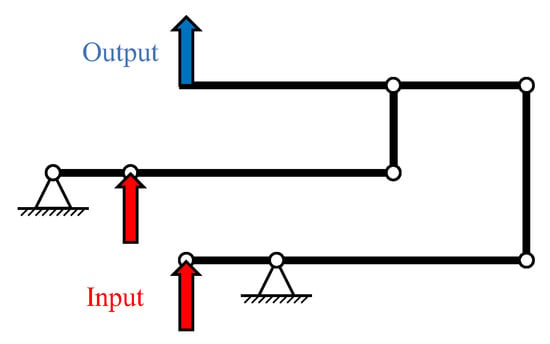
Figure 3.
Schematic diagram of a differential lever amplifier.
3.2. Bridge-Type Amplifier
Another popular type of amplifier is the bridge type. It can generate a pure linear output motion. Figure 4 shows a bridge amplifier with a right-circle flexure hinge. To obtain the same amplification ratio, the bridge amplification mechanism can be made more compact than the lever-type mechanism, but its analytical model is more complicated. In addition, the lateral stiffness of the bridge-type mechanism is lower than the lever-type. Therefore, guiding mechanisms are always used to overcome this disadvantage.
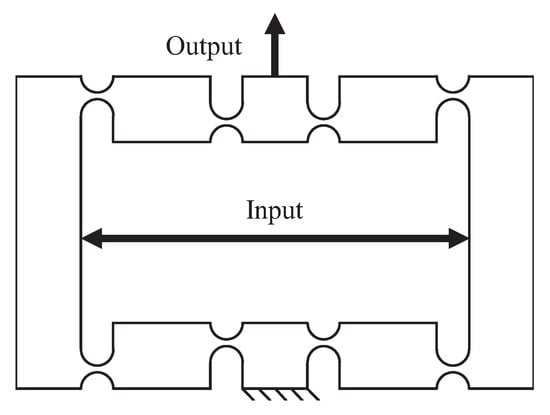
Figure 4.
Schematic diagram of a bridge amplifier.
Researchers have conducted many studies on the performance evaluation of the bridge amplifier and its derived types. For example, Lobontiu et al. [56] reviewed the literature and gave an analytical model of the bridge amplifier. Choi et al. [64] designed an amplifier with double-amplification mechanisms and two piezoelectric actuators to overcome the output force deterioration problem (see Figure 5a). With a similar structure, Kim et al. [65] integrated the compound guiding mechanism to form the self-guided bridge amplifier. Xu et al. [54] designed a bridge amplifier with compound design (see Figure 5b) to overcome the low lateral stiffness problem of the original bridge amplifier and derived the mathematical model by geometric relations and elastic analysis. Lee et al. [66] proposed a spatial compound bridge amplifier (Figure 5c) to reduce the height of a lifting stage. Zhu et al. [67] used the Z-shaped flexure hinges in the design of a half-bridge amplifier. Zhang et al. [68,69] designed two-level and three-level bridge amplifiers to obtain a larger amplification ratio, and the expression of the amplification ratio was also derived. Li et al. [70] presented a derivation of empirical compliance equations of the rectangular flexure hinge, which was verified by constructing a bridge amplifier. More recently, Dong et al. [71] proposed the design of a highly efficient bridge-type mechanism based on negative stiffness. Chen et al. [72] reported a three-dimensional bridge-type mechanism, which provides a large amplification ratio of 41.
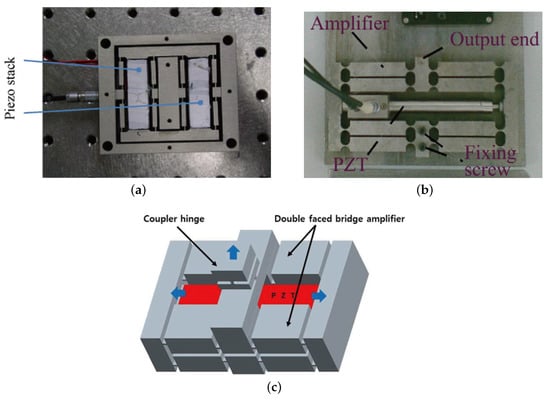
Figure 5.
(a) The double amplification mechanism [64]; (b) the compound bridge amplifier [54]; (c) the steric compound bridge amplifier [66].
3.3. Hybrid-Type Amplifier
In order to have a better utility of space and linearity of output motion, some researchers used the lever and bridge amplifier together in one design. In the literature, Yao et al. [73] presented an amplifier that is composed of two serially-jointed parallelogram four-bar linkages (Figure 6). The input end is located on one bar. The first level of amplification is carried by a lever mechanism, and then, the second level of amplification is realized by the two parallelogram four-bar linkages, which can be considered as a compound half-bridge amplifier. Clark et al. [74] designed a pure rotation stage with the use of a bridge amplifier and two three-level lever amplifiers. Zhang et al. [55] and Tzou et al. [75] both used two lever amplifiers in symmetry to obtain the amplified stroke, and then, a half-bridge amplifier was used to generate linear motion. Besides, Zhang and Xu [76] used lever amplifiers to amplify the output of the bridge amplifier, so as to increase the workspace of a 3-PSS (prismatic-spherical-spherical) parallel flexure stage.

Figure 6.
The hybrid amplifier constructed by serially-jointed parallelogram four-bar linkages [73].
4. Design of a Multi-DOF Stage
In order to carry out delicate and complicated operations, the micro-/nano-positioning stage needs more degrees-of-freedom (DOF). In the literature, there are three main schemes to design a multi-DOF stage, i.e., serial scheme, parallel scheme and serial-parallel scheme. In this section, different scheme designs are introduced, and the recommendation is proposed as a reference to choose a specific scheme.
4.1. Serial Scheme Design
The serial scheme is the simplest method to form a multi-DOF stage, which is realized by connecting one stage’s fixed end to another stage’s output end in series. Benefiting from this feature, the serial stages can be used modularly, e.g., several 1-DOF stages can be composed as an XY, XYZ or large stroke 1-DOF stage. Moreover, the serial stage is easy to design as a stacked structure, which can reduce the planar size and increase the compactness. To conclude, the serial scheme is recommended for the designs that require high modularity or flexibility to suit different application scenarios.
In the literature, Xu [77] introduced a dual-stage 1-DOF positioning system by serial connection of the VCM-driven and PEA-driven stages, which can provide a resolution of 500 nm and over a 10-mm stroke. Xue et al. [78] designed an ESA-driven XYZ serial stage, which has a workspace of 25.2 × 20.4 × 58.5 m. Lee et al. [79] designed a serial XY stage with a stacked structure (Figure 7), which has 50-nm resolution and an 80 × 80 m workspace. Liu et al. [80] used embedded structure to design a planar serial XY stage. It provides a resolution of 50 nm and a workspace of 41.6 × 42.9 m. Pinskier et al. [81] composed two modular 1-DOF stages in a stack to form an XY serial stage, which has a workspace of 39.1 × 42.1 m.
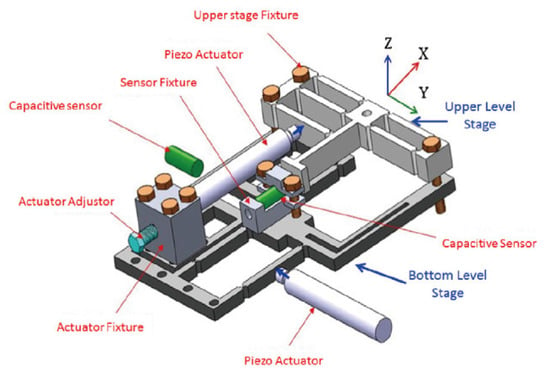
Figure 7.
Schematic diagrams of a serial XY stage with a stacked structure [79].
However, as for a multi-DOF serial stage, the positioning error of each stage will be accumulated and expressed in the final output. On the other hand, since the loading of each level is different, it will cause different dynamic performances for each stage. Thus, a better control and feedback system should be applied to overcome these problems.
4.2. Parallel Scheme Design
The parallel mechanisms, which are implemented by the connection of joints (revolute (R), prismatic (P), cylinder (C), spherical (S) and universal (U)) and rigid linkages, have been concluded well in previous research [82]. The related large-scale positioning stages have been widely used in industry such as multi-axis machining. Due to the properties such as no backlash and being frictionless, the compliant joint is an effective choice to replace the rigid joint, so as to construct a precision parallel stage. Therefore, the compliant parallel positioning stage has become a hot topic in recent years.
To develop a parallel stage, one method is connecting the output ends of different links together. It is a multiple-input multiple-output (MIMO) system as its output motion is coupled. Another method is using decoupling mechanisms as connectors to connect the output ends of different stages. The decoupling mechanisms or decouplers are used to reduce the coupling effect or even isolate the output motion of different axes of the stage. Because of the decoupled output motion, the system can be treated as a combination of multiple single-input single-output (SISO) systems. Some typical decouplers have been used in recent research (see Figure 8), such as parallelogram flexure (PF), compound parallelogram flexure (CPF) and the Roberts mechanism (RM) [83].
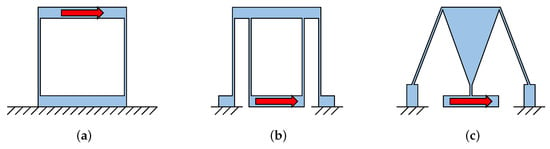
Figure 8.
Illustrations of (a) parallelogram flexure (PF), (b) compound parallelogram flexure (CPF) and (c) the Roberts mechanism (RM).
In comparison with the serial scheme, the parallel scheme can provide larger stiffness, faster response, no accumulated error and identical dynamic performance on each axis by applying a symmetrical design. This scheme is commonly used in applications that require high dynamic performance.
Recent research about parallel stage is mostly focused on three kinds of stage, i.e., XY stage, XY stage and XYZ stage, due to their high versatility. In addition, other designs are also presented for some certain applications, e.g., Hao and He [84] designed a stage for the implementation of a tip-tilt-piston motion. Since there are many related research works about the XY and XY stage in the literature, some of the fabricated stages are listed in Table 1 and Table 2. Due to the difficulty of manufacturing, there are only a few fabricated XYZ stages. Thus, Table 3 shows both fabricated prototypes and concept designs of XYZ stages.

Table 1.
Performance of recent XY parallel stages.

Table 2.
Performance of recent XY parallel stages.

Table 3.
Performance of recent XYZ parallel stages.
4.3. Serial-Parallel Scheme Design
Both serial and parallel schemes have their own advantages and disadvantages. In order to reduce the design difficulty and to obtain a reliable performance, the serial-parallel scheme is a compromise choice. Generally, the serial-parallel scheme provides a higher stiffness than the serial scheme and offers a larger workspace than the parallel scheme [103,104].
The serial-parallel scheme is normally adopted in the mechanical design, which needs three or more DOFs. In the literature, there are many research works about the serial-parallel stage using rigid mechanisms [105,106]. However, there are only a few of research works that adopt the compliant mechanism. Tang et al. [107] design an XYZ serial-parallel positioning stage with the use of two-axis flexure hinges. Cai et al. [108] serially connected two complementary 3-DOF parallel stages to form a 6-DOF compliant stage (Figure 9). The authors stated that this scheme has many benefits, e.g., simple structure, low manufacturing difficulty, low assembly error, high system stability and good dynamic performance.

Figure 9.
A 6-DOF compliant serial-parallel stage [108].
5. Optimization Methods
Structural parameter design is also an important part of designing a compliant micro-/nano-positioning stage, because it governs the performance of the stage dominantly, e.g., stiffness, strength, deflection shape or decoupling performance. An optimal design can guarantee the stability and reliability of the structure and increase the concerned efficiency, e.g., space and material utilization.
To obtain a reliable result in optimization, objective functions should be well prepared. In the field of mechanical design, finite element analysis (FEA) and mathematical modeling are two major methods to evaluate the performance before the prototype fabrication. FEA can provide a reasonable result, and its accuracy mainly relies on the fineness of meshing. There are many widely-used FEA software packages, such as ANSYS, COMSOL and ABAQUS, which provide ease-of-use environments for the user, but the computational cost is high. On the other hand, although the mathematical model could be solved within a short time, the accuracy of the model affects the reliability of the results. Researchers have proposed various methods, where the compliance matrix method [109,110,111] and pseudo-rigid-body model (PRBM) [112,113,114,115,116] are two of the most-used methods for modeling the flexure hinges. With years of practice, the reliability of both of these has been well verified. Besides, the low computational cost is a major benefit for optimizing the complex structure.
In the field of structure optimization, there are three types of methodologies, namely dimension optimization, shape optimization and topology optimization. During the mechanism design, the dimension and shape optimization are normally performed at a later stage, while topology optimization is conducted at the very beginning. In this section, different optimization methods and processes are introduced.
5.1. Dimension and Shape Optimization
The dimension of the mechanisms affects its performance greatly. In order to select the best values of the dimensions to improve the potential of a mechanism, an optimization should be done to enhance the performance. After defining the optimization problem, e.g., optimization objectives and the constraints of performance and design parameters, optimization methods should be chosen to complete the process. According to recent research, the optimization methods can be categorized into non-heuristic and heuristic algorithms.
5.1.1. Non-Heuristic Algorithms
Non-heuristic algorithms include mathematical algorithms (e.g., gradient descent, Newton’s method) and statistical methods (e.g., response surface method, grey relational analysis). Researchers have applied the algorithms to solve the optimization problem of structure design. For instance, Kim et al. [65] and Lee et al. [66] used the sequential quadratic programming (SQP) method to maximize the dynamic performance of their designs. Lai et al. [88] used the “fmincon” function, which is provided by MATLAB, to maximize the translational natural frequency of an XY stage. Dao et al. [60] applied the response surface methodology (RSM) and entropy measurement technique, which are based on the Taguchi method and grey relational analysis, to maximize both the displacement and first natural frequency of an XY parallel stage. Jiang et al. [117] defined the input coupling degree (ICD) to evaluate the decoupling performance of an XY parallel stage first, and then used the “fmincon” function to minimize the ICD.
5.1.2. Heuristic Algorithm
In order to further improve the performance, more freedom of design is required. Therefore, more design parameters should be tuned to fulfill the demand. As the number of design parameters increases, it is challenging work for the conventional optimization methods to obtain an optimal result. The reason lies in that the objective function may not be a convex function, and the local extremum may not be the global extremum. On the other hand, the screening method is also unpractical because of the large search space.
To solve this kind of optimization problem with an acceptable time and resource cost, heuristic algorithms become an alternative choice. In the literature, Xu et al. [59,100,118,119,120] used particle swarm optimization (PSO) to maximize the frequency of the designed stages. Lin et al. [121] and Liu et al. [122] applied the genetic algorithm (GA) to optimize their designs. In addition, Tian et al. [92] solved the optimization problem by using both PSO and GA, and obtained two similar results. This indicates the reliability of the two methods.
5.2. Topology Optimization
At present, the designs of most compliant mechanisms are inspired by or referenced to existing rigid mechanisms, i.e., using a compliant component to replace the rigid component. Although the dimension and shape optimization can improve the performance of the compliant stage to a certain extent, the design already has limited the potential. To improve the performance from the root, researchers have used topology optimization to design new compliant mechanisms starting from the end of the 20th Century [123,124]. The main idea of topology optimization is to achieve the best distribution and least usage of material. Therefore, unlike the frequency maximization objective in dimension and shape optimization, the objective of topology optimization is more flexible. Researchers can design various objectives according to their requirements.
Recent topology optimization research woks about compliant mechanisms have been mostly concentrated on the improvement of optimization methods. For instance, Lee et al. [125] proposed the strain-based solid isotropic microstructure with penalty (SIMP) method to reduce the localized high strain in the flexure hinge. Gaynor et al. [126] used the peak function method and the multivariate SIMP method to perform multiple material topology optimization. Huang et al. [127] proposed bi-directional evolutionary structural optimization (bi-directional ESO (BESO)) to implement the structure optimization with desired stiffness. Wang et al. [128] used the level set method to track the motion of the actuator and the independent point-wise density interpolation (iPDI) method to optimize the structure, so as to realize the optimization of both actuating position and structure. De Leon et al. [129] added the stress constraint in the optimization to avoid the one-node-connected hinge problem. In addition, Yoo et al. [130] used modified ant colony optimization (MACO) to improve the computational efficiency of SIMP.
Researchers have also used novel tools to design positioning stages. In the literature, Lum et al. [131] analyzed and optimized the compliant joints and then constructed an XY parallel stage by using the optimal results (see Figure 10a). Bharanidaran et al. [132] designed a stroke amplifier by topology optimization (Figure 10b), which obtained a half-bridge amplifier. This research demonstrated the reasonableness of bridge type amplifiers. Jin et al. [133] directly defined the design domain of XY and XY parallel stages (Figure 10c,d) and then fabricated and tested the prototypes with optimal results.
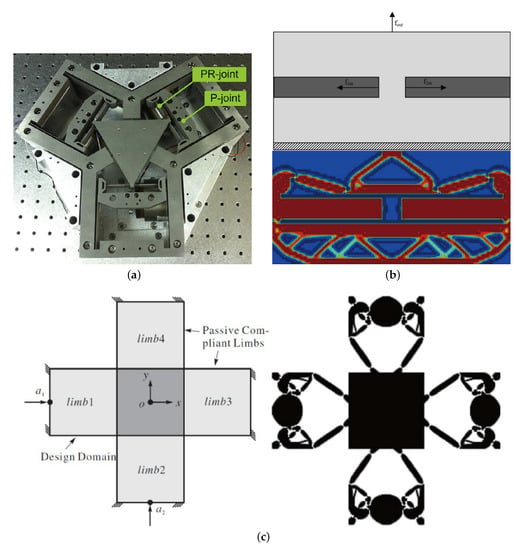
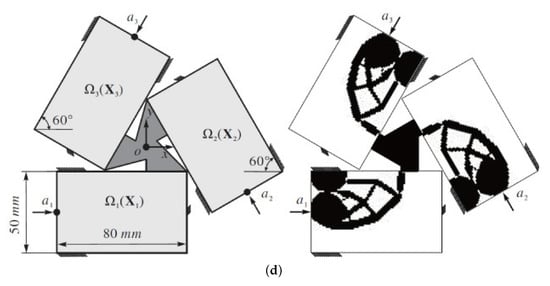
Figure 10.
(a) An XYθ parallel stage using an optimized compliant joint (P: prismatic; R: revolute) [131]; (b) design domain of a stroke amplifier and the result [132]; design domain of (c) an XY and (d) an XYθ parallel stage and the results [133].
6. Further Discussion
From the literature review, we can find that the performance of compliant mechanisms is commonly evaluated by their static and dynamic properties. For a compliant positioning stage, its static performance is mainly indicated by its workspace. However, a larger workspace means larger elastic deformation of the mechanism. Therefore, larger elastic force will be generated. As for the dynamic performance, it is mainly indicated by the natural frequency, which has a positive correlation with the mechanism’s stiffness. However, retaining the same deformation, a higher stiffness mechanism means larger elastic force. Hence, both static and dynamic performances highlight the importance and necessity of a larger actuating force. More recently, constant-force or statically-balanced compliant mechanisms have been investigated [134,135]. This emerges as a promising research topic of actuation technology for various manipulation tasks [136].
For a positioning stage with more than three DOFs, the designed components are usually not planar. On the other hand, the 2D topology optimization always gives the integrated and irregular structure. If topology optimization is applied to 3D solid model design, the optimization result can be more complex. However, the conventional manufacturing methods, e.g., computer numerical control (CNC) lathe machining and wire electrical discharge machining (WEDM), cannot fabricate such complex structures. Therefore, a complex structure needs to be partitioned into several components for manufacturing and then assembling together by screws. Nevertheless, the tolerance of the screw holes further enlarges the effect of manufacturing tolerance. To manufacture complex structure as an integral object with high precision, additive manufacturing (AM) has the greatest potential, e.g., selective laser sintering (SLS), selective laser melting (SLM), direct metal laser sintering (DMLS) and laser engineered net shaping (LENS) [137].
7. Conclusions
This paper has reviewed the recent designs of compliant micro-/nano-positioning stages in consideration of major processes and components in the design flow. With this concept, distinctive design issues are introduced and compared. Moreover, the problems and challenges of the design are concluded and discussed. As a reference, Figure 11 gives the design flow for designing a compliant micro-/nano-positioning stage.
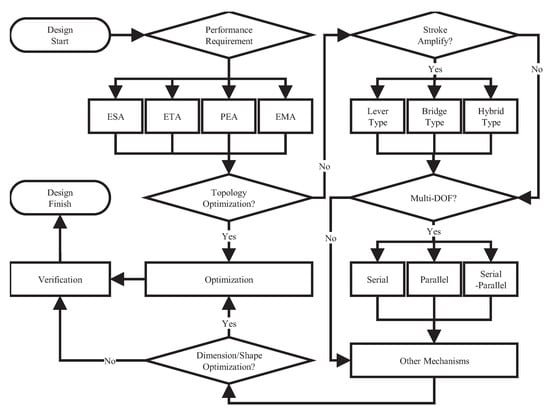
Figure 11.
Design flow for a compliant micro-/nano-positioning stage.
According to the flowchart, the design is oriented by the application. Thus, researchers should first choose the appropriate actuator for the stage according to the specific performance requirement. Once the actuator is selected, the design method needs to be considered, i.e., topology optimization or conventional design approach. For those who choose topology optimization to design the stage, the following step is the optimization; whereas, for those who follow the conventional design way, the next step is the mechanical design, e.g., stroke amplifier or decoupler, which depends on the design requirement and the chosen connecting scheme. Moreover, if an improved performance is desired, the dimension or shape optimization can be introduced as an extra step after the mechanical design. The processes of dimension/shape and topology optimization are similar, i.e., they need a clearly-defined optimization problem including the objectives and constraints, and then, the optimization can be performed by specific optimization algorithm. After the verification by the analytical model or FEA, the design process can be finished. Afterwards, prototype fabrication can be conducted for experimental investigation and application testing. With the advancement of related technologies, more and more micro-/nano-positioning stages will be devised in both academia and industry for pertinent applications.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant 51575545 and the Macao Science and Technology Development Fund under Grants 143/2016/A and 090/2015/A3.
Author Contributions
Zeyi Wu performed the literature view. Zeyi Wu and Qingsong Xu wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
References
- Preston, D.J.; Anders, A.; Barabadi, B.; Tio, E.; Zhu, Y.; Dai, D.A.; Wang, E.N. Electrowetting-on-dielectric actuation of a vertical translation and angular manipulation stage. Appl. Phys. Lett. 2016, 109, 244102. [Google Scholar] [CrossRef]
- Warnat, S.; King, H.; Wasay, A.; Sameoto, D.; Hubbard, T. Direct integration of MEMS, dielectric pumping and cell manipulation with reversibly bonded gecko adhesive microfluidics. J. Micromech. Microeng. 2016, 26, 097001. [Google Scholar] [CrossRef]
- Belfiore, N.P.; Verotti, M.; Crescenzi, R.; Balucani, M. Design, optimization and construction of MEMS-based micro grippers for cell manipulation. In Proceedings of the 2013 International Conference on System Science and Engineering (ICSSE), Budapest, Hungary, 4–6 July 2013; pp. 105–110. [Google Scholar]
- Jain, R.K.; Majumder, S.; Ghosh, B.; Saha, S. Design and manufacturing of mobile micro manipulation system with a compliant piezoelectric actuator based micro gripper. J. Manuf. Syst. 2015, 35, 76–91. [Google Scholar] [CrossRef]
- Cecil, J.; Vasquez, D.; Powell, D. A review of gripping and manipulation techniques for micro-assembly applications. Int. J. Prod. Res. 2005, 43, 819–828. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Tjiptoprodjo, R.C.; Zhang, W.J.; Yang, G.S. Micro-motion devices technology: The state of arts review. Int. J. Adv. Manuf. Technol. 2007, 38, 463–478. [Google Scholar] [CrossRef]
- Howell, L.L. Compliant Mechanisms. In 21st Century Kinematics; Springer: London, UK, 2013; pp. 189–216. [Google Scholar]
- Lobontiu, N. Compliant Mechanisms; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Xu, Q. Design and Implementation of Large-Range Compliant Micropositioning Systems; John Wiley & Sons Singapore Pte. Ltd.: Singapore, 2016. [Google Scholar]
- Ryu, J.W.; Gweon, D.G. Error analysis of a flexure hinge mechanism induced by machining imperfection. Precis. Eng. 1997, 21, 83–89. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. A Comprehensive Survey on Microgrippers Design: Mechanical Structure. J. Mech. Des. 2017, 139, 060801. [Google Scholar] [CrossRef]
- Dochshanov, A.; Verotti, M.; Belfiore, N.P. A Comprehensive Survey on Microgrippers Design: Operational Strategy. J. Mech. Des. 2017, 139, 070801. [Google Scholar] [CrossRef]
- Xu, Q. Design and Development of a Compact Flexure-Based XY Precision Positioning System with Centimeter Range. IEEE Trans. Ind. Electron. 2014, 61, 893–903. [Google Scholar] [CrossRef]
- Mekid, S.; Bashmal, S.; Ouakad, H.M. Nanoscale Manipulators: Review of Conceptual Designs Through Recent Patents. Recent Pat. Nanotechnol. 2016, 10, 44–58. [Google Scholar] [CrossRef] [PubMed]
- Nikoobin, A.; Niaki, M.H. Deriving and analyzing the effective parameters in microgrippers performance. Sci. Iran. 2012, 19, 1554–1563. [Google Scholar] [CrossRef]
- Hao, G.; Li, H.; He, X.; Kong, X. Conceptual design of compliant translational joints for high-precision applications. Front. Mech. Eng. 2014, 9, 331–343. [Google Scholar] [CrossRef]
- Hao, G.; Kong, X. A structure design method for compliant parallel manipulators with actuation isolation. Mech. Sci. 2016, 7, 247–253. [Google Scholar] [CrossRef]
- Hubbard, N.B.; Culpepper, M.L.; Howell, L.L. Actuators for Micropositioners and Nanopositioners. Appl. Mech. Rev. 2006, 59, 324. [Google Scholar] [CrossRef]
- Bell, D.J.; Lu, T.J.; Fleck, N.A.; Spearing, S.M. MEMS actuators and sensors: Observations on their performance and selection for purpose. J. Micromech. Microeng. 2005, 15, S153–S164. [Google Scholar] [CrossRef]
- Ghosh, A.; Corves, B. Introduction to Micromechanisms and Microactuators; Springer: New Delhi, India, 2015. [Google Scholar]
- Zhang, Z.; Liu, B.; Wang, P.; Yan, P. Design of an additive manufactured XY compliant manipulator with spatial redundant constraints. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 9149–9154. [Google Scholar]
- Wang, N.; Liang, X.; Zhang, X. Design and Analysis of a Novel XY Micro-positioning Stage Used Corrugated Flexure Beams. In Intelligent Robotics and Applications; Zhang, X., Liu, H., Chen, Z., Wang, N., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 586–595. [Google Scholar]
- Kim, D.H.; Kim, B.; Kang, H. Development of a piezoelectric polymer-based sensorized microgripper for microassembly and micromanipulation. Microsyst. Technol. 2004, 10, 275–280. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, M.G.; Kim, B.; Sun, Y. A superelastic alloy microgripper with embedded electromagnetic actuators and piezoelectric force sensors: A numerical and experimental study. Smart Mater. Struct. 2005, 14, 1265–1272. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, Q. MEMS Microgripper Actuators and Sensors: The State-of-the-Art Survey. Recent Pat. Mech. Eng. 2013, 6, 132–142. [Google Scholar] [CrossRef]
- Madou, M.J. Fundamentals of Microfabrication: The Science of Miniaturization, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Li, L.; Chew, Z. Microactuators: Design and technology. In Smart Sensors and Mems; Elsevier: Amsterdam, The Netherlands, 2014; pp. 305–348. [Google Scholar]
- Piriyanont, B.; Moheimani, S.O.R. MEMS Rotary Microgripper With Integrated Electrothermal Force Sensor. J. Microelectromech. Syst. 2014, 23, 1249–1251. [Google Scholar] [CrossRef]
- Yeh, J.A.; Chen, C.N.; Lui, Y.S. Large rotation actuated by in-plane rotary comb-drives with serpentine spring suspension. J. Micromech. Microeng. 2004, 15, 201–206. [Google Scholar] [CrossRef]
- Belfiore, N.P.; Broggiato, G.B.; Verotti, M.; Balucani, M.; Crescenzi, R.; Bagolini, A.; Bellutti, P.; Boscardin, M. Simulation and construction of a MEMS CSFH based microgripper. Int. J. Mech. Control 2015, 16, 21–30. [Google Scholar]
- Chang, H.; Zhao, H.; Ye, F.; Yuan, G.; Xie, J.; Kraft, M.; Yuan, W. A rotary comb-actuated microgripper with a large displacement range. Microsyst. Technol. 2013, 20, 119–126. [Google Scholar] [CrossRef]
- Cecchi, R.; Verotti, M.; Capata, R.; Dochshanov, A.; Broggiato, G.; Crescenzi, R.; Balucani, M.; Natali, S.; Razzano, G.; Lucchese, F.; et al. Development of Micro-Grippers for Tissue and Cell Manipulation with Direct Morphological Comparison. Micromachines 2015, 6, 1710–1728. [Google Scholar] [CrossRef]
- Piriyanont, B.; Fowler, A.G.; Moheimani, S.O.R. Force-Controlled MEMS Rotary Microgripper. J. Microelectromech. Syst. 2015, 24, 1164–1172. [Google Scholar] [CrossRef]
- Yeh, J.; Jiang, S.S.; Lee, C. MOEMS variable optical attenuators using rotary comb drive actuators. IEEE Photonics Technol. Lett. 2006, 18, 1170–1172. [Google Scholar] [CrossRef]
- Mita, M.; Arai, M.; Tensaka, S.; Kobayashi, D.; Fujita, H. A micromachined impact microactuator driven by electrostatic force. J. Microelectromech. Syst. 2003, 12, 37–41. [Google Scholar] [CrossRef]
- Maroufi, M.; Moheimani, S.O.R. Design, fabrication and characterization of a high-bandwidth 2DOF MEMS nanopositioner. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 335–340. [Google Scholar]
- Zhang, W.M.; Meng, G.; Chen, D. Stability, Nonlinearity and Reliability of Electrostatically Actuated MEMS Devices. Sensors 2007, 7, 760–796. [Google Scholar] [CrossRef]
- Bazaz, S.A.; Khan, F.; Shakoor, R.I. Design, simulation and testing of electrostatic SOI MUMPs based microgripper integrated with capacitive contact sensor. Sens. Actuators A Phys. 2011, 167, 44–53. [Google Scholar] [CrossRef]
- Wierzbicki, R.; Adda, C.; Hotzendorfer, H. Electrostatic Silicon Microgripper with Low Voltage of Actuation. In Proceedings of the 2007 International Symposium on Micro-NanoMechatronics and Human Science, Nagoya, Japan, 11–14 November 2007; pp. 344–349. [Google Scholar]
- Nakic, C.; Bieker, J.; Lammle, D.; Winterstein, T.; Schlaak, H.F.; Schaumann, G.; Abel, T. Development of an electrothermal micro positioning platform for laser targets with two degrees of freedom. In Proceedings of the 2016 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Paris, France, 18–22 July 2016; pp. 1–5. [Google Scholar]
- Fu, Y.; Luo, J.; Flewitt, A.; Milne, W. Smart microgrippers for bioMEMS applications. In MEMS for Biomedical Applications; Elsevier: Amsterdam, The Netherlands, 2012; pp. 291–336. [Google Scholar]
- Nikoobin, A.; Niaki, M.H. Describing the effective parameters in grippers, and designing the novel micro-nano gripper. In Proceedings of the 2nd International Conference on Control, Instrumentation and Automation, Shiraz, Iran, 27–29 December 2011; pp. 957–963. [Google Scholar]
- Tsai, Y.C.; Lei, S.H.; Sudin, H. Design and analysis of planar compliant microgripper based on kinematic approach. J. Micromech. Microeng. 2004, 15, 143–156. [Google Scholar] [CrossRef]
- Demaghsi, H.; Mirzajani, H.; Ghavifekr, H.B. Design and simulation of a novel metallic microgripper using vibration to release nano objects actively. Microsyst. Technol. 2013, 20, 65–72. [Google Scholar] [CrossRef]
- Varona, J.; Saenz, E.; Fiscal-Woodhouse, S.; Hamoui, A.A. Design and fabrication of a novel microgripper based on electrostatic actuation. In Proceedings of the 2009 52nd IEEE International Midwest Symposium on Circuits and Systems, Cancun, Mexico, 2–5 August 2009; pp. 827–832. [Google Scholar]
- Maluf, N. An Introduction to Microelectromechanical Systems Engineering. Meas. Sci. Technol. 2002, 13, 229. [Google Scholar] [CrossRef]
- Engelen, J.B. Optimization of Comb-Drive Actuators. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2011. [Google Scholar]
- Rakotondrabe, M.; Ivan, I.A. Development and Force/Position Control of a New Hybrid Thermo-Piezoelectric MicroGripper Dedicated to Micromanipulation Tasks. IEEE Trans. Autom. Sci. Eng. 2011, 8, 824–834. [Google Scholar] [CrossRef]
- Habineza, D.; Rakotondrabe, M.; Gorrec, Y.L. Bouc–Wen Modeling and Feedforward Control of Multivariable Hysteresis in Piezoelectric Systems: Application to a 3-DoF Piezotube Scanner. IEEE Trans. Control Syst. Technol. 2015, 23, 1797–1806. [Google Scholar] [CrossRef]
- Gu, G.Y.; Li, C.X.; Zhu, L.M.; Su, C.Y. Modeling and Identification of Piezoelectric-Actuated Stages Cascading Hysteresis Nonlinearity With Linear Dynamics. IEEE/ASME Trans. Mechatron. 2016, 21, 1792–1797. [Google Scholar] [CrossRef]
- Yang, M.J.; Li, C.X.; Gu, G.Y.; Zhu, L.M. Modeling and compensating the dynamic hysteresis of piezoelectric actuators via a modified rate-dependent Prandtl–Ishlinskii model. Smart Mater. Struct. 2015, 24, 125006-1–125006-12. [Google Scholar] [CrossRef]
- Xu, Q. Identification and Compensation of Piezoelectric Hysteresis Without Modeling Hysteresis Inverse. IEEE Trans. Ind. Electron. 2013, 60, 3927–3937. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Model Predictive Discrete-Time Sliding Mode Control of a Nanopositioning Piezostage Without Modeling Hysteresis. IEEE Trans. Control Syst. Technol. 2012, 20, 983–994. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Analytical modeling, optimization and testing of a compound bridge-type compliant displacement amplifier. Mech. Mach. Theory 2011, 46, 183–200. [Google Scholar] [CrossRef]
- Zhu, X.; Wen, Z.; Liu, P. A Piezo-Driven Compliant Nanopositioning Stage with Large Stroke for Micro/Nano Manipulation. MATEC Web Conf. 2016, 77, 01040. [Google Scholar] [CrossRef]
- Lobontiu, N.; Garcia, E. Analytical model of displacement amplification and stiffness optimization for a class of flexure-based compliant mechanisms. Comput. Struct. 2003, 81, 2797–2810. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X.; Li, H.; Wu, H. Full closed-loop controls of micro/nano positioning system with nonlinear hysteresis using micro-vision system. Sens. Actuators A Phys. 2017, 257, 125–133. [Google Scholar] [CrossRef]
- Bhagat, U.; Shirinzadeh, B.; Clark, L.; Chea, P.; Qin, Y.; Tian, Y.; Zhang, D. Design and analysis of a novel flexure-based 3-DOF mechanism. Mech. Mach. Theory 2014, 74, 173–187. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. Design and Optimization of an XYZ Parallel Micromanipulator with Flexure Hinges. J. Intell. Robot. Syst. 2008, 55, 377–402. [Google Scholar] [CrossRef]
- Dao, T.P.; Huang, S.C. Optimization of a two degrees of freedom compliant mechanism using Taguchi method-based grey relational analysis. Microsyst. Technol. 2017, 23, 4815–4830. [Google Scholar] [CrossRef]
- Qu, J.; Chen, W.; Zhang, J.; Chen, W. A piezo-driven 2-DOF compliant micropositioning stage with remote center of motion. Sens. Actuators A Phys. 2016, 239, 114–126. [Google Scholar] [CrossRef]
- Ren, G.; Zhang, Q.; Li, C.; Zhang, X. Research on a 3-DOF Compliant Precision Positioning Stage Based on Piezoelectric Actuators. In Intelligent Robotics and Applications; Huang, Y., Wu, H., Liu, H., Yin, Z., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 346–358. [Google Scholar]
- Gao, J.; Zeng, Z.; Tang, H.; Chen, X.; Qiu, Q.; He, S.; He, Y.; Yang, Z. Design and assessment of a piezo-actuated 3-DOF flexible nanopositioner with large stroke. In Proceedings of the 2016 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Chongqing, China, 18–22 July 2016; pp. 19–24. [Google Scholar]
- Choi, K.B.; Lee, J.J.; Hata, S. A piezo-driven compliant stage with double mechanical amplification mechanisms arranged in parallel. Sens. Actuators A Phys. 2010, 161, 173–181. [Google Scholar] [CrossRef]
- Kim, J.J.; Choi, Y.M.; Ahn, D.; Hwang, B.; Gweon, D.G.; Jeong, J. A millimeter-range flexure-based nano-positioning stage using a self-guided displacement amplification mechanism. Mech. Mach. Theory 2012, 50, 109–120. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, H.C.; Kim, H.Y.; Gweon, D.G. Optimal design and experiment of a three-axis out-of-plane nano positioning stage using a new compact bridge-type displacement amplifier. Rev. Sci. Instrum. 2013, 84, 115103. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Zhou, X.; Liu, Z.; Wang, R.; Zhu, L. Development of a piezoelectrically actuated two-degree-of-freedom fast tool servo with decoupled motions for micro-/nanomachining. Precis. Eng. 2014, 38, 809–820. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Mechanism design of a compact XYZ parallel flexure stage. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 953–957. [Google Scholar]
- Zhang, X.; Xu, Q. Design of a new flexure-based XYZ parallel nanopositioning stage. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 1962–1966. [Google Scholar]
- Li, T.; Du, Y.; Jiang, Y.; Zhang, J. Empirical Compliance Equations for Constant Rectangular Cross Section Flexure Hinges and Their Applications. Math. Probl. Eng. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Dong, W.; Chen, F.; Yang, M.; Du, Z.; Tang, J.; Zhang, D. Development of a highly efficient bridge-type mechanism based on negative stiffness. Smart Mater. Struct. 2017, 26, 095053. [Google Scholar] [CrossRef]
- Chen, F.; Du, Z.; Yang, M.; Gao, F.; Dong, W.; Zhang, D. Design and analysis of a three-dimensional bridge-type mechanism based on the stiffness distribution. Precis. Eng. 2018, 51, 48–58. [Google Scholar] [CrossRef]
- Yao, Q.; Dong, J.; Ferreira, P. Design, analysis, fabrication and testing of a parallel-kinematic micropositioning XY stage. Int. J. Mach. Tools Manuf. 2007, 47, 946–961. [Google Scholar] [CrossRef]
- Clark, L.; Shirinzadeh, B.; Zhong, Y.; Tian, Y.; Zhang, D. Design and analysis of a compact flexure-based precision pure rotation stage without actuator redundancy. Mech. Mach. Theory 2016, 105, 129–144. [Google Scholar] [CrossRef]
- Chu, C.L.; Chen, H.C.; Sie, M.H. Development of a XYθz 3-DOF nanopositioning stage with linear displacement amplification device. MATEC Web Conf. 2017, 123, 00006. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design and modeling of a novel 3-PSS flexure nanopositioning stage. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1322–1327. [Google Scholar]
- Xu, Q. Design and Development of a Flexure-Based Dual-Stage Nanopositioning System With Minimum Interference Behavior. IEEE Trans. Autom. Sci. Eng. 2012, 9, 554–563. [Google Scholar] [CrossRef]
- Xue, G.; Toda, M.; Ono, T. Comb-drive XYZ-microstage based on assembling technology for low temperature measurement systems. In Proceedings of the 2015 International Conference on Electronic Packaging and iMAPS All Asia Conference (ICEP-IAAC), Kyoto, Japan, 14–17 April 2015; pp. 83–88. [Google Scholar]
- Lee, J.W.; Li, Y.C.; Chen, K.S.; Liu, Y.H. Design and control of a cascaded piezoelectric actuated two-degrees-of-freedom positioning compliant stage. Precis. Eng. 2016, 45, 374–386. [Google Scholar] [CrossRef]
- Liu, X.; Huang, W.; Wang, Y. A novel 2D piezo-nanopositioning stage based on triangle amplifier mechanism. In Proceedings of the 2016 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Xi’an, China, 21–24 October 2016; pp. 314–318. [Google Scholar]
- Pinskier, J.; Shirinzadeh, B.; Clark, L.; Qin, Y.; Fatikow, S. Design, development and analysis of a haptic-enabled modular flexure-based manipulator. Mechatronics 2016, 40, 156–166. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J. Parallel Kinematics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Wan, S.; Zhang, Y.; Xu, Q. Design and development of a new large-stroke XY compliant micropositioning stage. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 3263–3276. [Google Scholar] [CrossRef]
- Hao, G.; He, X. Designing a monolithic tip-tilt-piston flexure manipulator. Arch. Civ. Mech. Eng. 2017, 17, 871–879. [Google Scholar] [CrossRef]
- Awtar, S.; Slocum, A.H. Constraint-Based Design of Parallel Kinematic XY Flexure Mechanisms. J. Mech. Des. 2007, 129, 816–830. [Google Scholar] [CrossRef]
- Awtar, S.; Parmar, G. Design of a Large Range XY Nanopositioning System. J. Mech. Robot. 2013, 5, 021008. [Google Scholar] [CrossRef]
- Xu, Q. New Flexure Parallel-Kinematic Micropositioning System with Large Workspace. IEEE Trans. Robot. 2012, 28, 478–491. [Google Scholar] [CrossRef]
- Lai, L.J.; Gu, G.Y.; Zhu, L.M. Design and control of a decoupled two degree of freedom translational parallel micro-positioning stage. Rev. Sci. Instrum. 2012, 83, 045105-1–045105-17. [Google Scholar] [CrossRef] [PubMed]
- Olfatnia, M.; Cui, L.; Chopra, P.; Awtar, S. Large range dual-axis micro-stage driven by electrostatic comb-drive actuators. J. Micromech. Microeng. 2013, 23, 105008-1–105008-11. [Google Scholar] [CrossRef]
- Qin, Y.; Shirinzadeh, B.; Tian, Y.; Zhang, D. Design issues in a decoupled XY stage: Static and dynamics modeling, hysteresis compensation, and tracking control. Sens. Actuators A Phys. 2013, 194, 95–105. [Google Scholar] [CrossRef]
- Xu, Q. A modular two-axis compliant parallel micropositioning stage with long travel range. In Proceedings of the 2013 IEEE International Conference on Information and Automation (ICIA), Yinchuan, China, 26–28 August 2013; pp. 898–903. [Google Scholar]
- Tian, Y.; Liu, C.; Liu, X.; Wang, F.; Li, X.; Qin, Y.; Zhang, D.; Shirinzadeh, B. Design, modelling and characterization of a 2-DOF precision positioning platform. Trans. Inst. Meas. Control 2014, 37, 396–405. [Google Scholar] [CrossRef]
- Huang, S.C.; Dao, T.P. Design and computational optimization of a flexure-based XY positioning platform using FEA-based response surface methodology. Int. J. Precis. Eng. Manuf. 2016, 17, 1035–1048. [Google Scholar] [CrossRef]
- Pang, J.; Liu, P.; Yan, P.; Zhang, Z. Modeling and experimental testing of a composite bridge type amplifier based nano-positioner. In Proceedings of the 2016 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), IEEE, Chongqing, China, 18–22 July 2016; pp. 25–30. [Google Scholar]
- Wan, S.; Xu, Q. Design and analysis of a new compliant XY micropositioning stage based on Roberts mechanism. Mech. Mach. Theory 2016, 95, 125–139. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Xu, Q. Design and control of a novel piezo-driven XY parallel nanopositioning stage. Microsyst. Technol. 2016, 23, 1067–1080. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, Y.; Liu, C.; Wang, F.; Liu, X.; Shirinzadeh, B.; Zhang, D. Design and control methodology of a 3-DOF flexure-based mechanism for micro-/nano-positioning. Robot. Comput.-Integr. Manuf. 2015, 32, 93–105. [Google Scholar] [CrossRef]
- Cai, K.; Tian, Y.; Wang, F.; Zhang, D.; Shirinzadeh, B. Development of a piezo-driven 3-DOF stage with T-shape flexible hinge mechanism. Robot. Comput.-Integr. Manuf. 2016, 37, 125–138. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, X. A planar 3-DOF nanopositioning platform with large magnification. Precis. Eng. 2016, 46, 221–231. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. A Totally Decoupled Piezo-Driven XYZ Flexure Parallel Micropositioning Stage for Micro/Nanomanipulation. IEEE Trans. Autom. Sci. Eng. 2011, 8, 265–279. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design of a new decoupled compliant XYZ parallel-kinematic nanopositioning stage. In Proceedings of the TENCON 2015—2015 IEEE Region 10 Conference, Macao, China, 1–4 November 2015; pp. 1–4. [Google Scholar]
- Zhang, X.; Xu, Q.; Macau, P. Design and Analysis of a New XYZ Parallel Flexure Stage. In Proceedings of the 14th IFToMM World Congress, Taibei, Taiwan, 25–30 October 2015; pp. 706–710. [Google Scholar]
- Merlet, J.P. Parallel Robots; Springer Science & Business Media: New York, NY, USA, 2006; Volume 128. [Google Scholar]
- Huang, Z.; Kong, L.; Fang, Y.F. Theory on Parallel Robotics and Control; Machinery Industry: Beijing, China, 1997; pp. 293–302. [Google Scholar]
- Law, M.; Ihlenfeldt, S.; Wabner, M.; Altintas, Y.; Neugebauer, R. Position-dependent dynamics and stability of serial-parallel kinematic machines. CIRP Ann. 2013, 62, 375–378. [Google Scholar] [CrossRef]
- Oba, Y.; Yamada, Y.; Igarashi, K.; Katsura, S.; Kakinuma, Y. Replication of skilled polishing technique with serial–parallel mechanism polishing machine. Precis. Eng. 2016, 45, 292–300. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, M.; Cao, G. Design and testing of a novel flexure-based 3-degree-of-freedom elliptical micro-/nano-positioning motion stage. Adv. Mech. Eng. 2017, 9, 168781401772524. [Google Scholar] [CrossRef]
- Cai, K.; Tian, Y.; Wang, F.; Zhang, D.; Liu, X.; Shirinzadeh, B. Design and control of a 6-degree-of-freedom precision positioning system. Robot. Comput.-Integr. Manuf. 2017, 44, 77–96. [Google Scholar] [CrossRef]
- Lobontiu, N. Compliance-based matrix method for modeling the quasi-static response of planar serial flexure-hinge mechanisms. Precis. Eng. 2014, 38, 639–650. [Google Scholar] [CrossRef]
- Koseki, Y.; Tanikawa, T.; Koyachi, N.; Arai, T. Kinematic analysis of a translational 3-DOF micro-parallel mechanism using the matrix method. Adv. Robot. 2002, 16, 251–264. [Google Scholar] [CrossRef]
- Pham, H.H.; Chen, I.M. Stiffness modeling of flexure parallel mechanism. Precis. Eng. 2005, 29, 467–478. [Google Scholar] [CrossRef]
- Venkiteswaran, V.K.; Su, H.J. Pseudo-Rigid-Body Models of Initially-Curved and Straight Beams for Designing Compliant Mechanisms. In Proceedings of the Volume 5A: 41st Mechanisms and Robotics Conference, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Li, N.; Su, H.J.; Zhang, X.P. Accuracy Assessment of Pseudo-Rigid-Body Model for Dynamic Analysis of Compliant Mechanisms. J. Mech. Robot. 2017, 9, 054503. [Google Scholar] [CrossRef]
- Verotti, M. Analysis of the center of rotation in primitive flexures: Uniform cantilever beams with constant curvature. Mech. Mach. Theory 2016, 97, 29–50. [Google Scholar] [CrossRef]
- Verotti, M. Effect of initial curvature in uniform flexures on position accuracy. Mech. Mach. Theory 2018, 119, 106–118. [Google Scholar] [CrossRef]
- Belfiore, N.P.; Balucani, M.; Crescenzi, R.; Verotti, M. Performance Analysis of Compliant MEMS Parallel Robots Through Pseudo-Rigid-Body Model Synthesis. In Proceedings of the ASME 2012 11th Biennial Conference on Engineering Systems Design and Analysis, Nantes, France, 2–4 July 2012; pp. 329–334. [Google Scholar]
- Jiang, Y.; Li, T.; Wang, L. Design, Development, and Application of a Compact Flexure-Based Decoupler With High Motion Transmission Efficiency and Excellent Input Decoupling Performance. IEEE/ASME Trans. Mechatron. 2017, 22, 1071–1081. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Optimal design and fabrication of a piezoactuated flexure XYZ parallel micropositioning stage. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taiwan, 18–22 October 2010; pp. 3682–3687. [Google Scholar]
- Li, Y.; Xu, Q. Design and Analysis of a Totally Decoupled Flexure-Based XY Parallel Micromanipulator. IEEE Trans. Robot. 2009, 25, 645–657. [Google Scholar]
- Li, Y.; Xu, Q. A Novel Piezoactuated XY Stage With Parallel, Decoupled, and Stacked Flexure Structure for Micro-/Nanopositioning. IEEE Trans. Ind. Electron. 2011, 58, 3601–3615. [Google Scholar] [CrossRef]
- Lin, S.; Jia, Y.; Lei, I.P.; Xu, Q. Design and optimization of a long-stroke compliant micropositioning stage driven by voice coil motor. In Proceedings of the 2012 12th International Conference on Control Automation Robotics & Vision (ICARCV). IEEE, Guangzhou, China, 5–7 December 2012; pp. 1716–1721. [Google Scholar]
- Liu, Y.; Wu, K.; Xu, D.; Xu, Q. Design of a microscope auto-focusing device based on multi-stage leaf spring. In Proceedings of the 2014 IEEE International Conference on Information and Automation (ICIA), Hailar, China, 28–30 July 2014; pp. 1–6. [Google Scholar]
- Sigmund, O. On the Design of Compliant Mechanisms Using Topology Optimization. Mech. Struct. Mach. 1997, 25, 493–524. [Google Scholar] [CrossRef]
- Jonsmann, J.; Sigmund, O.; Bouwstra, S. Compliant thermal microactuators. Sens. Actuators A Phys. 1999, 76, 463–469. [Google Scholar] [CrossRef]
- Lee, E.; Gea, H.C. A strain based topology optimization method for compliant mechanism design. Struct. Multidiscip. Optim. 2013, 49, 199–207. [Google Scholar] [CrossRef]
- Gaynor, A.T.; Meisel, N.A.; Williams, C.B.; Guest, J.K. Multiple-Material Topology Optimization of Compliant Mechanisms Created Via PolyJet Three-Dimensional Printing. J. Manuf. Sci. Eng. 2014, 136, 061015-1–061015-10. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Zhou, S.; Xie, Y. Topology optimization of compliant mechanisms with desired structural stiffness. Eng. Struct. 2014, 79, 13–21. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Z.; Zhang, X.; Kang, Z. Topological design of compliant smart structures with embedded movable actuators. Smart Mater. Struct. 2014, 23, 045024-1–045024-15. [Google Scholar] [CrossRef]
- Leon, D.M.D.; Alexandersen, J.; Fonseca, J.S.O.; Sigmund, O. Stress-constrained topology optimization for compliant mechanism design. Struct. Multidiscip. Optim. 2015, 52, 929–943. [Google Scholar] [CrossRef]
- Yoo, K.S.; Han, S.Y. Topology optimum design of compliant mechanisms using modified ant colony optimization. J. Mech. Sci. Technol. 2015, 29, 3321–3327. [Google Scholar] [CrossRef]
- Lum, G.Z.; Teo, T.J.; Yang, G.; Yeo, S.H.; Sitti, M. Integrating mechanism synthesis and topological optimization technique for stiffness-oriented design of a three degrees-of-freedom flexure-based parallel mechanism. Precis. Eng. 2015, 39, 125–133. [Google Scholar] [CrossRef]
- Bharanidaran, R.; Srikanth, S.A. A new method for designing a compliant mechanism based displacement amplifier. IOP Conf. Ser. Mater. Sci. Eng. 2016, 149, 012129-1–012129-7. [Google Scholar] [CrossRef]
- Jin, M.; Zhang, X. A new topology optimization method for planar compliant parallel mechanisms. Mech. Mach. Theory 2016, 95, 42–58. [Google Scholar] [CrossRef]
- Xu, Q. Design of a Large-Stroke Bistable Mechanism for the Application in Constant-Force Micropositioning Stage. J. Mech. Robot. 2016, 9, 011006-1–011006-7. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Q. Design of a flexure-based constant-force XY precision positioning stage. Mech. Mach. Theory 2017, 108, 1–13. [Google Scholar] [CrossRef]
- Xu, Q. Micromachines for Biological Micromanipulation; Springer: New York, NY, USA, 2018. [Google Scholar]
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive manufacturing methods and modelling approaches: A critical review. Int. J. Adv. Manuf. Technol. 2015, 83, 389–405. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).