Abstract
This paper deals with static stability in planar grasps of an object by multiple fingers. Differently from previous research, we focus on the case that each finger has redundant links and joints. Based on contact constraints between the object and fingers, the relationships among displacements of object’s pose, contact positions, and joint positions are formulated. Using the constraints, the redundant joints are reduced to independent parameters. The relationship between the displacement and reaction torque of each joint is modeled as a linear spring, and potential energy of the grasp is formulated. Not only for frictionless sliding contact but also for pure rolling contact, we derive stable conditions on the contact positions and joint positions. Based on the conditions, partially differentiating the potential energy, a wrench (force and moment) vector and a stiffness matrix applied to the object by each finger are derived. Summing up the wrenches and matrices of all the fingers, we obtain a wrench vector and a stiffness matrix of the grasp, and we evaluate the grasp stability. Because of our analytical formulation, grasp parameters such as local curvatures at contact points, joint stiffnesses, etc., are explicitly included in the derived matrices. Partially differentiating the wrenches and matrices by the grasp parameters, we clarify effects of the parameters on the stability. Moreover, the difference between the frictionless sliding contact and pure rolling contact is derived in the wrench vector and the stiffness matrix. Using numerical examples, we validate our analysis.
1. Introduction
Humans can dexterously grasp and manipulate various shaped objects using their hands. Even during assembly or contact tasks, it is possible to maintain the grasp without dropping or breaking the objects and accomplish the tasks. When performing assembly or contact tasks by human-like robots, it is necessary to grasp and manipulate an object by a multi-finger robotic hand stably against an external disturbance. In order to make stable grasps, grasp stability has been investigated for many years.
Hanafusa et al. [] explored stable grasps by a three-finger mechanical hand. Since the hand was composed of elastic fingers, they focused on the potential energy stored in the grasp. They pointed out that the grasp is stable if the potential energy is in the local minimum. Nguyen [,] replaced every finger with a virtual linear spring actuated by a motor control and formulated potential energy stored in the grasp system. The first- and second-order partial derivatives of the energy based on the object pose (position and orientation) displacement were derived. He pointed out that the grasp is stable if the first-order partial derivative is zero (wrench equilibrium) and the second-order partial derivative is positive definite. In the virtual spring model, for frictionless contact, each finger is replaced with one linear spring aligned in the normal direction at the contact point. For frictional contact, each finger is replaced by multiple linear springs connected at the contact point. Note that, in this paper, the first- and second-order partial derivatives are referred to as a grasp wrench (force and moment) and a grasp stiffness matrix, respectively.
Bicchi [,] considered form closure and force closure from the perspective of constraining a part (an object) with fixtures (fingers). The form-closure grasp is a grasp that geometrically constrains the pose displacement of the part by the part and fixtures’ shape and the fixtures’ arrangement. This grasp does not rely on surface friction and contact forces. Force-closure grasp is a grasp that can resist any external disturbance force generated on the part by contact forces generated by the fixtures. This grasp does not consider the object pose displacement but includes friction forces.
Montana [], Funahashi et al. [], Howard et al. [], and Rimon et al. [] introduced local curvatures at the contact points and investigated the grasp stability in planar or spatial grasps. Considering the curvatures, they included motion of the contact points on the object and fingers. Rimon et al. [] investigated a second-order mobility index. From the perspective of form closure, immobility of an object was discussed including local curvatures at contact points. Montana [], Yamada et al. [], and Luo et al. [] introduced the surface geometry at each contact point in spatial grasps, i.e., including not only curvature but also metric tensor and torsion. Differently from previous research, in Ref. [], the multiple virtual spring model is applied not only for frictional contact but also for frictionless contact. Differences in the surface friction condition were represented by differences in contact point movement.
Li et al. [] investigated form-closure grasps using a four-pin parallel gripper. A method for achieving stable grasps using reinforcement learning in a simulation space was proposed. Minami et al. [] investigated the alignment feasibility of a grasped part by two circular fingers from the perspective of second-order form closure. Xu et al. [] discussed a method for achieving force-closure grasps using a learning method. Gilart et al. [] investigated a method for determining grasp positions that achieve a force-closure grasp within reach of the fingers of a given hand. Li et al. [] investigated an algorithm for minimizing grasp forces from the perspective of force closure.
Harada et al. [] explored manipulation of multiple objects. Yamada et al. [] investigated grasp stability of multiple objects in two or three dimensions. The surface geometries at contact points between not only the object and fingers but also the objects were included.
Tsuji et al. [] introduced the concept of energy tolerance in potential field. Deformation of the elastic fingertip surface was discussed, the potential energy of the de-formation was formulated, and friction constraints were considered. Garate et al. [] proposed a method which controlled finger joints and regulated orientation of the primary axis of the grasp stiffness ellipsoid in order to maintain stable grasps. Nakashima et al. [] explored moment stability of grasps with soft finger contact. Harada et al. [] discussed grasp stability under soft finger contact and gravity. Dong et al. [] and Ma et al. [] discussed contact stiffness of soft fingertips.
Yamada et al. [] explored effects of grasp parameters on the grasp stability. Grasp parameters such as local curvatures, joint stiffnesses, contact forces, etc., are included in the grasp stiffness matrix. The grasp stiffness matrix was partially differentiated by the grasp parameters, and the effects of the grasp parameters were evaluated by positive definiteness of the derivatives. Yamada et al. [] proposed an algorithm for optimization of the grasp positions of the fingers based on the grasp stiffness matrix. The grasp stability is evaluated by the eigenvalues of the matrix. Using the partial derivative of the stiffness matrix, the relationship between the finger position parameter and positive definiteness of the stiffness matrix was derived. In order to maximize the eigenvalues, the grasp positions are regulated. In the algorithm, the contact forces inside friction cones are obtained and the wrench equilibrium is satisfied by using a linear programming problem.
Chirikjian et al. [] discussed kinematics and grasping of hyper-redundant robots. Firouzeh et al. [] handled grasps by fingers with redundant and underactuated joints. The gripper is a tendon-driven type with adjustable stiffness. Song et al. [] discussed grasping of a soft gripper whose shape is changeable by vacuum control. Surface curvature and finger stiffness are also changeable. Shan et al. [] investigated grasps by fingers with a cantilever spring-based variable stiffness mechanism. The finger is deformable due to the shape of objects.
Robotic fingers are composed of multiple links and joints. Prismatic or revolute joints exist in the joint types. In previous research on grasp stability [,], the fingertips move in translation only; i.e., the fingers are composed of prismatic joints. Yamada et al. [] introduced revolute joints into the grasp stability analysis in two dimensions. The number of joints of every finger is restricted to less than or equal to three.
In this paper, we deal with static stability in planar grasps of an object by multiple redundant fingers. Differently from previous research, we focus on each finger having redundant links and joints. A detailed analysis is performed, and the wrench vector and grasp stiffness matrix are derived in detail. The effects of grasp parameters are also investigated analytically. In Section 2, we explain assumptions, potential energy of the object and fingers, and contact constraints between the object and fingers. In Section 3, the stiffness matrices of the object pose applied by the fingers are derived in the case of frictionless sliding contact between the object and fingers. In Section 4, the stiffness matrices are derived in the case of pure rolling contact (rolling contact without sliding). In Section 5, the wrench vector and the stiffness matrix of the grasp are derived. In Section 6, we discuss effects of grasp parameters on the grasp stability. In Section 7, using numerical examples, we evaluate grasps and validate our analysis. In Section 8, we conclude this paper.
2. Problem Formulation
As shown in Figure 1, an object is grasped by multiple fingers with redundant joints. Every finger is composed of a series of links. A distal link of the finger maintains contact with the object. The distal link is referred to as a fingertip. We focus on quasi-static stability of the grasp. When the object is perturbed by an external disturbance, the grasp system is displaced from the initial grasp state. If the grasp system returns to the initial grasp after the disturbance dissipates, the grasp is stable. Hence, in this paper, the grasp is replaced by an elastic system, and the potential energy of the grasp is derived. The first- and second-order partial derivatives of the energy are derived. The grasp stability is evaluated by using positive definiteness of the energy at the initial grasp.
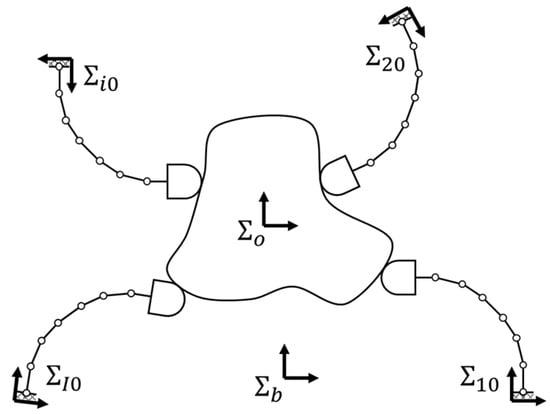
Figure 1.
An object grasped by multiple fingers with redundant joints.
2.1. Assumptions
We analyze the stability in the following assumptions:
(C1) The object and the finger links are rigid bodies.
(C2) Motion of the bodies is limited to infinitesimal displacement.
(C3) The relationship between position displacement and reaction torque of every joint is modeled as a linear spring.
(C4) At the contact points, the shapes of the object and distal links of the fingers are approximated by local curvatures.
(C5) In the initial grasp state, the fingers push the object, and the grasp is in wrench equilibrium.
Based on (C1), detailed geometrical formulations are performed when displacements of the object and fingers occur. Since the first- and second-order terms of Taylor expansion of grasp potential energy in the initial grasp state are focused on, (C2) is considered. Based on (C3), potential energy of the grasp system is formulated. In (C3), the linear property is actualized by computer control of a joint motor. Since at most second-order terms are focused on, the surface shapes are considered within the second-order geometry in (C4). Based on the potential energy, the grasp stability is analyzed in detail. Because the grasp position determination problem is not discussed, (C5) is assumed. The problem will be tackled in our future projects.
2.2. Symbols
The number of fingers is denoted by . Finger number is expressed by . The number of joints of the i-th finger is denoted by . Joint number is expressed by . For simplicity of the expression, subscript “” of is omitted as below. Symbol expresses a coordinate frame as follows (Figure 2):
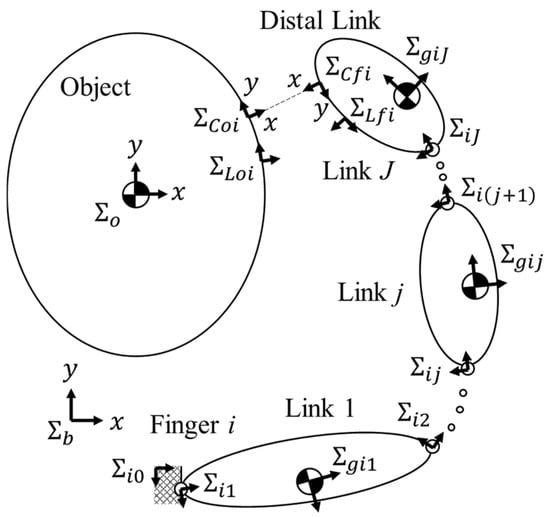
Figure 2.
Coordinate frames.
: Base coordinate frame.
: Object coordinate frame fixed at the mass center of the object.
: Moving frame at the current contact point on the object surface. The x- and y-axes of the frame are an outward normal vector and a tangent vector of the object surface, respectively.
: Moving frame at the current contact point on the finger surface. The x- and y-axes of the frame are set in a similar manner of .
, , : Initial frames of the frames , , and , respectively.
: Finger link coordinate frame fixed at the mass center of the j-th link of the i-th finger.
Vectors and matrices used in this paper are shown in Appendix A.
2.3. Displacements of the Object and Fingers
Due to an external disturbance applied to the grasp system, the object and fingers are displaced from the initial grasp state. In this subsection, the displacements and constraints of the bodies are formulated, and potential energies of the bodies are derived.
2.3.1. Displacement Parameters of the Object Pose
Pose (position and orientation) displacement of the object due to the external disturbance is denoted by , where is a translation component and is a rotation component. The pose of with respect to is expressed by the following homogeneous transformation matrix:
See (A2) in Appendix A.1 for the symbol . Hence, the pose of the object mass center frame with respect to the base frame is obtained by the following matrix:
The position component of is obtained by
The potential energy of the object mass is obtained by
where the vector is the gravity acceleration with respect to . The first and second partial derivatives of by at the initial state are obtained by
2.3.2. Displacement Parameters of the Finger Joints
Joint position of the j-th joint of the i-th finger is denoted by . The position is composed of three elements:
where is a natural position component, is a compressed position component by the initial contact force, and is generated by the object pose displacement . The joint positions of the finger are collected, so we have
Every joint of the fingers is replaced by linear spring stiffness. The stiffness is denoted by , and the potential energy stored in the i-th finger is expressed by
where . The pose of the finger link mass center frame with respect to is represented by
The position component of is obtained by
The finger link mass is denoted by . The potential energy of the finger is obtained by
Total potential energy of the i-th finger is obtained by
The energy is partially differentiated by , and the initial state is substituted into the differentiation; then we have the following torque vector:
The second partial derivative of at the initial state is given by
where the details of , , and are shown in Appendix B.1.
2.4. Contact Constraints of the Object and Fingers
2.4.1. Displacement Parameters of the Contact Positions
The initial contact frame is fixed on the object surface. The pose of with respect to is expressed by the following matrix:
The initial contact frame is fixed on the distal link surface of the finger (i.e., the fingertip). The pose of with respect to is expressed by
The contact positions on the object and fingertips move due to the displacements and . The displacements of the positions are expressed by and , and local curvatures at the contact positions are expressed by and , respectively. Note that the curvature represent a convex surface, represents a flat surface, and represents a concave surface. The pose of the moving contact frame with respect to the initial contact frame is expressed by the following homogeneous transformation matrices:
When the fingertip maintains contact with the object even in the presence of external disturbance, we obtain the following constraint:
where x- and y-axes of and those of are opposite; then the pose of with respect to is given by
The fingertip makes a single-point contact with the object. The fingertip surface does not overlap with the object surface at any other point; then we have .
2.4.2. Partial Derivative of the Constraints
In (18), the number of displacement parameters is (i.e., 3 for , 2 for , for ), and the number of constraints is 3 (i.e., 2 for translation, 1 for rotation). Considering constraint (18), the displacements can be reduced and are expressed by a function of independent parameters in the following form:
where the parameter is represented by
Considering (20), and partially differentiating Equations (18) and (21), we have the following form (See Appendix C):
where the symbol is an order identity matrix. The matrix and the Jacobian matrix are obtained by
We assume that the left-hand coefficient matrix of (22) is nonsingular, and the following condition is satisfied.
The matrix can be obtained from independent rows of the matrix . We express the inverse matrix of the coefficient matrix as
Then we have
Considering (24b), the matrices and are represented by
2.4.3. Potential Energy of the Finger Considering the Constraints
Considering constraint (18) and form (20), the energy is rewritten by
If (28) is partially differentiated by the displacements , and the initial state is substituted, we have the following vectors:
where the vector is given by the following form:
The vector represents contact wrench (force and moment) generated by the joint torque and is represented in the frame . Deriving the second partial derivative (28), we have the following form:
where . The matrix includes the local curvatures, the contact force, and contact positions with respect to the object center. The matrix includes the joint spring stiffnesses, the matrix includes the masses and positions of the finger links with respect to the joint positions, and the matrix includes contact positions and contact forces. The details of the matrices and are shown in Appendix B.2.
3. Frictionless Sliding Contact
In the previous section, we only considered constraint (18). At the contact point, the movement of the fingers on the object surface depends on friction. In this section, we focus on frictionless sliding contact.
3.1. Stable Condition of the Finger with the Sliding Contacct
When the energy is locally minimum, the contact position displacement and the joint position parameter are stable. Consequently, in the case of frictionless sliding contact, we have the following conditions on the first and second partial derivatives:
Substituting the initial state, we have
From (32b), we have
From (29) and (33a), we have
Consequently, the tangent and moment components of the contact wrench have to be zero, and the normal component remains. Since the wrench applied by each finger is restricted in (35), the contact force has to be aligned in the normal direction at the contact point.
Considering (25), (30), and (35), the relationship between the joint torque and the contact force is obtained by the following form:
Substituting the wrench condition, the derivative (31) is rewritten by
where the details of and are shown in Appendix B.3.
3.2. Wrench Vector and Stiffness Matrix of the Finger with the Sliding Contacct
Partially differentiating (32a) and substituting the initial state, we have
In (32a), the number of constraints is . Consequently, the parameters and can be reduced, and the energy (28) is represented by a function of as follows:
The first partial derivative of by at the initial state is obtained by
The vector is a wrench vector applied to the object center by the i-th finger. The wrench vector is generated only by the normal force component at the contact point. Considering (38), the second partial derivative of is obtained by
where
See Appendix D.1 for the derivation. The matrix is a stiffness matrix of the object pose applied by the finger. The first term is affected by the contact positions on the object and the finger configurations. The second term is affected by the local curvatures and the finger configurations. Considering condition (34a), positive definiteness of decreases due to the contact position movement. The third term is affected by the redundant joints. Considering condition (34b), the positive definiteness of decreases due to the redundant joints.
Note that the vector and the matrix are independent of the selection of the matrix (see Appendix D.2).
4. Pure Rolling Contact
In this section, we focus on the case that the fingertip rolls on the object surface without sliding (i.e., pure rolling contact).
4.1. Stable Condition of the Finger with the Rolling Contact
In the case of pure rolling contact, the contact displacement parameters and are restricted by
From this condition, the parameters included in the energy are reduced to the following form:
When the energy is in the local minimum, the displacements are stable. Then we have
Substituting the initial state, we have
From (45b), we have
From (29) and (43), we have the following first partial derivatives:
From (45a) and (47), the following conditions have to be satisfied.
Considering , we have
This condition means that no moment component occurs at the contact point and the force component remains. Since the contact wrench applied by each finger is restricted in (49), the translational components of the wrench have no restrictions. However, the contact force has to be inside the friction cone at the contact point for the pure rolling contact. In this paper, we suppose that the contact force stays inside the friction cone.
The second partial derivatives are represented in the following form:
4.2. Wrench Vector and Stiffness Matrix of the Finger with the Rolling Contact
Partially differentiating (44a) and substituting the initial state, we have
Considering condition (44a), the parameters are redundant, and the energy is rewritten by
The first partial derivative of by is obtained by
The vector is a wrench vector applied to the object center. Considering (51), the second partial derivative of is obtained by
where
The matrix is a stiffness matrix of the object pose applied by the finger and is composed of three terms. The first term is affected by the contact position. The second term is affected by the local curvatures and decreases the positive definiteness of due to (46a). The third them is affected by the redundant joints and decreases the positive definiteness of due to (46b).
Note that the vector and the matrix are also independent of the selection of the matrix .
5. Wrench Vector and Stiffness Matrix of the Grasp
The grasp is composed of the object and fingers. Considering (4), (39) and (52), the total potential energy of the grasp is given by summarizing the bodies.
where the right-hand superscript “” means
The first- and second-order partial derivatives are obtained by
From the viewpoint of the potential energy method, the grasp is stable when the potential energy is in the local minimum at the initial state. If the first partial derivative is in wrench equilibrium (), and the second partial derivative is positive definite (), then the grasp is stable. The positive definiteness is evaluated by the eigenvalues of the matrix. Since the matrix is a real symmetric matrix, its eigenvalues and eigenvectors are obtained in real values and real vectors. If the matrix is positive definite, all eigenvalues are positive. If the matrix is not positive definite, zero or negative eigenvalues are obtained, and the grasp is not guaranteed to be stable.
6. Parameter Effects
In our formulation, the vector and the matrix are analytically derived. In this section, we analyze effects of the grasp parameters. See Appendix E for detailed derivations.
6.1. Effects in the Case of the Sliding Contact
In this subsection, we focus on the case of frictionless sliding contact. Effects of the grasp parameters in and are analyzed.
6.1.1. Effects of the Local Curvatures in the Sliding Contact
The wrench vector is partially differentiated by the local curvatures and ; we have
The wrench vector is independent of the local curvatures. The stiffness matrix is also partially differentiated; we have
The matrix depends on the local curvatures. Because of , the derivatives are negative semi-definite. This means that as the local curvatures increase, the grasp stability decreases. Effects of the local curvatures’ deviation appear in the object motion directions and .
6.1.2. Effects of the Joint Stiffness in the Sliding Contact
The vector and the matrix are partially differentiated by the joint stiffness ; we have
The vector is not affected by deviation of the joint stiffness. Because the partial derivative of is negative semi-definite, when the joint stiffness increases, the grasp stability enhances. Effect of the deviation appears in the object displacement direction .
6.2. Effects in the Case of the Rolling Contact
In this subsection, we focus on the case of pure rolling contact. Effects of the grasp parameters in and are analyzed.
6.2.1. Effects of the Local Curvatures in the Rolling Contact
The vector and the matrix are partially differentiated by the local curvatures; we have
The vector is not affected by the local curvatures. The derivative of is negative semi-definite. When the local curvatures increase, the grasp stability decreases. Effects of deviations of the curvatures appear in the object displacement direction .
6.2.2. Effects of the Joint Stiffness in the Rolling Contact
The partial derivatives of and by are obtained by
The vector is not affected by the joint stiffness. The derivative of is positive semi-definite. When the joint stiffness increases, the grasp stability enhances. The effect appears in the object displacement direction .
6.3. Difference Between Frictionless Sliding Contact and Pure Rolling Contact
We focus on the difference between the sliding contact and the rolling contact. The difference in the wrench vector is obtained as
In this difference, the tangent component of the contact force remains. To set the same condition between the contacts, we consider . Then we have
Equation (63a) is obtained in a similar manner to (37) in Ref. []. From (63a), the difference matrix is positive semi-definite. It is shown that positive definiteness of is larger than that of , and the grasp stability is enhanced by rolling contact. The effect appears in the direction of the vector . From (63a), the effect of the contact friction condition is demonstrated quantitatively.
7. Numerical Examples
7.1. Grasp by Two Fingers Composed of Four Joints
We investigate a grasp by two fingers which are composed of four joints, as shown in Figure 3. The coordinate frames of the initial grasp are represented by the homogeneous transformation matrices shown in Table 1. The length of links, the local curvatures, and the contact forces are shown in Table 2. To simplify the example, all masses are zero; i.e., we assume that the grasp is considered in the horizontal plane. The contact forces generated by the fingers are aligned in the normal directions at contact points. Since every contact force is assigned inside the friction cone at the contact point, the detailed value of the friction coefficient is omitted in this paper.
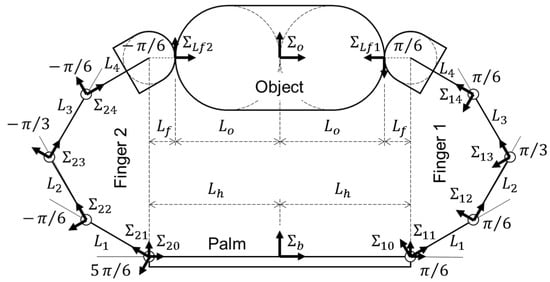
Figure 3.
Example 1. An object is grasped by 2 fingers; each finger is composed of 4 joints and 4 links.

Table 1.
Settings of the finger links for Example 1.

Table 2.
Settings of the shape and parameters.
Our method can be used even when the number of fingers is increased. As easy-to-understand examples that are consistent with intuition, two-finger grasps are shown in numerical examples.
7.1.1. Frictionless Sliding Contact in Example 1
The wrench vectors are calculated as
This grasp is in wrench equilibrium. For , condition (34) is calculated as
The eigenvalues of are and ; then is positive definite. From (65), the contact position and finger joints are stable. The stiffness matrices of the object pose applied by the fingers are calculated as the following elements:
The grasp stiffness matrix is calculated as the following elements:
Eigenvalues and unit eigenvectors of the matrix are shown in Table 3. Because two eigenvalues are negative, the grasp is unstable. The unstable directions of the object motion are given mainly in rotation and y-axis translation.

Table 3.
Eigenvalues and unit eigenvectors of in (67).
In Table 3, the eigenvalues are arranged in descending order, regardless of the units. The units of the eigenvalues are mixed from the elements of the matrix (67). The units of the eigenvectors are obtained from the eigenvalue decomposition:
In this paper, the vector is set in units of (m, m, rad). When the other units ( for example mm, mm, deg) are selected, the eigenvalues are obtained from the matrix shown in (69).
The matrices and are real symmetric matrices, so these eigenvalues are obtained in real values. Depending on the weight matrix , the eigenvalues of are variant from those of . However, the numbers of positive, zero, and negative signs are invariant. Considering grasp environments, we can select the elements of . When the translational stability has to be emphasized, the translational weights of are increased. When the rotational stability has to be emphasized, the rotational weight of is increased. The grasp stability is evaluated by the eigenvalues depending on .
The direction vectors of the parameter effects, , , and , are shown in Table 4. These vectors are represented in the object coordinate frame . Because of the symmetrical grasp, the x-translation and rotation components are the same values for i = 1, 2, and the y-translation components are opposite signs. In the vector , the absolute value of the y-component is more than three times that of the x-component. The change in the curvature affects the grasp stability mainly in the y-translation motion of the object. In the vector , the absolute value of the x-component is about two to eight times more than that of the y-component. The change in the stiffnesses affects the grasp stability mainly in the x-translation motion of the object. Because of frictionless contact, it is thought that the change in joint stiffness affects the grasp stiffness mainly in the normal direction at the contact point, i.e., in the x-direction of the object frame.

Table 4.
Direction vectors , , and as parameter effects in Example 1.
The local curvatures and/or are made smaller; the grasp stability is enhanced as shown in (60b). For example, when the curvatures are set at or , all eigenvalues become positive and the grasp is stable. The detailed results are omitted for page space. The object is not immobilized within the contact wrenches (first-order evaluation), while it is stabilized by the grasp stiffness matrix (second-order evaluation).
In Appendix F, we explain the condition of the first-order immobilization, and we show an example where the object is immobilized in the first-order evaluation.
7.1.2. Pure Rolling Contact in Example 1
For , condition (46) is calculated as
From (70), the contact position and finger joints are stable. The stiffness matrices of the object pose applied by the fingers are calculated as the following elements:
The grasp stiffness matrix is obtained in the following form:
Eigenvalues and unit eigenvectors of (72) are shown in Table 5. Because all eigenvalues are positive, the grasp is stable. Note that, for example, when or , one eigenvalue becomes negative, and the grasp is unstable.

Table 5.
Eigenvalues and unit eigenvectors of in (72).
The direction vectors of the parameter effects, and , are shown in Table 6. Because of the symmetrical grasp, the y-components have opposite signs for i = 1,2. In the vector , the absolute value of the y-component is larger than that of the x-component. The change of the curvature affects the stability in the y-translation more than the x-translation. In the vector for j = 3, 4, the absolute value of the y-component is three times larger than that of the x-component. For the third and fourth joints, the change in stiffnesses affects the grasp stability in the y-translation of the object motion more than the x-translation.

Table 6.
Direction vectors and as parameter effects in Example 1.
7.2. Grasp by Two Fingers Composed of Five Joints
We investigate the grasp by two fingers which are composed of five joints. The grasp is shown in Figure 4. The grasp is obtained as follows: Both one link and one joint are added to each finger shown in Figure 3. The angle of the third joint () is distributed to the angles of two joints (). The length of the links is the same as the other links. Homogeneous transformation matrices of the grasp are shown in Table 7. The values of the joint stiffnesses and the initial fingers are the same as shown in Table 2.
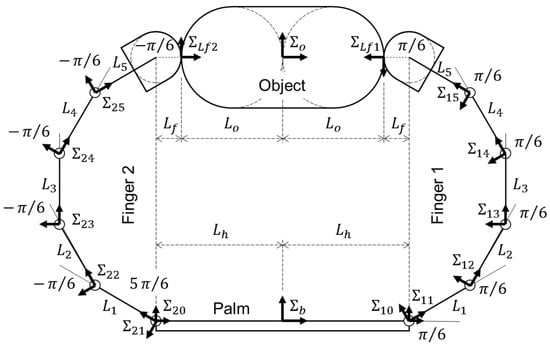
Figure 4.
Example 2. An object is grasped by 2 fingers; each finger is composed of 5 joints and 5 links.

Table 7.
Settings of the fingers for Example 2.
7.2.1. Frictionless Sliding Contact in Example 2
Condition (34) is calculated as
Eigenvalues of are and . Eigenvalues of are 17.7 and 2.37. From (73), the contact positions and the finger joints are stable. The grasp stiffness matrix is given in the following form:
Eigenvalues and unit eigenvectors of (74) are shown in Table 8. Because two eigenvalues are negative and one eigenvalue is positive, the grasp is unstable. The unstable directions of the object motion are given mainly in rotation and y-translation.

Table 8.
Eigenvalues and unit eigenvectors of in (74).
The direction vectors of the parameter effects, , , and , are shown in Table 9. Because of the symmetrical grasp, for i = 1,2, the y-components have opposite signs. In the vector and , the absolute value of the y-component is larger than that of the x-component. The change in the local curvatures affects the grasp stability in the y-translation more than x-translation of the object motion. In the vector , the absolute value of the x-component is larger than that of the y-component. The change in the joint stiffness affects the grasp stability in the x-translation more than the y-translation of the object motion.

Table 9.
Direction vectors , , and as parameter effects in Example 2.
7.2.2. Pure Rolling Contact in Example 2
Condition (46) is calculated as
Eigenvalues of (75b) are 1.76 and 2.37. From (75), the contact position and the finger joints are stable. Grasp stiffness matrix is given by the following form:
Eigenvalues and unit eigenvectors of (76) are shown in Table 10. All eigenvalues are positive, so the grasp is stable. Note that, for example, when or , one eigenvalue becomes negative, and the grasp is unstable.

Table 10.
Eigenvalues and unit eigenvectors of in (76).
The direction vectors of the parameter effects, and , are shown in Table 11. Because of the symmetrical grasp, for i = 1, 2, the y-components have opposite signs. In the vector , the absolute value of the y-component is larger than that of the x-component. The change in the local curvatures affects the grasp stability in the y-translation more than x-translation of the object motion. In the vector , for j = 3, 4, 5, the absolute value of the y-component is larger than that of the x-component. The change in the stiffness of the third to fifth joints affects the grasp stability in the y-translation more than x-translation of the object motion.

Table 11.
Direction vectors and as parameter effects in Example 2.
8. Conclusions
The distinctive feature of this paper was to analyze grasp stability in detail. In particular, grasps by multiple fingers with redundant joints have been investigated.
The contact constraints between the object and fingers were formulated. The relationships among the displacements of object pose, contact positions, and joint position were formulated when the object was moved by an external disturbance. Each joint was modeled as a linear spring, and the potential energy of the grasp was formulated.
The displacement parameters were reduced, and the wrench vectors and the stiffness matrices of the object generated by the fingers were derived using partial derivatives of the potential energy. Stable conditions of contact positions and joint positions were also formulated.
In the wrench vectors and stiffness matrices, the grasp parameters such as the local curvatures, joint stiffnesses, etc., were included explicitly. Partial derivatives of the wrenches and matrices by the parameters were derived. Effects of the parameters on the grasp stability are evaluated based on positive definiteness of the derivatives. These features were obtained through detailed analysis.
In numerical examples of grasps with redundant joints, the wrench vectors and stiffness matrices of the grasps were calculated. The grasp stability is evaluated by the eigenvalues of the matrices, and the stable and unstable directions of the grasp are obtained by the eigenvectors. The stable conditions of the contact positions and the joint positions were checked. The directions in which the changes in the grasp parameters affect the grasp stability were also calculated.
In our future projects, we will explore various types of grasps such as grasps with elastic surfaces, inner link grasps, enveloping grasps, spatial grasps, multiple-object grasps, and so on. We will also tackle a grasp optimization problem based on our analysis.
Funding
This research received no external funding.
Data Availability Statement
The dataset is available on request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Vectors and Matrices
This paper uses the following vectors and matrices:
Homogeneous transformation matrices are defined as follows:
The following matrices are also used in this paper.
Appendix A.2. Partial Derivatives of the Homogeneous Transformation Matrices
Translation and rotation displacements are represented by homogeneous transformation matrices for prismatic and revolute joints, respectively.
Partial derivatives of the homogeneous transformation matrices are represented by the following form:
Partial derivatives of the translational displacements are represented by the following forms:
Partial derivative of the rotational displacement is represented by the following form:
We organize the form obtained by the first partial derivative.
Then we have the following form:
We organize the form obtained by the second partial derivative.
Appendix B. The Partial Derivatives of the Potential Energy
Appendix B.1. Joint Torque and Link Mass Effects
Joint torques are obtained by the following form:
and
The matrix is given by the following form:
Appendix B.2. Elements of the Second Partial Derivatives
The matrix is obtained by
The local curvatures and are included in . The matrix is obtained by
Force and moment components are included in .
Appendix B.3. Frictionless Sliding Contact
In the case of frictionless sliding contact, the contact force generates only in the contact normal direction. The matrices and are rewritten as and , respectively.
Appendix C. The Partial Derivatives of (18)
Equation (18) is transformed to
The partial derivative of this equation is determined by one of the parameters:
Considering the initial states, we have
This equation is transformed with respect to , and using (A8), we have
This equation is simplified in the following form:
Using the derivatives by all parameters, the first row block of (22) is obtained. The other derivatives in this paper are obtained in a similar manner. In the second partial derivatives, using the form (A10), we have (31).
Appendix D. Stiffness Matrix of the Fingers
Appendix D.1. Derivation of (41)
The matrix of (33b) is transformed as follows:
We have the conditions (34). Equation (41) is obtained as follows:
Equations (46) and (54) are obtained in a similar manner.
Appendix D.2. Uniqueness of the Matrix (Independent of the Selection )
In order to prove that the matrix is uniquely determined, i.e., it is independent of the selection of the matrix , the matrix is represented by a product of matrices and , where and satisfy
Selection arbitrariness of is expressed by . The matrix is rewritten as
Matrix (37) is rewritten as
The matrix is independent of the matrix . From (41c), the element is eliminated as follows:
Consequently, the matrix is independent of arbitrariness of the selection . In a similar manner, the matrix is also independent of that.
Appendix E. Partial Derivative of Grasp Stiffness Matrix by Grasp Parameters
Appendix E.1. Frictionless Sliding Contact
The effect of the local curvature at the contact point on contact point displacement is represented as
Each term in Equation (41) is partially differentiated by the local curvature , so we have
Equation (A29b) is the same form as Equation (28) in Ref. []. Equation (58a) is obtained by summarizing (A29). In a similar manner, we have
The joint stiffness effect is obtained by partially differentiating by .
Appendix E.2. Pure Rolling Contact
Differentiating the matrix by the local curvatures at contact points, we analyze the effect of the curvatures on grasp stability. We have the following partial derivatives:
The partial derivative of by is obtained by
Appendix F. Four-Finger Grasp for an Example of Force-Closure Grasp
If the object is required to be immobilized in the first-order evaluation, we consider the grasp wrench vector (56a).
If the coefficient matrix satisfies the force-closure condition [,], the object can be immobilized.
For example, based on Figure 3, we consider that the object is grasped by four fingers as shown in Figure A1. Note that the figure is rotated 90 degrees from Figure 3 for page space. The sizes of the object and finger links are the same as those of Figure 3. The contact positions on the object are assigned as the following values:
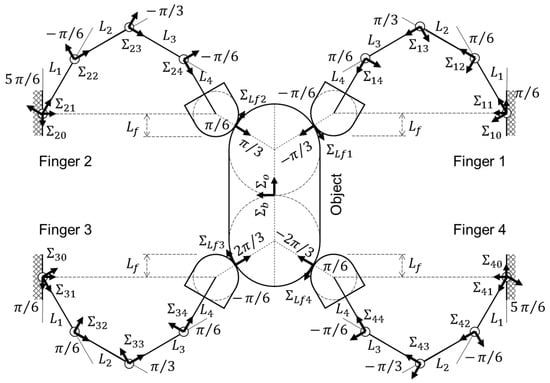
Figure A1.
Four-finger grasp for the 1st-order evaluation.
The joint positions are the same as those of Figure 3, but the contact positions on the fingers are changed as shown in Table A1. In this case, the coefficient matrix is obtained as the following row full-rank matrix, which satisfies the force-closure condition:
The grasp stiffness matrix is obtained as the following positive definite matrix:
As a result, the object is immobilized within the first-order evaluation, and the grasp is also stabilized in the second-order evaluation. The detailed results are omitted for page space.

Table A1.
Settings of the finger links for the grasp shown in Figure A1.
Table A1.
Settings of the finger links for the grasp shown in Figure A1.
| Fingers 1, 3 | Fingers 2, 4 | |
|---|---|---|
References
- Hanafusa, H.; Asada, H. Stable Prehension of Objects by the Robot Hand with Elastic Fingers. SICE 1977, 13, 370–377. [Google Scholar] [CrossRef]
- Nguyen, V.D. The synthesis of stable grasps in the plane. In Proceedings of the 1986 IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 7–10 April 1986; pp. 884–889. [Google Scholar] [CrossRef]
- Nguyen, V.D. Constructing Stable Grasps in 3D. In Proceedings of the 1987 IEEE International Conference on Robotics and Automation, Raleigh, NC, USA, 31 March–3 April 1987; pp. 234–239. [Google Scholar] [CrossRef]
- Bicchi, A. On the Force-Closure Property of Robotic Grasping. IFAC Proc. Vol. 1994, 27, 213–218. [Google Scholar] [CrossRef]
- Bicchi, A. On the Form-Closure Property of Robotic Grasping. IFAC Proc. Vol. 1994, 27, 219–224. [Google Scholar] [CrossRef]
- Montana, D.J. Contact Stability for Two-Fingered Grasps. IEEE Trans. Robot. Autom. 1992, 8, 421–430. [Google Scholar] [CrossRef]
- Funahashi, Y.; Yamada, T.; Tate, M.; Suzuki, Y. Grasp stability analysis considering the curvatures at contact points. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; pp. 3040–3046. [Google Scholar] [CrossRef]
- Howard, W.S.; Kumar, V. On the Stability of Grasped Objects. IEEE Trans. Robot. Autom. 1996, 12, 904–917. [Google Scholar] [CrossRef]
- Rimon, E.; Burdick, J.W. Mobility of Bodies in Contact—Part II: How Forces are Generated by Curvature Effects. IEEE Trans. Robot. Autom. 1998, 14, 709–717. [Google Scholar] [CrossRef]
- Rimon, E.; Burdick, J.W. Mobility of Bodies in Contact—Part I: A 2nd-Order Mobility Index for Multiple-Finger Grasps. IEEE Trans. Robot. Autom. 1998, 14, 696–708. [Google Scholar] [CrossRef]
- Montana, D.J. The Kinematics of Contact and Grasp. Int. J. Robot. Res. IJRR 1988, 7, 17–32. [Google Scholar] [CrossRef]
- Yamada, T.; Taki, T.; Yamada, M.; Yamamoto, Y.F.H. Static Stability Analysis of Spatial Grasps Including Contact Surface Geometry. Adv. Robot. 2011, 25, 447–472. [Google Scholar] [CrossRef]
- Luo, C.; Zhu, L.; Ding, H. A novel curvature-based method for analyzing the second-order immobility of frictionless grasp. Robotica 2012, 30, 613–625. [Google Scholar] [CrossRef]
- Li, R.; Liu, S.; Su, X. Learning Form Closure Grasping with a Four-Pin Parallel Gripper. Appl. Sci. 2023, 13, 2506. [Google Scholar] [CrossRef]
- Minami, M.; Dobashi, H. Fundamental Study on the Feasibility of Alignment of Parts for 2nd-order Form Closure Grasps by Two Circular Fingers. J. Robot. Soc. Jpn. 2022, 40, 453–456. [Google Scholar] [CrossRef]
- Xu, W.; Guo, W.; Shi, X.; Sheng, X.; Zhu, X. Fast Force-Closure Grasp Synthesis With Learning-Based Sampling. IEEE Robot. Autom. Lett. 2023, 8, 4275–4282. [Google Scholar] [CrossRef]
- Gilart, F.; Suárez, R. Determining Force-Closure Grasps Reachable by a Given Hand. IFAC Proc. Vol. 2012, 45, 235–240. [Google Scholar] [CrossRef]
- Li, Y.; Cong, M.; Liu, D.; Du, Y.; Xu, X. Stable grasp planning based on minimum force for dexterous hands. Intell. Serv. Robot. 2020, 13, 251–262. [Google Scholar] [CrossRef]
- Harada, K.; Kaneko, M. Enveloping Grasp for Multiple Objects—Kinematics and Shovelling up Condition. J. Robot. Soc. jpn 1998, 16, 860–867. [Google Scholar] [CrossRef]
- Yamanaka, T.Y.S.; Yamada, M.; Funahashi, Y.; Yamamoto, H. Static Stability Analysis Of Grasping Multiple Objects in 2D. Int. J. Inf. Acquis. 2010, 7, 119–134. [Google Scholar] [CrossRef]
- Tsuji, T.; Baba, K.; Tahara, K.; Harada, K.; Morooka, K.; Kurazume, R. Grasp Stability Evaluation based on Energy Tolerance in Potential Field. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 2311–2316. [Google Scholar] [CrossRef]
- Garate, V.R.; Pozzi, M.; Prattichizzo, D.; Tsagarakis, N.; Ajoudani, A. Grasp Stiffness Control in Robotic Hands through Coordinated Optimization of Pose and Joint Stiffness. IEEE Robot. Autom. Lett. 2018, 3, 3952–3959. [Google Scholar] [CrossRef]
- Nakashima, A.; Hayakawa, Y. Stability Analysis of Grasped Object by Soft-Fingers with 3-Dimensional Deformation based on Moment Stability. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 8192–8199. [Google Scholar] [CrossRef]
- Harada, K.; Tsuji, T.; Uto, S.; Yamanobe, N.; Nagata, K.; Kitagaki, K. Stability of Soft-Finger Grasp under Gravity. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 883–888. [Google Scholar] [CrossRef]
- Dong, H.; Qiu, C.; Prasad, D.K.; Pan, Y.; Dai, J.; Chen, I.-M. Enabling Grasp Action: Generalized Quality Evaluation of Grasp Stability via Contact Stiffness from Contact Mechanics Insight. Mech. Mach. Theory 2019, 134, 625–644. [Google Scholar] [CrossRef]
- Ma, X.; Chen, L.; Gao, Y.; Liu, D.; Wang, B. Modeling Contact Stiffness of Soft Fingertips for Grasping Applications. Biomimetics 2023, 8, 398. [Google Scholar] [CrossRef]
- Yamada, T.; Yamamoto, H. Analysis of Grasp Parameter Effects for Static Stability of Planar Grasps. J. Instrum. Autom. Syst. 2015, 2, 10–21. [Google Scholar] [CrossRef]
- Yamada, T.; Niwa, K.; Yamamoto, H.; Kawasaki, H.; Mouri, T. Automatic generation of grasp positions using the partial differentiation of the grasp stiffness matrix. J. Robot. Mechatron. Syst. 2017, 2, 1–15. [Google Scholar]
- Chirikjian, G.S.; Burdick, J.W. Hyper-Redundant Robot Mechanisms and Their Applications. In Proceedings of the IROS ’91: IEEE/RSJ International Workshop on Intelligent Robots and Systems ’91, Osaka, Japan, 3–5 November 1991; pp. 185–190. [Google Scholar] [CrossRef]
- Firouzeh, A.; Paik, J. Grasp Mode and Compliance Control of an Underactuated Origami Gripper Using Adjustable Stiffness Joints. IEEE/ASME Trans. Mechatron. 2017, 22, 2165–2173. [Google Scholar] [CrossRef]
- Song, E.J.; Lee, J.S.; Moon, H.; Choi, H.R.; Koo, J.C. A Multi-Curvature, Variable Stiffness Soft Gripper for Enhanced Grasping Operations. Actuators 2021, 10, 316. [Google Scholar] [CrossRef]
- Shan, H.; Xu, L.; Li, X. A variable stiffness design method for soft robotic fingers based on grasping force compensation and linearization. Robotica 2024, 42, 2061–2083. [Google Scholar] [CrossRef]
- Yamada, T.; Johansson, R.; Robertsson, A.; Yamamoto, H. Static Stability Analysis of a Planar Object Grasped by Multifingers with Three Joints. Robotics 2015, 4, 464–491. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).