Abstract
The automotive industries currently face challenges such as emission limits, traffic congestion, and limited parking, which have prompted shifts in consumer preferences and modern passenger vehicle requirements towards compact vehicles. However, given the inherent limited width of compact vehicles, the potential risk of vehicle rollover is greater than that of regular vehicles. This paper addresses the safety concerns associated with vehicle rollover, focusing on narrow tilting vehicles (NTVs). Quantifying stability involves numerical indicators such as the lateral load transfer ratio (LTR). Additionally, a unique approach is taken by applying ZMP (zero moment point), commonly used in the robotics field, as an indicator of vehicle stability. Effective roll control requires a detailed analysis of the vehicle’s characteristic model and the derivation of lateral and roll dynamics. The paper presents the detailed roll dynamics of an NTV with a MacPherson strut-type suspension. A stability-enhancing method is proposed using a cascade structure based on the internal robust position controller and outer roll stability controller, addressing challenges posed by disturbances. Experimental verification using Simscape Multibody and CarSim validates the dynamic model and controller’s effectiveness, ensuring the reliability of the proposed tilting control for NTVs in practical scenarios.
1. Introduction
As global populations continue to surge alongside rapid economic development, demand for automobiles is increasing, and transportation problems such as lack of parking spaces and air pollution are also increasing. In response to this, there has been a heightened focus on compact vehicles as a potential solution to mitigate the challenges associated with increased vehicular density [1,2]. However, because compact vehicles are generally narrow, the potential risk of vehicle rollover is greater than that of regular vehicles. Various studies have been conducted to supplement the safety of such a roll [3], and many studies suggest methods for stable driving by adding a structure that makes the vehicle tilt [4,5]. Commonly, a narrow vehicle with a structure that allows the vehicle to be tilted is collectively referred to as a narrow tilting vehicle (NTV).
NTV’s ability to actively create roll angles is similar to that of two-wheeled vehicles, especially motorcycles. Similar to two-wheeled vehicles, which achieve stability during cornering by tilting inwards relative to the turn radius, the NTV employs a lean towards the turn’s inner radius to enhance stability. However, relying solely on a tilting angle is insufficient for numerically determining stability, necessitating the use of indicators based on a numerical model of the vehicle. One such indicator for evaluating the roll stability of the vehicle is the lateral load transfer ratio (LTR) [6,7,8,9]. This value, determined through the vertical load difference between the left and right wheels, provides quantitative criteria for roll stability. Additionally, there is another stability criterion, which is named zero moment point (ZMP) [10,11], based on the lateral force generated at the center of mass in the pedestrian robot and the rotational moment generated when viewed from the ground. Although this criterion is commonly used in robotics, our study marks the pioneering application of this metric in the context of vehicles, showing a novel integration of established robotic principles into the automotive domain. ZMP, the proposed roll stability index of the vehicle in this paper, can easily show from a visual perspective how a vehicle’s roll occurs by observing the point at which the turning moment becomes zero relative to the ground.
Effective roll control is not possible merely by defining and calculating vehicle stability criteria. Control logic fundamentally relies on the physical characteristics and dynamic equations of a vehicle. Therefore, a prerequisite for roll control involves a detailed analysis of the vehicle’s characteristic model and the derivation of lateral and roll dynamics. Formulas describing the lateral dynamics during cornering can be obtained through the basic vehicle dynamics equations [12]. To analyze the characteristics related to roll, derivation must be performed, and equations must include the effects of lateral motions during cornering situations. Finally, incorporating the influence of tilting actuators allows for the derivation of the roll dynamics equation. Several studies have conducted a mathematical approach to NTV, which has a structure in which an actuator attached to an unsprung mass directly applies torque to the vehicle body [3,13]. Based on the basic lateral dynamics of the vehicle, this paper provides detailed roll dynamics of a tilting structure mechanically connected to a MacPherson strut suspension rather than a structure that directly transmits drive torque.
Understanding the roll dynamics of tilting vehicles provides a foundation for applying various roll stability control strategies. While some studies focus on securing roll stability solely through the tilting actuator torque generation [14,15,16,17], some others assume that steering intervention is possible and present integrated control between steering and tilting mechanisms [18,19]. Although many studies propose torque inputs based on the vehicle model, this approach may struggle to ensure stability in the presence of disturbances like crosswinds. In this paper, a stability-enhancing method is proposed, which adopts a cascade structure based on an internal robust position controller, mitigating the effects of disturbances and model uncertainty.
Experimental verification is necessary to confirm the validity of the previously derived dynamic model and the controller based on it. In this study, experiments were conducted using a simulation model based on an existing physical vehicle model. Simulation models were implemented using Simscape Multibody, and parameter matching was performed to align them closely with the real vehicle through a comparison with the physically constructed prototype. The designed model was then integrated with the CarSim driving simulator to implement driving scenarios and validate the effectiveness of the proposed tilting control. In addition, the stability results were analyzed in detail based on the suggested stability criteria.
2. System Modeling
The narrow tilting vehicle (NTV) aims to prevent rollovers by allowing rotation of the vehicle body. The tilting structures proposed in many other studies are based on a double wishbone-type suspension. One of the models considered in this study is a system with a tilting structure at the top of a vehicle equipped with a double wishbone-type suspension, as shown in Figure 1a. However, considering the pros and cons of two types of suspension systems, as shown in Figure 1, the tilting mechanism concept implemented within the MacPherson strut-type suspension structure is proposed in this study. The mechanism achieves vehicle inclination through the controlled rotation of the upper strut mount. The upper plate of the suspension is attached to the axis of the tilting actuator motor, and the motor is mounted on the vehicle cabin. Applying the MacPherson strut-type method has the advantage of simplifying the structure of the tilting mechanism and reducing the vehicle weight.
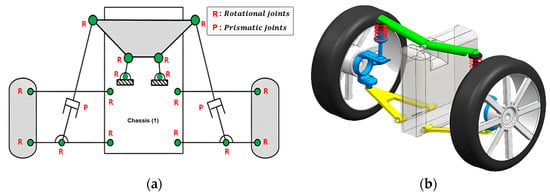
Figure 1.
The tilting structures with the suspensions: (a) double wishbone-type suspension and (b) MacPherson strut-type suspension.
Through the implementation of a simple tilting structure in the hardware-in-the-loop system, as shown in Figure 2, it was observed that vehicles with tilting exhibited a lower risk of rollovers. However, due to the challenges in analyzing the behavior of tilting vehicles through simplistic simulations, it is necessary to derive an accurate mathematical model for such vehicles. Lateral dynamics of the narrow tilting vehicle mechanism significantly differs from conventional vehicles, primarily due to the roll motion. The derivation of dynamic equations of the NTV is necessary due to the motion generated by the actuator. The first step in deriving the model equations is to calculate the dynamic equations for the lateral and roll movements that occur in cornering situations. As a next step, dynamic equations need to be derived for the lateral motion when the central actuator of the vehicle transmits force to the main body frame. Subsequently, the dynamic model is derived based on the forces transmitted to the mainframe and suspension as the motor operates. Through this process, this section presents the dynamic equations of the tilting vehicle.

Figure 2.
Hardware-in-the-loop simulation of the narrow vehicle: (a) normal vehicle and (b) simple tilting vehicle.
2.1. Lateral Dynamics for Narrow Tilting Vehicle
In conventional vehicles, the roll dynamics is basically based on the difference in load between the left and right suspension due to lateral force in cornering situations. In contrast, tilting vehicles can actively make the roll angle through actuators. Based on the lateral dynamics of a general vehicle and adding the effect of the tilting structure, the dynamics equation for the tilting vehicle can be derived. The lateral force during cornering situations, as depicted in Figure 3a, can be derived similarly to conventional vehicles, and its equations are derived as Equations (1)–(4).
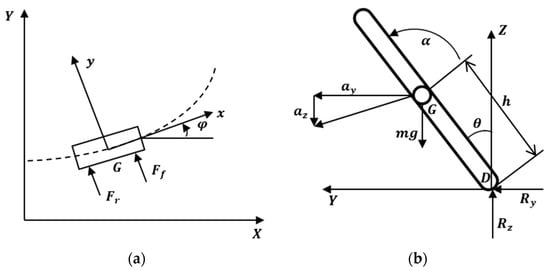
Figure 3.
The vehicle dynamics model: (a) lateral dynamics model when cornering and (b) roll dynamics model.
The lateral dynamics of a tilting vehicle, as depicted in Figure 3b, can be expressed in terms of lateral forces acting on the ground, lateral acceleration, and the vehicle’s roll angle. Equation of the dynamics for the lateral force and vertical force acting on the tire from the ground is derived as Equations (5) and (6).
When considering the rotational moment generated by the actuator at the center of gravity as , the equation of the roll dynamics is derived as follows:
2.2. Tilting Mechanism Dynamics
The tilting structure of the vehicle proposed in this paper is mechanically connected to a MacPherson strut-type suspension through a rotating plate. The torque generated by the tilting actuator is not directly transmitted to the vehicle’s body moment. Instead, it is configured in a complex structure of 2DOF with suspension parts and body parts. Unlike a structure where the motor is fixed at a specific position to generate torque, this system is designed to transmit torque to both the rotor and stator sides. The housing containing the motor’s stator is attached to the body, which corresponds to the sprung mass. The rotor and shaft are connected to a plate attached to the upper part of the suspension. The structure of the tilting part can be expressed as shown in Figure 4.
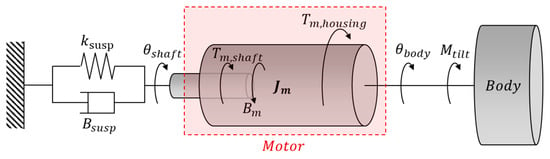
Figure 4.
Simplified dynamics model of tilting structure.
The linear motion of the suspension resulting from the rotation of the plate connected to the motor shaft in Figure 4 is represented as a single rotational component. The torque generated between the rotor and stator is transmitted through the housing and motor shaft. The torque applied to the motor shaft is transmitted through the rotating plate, generating the motion of the suspension. As the motor housing is connected to the vehicle’s body, its force acts as the body moment. This force relationship can be expressed mathematically as follows:
The tilting structure can be defined by the equation of the angle of the motor shaft () and the roll angle of the body (), where the difference between the two angles is , defined as . Based on this relationship, the dynamics of the tilting actuator can be derived as Equation (9).
3. Design of the Roll Stability Criteria
The objective of this paper is to improve the stability of roll through the control of tilting vehicles. Therefore, it is necessary to define stability criteria for evaluating roll stability. Tilting vehicles can be conceptually likened to motorcycles in their ability to generate roll angles. Generally, in the context of a two-wheeled system like a motorcycle, the driver feels safe about lateral motion when the lateral acceleration of the driver converges to zero. Hence, the driver’s lateral acceleration can be one of the criteria for evaluating roll stability. In addition to lateral acceleration, two more specific stability criteria are proposed, which are directly associated with the rollover and can be evaluated numerically.
3.1. Lateral Load Transfer Ratio
One of the criteria for evaluating the roll stability of a vehicle is the lateral load transfer ratio (LTR), which is defined as follows:
This index represents the ratio of the difference in vertical loads between the left and right sides. In a situation where there is no difference in vertical load between the left and right sides, this index is measured as 0. As the difference in vertical loads increases, the absolute value of this index increases. In a scenario where one wheel of the vehicle loses contact with the ground, leading to a rollover situation, one vertical load becomes 0, resulting in the LTR becoming either 1 or −1. Therefore, maintaining this value within a certain range is crucial for preventing vehicle rollover.
The sum of the vertical loads on the left and right sides of the vehicle is equivalent to the total vertical load and can be simply expressed as . The difference in vertical loads between the left and right sides, as shown in Figure 5, is influenced by the lateral acceleration due to the cornering and the force of gravity. Furthermore, considering the effect of angular acceleration, this difference can be expressed by Equation (11).
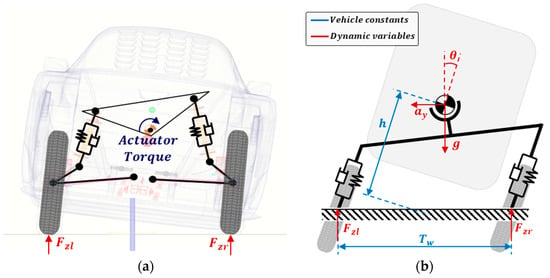
Figure 5.
The narrow tilting vehicle structure: (a) structure of the tilting vehicle with rotational plate and (b) simplified dynamics model of the tilting vehicle.
Consequently, the LTR value can be derived as Equation (12) by considering the lateral acceleration and roll angle.
3.2. Zero Moment Point
The concept of the zero moment point (ZMP) is a critical parameter in the field of humanoid robotics and dynamic stability analysis. ZMP refers to the point on the ground at which the moment acting on the center of mass of the walking or balancing system is equal to zero. Mathematically, the ZMP can be defined as the point on the ground plane where the sum of the moments is zero.
Applying this concept to vehicles enables the detection of vehicle stability through the position of the ZMP. When the ZMP is located between the left and right wheels of the vehicle, rollover does not occur because the point where the moment becomes 0 is inside the contact point. A rollover occurs when the ZMP is located outside the vehicle’s wheels, causing a rotating moment outside the vehicle. Therefore, it can be considered safer when the ZMP is closer to the midpoint between the two wheels, and this point can be used as stability criteria.
In tilting vehicles, the ZMP can be defined as the point where the resultant force of lateral and gravitational contacts the ground. Assuming that the lateral acceleration of the vehicle can be measured, the direction of the force vector originating from the center of mass can be expressed as Equation (13).
Extending this vector and performing the mathematical intersection with the ground, as illustrated in Figure 6b, we obtain the contact point. When considering the midpoint between the two wheels as the reference point, the displacement of the vehicle’s center of mass, influenced by the vehicle’s rotation, is given by a -axis position of and a -axis position of . Through this, distance from the center point of the two wheels to the ZMP can be calculated, and the formula of the ZMP is derived as follows:
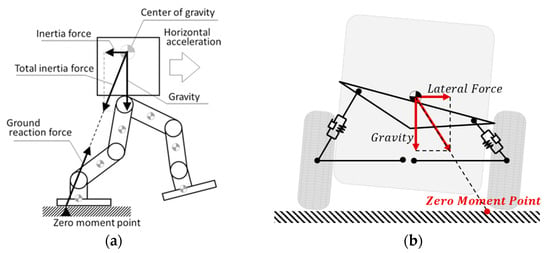
Figure 6.
The zero moment point (ZMP): (a) ZMP of the walking system and (b) ZMP of the tilting vehicle.
4. Design of a Robust Tilting Control System
The control block diagram is designed as a cascade structure to enhance roll stability, as illustrated in Figure 7. The cascade structure offers several advantages, including improved performance, robustness, and easier tuning. By separating the control tasks into inner and outer loops, the cascade structure allows each loop to be tuned independently, simplifying the overall control design. The inner loop can be optimized for fast and accurate roll angle control, while the outer loop can focus on adapting to different driving conditions. This hierarchical approach improves the system’s robustness against disturbances and enhances the vehicle’s overall handling performance.
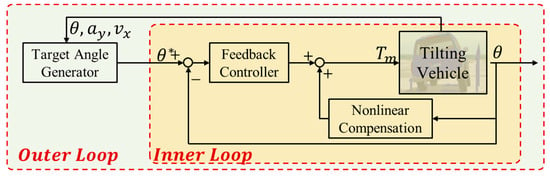
Figure 7.
Block diagram of the vehicle controller.
The inner loop controller is designed as a roll angle control loop. Its primary function is to track the desired roll angle with high precision and quick response. By focusing on the roll angle directly, the inner loop ensures rapid correction, thereby enhancing the vehicle’s stability in real time.
The outer loop, on the other hand, generates the target roll angle() based on the vehicle’s overall state, including speed, lateral acceleration, and other dynamic parameters. This loop takes a broader view of the vehicle’s dynamics and adjusts the target roll angle to optimize stability under varying conditions.
4.1. Roll Angle Controller
The roll angle controller of the vehicle is designed based on the dynamic model between the vehicle’s roll angle and motor torque. The relationship between the motor angle and the roll angle, previously expressed in a 2DOF, is simplified into a 1DOF rotational model. The nominal model in the control logic is expressed as simply as possible, and an additional robust controller is applied. Inertia coefficient Jn is the nominal roll inertia for the entire vehicle, while Bn is the nominal damping, such as friction from bushings and reduction gear in the vehicle. The dynamic equation of the model is expressed as follows:
The roll angle controller for the vehicle consists of feedback, feedforward, and disturbance observer (DOB) based on the nominal model. A complete block diagram of the roll angle controller is shown in Figure 8. The feedback controller is designed using pole-zero cancellation based on the nominal model in Equation (15). The feedback control equation with tuning parameter is expressed as follows:
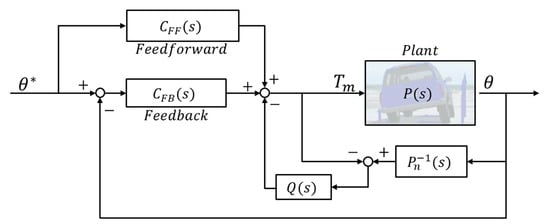
Figure 8.
Block diagram of the roll angle controller.
To improve the position control response time, the feedforward is designed by taking the inverse of the nominal model and multiplying it with a second-order order low-pass filter for stability. The equation of the feedforward controller is expressed as follows:
The tracking performance of the position control may be unstable due to the model uncertainty if only feedback and feedforward controllers are used. Additionally, in cornering situations, the lateral force is transmitted to the motors, resulting in high position error. To compensate for these model uncertainties and disturbances, a disturbance observer (DOB) is used as an additional control structure. DOB predicts the current input of the nominal model and compares it to the actual input, predicting the difference as a disturbance. This predicted disturbance passes through a second-order low-pass filter, which is expressed as , to observe disturbances below a certain frequency, while signals beyond this frequency range are blocked. This structure can predict and compensate for disturbances, effectively removing noise and enhancing the tracking performance of the position control. The mathematical expression for the second-order low-pass filter is expressed as follows:
4.2. Roll Stability Controller
The outer control loop, which generates the target roll angle of the tilting vehicle, is based on lateral acceleration during cornering. The lateral acceleration of the vehicle’s body, originating from the center of gravity, is typically expressed as shown in Equation (19).
The target roll angle is calculated to converge lateral acceleration to zero based on this equation. For simplicity, the lateral acceleration caused by the side slip and the angular acceleration are assumed to be zero in the equation. The vehicle’s yaw rate is calculated as , and the cornering radius can be expressed in relation to the steering angle and the wheelbase . The formula for calculating the target roll angle is represented as a function of the vehicle’s longitudinal velocity and steering angle, as shown in Equation (20).
Directly using the values generated by vehicle speed and steering can result in a too-rapid response in comparison to the steering angle, potentially causing discomfort for the driver. To control the response speed of the target roll angle, a steering response coefficient has been added to the controller. Additionally, to prevent the excessive roll angle, has been included as a tuning parameter for the target roll angle. The transfer function for tuning the roll angle is expressed in Equation (21), and the final formula for generating the target roll angle is represented as shown in Equation (22).
5. Simulation Result
The tilting vehicle introduced in this paper is based on an actual vehicle with tilting attached to a MacPherson strut-type suspension. For the simulation, the Simscape Multibody model is constructed based on 3D drawings of the actual vehicle. The connection structure between each component is constructed based on rotational and linear movements, giving each part the necessary degree of freedom to allow movement of each part. The component connection of the physical model is designed to be as similar as possible to the actual system, but since the model is too complex to measure and consider all friction and deformation of each part. Therefore, the multibody model is constructed by prioritizing simplicity while preserving similarity, such as applying friction only to areas with significant friction components. Components related to the tilting structure, including the actuator motor and suspension, are designed by combining analytically derived models proposed in equation 11 and multibody physical models to ensure the accuracy of the simulation model.
A parameter matching process is performed to ensure similarity between the simulation model and the actual model. Various sine signals of different magnitudes and frequencies are applied to perform parameter matching based on the roll angle and motor position. The parameters such as friction, inertia, and spring constant are adjusted to match the results with the actual vehicle’s behavior. The results for sine input response comparison are shown in Figure 9 and Figure 10. It is difficult to obtain the same results due to the differences between the actual vehicle and the simulation model, such as left and right friction conditions, initial position, and gear backlash. Therefore, parameter matching is performed to produce as similar behavior as possible by focusing on the phase and magnitude when various signals are given. The parameters applied in Simulink multibody are listed in Table 1.
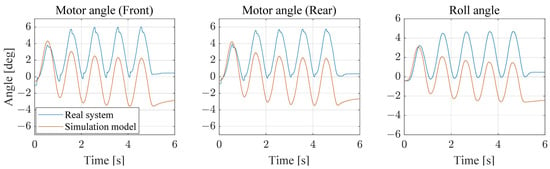
Figure 9.
Position response of the real system and simulation.
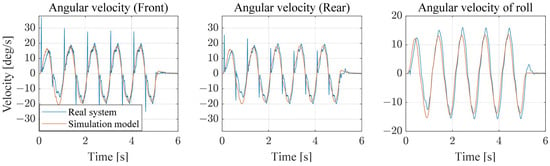
Figure 10.
Velocity response of the real system and simulation.

Table 1.
The parameters of the simulation model.
The controller designed in this paper adopts a cascade structure with an internal roll angle control loop. To ensure the performance and safety of the external control logic, it is essential to first verify the performance of the internal control loop. To evaluate the performance of the internal roll angle control, a simulation is conducted in the multibody environment using roll position inputs for trapezoidal, random, and double lane change scenarios. The trapezoidal signal has an angular velocity of 10 deg/s with a convergence angle of 6 deg, and the random signal is a 1 Hz Gaussian noise with a maximum position of 5 deg.
The simulation results are presented in Figure 11, confirming that the roll command tracking error is below 0.66 deg. Furthermore, for the model with a disturbance observer (DOB), the maximum error is 0.3040 deg, and the root mean square (RMS) error is 0.0847 deg in the case of the random signal. These values are smaller compared to the model without DOB, which has a maximum error of 0.3078 and an RMS error of 0.0922. Although these results indicate that the performance with DOB is better, the difference is not significant enough to fully demonstrate the robustness of DOB. This is because the simulation model presented in Figure 11 was conducted without external disturbances, representing conditions when the vehicle is stationary state. However, in real driving situations, numerous disturbances occur.
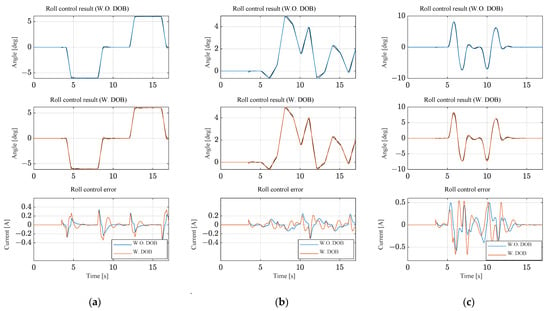
Figure 11.
Roll angle control results without external forces: (a) trapezoidal input; (b) random input; and (c) double lane change input.
To simulate various disturbances encountered during driving, a random external force was applied to the center of mass. The simulation results under these conditions are shown in Figure 12. Unlike the disturbance-free scenario, the graphs reveal a significant difference in control performance. The RMS error decreased from 0.3335 to 0.2053, representing a 38% reduction, while the peak error decreased from 0.7002 to 0.5948, representing a 15% reduction. These results confirm the advantages of robust control provided by the DOB.
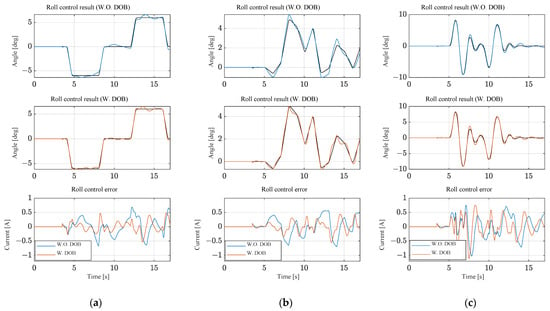
Figure 12.
Roll angle control results with external forces: (a) trapezoidal input; (b) random input; and (c) double lane change input.
While multibody simulations are suitable for the lateral behavior in a static state, creating a dynamic driving environment is challenging. Therefore, a driving simulation tool is additionally needed, and CarSim2019 is a useful co-simulation software that can be used with Simulink. Factors such as lateral acceleration, lateral force, and driver’s steering during driving situations are imported from CarSim to multibody to generate lateral behavior. Conversely, the vehicle’s roll angle resulting from lateral behavior is imported into CarSim based on the values obtained from the multibody. The entire co-simulation environment is shown in Figure 13.
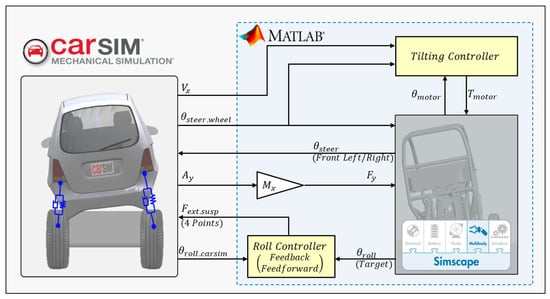
Figure 13.
Co-simulation diagram of the system.
The driving scenarios for the tilting vehicle include double lane changes and step steer conditions. The maximum driving speed of the tilting vehicle is set as 60 km/h, and the simulation for a single lane change is conducted under constant speed conditions of 50 km/h. In the step steer simulation, 120 degrees of steering angle is applied at a constant driving speed. To compare the effect of the tilting control, two vehicle control methods were applied. For regular vehicles without tilting, the plate used to rotate the vehicle is fixed to the vehicle’s body. The motor shaft for tilting motion is fixed at zero, and this model operates like a conventional vehicle with a standard suspension. The model with the tilting control is designed to actively create a roll angle based on the controller suggested in Figure 7.
Roll stability of the vehicle is evaluated by the driver’s lateral acceleration, LTR, and ZMP. From the perspective of the roll angle of the vehicle, drivers feel safe when tilting control is applied as the vehicle leans inside of the cornering radius. In contrast, without control, the vehicle leans outward of the cornering radius, which can cause rollover. Similarly, the driver’s lateral acceleration significantly decreases when controlled, making the driver feel more stable. In terms of LTR, the roll stability is significantly reduced by more than 40% in RMS compared to the uncontrolled scenario. The increase of stability is seen in both the single lane change driving, shown in Figure 14, and the constant radius cornering driving shown in Figure 15. These results show that the lateral loads on the vehicle are well distributed, reducing the risk of one side lifting off the ground. When evaluating stability based on the ZMP, the results show that the ZMP of the vehicle with tilting control is stably positioned near the center. This indicates that the tilting control effectively contributes to stability in terms of ZMP.
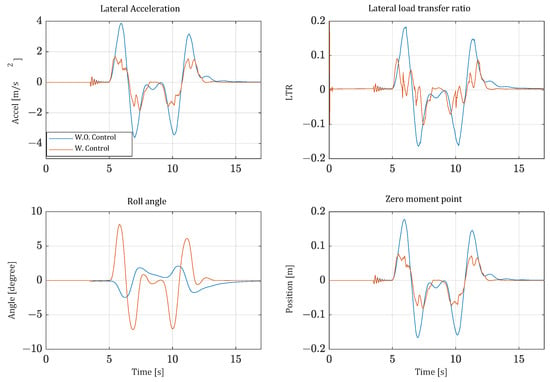
Figure 14.
The simulation results of the double lane change.
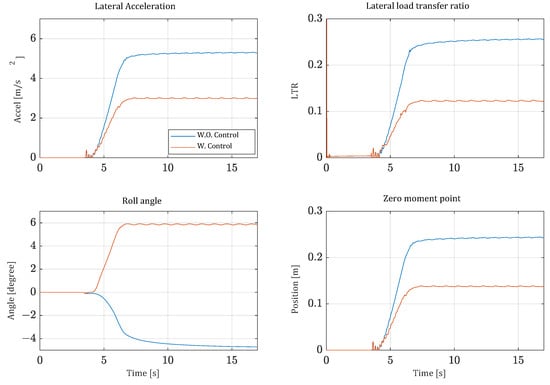
Figure 15.
The simulation results of step steer.
6. Conclusions
This paper investigates the roll stability control of a narrow tilting vehicle (NTV) with a novel tilting structure, leveraging a real vehicle model to enhance its practical relevance. Accurate and detailed dynamic equations were derived using the 3D model of the actual vehicle, and through parameter matching, the simulation model was implemented to replicate real vehicle conditions. As a control structure, the cascade structure consisting of an inner robustness control loop and an outer stability control loop was adopted. This approach secures robust angle control in the inner loop while effectively managing roll stability in the outer loop. The proposed roll angle controller simplifies the model to reduce instability, and the incorporation of a disturbance observer (DOB) mitigates the effects of external disturbances and model errors, demonstrating an improvement in control performance. Moreover, this study enhances the evaluation of vehicle roll stability by introducing the zero moment point (ZMP) criterion, traditionally used in pedestrian robot research, alongside the commonly utilized lateral tire force ratio (LTR). By applying both LTR and ZMP as stability indicators, the research provides a comprehensive assessment of the tilting vehicle’s roll stability from multiple perspectives.
Author Contributions
Conceptualization, H.C.; methodology, S.L. and K.N.; software, S.L.; validation, S.L., H.C. and K.N.; formal analysis, S.L. and K.N.; investigation, S.L. and H.C.; resources, H.C.; data curation, S.L.; writing—original draft preparation, S.L.; writing—review and editing, K.N.; visualization, S.L.; supervision, K.N.; project administration, H.C.; funding acquisition, K.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2022R1C1C1011785) and by the Korea Evaluation Institute of Industrial Technology (KEIT) grant funded by the Korean government (MOTIE) (No. 20023833).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.
Conflicts of Interest
Author Hyeonseok Cho was employed by the company Hyundai (Kia Namyang) Research and Development Center. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Kockelman, K.M.; Zhao, Y. Behavioral Distinctions: The Use of Light-Duty Trucks and Passenger Cars. J. Transp. Stat. 2000, 3, 47–60. [Google Scholar] [CrossRef]
- Grzegożek, W.A. Analysis of a Construction Solution for Narrow Track Vehicle (NTV). IOP Conf. Ser. Mater. Sci. Eng. 2018, 421, 022012. [Google Scholar] [CrossRef]
- Poelgeest, A. The Dynamics and Control of a Three-Wheeled Tilting Vehicle. Ph.D. Thesis, University of Bath, Bath, UK, 2011. [Google Scholar]
- Chatterjee, M.; Kale, M.; Chaudhari, B.N. Mathematical Modelling of Chassis Dynamics of Electric Narrow Tilting Three Wheeled Vehicle. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Chiou, J.-C.; Chen, C.-L. Modeling and Verification of a Diamond-Shape Narrow-Tilting Vehicle. IEEE/ASME Trans. Mechatron. 2008, 13, 678–691. [Google Scholar] [CrossRef]
- Larish, C.; Piyabongkarn, D.; Tsourapas, V.; Rajamani, R. A New Predictive Lateral Load Transfer Ratio for Rollover Prevention Systems. IEEE Trans. Veh. Technol. 2013, 62, 2928–2936. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Z.; Zhang, L. A Vehicle Rollover Prediction System Based on Lateral Load Transfer Ratio. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 7256–7261. [Google Scholar]
- Tsourapas, V.; Piyabongkarn, D.; Williams, A.C.; Rajamani, R. New Method of Identifying Real-Time Predictive Lateral Load Transfer Ratio for Rollover Prevention Systems. In Proceedings of the 2009 American Control Conference, Saint Louis, MO, USA, 10–12 June 2009; pp. 439–444. [Google Scholar]
- Shin, D.; Woo, S.; Park, M. Rollover Index for Rollover Mitigation Function of Intelligent Commercial Vehicle’s Electronic Stability Control. Electronics 2021, 10, 2605. [Google Scholar] [CrossRef]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped Walking Pattern Generation by Using Preview Control of Zero-Moment Point. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 14–19 September 2003; Volume 2, pp. 1620–1626. [Google Scholar]
- Erbatur, K.; Okazaki, A.; Obiya, K.; Takahashi, T.; Kawamura, A. A Study on the Zero Moment Point Measurement for Biped Walking Robots. In Proceedings of the 7th International Workshop on Advanced Motion Control. Proceedings (Cat. No.02TH8623), Maribor, Slovenia, 3–5 July 2002; pp. 431–436. [Google Scholar]
- Rajamani, R.; Piyabongkarn, D.; Tsourapas, V.; Lew, J.Y. Parameter and State Estimation in Vehicle Roll Dynamics. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1558–1567. [Google Scholar] [CrossRef]
- Rajamani, R.; Gohl, J.; Alexander, L.; Starr, P. Dynamics of Narrow Tilting Vehicles. Math. Comput. Model. Dyn. Syst. 2003, 9, 209–231. [Google Scholar] [CrossRef]
- Piyabongkarn, D.; Keviczky, T.; Rajamani, R. Active direct tilt control for stability enhancement of a narrow commuter vehicle. Int. J. Automot. Technol. 2004, 5, 77–88. [Google Scholar]
- Kidane, S.; Rajamani, R.; Alexander, L.; Starr, P.J.; Donath, M. Development and Experimental Evaluation of a Tilt Stability Control System for Narrow Commuter Vehicles. IEEE Trans. Control. Syst. Technol. 2010, 18, 1266–1279. [Google Scholar] [CrossRef]
- Tang, C.; Ataei, M.; Khajepour, A. A Reconfigurable Integrated Control for Narrow Tilting Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 234–244. [Google Scholar] [CrossRef]
- Tang, C.; Khajepour, A. Integrated Stability Control for Narrow Tilting Vehicles: An Envelope Approach. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3158–3166. [Google Scholar] [CrossRef]
- Tang, C.; Khajepour, A. Narrow Tilting Vehicles: Mechanism, Dynamics, and Control; Morgan & Claypool Publishers: San Rafael, CA, USA, 2019; ISBN 978-3-031-01501-4. [Google Scholar]
- Ren, Y.; Dinh, T.Q.; Marco, J.; Greenwood, D.; Hessar, C. Nonlinearity Compensation Based Tilting Controller for Electric Narrow Tilting Vehicles. In Proceedings of the 2018 5th International Conference on Control, Decision and Information Technologies (CoDIT), Thessaloniki, Greece, 10–13 April 2018; pp. 1085–1090. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).