Abstract
An adaptive cruise control (ACC) system can reduce driver workload and improve safety by taking over the longitudinal control of vehicles. Nowadays, with the development of range sensors and V2X technology, the ACC system has been applied to curved conditions. Therefore, in the curving car-following process, it is necessary to simultaneously consider the car-following performance, longitudinal ride comfort, fuel economy and lateral stability of ACC vehicle. The direct yaw moment control (DYC) system can effectively improve the vehicle lateral stability by applying different longitudinal forces to different wheels. However, the various control objectives above will conflict with each other in some cases. To improve the overall performance of ACC vehicle and realize the coordination between these control objectives, the extension control is introduced to design the real-time weight matrix under a multi-objective model predictive control (MPC) framework. The driver-in-the-loop (DIL) tests on a driving simulator are conducted and the results show that the proposed method can effectively improve the overall performance of vehicle control system and realize the coordination of various control objectives.
1. Introduction
1.1. Background
An adaptive cruise control system is a key basic function of the advanced driver assistant systems (ADAS) developed to enhance driving comfort, reduce driving errors, improve safety, increase traffic capacity and reduce fuel consumption [1]. The ACC system is developed from the conventional cruise control (CC) system. It measures the distance and relative longitudinal speed between the host vehicle and preceding vehicle by range sensors (such as radar, lidar or video camera), then the throttle and brake will be controlled by ACC algorithm to realize the longitudinal motion control of the vehicle. As the ACC system takes over the longitudinal motion control of vehicle, the driver workload is largely reduced.
1.2. Literature Review and Analysis
A lot of research has been done on improving the longitudinal car-following performance of ACC vehicles. Moon et al. proposed a multiple-target tracking adaptive cruise control system to improve the system performance [2]. Martinez and Canudas-de-Wit proposed a novel reference model-based control approach for automotive longitudinal control [3]. Ganji et al. proposed an adaptive cruise control for a hybrid electric vehicle based on a sliding mode controller which can deal with the problem of variable set-point of ACC [4]. Lin proposed an adaptive neuro-fuzzy predictor-based control approach to enhance the fuel efficiency [5]. Althoff proposed an exchangeable nominal controller to ensure comfort [6].
In recent years, in order to save energy, reduce emission and improve the passenger comfort, in addition to improving the longitudinal car-following performance of ACC system, some scholars have also considered the fuel economy, longitudinal ride comfort, safety into the design of ACC system. Moser proposed a stochastic model predictive control (MPC) to optimize the fuel consumption in a vehicle following context [7]. Luo et al. proposed an adaptive cruise control algorithm with multiple objectives based on a model predictive control framework [8]. Li et al. proposed a novel vehicular adaptive cruise control system to comprehensively address the issues of tracking ability, fuel economy and driver desired response [9]. Luo et al. proposed a novel ACC system for intelligent HEVs to improve the energy efficiency and control system integration [10]. Ren et al. proposed a hierarchical adaptive cruise control system to get a balance among the driver’s expectation, collision risk and ride comfort [11]. Asadi and Vahidi proposed a method which used the upcoming traffic signal information within the vehicle’s adaptive cruise control system to reduce idle time at stop lights and fuel consumption [12].
Most of the above studies usually assumed that the vehicle was running along the straight lane. With the development of radar detection range and V2 X technology, it enables ACC vehicle to detect the preceding vehicle on the curved road. Thus, in order to expand the application of ACC system, some studies have been done under the condition that the ACC vehicle runs on a curved road. D. Zhang et al. presented a curving adaptive cruise control system to coordinate the direct yaw moment control system and considered both longitudinal car-following capability and lateral stability on curved roads [13]. Cheng et al. proposed a multiple-objective ACC integrated with direct yaw moment control to ensure vehicle dynamics stability and improve driving comfort on the premise of car following performance [14]. Idriz et al. proposed an integrated control strategy for adaptive cruise control with auto-steering for highway driving [15]. The references above have considered the car-following performance, longitudinal ride comfort, fuel economy and lateral stability of ACC vehicle. However, when an ACC vehicle drives on a curved road, these control objectives usually conflict with each other. For example, in order to obtain better car-following performance, ACC vehicles usually tend to adopt larger acceleration and acceleration rate to adapt to the preceding vehicle, which will lead to poor longitudinal ride comfort. Moreover, in order to ensure vehicle lateral stability, the differential braking forces generated by the DYC system are usually applied to track the desired vehicle sideslip angle and yaw rate, whereas the additional braking forces will make the car-following performance worse, especially when the ACC vehicle is in an accelerating process. Meanwhile, to ensure the car-following performance when the additional braking force acts on the wheel, the ACC vehicles will increase the throttle opening to track the desired longitudinal acceleration, which usually means the increase of fuel consumption. The traditional constant weight matrix MPC has been unable to adapt to various complex conditions. In this paper, the extension control is introduced to design the real-time weight matrix under the MPC framework to coordinate the control objectives including longitudinal car-following capability, lateral stability, fuel economy and longitudinal ride comfort and improve the overall performance of vehicle control system.
Extension control is developed from the extension theory founded by Wen Cai. It is a new type of intelligent control that combines extenics and control. It can imitate people’s ability to summarize, study and solve the incompatible issue [16]. Its basic idea is to deal with the control problems from the perspective of information conversion. In other words, the qualified degree (dependent degree) of control input information is used as the basis to determine the correction value of control output, then the controlled information will be converted to the qualified range [17]. Extension control is a cross-discipline method which has been applied into various engineering control domain. Currently, the extension control has also been applied into vehicle stability control [18,19,20], and these studies showed that the extension control could improve the performance of control system effectively. In this paper, the extension control is used to supervise the control effect of longitudinal car-following distance error and the risk of losing vehicle lateral stability and then adjust the weight matrix in the MPC framework.
1.3. Contribution and Organization
The main contribution of this paper is as follows.
The extension sets are designed to supervise the control effect of longitudinal car-following distance error and the risk of losing vehicle lateral stability. Both the control effect and the risk can be reflected by the corresponding extension distance. Then, the control system is designed by the following purpose. That is, on the premise of ensuring longitudinal car-following performance and lateral stability, the fuel economy and longitudinal ride comfort should be improved as much as possible.
Based on the system integrating ACC with DYC, this paper introduces the extension control to design the real-time weight matrix under a multi-objective MPC framework to solve the contradiction among the control objectives above. It can coordinate various control objectives and improve the comprehensive performance of vehicle control system under different conditions. Then, the DIL tests are carried out to validate the effectiveness of the proposed control strategy.
2. Vehicle Models
2.1. Longitudinal Dynamics Model
Newton’s second law is applied to establish the vehicle longitudinal dynamics model. As shown in Figure 1, the longitudinal forces acting on the vehicle are expressed as the acceleration, rolling, gravitational, and drag [4]. The longitudinal dynamics equation is shown in Equation (1).
where Fd represents the net traction force, m is the vehicle mass, ax is vehicle longitudinal acceleration, g is the gravitational acceleration, f denotes the rolling coefficient, θ is the grade of road, and Fw is the aerodynamic drag as shown in Equation (2).
where ρ is the air density, CD is the drag coefficient, A is the windward area of the vehicle, and vx represents vehicle longitudinal speed.
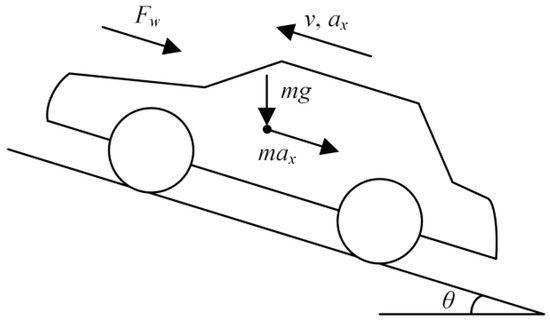
Figure 1.
Vehicle longitudinal dynamics model.
2.2. Four-Wheel Vehicle Dynamics Model
In this paper, the longitudinal, lateral and yaw motion of vehicle are considered, and the pitch, roll and vertical motion of the vehicle are neglected. The simplified four-wheel vehicle dynamics model [14] is established as shown in Figure 2, where Fxi and Fyi are the longitudinal and lateral forces of the four wheels respectively, and the subscript i is 1, 2, 3, and 4, representing the front-left, front-right, rear-left and rear-right wheel respectively; δf is the front wheel steering angle, lf and lr are the distance from vehicle gravity center to the front axle and rear axle, respectively; l is the wheelbase, and T is the track width. The longitudinal, lateral and yaw motion are presented as follows:
where vy represents vehicle lateral velocity, β and ω represent vehicle sideslip angle and yaw rate respectively, and Iz represents the inertia moment.
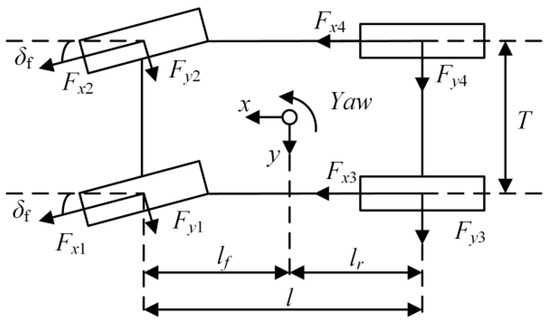
Figure 2.
Vehicle dynamics model.
2.3. Tire Model
In this paper, Pacejka’s magic formula [21] is used to describe the dynamics of tire. The longitudinal and lateral tire force can be calculated by Pacejka’s magic formula. It can be depicted as follows:
where Y represent longitudinal force Fx, lateral force Fy or aligning torques Mz, X is wheel slip ratio or wheel sideslip angle, B is stiffness coefficient, C is shape coefficient, D is peak value, E is curvature coefficient, SH is horizontal offset, and SV is vertical offset.
3. Control System Design
In the car-following process, the host vehicle sometimes needs to consider the lateral stability. For example, when the preceding vehicle drives away from the curve and accelerates into the straight lane, the host vehicle may still run on the curve, and it will also be accelerated to ensure the car-following performance. At this moment, the acceleration, steering and high longitudinal speed of host vehicle will increase the risk of losing lateral stability. Thus, it is necessary to consider the car-following performance and lateral stability simultaneously. Moreover, to improve driver satisfaction and reduce fuel consumption, the longitudinal ride comfort and fuel economy should also be considered into the control system design.
The extension control is introduced to design the weight matrix under the multi-objective MPC framework to coordinate the above control objectives and improve the overall performance of vehicle control system. The framework of control system is shown in Figure 3.
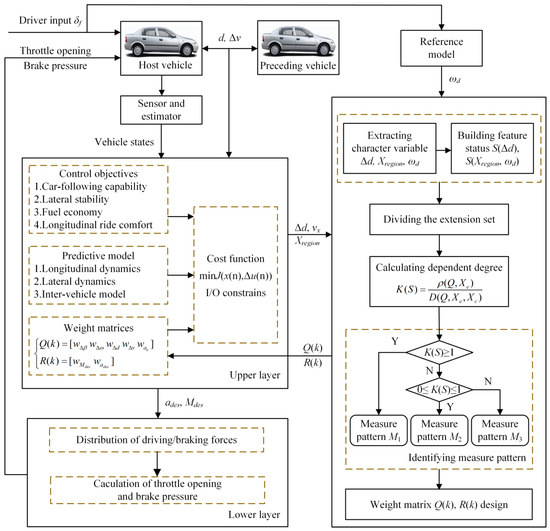
Figure 3.
Framework of the proposed control.
This paper mainly focuses on the design of coordinated control system and there are many studies have been done on estimation of the key variables [22,23,24]. Therefore, it is assumed that vehicle states such as sideslip angle, sideslip angle rate and road friction coefficient can be estimated accurately.
The purpose of the vehicle control system in this paper is as follows:
- On the premise of ensuring vehicle lateral stability, the additional yaw moment should be as small as possible to reduce the impact on longitudinal car-following performance and improve the fuel economy.
- On the premise of ensuring the longitudinal car-following performance, the longitudinal acceleration and its change rate should be as small as possible to improve the longitudinal ride comfort.
3.1. Predictive Model
3.1.1. Longitudinal Car-Following Model
The function of ACC is to take over the longitudinal motion control of host vehicle to make it run at the driver’s preset longitudinal speed or car-following distance. The longitudinal kinematic diagram of host vehicle and preceding vehicle is shown in Figure 4.
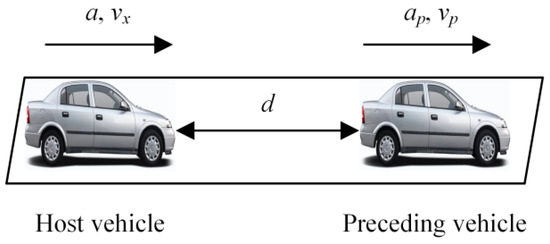
Figure 4.
Vehicle following model.
The desired car-following distance between the host vehicle and the preceding vehicle is calculated by using the constant time headway, as shown in Equation (7).
where ddes is the desired car-following distance, Th is the time headway, vx is the longitudinal speed of host vehicle, and d0 is the static inter-vehicle distance. Here, Th = 2, d0 = 10.
Usually, the longitudinal car-following performance can be represented by relative speed Δv and the car-following distance error Δd between the actual car-following distance d and the desired car-following distance ddes, as shown in Equation (8).
where vp is the longitudinal speed of the preceding vehicle. The derivative of Equation (8) can be derived as follows:
where ap is the longitudinal acceleration of preceding vehicle.
The relationship between the desired acceleration and the actual longitudinal acceleration can be described by the first-order inertial system [13], as shown in the following Equation (10).
where ax and ades are the actual longitudinal acceleration and desired longitudinal acceleration of host vehicle respectively, Tax is time-constant and Tax = 0.45.
3.1.2. Lateral Dynamic Model
A 2-DOF vehicle model is usually used to design the lateral stability controller [25], as shown in Equation (11).
where Cf and Cr are the cornering stiffness of the front wheel and rear wheel, respectively, and Mdes is the desired additional yaw moment.
The desired values of yaw rate ωd and side slip angle βd are defined according to vehicle parameters, longitudinal speed, and front steering angle δf directly manipulated by driver’s steering action [26], as shown in Equation (12).
Considering the road friction limitation, the desired yaw rate and side slip angle are modified as follows:
The yaw rate error and the vehicle sideslip angle error can be calculated by Equation (14).
The error between the desired value and the actual value reflects the stability of the vehicle. When the error of yaw rate or vehicle sideslip angle is small, the vehicle is in a steady status. When the error is large, it means that the vehicle is out of control or loses its stability.
3.1.3. Model Discretization
By combining (7)–(10), the state-space equation can be obtained as shown in Equation (15).
where , , , and the matrix expression is shown in Equations (16)–(18).
In order to get the numerical solution of rolling optimization, the Taylor expansion method is applied to discretize Equation (15) to obtain the discrete state-space equation as shown in Equation (19).
where Ad, Bd, Dd can be calculated by Taylor expansion method, as shown in Equation (20).
where Ts is the sampling time and I is the unit matrix.
3.2. Performance Index
3.2.1. Longitudinal Car-Following Performance
The longitudinal car-following performance of ACC system is usually evaluated by the distance error and relative speed between host vehicle and preceding vehicle. To ensure the longitudinal car-following performance, the distance error and relative speed are used to build the cost function for longitudinal car-following capability, as shown in Equation (21).
where the reference value of Δdref, Δvref, ax,ref are set as zero.
3.2.2. Lateral Dynamics Stability
Vehicle yaw rate error and sideslip angle error are usually used to describe vehicle lateral stability. When the error is small, it means that the vehicle status is in a stability area; when the error is large, it means that the vehicle loses control or loses the stability. The DYC system is usually applied to ensure the lateral stability of vehicle. However, the additional yaw moment required by DYC system is usually generated by the braking pressure of different wheels, the additional yaw moment will affect the longitudinal car-following performance and fuel economy of ACC vehicles. Therefore, on the premise of ensuring the vehicle lateral stability, the additional yaw moment is expected to be as small as possible. The quadratic form of Δω, Δβ and the additional yaw moment Mdes is used to form the cost function for lateral stability, as shown in Equation (22).
3.2.3. Longitudinal Ride Comfort
In order to improve driver satisfaction and ensure the longitudinal ride comfort, the absolute value of longitudinal acceleration and jerk caused by the change of longitudinal acceleration are used to describe the longitudinal ride comfort performance index of ACC vehicle. Therefore, the absolute value of longitudinal acceleration and jerk are set as the constrains to ensure the longitudinal ride comfort, as shown in Equation (23).
3.2.4. Cost Function Design
By combining Equations (21) and (22), the cost function for the multi-objective control is formed as shown in Equation (24).
Then, the predictive expression of the cost function can be obtained, as shown in Equation (25).
where Np and Nc denote the predictive horizon and control horizon, respectively. Q(k) and R(k) are non-negative weight matrices, as shown in Equation (26). xref is the reference value of MPC, and xref = [βd ωd 0 0 0]T.
Then the desired longitudinal acceleration and additional yaw moment can be obtained by minimizing the cost function as shown in Equation (25) subject to the car-following model, vehicle dynamics model, and the constraints as shown in Equation (23).
3.3. Extension Control Design
In order to improve the performance of MPC and make it adapt to various conditions, that is, the deceleration process, constant speed process and acceleration process of host vehicle in the curve. The extension control is introduced to design the real-time weight matrix under the framework of MPC. The design process is as follows:
3.3.1. Extracting Character Variable
In terms of the longitudinal car-following performance, due to the drivers are more sensitive to the distance error than the relative speed during the car-following process [13], this paper selects the car-following distance error to adjust the weight wΔd of the distance error, and sets the weight wΔv of the relative speed as a constant, then the distance error is selected to form the longitudinal car-following feature status S(Δd).
In terms of vehicle lateral stability, the phase plane method composed of the sideslip angle and the sideslip angle rate is usually used to judge the lateral stability of vehicle [25] because its good identification of vehicle stability condition. The phase plane method can be expressed as Equation (27).
where B1 and B2 are the parameters related to the road friction coefficient μ, here B1 = 0.064 and B2 = 0.214 [27].
The vehicle phase plane can be divided into ‘stability region’ and ‘instability region’ by Equation (27), as shown in Figure 5. The area ‘stability region’ means vehicle status in this area is safe and stable, while the remaining area is ‘instability region’, which means vehicle status in this area is risky in losing stability and unsafe [25].
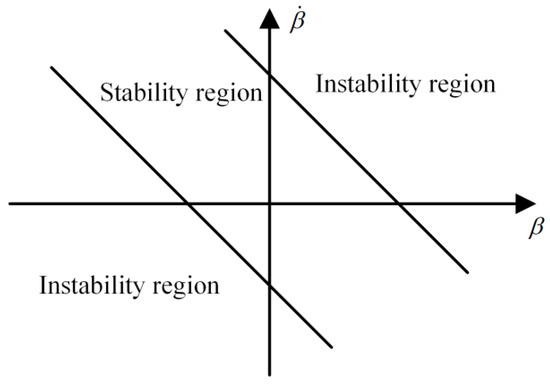
Figure 5.
Sideslip angle phase plane division region.
It is also a challenge to ensure vehicle lateral stability when the driver desired yaw rate is in a large range. Thus, the value of Xregion and the desired yaw rate ωd are selected as the character variables of lateral stability to form the feature status S(Xregion, ωd).
3.3.2. Dividing the Extension Set
The one-dimensional (1-D) extension set of the longitudinal car-following distance error is shown in the Figure 6, where Δd1 and Δd2 are the boundaries of the classic domain and the extension domain, respectively. The distance error should be in driver’s permissible longitudinal car-following range to reduce the driver intervention. The boundary of extension domain reflects the boundary of permissible region and impermissible region. Therefore, Δd2 is set to the driver’s maximum permissible value. The driver’s permissible longitudinal car-following range [13] is shown in Equation (28).
where SDE is the driver’s sensitivity to distance error. The boundary of extension domain is calculated as Δd2 = Δdmax·SDE−1. The SDE−1 is calculated as follows:
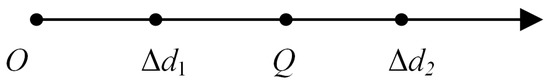
Figure 6.
1-D extension set of car-following distance error.
The parameters in Equations (28) and (29) are identified by driver experiment data in highway and city road traffic conditions [13]. Here, Δdmax = 7.2 m, kSDE = 0.06, and dSDE = 0.12. The boundary of classic domain Δd1 is set to a relatively small value and Δd1 = 0.1 × Δd2.
The lateral stability is represented by a two-dimensional (2-D) extension set, including classic domain, extension domain and non-domain. In the classic domain, it indicates the vehicle is stable; in the extension domain, it indicates the vehicle is transiting from stability to instability, and the vehicle state can be converted into the stable state by control; while in the non-domain, the vehicle is instable. The x-axis is desired yaw rate, and the y-axis is Xregion, as shown in the Figure 7, where ω1 and ω2 are the boundaries of the classic domain and the extension domain in the x-axis direction, Xregion1 and Xregion2 are the boundaries of the classic domain and the extension domain in the y-axis direction, respectively. Here, Xregion1 and Xregion2 are set to 0.1 and 1 respectively. The extension boundary ω2 in the x-axis direction reflects the boundary under large steering condition. Based on the experience and previous works [25], 0.2 μrad/s is set as the threshold of large steering condition. Therefore, the boundary ω2 is set as 0.2 μrad/s. The classic boundary ω1 is set as 0.1 × ω2.
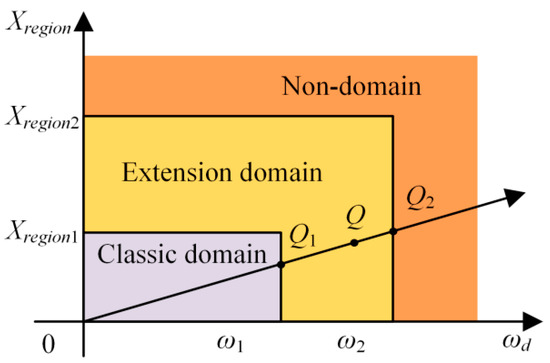
Figure 7.
2-D extension set of lateral stability.
Here, the “classic domain” and “extension domain” correspond to the stability region, and the “non-domain” corresponds to the instability region of vehicle. The “extension domain” can be understand as a transition domain.
3.3.3. Calculating Dependent Degree
Compared with the result of whether the vehicle status is in the stable region or not, it will help to improve the performance of control system if more detailed information, i.e., the degree of vehicle lateral status is known, and then we can design the control method according to that degree. In extension control, the “degree” above was defined as “dependent degree”. The ideal point in the extension set is the original point O which represents the longitudinal car-following distance error, Xregion and ωd are zero. The point Q is supposed as a point in the extension domain. Connecting the point O with the point Q, the intersection points of the line OQ and the domains’ boundaries are the points Q1 and Q2, respectively. Obviously, in 1-D extension set of car-following distance error, the points Q1 and Q2 correspond to Δd1 and Δd2 respectively. As shown in the Figure 7, the line segment OQ is the shortest distance for the point Q to approach the ideal point O. In the extension sets, the extension distance is defined as the distance from a point to a set, which is defined in a 1-D coordinate system. Therefore, it is required to convert the extension distance of 2-D extension set of lateral stability to a 1-D extension form, as shown in Figure 8.
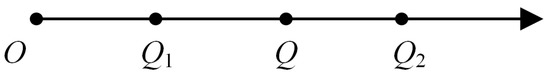
Figure 8.
1-D extension set.
Set the classic domain <O, Q1> = Xc, the extension domain <Q1, Q2> = Xe. The extension distance from the point Q to classic domain is represented as ρ(Q, Xc), and the extension distance from point Q to extension domain is represented as ρ(Q, Xe). The extension distance can be calculated as follows:
Thus, the dependent degree K(S), also known as correlation function, can be calculated as follows:
3.3.4. Identifying Measure Pattern
The dependent degree of any point Q in the extension set can be described quantitatively by the dependent degree K(S). The measure pattern can be divided as follows:
The classic domain, extension domain and non-domain correspond to the measure pattern M1, M2 and M3, respectively.
3.3.5. Weight Matrix Design
After the dependent degree K(S) is calculated, it is used to design the real-time weight matrix because it can reflect the degree of longitudinal car-following distance error and the risk of losing lateral stability. The weights for wΔβ, wΔω and wΔd are set as the real-time weights which are adjusted by the corresponding values of the dependent degree K(S), and the other weights wΔv, wae, wMdes, wades are set as constants.
When the car-following distance error belongs to the measure pattern M1, it means that the distance error is in a small range, and it is not necessary to increase the corresponding weight. When the car-following distance error belongs to the measure pattern M2, the distance error is in a relatively large range, and it is possible to exceed the driver’s sensitivity limit of the distance error if the corresponding weight is not adjusted timely. When the car-following distance error belongs to the measure pattern M3, the distance error exceeds the driver’s sensitivity limit, and the corresponding weight should be maximized to reduce the distance error by control. The real-time weight for longitudinal car-following distance is designed as follows:
where , kACC and KACC(S) are defined as the adjustment factor and dependent degree for vehicle longitudinal control.
Similarly, when the lateral stability status belongs to the measure pattern M1, it indicates that the vehicle lateral stability status is in a stability region, and it is not necessary to adjust the corresponding weight. When the lateral stability status belongs to the measure pattern M2, the lateral stability status is in the area between stability region and instability region and the vehicle may lose stability if the corresponding weight is not adjusted timely. When the lateral stability status belongs to the measure pattern M3, the lateral stability status is in the instability region, the corresponding weight should be maximized to maintain vehicle lateral stability by control. The real-time weights for lateral stability are designed as follows:
where , kVLS and KVLS(S) are defined as the adjustment factor and dependent degree for vehicle stability control.
The real-time weight matrices of the proposed control are designed as follows:
To show the effectiveness of the proposed control, a constant weight ACC and a constant weight ACC&DYC are used for comparison. The constant weight matrices of conventional ACC are shown in Equation (37).
The constant weight matrices of conventional ACC&DYC are shown in (38).
3.4. Lower Layer Design
After the desired longitudinal acceleration and additional yaw moment are obtained from MPC in the upper layer, the lower layer of the control system is to realize these objectives by the throttle opening and brake pressure. The desired longitudinal force on rear wheels can be obtained by Equation (39).
Simplifying the power-train, consider the constant efficiencies at final drive, transmission, torque converter and neglecting the slip in wheels [4].
The fuel consumption is shown in Figure 9a. The desired longitudinal acceleration is realized by the engine map which is shown in Figure 9b. The throttle opening is determined through the look-up table by utilizing engine speed and desired engine torque. The brake pressure of rear wheel is calculated by inverse brake system. As ACC and DYC system usually does not need too large braking deceleration, it can be considered that there is a linear relationship between the brake pressure Pb and braking torque Tb at the wheels [28], as shown in Equation (40).
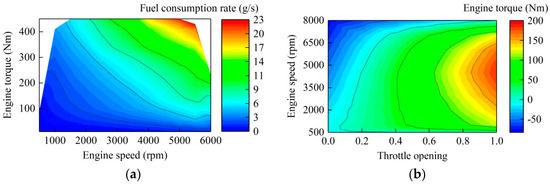
Figure 9.
Fuel consumption rate and map of engine: (a) fuel consumption rate of engine; (b) engine map.
The relationship between Fd and engine output torque Te is as follows [14].
where η represents mechanical efficiency, f(ωt/ωe) is the torque characteristic function of torque converter, and ig and io denote the transmission ratio of the gearbox and main reducer, respectively.
4. DIL Test Results and Analysis
As ACC and DYC systems always work with the driver, a closed DIL evaluation would be more effective than the open-loop simulations because of the real action of drivers’ steering behavior [13]. Therefore, a driving simulator is used in the DIL tests for coordinated multi-objective ACC, as shown in Figure 10. In the simulator, the vehicle model is built in the vehicle simulation software, CarMaker. The coordinated multi-objective ACC controller is implemented with MATLAB/Simulink.
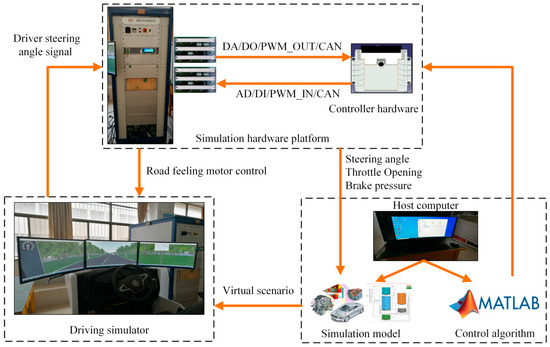
Figure 10.
DIL test hardware platform.
The driving simulator contains the steering wheel, monitor, brake pedal, accelerator pedal and a road feeling motor. The driver’s steering angle signal is obtained by steering wheel, the virtual scenario in CarMaker is displayed on the monitor. Due to the ACC system takes over the longitudinal control, the brake pedal and accelerator pedal are not used here. The road feeling motor can make the driver perceive the road feeling information of the vehicle through the steering wheel. The simulation hardware platform contains the controller hardware, board card, CAN card, NI PXI real-time processor and the platform is used to simulate all the input signals required by the normal operation of the controller to be tested, and collect the control commands from the controller.
The traditional constant weight ACC and the constant weight ACC and DYC are denoted as “ACC” and “ACC&DYC” in the simulation results, respectively. The parameters in the simulation model are shown in Table 1. The type of tire model used in CarMaker is magic formula tire model “MF_205_60R15”. The values “205”, “60” in name “MF_205_60R15” represent the tread width and flat ratio of tire. The letter “R15” indicates that the tire is a radial tire and “15” is the outer diameter of rim.

Table 1.
Parameters in the simulation model.
A common scenario is conducted to show the effectiveness of the proposed controller. The preceding vehicle and host vehicle go through a curved path which is shown in Figure 11. Before entering the curve, the preceding vehicle drives at a constant speed 110 km/h. Then the preceding vehicle slows into the curve with a deceleration of –1 m/s2 and drives at a low constant speed 54 km/h in the curve, as shown in Figure 12a. Finally, the preceding vehicle speeds up with an acceleration of 1 m/s2 to drive away from the curve. During the driver in the loop test, in order to reduce the influence of driver’s subjective factors on the results, the driver is not told what kind the controller is, and the steering wheel angle from driver is shown in Figure 12b. It can be seen that the driver’s steering angle under the three controllers is almost the same as a whole, and the driver’s steering wheel angle is little different with the different three controllers.
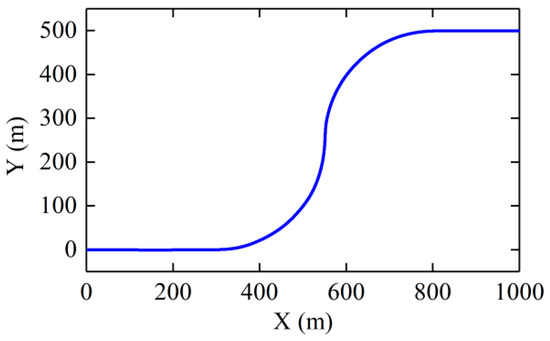
Figure 11.
Curve path in the simulation model.
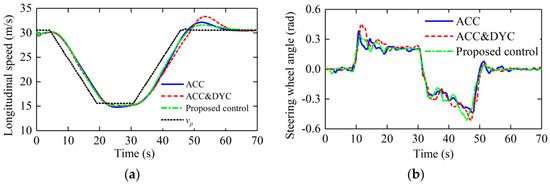
Figure 12.
Longitudinal speed and steering wheel angle: (a) longitudinal speed; (b) steering wheel angle.
The longitudinal car-following errors, lateral stability error and phase plane of errors are shown in Figure 13, Figure 14 and Figure 15, respectively.
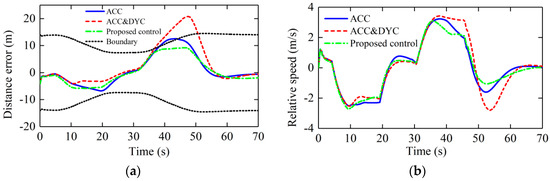
Figure 13.
Longitudinal car-following errors, (a) Longitudinal car-following distance error, (b) Relative speed.
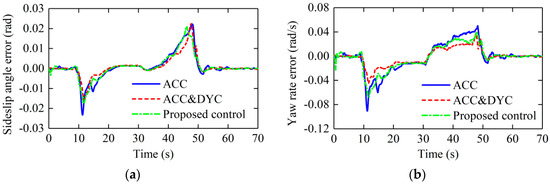
Figure 14.
Lateral stability errors: (a) vehicle sideslip angle error; (b) yaw rate error.
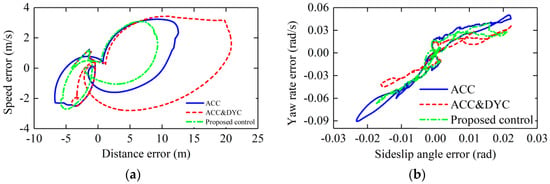
Figure 15.
Phase plane of errors: (a) phase plane of longitudinal car-following errors; (b) phase plane of lateral errors.
It can be seen from Figure 13 that for the constant weight ACC&DYC, when the host vehicle decelerates, the additional braking force will make the longitudinal car-following errors smaller than the constant weight ACC and proposed control, but when the host vehicle is in an accelerating process, the additional braking force will make the longitudinal car-following capability worse. When the distance error is close to the limit value, the proposed control will increase its weight according to the degree of approaching the limit value to keep the distance error within the limit value as far as possible. As can be seen in Figure 13a, the distance error with the proposed control is kept within the driver sensitivity limit, while the errors with the other two controllers exceed the limit value.
In terms of lateral stability control, as can be seen in Figure 14, the maximum yaw rate errors with constant weight ACC, constant ACC&DYC and the proposed control are about 0.091 rad/s, −0.045 rad/s and 0.067 rad/s, and the maximum sideslip angle errors with constant weight ACC, constant ACC&DYC and the proposed control are about 0.023 rad, −0.023 rad and 0.021 rad. With the proposed control, the maximum yaw rate error and sideslip angle error are both in a small range. As shown in Figure 15, in the aspect of lateral stability errors, ACC&DYC has the best control effect. However, in the aspect of longitudinal tracking errors, the maximum distance error with ACC&DYC has exceeded 20 m which is too large for driver’s sensitivity limit. Although the lateral stability errors are smaller with ACC&DYC, it sacrifices too much longitudinal car-following performance. By supervising the risk of losing lateral stability and then apply the corresponding control strength of DYC system, the proposed control realized coordination of car-following performance and lateral stability, so as to ensure that the car-following errors and lateral stability errors are both in a relatively acceptable range.
The proposed control determines the weight of the distance error by the dependent degree KACC(S) which can reflect the control effect of the longitudinal control. The proposed control determines the weights of sideslip angle error and yaw rate error by the dependent degree KVLS(S) which can reflect the risk of losing vehicle lateral stability. As can be seen from Figure 16b, when the longitudinal distance error increases, the KACC will be increased to adjust the weights and ensure the longitudinal car-following capability; when the value of driver steering wheel angle and Xregion increase, the KVLS will be increased to adjust the weights and ensure the lateral stability. The maximum errors and Xregion with three controllers are shown in Table 2. Obviously, the overall performance of the control system is improved. The proposed control can intelligently determine the weight matrices by the control effect of the longitudinal distance error and the risk of losing lateral stability. Thus, on the premise of ensuring the car-following performance and lateral stability, the fuel economy and longitudinal ride comfort are improved as much as possible.
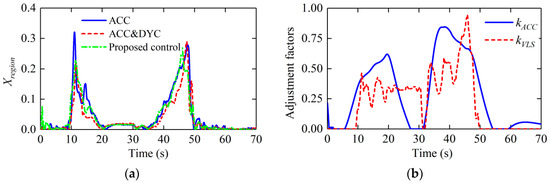
Figure 16.
Xregion and adjustment factors: (a) Xregion; (b) adjustment factors.

Table 2.
Maximum errors and Xregion with the three controllers.
From the perspective of fuel economy and longitudinal ride comfort, the fuel consumption with ACC is the lowest because of zero additional yaw moment, i.e., additional braking forces are zero. The fuel consumption with ACC&DYC is the highest because of the biggest control strength of DYC system. The fuel consumption with the proposed control is in a medium range so that the vehicle can improve the fuel economy as much as possible on the premise of ensuring the lateral stability.
As can be seen in Figure 17, the longitudinal acceleration of host vehicle with the proposed control increases rapidly at about 35 s. The reason is that the distance error is about to reach the sensitivity limit. Therefore, it is necessary to increase the weights and the control strength in the longitudinal control. When the distance error is in a relatively small range, the proposed control will decrease the weights to improve the longitudinal ride comfort as much as possible. The control outputs and brake pressure are shown in Figure 18 and Figure 19, respectively. It can be seen from the Figure 18 and Figure 19 that the throttle opening of ACC&DYC control method is greater than 0 between 10 s and 20 s, while the throttle opening of the other two methods is 0. This is because the ACC&DYC method needs to provide additional relatively large yaw moment during deceleration, which is the same between 40 s and 50 s. This is also one of the reasons for the high fuel consumption of ACC&DYC, because some fuel energy is converted into heat energy during differential braking process, which is also reflected both in larger throttle opening and brake pressure. This is the conflict between ACC (car-following performance) and DYC (lateral stability). The proposed control gets a balance between car-following performance and lateral stability. Meanwhile, the fuel economy has been improved by reducing such conflict.
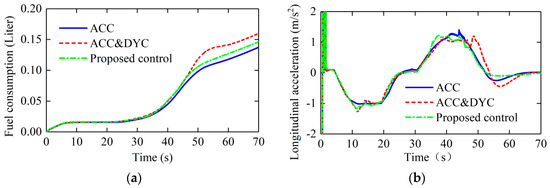
Figure 17.
Fuel consumption and longitudinal acceleration: (a) fuel consumption; (b) longitudinal acceleration.
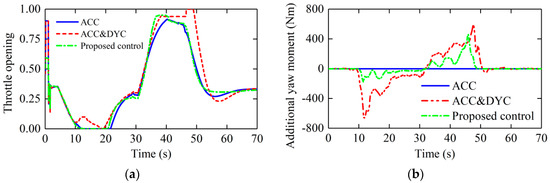
Figure 18.
Control outputs: (a) throttle opening; (b) additional yaw moment.
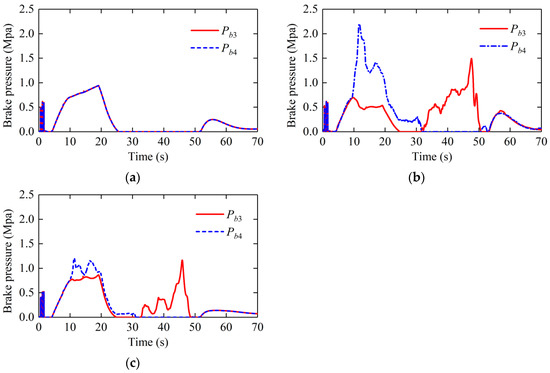
Figure 19.
Brake pressure on wheels: (a) brake pressure with ACC; (b) brake pressure with ACC&DYC; (c) brake pressure with proposed control.
To summarize, compared with the traditional constant weight ACC and ACC&DYC, the proposed control can both ensure the car-following performance and lateral stability by intelligently designing the real-time weight matrices. It solves the problem of excessive sacrifice of other performances when improving one performance during car-following process.
5. Conclusions
A coordinated multi-objective ACC integrated with DYC under the MPC framework was proposed in this paper. The extension control is introduced into the real-time weight matrix design to realize the coordination of various control objectives. The extension control can intelligently adjust the weight matrix by evaluating the control effect of ACC and the risk of losing lateral stability.
The longitudinal car-following performance, lateral stability, fuel economy and longitudinal ride comfort are considered in the control design. On the premise of ensuring longitudinal car-following performance and lateral stability, the fuel economy and longitudinal ride comfort are improved as much as possible.
With the proposed control, the longitudinal car-following distance error was kept within the driver sensitivity limit. The lateral stability was ensured by applying DYC system. Compared with the other two constant weight-matrix MPCs, the proposed control can improve the overall performance of vehicle control system and realize the coordination of longitudinal car-following capability, lateral stability, fuel economy and longitudinal ride comfort. The application of extension coordinated control enables ACC vehicles to deal with the problem of multi-objective coordinated control on curved roads. From a practical point of view, it is conducive to reduce traffic accidents, reduce energy consumption and improve driver comfort and vehicle safety.
Author Contributions
Conceptualization, H.W. and Y.S.; methodology, H.W. and Y.S.; software, Y.S.; validation, Y.S.; formal analysis, H.W., Y.S. and Z.G.; investigation, Y.S. and Z.G.; resources, H.W.; data curation, Y.S. and L.C.; writing—original draft preparation, H.W., Y.S. and Z.G.; writing—review and editing, H.W. and Y.S.; visualization, Y.S. and L.C.; supervision, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by National Natural Science Foundation of China (U1564201), Science Fund of Anhui Intelligent Vehicle Engineering Laboratory (PA2018AFGS0026), Natural Science Foundation of Inner Mongolia (2021MS05051), Research Program of science and technology at Universities of Inner Mongolia Autonomous Region (NJZZ21058) and Key Technology Research Project of Inner Mongolia Science and Technology Department (2020GG0200).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xiao, L.; Gao, F. A comprehensive review of the development of adaptive cruise control systems. Veh. Syst. Dyn. 2010, 48, 1167–1192. [Google Scholar] [CrossRef]
- Moon, I.-K.; Yi, K.; Caveney, D.; Hedrick, J.K. A multi-target tracking algorithm for application to adaptive cruise control. J. Mech. Sci. Technol. 2005, 19, 1742–1752. [Google Scholar] [CrossRef]
- Martinez, J.J.; Canudas-de-Wit, C. A safe longitudinal control for adaptive cruise control and stop-and-go scenarios. IEEE Trans. Control Syst. Technol. 2007, 15, 246–258. [Google Scholar] [CrossRef]
- Ganji, B.; Kouzani, A.Z.; Khoo, S.Y.; Shams-Zahraei, M. Adaptive cruise control of a HEV using sliding mode control. Expert Syst. Appl. 2014, 41, 607–615. [Google Scholar] [CrossRef]
- Lin, Y.; Nguyen, H.L.T. Adaptive Neuro-Fuzzy Predictor-Based Control for Cooperative Adaptive Cruise Control System. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1054–1063. [Google Scholar] [CrossRef]
- Althoff, M.; Maierhofer, S.; Pek, C. Provably-Correct and Comfortable Adaptive Cruise Control. IEEE Trans. Intell. Veh. 2021, 6, 159–174. [Google Scholar] [CrossRef]
- Moser, D.; Schmied, R.; Waschl, H.; del Re, L. Flexible Spacing Adaptive Cruise Control Using Stochastic Model Predictive Control. IEEE Trans. Control Syst. Technol. 2018, 26, 114–127. [Google Scholar] [CrossRef]
- Luo, L.; Liu, H.; Li, P.; Wang, H. Model predictive control for adaptive cruise control with multi-objectives comfort, fuel-economy, safety and car-following. J. Zhejiang Univ. Sci. A 2010, 11, 191–201. [Google Scholar] [CrossRef]
- Li, S.; Li, K.; Rajamani, R.; Wang, J. Model Predictive Multi-Objective Vehicular Adaptive Cruise Control. IEEE Trans. Control Syst. Technol. 2011, 19, 556–566. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, T.; Zhang, S.; Li, K. Intelligent Hybrid Electric Vehicle ACC With Coordinated Control of Tracking Ability, Fuel Economy, and Ride Comfort. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2303–2308. [Google Scholar] [CrossRef]
- Ren, Y.; Zheng, L.; Yang, W.; Li, Y. Potential field-based hierarchical adaptive cruise control for semi-autonomous electrc vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 2479–2491. [Google Scholar] [CrossRef]
- Asadi, B.; Vahidi, A. Predictive Cruise Control: Utilizing Upcoming Traffic Signal Information for Improving Fuel Economy and Reducing Trip Time. IEEE Trans. Control Syst. Technol. 2011, 19, 707–714. [Google Scholar] [CrossRef]
- Zhang, D.; Li, K.; Wang, J. A curving ACC system with coordination control of longitudinal car following and lateral stability. Veh. Syst. Dyn. 2012, 50, 1085–1102. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Mei, M.; Nie, Y.-L.; Zhao, L. Multiple-Objective Adaptive Cruise Control System Integrated With DYC. IEEE Trans. Veh. Technol. 2019, 68, 4550–4559. [Google Scholar] [CrossRef]
- Idriz, A.F.; Rachman, A.S.; Baldi, S. Integration of auto-steering with adaptive cruise control for improved cornering behaviour. IET Intell. Transp.Syst. 2017, 11, 667–675. [Google Scholar] [CrossRef] [Green Version]
- Cai, W. The extension set and non-compatible problems. In Advances in Applied Mathematics and Mechanics in China; International Academic Publishers: Lausanne, Switzerland, 1990; Volume 2, pp. 1–21. [Google Scholar]
- Li, J.; Wang, S. Primary research on extension control. In Proceedings of the AMSE International Conference on Information and Systems, New York, NY, USA, 16–18 December 1991; Volume 1, pp. 392–395. [Google Scholar]
- Chen, W.; Wang, H. Function allocation based vehicle suspension/steering system extension control and stability analysis. J. Mech. Eng. 2013, 49, 67–75. [Google Scholar] [CrossRef]
- Zhao, W.; Fan, M.; Wang, C.; Jin, Z.; Li, Y. H∞/extension stability control of automotive active front steering system. Mech. Syst. Signal Process. 2019, 115, 621–636. [Google Scholar] [CrossRef]
- Chen, W.; Liang, X.; Wang, Q.; Zhao, L.; Wang, X. Extension coordinated control of four wheel independent drive electric vehicles by AFS and DYC. Control Eng. Pract. 2020, 101, 1–12. [Google Scholar] [CrossRef]
- Pacejka, H. Tire and Vehicle Dynamics; Butterworth Heinemann: Oxford, UK, 2012. [Google Scholar]
- Hu, J.; Rakheja, S.; Zhang, Y. Real-time estimation of tire—Road friction coefficient based on lateral vehicle dynamics. Proc. IMechE Part D J. Automob. Eng. 2020, 234, 2444–2457. [Google Scholar] [CrossRef]
- Kim, D.; Min, K.; Kim, H.; Huh, K. Vehicle sideslip angle estimation using deep ensemble-based adaptive Kalman filter. Mech. Syst. Signal Process. 2020, 144, 1–17. [Google Scholar] [CrossRef]
- Bascetta, L.; Baur, M.; Ferretti, G. A simple and reliable technique to design kinematic-based sideslip estimators. Control Eng. Pract. 2020, 96, 1–17. [Google Scholar] [CrossRef]
- Liang, Y.; Li, Y.; Yu, Y.; Zheng, L. Integrated lateral control for 4WID/4WIS vehicle in high-speed condition considering the magnitude of steering. Veh. Syst. Dyn. 2020, 58, 1711–1735. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science: Boston, MA, USA, 2006. [Google Scholar]
- Inagaki, S.; Kushiro, I.; Yamamoto, M. Analysis on vehicle stability in critical cornering using phase-plane method. JSAE Rev. 1995, 16, 287–292. [Google Scholar]
- Zhan, J. Research on model of brake system based on ACC system. China Mech. Eng. 2005, 16, 450–452. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).