Multilevel Intersectional Analysis to Identify Extreme Profiles in Italian Student Achievement Data
Abstract
1. Introduction
1.1. Determinants of Educational Inequalities
1.2. Intersectionality
1.3. MAIHDA
2. Materials and Methods
2.1. Dataset
2.2. Handling of Missing Values
2.3. Descriptive Statistics
2.4. Statistical Models
3. Results
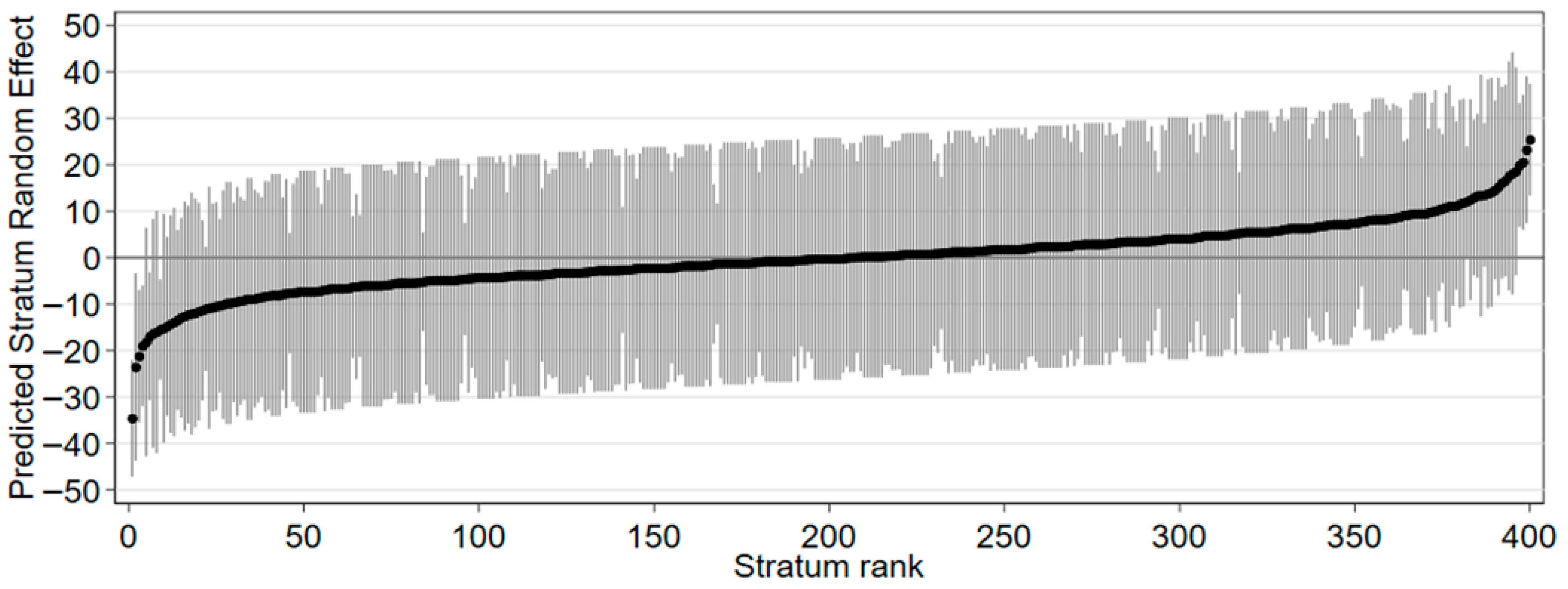
3.1. Variance Partitioning from Model 1 and Model 2
3.2. Regression Coefficient Estimates from Model 2
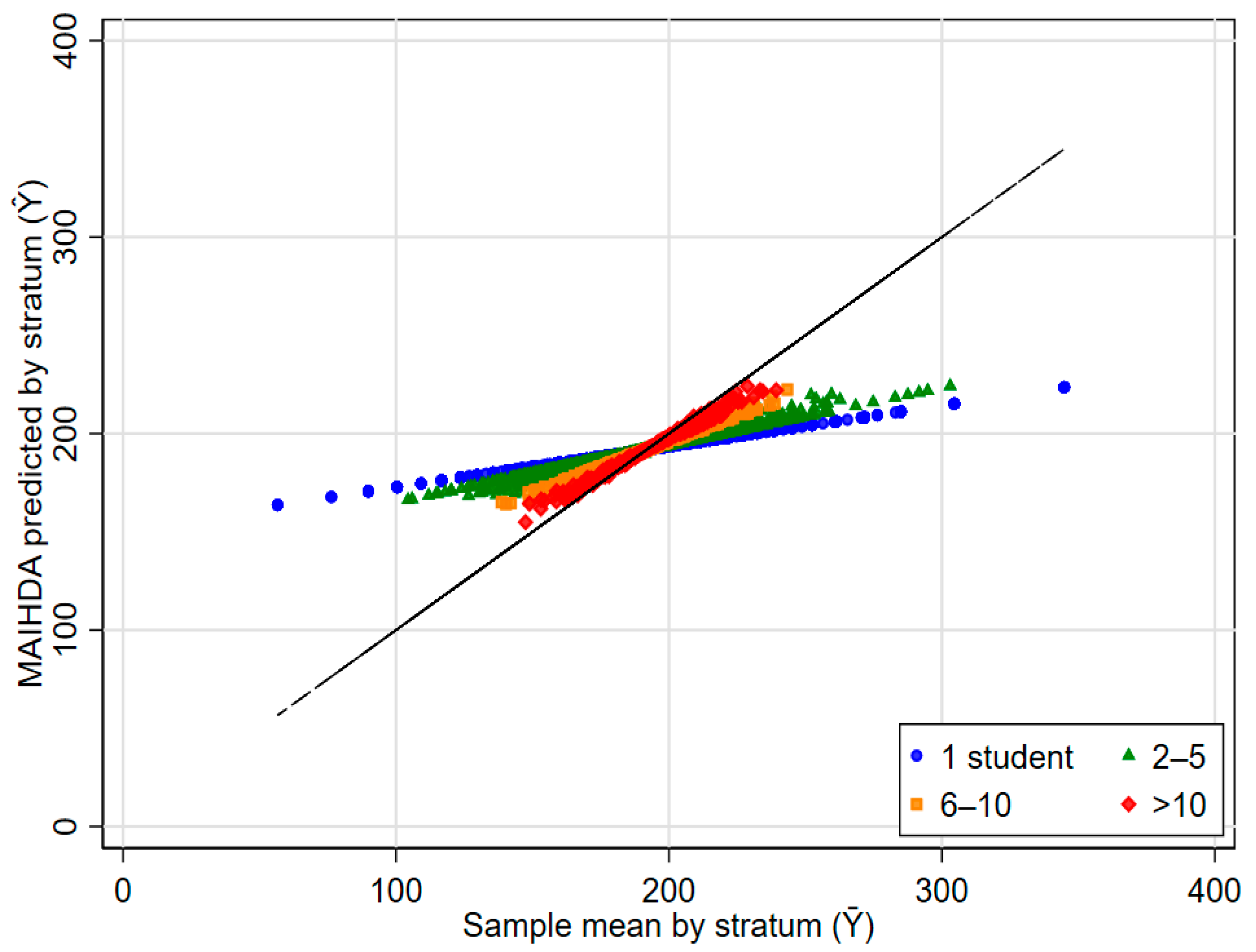
3.3. Most and Least Advantaged Student Profiles from Model 1
4. Discussion
5. Limitations and Final Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aparicio Fenoll, Ainhoa. 2017. English Proficiency and Test Scores of Immigrant Children in the US. (No. 10848). IZA Discussion Papers. Bonn: Institute for the Study of Labor (IZA). [Google Scholar]
- Álvarez, Ana Suárez, and Ana Jesús López Menéndez. 2023. The role of family background and education in shaping inequalities. Evidence from the Spanish regions. Social Policy and Society 24: 355–72. [Google Scholar] [CrossRef]
- Bauer, Greta R., Siobhan M. Churchill, Mayuri Mahendran, Chantel Walwyn, Daniel Lizotte, and Alma Angelica Villa-Rueda. 2021. Intersectionality in quantitative research: A systematic review of its emergence and applications of theory and methods. SSM-Population Health 14: 100798. [Google Scholar] [CrossRef]
- Bell, Andrew, Clare R. Evans, Dan Holman, and George Leckie. 2024. Extending intersectional multilevel analysis of individual heterogeneity and discriminatory accuracy (MAIHDA) to study individual longitudinal trajectories, with application to mental health in the UK. Social Science & Medicine 351: 116955. [Google Scholar] [CrossRef] [PubMed]
- Buchmann, Claudia, Thomas A. DiPrete, and Anne McDaniel. 2008. Gender inequalities in education. Annual Review of Sociology 34: 319–37. [Google Scholar] [CrossRef]
- Burgess, Simon, Ellen Greaves, Anna Vignoles, and Deborah Wilson. 2015. What parents want: School preferences and school choice. The Economic Journal 125: 1262–89. [Google Scholar] [CrossRef]
- Chetty, Raj, Nathaniel Hendren, Patrick Kline, and Emmanuel Saez. 2014. Where is the land of opportunity? The geography of intergenerational mobility in the United States. The Quarterly Journal of Economics 129: 1553–623. [Google Scholar] [CrossRef]
- Collins, Patricia Hill, Elaini Cristina Gonzaga da Silva, Emek Ergun, Inger Furseth, Kanisha D. Bond, and Jone Martínez-Palacios. 2021. Intersectionality as critical social theory: Intersectionality as critical social theory. Contemporary Political Theory 20: 690. [Google Scholar] [CrossRef]
- Dupriez, Vincent, Xavier Dumay, and Anne Vause. 2008. How do school systems manage pupils’ heterogeneity? Comparative Education Review 52: 245–73. [Google Scholar] [CrossRef]
- Evans, Clare R. 2019. Reintegrating contexts into quantitative intersectional analyses of health inequalities. Health and Place 60: 102214. [Google Scholar] [CrossRef] [PubMed]
- Evans, Clare R., David R. Williams, Jukka-Pekka Onnela, and Sankaran Venkata Subramanian. 2018. A multilevel approach to modelling health inequalities at the intersection of multiple social identities. Social Science & Medicine 203: 64–73. [Google Scholar] [CrossRef]
- Evans, Clare R., George Leckie, Sankaran Venkata Subramanian, Andrew Bell, and Juan Merlo. 2024. A tutorial for conducting intersectional multilevel analysis of individual heterogeneity and discriminatory accuracy (MAIHDA). SSM-Population Health 26: 101664. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, Francisco H., and Jérémie Gignoux. 2014. The measurement of educational inequality: Achievement and opportunity. The World Bank Economic Review 28: 210–46. [Google Scholar] [CrossRef]
- Ferri, Valentina, Giovanna Di Castro, and Salvatore Marsiglia. 2023. Does the immigrant background affect student achievement? Cross-country comparisons of PISA scores. Rivista Italiana di Economia Demografia e Statistica 77: 91–102. [Google Scholar] [CrossRef]
- Gamoran, Adam. 2001. American schooling and educational inequality: A forecast for the 21st century. Sociology of Education 74: 135–53. [Google Scholar] [CrossRef]
- Green, Mark A., Clare R. Evans, and Sankaran Venkata Subramanian. 2017. Can intersectionality theory enrich population health research? Social Science & Medicine 178: 214–16. [Google Scholar] [CrossRef]
- Groves, Robert M., Floyd J. Fowler, Jr., Mick P. Couper, James M. Lepkowski, Eleanor Singer, and Roger Tourangeau. 2011. Survey Methodology. Hoboken: John Wiley and Sons. [Google Scholar]
- Guez, Ava, Hugo Peyre, and Frank Ramus. 2020. Sex differences in academic achievement are modulated by evaluation type. Learning and Individual Differences 83: 101935. [Google Scholar] [CrossRef]
- Iannelli, Cristina. 2017. The role of the school curriculum in social mobility. In Education and Social Mobility. Abingdon: Routledge, pp. 289–310. [Google Scholar]
- Jensen, Simon Skovgaard, Michael Kühhirt, and Felix Weiss. 2024. Parental unemployment and children’s well-being at school: The role of duration, reemployment, and socioeconomic status. Acta Sociologica 68: 217–37. [Google Scholar] [CrossRef]
- Jæger, Mads Meier. 2022. Cultural capital and educational inequality: An assessment of the state of the art. In Handbook of Sociological Science. Cheltenham and Northampton: Edward Elgar Publishing, pp. 121–34. [Google Scholar] [CrossRef]
- Kalmijn, Matthijs. 1994. Mother’s occupational status and children’s schooling. American Sociological Review 59: 257–75. [Google Scholar] [CrossRef]
- Keller, Lena, Elisa Oppermann, and Camilla Rjosk. 2024. Intersectionality in Educational Contexts. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie 56: 1–6. [Google Scholar] [CrossRef]
- Keller, Lena, Oliver Lüdtke, Franzis Preckel, and Martin Brunner. 2023. Educational inequalities at the intersection of multiple social categories: An introduction and systematic review of the Multilevel Analysis of Individual Heterogeneity and Discriminatory Accuracy (MAIHDA) approach. Educational Psychology Review 35: 1–37. [Google Scholar] [CrossRef]
- King, Deborah K. 1988. Multiple jeopardy, multiple consciousness: The context of a Black feminist ideology. Signs: Journal of Women in Culture and Society 14: 42–72. [Google Scholar] [CrossRef]
- Kristen, Cornelia, and Nadia Granato. 2007. The educational attainment of the second generation in Germany: Social origins and ethnic inequality. Ethnicities 7: 343–66. [Google Scholar] [CrossRef]
- Lareau, Annette. 2018. Unequal childhoods: Class, race, and family life. In Inequality in the 21st Century. Abingdon: Routledge, pp. 444–51. [Google Scholar]
- Le, Vy, Grace Angell, Jayson Nissen, and Ben Van Dusen. 2025. Challenging the Model Minority Myth: A MAIHDA Study of Asian Student Outcomes in Introductory Physics. arXiv arXiv:2509.19049. [Google Scholar] [CrossRef]
- Lindemann, Kristina, and Ellu Saar. 2011. Ethnic inequalities in education. In The Russian Second Generation in Tallinn and Kohtla-Järve: The TIES Study in Estonia. Edited by Raivo Vetik and Jelena Helemäe. Amsterdam: Taylor & Francis, pp. 59–92. [Google Scholar]
- Lister, Jennie, Catherine Hewitt, and Josie Dickerson. 2024. Using I-MAIHDA to extend understanding of engagement in early years interventions: An example using the Born in Bradford’s Better Start (BiBBS) birth cohort data. Social Sciences & Humanities Open 10: 100935. [Google Scholar] [CrossRef]
- Liu, Yan. 2024. The relationship and heterogeneity of family participation and social participation among older adults: From an intersectionality perspective. BMC Geriatrics 24: 949. [Google Scholar] [CrossRef] [PubMed]
- Ljungman, Hanna, Maria Wemrell, Raquel Perez-Vicente, Kani Khalaf, Juan Merlo, and George Leckie. 2021. Antidepressant use in Sweden: An intersectional multilevel analysis of individual heterogeneity and discriminatory accuracy (MAIHDA). Scandinavian Journal of Public Health 50: 395–403. [Google Scholar] [CrossRef]
- Machin, Stephen, and Anna Vignoles. 2004. Educational inequality: The widening socio-economic gap. Fiscal Studies 25: 107–28. [Google Scholar] [CrossRef]
- Mahendran, Mayuri, Daniel Lizotte, and Greta R. Bauer. 2022. Describing intersectional health outcomes: An evaluation of data analysis methods. Epidemiology 33: 395–405. [Google Scholar] [CrossRef]
- Marone, Francesca, and Francesca Buccini. 2020. Disability and migration: New alliances for inclusion. Educazione Interculturale 18: 97–111. [Google Scholar] [CrossRef]
- Merlo, Juan. 2018. Multilevel analysis of individual heterogeneity and discriminatory accuracy (MAIHDA) within an intersectional framework. Social Science & Medicine 203: 74–80. [Google Scholar] [CrossRef]
- Nieves, Christina I., Luisa N. Borrell, Clare R. Evans, Heidi E. Jones, and Mary Huynh. 2023. The application of intersectional multilevel analysis of individual heterogeneity and discriminatory accuracy (MAIHDA) to examine birthweight inequities in New York City. Health & Place 81: 103029. [Google Scholar] [CrossRef] [PubMed]
- OECD. 2018. Equity in Education: Breaking Down Barriers to Social Mobility. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- OECD. 2019. PISA 2018 Results (Volume I): What Students Know and Can Do. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- OECD. 2023. PISA 2022 Results (Volume I): The State of Learning and Equity in Education. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- Patall, Erika A., Harris Cooper, and Ashley Batts Allen. 2010. Extending the school day or school year: A systematic review of research (1985–2009). Review of Educational Research 80: 401–36. [Google Scholar] [CrossRef]
- Pensiero, Nicola, Orazio Giancola, and Carlo Barone. 2019. Socioeconomic inequality and student outcomes in Italy. In Socioeconomic Inequality and Student Outcomes: Cross-National Trends, Policies, and Practices. Singapore: Springer, pp. 81–94. [Google Scholar] [CrossRef]
- Pfeffer, Fabian T. 2008. Persistent inequality in educational attainment and its institutional context. European Sociological Review 24: 543–65. [Google Scholar] [CrossRef]
- Prior, Lucy, and George Leckie. 2024. Student intersectional sociodemographic and school variation in GCSE final grades in England following COVID-19 examination cancellations. Oxford Review of Education 51: 763–84. [Google Scholar] [CrossRef]
- Prior, Lucy, Clare R. Evans, Juan Merlo, and George Leckie. 2024. Socio-demographic Inequalities in Student Achievement: An Intersectional Multilevel Analysis of Individual Heterogeneity and Discriminatory Accuracy (MAIHDA). Sociology of Race and Ethnicity 11: 351–69. [Google Scholar] [CrossRef]
- Rosen, Maya L., Margaret A. Sheridan, Kelly A. Sambrook, Andrew N. Meltzoff, and Katie A. McLaughlin. 2018. Socioeconomic disparities in academic achievement: A multi-modal investigation of neural mechanisms in children and adolescents. NeuroImage 173: 298–310. [Google Scholar] [CrossRef]
- Rossetti, Sara. 2022. Intersezionalità e decolonialità: Nuove lenti sugli studi delle migrazioni femminili attraverso il caso studio delle donne originarie del Subcontinente indiano in Italia. Culture e Studi del Sociale 7: 152–64. [Google Scholar]
- Rothstein, Richard. 2015. The racial achievement gap, segregated schools, and segregated neighborhoods: A constitutional insult. Race and Social Problems 7: 21–30. [Google Scholar] [CrossRef]
- Schildberg-Hörisch, Hannah. 2016. Parental Employment and Children’s Academic Achievement. Bonn: IZA World of Labor. [Google Scholar] [CrossRef]
- Schmidt, William H., Nathan A. Burroughs, Pablo Zoido, and Richard T. Houang. 2015. The role of schooling in perpetuating educational inequality: An international perspective. Educational Researcher 44: 371–86. [Google Scholar] [CrossRef]
- StataCorp. 2023. Stata Statistical Software: Release 18. College Station: StataCorp LLC. [Google Scholar]
- Terrin, Éder, and Moris Triventi. 2023. The effect of school tracking on student achievement and inequality: A meta-analysis. Review of Educational Research 93: 236–74. [Google Scholar] [CrossRef]
- Triventi, Moris, Elisa Vlach, and Elisa Pini. 2022. Understanding why immigrant children underperform: Evidence from Italian compulsory education. Journal of Ethnic and Migration Studies 48: 2324–46. [Google Scholar] [CrossRef]
- Voyer, Daniel, and Susan D. Voyer. 2014. Gender differences in scholastic achievement: A meta-analysis. Psychological Bulletin 140: 1174. [Google Scholar] [CrossRef]
- Willms, J. Douglas. 2010. School composition and contextual effects on student outcomes. Teachers College Record 112: 1008–37. [Google Scholar] [CrossRef]
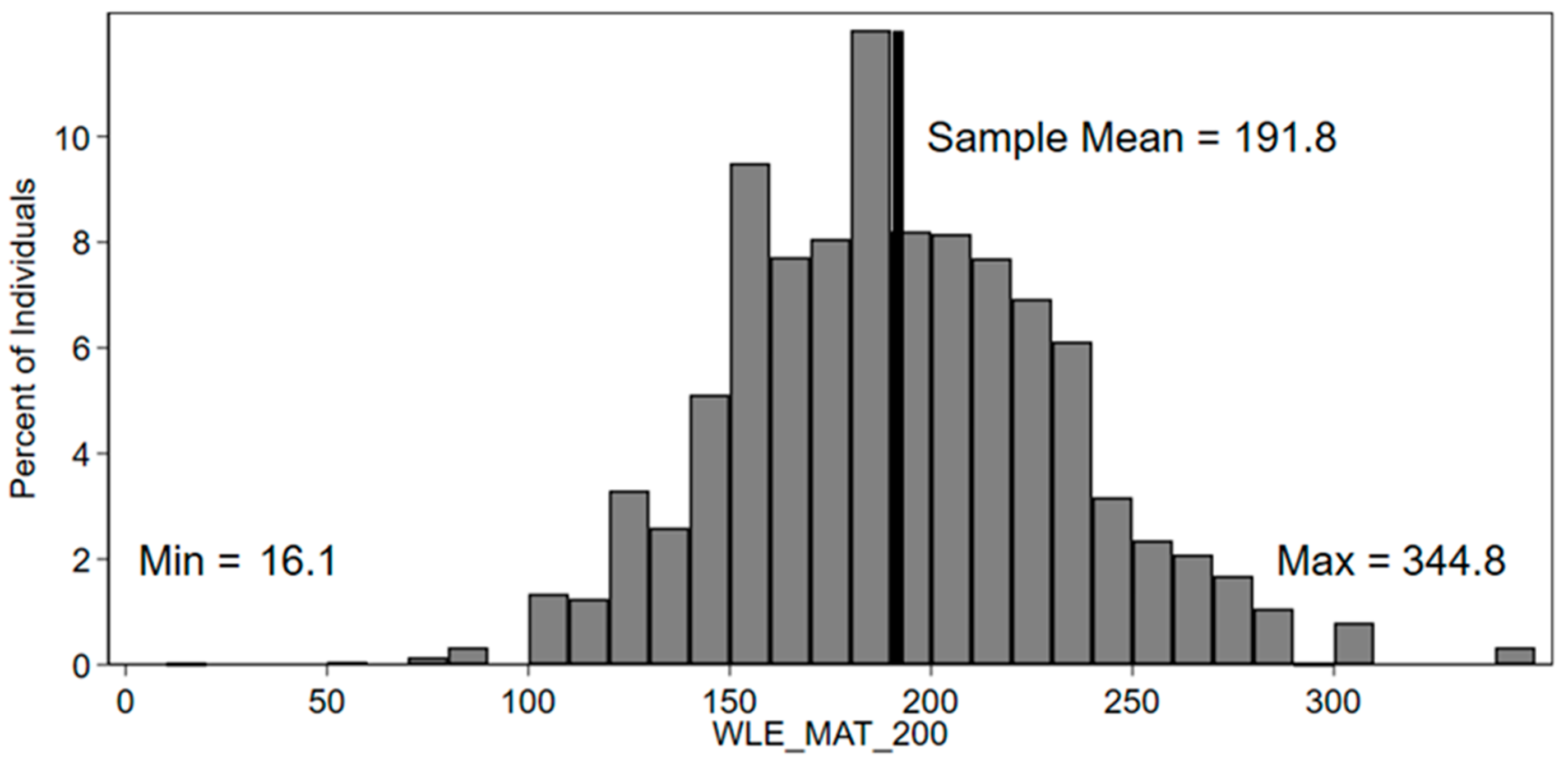
| Sample Statistics | N. Students | % Students | |
|---|---|---|---|
| Total | 16,011 | 100 | |
| Sex | Male | 8023 | 50.11 |
| Female | 7988 | 49.89 | |
| Origin | Native | 14,065 | 87.85 |
| 1st-gen immigrant | 481 | 3.00 | |
| 2nd-gen immigrant | 1465 | 9.15 | |
| FAMENV | 1 | 4009 | 25.04 |
| (quartiles of the score from an IRT model) | 2 | 4038 | 25.22 |
| 3 | 3962 | 24.75 | |
| 4 | 4000 | 25.00 |
| Sample Statistics | N. Students (Father) | N. Students (Mother) | % Students (Father) | % Students (Mother) | |
|---|---|---|---|---|---|
| Parental education | Compulsory | 3518 | 2641 | 21.97 | 16.49 |
| High school | 6258 | 6127 | 39.09 | 38.27 | |
| Bachelor’s degree | 1024 | 1439 | 6.40 | 8.99 | |
| Master or more | 1687 | 2494 | 10.54 | 15.58 | |
| Unknown | 3524 | 3310 | 22.01 | 20.67 | |
| Parental occupation | Unemployed or retired | 557 | 4168 | 3.48 | 26.03 |
| Manager or clerk | 3046 | 3967 | 19.02 | 24.78 | |
| Self-employed | 2971 | 1190 | 18.56 | 7.43 | |
| Blue-collar | 3840 | 1857 | 23.98 | 11.60 | |
| Professional | 2030 | 1595 | 12.68 | 9.96 | |
| Unknown | 3567 | 3234 | 22.28 | 20.20 |
| Model 1 | Model 2 | PCV | |
|---|---|---|---|
| Variances of random terms | |||
| Between strata | 200.48 | 6.13 | 96.94% |
| Between schools | 151.28 | 166.83 | −10.27% |
| Student | 1341.00 | 1335.58 | |
| Total | 1692.76 | 1508.54 | |
| VPC | |||
| Strata | 11.84% | 0.41% | |
| Schools | 8.93% | 11.06% |
| Estimate | 95% conf. int. | ||
|---|---|---|---|
| Intercept | 160.84 | [157.12, 164.56] | |
| Sex | Female (Ref) | - | - |
| Male | 8.51 | [7.22, 9.81] | |
| Origin | Native (Ref) | - | - |
| 1st-gen imm. | −14.53 | [−18.19, −10.86] | |
| 2nd-gen imm. | −4.93 | [−7.19, −2.66] | |
| FAMENV | 1 (Ref) | - | - |
| 2 | 3.85 | [2.02, 5.67] | |
| 3 | 7.85 | [6.00, 9.70] | |
| 4 | 12.54 | [10.66, 14.42] |
| Father | Mother | ||||
|---|---|---|---|---|---|
| Estimate | 95% conf. int. | Estimate | 95% conf. int. | ||
| Parental education | Compulsory education (Ref) | - | - | - | - |
| High school diploma | 7.32 | [5.49, 9.16] | 8.36 | [6.35, 10.37] | |
| Bachelor’s degree | 11.41 | [8.15, 14.67] | 9.44 | [6.42, 12.46] | |
| Master or more | 12.47 | [9.57, 15.37] | 14.12 | [11.34, 16.91] | |
| Unknown | 4.19 | [0.85, 7.53] | 8.80 | [5.40, 12.20] | |
| Parental occupation | Unemployed or retired (Ref) | - | - | - | - |
| Manager or clerk | 9.12 | [5.37, 12.87] | 5.51 | [3.50, 7.52] | |
| Self-employed | 6.83 | [3.19, 10.47] | 3.44 | [0.80, 6.08] | |
| Blue-collar worker | 4.37 | [0.82, 7.92] | 1.22 | [−1.00, 3.43] | |
| Professional | 7.42 | [3.51, 11.32] | 6.20 | [3.56, 8.85] | |
| Unknown | 1.37 | [−2.81, 5.56] | .96 | [−1.93, 3.86] | |
| Sex | Origin | FAMENV | Father’s Education | Mother’s Education | Father’s Occupation | Mother’s Occupation | Predicted Random Effect | Sample Average Score |
|---|---|---|---|---|---|---|---|---|
| male | native | 4 | master or more | master or more | professional | professional | 31.695 | 228.706 (n = 47) |
| male | native | 4 | master or more | master or more | manager or clerk | manager or clerk | 29.159 | 224.407 (n = 63) |
| male | native | 4 | master or more | master or more | manager or clerk | professional | 28.681 | 233.366 (n = 17) |
| male | native | 4 | high school | high school | self-employed | professional | 28.355 | 239.315 (n = 11) |
| female | native | 3 | bachelor | bachelor | manager or clerk | manager or clerk | 28.247 | 243.382 (n = 9) |
| female | 2nd imm. | 1 | compulsory | compulsory | blue-collar | blue-collar | −24.932 | 140.328 (n = 7) |
| female | native | 2 | compulsory | compulsory | blue-collar | blue-collar | −25.336 | 158.738 (n = 25) |
| female | native | 1 | compulsory | compulsory | self-employed | blue-collar | −25.583 | 148.878 (n = 11) |
| female | 1st imm. | 1 | unknown | unknown | unknown | unknown | −28.930 | 153.054 (n = 22) |
| male | native | 1 | compulsory | compulsory | unemployed or retired | unemployed or retired | −34.578 | 147.468 (n = 31) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contin, E.; Grilli, L. Multilevel Intersectional Analysis to Identify Extreme Profiles in Italian Student Achievement Data. Soc. Sci. 2025, 14, 672. https://doi.org/10.3390/socsci14110672
Contin E, Grilli L. Multilevel Intersectional Analysis to Identify Extreme Profiles in Italian Student Achievement Data. Social Sciences. 2025; 14(11):672. https://doi.org/10.3390/socsci14110672
Chicago/Turabian StyleContin, Enrico, and Leonardo Grilli. 2025. "Multilevel Intersectional Analysis to Identify Extreme Profiles in Italian Student Achievement Data" Social Sciences 14, no. 11: 672. https://doi.org/10.3390/socsci14110672
APA StyleContin, E., & Grilli, L. (2025). Multilevel Intersectional Analysis to Identify Extreme Profiles in Italian Student Achievement Data. Social Sciences, 14(11), 672. https://doi.org/10.3390/socsci14110672







